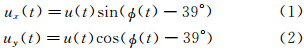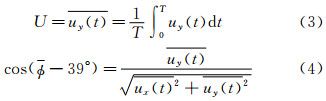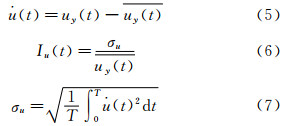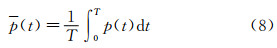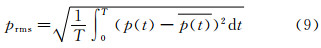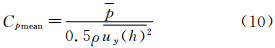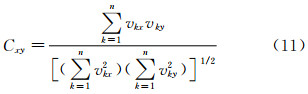由于现代高层建筑呈现出质量轻、柔性大、阻尼低等特点,其对风的敏感性也随着这一特征的放大而增加,高层建筑(尤其是沿海多台风地区的高层建筑)的风荷载研究变得越来越重要和必不可少。 现场实测作为结构风荷载研究最直接、最有效的方法之一,近年来在国内风工程领域逐步兴起,并取得了一些实质性的突破和发展。但由于受台风实测全尺度测量条件、露天环境恶劣、实测成本高等因素的制约,结构抗风的实测研究相对来说还比较少,特别是高层建筑结构抗风方面的实测数据更是缺乏,开展这方面的现场实测,对高层建筑抗风具有十分重要的意义[1, 2]。
研究分析各国的结构设计荷载规范可知[3, 4],在风荷载计算时,首先需要确定的是基本风速和基本风压,而这又与平均风速的确定直接相关。平均风速与所取某一中心时刻附近的时距有关,随着所取平均风时距的缩短,对应于这一时距的最大平均风速将增大,因为在较小的时距内能集中反映较大波峰的影响[5],而较小的波峰未能得以反应。各国荷载规范对平均风时距的规定不尽相同,国际上许多国家(包括我国) 将平均风速计算时距值取为 10min,但也有国家取为1h(如加拿大等),甚至有的国家取为3~5s时距的瞬时风速(如美国规范取为3s)。英国规范规定对所有围护构件、玻璃及屋面,都采用3s阵风风速。对于竖向和水平最大尺寸大于50m的房屋或结构物,采用15s的平均风速。显然在风荷载计算时,取不同的时距得到的结果是不同的。对于超高层建筑而言,究竟时距长度取何值时最为适宜,在国内外尚没有定论。本文通过对厦门观音山商业运用中心11号楼在台风“天兔”登陆时的风场及其迎风墙面风压的实测数据进行了相关性分析,研究了时距和来流风向角对风场和风压相关性大小的影响,以供今后在高层建筑抗风研究中,在基本时距选取时作一个参考。 1 观测位置和仪器
为了获取在台风“天兔”作用下超高层建筑的风场特性及建筑迎风墙面风压场特征,在位于厦门观音山商业运营中心的11号楼顶部安装了一个风速风向仪,风速风向仪安装位置如图 1所示,其高出屋面栅栏6.4m,超出栅栏4.2m,比前方屋面高出约15m。并在该栋楼的第17层(避难层)幕墙外表面布置了18个风压测点。该楼距离海边大概450m左右,地貌类别为A类。该建筑主体为36层,地上部分的高度为149.8m。现场实测中采用RM Young 05103v螺旋桨式风速风向仪,在实测时,风速仪零度风向角对应的地理方向为正北方向,角度按顺时针方向递增(图 2),此处定义结构主轴X向为建筑物的长边方向,结构主轴Y向为建筑物的短边方向;在该楼的第17层(避难层,离地面的高度约为70m)开展风压实测,风压传感器采用CY2000FA1P型风压传感器。风压传感器粘贴在东北和东南的外墙面上,测点布置如图 2所示,共布置了18个测点(本文只采用了1~15测点的数据)。当台风“天兔”2013年9月20日16 时32分登陆福建沿海地区时,对该楼的楼顶风场和避难层的风压情况进行了现场实测,风速和风压的实测频率分别为20Hz和25.6Hz,同步连续记录了从2013年9月20日16时至9月23日9时长达65h的风场及风压数据。
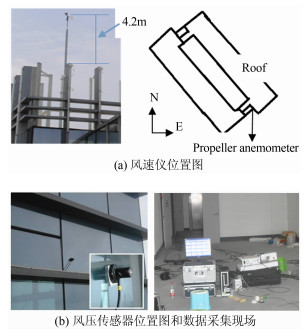 |
| 图 1 实测现场信息图 Fig 1 The scene graph of measured information |
论文在数据选取时,主要选取风向角与迎风墙面基本垂直范围内的风场数据。同时,文献[10]中指出风压传感器所测到的风压理论上为垂直于墙面的风压,平行于墙面的部分可以忽略。因此,本文提取风速垂直于墙面的分量进行分析。并且,在风速的分解中发现,所取风向范围内的横风向风速很小,基本可不做考虑。在后续的风场参数的定义中均以垂直于墙面的风速分量作为基本参数进行定义与计算分析,以保持风场参数方向与所测风压一致。
根据上文的分析,本文在进行数据选取时,选取了来流风向角基本与建筑物迎风墙面垂直,风速变化比较平稳的一段4h内风场时程作计算分析,风压取时间上同风场同步的实测风压数据。基于以上考虑,本文对实测风速进行如图 2所示的Y和X两个方向进行实时分解,得到Y方向的风速时程,在此基础上再求Y方向的平均风速和湍流度等风场特性值。
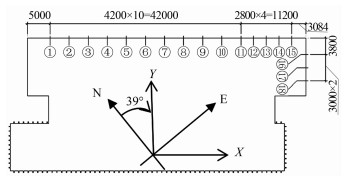 |
| 图 2 风压传感器的平面布置图 Fig 2 Plan view of wind pressure sensor location |
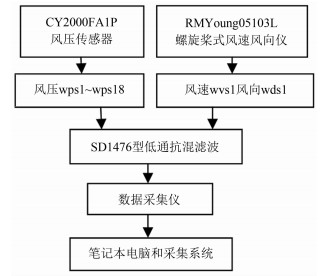 |
| 图 3 实测流程线路图 Fig 3 Flowchart of measurement |
实测的风速、风向记录分为2个时间序列,即水平风速u(t)和风向φ(t)。其随时间变化的时程图如图 5所示。风速可根据以下公式分解为2个坐标轴方向的分量ux(t)(建筑物长边方向)和uy(t)(建筑物短边方向),如图 4所示:
计算分析取T为基本时距,Y方向的平均风速U和水平风向角可表示为:
其中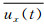 (其定义公式同
(其定义公式同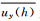 一致),
一致),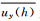 分别为T时距时所取样本的二维风速平均值。
分别为T时距时所取样本的二维风速平均值。
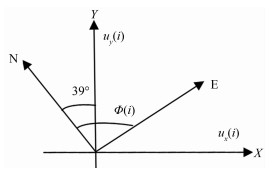 |
| 图 4 风速、风向示意图 Fig 4 Coordinate of wind speed and wind direction |
实测风速仪零度风向角对应于地理上的正北方向,而上述Y方向与地理正北方向之间的夹角为39°(风向角沿着顺时针方向增大)。本文所有提及的风场特征值(除风向角外,其它的风场特征值),如无特别说明,均指实际量在Y方向的分量。
经公式(2)实时分解后Y方向的风速时程如图 5(c)所示,由于所取风场数据段的风向角基本与建筑迎风墙面垂直(Y方向),因此经公式(2)分解后Y方向的风速时程同水平风速时程相比,其值变化不大,变化趋势基本一致,由于所取水平风速可假定是平稳随机过程[6],因此Y方向的风速时程也可以认为是平稳随机过程。
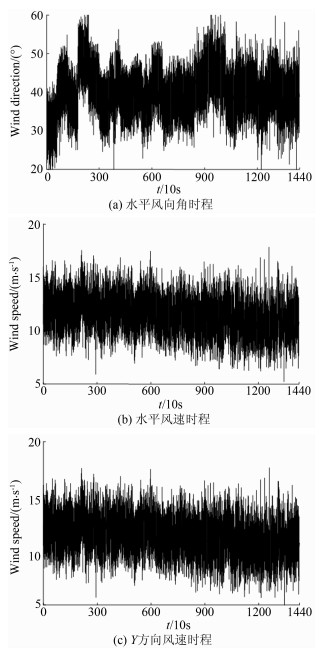 |
| 图 5 水平风速风向及Y方向风速时程 Fig 5 Time series of the horizontal wind speed and direction,wind speed in Y direction |
在本次台风实测的时程数据中选取4h的实测数据进行分析,以10min为基本时距的Y方向平均风速和风向图如图 6所示,本次观测的Y方向分量风的总体平均风速为11.08m/s,最大10min平均风速为12.46m/s,顺风向的最大瞬时风速为16.77m/s。实测的平均风向角先变大,然后趋于平稳,平均风向处于东北偏东方向。由图及以上分析可知风速和风向变化较为平稳,表明台风登陆后,陆地上的风速和风向趋于稳定。此外,同水平方向平均风速相比,Y方向的平均风速略小,但其变化趋势基本一致。
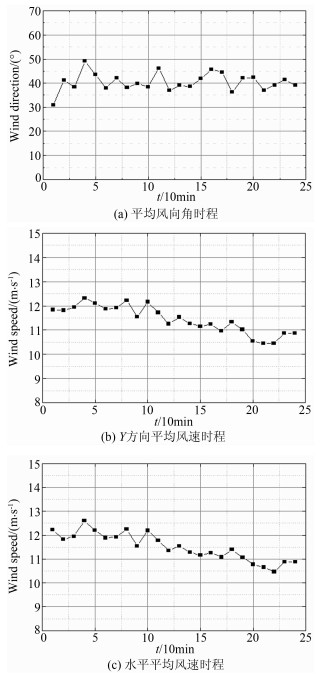 |
| 图 6 10min Y方向平均风速和平均风向时程,水平平均风速时程 Fig 6 Time series of 10min mean wind in Y direction and mean wind direction,the level of average wind speed |
在结构抗风中,风的湍流特征对于柔性结构的共振和刚性结构的振动有着重要的作用。湍流度是结构抗风设计中基本的湍流特征信息之一。Y方向风的脉动风速、湍流度、脉动风速均方根值定义公式如下:
其中uy(t),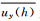 的定义同3.1节,σu为10min脉动风速(t)的均方根值。其它时距条件下也可以采用同样的方法求解。
的定义同3.1节,σu为10min脉动风速(t)的均方根值。其它时距条件下也可以采用同样的方法求解。
风场中脉动风速的变化过程可以看作是一个随机过程[6, 7, 8],进而可利用随机过程理论建立脉动风速模型,在满足工程计算精度要求的前提下,可以假定脉动风速是零均值的平稳随机过程[9]。理论上,假定脉动风速和脉动风压是平稳随机过程(对本文公式(5)等号两边求平均,可知等号右边的值为0)。但是,通过现场实测得到的脉动风速和脉动风压的均值不是0,而是接近于0的值,且随着基本时距的增大而趋向于0。因此,本文采用脉动风压的均方根,并分析基本时距对两者之间的相关性的影响规律。以10min作为基本时距,选择垂直于建筑物迎风墙面方向的脉动风速均方根值做为脉动风速特征值,其随时间的变化历程如图 7(a)所示。从图中可以看出,在所取的4h内的脉动风速均方根值历程中,在小范围内有较大波动,但波动范围不大,总体变化比较平稳。
图 7(b)描述了Y方向实测风速的10min平均湍流度,湍流度的变化范围为7.8%~12.3%,平均湍流度为9.3%,可以看出10min平均湍流度的变化平缓,波动不是很大。
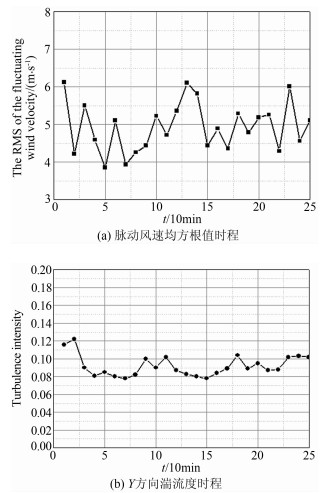 |
| 图 7 脉动风速均方根值和湍流度时程 Fig 7 Variation of fluctuating wind speed and turbulence intensity |
实测风场是随机的,因此风速和风向是随机过程,导致建筑物表面所测得的风压显然也是随机过程[9]。由于来流与建筑物呈一交角,因此作用于建筑物表面的风压可分为沿法线方向和切线方向的2个分量,由于空气的粘性很小,抗剪能力较差,因此起主要作用的是沿结构法线方向的风压[10],即垂直于结构表面的风压。同风速一样,风压也可以提取一系列代表风压的特征值,本文主要计算了建筑物表面实测的平均风压、脉动风压均方根值。平均风压的计算公式如下:
T为计算时所取基本时距,本节T的取值为10min,其它时距下也可以采用该式求解。由于风场的随机性,由前文可知,脉动风速为一定时距上均值为零的平稳随机过程,因此脉动风压也可以认为是一定时距上均值为零的平稳随机过程,因此,同3.2节中的脉动风速一样,将脉动风压均方根值作为风压脉动的特征值,用于后文的相关性分析,其定义如下:
T为计算所取的基本时距,同前面风场特性的定义一致。以10min为基本时距,计算了迎风墙面测点7的平均风压和脉动风压均方根值与风场同步4h内时间变化历程,如图 8所示。
从图 8和图 6(b)、图 7(a)对比可以看出,风压的变化趋势同风场特性的变化趋势相一致,说明实测风场数据与实测的风压数据呈现某种程度的相关性,对于迎风墙面的其它测点采用同样的方法分析,得到类似的结论。对于其它时距条件,也可以采用同样的方法进行分析与计算。
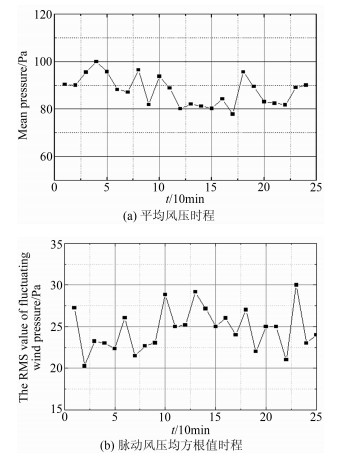 |
| 图 8 10min平均风压和脉动风压均方根值时程 Fig 8 Time series of 10min mean wind pressure and the RMS value of fluctuating wind pressure |
根据文献[11],在风压的全尺度实测中,平均风压系数定义如下[11]:
式中: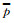 为实测迎风墙面基本时距为10min时风压的平均值;ρ为空气密度;
为实测迎风墙面基本时距为10min时风压的平均值;ρ为空气密度;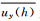 为h高度处的平均风速。h指风速仪的高度,
为h高度处的平均风速。h指风速仪的高度,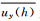 的定义同式(3)。
的定义同式(3)。
将式中的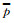 换成均方根风压prms后,则可得到脉动风压均方根系数Cprms,prms的定义同式(9)。
换成均方根风压prms后,则可得到脉动风压均方根系数Cprms,prms的定义同式(9)。
各测点的风压系数值如表 1所示。平均风压系数呈现中间大、两头小的规律,且均为小于1的正值,但靠近东边的测点与靠近西边的对称测点相比,平均风压系数要大,这可能与风是从东北偏东方向吹来有关。各测点均方根风压系数有类似规律。
| 测点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Cpmean | 0.6721 | 0.7244 | 0.7767 | 0.829 | 0.8813 | 0.7341 | 0.7791 | 0.9031 |
| Cprms | 0.1276 | 0.1364 | 0.1958 | 0.1701 | 0.1729 | 0.1881 | 0.2516 | 0.2433 |
| 测点 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| Cpmean | 0.7655 | 0.7094 | 0.7145 | 0.6611 | 0.6921 | 0.6816 | 0.6347 | |
| Cprms | 0.2053 | 0.1872 | 0.1954 | 0.1728 | 0.1562 | 0.1368 | 0.1416 |
图 9为各测点在10min时距下的平均风压系数随风向角变化趋势。由图可知,迎风墙面各测点随着风向角的变化趋势基本趋于一致,从中间测点往两边测点呈现递减的规律,这可能与转角处的脉动较大有关。在不同风向角下,靠近北面的各测点平均风压系数随风向角的增大而减小,而靠近南面的各测点的平均风压系数随风向角的变化趋势刚好相反,中间测点随着风向角呈现先增大后减小的趋势。这说明同来流风向靠近的测点风压更大,而远端的测点相对要小。中间测点始终是最大的,这可能与靠边测点的脉动较大有关。
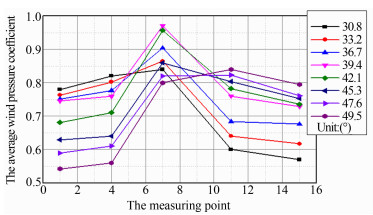 |
| 图 9 不同风向角下各测点的平均风压系数 Fig 9 Mean pressure coefficient distributions of every test point in different wind directions |
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素相关程度的一种分析手段。参与分析的各元素之间需要存在一定的联系或者概率才可以进行相关性分析[12]。由前文可知,风场和风压显然满足相关性分析的条件。
为了探讨基本时距和风向角对风场和风压相关性的影响,本文将根据前述实测所获得的风场数据和风压场数据,通过相关性分析的方法研究在不同的时距条件下两者之间的相关性,进而通过比较在不同时距条件下的相关性,确定相关性较大时所对应的时距。另外对比了10min基本时距时,不同来流风向角下二者的相关性,以期得到相关性最大时来流的角度。具体的计算方法和公式介绍如下。 5.1 相关性及其计算[13]
对于一组复杂数据可以使用一定的数学手段产生一个相对简单的类结构,进行“相关性”或“相似性”分析,最常用的是使用相似系数Cxy来表示指标x和指标y之间的相似关系。Cxy的取值在-1~1之间,其绝对值越接近1,表示指标x和指标y之间的关系越密切,其绝对值越接近0,表示指标x和指标y之间的关系越疏远。对于两条曲线形状变化规律之间的间隔尺度,常用的相似系数有夹角余弦和相关系数。
(1)夹角余弦;这是受相似形的启发而来,对于两条曲线,如果长度不一,但是形状相似,当长度不是主要矛盾时,可以定义一种相似系数来表示两条曲线之间比较密切的相似关系从而加以描述。通常用夹角余弦来描述这种关系,其定义为
式中,vkx,vky表示所要研究的两个指标向量,在本文研究分析中,vkx分别对应于平均风速、脉动风速均方根值和湍流度;vky分别对应于平均风压、脉动风压均方根值,k表示指标向量的第k个元素,n表示指标向量中元素的个数。
(2)相关系数;相关系数Cxy就是求将数据标准化 (将指标向量的每个元素减去指标向量元素平均值) 后的夹角余弦。为了简便计,在计算分析时,相关性系数取计算各指标向量之间的夹角余弦。 5.2 相关性分析结果
在研究不同时距和不同来流风向角下风场与建筑物迎风墙面风压场的相关性时,集中计算了在不同平均风时距和不同风向角下平均风速同平均风压,脉动风速均方根值、湍流度分别同脉动风压均方根值的相关性。从数理统计的角度而言,参与计算的数据个数的多少对于相关性系数的值有一定的影响。 5.2.1 不同的基本时距条件下风场和风压的相关性分析结果
在总的采样时间长度相同,不同基本时距条件下划分的数据段个数显然是不同的,平均风时距越大划分的数据段个数越少,而采用上述相关性分析方法,数据段个数的多少会直接影响到计算得到的相关系数值。因此,为了体现最后结果的一般性,本文分别取等时间长度(取计算总时长为1h)和等数据段个数(在不同时距条件取相同的数据段个数(60个))两种情况进行分析。本文选取了1s,2s,3s,10s,0.5min,1min,3min,10min共8个时距下的相关性分析。
(1) 等时间长度时的相关度
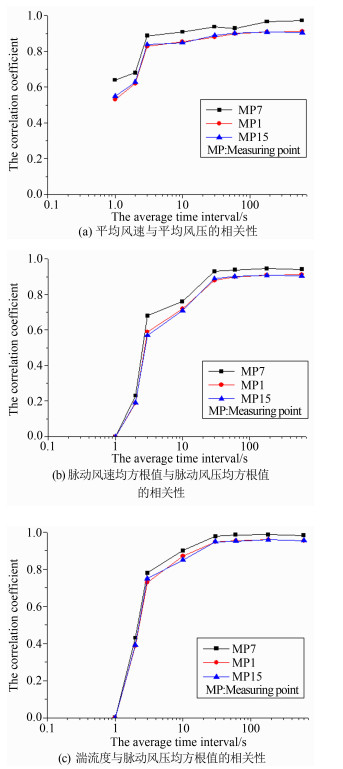
取计算的时间长度为1h,在此条件下,计算得到了在不同时距条件下,平均风速同平均风压以及脉动风速均方根值和湍流度分别同脉动分压均方根值的的相关性。具体计算结果如图 10所示。
由图 10可知,对于脉动风速均方根值同脉动风压均方根值以及湍流度同脉动风压均方根值的相关性变化趋势基本一致,由脉动风速均方根值同湍流度的关系可知,此时平均风速对其相关性的影响较小。具体来说,当时距小于3s时,相关性呈现陡降的趋势,当时距取为1s时,基本上没有相关性。这可能与脉动风速的周期正好处于这一时距段,因而得到的数据随机性大有关。当时距处于3s~0.5min的区间时,相关性呈现稳步递增的趋势,变化相对比较平稳。当时距大于0.5min时,相关性系数基本呈一常数。分析原因可知,随着时距的增大,脉动的瞬时性减弱,而呈现出长时距上的整体平均,偏离脉动风自身的周期越大,这种现象越为明显。平均风速同平均风压的相关性在时距大于等于3s这一时距区间内基本呈现和上述脉动风速均方根值和脉动风压均方根值之间相同的变化趋势。当时距小于3s时,虽然相关性系数有所下降,但下降得不多,且在这一低时距区间内,还呈现出一定的相关性。这可能与平均风的计算分析与脉动风的周期计算相关不大有关系,再有,当时距小时参与相关性计算的数据个数比时距大时要多,更能详尽描述两条曲线的变化趋势,因此,在较小的时距段均呈现较低或几乎没有相关性。此外,为了分析迎风墙面各个测点的相关性,分别对迎风墙面中间测点7、边测点1和边测点15进行了分析,由图可知3组数据下的相关性曲线走势基本相同,对其它的测点进行同样的分析也有类似的结果。这说明,迎风墙面各个测点的风压同风场有一致的相关性。
 |
| 图 10 风场和风压的相关性 Fig 10 The correlation between the measured wind field and wind pressure |
(2) 等数据个数时相关性结果
在相关性系数计算的数学模型中,参与计算的数据个数对相关性系数值有影响。当参与分析的数据个数比较少时,不能详尽描述2个随机变量之间或2条曲线变化趋势的相似程度,这往往会导致计算出来的相关性系数比较大。为了消除这种影响,对不同时距条件下的数据均取60个进行分析。
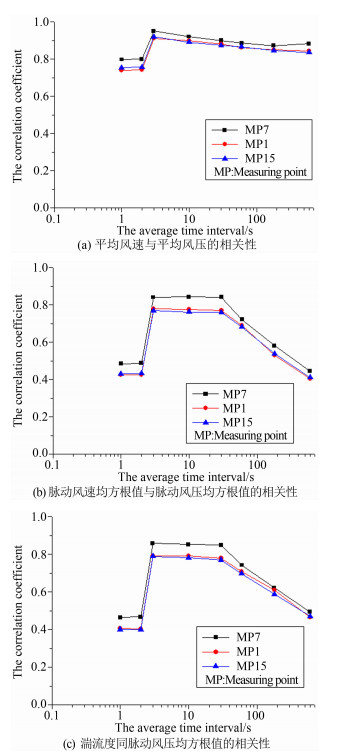
由图 11可知,取相同数据个数分析时,在时距大的区间内相关性有所降低,而时距小的区间内相关性有所增加。具体来说,对平均风速和平均风压之间的相关性,当时距小于等于2s时,基本为一常数,同图 10比较可知,在这一时距区间内相关性增大,说明参与分析的数据个数越少,相关性会越大。3s~2s的区间存在陡降趋势,当大于3s时,呈现递减趋势,但是变化不大。在这一时距区间内有所减小,说明时距的影响对平均风成分的影响是有限的。对脉动风速均方根值和湍流度同脉动风压均方根值的相关性,当时距小于等于2s时,相关性基本呈一常数,3s~2s的区间存在陡降趋势。说明所取时距小于脉动风速的周期时,由于脉动风场的瞬时性,在此时距区间内的相关性较低,由于参与分析的数据个数相对图 10的情况来说很少,因此分析时还是有很小的相关性。3s~0.5min的区间内,基本呈一常数,当时距大于0.5min时,相关性呈下降趋势,且下降比较多。这可能与所取时距过长,脉动成分表现出被中和抵消的情况有关,但同图 10的情况相比,相关性下降较多,这与在大的时距区间参与分析数据的个数比图 10的情况要多有关。综合以上分析可知,基本时距取3s时,风场和风压之间各参数的相关性较大。
 |
| 图 11 风场和风压的相关性 Fig 11 The correlation between the measured wind field and wind pressure |
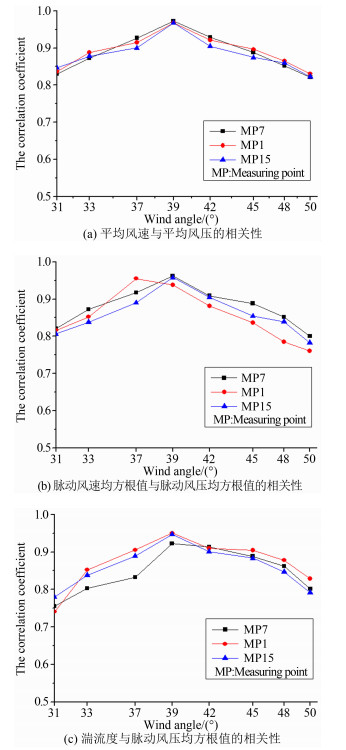
取来流风向角稳定在42°~65°时,1h的风场和风压数据,集中研究了当基本时距取10min时,在不同风向角下平均风速同平均风压,脉动风速均方根值和湍流度分别同脉动风压均方根值的相关性。当来流风向同建筑物表面呈一夹角时,随着相交角度的变化,风压随着风速变化的影响程度显然是不一样的。在不同风向角下,风场同风压的相关性如图 12所示。
 |
| 图 12 风场和风压的相关性 Fig 12 The correlation between the measured wind field and wind pressure |
由图 12可知,随着来流角度的增大,相关性系数呈现先增大后减小的规律,表明来流风向角对相关性影响较大,由于规定正北方向为来流风向的零度角,当来流风向为39°时,来流风速恰好与建筑物迎风墙面垂直,由图可知当风向角为39.4°,各测点风场同风压之间各个对应参数之间的相关性最大。说明来流风向与迎风墙面垂直时,相关性最大。对于其它风向角下的相关性,当风向角从39.4°往两边变化基本呈对称递减的特征。因为建筑物表面粘贴的风压传感器所能感应到的风是垂直于建筑物表面方向的风速分量,因此由分析可知,当风速垂直吹向风压传感器时,测到的风压更能准确地反映风速大小的变化,两者的变化趋势自然会呈现高度的相似,因此实测相关性分析得到的结果同我们理论分析的结果相同。
6 结 论通过上述对风场和建筑物迎风墙面实测风压及风场参数和风压场参数的相似性分析得到的结果,得出以下结论:
(1) 通过对风场特性及风压特性实测数据的分析,强风“天兔”的风速和风向变化比较平稳,湍流度不是很大,脉动风速均方根值比较小,且随着风速的增加变化比较平稳;
(2) 实测风压场与Y方向风速的变化趋势类似,对于迎风墙面各测点风压系数呈现出中间大、两头小的特征,但差别不是很大;
(3) 通过对风场参数与风压参数的相关性分析,当取等时长1h进行分析时,由于各个时距下,参与分析的数据个数不同,在时距大于等于0.5min时,相关性最高且基本呈一常数,当时距小于3s时,相关性较低,尤其是脉动风压均方根值同湍流度及脉动风速均方根值的相关度非常小,下降比较快。当基本时距为3s时,呈现比较高的相关性,3s~0.5min的区间内稳步上升。
(4) 当取相同的数据个数进行分析时,时距为3s时的相关性最高,3s~2s的区间内呈现陡降趋势,小于等于2s时相关性基本呈一常数,且数值较低。当时距大于等于3s时,随着时距的增加,平均风速同平均风压之间的相关性越来越小,但减小比较缓慢。脉动风压均方根值同脉动风速均方根值以及湍流度的相关度,在3s~0.5min的区间内基本不变,当时距大于0.5min时,相关性值越来越小,且下降比较多。
(5) 当基本时距取3s时,风场同风压场的相关性较高;当来流风向垂直于结构迎风墙面时,风场同风压场的相关系数值较高,以上结果是在特定台风下的研究结果,结论是否具有普遍性,还有待进一步探索。
| [1] | Li Q S, Fang J Q, Jeary A P, et al. Full-scale measurement of wind effects on tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 741-750. |
| [2] | Li Q S, Wu J R, Liang S G, et al. Full-scale measurements and numerical evaluation of wind-induced vibration of a 63-story rein-forced concrete super-tall building[J]. Engineering Structures, 2004, 26: 1779-1794. |
| [3] | 张相庭. 国内外风载规范的评估和展望[J]. 同济大学学报: 自然科学版, 2002, 30(5): 539-543. Zhang Xiangting. Evaluation and prosper for wind loading codes at home and abroad[J]. Journal Tongji University: Natural Science Edition, 2002, 30(5): 539-543. |
| [4] | GB50009-2001. 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2006. GB50009-2001. Load code for the design building structure[S]. Beijing: China Architecture & Building Press, 2006. |
| [5] | 黄本才, 汪丛军. 结构抗风分析原理及应用[M]. 第二版. 上海: 同济大学出版社, 2008: 28. Huang Bencai, Wang Congjun. Wind resistant analysis of the principle and application[M]. 2nd ed. Shanghai: Tongji University, 2008: 28. |
| [6] | 陈严, 张锦源, 王楠, 等. 风力机风场模型的研究及紊流风场的Matlab数值模拟[J]. 太阳能学报, 2006, 27(9): 955-960. Chen Yan, Zhang Jinyuan, Wang Nan, et al. Study on turbine wind-field model and numerical simulation in turbulent flow[J]. Acta Energiae Solaris Sinica, 2006, 27(9): 955-960. |
| [7] | 谷兴凯, 范高锋, 王晓蓉, 等. 风电功率预测技术综述[J]. 电网技术, 2007, 31(S2): 335-338. Gu Xingkai, Fan Gaofeng, Wang Xiaorong, et al. Summarization of wind power technology[J]. Power System Technology, 2007, 31(S2): 335-338. |
| [8] | 娄素华, 李志恒, 高苏杰, 等. 风电场模型及其对电力系统的影响[J]. 电网技术, 2007, 31(S2): 330-334. Lou Suhua, Li Zhiheng, Gao Sujie, et al. Wind farms models and its impacts on wind farms integration into power system[J]. Power System Technology, 2007, 31(S2): 330-334. |
| [9] | 舒新玲, 周岱. 风速时程AR模型及其快速实现[J]. 空间结构, 2004, 9(4): 27-32. Shu Xinling, Zhou Dai. AR model of wind speed time series and its rapid implementation[J]. Spatial Structures, 2004, 9(4): 27-32. |
| [10] | 杨庆山, 黄韬颖. 中美澳三国风荷载规范简介及其关于设计风速规定之比较[C]//第十三届全国结构风工程学术会议论文集 (下册), 2007. Yang Qingshan, Huang Taoying. Brief introduction and comparative study on the design wind speed regulation of wind loads among the codes of China, America and Australia[C]//Proceedings of the Thirteenth National Academic Conference on Wind Engineering Structure, 2007. |
| [11] | Simiu E, Scanlan R H. Wind effects on structures[M]. Wiley, 1996. |
| [12] | 白丽, 张向阳. 广州大学生网上创业与高校创业教育相关性探讨[J]. 继续教育研究, 2012, 2012(6): 123-125. Bai Li, Zhang Xiangyang. Correlation discussion between Guangzhou college students' internet entrepreneurship and entrepreneurship education in colleges and universities[J]. Continue Education Research, 2012, 2012(6): 123-125. |
| [13] | 李正农, 宋克, 李秋胜, 等. 广州中信广场台风特性与结构响应的相关性分析[J]. 实验流体力学, 2009, 23(04): 21-27. Li Zhengnong, Song Ke, Li Qiusheng, et al. Correlation analysis of wind characteristic and wind-induced response of CITIC Plaza[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(4): 21-27. |