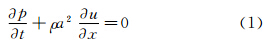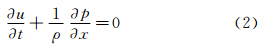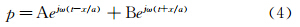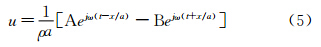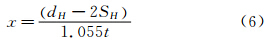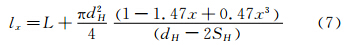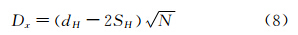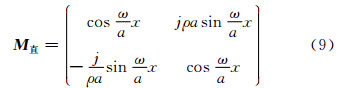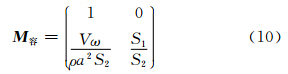2. 西安交通大学航天航空学院 机械结构强度与振动国家重点实验室, 西安 710049
2. State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi'an Jiao Tong University, Xi'an 710049, China
往复式压缩机管道系统中气柱的共振是引起管道振动的主要原因之一。因此,在已知压缩机激发频率的情况下,准确计算管道系统各阶气柱固有频率,对避免气柱共振和消减管道内气流压力脉动具有重要的理论意义和工程实用价值。
近几十年来对于往复式压缩机管道系统气柱固有频率问题的研究,很多学者做出了贡献:西安交大管道振动研究室编著了有关气柱固有频率和气流脉动方面的专著[1]并开发了相关的计算程序;CYKLIS P.等人利用传递矩阵法计算管道系统的气柱固有频率及气流脉动[2];谢壮宁利用频响函数法计算了复杂管道系统的气柱固有频率,分析了阻尼对气柱固有频率的影响[3];刁安娜通过对数值模拟和试验研究,分析了不同孔板安装位置和孔板内径对气柱系统固有频率及气流脉动幅值的影响[4];刘智勇等人通过管路内气体的运动推算了气柱固有频率的计算方法[5]; 姜文全、薛玮飞,Brian C.Howes,Shellev D,Enzo Giacomelli等人用有限元方法计算管道系统气流脉动及气柱固有频率[6, 7, 8, 9]。然而随着生产能力的提高,为了得到高压气体,需要多级压缩,压缩后的气体温度很高,在进入后一级压缩时需要冷却,因而在管系中空冷器作为一个重要辅助结构对气柱固有频率有一定的影响。现有的研究方法和计算程序在处理含空冷器管道系统气柱固有频率问题时均没有一个具体的计算模型,只能凭借经验或作简化近似计算,这样也难于获得准确结果。
本文基于数值模拟与实验的方法提出空冷器作为管路原件时的参数化模型,并验证利用此模型计算管道系统气柱固有频率的正确性。
1 气柱固有频率实验及管道系统计算模型 1.1 气柱固有频率实验本文仅考虑空冷器结构对管系气柱固有频率的影响,故只根据现场常见空冷器(见图 1)和空冷器国标GB/T-15386-94[10]制造空冷器结构模型,如图 2~3所示,对其引风冷却结构不做分析。
 |
| 图 1 工程现场管束结构空冷器 Fig. 1 Air coolers used in engineering |
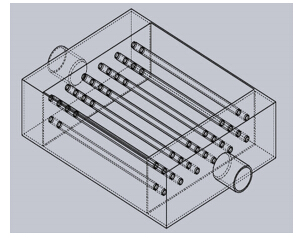 |
| 图 2 实验室空冷器结构图 Fig. 2 Structure of laboratory air cooler |
 |
| 图 3 实验室空冷器模型 Fig. 3 Laboratory air cooler model |
首先依照实验流程图 4建立图 5所示含空冷器管道系统系统气柱固有频率测试实验平台,采用扫频法进行气柱固有频率分析实验。测试系统主要由数字信号发生器、功率放大器、扬声器、管道系统、拾音器、数字信号示波器、数据采集及分析系统组成。测试原理为:由数字信号发生器产生易于变频的正弦波信号,经过功率放大后驱动扬声器作为激励源,当扬声器以某一频率发生正弦波时,就激发管系内的气柱做受迫振动。其声压由塞入管内的电容话筒来拾取,如图 5所示,并可在数字信号示波器上计量显示,同时用DaqBook2000A振动信号数据采集系统采集声压数据。当扬声器的激发频率与管系气柱固有频率之一相重时,管系内的气柱便处于共振状态,声压就达到一极大值,波形为正弦波。不断改变扬声器的频率就能获得一系列的声压极大值,与这些声压极大值所对应的的一系列频率就是管系的气柱固有频率。最后利用MATLAB对所采集到的声压信号进行分析处理后可得到时域信号的频谱分析结果。数字信号发生器的扫频范围设定为1~500Hz。
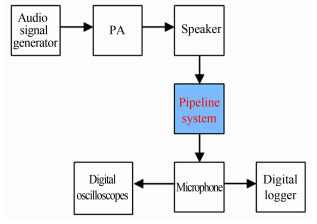 |
| 图 4 气柱固有频率实验流程图 Fig. 4 Flow chart of gas natural frequency test |
 |
| 图 5 含空冷器管道系统实验平台 Fig. 5 Experimental platform of pipeline with air cooler experimental system |
根据搭建的管道系统实验平台,利用三维建模软件CATIA建立了含空冷器管道系统的实体模型,如图 6所示。将实体模型导入Gambit中分割并划分网格,其中2端的圆管及空冷器内的圆管束是利用Cooper方法划分的六面体网格单元,空冷器两端的腔体是利用Tri/hybrid的方法划分的四面体网格单元,如图 7所示。最后在Gambit中对管道系统添加边界条件,入口边界条件采用非定常压力入口边界条件,出口边界条件为压力出口边界条件。
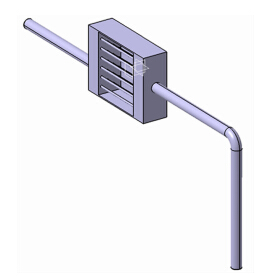 |
| 图 6 管道系统几何模型 Fig. 6 Geometric model of pipe system |
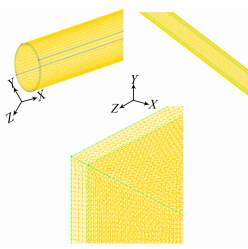 |
| 图 7 模型有限元网格(圆管、管束、腔体) Fig. 7 The mesh of FEM |
设置数字信号发生器频率变化时间Δt=0.1s,从0~500Hz共需扫频时间t=50s。在数采系统中设定采样频率fd=1000,数据长度L=50000,采样点数N=53008,利用MATLAB编制程序对其做快速傅里叶变换得到频谱图如图 8所示,其中纵坐标是具有压力量纲的相对值。
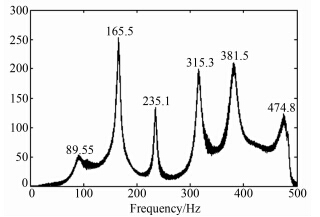 |
| 图 8 实验测得气柱固有频率 Fig. 8 The test result of natural frequency |
将在Gambit中划分好的网格模型导入Fluent中,在Fluent中根据管道内部介质的性质采用基于密度(耦合式)的隐式3ddp(三维双精度)求解器,并指定其计算模式为非稳态;计算模型选择标准k-ε双方程湍流模型;流体类材料为理想空气。为了便于计算,入口边界条 件采用非定常压力边界条件:p=101325[1+0.05(sinft)],其中f=2πn,n在0~500Hz之间 且频率变化率为1(根据其公式用C语言编译非定常速度UDF函数),出口边界条件采用定常压力边界条件(出口端与与大气直接相通),文中设定为101325Pa。根据以上设置分别计算0~500Hz中每一个频率下的气流压力脉动情况,依据计算结果得出不同频率下的压力脉动相对值如图 9所示,并将其与实验结果作对比如表 1所示。
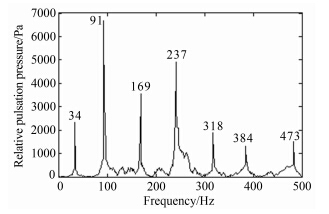 |
| 图 9 模拟所得气柱固有频率 Fig. 9 Numerical simulation of natural frequency |
| 阶次 | 模拟结果 fs/Hz | 实验结果 fe/Hz | 误差 fs-fe/fe |
| 1 | 34 | —— | —— |
| 2 | 91 | 89.55 | 1.619% |
| 3 | 169 | 165.5 | 2.115% |
| 4 | 237 | 235.1 | 0.808% |
| 5 | 318 | 315.3 | 0.856% |
| 6 | 384 | 381.5 | 0.655% |
| 7 | 473 | 474.8 | 0.379% |
由表 1可看出,除第一阶外其余各阶模拟结果与实验结果均较为相近,且误差也在工程允许范围之内。实验结果中第一阶固有频率缺失的原因是扬声器的低频性能差,对30Hz以下音频信号反应弱,故数值模拟结果准确可靠。未来研究中将采用低频性能强的音频传感器对此实验进行完善。对比模拟和实验结果可知:在进行管道系统气柱固有频率实验测试时扫频法具有高效、连续、测试结果相对准确的特点;同时Fluent中利用“频率-响应”方法计算气柱固有频率时,虽计算量较大但计算结果相对准确且不易漏根。
3 空冷器参数化模型的建立及管道系统气柱固有频率理论计算 3.1 管道系统气柱固有频率的基本计算理论由于管道中流体的流动可视为一维非定常流动,且正常情况下管道中的压力脉动值相对于压力平均值很小(工程中一般在8%以内);气流速度相对于声速很小,阻尼也很小(可忽略),流体可压缩,因此管道中的介质波动现象可以用研究声波的基本方程(波动方程)来描绘。以管内一段流体微团为研究对象,结合波动方程的上述假设,由控制体内的质量守恒 原理可得连续方程:
根据牛顿第二定律对微团进行受力分析得运动方程:
由(1)、(2) 2式可得出波动方程:
此为关于脉动压力的偏微分方程,其解为:
将(4)代入运动方程(2)中得:
式中: ρ为流体密度,x为沿管轴线的坐标,t为时间,a为声速,p为脉动压力,u为脉动流速,(4)和(5)式中的A、B为复数常数,由管道的边界条件确定,ω为脉动的圆频率。由于管道系统是由各种基本管道元件组成,即可以将管道系统拆分为闭端、等截面直管、体积元件、回路管、三通汇流管、异径管和开端等,依据线性波动理论可依次计算出每一管道元件进出口物理状态(脉动压力和脉动速度)的转移矩阵。在管系内选择一条主线,沿主线建立整个管系的转移矩阵,便可得到末端和起始端的压力与流速脉动关系。再根据起始点和末端的边界条件列出频率方程,并用数值解法找到其解,即可得复杂管系的气柱固有频率值。
3.2 参数化模型的建立与计算在天然气输送现场,经常使用的是引风式丝堵式管束结构的空冷器,由于本文仅考虑空冷器结构对管道系统气柱固有频率的影响,且根据现场常见空冷器和空冷器国标GB/T-15386-94制造空冷器结构模型,如图 1所示,对其引风冷却结构不做分析。由于空冷气两端为2个标准长方体腔体,腔体中间为错列式排列的管束,因此根据试验与模拟结果可将空冷器等效为“容-管-容”2种管路基本原件。其中错列式管束亦可用“当量管长、当量管径”[11]来等效,同时结合模拟与实验结果对其修正可得如下计算模型:
管束的当量管长
式中:x为中间变量,t为节距,SH为管壁厚,L为单根管总长,dH为单根管外径。
管束的当量管径
式中:Dx为当量管径,N为每列管数。
由于管道系统是由各种基本管道元件组成,依据线性波动理论可依次计算出每一管道元件进出口物理状态(脉动压力和脉动速度)的转移矩阵。本文仅需要等截面管和体积原件的转移矩阵:
等截面管的转移矩阵
这个方阵的意义是将x=0处的脉动量转换成直管中距离x处截面的脉动量。体积元件的转移矩阵
其中S1和S2分别为体积元件前后管子的横截面积,V为容器的体积。
实验室中空器两边腔体的体积均为v=0.0157m3;管束之间的节距t=70mm,管壁厚SH= 1.1mm,单根管长L=619.16mm,单根管经dH=20.2mm,每列管束N=6,由公式(12)和(13)计算其当量管长为lx= 601mm ,当量管径Dx=44.09mm。因此可将管路系统简化为图 10所示计算模型,依据传递矩阵法计算管道系统的气柱固有频率,其理论计算结果与实验和模拟结果对比情况如表 2所示。
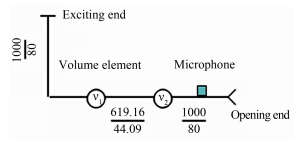 |
| 图 10 管道气柱固有频率计算简图 Fig. 10 The scheme of natural frequency calculation |
| 阶次 | PAP计算结果 ft/Hz | 模拟结果 fs/Hz | 实验结果 fe/Hz |
| 1 | 32.41 | 34 | —— |
| 2 | 91.73 | 91 | 89.55 |
| 3 | 167.29 | 169 | 165.5 |
| 4 | 238.06 | 237 | 235.1 |
| 5 | 316.13 | 318 | 315.3 |
| 6 | 381.76 | 384 | 381.5 |
| 7 | 477.94 | 473 | 474.8 |
由对比结果可以看出将空冷器等效为“容-管-容”且中间管束以当量直径和当量管长来近似能够满足气柱固有频率的工程计算需求。
4 结 论通过对含空冷器管道系统气柱固有频率的数值、试验及理论计算对比研究得到如下2点结论:
(1) 基于CFD方法,根据所搭建的含空冷器管道系统系统气柱固有频率实验测试平台,建立了管道系统流体动力学模型;通过模拟结果与实验数据的对比,证明了本文所提实验与模拟方法的正确性,并且有很好的工程应用价值;
(2) 根据空冷器国标GB/T-15386-94和工程中惯用空冷器结构模型,基于实验和模拟结果提出了空冷器作为管道系统中特殊管路元件时合理的参数化模型即“容-管-容”参数化模型,为工程中计算含空冷器管道系统气柱固有频率提供了直接有效的方法。
| [1] | 党锡淇, 陈守五. 活塞式压缩机气流脉动与管道振动[M]. 西安: 西安交通大学出版社, 1984. Dang Xiqi, Chen Shouwu. Gas pulsation and pipe vibration research on reciprocating compressor piping system[M]. Xi'an: Xi'an Jiao tong University Press, 1984. |
| [2] | Cyklis P. Experiment identification of the transmittance matrix for any element of the pulsating gas manifold[J]. Journal of Sound and Vibration, 2001, 244 (5): 859-870. |
| [3] | 谢壮宁. 采用频响函数法计算复杂管系气柱固有频率[J]. 流体机械, 1995, 23(7): 17-20. Xie Zhuangning. Calculating the gas natural frequency of pipeling system with FRF france[J]. Fluid Machinery, 1995, 23(7): 17-20. |
| [4] | 刁安娜. 孔板对压缩机管路气流脉动影响的理论与实验研究[D]. 西安: 西安交通大学, 2008. Diao Anna. Numerical simulation and experimental research on orifice plate reducing gas pulsation[D]. Xi'an: Xi'an Jiao tong University, 2008. |
| [5] | 刘智勇, 高梦里. 活塞式压缩机管路设计中气柱固有频率的计算方法[J]. 化工机械, 2008, 35(4): 212-216. Liu Zhiyong, Gao Mengli. Calculation method of the gas pole immanence frequency in the design of the pipelines of a reciprocating compressor[J]. Chemical Machinery, 2008, 35(4): 212-216. |
| [6] | 姜文全, 杨帆, 王茂廷, 等. 基于ansys的往复式压缩机管系气柱固有频率计算[J]. 压缩机技术, 2008, 6: 13-16. Jiang Wenquan, Yang Fan, Wang Maoting, et al. Calculation of the natural frequency of the gas columns in reciprocating compressor pipelines on ANSYS[J]. Compressor Technique, 2008, 6: 13-16. |
| [7] | 薛玮飞, 杨晓翔. 复杂管系气柱固有频率的有限元计算[J]. 化工机械, 2003, 30(3): 152-156. Xue Weifei, Yang Xiaoxiang. Finite element method calculation of the natural frequency of the gas columns in complex pipelines[J]. Chemical Machinery, 2003, 30(3): 152-156. |
| [8] | Brian C Howes, Shellev D Greenfield. Guidelines in pulsation studies for reciprocating compressors[J]. Proceedings of the International Pipeline Conference, 2002, 30(3): 1241-1250. |
| [9] | Enzo Giacomelli, Marco Passeri.Control of pulsation and vibrations in hyper compressors for LDPE plants[C]. ASME-PVP2004 Pressure Vessel & Piping Conference, San Diego, California, 2004. |
| [10] | 空冷式换热器 GB/T 15386-94[S]. 国家技术监督局, 1995. |
| [11] | 李志博. 活塞压缩机管道系统气流脉动数值模拟及实验研究[D]. 西安: 西安交通大学, 2003. Li Zhibo. Gas pulsation analysis and experimental research on reciprocating compressor piping system[D]. Xi'an: Xi'an Jiao tong University, 2003. |