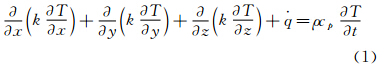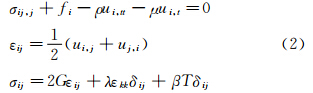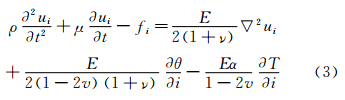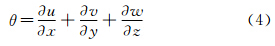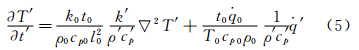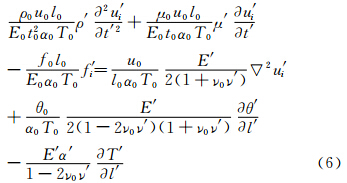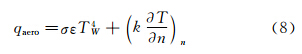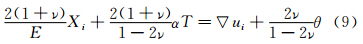以往的数据换算主要针对模型气动加热影响进行,而对于现代高超声速飞行器,一些新的外形特点,如前缘尖锐,致使驻点热流很高,再加上飞行时间长,[CM(22*2]累计的加热量很大,使得结构外部温升严重,整个防热结构存在较大的温度梯度,热应力问题也十分突出。因此,对飞行器模型进行热结构试验,并通过相似准则得到实际飞行器结构温度场/应力场,为飞行器防热布局设计提供有效数据支撑是十分必要的。朱伯芳[1]早在20世纪50年代就对建筑物温度应力的相似律进行了研究;唐新成[2]等人在上世纪末又针对工艺应力模拟技术中的热相似律进行了细致讨论;相似理论在流体力学和传热学中已有大量的应用研究[3, 4, 5];针对飞行器部件的热相似问题之前也有一些研究[6, 7]。但针对风洞试验的特殊耦合环境相似准则一直未得到深入发展。
本文通 过热传导方程和热弹性动力学方程组,对其中的模型相似参数进行讨论,并根据模型试验边界情况进行讨论研究。提出适用于热气动弹性问题的地面考核试验相似准则,并建立不同试验类型情况下需要遵循的相似准则条件。通过飞行器尖锐前缘模型算例进行考核计算与分析。
1 基本控制方程与相似准则温度场规律可由热扩散方程表征,在直角坐标系下热传导方程的普通形式为:
应力场规律由热弹性控制方程表征,考虑到问题还涉及动力响应问题,此处采用三维弹性动力学方程组,该基本方程组为:
将上式中的平衡方程和几何方程代入本构方程,并代入β=- E 1-2v α,可得如下变换形式:
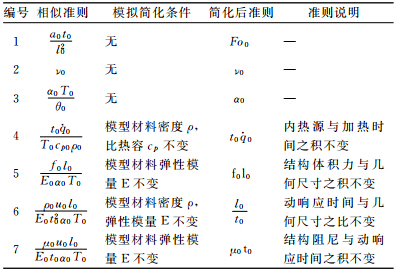
其中, 取T0、t0、l0、u0、θ0、 0和f0为无量纲参考量,其可视为参考模型的固有特征量,如l0为模型的特征长度。则原控制方程组变为:为保证无量纲方程与原方程一致,即2个物理问题保持相似,则可将2个问题的参数要求归纳为如表 1所示的相似准则:除控制方程外,还需考虑热结构考核试验的边界条件相似关系,才能唯一确定模型间的相似性。在热结构考核试验中,考核件的实际边界条件分为2类:热边界条件和力边界条件。对于热边界条件,这里主要为综合性的热流边界条件,其边界热平衡时满足以下关系式:
式中:qaero表示总的气动热流;qrad为壁面辐射到外部环境中的热流;qcond为通过导热传入结构内部的热量。由此可得到边界条件为:
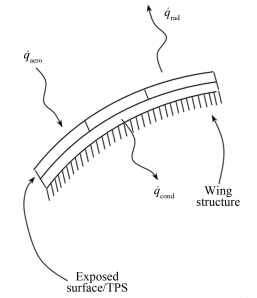 |
| 图 1 气动加热边界热平衡示意图 Fig. 1 Schematic diagram of the boundary thermal equilibrium |
除热流边界外,还需考虑气动力边界。现有高超声速气动力工程预测方法,都是建立在高超声速无粘流动分析的基础上,具备牛顿流特性,表面压强正比于来流速度与密度。则由三维弹性动力学方程的本构关系可得下式:
其中,Xi为边界上在i方向的表面力(压强)。经过与控制方程相同的无量纲化,可得到考虑边界条件的相似准则如表 2所示。根据不同的考核试验类型与要求,可将相似准则要求进行如表 3所示的分类。在进行相应的试验时,遵循列出的相似准则即可。
| 编号 | 试验类型 | 需遵循的相似准则 |
| Ⅰ | 无内热源的结构环境与温度场考核 | 1、8、9 |
| Ⅱ | 含内热源的结构环境与温度场考核 | 1、4、8、9 |
| Ⅲ | 应力/应变考核(不考虑气动加热) | 2、10 |
| Ⅳ | 应力/应变考核(考虑气动加热) | 1、2、3、5、8、9、10 |
| Ⅴ | 结构动力响应试验(不考虑气动加热) | 2、5、6、7、10 |
| Ⅵ | 结构动力响应试验(考虑气动加热) | 1~10 |
当然,也可根据实际需要,调整需遵循的相似准则。如不考虑辐射影响时,就可以不考虑相似准则8。从上表还可以看出,当考核时只考核结构温度或者结构应力情况时,满足部分相似准则即可。而需要进行热结构动力响应模拟时,需要满足全部10条相似准则。
需要特别注意的是,在某些特殊情况下相似准则间会出现矛盾现象,如何取舍需要根据试验要求和主要目的判断。例如进行上表中试验类型VI的考虑气动加热的结构动力响应考核,假设试验模型是真实模型的1/4,则根据相似准则1可知,结构加热时间为真实模型的1/16。同时,根据相似准则5,结构体积力(重力)也应满足真实模型的4倍要求。而此时再根据相似准则6和准则7可知,结构动响应时间为真实模型的1/2。因此,结构动响应与结构加热时间不一致。也即是说,在进行考虑气动加热条件下的结构动力响应试验时,如模型尺寸与真实模型不同,则无法真实模拟原模型的动力响应特性。以下就讨论获得的相似准则进行算例分析。
2 算例考核与分析图 2为某飞行器尖锐前缘模型。该模型楔角18°,两端经倒圆处理。由于前缘处于高热流区,其结构温度和应力都是在飞行前的考核试验中应该完成的考核内容。由于该尖锐前缘尺寸很小,在试验中,布置测点难度较高。如果放大前缘尺寸则能很好地解决这一问题。
 |
| 图 2 尖锐前缘模型计算网格 Fig. 2 Sharp leading edge model and calculation grid |
为模拟尖前缘模型在飞行情况下的实际加热状态,此处以模型在假定的飞行条件下的气动加热情况为基础,并根据相似准则调整相关参数,以期达到与真实模型一致的结构温度场和应力/应变场。假设本模型需完成试验类型Ⅳ的考虑气动加热的应力/应变考核试验。假设风洞模型为真实模型的2倍大小。根据相似准则要求,本试验需满足相似准则1、2、3、5、8、9和10。需要特别说明的是,相似准则10要求气动力载荷分布不变。而模型大小改变时,即使风洞来流状态不变,模型气动力载荷分布也会发生一定变化,但风洞气动力载荷通常在MPa量级,远小于结构温度温升引起的内应力。因此,这里暂且忽略气动力载荷影响。
根据以上描述,可设计如下表 4所列考核状态。
| 真实模型 | 考核一 | 考核二 | 考核三 | |
| 加热时间/s | 64 | 256 | 256 | 256 |
| 热流比 | 1 | 1/2 | 1 | 1 |
| 辐射系数 | 0.8 | 0.4 | 0.8 | 0.8 |
| 热传导系数/(J·(K·m)-3) | 50 | 50 | 100 | 100 |
| 材料密度/(kg·m-3) | 4960 | 4960 | 9920 | 4960 |
| 材料比热容/(J·(kg·K)-1) | 1116 | 1116 | 1116 | 2232 |
如图 4~6所示,分别为尖前缘中点(A点)、层流区域点(B点)和结构内点(C点)温度随时间变化图。通过监控对应位置点的温度时间曲线即可初步判断温度场的相似性。从曲线图可以看出,通过相似准则确定的3种考核方案中,虽然考核模型大小均为真实模型的2倍,但前缘和3个监控点的温度随傅里叶数(时间)变化完全一致。也即考核模型温度场和真实模型温度场相同。
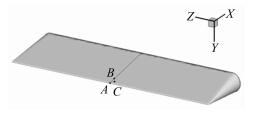 |
| 图 3 结构监控点位置示意图 Fig. 3 Schematic diagram of structural monitoring points |
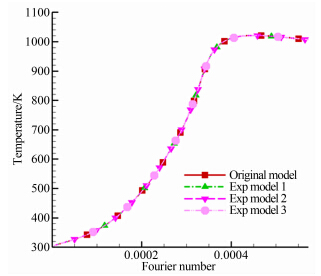 |
| 图 4 A点温度随时间变化图 Fig. 4 Temperature versus Fourier number on point A |
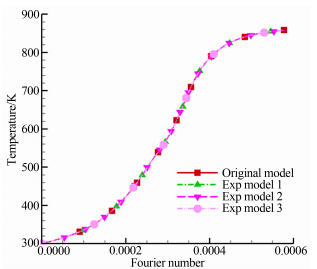 |
| 图 5 B点温度随时间变化图Fig. 5 Temperature versus Fourier number on point B |
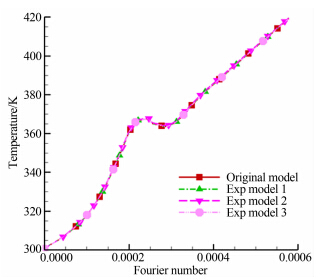 |
| 图 6 C点温度随时间变化图Fig. 6 Temperature versus Fourier number on point C |
| 坐标点 | 坐标值/m |
| A | (0,0,0) |
| B | (0.012,0.003,0) |
| C | (0.09,0.0155,0) |
图 7为模型加热10s时刻的结构等效应力云图。图 8为考核状态一模型加热40s时刻的结构等效应力云图。从图中可以看出,真实模型和风洞模型在对应时间点上,结构应力情况同样完全一致。
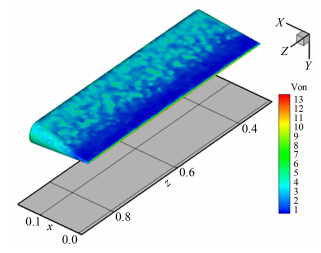 |
| 图 7 真实模型等效应力云图Fig. 7 Von.Mises stress nephogram in 35s of actual model |
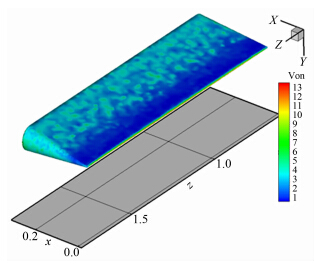 |
| 图 8 风洞模型等效应力云图Fig. 8 Von.Mises stress nephogram in 35s of test model Ⅰ |
通过对热传导方程、热弹性方程组和边界条件进行无量纲变换,提出了适用于热气动弹性问题的地面考核试验相似准则。并建立了不同试验类型情况下需要遵循的相似准则条件。计算结果表明,该相似准则具有较大的灵活度,且具有较高实用价值。主要体现在:
(1) 当真实材料无法直接进行考核时,可方便选取其它材料完成考核,并通过本相似准则完成考核状态与模型尺寸的确定;
(2) 对于尖锐前缘等结构太小无法测量,或真实模型太大无法试验等情况,可根据需要进行缩放,再根据相似准则选取材料;
(3) 对于无法模拟真实飞行条件的考核,可通过本相似准则确定达成考核目标最需要的相似条件,其它冲突准则可予以忽略,最大限度地满足考核要求。
| [1] | 朱伯芳. 建筑物温度应力试验的相似律[J]. 土木工程学报, 1958, 5(4): 271-277. Zhu Bofang. Similarity law for model tests of temperature stress in structure[J]. Chinese Journal of Civil Engineering, 1958, 5(4): 271-277. |
| [2] | 唐新成, 赖曾美, 张鸿庆. 工艺应力模拟技术中的热相似律[J]. 实验力学, 1993, 8(4): 311-317. Tang Xincheng, Lai Zengmei, Zhang Hongqing. Thermo-similarity in simulation of processing stress[J]. Journal of Experimental Mechanics, 1993, 8(4): 311-317. |
| [3] | 徐丹. 流体动力相似理论在旋流器中的建模[J]. 南通工学院学报, 2002, 1(1): 71-75. Xu Dan. To build a model in hydrocycloning by hydrokinetics similar theory[J]. Journal of Nantong Institute of Technology, 2002, 1(1): 71-75. |
| [4] | 杨锐玲, 朱永华. 相似理论在有缺陷混凝土热传导模型试验中的应用[J]. 红外, 2005, 3: 1-5. Yang Ruiling, Zhu Yonghua. Application of similarity theories in model experiment of conductive heat transfer in decaying concrete[J]. Infrared, 2005, 3: 1-5. |
| [5] | 蔡志鹏, 赵海燕, 鹿安理, 等. 焊接温度场、应力场和应力场相似准则的推导及验证[J]. 中国机械工程, 2001, 12(10): 1165-1168. Cai Zhipeng, Zhao Haiyan, Lu Anli, et al. Research on similitude principles of welding temperature, strain and stress fields[J]. China Mechanical Engineering, 2001, 12(10): 1165-1168. |
| [6] | Tsien Hsueshen. Similarity laws for stressing heated wings[J]. Journal of the Aeronautical Sciences, 1953, 20(1): 1-11. |
| [7] | Liu Lei, Gui Yewei, Du Yanxia, et al. Study on the similarity criteria of aircraft structure temperature/stress/dynamic response[J]. Journal of Thermal Science and Technology, 7: 262-271. |
| [8] | 王玉恒, 刘峰. 强激光辐照充压圆柱壳体热力效应的相似性数值模拟[J]. 激光杂志, 2008, 29(5): 62-63. Wang Yuheng, Liu Feng. Numerical simulation on similarity of thermal-mechanical effects of cylindrical shell subjected to inner pressure and irradiated by intense laser[J]. Laser Journal, 2008, 29(5): 62-63. |
| [9] | Canfield Stephen L, Peddieson John. Similarity criteria and associated design procedures for scaling solar sail systems[J]. Journal of Spacecraft and Rockets, 2011, 48(1): 218-221. |
| [10] | Zienkiewicz O C, Taylor K L. The finite element method[M]. Fifth Edition. Butterworth Heinemann, 2000. |
| [11] | Dhawan S, Narasimha R. Some properties of boundary layer low during transition from laminar to turbulent motion[J]. Journal of Fluid Mechanics, 1958, 3: 418-436. |
| [12] | Zoby E V, Moss J N, Sutton K. Approximate convective heating equations for hypersonic flows[R]. AIAA-79-1078. |