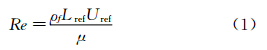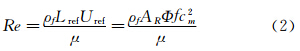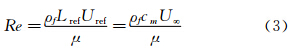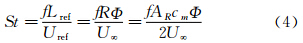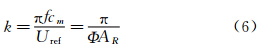2. 中国航空工业集团公司 第一飞机设计研究院, 西安 710089
2. The First Institute of Aircraft Design, AVIC, Xi'an 710089, China
微型仿生飞行器由于突出的仿生外形和飞行特性,以及小尺寸具有的机动灵活性,有望为环境监测、安保监控等重要应用的信息获取方式带来革命性的改进[1, 2]。从本世纪初掀起的微型飞行器研究热潮到如今,经过十几年的发展,微型仿生飞行器的研究已经取得了相当的进展。扑翼飞行器是仿生飞行器的代表,与传统飞行器的飞行方式不同,它采用自然界生物的扑动翼的飞行方式来同时产生飞行所需的升力和推力。具有合适外形、刚度及运动方式的扑翼可以产生理想的升力和推力,从飞行生物身上可以看到扑翼飞行的潜力,比如小小的蜜蜂可以带动比自身更重的花粉来飞行,老鹰甚至可以带动一只山羊飞行。且扑翼飞行可随时调整扑动的频率、幅度以适应不同的飞行状况,甚至可以停止扑动采用滑翔飞行方式来节省体能。
由于微型飞行器质量小、飞行速度低,突风对其飞行性能影响非常大,而采用柔性翼结构后,遭遇突风产生相应变形可以起到一定的抗风作用[3, 4]。柔性结构还可以充分利用结构变形对气动力的重新分布影响进行详细设计,进而改进飞行器的气动性能。飞行生物也采用了柔性翼结构,用于抵抗突风,提高飞行的机动能力。
扑翼飞行的一个重要优势是可以充分利用涡的能量。对于传统固定翼飞行器而言,翼尖涡会消耗能量,所以采用翼稍小翼等技术将其影响尽量减小。但对于扑翼,翼尖涡却可以和前缘涡同时作用,起到增强升力的效果。柔性结构的扑翼,弦向结构变形导致气动力重新分布,可显著增强推力。沿着展向的结构变形会改变迎角在展向的分布,同时改变所产生气动力的相位。
前飞时柔性扑翼的推力主要包括2部分,前缘吸力和由于弦向变形导致的压力分布变化。当翼型后部的柔性变形增加时,可以增加推力的分量,效果相当于增加了有效迎角。当弦向柔性在一定范围内增加时,尽管有效迎角和总气动力由于弦向外形变化而减少,但平均推力和瞬时推力都会由于气动力方向的改变而显著增加。对于展向柔性变形,在一定的合适范围内,可以增加推力。
翼型和翼面形状对扑翼的气动特性影响显著,涌现出大量关于不同外形扑翼结构柔性特性的研究。理论上结构变形有一个合适范围,可以改善气动特性。但该方面还需要开展深入的工作,以了解结构柔性变形和气动性能的影响机理,特别是在遭遇不可预见突风等复杂情况下。
由于柔性翼对飞行器的气动特性有显著的影响,众多文献都展开了研究,但目前的研究还仅限于探索性的初步研究,很多关键的研究问题尚未解决,突出的难点包括:几何非线性的作用及结构各向异性如何影响扑翼飞行的空气动力学特性;扑翼飞行如何通过结构变形提高稳定性等。
上述问题均不是独立存在,而是需要在扑翼飞行器设计的运动学、动力学及柔性结构特性等多个方面同时开展深入的综合研究,才能设计出具有高性能的飞行器。
有大量的文献表明关于上述内容已经开展了相关的研究。近年来,已发表的研究内容也有逐步深入和细化的趋势。本文的目的是综述目前相关的气动特性研究进展,并指出未来研究的发展方向,及面临的难点与挑战。 1 尺度律与关键无量纲参数
尺度律的研究对于减少参数数量,清晰描述一个系统的参数特性有重要意义,可以指出各参数的重要性[5]。对于扑翼的研究,主要的无量纲参数为:
(1) 雷诺数Re描述的是惯性力和粘性力的比值。定义为:
式中:ρf为流体密度,Lref为参考长度,Uref为参考速度,μ为粘性系数。
在扑翼飞行中,由于升力和推力都是依靠扑翼的扑动运动而产生,参考长度通常取平均气动弦长,参考时间取扑动周期,参考速度需要根据飞行情况和翼的运动规律来决定。
悬停飞行时,参考速度取翼尖平均速度。此时,雷诺数的形式如公式(2)所示,与扑动幅度、扑动频率、平均气动弦长的平方及展弦比成正比。
式中:AR为展弦比,Φ为扑动幅度,f为扑动频率,cm为平均气动弦长。
前飞时,参考速度有多种考虑,可以用前飞速度或者翼尖平均扑动速度。当选择前飞速度作为参考速度时,雷诺数的形式如公式(3)所示,正比于平均气动弦长和飞行速度,与扑动频率和扑动幅度无关。
式中:U∞为前飞速度或来流速度。
(2) 斯特劳哈尔数St描述的是前飞速度和扑动速度的比值。该参数描述了飞行中涡量脱落的效果[6]。对于扑翼飞行,该参数定义为:
从定义可以看出,该参数可以作为扑翼前飞时推进效率的度量。
(3)减缩频率k描述的是扑动运动的非定常度,含义为流体扰动的空间尺度与弦长的比较[7]。定义为:
当参考翼尖平均速度时,减缩频率可以表示为:
注意到该定义中减缩频率和扑动幅度及展弦比成反比,和扑动频率无关。
当参考前飞速度时,减缩频率可以表达为:
此时,减缩频率正比于扑动频率和平均气动弦长,与飞行速度成反比。前飞速度作为参考值时,减缩频率和斯特劳哈尔数的关系为:
总的来说,在几何相似的前提下,基于2种参考速度的扑翼飞行尺度律如表 1所示。可以根据表 1各个参数的依赖关系来研究其影响规律。
| 无量纲参数 |
参考翼尖扑动速度 Uref=Utip | 参考前飞速度 Uref=U∞ | |||
| 长度 | 频率 | 长度 | 频率 | 速度 | |
| 雷诺数Re | c2m | f | cm | 无关 | U∞ |
| 斯特劳哈尔数St | 无关 | 无关 | cm | f | U-1∞ |
| 减缩频率k | 无关 | 无关 | cm | f | U-1∞ |
自然界飞行生物利用高效飞行机制同时产生升力和推力来飞行。影响这些机制的主要因素包括流动产生的涡的脱落方式,翼的外形及结构的柔性,需要深入分析翼涡交互作用及流固耦合的影响关系。本节总结了文献中提到较多的非定常流动机理。
(1) 拍-挥机制Weis-Fogh[8]提出了昆虫产生高升力机制。通过观察一种小蜂的飞行得知,小蜂首先将两翅拍到一起,然后再迅速挥动开,使得空气可以充满间隙。基于定常估算,该蜂翅膀产生的升力不可能支持其飞行。Weis-Fogh认为在挥动运动中,翅膀快速打开后,绕翅膀的空气形成了环量产生了升力,如图 1所示。Lighthill[9]通过理论分析,Lehmann[10]通过试验验证了该现象,还有数值模拟的研究成果也证明了该机理[11]。拍-挥机制增强升力主要依靠扑动运动,可有效利用能量,自然界很多生物都依靠这种机制产生升力,如飞蛾、蝴蝶、果蝇等[12]。
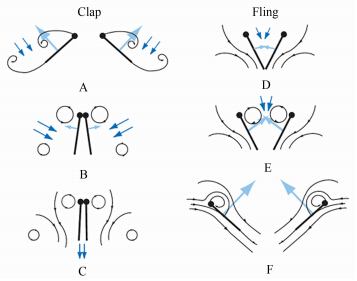 |
| 图 1 扑翼的拍-挥机制 Fig 1 Clap-fling mechanism of flapping wing |
Dickinson等[13]发现,在每次扑动结束时刻,昆虫的扑翼通常会有一个快速旋转的运动,可增强气动力,如图 2所示。通过控制平移运动和旋转运动的相位差来实现,如果在扑动运动结束前就朝正确方向快速翻转即可有效增强升力,称为提前旋转。如果推后旋转,则会减小升力[14],快速的旋转可以有效增加升力[15]。
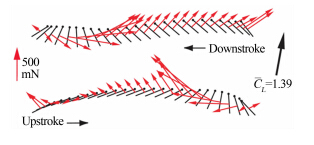 |
| 图 2 扑翼的快速旋转机制 Fig 2 Rapid pitch rotation of flapping wing |
Ellington等[16]提出前缘涡导致的失速延迟可以显著增强扑翼产生的升力。他观察到鹰蛾翅膀上的失速涡在整个拍动过程中均不脱落。前缘涡使得翼面产生低压区,对翼表面产生吸力因而可以增加升力,如图 3所示。但前缘涡受到很多参数的影响,雷诺数、减缩频率、斯特劳哈尔数、翼的柔性以及扑动规律等。Rival等[17]利用PIV方法试验研究了雷诺数为30000时前缘涡和运动参数的相关性,研究发现细致调节扑翼的运动规律可以保持前缘涡稳定,从而延迟失速,展向流动为稳定前缘涡做出了相当的贡献。
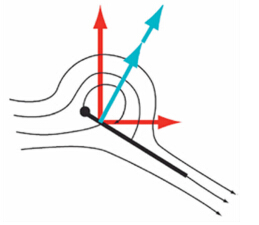 |
| 图 3 前缘涡增加升力的机理 Fig 3 Lift enhancement of leading edge vortex |
尾迹捕捉机制通常可以在翼涡交互作用中观察到,当扑翼转换扑动方向时,会遇到前次扑动产生的涡,导致翼面流动速度增加并产生额外的升力峰值。研究表明,尾迹捕捉的效果和涡量的分布与大小的时间变化规律有关[18]。Wang[19]和Shyy等[20]利用二维翼型的数值模拟分析了尾迹捕捉的升力增强原理,如图 4所示。
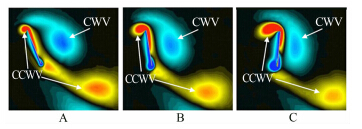 |
| 图 4 尾迹捕捉机制 Fig 4 Wake capture mechanism |
扑动反向时,受到惯性力的作用,扑翼会扭转变形产生一个类似被动俯仰的运动。该俯仰现象与扑动运动的相位对比可以分为延迟、同步和提前这3种模式。研究发现扑动频率和结构固有频率决定了被动俯仰的模式。当扑动频率小于固有频率时,扑翼为提前俯仰模式。这种情况下,2个扑动周期间的尾迹交互作用可对升力起到增强作用[21]。在二维翼型的流动结构中可以观察到,发生被动俯仰的柔性翼表面的前缘涡比刚性翼保持得更久[22],如图 5所示。
 |
| 图 5 被动俯仰机制(左列为柔性翼,右列为刚性翼) Fig 5 Passive pitching mechanism (left column is flexible wing,and right column is rigid wing) |
对于有限翼展的固定翼来说,翼尖涡会造成升力损失和阻力增加[23]。然而非定常流动中,翼尖涡在翼尖附件产生一个低压区,和前缘涡产生一定交互作 用,不断脱落构成各种结构的涡系。在扑翼悬停飞行 中,以特定的方式扑动,则可以使翼尖涡产生好的影响,如图 6所示的翼尖涡有效增强了升力。
 |
| 图 6 翼尖涡的增升作用 Fig 6 Lift enhancement of tip vortex |
对生物飞行空气动力学的研究有助于人们深入理解扑翼飞行的气动机理,这是成功研制高性能仿生扑翼飞行器的关键之一。早在1984年,Ellington[24]就详细解释和证明了准定常空气动力学不能完全解释昆虫的飞行机理,并通过记录多个物种的形态学和运动学数据,证明了昆虫飞行过程中存在非定常高升力机制。
对昆虫飞行空气动力学机理的实验研究是扑翼非定常空气动力学研究的开始。
1997年,Willmott等[25]利用带有点燃的烟苗的立体摄影技术,通过4个高倍的频闪观测仪来捕捉天蛾翅膀的非定常空气流动。从拍到的照片能够观察到天蛾飞行过程中产生的涡,从而解释天蛾飞行的非定常空气动力效应。同年,Van den Berg和Ellington[26]为了研究天蛾飞行时产生的尾涡结构,利用一个带有扑动机构的天蛾模型模拟了其悬停运动。随后他们又对天蛾飞行过程中产生的三维前缘涡进行研究,发现前缘涡的形成和发展是天蛾产生高升力的主要原因[27]。1999年,Ellington[28]总结了之前的研究工作,进一步探讨了非定常流动机理在微型扑翼飞行器中的应用。同年,Dickinson等[13]研究了昆虫飞行中翅膀旋转运动与非定常气动力产生之间的关系。2001年,Birch等[29]通过实验研究发现了昆虫飞行中的另外一个流动特性:展向流动和前缘涡的再附着。他们通过可靠的实验结果否定了之前的关于昆虫飞行中产生的前缘涡再附着现象与三角翼飞机中的流动机制类似的假设。这是昆虫空气动力学领域一个很重要的发现。2004年,Dickson等[30]通过对昆虫悬停过程采用准定常假设,研究了前进比对昆虫气动特性的影响。2005年,Fry等[31]制作出了模拟昆虫运动的扑翼飞行器,并且成功估算出了其飞行时的空气动力载荷。
在对昆虫非定常空气动力学进行理论研究的同时,人们也利用日益成熟的风洞实验技术对昆虫飞行时的流动细节进行测量,从而进一步加深了对昆虫飞行机理的理解。2005年,Lehmann等[32]使用数字粒子图像测速技术(DPIV)研究了昆虫做翻转运动时产生的高升力机理。Poelma等[33]将流场可视化工作进一步推广到重建昆虫运动的瞬时全场流动速度。他们利用现代的电机驱动、力测量以及流动可视化技术对低雷诺数昆虫飞行空气动力学进行了系统的研究。
由于对动物的飞行实验研究需要活的动物标本,而且所需的实验条件也很复杂,所以人们在之前对飞行动物空气动力特性的研究基础上,开始制作简化的扑翼飞行器模型来测量其气动特性。
2003年,Mueller等[34]总结了微型扑翼飞行器的一般空气动力学特性,包括各种实际扑翼飞行器模型和实验测量方法。Rozhdestvensky等[35]研究了微型扑翼飞行器运动的空气动力推进机理。2004年,Heathcote等[36]研究了在无自由来流情况下的柔性翼型的俯仰/沉浮运动所产生的推力特性。2005年,Tarascio等[37]实现了模仿昆虫悬停的扑动机构,并且用实验测量出了其流场特性,但是最终只得到了定性的结果。2006年,Lu等[38]利用DPIV技术研究证实了扑翼前缘涡与升力产生间的关系。研究涵盖了不同展弦比、迎角和低雷诺数范围,研究数据为以后微型扑翼飞行器空气动力学研究提供了重要参考。
国内对微型扑翼气动特性的研究开展得比国外要晚,主要开始于2000年后。但通过最近几年科研人员的努力工作,也取得了不凡的成果。
2003年,南京航空航天大学曾锐等[39]根据绿头鸭飞行的录像片断,对其平飞时翅膀的扑动模型进行简化,较详细地分析了扑翼平均升力系数随着扑动幅度、俯仰幅度以及扑动频率等各种扑动参数的变化曲线,为微型扑翼机的设计提供了一定的参考依据。
2007年,西北工业大学邵立民等[40]利用西北工业大学微型飞行器专用风洞对微型扑翼飞行器机翼进行初步风洞试验。2008年,王利光[41]对扑翼风洞试验系统进行了改进,能够对扑翼的气动、动力、能源等系统进行实验测量与分析。2014年,王利光等进一步改进扑翼风洞试验系统,提高了测量精度,并实现了与DIC系统的融合与同步测量,开展了柔性扑翼变形与气动特性对应关系的研究[42, 43, 44]。 4 扑翼飞行空气动力学数值模拟研究
20世纪90年代以来,随着计算机技术的飞速发展,数值模拟方法也在微型扑翼空气动力学研究中发挥了越来越重要的作用。
1996年,Vest等[45]利用非定常气动模型数值模拟了微型扑翼的推力特性;Smith等[46]利用面元法数值模拟了刚性扑翼产生的大尺度尾涡结构以及气动力,并且证明了此方法优于准定常方法。1998年,Liu等[47]通过求解基于时间推进的三维非定常Navier-Stokes方程,数值模拟了昆虫的非定常流场结构,并且与实验值进行比较,分析发现在昆虫飞行的低雷诺数范围内翼尖前缘涡对“高升力”的产生起非常重要的作用。2002年,Ramamurti等[48]利用基于有限元方法的求解器数值模拟了果蝇的三维非定常流动特性,计算结果与相关实验值吻合良好。2004年,Wu等[49]通过数值求解三维非定常Navier-Stokes方程模拟了果蝇的非定常气动力;Fritz等[50]利用非定常涡方法计算了有限翼展机翼做俯仰、沉浮运动时非定常气动特性。
国内对微型扑翼的气动特性数值模拟研究工作也取得了不小的进展。
2002年北京航空航天大学流体力学研究所的孙茂[51]利用N-S方程数值模拟方法,采用全层流假设,对昆虫的飞行机理以及高升力产生机理进行了深入细致的研究。
2003年南京航空航天大学的曾锐、昂海松等提出了一种新的变速-折叠扑翼仿鸟扑动模型。通过非定常涡格法的计算研究表明,在一个周期内,新扑翼模型的平均升力系数较原有的匀角速度刚性模型有显著增加[39]。随后,曾锐等又在原有扑翼刚性匀速运动模型基础上,加入了扑动速率变化和形状变化,使之更接近鸟翼真实飞行情况。通过计算发现,柔性变形对扑翼的升力和推力有着显著的影响,如果柔性变形控制得当,可以大大改善扑翼的气动特性[52]。2007年,昂海松等利用风洞实验和模型飞行实验的方法,探讨了柔性扑翼微型飞行器产生升力和推力的流动机理,并研究了不同扑动频率、迎角、速度下扑翼升力和推力的变化情况,为微型扑翼机的设计研制提供了参考依据[53]。
自2000年以来,西北工业大学针对微型扑翼飞行器的研究开展了许多工作。2003年,龚凯等利用求解Euler方程的方法建立了一套扑翼气动特性的计算程序,在此基础上研究了不同参数对扑翼的气动特性的影响[54]。2006年,杨淑利等根据微型扑翼产生升力和推力的机理,利用改进的片条理论方法建立了一套扑翼气动特性的工程估算软件,并通过风洞实验验证了估算软件的可靠性,在此基础上研究了不同扑翼形状下扑翼的气动特性[55]。2007年,何飞等通过对XFOIL程序进行改造和扩充,完成了对振荡来流下柔性翼型的气动特性的研究,并通过求解N-S方程研究了三维柔性固定翼的气动特性[56]。2008年,谢辉等[57]发展了一套基于广义无限插值理论的扑翼运动网格自动生成程序,并且应用有限体积法结合双时间推进技术数值求解了预处理后的三维非定常N-S方程组,实现微型扑翼在低速、低雷诺数下粘性绕流的数值模拟。2010年,杨文青等随后发展了基于距离减缩法的嵌套网格技术,实现了对微型扑翼全机绕流特性的数值模拟[58, 59, 60]。2013年,陈利丽[61]在此基础上,嵌入了适用性更强的k-ω SST湍流模型模块和精度更高的高分辨率空间离散格式,提高了对扑翼绕流数值模拟的精度。 5 扑翼气动结构耦合研究
昆虫和鸟类的翅膀在飞行过程中常常会产生显著的柔性变形,如图 7所示,这主要是通过翅膀的关节运动或肌肉收缩来控制的:昆虫通过调节内部压力从而改变翅膀刚度;蜂鸟通过控制羽毛的分布改变翅膀的平面形状来获得所需的升力;瓢虫利用其柔软并且可折叠的翅膀,在飞行时产生一定的“拱形”翅膀剖面来提高升力特性。
 |
| 图 7 飞行生物翅膀柔性变形 Fig 7 Flexible wings of natural flyers |
对于人造微型扑翼飞行器来说,也可以考虑利用结构的柔性变形来提高气动特性。国内外研究学者分别通过实验和计算2种方法对微型扑翼飞行器气动结构耦合特性进行了一些研究。
Heathcote等[62]通过实验方法对做沉浮运动的柔性扑翼刚度对推力特性的影响进行了研究,结果表明,与刚性扑翼相比,柔性扑翼能够产生更大的推力,并通过水洞实验对半展弦比为3,做沉浮运动的NACA0012矩形机翼气动特性进行测量,发现展向柔性变形能够显著提高扑翼的推力。
Frampton等[63]通过实验方法研究了产生最佳推力特性的柔性扑翼展向弯曲变形与弦向扭转变形之间的关系,发现柔性弯曲和扭转变形的相位关系对于推力特性的产生是至关重要的,当扭转变形滞后弯曲变形90°时,能够产生最大的推力。
Singh等[64, 65]利用自行开发的实验装置和仿生扑动机构来测量机翼结构的推力特性,结果表明,在其实验状态范围内,惯性力对机翼结构变形起主导作用。由此说明,在相关气动结构耦合研究中考虑惯性力的影响是非常必要的。
Wu等[66]发展了一种多学科耦合实验方法,测量了6副不同结构(每副机翼均为板条-薄膜结构)的微型扑翼做单自由度扑动运动时的气动弹性响应和气动特性。通过数字图像关联系统测量结构变形,通过载荷传感器记录作用于扑翼上的气动载荷,利用数字粒子图像测速技术(DPIV)测量流场特性。他们的研究结果表明,不同的机翼结构之间的气动弹性特性差异是很大的,通过适当的柔性结构变形,能够获得更好的气动特性。
国内外研究者不仅在扑翼气动弹性实验方面进行了一些研究工作,而且在数值模拟方面也取得了一定的进展。
Hamamoto等[67]采用有限元方法数值模拟了蜻蜓悬停时的气动结构耦合特性,对柔性结构的利弊进行了初步探讨。
Zhu等[68]发展了一套基于三维边界元法和二维非线性薄钢板结构动力学模型方法的气动结构耦合分析求解器,并将数值模拟结果与Heathcote[62]做沉浮运动的柔性扑翼实验结果进行对比,验证了算法的正确性。他还分析了惯性载荷在机翼柔性结构变形中所起的作用,并且探讨了展向柔性变形和弦向柔性变形对气动力的影响,结果表明,展向柔性结构变形能够明显提高扑翼的推力特性。
Liani等[69]发展了一套基于非定常面元法和二维结构动力学方程的气动结构耦合求解器,研究了不同频率下柔性扑翼的气动弹性响应,通过对做沉浮运动的碳纤维平板矩形机翼在不同频率下的气动结构耦合特性进行数值计算,发现在计算考虑的所有频率范围内,柔性结构变形对扑翼气动特性有显著影响。
Kim等[70]提出了一种采用基于修正的片条理论模型作为气动分析工具的气动结构耦合研究方法。该模型能够考虑大迎角和动态失速的影响。利用该方法对矩形直机翼的气动结构耦合特性进行了数值模拟,其结果与实验值吻合良好,从而验证了算法的可靠性。
Unger等[71]发展了一套基于非定常雷诺平均N-S方程和非线性结构有限元方法的扑翼气动结构耦合求解器,研究了固定展向刚度、仅保持弦向柔性特性的沉浮/俯仰运动扑翼的气动结构耦合特性,发现柔性扑翼模型的上下表面层流分离泡从后缘有向前缘移动的趋势。
西北工业大学针对微型扑翼气动结构耦合特性开展了一些研究工作。杨文青等[72]发展了基于非定常雷诺平均N-S方程和静态结构有限元方法的气动结构耦合求解器,初步研究了考虑柔性变形的微型扑翼气动特性。陈丽利等[73, 74]进一步发展了基于结构动力学方法的扑翼CFD/CSD耦合求解程序,通过考虑惯性力的影响,更准确地模拟柔性扑翼的气动结构特性。 6 结 论
本文综述了仿生微型扑翼飞行器相关的空气动力学研究进展,并重点分析了柔性扑翼飞行的气动结构耦合特性研究。总的来说,尽管目前相关的研究手段及气动机理等方面已经取得了相当显著的进展,然而在进一步研究高性能的仿生微型扑翼飞行器,分析其同时产生升力和推力、可悬停、高机动飞行,同时又节约能量的种种优越特性时,研究者需要开展扑翼流固耦合特性及相关的非定常空气动力学等所必须的试验、计算与理论分析,更进一步的研究具体体现在以下4个方面:
(1) 仿生微型扑翼飞行器小尺度与低速度带来的低雷诺数空气动力学问题,同时扑翼与柔性翼还带来了非定常流动问题。微型飞行器所处的雷诺数为103~105量级,根据Mueller[75]的研究,属于对转捩与湍流非常敏感的区域,相关的气动机理复杂。
(2) 微型柔性翼在飞行中密切相关的动气动弹性问题。柔性变形可以显著影响柔性翼的气动特性,包括固定翼和扑翼,在飞行中产生特殊的气动现象,如柔性固定翼的后缘振动及柔性扑翼的大幅度动态变形。当飞行器的尺度改变时,由于柔性结构特性使得尺度参数不能同时保证。所以为了开展精确的测试,很多研究都无法采用缩比模型研究,研究受到很多限制。因此建立准确的计算模型就显得十分重要,且更适合用于优化设计和增强鲁棒性的研究。
(3) 高机动性的研究,及其带来的动气动弹性耦合飞行力学问题。包括起飞、不同速度前飞、突风响应、悬停、栖息、威胁躲避、位置跟踪、载荷变化等情况,需同时考虑身体和翼的相对运动变化。可借鉴自然界生物的尺度和扑动模式的变化,需在运动规律与气动特性的影响方面进行深入研究并加深理解。
(4) 扑翼飞行的动力学和稳定性影响,对应的闭环主动控制,以达到所需的气动性能,减少扰动对飞行的影响。扑翼飞行的复杂姿态及产生的气动力对飞控系统的挑战及反馈耦合算法的设计等。自适应控制技术对扑翼飞行性能有重要意义,该技术需要大量的数据,此时还需要建立合适的代理模型来估算柔性扑翼的气动力。
这些层层深入的多学科耦合难题导致了目前具备的研究手段不能为仿生微型扑翼飞行器的研究提供定量的分析与改进设计。在解决上述难题的基础上,未来可进一步在高机动灵活飞行姿态方面进行深入研究,对柔性翼的刚度分布开展详细设计,使仿生飞行器具有像自然界飞行生物一样的主动变形能力,可在复杂的环境下具备高机动飞行能力,最终实现高仿生外形和性能的人造飞鸟或人造飞虫。
以上分析可以看出,目前的成果像是冰山一角般揭开了仿生扑翼飞行相关研究的序幕,未来需要科研工作者积极探索,开展更加深入的研究。
| [1] | Hundley R O, Gritton E C. Future technology-driven revolutions in military operations[R]. Documented Briefing of the RAND National Defense Research Institute. December, 1992. |
| [2] | Steven A S. Palm-size spyplane[J]. Mechanical Engineering, 1998, 11(3): 74-78. |
| [3] | Shyy W, Lian Y, Tang J, et al. Aerodynamics of low Reynolds number flyers[M]. New York: Cambridge University Press, 2008. |
| [4] | Shyy W, Berg M, Ljungqvist D. Flapping and flexible wings for biological and micro air vehicles[J]. Progress in Aerospace Sciences, 1999, 35(5): 455-505. |
| [5] | Shyy W, Aono H, Chimakurthi S K, et al. Recent progress in flapping wing aerodynamics and aeroelasticity[J]. Progress in Aerospace Sciences, 2010, 46(8): 284-327. |
| [6] | Triantafyllou M S, Triantafyllou G S, Yue D K P. Hydrodynamics of fishlike swimming[J]. Annual Review of Fluid Mechanics, 2000, 32: 33-53. |
| [7] | Christensen R M. Mechanics of composite materials[M]. Reprinted. New York: Dover Publications Inc, 2005. |
| [8] | Weis-Fogh T. Quick estimates of flight fitness in hovering animals, including novel mechanism for lift production[J]. Journal of Experimental Biology, 1973, 59: 169-230. |
| [9] | Lighthill M J. On the weis-fogh mechanism of lift generation[J]. Journal of Fluid Mechanics, 1973, 60: 1-17. |
| [10] | Lehmann F O, Sane S P, Dickinson M H. The aerodynamic effects of wing-wing interaction in flapping insect wings[J]. Journal of Experimental Biology, 2005, 208: 3075-3092. |
| [11] | Sun M, Yu X. Flows around two airfoils performing fling and subsequent translation and translation and subsequent clap[J]. Acta Mechanica Sinica, 2003, 19(2): 103-117. |
| [12] | Srygley R B, Thomas A L R. Unconventional lift-generating mechanisms in free-flying butter flies[J]. Nature, 2002, 420: 660-664. |
| [13] | Dickinson M H, Lehmann F O, Sane S P. Wing rotation and the aerodynamic basis of insect flight[J]. Science, 1999, 284(5422): 1954-1960. |
| [14] | Sane S P, Dickinson M H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight[J]. Journal of Experimental Biology, 2002, 205: 1087-1096. |
| [15] | Sun M, Tang J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J]. Journal of Experimental Biology, 2002, 205: 55-70. |
| [16] | Ellington C P, vanden Berg C, Willmott A P, et al. Leading-edge vortices in insect flight[J]. Nature, 1996, 384: 626-630. |
| [17] | Rival D, Prangemeier T, Tropea C. The influence of airfoil kinematics on the formation of leading-edge vortices in bio-inspired flight[J]. Experiments in Fluids, 2009, 46: 823-833. |
| [18] | Birch J M, Dickinson M H. The influence of wing-wake interactions on the production of aerodynamic forces in flapping flight[J]. Journal of Experimental Biology, 2003, 206: 2257-2272. |
| [19] | Wang Z J. Dissecting insectflight[J]. Annual Review of Fluid Mechanics, 2005, 37: 183-210. |
| [20] | Shyy W, Trizila P, Kang C, et al. Can tip vortices enhance lift of a flapping wing?[J]. AIAA Journal, 2009, 47(2): 289-293. |
| [21] | Ishihara D, Horie T, Denda M. A two-dimensional computational study on the fluid-structure interaction cause of wing pitch changes in dipteran flapping flight[J]. Journal of Experimental Biology, 2009, 212: 1-10. |
| [22] | Vanella M, Fitzgerald T, Preidikman S, et al. Influence of flexibility on the aerodynamic performance of a hovering wing[J]. Journal of Experimental Biology, 2009, 212: 95-105. |
| [23] | Anderson J D. Fundamentals of aerodynamics[M]. 4th Ed. New York: McGraw Hill Higher Education, 2006. |
| [24] | Ellington C P. The aerodynamics of hovering insect flight III[J]. Kinematics, Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 1984, 305(1122): 41-78. |
| [25] | Willmott A P, Ellington C P, Thomas A L R. Flow visualization and unsteady aerodynamics in the flight of the hawkmoth, manduca sexta[J]. Biological Sciences, 1997, 352(1351): 303-316. |
| [26] | Van den Berg C, Ellington C P. The vortex wake of a hovering model hawkmoth[J]. Biological Sciences, 1997, 352(1351): 317-328. |
| [27] | Van Den Berg C, Ellington C P. The three-dimensional leading-edge vortex of a 'hovering'model hawkmoth[J]. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 1997, 352(1351): 329-340. |
| [28] | Ellington C P. The novel aerodynamics of insect flight: applications to micro-air vehicles[J]. Journal of Experimental Biology, 1999, 202(23): 3439-3448. |
| [29] | Birch J M, Dickinson M H. Spanwise flow and the attachment of the leading-edge vortex on insect wings[J]. Nature, 2001, 412(6848): 729-733. |
| [30] | Dickson W B, Dickinson M H. The effect of advance ratio on the aerodynamics of revolving wings[J]. Journal of Experimental Biology, 2004, 207(24): 4269-4281. |
| [31] | Fry S N, Sayaman R, Dickinson M H. The aerodynamics of hovering flight in Drosophila[J]. Journal of Experimental Biology, 2005, 208(12): 2303-2318. |
| [32] | Lehmann F O, Sane S P, Dickinson M. The aerodynamic effects of wing-wing interaction in flapping insectwings[J]. Journal of Experimental Biology, 2005, 208(16): 3075-3092. |
| [33] | Poelma C, Dickson W B, Dickinson M H. Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing[J]. Experiments in Fluids, 2006, 41(2): 213-225. |
| [34] | Mueller T J, DeLaurier J D. Aerodynamics of small vehicles[J]. Annual Review of Fluid Mechanics, 2003, 35(1): 89-111. |
| [35] | Rozhdestvensky K V, Ryzhov V A. Aerohydrodynamics of flapping-wing propulsors[J]. Progress in Aerospace Sciences, 2003, 39(8): 585-633. |
| [36] | Heathcote S, Martin D, Gursul I. Flexible flapping airfoil propulsion at zero freestream velocity[J]. AIAA Journal, 2004, 42(11): 2196-2204. |
| [37] | Tarascio M J, Ramasamy M, Chopra I, et al. Flow visualization of micro air vehicle scaled insect-based flapping wings[J]. Journal of Aircraft, 2005, 42(2): 385-390. |
| [38] | Lu Y, Shen G X, Lai G J. Dual leading-edge vortices on flapping wings[J]. Journal of Experimental Biology, 2006, 209(24): 5005-5016. |
| [39] | 曾锐, 昂海松. 仿鸟复合振动的扑翼气动分析[J]. 南京航空航天大学学报, 2003, 35(1): 6-12. Zeng Rui, Ang Haisong. Aerodynamic computation of flapping-wing simulating bird wings[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2003, 35(1): 6-12. |
| [40] | 邵立民, 宋笔锋, 熊超, 等. 微型扑翼飞行器风洞试验初步研究[J]. 航空学报, 2007, 28(2): 275-280. Shao Limin, Song Bifeng, Xiong Chao, et al. Experimental investigation of flapping-wing MAV in wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 275-280. |
| [41] | 王利光. 微型扑翼飞行器动力系统设计与优化[D]. 西安: 西北工业大学, 2008. Wang Liguang. Design and optimization for the propulsion system of the flapping-wing micro airvehicle[D]. Xi'an: Northwestern Polytechnical University, 2008. |
| [42] | Wang L, Song B, Yang W, et al. Experimental characterization of a flexible membrane flapping-wing in forward flight[C]. ICAS2014. St. Petersburg. Russia, Sep 7-12, 2014. |
| [43] | Yang W, Song B, Song W, et al. Aerodynamic research of flexible flapping wing by combining DIC and CFD approaches[C]. ICAS2014. St. Petersburg. Russia, Sep 7-12, 2014. |
| [44] | Fu P, Song B, Wang L. An experimental study on the influence of passive deformation to lift and thrust generation in flexible flapping wing[C]. ICAS2014. St. Petersburg. Russia, Sep 7-12, 2014. |
| [45] | Vest M S, Katz J. Unsteady aerodynamic model of flapping wings[J]. AIAA Journal, 1996, 34(7): 1435-1440. |
| [46] | Smith M, Wilkin P, Williams M. The advantages of an unsteady panel method in modelling the aerodynamic forces on rigid flapping wings[J]. Journal of Experimental Biology, 1996, 199(5): 1073-1083. |
| [47] | Liu H, Kawachi K. A numerical study of insect flight[J]. Journal of Computational Physics, 1998, 146(1): 124-156. |
| [48] | Ramamurti R, Sandberg W C. A three-dimensional computational study of the aerodynamic mechanisms of insect flight[J]. Journal of Experimental Biology, 2002, 205(10): 1507-1518. |
| [49] | Wu J H, Sun M. Unsteady aerodynamic forces of a flapping wing[J]. Journal of Experimental Biology, 2004, 207(7): 1137-1150. |
| [50] | Fritz T E, Long L N. Object-oriented unsteady vortex lattice method for flapping flight[J]. Journal of Aircraft, 2004, 41(6): 1275-1290. |
| [51] | 孙茂. 昆虫飞行的高升力机理[J]. 力学进展, 2002, 32(3): 425-434. Sun Mao. Unsteady lift mechanisms in insect flight[J]. Advances in Mechanics, 2002, 32(3): 425-434. |
| [52] | 曾锐, 昂海松, 梅源, 等. 扑翼柔性及其对气动特性的影响[J]. 计算力学学报, 2005, 22(6): 750-754. Zeng Rui, Ang Haisong, Mei Yuan, et al. Flexibility of flapping wing and its effect on aerodynamic characteristic[J]. Chinese Journal of Computational Mechanics, 2005, 22(6): 750-754. |
| [53] | 昂海松, 曾锐, 段文博, 等. 柔性扑翼微型飞行器升力和推力机理的风洞实验和飞行实验[J]. 航空动力学报, 2007, 22(11): 1838-1845. Ang Haisong, Zeng Rui, Duan Wenbo, et al. Aerodynamic experimental investigation for mechanism of lift and thrust of flexible flapping-wing MAV[J]. Journal of Aerospace Power, 2007, 22(11): 1838-1845. |
| [54] | 龚凯. 有限翼展扑动翼的欧拉方程数值模拟[D]. 西安: 西北工业大学, 2003. Gong Kai. Numerical simulation of finite-span flapping wing by euler equations[D]. Xi'an: Northwestern Polytechnical University, 2003. |
| [55] | 杨淑利, 宋文萍, 宋笔锋, 等. 微型扑翼飞行器机翼气动特性研究[J]. 西北工业大学学报, 2006, 24(6): 768-773. Yang Shuli, Song Wenping, Song Bifeng, et al. Achieving reliability and validity of predicted aerodynamic performance of flapping wings for micro air vehicle (MAV)[J]. Journal of Northwestern Polytechnical University, 2006, 24(6): 768-773. |
| [56] | 何飞. 微型飞行器柔性翼气动及抗风特性研究[D]. 西安: 西北工业大学, 2007. He Fei. Aerodynamics and anti-gust research of flexible-wing MAV[D]. Xi'an: Northwestern Polytechnical University, 2007. |
| [57] | 谢辉, 宋文萍, 宋笔锋. 微型扑翼绕流的N-S方程数值模拟[J]. 西北工业大学学报, 2008, 26(1): 104-109. Xie Hui, Song Wenping, Song Bifeng. Numerical solution of Navier-Stokes equations for flow over a flapping wing[J]. Journal of Northwestern Polytechnical University, 2008, 26(1): 104-109. |
| [58] | 杨文青, 宋笔锋, 宋文萍. 翼型对微型扑翼气动特性影响研究[J]. 计算力学学报, 2011, 28(2): 214-220. Yang Wenqing, Song Bifeng, Song Wenping. The effect of airfoil to aerodynamic characteristics of flapping wing by numerical simulation on Navier-Stokes equations[J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 214-220. |
| [59] | 杨文青, 宋笔锋, 宋文萍, 等. 微型扑翼低雷诺数绕流气动特性研究[J]. 空气动力学学报, 2011, 29(1): 32-38. Yang Wenqing, Song Bifeng, Song Wenping, et al. Aerodynamic performance research of micro flapping-wing in low Reynolds number flow[J]. Acta Aerodynamica Sinica, 2011, 29(1): 32-38. |
| [60] | 杨文青, 宋笔锋, 宋文萍. 高效确定重叠网格对应关系的距离减缩法及其应用[J]. 航空学报, 2009, 30(2): 205-212. Yang Wenqing, Song Bifeng, Song Wenping. Distance decreasing method for confirming corresponding cells of overset grids and its application[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(2): 205-212. |
| [61] | 陈利丽. 微型扑翼气动结构耦合计算及优化设计研究[D]. 西安: 西北工业大学, 2013. Chen Lili. Aeroelastic analysis and optimization of flapping-wing micro air vehicle by numerical simulation[D]. Xi'an: Northwestern Polytechnical University, 2013 |
| [62] | Heathcote S, Wang Z, Gursul I. Effect of spanwise flexibility on flapping wing propulsion[J]. Journal of Fluids and Structures, 2008, 24(2): 183-199. |
| [63] | Frampton K D, Goldfarb M, Monopoli D, et al. Passive aeroelastic tailoring for optimal flapping wings[J]. Progress in Astronautics and Aeronautics, 2001, 195: 473-482. |
| [64] | Singh B, Chopra I. Insect-based flapping wings for micro hovering air vehicles: experimental investigations[C]. American Helicopter Society International Specialists Meeting on Unmanned Rotorcraft, Arizona, 2004. |
| [65] | Singh B, Chopra I. Dynamics of insect-based flapping wings: Loads validation[R]. AIAA-2006-1663. |
| [66] | Wu P, Ifju P, Stanford B, et al. A multidisciplinary experimental study of flapping wing aeroelasticity in thrust production[C]. AIAA Structures, Structural Dynamics, and Materials Conference, 2009: 4-7. |
| [67] | Hamamoto M. Application of fluid-structure interaction inalysis to flapping flight of insects with deformable wings[J]. Advanced Robotics, 2007, 21(1-2): 1-21. |
| [68] | Zhu Q. Numerical simulation of a flapping foil with chordwise or spanwise flexibility[J]. AIAA Journal, 2007, 45(10): 2448-2457. |
| [69] | Liani E. Aeroelastic effect on flapping wing performance[R]. AIAA-2007-2412. |
| [70] | Kim D K, Lee J S, Lee J Y, et al. Anaeroelastic analysis of a flexible flapping wing using modified strip theory[C]. International Society for Optical Engineering (SPIE), 2008. |
| [71] | Unger R, Haupt M C, Horst P, et al. Structural design and aeroelastic analysis of an oscillating airfoil for flapping wing propulsion[R]. AIAA-2008-306. |
| [72] | Yang W, Song B, Song W. Fluid-structure coupling research for micro flapping-wing[C]. ICAS2010. Nice, France. Sep, 19-24, 2010. |
| [73] | 陈利丽, 宋笔锋, 宋文萍, 等. 基于结构动力学的平板扑翼气动弹性方法研究[J]. 空气动力学学报, 2013, 31(2): 175-180. Chen Lili, Song Bifeng, Song Wenping, et al. Dynamic fluid-structure coupling research for micro flapping wing[J]. Acta Aerodynamica Sinica, 2013, 31(2): 175-180. |
| [74] | 陈利丽, 宋笔锋, 宋文萍, 等. 一种基于结构动力学的柔性扑翼气动结构耦合方法研究[J]. 航空学报, 2013, 34(12): 2668-2681. Chen Lili, Song Bifeng, Song Wenping, et al. Research on aerodynamic-structural coupling of flexible flapping wing[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(12): 2668-2681. |
| [75] | Mueller T J. Aerodynamic measurements at low Reynolds numbers for fixed wing micro-air vehicles[C] //Development and Operation of UAVs for Military and Civil Applications. VKI, Belgium, September 13-17, 1999. |