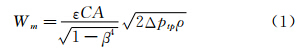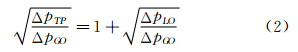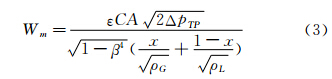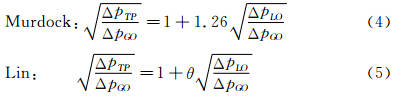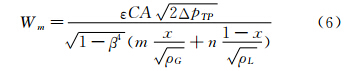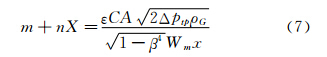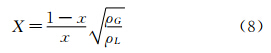气液两相流广泛存在于化工、动力、航空航天、油气开采与输送等领域,其参数的传感与测量是工业系统中难以回避的一个难题。几十年来,国内外科技工作者在解决两相流流动参数的检测问题上开展了大量的理论与实验研究,诸多传统单相流传感方法及新方法、技术被尝试用于气液两相流参数的测量[1, 2, 3, 4, 5, 6, 7]。差压式流量计由于具有结构简单,安装方便等优点,利用传统差压式流量计结合两相流测量模型的方法成为气液两相流参数测量的重要方法之一,Huang等[8]利用文丘里管结合电容层析成像技术对油气两相流进行了测量研究,实现了流型及分相含率的测量;Fang等[9]提出了一种狭缝文丘里气液两相流测量系统,实现了不同流型下气液两相流流量的测量;Dong等[10]利用内锥式流量计实验修正了气液两相流模型,实现了两相流流量的测量。虽然众多学者致力于气液两相流测量的研究,但是成功商业化的产品非常少,还无法满足实际工业应用的需求。因此,有必要对气液两相流参数尤其是流量的测量进行进一步的研究。
本文提出一种双锥结构的新型流量测量方法,设计并加工直径比分别为0.5、0.6、0.7、0.8和0.9的双锥流量计。Liang等[11]对其进行了单相流仿真与实验研究,结果表明其具有量程比大,直管段要求短,压损小等优点。本文在50mm管径的水平管路中对气液两相流流量进行了系列实验,通过研究Lockhart-Martinelli常数与准气相流量比的关系,建立了适用于双锥流量计的气液两相流流量测量模型。 1 一次部件结构和测量原理 1.1 双锥流量计结构
双锥流量计是一种基于V锥流量计改进的新型差压式流量计,其结构包括2部分:锥体和锥体支架。锥体部分前后2锥角对称,3个片状支架将喉部固定在管道中心与管道同轴,将锥体支架安装在管道中构成双锥流量计。与V锥流量计相比,其尾部通过一段喉部连接1个与前锥角同角度的锥体,对尾部的流体有一定的导流作用,减少漩涡,从而有效地降低压力损失。双锥流量计的加工实物图及结构示意图分别如图 1和2所示。
 |
| 图 1 双锥流量计实物图Fig. 1 The double-cone flowmeter |
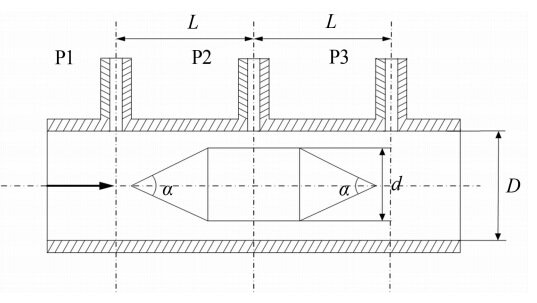 |
| 图 2 双锥流量计结构简图Fig. 2 Scheme of the flowmeter structure |
P1,P2,P3为3个取压口,当流体到达最小截面处即P2所在截面时,流速达到最大,压力降至最低,通过P1和P2两取压口可获得最大差压信号。D为管道内径,d为喉部直径,d/D为直径比,是影响双锥流量计测量特性的最重要因素之一。为分析不同直径比下的测量特性,分别加工了直径比为0.5、0.6、0.7、0.8和0.9的5个双锥流量计。
1.2 测量原理双锥流量计的测量原理遵循一般的差压式流量计测量原理,在同一密闭管道中根据伯努利方程和流动连续性方程,可得单相流流量基本测量模型为:
式中:Δptp为差压;ρ为单相流流体的密度;C流出系数;A为流束的最小流通面积,πβ2D2/4;ε为流体的可膨胀系数,对于不可压缩流体ε=1;β为等效直径比,即最小流通面积和管道截面积的比值,采用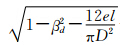 计算,其中βd为双锥直径比d/D,e、l分别为支撑叶片的厚度和长度,直径比0.5、0.6、0.7、0.8和0.9对应的等效直径比分别为0.840、0.780、0.697、0.586和0.424。
计算,其中βd为双锥直径比d/D,e、l分别为支撑叶片的厚度和长度,直径比0.5、0.6、0.7、0.8和0.9对应的等效直径比分别为0.840、0.780、0.697、0.586和0.424。
双锥流量计不是标准节流装置,因此使用之前需要对其流出系数进行标定。以水为实验介质在液体流量标准装置上对5个双锥流量计进行了标定。数据分析可知,直径比为0.7、0.8和0.9的双锥流量计在雷诺数大于45000后,流出系数趋于稳定;直径比为0.5和0.6的双锥流量计在雷诺数大于53000后,流出系数趋于稳定。取其稳定后数据的平均值作为双锥流量计的流出系数,各流出系数如表 1所示。
| βd | C |
| 0.5 | 0.996 |
| 0.6 | 0.966 |
| 0.7 | 0.993 |
| 0.8 | 0.972 |
| 0.9 | 0.845 |
常用的气液两相流测量模型包括分相流模型、均相流模型、James模型[12]、Murdock模型[13]和林宗虎模型[14]等。
分相流模型假设气液两相流是完全分开的,两相均为不可压缩流体且流出系数相同,各相具有不同的流动速度并各自占据流通面积,流经节流元件时各相产生的压力降等于两相流体流过节流元件时的压力降。当两相同时经过节流件时则有:
式中:ΔpGO为气相单独通过节流件时产生的压降;ΔpLO为液相单独通过节流件时产生的压降。由式(2)可以得到两相流质量流量式:
式中:x为干度;ρL为液相密度;ρG为气相密度。在实际测量过程中,Murdock,Lin等通过大量的实验,得到气液两相流总流量差压和各分相差压间的关系分别为:
通过差压关系式分别得到质量流量关系式。 2.2 双锥流量计气液两相流流量测量模型
上述这些模型是通过孔板及内锥式流量计获得,并且仅仅适用于特定的实验室工况条件,将它们用于其它工况误差较大。因此,需要建立适合双锥流量计的两相流模型。结合式(2)~(5),假设双锥流量计流量测量关系式为:
式中:m,n为各种工况条件下流量测量关系式修正系数,式(6)可改写为如下形式:
等式的右边可以看作准气相流量比,用M表示,可由实验得到;X为Lockhart-Martinelli常数,由下式计算:
通过研究M与X的关系即可确定m和n,得到双锥流量计流量测量模型。 3 实验与结果分析 3.1 实验装置
双锥流量计气液两相流实验是在中国计量学院油气水多相流实验室进行的,实验介质为空气和水,工况温度为20.5℃,实验系统结构简图如图 3所示。
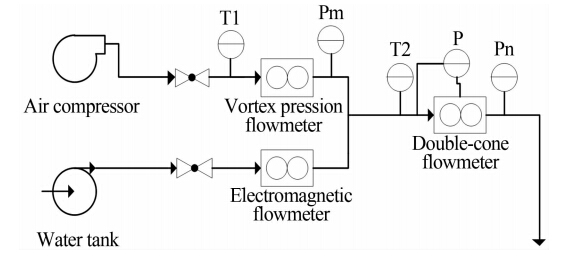 |
| 图 3 气液两相流实验系统简图Fig. 3 The simplified structure of the experimental system |
实验段有8m长的直管段,以保证气液两相流的充分发展。液体稳压罐稳压范围为0.2~0.21MPa,气体稳压罐稳压范围为0.39~0.41MPa,直管段以及实验管段管径为50mm。
利用研华数据采集卡PCI1710对差压变送器所得差压信号进行采集,采集频率为500Hz,每个流量点采集时间15s。选用的两个应变式差压变送器量程分别为0~65kPa和0~100kPa,输出信号为4~20mA电流信号,精度等级分别为0.25%FS和0.2%FS;选用应变式压力变送器Pm、Pn对标准表处及工作点压力进行测量,量程分别为0~1MPa、0~400kPa,输出均为4~20mA电流信号,精度等级均为0.25%FS;由于在实验过程中温度变化不大,T1和T2两处温度的测量选用的是玻璃水银温度计。 3.2 测量模型建立
分别利用直径比为0.5、0.6、0.7、0.8和0.9的5个双锥进行实验。实验过程中实验温度为18~20℃,水流量范围为1.25~7.07kg/s,空气流量范围为0.007~0.040kg/s,干度范围为0.0025~0.03(体积含气率为20%~95%),涉及的流型有泡状流、塞状流和弹状流。图 4显示了利用各直径比双锥流量计实验计算得到的准气相流量比M和Lockhart-Martinelli常数X的关系图。
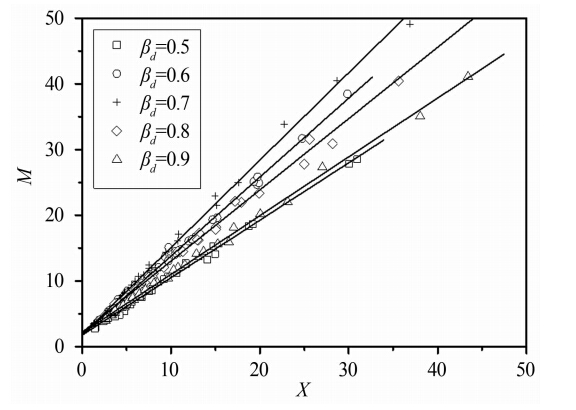 |
| 图 4 各直径比准气相流量比M和Lockhart-Martinelli常数X关系图 Fig. 4 Relationship between Lockhart-Martinelli number and gas flowrate ratio |
从图中可以看到,在实验涉及的3种流型下,5个双锥流量计实验所得准气相流量比M和Lockhart- Martinelli常数X均呈现良好的线性关系。通过对5组数据进行线性拟合,得到各直径比双锥流量计准气相流量比M和Lockhart-Martinelli常数X的关系式,从而得到总质量流量测量模型各参数,如表 2所示。将各参数代入式(6)即可得到双锥流量计模型。
| βd | m | n |
| 0.5 | 1.7631 | 0.8742 |
| 0.6 | 1.7775 | 1.2017 |
| 0.7 | 1.7894 | 1.3302 |
| 0.8 | 2.1827 | 1.0845 |
| 0.9 | 1.8839 | 0.9034 |
以混合前的液体流量和气体流量之和作为参考气液总流量,对测量相对误差及均方根误差进行了分析。首先以直径比为0.9的双锥流量计实验结果为例,将分相流模型、Murdock模型和Lin模型用于双锥流量计气液两相流的测量进行对比,图 5~7显示了各流量测量模型随干度x变化的测量误差。
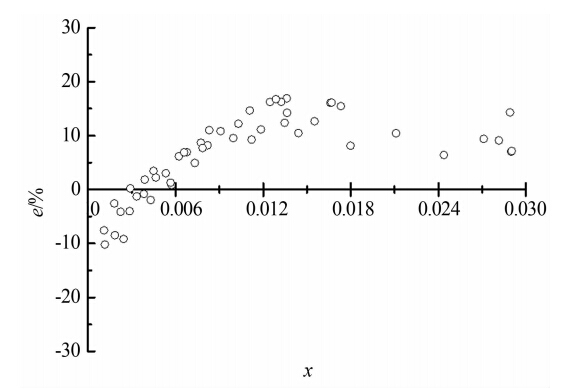 |
| 图 5 βd=0.9 分相流模型流量测量误差Fig. 5 Relative errors of total mass flowrate of the Separated model when βd=0.9 |
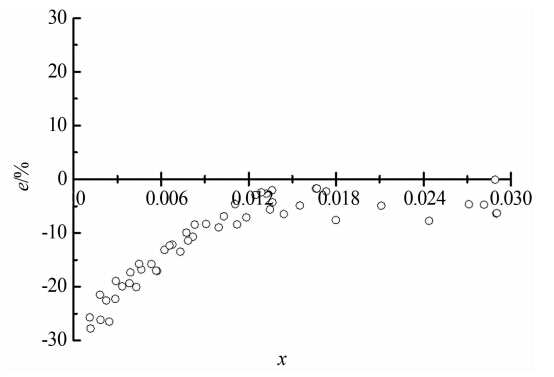 |
| 图 6 βd=0.9 Murdock模型流量测量误差Fig. 6 Relative errors of total mass flowrate of the Murdock model when βd=0.9 |
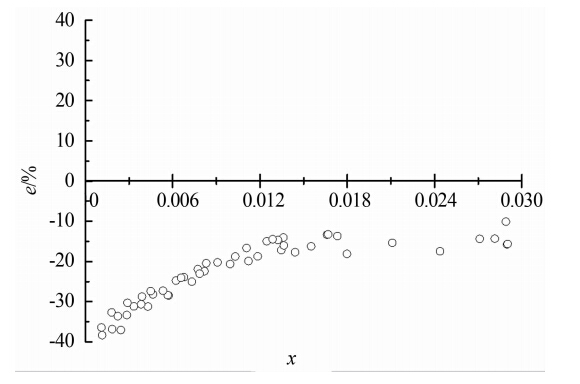 |
| 图 7 βd=0.9 Lin 模型流量测量误差Fig. 7 Relative errors of total mass flowrate of the Lin model when βd=0.9 |
由图 5~7可以看出,3种常用模型用于双锥流量计流量测量误差都较大,由于Murdock模型和Lin模型都是基于分相流模型修正得到的,因此3种模型表现出的误差趋势大致相同。理论上来讲,几种模型 中,分相流模型适用范围最广,但是其假设条件过于理想,两相流流动复杂,其相间传热及相间作用不容忽略,因此实际应用中分相流模型误差较大。Murdock模 型与Lin模型整体测量误差为负,随着干度的增大,其测量误差变小。其中Lin模型误差最大,最小测量误差大于10%。当干度小于0.008时,Murdock模型测量误差在-30%~-10%之间;当干度大于0.008时,其测量误差可以达到10%以内。分析其原因,首先,Murdock模型和Lin模型的获取实验工况与本实验有着较大的差异,实验工况超出了模型适用范围;其次,2种模型都是通过孔板流量计得到的,孔板节流件与双锥节流件在结构上有很大的不同,节流件的差别是导致2种模型不适用于双锥流量计两相流流量测量的重要原因。
图 8~12显示了5个双锥流量计配合所建双锥流量计测量模型流量测量相对误差。
 |
| 图 7 βd=0.9 Lin 模型流量测量误差Fig. 7 Relative errors of total mass flowrate of the Lin model when βd=0.9 |
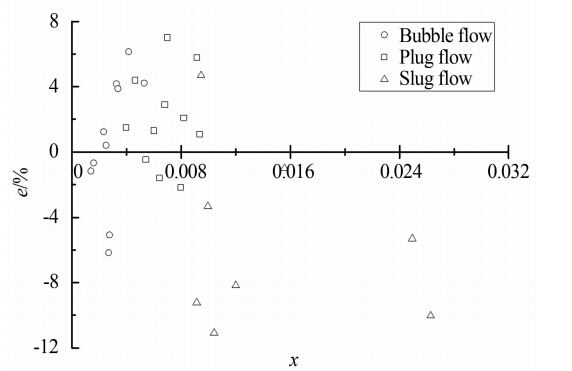 |
| 图 8 βd=0.5 总质量流量测量相对误差Fig. 8 Relative errors of total mass flowrate when βd=0.5 |
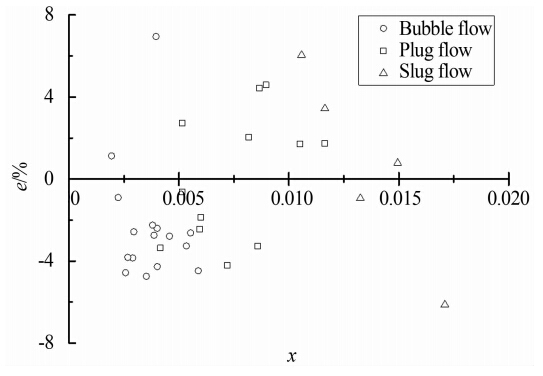 |
| 图 9 βd=0.6 总质量流量测量相对误差Fig. 9 Relative errors of total mass flowrate when βd=0.6 |
由图 8~12可知,除个别点外,直径比为0.5的双锥流量计总质量流量测量相对误差在-8%~8%之间,直径比为0.6、0.7、0.8和0.9的双锥流量计总质量流量相对误差在-6%~6%之间。所建模型测量误差较为稳定,误差与干度、流型之间没有明显的规律。与其它常用模型相比,利用新建的双锥流量计流量测量模型精度得到了很大的提升。定义均方根误差:
式中:n为测量点数;Wm(calculated)为计算所得气液两相总质量流量值;Wm(actual)为实测的气液两相总质量流量值。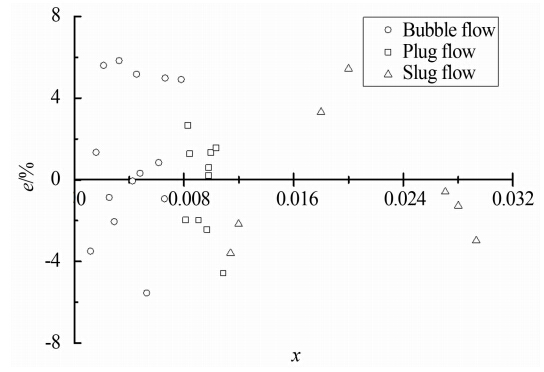 |
| 图 10 βd=0.7 总质量流量测量相对误差Fig. 10 Relative errors of total mass flowrate when βd=0.7 |
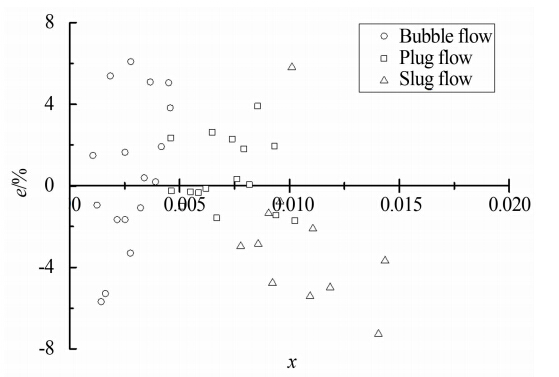 |
| 图 11 βd=0.8 总质量流量测量相对误差Fig. 11 Relative errors of total mass flowrate when βd=0.8 |
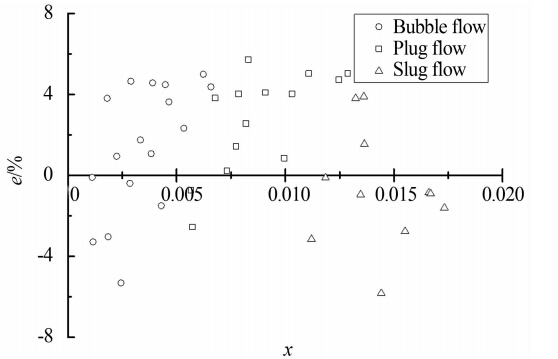 |
| 图 12 βd=0.9 总质量流量测量相对误差Fig. 12 Relative errors of total mass flowrate when βd=0.9 |
计算得到各双锥流量计总质量流量测量均方根误差,如表 3所示:
| βd | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| σ | 5.16% | 3.40% | 3.97% | 3.27% | 3.06% |
由表 3可知,除直径比为0.5的双锥流量计其测量均方根误差为5.16%外,其余4个双锥流量计测量均方根误差可以保持在4%以内。 4 结 论
本文提出了一种新型的双锥流量测量方法并在水平管多相流系统中开展了气液两相流流量测量实验。初步研究表明,在本实验工况条件下,结合所建模型,直径比为0.5的双锥流量计对气液两相流总流量测量的相对误差在±8%以内,均方根误差为5.16%;直径比为0.6、0.7、0.8和0.9的双锥流量计对总流量测量的相对误差在±6%以内,均方根误差在4%以内。结果显示,所提出的双锥流量传感方法具有较好的测量特性,可用于双锥流量计气液两相流流量的测量。
| [1] | 孙波, 孙立成, 幸奠川, 等. 漂移流模型在大管内气液两相流动的适用性研究[J]. 实验流体力学, 2013, 27(3): 56-59. Sun Bo, Sun Licheng, Xing Dianchuang, et al. A study of the application of drift-flux model in gas-liquid two-phase flow in a large tube[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(3): 56-59. |
| [2] | 张立峰, 王化祥. 基于SVM及电容层析成像的两相流流型识别[J]. 仪器仪表学报, 2009, 30(4): 812-816. Zhang Lifeng, Wang Huaxiang. Identification of two-phase flow regime based on support vector machine and electrical capacitance tomography technique[J]. Chinese Journal of Scientific Instrument, 2009, 30(4): 812-816. |
| [3] | 陈飞, 孙斌, 王二鹏, 等. 不同节流装置测量气液两相流的动态特性研究[J]. 实验流体力学, 2012, 26(1): 55-60. Chen Fei, Sun Bin, Wang Erpeng, et al. Research on the dynamic characteristics of gas-liquid two phase flow measurement with different throttle devices[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1): 55-60. |
| [4] | Meng Z Z, Huang Z Y, Wang B L, et al. Air-water two-phase flow measurement using a Venturi meter and an electrical resistance tomography sensor[J]. Flow Measurement and Instrumentation, 2010, 21(3): 268-276. |
| [5] | 谭超, 董峰, 许聪, 等. 用于两相流检测的电阻层析成像系统[J]. 东南大学学报(自然科学版), 2011, 41(S1): 125-129. Tan Chao, Dong Feng, Xu Cong, et al. Electrical resistance tomography system for two-phase flow monitoring[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(S1): 125-129. |
| [6] | 周云龙, 衣得武, 高云鹏. 用于气液两相流流型识别的ECT传感器的优化设计[J]. 电机与控制学报, 2011, 15(6): 62-66. Zhou Yunlong, Yi Dewu, Gao Yunpeng. Optimal design of ECT sensor for gas-liquid two-phase flow pattern identification[J]. Electric Machines and Control, 2011, 15(6): 62-66. |
| [7] | 黄春辉, 胡金海, 刘兴斌, 等. 电导相关流量测井仪在气/水两相流下响应规律的实验研究[J]. 测井技术, 2011, 35(6): 508-511. Huang Chunhui, Hu Jinhai, Liu Xingbin, et al. Experimental analysis of conductance correlation flowmeter in gas-water two-phase flow[J]. Well Logging Technology, 2011, 35(6): 508-511. |
| [8] | Huang Z Y, Xie D L, Zhang H J, et al. Gas-oil two-phase flow measurement using an ecectrical capacitance tomography system and a Venturimeter[J]. Flow Measurement and Instrument, 2005, 16(2-3): 177-182. |
| [9] | 方立德, 张涛, 徐英. 基于狭缝文丘里管的气液两相流测量[J]. 传感技术学报, 2008, 21(8): 1458-1465. Fang Lide, Zhang Tao, Xu Ying. Gas-liquid two-phase flow measurement based on a slot venturi[J]. Chinese Journal of Sensors and Actuators, 2008, 21(8): 1458-1465. |
| [10] | Dong F, Hu J. Study of the gas-liquid two-phase flow measuring method based on the V-cone flow meter[C]. The 5th International Symposium on Measurement Techniques for Multiphase Flows, Macao, China, 2006: 214-220. |
| [11] | 梁佳娜, 梁国伟, 沈平平. 双锥流量计实验研究与计算模拟[J]. 中国计量学院学报, 2010, 21(3): 201-205. Liang Jiana, Liang Guowei, Shen Pingping. Experimental study and computational simulation on double-cone flow-meters[J]. Journal of China Jiliang University, 2010, 21(3): 201-205. |
| [12] | JAMES R. Metering of steam-water two-phase flow by sharp edged orifices[J]. Proc Inst Meech, 1965, 180(23): 594-566. |
| [13] | MURDOCK J W. Two-phase flow through measurement with orifices[J]. Journal of Basic Engineering, 1962, 84(4): 419-433. |
| [14] | LIN Z H. Two-phase flow measurement with sharp-edged orifices[J]. International Journal of Multiphase Flow, 1982, 8(6): 683-693. |