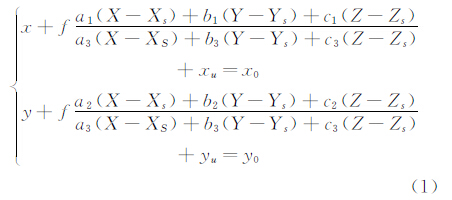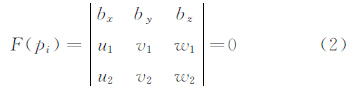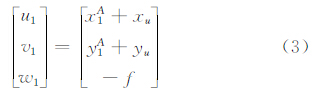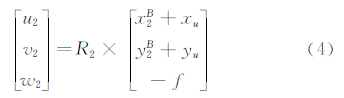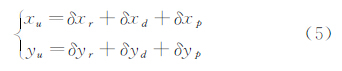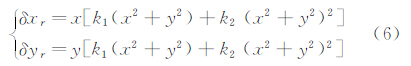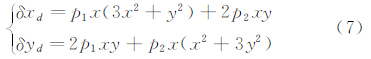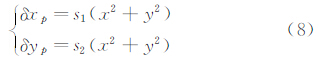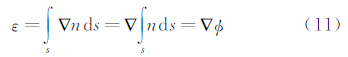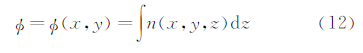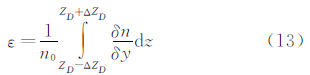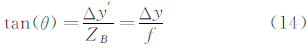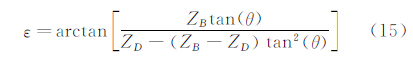由于现代飞行器的精益设计对风洞试验数据的精准度要求越来越高,亟需基于视频测量的弹性角修正技术与模型变形影响修正技术,修正风洞试验中因模型及其支撑机构弹性变形所致的气动力测量误差[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]。超声速巡航弹、超高速反舰导弹等型号的红外成像精确制导设备和上升段反导用途的机载激光武器亟需气动光学风洞试验技术,度量气动光学效应[12, 13, 14, 15]。
风洞试验中的视频测量技术[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]是利用光学成像技术无干扰测量试验模型在气动载荷下的姿态和变形量,实现弹性角修正与模型变形的影响修正,另一方面,将光束偏折位移场测量值转化为光束从摄影中心出发穿过扰流区到人工点的光程差,定量试验模型绕流导致的气动光学效应、提供流场结构及其变化过程的观察手段[12, 15]。
另一方面,视频测量技术以非接触方式测量风洞试验相关信息,具有直观、简洁、不干扰风洞试验模型 和流场的优势,可以为风洞试验提供一种新的测量手段和途径,辅佐和弥补现有基于天平、应变片、传感器等的传统测量技术,在试验精细化、简洁实用化和测量技术完善化方面,可大力增强高速风洞试验的测量能力,促进风洞试验技术的发展,如通过对气动力和姿态与外形的准确对应测量数据,进行时序分析,为研究人员发现新的流动现象和形成飞行器设计新概念提供了科学实验研究的有力工具[1, 2]。
为此,本文阐述了视频测量技术在CARDC高速风洞试验中的研究进展。
1 视频测量原理共线方程描述了相机、试验模型上粘印待测点及其像点三者的数学模型,表达式为
其中:(x0,y0)分别为相机像平面中心,f为相机焦距,xu与yu为通过相机标定得到的畸变参数,(Xs,Ys,Zs)分别为相机在地面坐标系下的位置坐标,(x,y)与(X,Y,Z)分别为粘印点的像平面坐标与地面坐标系下的坐标,(a1,a2,a3,b1,b2,b3,c1,c2,c3)为相机姿态角(φ,ω,κ)所组成的旋转矩阵R中9个方向余弦。共面方程指位于不同视角图片上的同一测量点(称为同名像对)共面。对于给定2张图片IA和IB,其同名像对的集合为 P ,pi∈ P ,pi=(piA,piB),SAu1v1w1与SBu2v2w2分别为piA和piB对应的像空间辅助坐标系,S1与S2分别为S1u1v1w1与S2u2v2w2的原点,对应的坐标分别为(u1,v1,w1)和(u2,v2,w2),S2在S1u1v1w1中的坐标为(bx,by,bz);piA和piB的共面方程式可表示为:
式中 其中:f为焦距,(x1A,y1A)和(x2B,y2B)分别为piA和piB对应的像平面坐标,R2为S2u2v2w2相对S1u1v1w1的3个角元素(φ,ω,κ)组成的旋转矩阵。因bx只涉及模型比例尺,故,只要 P 中同名像对总数超过5,联解式(2)即可得到5个相对定向元素(by,bz,φ,ω,κ),再代入式(1)并通过坐标变换即可得到试验模型上粘印待测点在风洞坐标系下的坐标。 2 高速风洞试验中的视频测量技术如图 1所示,CARDC高速风洞视频测量系统采用DALSA工业相机(分辨率为2352×1728),定焦镜头,Camera Link光纤中继器和图像采集电脑(图像采集卡通过PCI插槽安装在图像采集电脑上)[6];相机通过安装架固定在风洞试验段侧壁的观察孔前。试验开始时,通过控制信号启动图像的采集,并保存在采集计算机的硬盘中。试验结束后,通过控制信号关闭图像采集,采集到的图像通过网络传输至坐标解算计算机中,调用自主开发的三维坐标解算程序,读取采集到的图像,计算试验模型在气动载荷下的姿态、变形和光偏折角等。
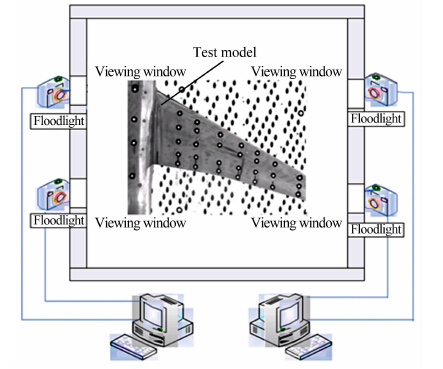 |
| 图 1 CARDC高速风洞视频测量示意图 Fig 1 Videogrammetric measurement schedule of CARDC high speed wind tunnel |
受风洞试验段的观察窗大小与位置限制,以及试验现场测量空间的限制,在高速风洞试验中往往不得不采用大角度大重叠视频图像采集方式,加之试验过程振动又较大,需要高精度的大角度外方位元素解算技术[9, 10]。
传统(航空)摄影测量是近似于垂直的摄影,因此可用小角度的线性化模型解得正确的相机位置与姿态角,但对于大角度重叠的摄影,必须考虑共线方程与共面方程的非线性特征,才能准确获得每张采集照片的相机位置坐标与姿态角,进而利用前方交会确定模型上被测点的三维坐标。
CARDC提出蒙特卡洛搜索域与摄影角间的数学模型[9, 10],建立3控制点的相机位置与姿态确定技术,在2m量级的高速风洞试验中能够解得正确的外方位元素。
2.2 标记点及其图像处理如图 2所示,通过测量粘印在洞体上的编码标志点坐标,建立风洞坐标系,实现高精度的外方位元素自动求解。其中,编码标志点利用同心环式标记点的编码与解码原理,将位于中心的圆点用于定位,编码点分布在与中心圆同心的圆周上,圆周上不同位置的组合代表了不同的编码值,通过图像识别技术得到不同视角每幅图像的编码标记点编码值,相同编码值的编码标记点即为同名像对,实现自动匹配。
 |
| 图 2 本文软件采用轮廓叠加图片方式显示界面 Fig 2 Software UI for contours of coded points |
采用Canny边缘检测算子,提取图 1编码标记点定位圆图像和圆形标志点图像的边缘;再采用中值滤波以过滤掉图像椭圆内部的噪声,利用灰度重心法、最小二乘拟合法或灰度重心加权等实现0.01~0.03个像素定位精度。如图 1所示,图中白色轮廓为编码点的定位圆的轮廓,红色轮廓为编码点的编码环轮廓。
2.3 标 定美国国家航空航天局(NASA)采用的标定块,其标定方法包含了确定相机位置与姿态的最小二乘法和确定相机畸变与焦距等参数的最优化方法[1, 2],但制造与维护成本高(尤其是台阶标定板尺寸超过1m后,其制造与维护费用剧增至十几万到几十万),因为其上标志点的坐标都要非常精确,并需要恒温恒湿存放环境[16, 17]。
CARDC提出基于式(4)的摄像机非线性畸变自校正技术,同时考虑了径向畸变、偏心畸变和薄棱镜畸变[18]。相应的畸变计算公式为
式中从多个角度拍摄一组图像序列,确保标尺编码点在相机CCD上的成像坐标不同,并尽量使图像序列中标尺编码点在相机CCD各个方位都有成像;另外,要求标尺成像清晰、亮度与对比度好,对选取的图像进行编码点识别,得到编码点中心的图像坐标。利用式(2)可得到6个镜头畸变参数k1、k2、p1、p2、s1和s2[12]。
 |
| 图 3 相机标定采用的标尺 Fig 3 Calibration rule |
按照气动光学波面畸变原理与光线追迹理论[1],光线穿过扰流产生的折射角为
式中n为折射率,则光程(OPL)为 有 即,光线穿过流场总偏折角与光程的梯度直接相关。因气动光学应用中,偏折角和通过介质总光程比较小,可近似认为ds=dz,则 故,通过计算偏折角即可得到气动光学波前畸变参数(光程差),如图 4所示,光线偏折角为沿光线路径折射率梯度的积分,有 式中密度梯度区域ΔZD《 ZD。由于 式中Δy′为世界坐标位移量,Δy为像空间位移量;ZB为镜头与纹案的距离,f为像平面到镜头的距离即焦距,则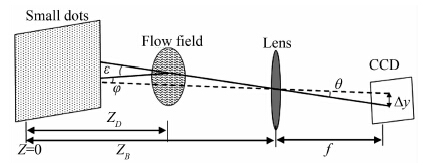 |
| 图 4 光束折射示意图 Fig 4 Principle of a beam refraction |
将式(15)代入式(11),即可通过测量图 4上每个圆点的位移,获得气动光学的波前畸变,但从式(14) 与(15)中可知偏折角ε与背景圆点到摄影中心的距 离ZB、背景圆点到飞行器模型距离ZD以及圆点像平面位移Δy相关,其测量精度严重影响气动光学的波前畸变的测量精度,需要采用式(1)计算小圆点与飞行器模型到摄影中心的距离。
3 实验研究 3.1 某标模5次重复性试验迎角测量分析在2m×2m超声速风洞的某标模试验中,5次同期重复试验迎角实测阶梯为-8°、-6°、-4°、-2°、0°、2°、4°、6°和8°。表 1为各名义角度阶梯的迎角实测数据,在-8°、-6°、-4°、-2°、0°、2°、4°、6°和8°阶梯上,5次同期试验迎角实测数据的最大平均值标准差为0.0027°,最小平均值标准差为0.001。
| 测量阶梯名义迎角/(°) | 车次号 | 平均值 /(°) | 标准差 /(°) | 平均值标准差/(°) | ||||
| 339次 | 342次 | 343次 | 344次 | 345次 | ||||
| -8 | -8.2752 | -8.2868 | -8.2823 | -8.2883 | -8.2820 | -8.2829 | 0.0051 | 0.0023 |
| -6 | -6.1996 | -6.2017 | -6.1995 | -6.2051 | -6.1995 | -6.2011 | 0.0024 | 0.0011 |
| -4 | -4.1167 | -4.1191 | -4.1156 | -4.1213 | -4.1189 | -4.1183 | 0.0022 | 0.001 |
| -2 | -2.0385 | -2.0375 | -2.0323 | -2.0402 | -2.0351 | -2.0367 | 0.0031 | 0.0014 |
| 0 | 0.0493 | 0.0507 | 0.0555 | 0.0471 | 0.0524 | 0.0510 | 0.0032 | 0.00143 |
| 2 | 2.1500 | 2.1514 | 2.1568 | 2.1462 | 2.1496 | 2.1508 | 0.0039 | 0.0017 |
| 4 | 4.2642 | 4.2584 | 4.2626 | 4.2526 | 4.2590 | 4.2594 | 0.0045 | 0.0022 |
| 6 | 6.4004 | 6.3942 | 6.4008 | 6.3896 | 6.3964 | 6.3963 | 0.0047 | 0.00221 |
| 8 | 8.5452 | 8.5481 | 8.5591 | 8.5410 | 8.5559 | 8.5499 | 0.0075 | 0.0027 |
如表 2所示,视频测量与天平测量的弹性角之差最大为-0.0256°、最小为-0.0119°。因为目前采用高精度数显倾斜仪确定天平和姿态角视频测量系统的俯仰方向基准,而高精度数显倾斜仪精度为0.01°,这 种准度上的误差可通过采用更高精度的倾斜仪以系统误差补偿的方法降低。
| 名义角度/(°) | -8 | -6 | -4 | -2 | 0 | 2 | 4 | 6 | 8 |
| 均值之差/(°) | -0.0256 | -0.0270 | -0.0220 | -0.0175 | -0.0149 | -0.0130 | -0.0161 | -0.0128 | -0.0119 |
受测压试验条件限制,一般无法安装测力天平,试验中只能得到弯刀支撑机构的名义迎角,无法获得模型及支杆 因弹性变形引起的弹性角,使测压数据对应的模型实际迎角出现严重偏差。近期在2m×2m超声速风洞进行的某飞机测压试验就明确提出高精度测量弹性角的要求。图 5和6为其中2次车的弹性角视频测量结果。由于本试验使用了高强度支杆,确保模型与支杆组成系统的弹性变形为线性弹性变形,图 5~6中弹性角实测数据与名义攻角的线性拟合的决定系数, 最大为0.9997,最小为0.9987。从另一方面,表明本文测量系统的测量结果正确可信。
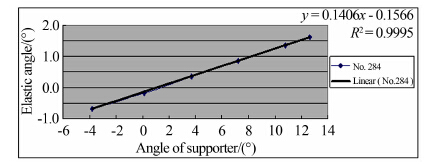 |
| 图 5 Ma1.5 284次车的弹性角测量结果 Fig 5 Results of elastic angle at Ma1.5 in test 284 |
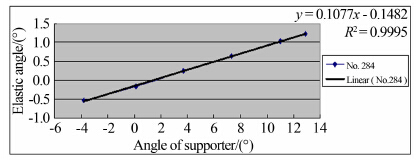 |
| 图 6 Ma2.0 287次车的的弹性角测量结果 Fig 6 Results of elastic angle at Ma2.0 in test 287 |
试验设备为2.4m×2.4m跨声速风洞,标记点在全尺寸弹舱舱门上的位置与编号如图 7所示,16个标记点Z坐标变形量如图 8所示。为了研究动态变形视频测量的精度,在马赫数1.4时,开展了4次全尺寸内埋弹舱舱门动态变形测量的重复性实验,测量1号测量点变形数据。表 3给出该点变形测量值不确定度估计,其4次的样本均值之间标准差1号点为0.082mm,说明本文采用的视频测量技术的动态测量精度高。表 3中1号测量点单次变形测量值的标准差表明:被测舱门1号点位置随时间动态变动范围(标准差)的平均值为1.515mm,但其标准不确定度最大不超过0.095mm,表明4次重复性实验的1号点位置动态变化均值可信度仍较高。
 |
| 图 7 标记点在舱门上的位置与编号Fig 7 Mark points on the full size embedded door |
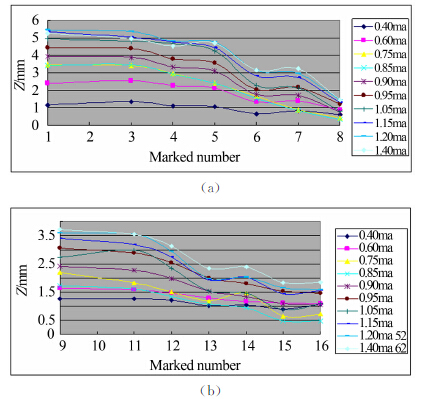 |
| 图 8 标记点Z坐标变形量与标记点位置关系Fig 8 Displacements of mark points at the Z direction |
| 第1次 | 第2次 | 第3次 | 第4次 | 4次重复 试验均值 | 4次重复 试验标准差 | |
| 采样频率/Hz | 80 | 80 | 80 | 80 | - | - |
| 样本个数 | 600 | 1200 | 360 | 320 | - | - |
| 持续时间/s | 7.5 | 15 | 4.5 | 4 | - | - |
| 变形量均值/mm | 5.120 | 5.246 | 5.348 | 5.215 | 5.232 | 0.082 |
| 变形量标准差/mm | 1.651 | 1.543 | 1.474 | 1.391 | 1.515 | 0.095 |
| 标准不确定度/mm | 0.067 | 0.045 | 0.078 | 0.078 | - | - |
| 动态不确定度/mm | 0.084 | 0.079 | 0.075 | 0.060 | - | - |
另一方面,根据动态不确定度计算公式,本文给出变形随时间变化的动态不确定度如表 3中末行,进一步从动态测量角度说明本文视频测量值的精度。
3.4 气动光学波前畸变场测量在2m×2m超声速风洞开展了气动光学波前畸变场测量,试验对象为某跨大气层飞行器风洞模型,马赫数为3.0下的光程差测量数据与Zernike多项式重构的光程差云图如图 9和10所示。图 11为采用本文技术测得的电吹风喷出气流的光偏转位移矢量场图。
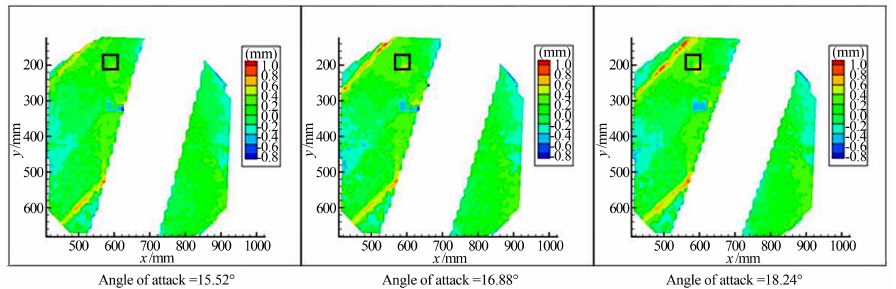 |
| 图 9 不同迎角下的光程差测量值Fig 9 OPD measurements |
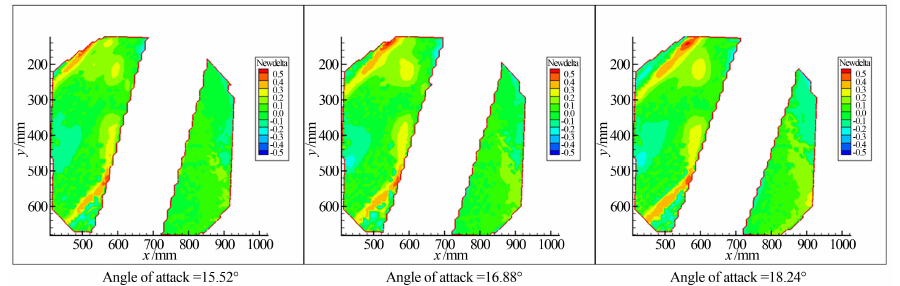 |
| 图 10 不同迎角下光程差Zernike多项式重构云图Fig 10 OPD described by Zernike polynomial |
 |
| 图 11 电吹风喷出气流的光偏转位移矢量图Fig 11 Displacement field induced by an electric drier |
多个试验模型的迎角与变形、气动光学畸变场等视频测量实例表明:
(1) 同期试验迎角视频实测数据的标准差≤0.0075°;
(2) 同期试验动态变形实测数据的标准差为0.082mm;
(3) 与基于相位或光强的传统气动光学现象测量方法不同,本文利用视频测量技术定量测量波前畸变场,测得机头与机翼的斜激波所致的波前畸变结构正确,该方法光路简单、无需使用价格昂贵的相干光源。
因此,视频测量技术既可为弹性角修正与模型变形的影响修正提供数据,又为气动光学效应的测试及校正技术的研究提供了新途径,因此具有巨大应用前景。
| [1] | Danny A B. Videogrammetric model deformation measurement technique for wind tunnel applications[R]. AIAA Paper 2007-1163. |
| [2] | Liu T, Burner A W, Pappa R. Photogrammetric techniques for aerospace applications[R]. AIAA Press, 2008. |
| [3] | Zhang Zhengyu, Wang S L. Videogrammetric measurement for model displacement in wind tunnel test[J]. Applied Mechanics and Materials, 2011, (130-134): 103-107. |
| [4] | 张孝棣, 蒋甲利, 贾元胜, 等. 视频测量力法在风洞模型姿态角测量中的应用[J]. 实验流体力学, 2005, 19(3): 21-25. Zhang Xiaodi, Jiang Jiali, Jia Yuansheng, et al. Videogrammetry application in wind tunnel model attitude measurement[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(3): 21-25. |
| [5] | Thomas W Jones, Charles B Lunsford. Design and development of a real-time model attitude measurement system for hypersonic facilities[C]. 43rd AIAA Aerospace Sciences Meeting and Exhibit 10-13 January 2005, Reno, Nevada, AIAA 2005-1411. |
| [6] | 孙岩, 张征宇, 黄诗捷, 等. 风洞试验中模型攻角视频测量技术研究[J]. 航空学报, 2013, 34(1): 1-7. Sun Yan, Zhang Zhengyu, Huang Shijie, et al. Vision measurement technology research for mode/angle of attack in wind tunnel tests[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 1-7. |
| [7] | 孙岩, 张征宇, 吕彬彬, 等. T型尾翼颤振模型光学测量实验与弯扭特性解算[J]. 实验流体力学, 2012, 26(1): 100-104. Sun Yan, Zhang Zhengyu, Lyu Binbin, et al. Optical measurement experiments on T-tails flutter model and bending-torsion characteristics calculation[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1): 100-104. |
| [8] | 王超, 张征宇, 殷国富, 等. 基于摄影测量的飞机静弹性风洞模型刚度识别方法[J]. 四川大学学报, 2013, 45(3): 183-188. Wang Chao, Zhang Zhengyu, Yin Guofu, et al. Stiffness identification for static aeroelasticity wind tunnel model of aircraft based on photogrammetry[J]. Journal of Sichuan University, 2013, 45(3): 183-188. |
| [9] | 罗川, 张征宇, 孙岩, 等. 模型变形视频测量的相机位置坐标与姿态角确定[J]. 实验流体力学, 2010, 24(6): 88-91. Luo Chuan, Zhang Zhengyu, Sun Yan, et al. Exterior orientation for video grammetric model deformation measurement[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(6) : 88-91. |
| [10] | 张征宇, 罗川, 孙岩, 等. 振动环境中相机位置坐标与姿态角解算的试验研究[J]. 实验流体力学, 2011, 25(3): 56-59. Zhang Zhengyu, Luo Chuan, Sun Yan, et al. Experimental investigation on exterior orientation in vibration environment[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3): 56-59. |
| [11] | 张征宇, 喻波, 罗川, 等. 2.4m跨声速风洞的模型位移视频测量精度研究[J]. 实验流体力学, 2011, 25(4): 56-60. Zhang Zhengyu, Yu Bo, Luo Chuan, et al. Precision investigation on model displacement videogrammetric measurement in 2.4m transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 79-82. |
| [12] | 赵涛, 张征宇, 王水亮, 等. 大幅面气动光学波前崎变场测量与重构[J]. 光学学报, 2013, 33(10): 10120031-10120037. Zhao Tao, Zhang Zhengyu, Wang Shuiliang, et al. Measurement and reconstruction for large aero-optics wavefront distortion field[J]. Acta Optica Sinica, 2013,33(10): 10120031-10120037 |
| [7] | 孙岩, 张征宇, 吕彬彬, 等. T型尾翼颤振模型光学测量实验与弯扭特性解算[J]. 实验流体力学, 2012, 26(1): 100-104. Sun Yan, Zhang Zhengyu, Lyu Binbin, et al. Optical measurement experiments on T-tails flutter model and bending-torsion characteristics calculation[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1): 100-104. |
| [14] | 赵玉新, 易仕和, 田立丰. 超声速混合层气动光学畸变与抖动[J]. 中国科学: 物理学 力学 天文学, 2010, 40(1): 33-46. Zhao Yuxin, Yi Shihe, Tian Lifeng. Aero-optic distortion and fitter in supersonic mixing layer[J]. Science China: Physics Mechanics Astronomy, 2010, 40(1): 33-46. |
| [15] | Zhang Zhengyu, Huang X H, Yin J. Measurement and visualization of large aero-optics wavefront distortion field in wind tunnel testing[J]. Applied Mechanics and Materials, 2013, (389): 1053-1057. |
| [16] | Ahmed Moumen, Farag Aly. Nonmetric calibration of camera lens distortion: differential methods and robust estimation[J]. IEEE Transactions on Image Processing, 2005, 14 (8): 1215-1230. |
| [17] | Zhang Zhengyu. Camera calibration with one-dimensional objects[J]. IEEE Trans on Pattern Analysis and Machine Intellingence, 2004, 26(7): 892-8990. |
| [18] | 张征宇, 黄诗捷, 罗川, 等. 基于共面条件的摄像机非线性畸变自校正[J]. 光学学报, 2012, 32(1): 0115002-1-0115002-6. Zhang Zhengyu, Huang Shijie, Luo Chuan, et al. Nonlinear distortion correction of camera based on coplanar condition equations[J]. Acta Optica Sinica, 2012, 32(1): 0115002-1-0115002-6. |