激波聚焦是指在一定条件下激波在其传播方向上发生收敛的行为,由于能够在聚焦中心产生局部高能量密度的高压区域,因此激波聚焦具有广泛的工程应用背景。在惯性约束核聚变[1]、体外激波碎石机[2]、激波聚焦点火[3]和超新星爆发[4]等研究领域都涉及到汇聚激波。尤其是近些年来,生成初始均匀的汇聚激波以及研究汇聚激波与不同流场结构相互作用的现象,如Richtmyer-Meshkov(RM)不稳定性[5,6],得到了众多科研工作者的关注。相比平面激波而言,汇聚激波结构和性质更为复杂,任何小扰动都会对汇聚激波产生干扰,因此在实验室条件下,生成汇聚激波一直是一个难题。早在20世纪50年代,Perry & Kantrowitz[7]利用水平环形的同轴激波管第一次成功地生成了环形汇聚激波,但生成的汇聚激波强度有一定的限制。Baronets[8]利用脉冲放电方法,在柱形腔中形成汇聚激波,并研究了汇聚激波在惰性气体中的传播规律。日本激波研究中心Takayama小组[9]一直致力于汇聚激波的实验研究,先后搭建了多套环形的同轴激波管,在改进的竖直激波管中得到了柱状环形汇聚激波并实验研究了环形激波条件下的RM不稳定性。加州理工Dimotakis & Samtaney[10]通过气体透镜原理,让平面激波穿过弧形气体界面,通过界面折射作用在二维楔形结构中产生柱状汇聚激波。这种方法理论上可以得到完美的汇聚激波,但对界面的属性要求较高而且每次实验前都必须对界面进行精确的安装,从而增大了实验的难度。Kjellander等人[11]利用水平同轴激波管生成柱状汇聚激波,通过纹影法和多重曝光技术捕捉激波位置,研究了气体比热比对激波运动规律的影响。然后通过数值方法的修正加工了可以产生球形汇聚激波的激波管[12],并通过光纤收集气体由于高温受激发而产生激发光的光谱来说明激波的汇聚效应。董刚等人[13]采用高速摄影技术和数值模拟方法,对入射激波在2种不同形状的抛物形反射器表面聚焦和反射的过程进行了研究。翟志刚等人[14]基于激波动力学理论提出了一种简单有效的方法,即利用连续光滑弯曲的壁面将平面激波转化为柱状汇聚激波。从前人的研究工作可以看出汇聚激波得到了诸多的关注与研究,但多集中于研究汇聚激波的生成及其性能,而由于汇聚激波管内部结构的限制,关于汇聚激波与不同流场结构相互作用的实验研究则开展较少。
基于Takayama小组的同轴激波管设计思想[9],本文加工一套小的竖直环形激波管,采用更小的实验段高度,从而减小重力的影响,同时改进流场的观测手段,既可以采用纹影光路显示流场,也可以采用片光技术显示流场。实验中还采用细丝约束肥皂膜的方法形成正八边形气体界面,通过连续激波片光结合高速摄影技术实现了对流场的显示,获得汇聚激波作用下正八边形气体界面的发展过程。 1 激波管的设计
激波管的设计基于Takayama小组的同轴激波管思想[9],其结构如图 1所示,分为底座、高压段、低压段和实验段4个部分。底座高165mm,为中空结构,包含1个辅助高压段和1个与实验段相 连的排气口。高压段由同轴的高压管和低压段外管组成,高为600mm,内径为180mm,外径为260mm;低压段由同轴的低压段内管和外管组成,高为1500mm,内径为140mm,外径为160mm。高压段与低压段之间由硅胶板隔开。实验段在激波管顶端,高度为5mm,侧面为片光入口,顶部为观察窗。当辅助高压段破膜时,该区域内压力迅速降低,硅胶板快速向下运动,高压段与低压段连通,在低压段内产生压缩波,进而发展成向上运动的环形平面激波。当入射的环形平面激波运动到实验段时,向内汇聚,最终在实验段内形成向中心运动的环形汇聚激波。当激波从低压段运动到实验段时会发生90°的偏折,为了减弱转角处产生的杂波,转角处内 外两侧均做了半径为5mm的圆滑过渡处理。
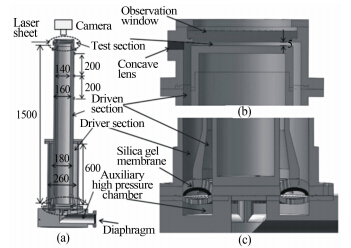 |
| 图 1 激波管总体图(a),实验段细节图(b),底座细节图(c) Fig. 1 General diagram of the shock tube (a),details of the test section (b) and details of the base (c) |
本文分别采用实验和数值方法对产生的环形汇聚激波进行验证。计算方法是基于Sun & Takayama编写的VAS2D(2-Dimensional & Axisymmetric Vectorized Adaptive Solver)程序[15]。VAS2D算法通过求解二维轴对称的欧拉方程,能够很好地模拟可压缩流动的问题。该数值方法采用非结构的四边形网格,基于MUSCL-Hancock格式达到时间二阶和空间二阶精度,采用有限体积法,结合非结构网格自适应技术对参数变化剧烈的复杂流场区域进行局部加密,可以用来求解有粘或无粘、定常或非定常、平衡或非平衡的可压缩流动问题。该程序的可靠性已经过课题组的大量验证,在平面激波与气泡相互作用的研究中得到了和实验吻合的结果[16],也在平面激波冲击不同形状界面问题的数值模拟中得到了和实验一致的结果[17],更进一步的程序验证可参考文献[15]。由于环形激波管呈轴对称结构,因此本文采用简化的轴对称模型。计算中激波管的尺寸与实验激波管尺寸相同,为了减小计算量,低压段只取一部分,设置初始入射激波在离实验段很近的位置,向上运行,如图 2所示。
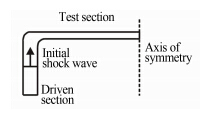 |
| 图 2 数值模拟初始流场示意图Fig. 2 Schematic of the initial condition for computation |
实验中为了判断低压段内产生的环形激波是否为平面激波以及为了测量初始激波马赫数,我们在低压段侧壁上安装了3个压力传感器ch1、ch2和ch3,其中ch2与ch3高度一样,用于检验入射激波的平面性。同时为了测量环形汇聚激波波后压力,在实验段顶部距离中心位置r=0,30,40和50mm处分别安装了压力传感器,测压点位置如图 3 (a)所示。实验中高压段压力为2atm,低压段压力为1atm,低压段侧壁测压点的压力曲线如图 3(b)所示。通过ch1和ch2传感器的压力响应时间差,可以计算出入射平面激波马赫数为Ms=1.17 (声速为340m/s)。通过ch2和ch3传感器的压力信号,如图 3(c)所示,可以判断低压段入射激波为平面激波。
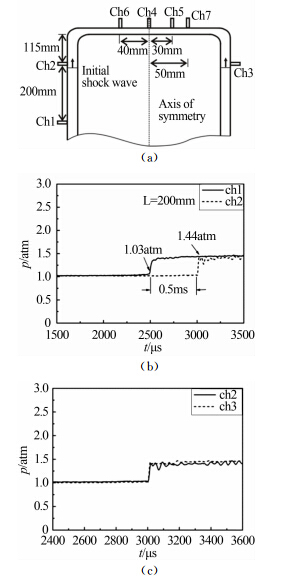 |
| 图 3 测压点位置示意图(a),ch1和ch2的压力曲线(b),ch2和ch3的压力曲线 (c)Fig. 3 (a) Schematic of measuring position,(b) pressure histories at ch1 and ch2,and (c) pressure histories at ch2 and ch3 |
图 4通过数值模拟给出了激波运行过程中的压力分布情况,3个时刻分别代表初始时刻、激波到达拐角时刻和激波即将到达汇聚中心时刻。从图中可以定性地观察到,随着激波向中心汇聚,波后压力逐渐增大。
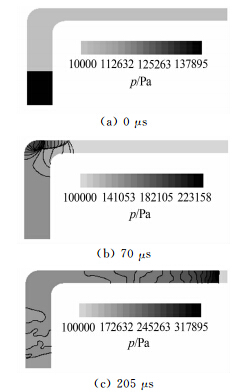 |
| 图 4 激波运行不同时刻的压力云图Fig. 4 Pressure contour at different times |
图 5通过实验和数值方法给出了不同位置测压点的压力变化情况。从图中可以看出,除了r=0mm附近的压力峰值变化差距较大外,其他位置压力变化的实验值和计算值吻合较好。当入射汇聚激波到达测压点时,压力曲线出现第1个阶跃。随着时间的推移,由于气体不断向实验段中心压缩,测压点处的压力值不断增大,反射激波经过测压点,导致压力曲线出现第2个阶跃。在整个汇聚激波运行的过程中,测压点压力值在反射激波经过测压点后达到最大。由于r=0mm的位置理论上为奇点,所以数值模拟得到压力峰值较大,与实验结果有一定的差距。而在其 它位置测压结果中,实验结果也总是小于计算结果。一方面实验中采用的压力传感器探头直径为8mm, 测得的压力值是探头表面的平均压力,在激波汇聚过程中,中心区域压力值变化剧烈,因此实验测得的值偏小。另一方面,数值方法中忽略了粘性项和热传导项,而实际情况中存在粘性扩散以及热传导,这也会导致实验值和计算值之间的差别。
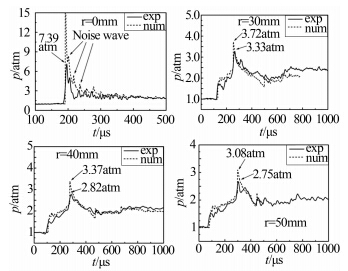 |
| 图 5 实验和数值模拟得到的不同位置测压点压力变化的比较Fig. 5 Comparison of the pressure variation with time obtained from experiment and computation at different positions |
在验证了环形汇聚激波之后,本文开展环形汇聚激波作用下界面不稳定性的实验研究。在界面形成方面,利用八根细丝约束肥皂膜可以形成八边形界面,如图 6(左)所示。在实验段上下侧有机玻璃板(观察窗) 上打直径为0.3 mm的小孔,细丝直径只有0.1 mm,用胶带把细丝粘到上侧玻璃上,由于细丝直径很小,几乎不影响流场观测。实验段下侧的细丝绑在一个重物上,使细丝绷紧,从而形成严格的正八边形二维界面,实验拍到的初始八边形界面如图 6(右)所示,界面外侧为空气,内侧为SF6。本文中正八边形界面各个顶点到中心的距离为20mm,界面高度为5mm。激波作用后的流场采用连续激光片光结合高速摄影相机进行显示,如图 7所示。连续激光器(SDL-532-15000T,15W,532nm)的初始光斑直径为10mm,依次通过柱凹面镜(f=50mm)和凸透镜(f=350mm)形成厚度约1 mm的片光,再经过实验段壁面上的柱面镜,进一步扩大片光范围(70mm),照亮整个流场。当激波穿过肥皂膜后,肥皂膜破碎成大量小液滴,在激光照射下,小液滴发出Mie 散射光,其运动轨迹可以被高速摄影相机记录下来,从而得到界面随着时间演化发展的整个过程。
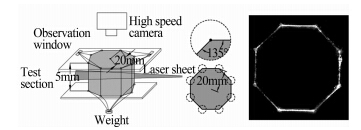 |
| 图 6 正八边形界面生成示意图(左)及实验拍到的初始界面(右)Fig. 6 Schematic of the regular octagon interface formation (left) and the corresponding picture from the experiment (right) |
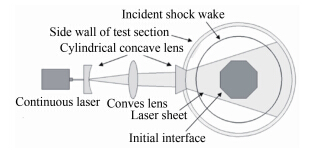 |
| 图 7 测量系统示意图(实验段俯视图)Fig. 7 Schematic of the visualizing system (top view) |
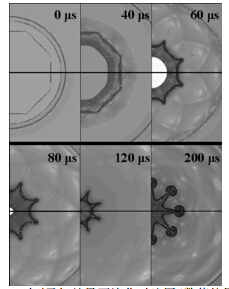
由于本文采用细丝对肥皂膜界面进行约束,而肥皂膜界面的可靠性已经在前人工作中得到了验证[18],因此首先采用数值方法考察了细丝对界面发展的影响。图 8给出了在环形汇聚激波的作用下,正八边形SF6气体界面在有无细丝约束条件下的发展演化。细丝在流场中是被当成固壁,以细丝为中心,半径为0.3 mm区域内单独划分更细的网格(最小尺寸为0.005mm)。由于激波与界面都是轴对称的,为了减少计算量,只模拟了1/4界面,图中上半部分为有细丝约束的结果,下半部分是没有细丝约束的结果。初始汇聚激波位于r=23 mm处,马赫数为1.337,界面位置与实验情况相同。从图中可以看到,上下2部分界面发展情况即有无细丝情况几乎对称,从而可以认为细丝对流场的影响很小。在验证界面形成方法之后,本文采用连续激光片光结合高速摄影技术得到了环形汇聚激波冲击下SF6正八边形界面演化过程,如图 9所示,同时对该过程进行了数值模拟研究。图中上侧是片光实验结果,下侧是与之对应的数值纹影图,第1幅图为初始界面。从图中可以看到,当激波作用在正八边形界面上之后,在激波的压缩下界面开始向中心运动。由于界面处压力梯度与密度梯度不重合,斜压涡量沉积在界面处,导致在界面的顶点以及边界上逐渐出现了尖钉与气泡结构,并随时间逐渐增长。当入射激波运动到中心会产生反射激波,反射激波会再次作用在正在演变的界面上。由于反射激波与入射激波引起的压力梯度正好相反,因此反射激波诱导产生的斜压涡量与入射激波诱导产生的斜压涡量正好相反,导致界面出现反相现象,原尖钉位置逐渐发展成气泡结构,而原气泡位置则逐渐发展成为尖钉结构。从图中可以看出,界面发展比较对称,实验与计算结果吻合较好。
 |
| 图 8 有/无细丝界面演化对比图(数值纹影)Fig. 8 Comparison of the interface evolution with (upper) and without (lower) the thin wire by simulation |
 |
| 图 9 SF6正八边形界面演化过程,实验和计算的对比,第一幅图为初始界面,Δt=16 μsFig. 9 The evolution of regular octagon interface after initial and reflected shock impact. The first frame gives the initial status and Δt=16 μs. Upper: experiment,Lower: simulation |
图 10定量给出了界面顶点以及界面边界中心位移随时间的变化,这里以界面中心作为参考点,取所有界面顶点或界面边界中心相对位移的平均值,误差棒表示最大、最小值与平均值之差。在入射激波压缩下,顶点及边界都向着界面中心运动,位移逐渐减小。界面顶点处形成尖钉结构,边界处形成气泡结构。反射激波作用后,界面顶点处产生气泡结构,而边界处产生尖钉结构。此时界面顶点位移以气泡位置为参考,界面边界中心位移则以尖钉位置为参考。可以看出,界面边界中心的位移在反射激波作用之后由于尖钉结构的增大而逐渐增大,而界面顶点的位移在反射激波作用后一段时间内仍是减小的,之后由于界面不稳定性的发展才逐渐增大。实验和计算结果中界面边界中心位移的变化趋势吻合较好,而界面顶点位移的变化则出现较大的差距。一方面可能是由于界面内气体纯度的影响导致初始界面上涡量幅度不同,从而导致尖钉结构尺寸不同;另一方面,在尖钉结构转变为气泡结构的过程中,实验测量存在较大的误差。
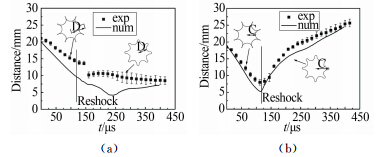 |
| 图 10 界面顶点位移变化(a),界面边界中心位移变化(b),以界面中心为参考点Fig. 10 Comparison of the displacement variations of interface vertex (a) and boundary center (b) between experiment and computation. The interface center is treated as the reference |
设计并加工了1套竖直环形激波管,通过实验测量激波管不同位置的压力变化,验证了该竖直同轴激波管形成环形汇聚激波的可行性,并通过实验结合数值模拟的手段,定量得到了环形汇聚激波运动过程中压力等参数变化信息。结果表明随着环形激波的汇聚,波后的压力等参数是逐渐增大的。之后在该激波管中开展了汇聚激波作用下RM不稳定性的实验研究。利用细丝约束肥皂膜技术形成正八边形界面,并通过数值模拟验证了细丝对界面前期演化的影响很小。通过片光技术结合高速摄影,得到了界面在入射激波及其反射激波冲击下的发展,并与计算结果进行对比,获得了较好的一致性,证明了实验方法的可行性。
| [1] |
张杰. 浅谈惯性约束核聚变[J]. 物理, 1999, 3: 142-152. Zhang Jie. An overview of inertial confinement fusion[J]. Physics, 1999, 3: 142-152. |
| [2] |
陈景秋, 韦春霞, 邓艇, 等. 体外冲击波碎石技术的力学机理的研究[J]. 力学进展, 2007, 37(4): 590-600. Chen Jingqiu, Wei Chunxia, Deng Ting, et al. Studies on mechanical mechanism about stone comminution and tissue trauma in extracorporeal shock wave lithotripsy[J]. Advances in Mechanics, 2007, 37(4): 590-600. |
| [3] |
滕宏辉, 王春, 邓博, 等. 可燃气体中激波聚焦的点火特性[J]. 力学学报, 2007, 39(2): 171-180. Teng Honghui, Wang Chun, Deng Bo, et al. Ignition characteristics of the shock wave focusing in combustive gases[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(2): 171-180. |
| [4] | Arnett W D, Bahcall J N, Kirshner R P, et al. Supernova 1987A[J]. Annual Review of Astronomy and Astrophysics, 1989, 27: 629-700. |
| [5] | Richtmyer R D. Taylor instability in shock acceleration of compressible fluids[J]. Communication on Pure and Applied Mathematics, 1960, 13: 297-319. |
| [6] | Meshkov E E. Instability of the interface of two gases accelerated rated by a shock wave[J]. Fluid Dynamics, 1969, 4: 151-157. |
| [7] | Perrt R W, Kantrowitz A. The production and stability of converging shock waves[J]. Journal of Applied Physics, 1951, 22: 878-886. |
| [8] | Baronets P. Imploding shock waves in a pulsed induction discharge[J]. Fluid Dynamics, 1984, 19: 503-508. |
| [9] | Hosseini S H R, Takayama K. Experimental study of Richtmyer-Meshkov instability induced by cylindrical shock waves[J]. Physics of Fluids, 2005, 17: 084101. |
| [10] | Dimotakis P E, Samtaney R. Planar shock cylindrical focusing by a perfect-gas lens[J]. Physics of Fluids, 2006, 18: 031705. |
| [11] | Kjelander M, Tillmark N, Apazidis N. Experimental determination of self-similarity constant for converging cylindrical shocks[J]. Physics of Fluids, 23: 116103. |
| [12] | Kjelander M, Tillmark N, Apazidis N. Energy concentration by spherical converging shocks generated in shock tube[J]. Physics of Fluids, 2012, 24, 126103. |
| [13] |
董刚, 叶经方, 范宝春. 激波聚焦反射的实验和数值研究[[J]. 高压物理学报, 2006, 20(4): 359-364. Dong Gang, Ye Jingfang, Fan Baochun. Experimental and numerical investigation of shock wave focusing and reflection[J]. Chinese Journal of High Pressure Physics, 2006, 20(4): 359-364. |
| [14] | Zhai Z, Liu C, Qin F, et al. Generation of cylindrical converging shock waves based on shock dynamics theory[J]. Physics of Fluids, 2010, 22: 041701. |
| [15] | Sun M, Takayama K. Conservative smoothing on an adaptive quadrilateral grid[J]. Journal of Computational Physics, 1999, 150: 143-180. |
| [16] | Zhai Z, Si T, Luo X, et al. On the evolution of spherical gas interface accelerated by a planar shock wave[J]. Physics of Fluids, 2011, 23: 084104. |
| [17] | Fan M, Zhai Z, Si T, et al. Numerical study on the evolution of the shock-accelerated SF6 interface: Influence of the interface shape[J]. Science China, Physics, Mechanics & Astronomy, 2012, 55: 284-296. |
| [18] |
罗喜胜, 王显圣, 陈模军, 等. 可控肥皂膜气柱界面与激波相互作用的实验研究[J]. 实验流体力学, 2014, 28(2): 7-13. Luo Xisheng, Wang Xianshen, Chen Mojun, et al. Experimental study of shock interacting with well-controlled gas cylinder generated by soap film[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 7-13. |


