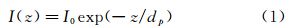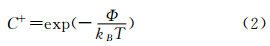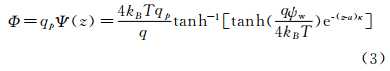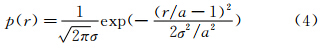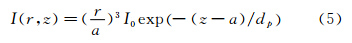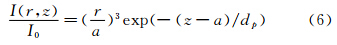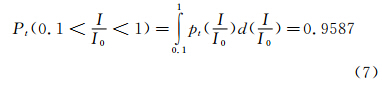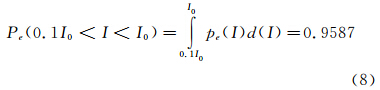2. 中国科学院 力学研究所, 北京 100190
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
全内反射测速技术(TIRV)利用壁面隐失波将观测区域限制在壁面附近几百纳米的薄层内,因此,相比传统体照明显微技术,该技术具有较高的信噪比 和分辨率[1]。隐失波照明最早在生物医学领域使用, 近年来一些研究者尝试将该技术用于受限布朗运动的测量和近壁区速度滑移的测量。Kihm、Banerjee等人采用全内反射荧光技术测量了近壁几百纳米区域内φ50-500nm粒子受限布朗运动[2,3]。Huang等采用TIRV测量了光滑玻璃表面的速度滑移[4]。Bouzigues等采用该技术研究了德拜长度内亲疏水表面速度滑移并讨论了静电力和表面电势的作用[5]。最近，Yoda和Kazoe采用隐失波照明技术测量了压力驱动流和电渗流中近壁500nm以内区域的速度分布[6]。这些研究都表明TIRV技术在微纳流动近壁测量中可以发挥重要的作用。可以说，基于全内反射隐失波的测速技术是目前最有效的百纳米量级空间分辨率的流动显示测量技术。更进一步，最新的一些结果显示，隐失波技术用于考察界面附近的物理问题仍有广阔的空间[7]。但是，该技术仍有些关键技术问题需要进一步解决。
在TIRV中，隐失波光强分布和其到壁面的距离成指数衰减的关系[8]，即
其中I0为界面处的隐失波基准光强，dp=λ/(4π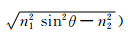
为穿透深度，n1为光密介质的折射率，n2为光疏介质的折射率，θ为入射角，λ为入射激光的波长。当荧光粒子处于隐失波照明场中时，其荧光光强的分布也符合这一规律。根据这一特性，测量粒子的亮度就可以获得粒子垂向位置z。隐失波照明技术中，基准光强I0对定位的准确性有至关重要的影响，然而入射光经过介质到达界面时，其亮度是未知量。上述文献中大多采用粘附在壁面上的粒子的亮度作为基准光强I0，但这种方法确定的基准光强存在很大的误差。Bouzigues等[5]提到，实验中测得粘附在壁面的粒子亮度有17%的标准偏差，这导致后续的粒子定位产生约17nm的误差。Yoda等[6]指出，粒子的z向定位误差最大来源是I0的不确定度，实验中采用的示踪粒子粒径分散性大于6%，测量粘附壁面粒子的亮度作为I0，其偏差大于10%，这主要是由于荧光粒子粒径的多分散性导致。Kazoe等[9]在研究近壁受限布朗运动时发现，实验中粒子z向定位误差在4.5~12nm，这主要来源于I0的确定有10%的误差。Wang等[10]指出在隐失波照明场中，粒径分散性将会给粒子垂向定位引入误差。Choi等[11]采用了测量大量(100个以上)粘附在壁面上的粒子的平均亮度作为基准光强I0，但是粒子在水溶液中由于双电层的排斥力，只有少量的粒子能够吸附在壁面上。他们采用了100mMol/L的NaCl溶液以减小粒子和壁面之间的双电层厚度，使得大量的粒子能够粘附在壁面上，进而测量其亮度值。这种方法因采用大量平均而减少了I0的误差，但是此方法受限于高浓度盐溶液，不容易推广到一般水溶液的测量中。我们还发现由于长时间暴露在激光照明场内，光漂白使得粘附在壁面的粒子亮度迅速降低，更增加了确定I0的难度。这些因素都给基准光强I0的确定及后续的粒子垂向定位带来了很大困难。
考虑到TIRV测量中，只有粒子亮度分布是最原始的测量数据，是否可以从亮度分布中找到可依据的信息来确定基准光强I0呢？Huang、Wang等人[4,10]曾根据近壁区的粒子浓度分布及粒子亮度指数衰减关系，并考虑了粒子的粒径分散性，给出了粒子亮度的概率密度函数。然而其中的I0为未知参数，解析求解有很大难度。本文从统计大量粒子的亮度分布规律着手，同样引入粒径分散性、粒子的浓度分布来定量描述粒子亮度的统计规律，给出粒子无量纲亮度I/I0理论分布的数值解。同时实验测量了隐失波光场内全部粒子亮度，得到了粒子亮度分布曲线，根据实验和理论分布相同的原则，可以定量确定基准光强I0。这种方法不受实验条件的限制，可以广泛用于各种溶液和示踪粒子。该方法定量的过程基于大量统计，可以进一步减小确定I0过程中的误差；同时还能描述粒子浓度分布及粒子粒径分散性对测量的影响。在此方法准确确定基准光强I0的基础上，可以进一步测量距离壁面百纳米附近流场的速度分布及纳米粒子的动力学特性。 1 理论分析
依据近壁区示踪粒子亮度的概率密度分布来确定界面处隐失波基准光强I0，首先要确定粒子亮度的概率密度分布。我们认为示踪粒子在壁面附近的浓度分布符合Boltzmann分布[12]，即
其中C+表示粒子浓度的无量纲分布，Φ为粒子与壁面的静电作用能，其表达式为:
其中ψ(z)为静电势，ψw为壁面的表面电势，q为单电荷电量，qp为粒子的当量电量，kB为Boltzmann常数，T为温度，κ为德拜长度的倒数，z为粒子中心到壁面的距离，a为粒子半径的均值。式(3)为粒子在静止流场液固界面附近的Boltzmann分布。根据我们前期的实验[13]，在较小壁面剪切率下(如2000s-1以下)，剪切流对近壁区粒子浓度分布影响可以忽略，Boltzmann分布仍然适用，在较大剪切率下，可以采用修正的Boltzmann分布。
如果纳米粒子的粒径分布符合高斯分布的特性，则其概率密度函数PDF(Probability Density Function)为，
其中，r为粒子半径，σ为其标准偏差。由于荧光粒子的激发光强和粒子的体积(即粒径的立方)成正比[2]，结合(1)式，粒子的亮度I(r，z)是其到壁面距离和粒径的函数，可用下式表示，
将粒子的亮度采用I0归一化处理，即
基于上述理论，利用Matlab数值解法，得到粒子亮度的概率密度函数的理论曲线。具体做法为，首先根据(2)、(3)式的Boltzmann分布生成总数N个粒子的垂向位置zi(i代表第i个粒子)，根据(4)式正态分布生成N个粒子的半径ri，然后根据(6)式计算这N个粒子的归一化亮度Ii(ri,zi)/I0。至此，N个粒径服从高斯分布，垂向位置服从Boltzmann浓度分布，并且亮度满足垂向指数衰减规律的粒子生成完毕。最后，采取统计的方法计算所有生成的N个粒子的归一化亮度I/I0的概率密度函数p(I/I0)。为了保证此计算统计量充足，粒子个数N达到5万个以上。这里需要说明的是，式(2)、(3)和(4)中相关的参数，如粒子粒径均值及标准偏差、静电作用相关的粒子电量、壁面电势和德拜长度，都可以通过独立实验测量确定。因此，对于不同工况的实验，我们均可给出其归一化亮度的概率密度函数)p(I/I0的曲线。
图 1为直径为100nm荧光粒子归一化亮度的理论概率密度函数p(I/I0)曲线，其中红色实线是粒子粒径相对标准偏差为17.5%时(此标准偏差值为实验实测值)的理论预测亮度PDF，蓝色虚线为粒径均一时(相对标准偏差为0%)的理论预测亮度PDF。可以看出，粒径分散性对粒子亮度分布PDF的影响主要体现在I/I0≈1附近的区域，也就是较亮粒子的分布区域。粒径均一时，最大亮度Imax=I0；而粒径标准偏差为17.5%时，最大粒径的粒子亮度会达到约2I0。此方法可以有效定量描述粒径分散性的影响。
 |
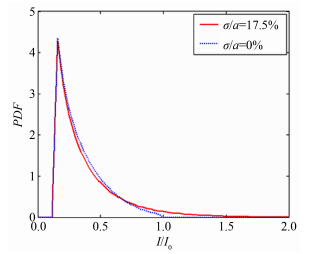| 图 1 φ100nm纳米粒子理论亮度分布 Fig. 1 Theoretical intensity distribution of φ100nm nanotracers |
实验观察采用Olympus IX71倒置荧光显微镜，配有100倍/NA=1.45全内反射专用油镜，如图 2所示。图像采集使用Andor ixon897 EMCCD，全幅模式下为512pixel×512pixel，单像素宽为160nm，实验中采用子区域拍摄，拍摄区域大小为80pixel×150pixel。荧光粒子采用标称直径分别为100和250nm的聚苯乙烯小球，采用动态光散射测量其粒径均值和标准偏差，分别约116.2±21nm和259.3±5.2nm，相对标准偏差分别为s=17.5%和s=2%。采用波长488nm的连续激光照明。
 |
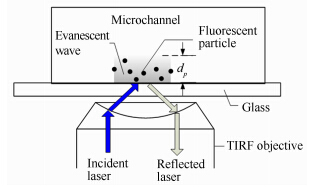| 图 2 实验装置简要示意图Fig. 2 Schematic of the experimental setup |
选取超纯水配置溶液，荧光粒子的体积浓度约为0.002%。实验在矩形截面管道中进行，管道的尺寸 为19.1μm×56.0μm×30.0mm，实际测量区域为管道中间部分约12.8μm×24.0μm的区域。将配置好的溶液注入管道，待溶液稳定后，用EMCDD记录粒子的图像，连续两帧图像的时间间隔Δt7ms，其中曝光时间te为0.4ms，同一位置连续拍摄10000张。拍摄时，以粘附在壁面的粒子为参考，采用具有纳米定位精度的压电传感器协助定位，把焦平面定位在壁面上。同一种实验条件下，改变位置拍摄5组图像。实验时，温度变化范围在19~21℃，相对湿度为20%~40% 。
根据实验观测，由于光漂白的作用，粘附在壁面的粒子在受较强隐失波照射约10s后，其亮度就会明显衰减，粒子亮度衰减一半的时间约为30s。对于流体内部的粒子，只有它们进入隐失波照明区域才会受光漂白的影响。而运动的粒子在照明区域内一般连续出现1~3帧(2帧时间间隔为7ms)即7~21ms，远小于光漂白作用约10s量级的衰减特征时间。因此，流体内的粒子受光漂白影响可以忽略。
采用Matlab软件处理实验图像，获取纳米示踪粒子的亮度信息，以测量其亮度分布，其中采用图像的灰度值表征亮度。具体的图像处理过程可分为图像滤波、粒子识别、亮度确定3个步骤。为了保留粒子的原始亮度信息，在进行图像滤波之前先复制原始图像，在副本上进行图像滤波、粒子识别处理，获取粒子的坐标以后，返回原始图像读取粒子的最大亮度。图像滤波是为了减小图像中的单点噪声，由于全内反射技术拍摄的图像质量较好，粒子无光晕，采用灰度阈值即可滤除噪音点。粒子识别过程中先对图像矩阵作出灰度值等值线，等值线围起来的灰度峰值区域判断为粒子区域，再根据质心法初步计算粒子位置。由于粒子光斑近似服从高斯分布，为了更精确地获得亚像素精度的粒子位置，我们采用高斯拟合法对粒子初步位置附近5个像素范围内进行二次定位，通过邻域内的像素灰度值进行高斯拟合，获得亚像素精度的粒子坐标。亮度确定是根据记录到的粒子坐标，在其周围5个像素的区域内查找最大灰度值像素点，作为粒子的亮度。图 3给出了连续3帧图像中2个φ250nm粒子的运动过程，从图中可以看出，粒子在运动的过程中其亮度有明暗变化，表征了粒子的垂向运动。
 |
| 图 3 连续3帧图像中2个φ250nm粒子的运动过程Fig. 3 Movement of two φ250nm particles in three consecutive images |
拍摄的图像经软件处理后，得到粒子的亮度信息。由于亮度太低的粒子接近背景亮度Ib，粒子识别误差较大，统计时首先选取约1.5Ib的亮度阈值滤除这部分粒子的干扰。对于φ100nm粒子，共统计约12600个粒子，粒子的概率密度分布如图 4所示。拍摄的粒子中亮度最大值Imax=1752，而拍摄时粘附在壁面上的粒子亮度由于光漂白作用仅为450。
 |
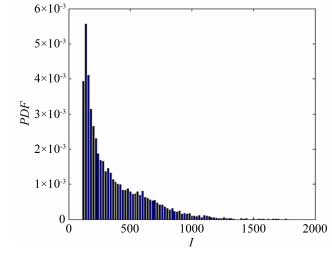| 图 4 φ100nm纳米粒子测量亮度分布Fig. 4 Measured intensity distribution of φ100nm nanotracers |
由于粒子理论亮度分布曲线(图 1)中各参数均由实验测量确定，我们认为实测粒子亮度和理论亮度(图 4)具有相同的分布，由此可以计算出待测参数I0。具体做法如下：根据理论曲线(图 1)计算得到归一化亮度范围0.1≤I/I0≤1内粒子的概率为:
对于实验数据(图 4)，令:
采用数值积分，求得I0=880。显然，采用此方法确定的基准亮度I0大于粘附在壁面上的粒子亮度(450)且小于最亮粒子亮度(1752)。此结果说明，目前不同方法之间确定I0有很大的不同，如果不采取有效的方法来确定I0可能引入很大的测量误差。
图 5(a)给出了φ100nm粒子的测量亮度概率密度分布和理论概率密度分布的比较，纵坐标为概率密度(PDF)，横坐标为归一化亮度I/I0。从图 5(a)中看出，在低亮度区域有一个位于I/I0=0.15的峰值。根据Boltzmann浓度分布，远离壁面的粒子浓度较大，使得低亮度区的粒子较多。值得注意的是，有部分粒子的亮度超过基准光强I0，这体现了粒子粒径分散性的影响。
 |
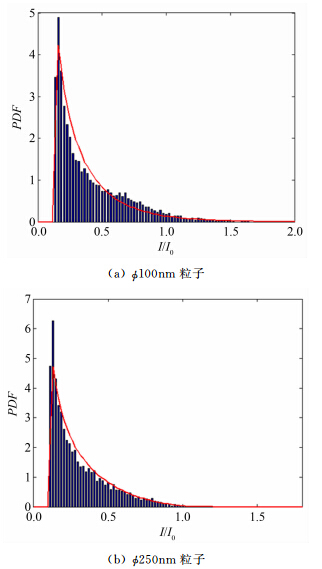| 图 5 粒子测量亮度分布和理论分布比较Fig. 5 Comparison between the measured and the theoretical intensity distributions of nanotracers |
采用同样的办法，计算并实测了φ250nm粒子亮度概率密度分布(图 5(b))，得到I0=1020。对比图 5(a)和(b)可以看出，由于φ250nm粒子的粒径分散性(s=2%)远小于φ100nm粒子的分散性(s=17.5%)，所以其亮度分布中，超过I0的粒子较少。同时，从测量的粒子亮度分布中可以看到，由于存在粒子粒径分布不均匀性，拍摄到的粒子无量纲最大亮度Imax/I0可以达到约1.3(φ250nm粒子)和2.0(φ100nm粒子)。这也恰说明，简单地从所有拍摄图像中取粒子最大亮度来确定I0，会引入约30%甚至更高的定位误差。 4 速度测量初步结果
我们还进行了矩形截面管道壁面附近速度测量，实验条件和上述实验相同，采用φ100nm聚苯乙烯小球作为示踪粒子。在此基础上，采用气泵加压驱动流动，压力为2000Pa。首先，按照第2节中图像处理方法对拍摄的图像进行处理，得到所有粒子的水平位置(x,y)和亮度信息I；然后，采用上述方法确定I0，再根据式(1)计算粒子的垂向位置z。如前文所述，本文方法假设近壁粒子符合Boltzmann分布在静态及低流速下适用。最后，根据粒子的水平位移计算粒子的速度。设在t时刻某一粒子的三维坐标为Mt(xt,yt,zt)，在t+Δt时刻，该粒子的坐标为Mt+Δt(xt+Δt,yt+Δt,zt+Δt)，流体流动方向为x方向，则粒子的速度V=(xt+Δt－xt)/Δt，垂向位置为zV=(zt+zt+Δt)/2。对所有拍摄到的粒子计算其在Δt内的速度V和垂向位置zV，根据粒子的垂向位置zV按照80nm的间距分层，统计每一层内的平均速度。
测量结果如图 6所示，图中蓝色实线为理论速度分布，空心圆圈是采用本文方法确定I0的速度测量结果，可见采用本文方法的测量速度基本与理论速度一致。图中误差条的长度根据同一层内所有统计的速度值的标准偏差给出，这是由纳米粒子的布朗运动导致，通过大量统计平均消除。作为比较，我们还采用拍摄到的粒子最大亮度作为I0的方法，同样给出了速度的分层测量结果，如图 6中实心圆圈所示。显然，简单由最亮粒子的亮度来确定I0，会导致粒子z定位30%以上的误差，使得测量速度出现极大的误差。这部分结果既是对本文方法可靠性的验证，也说明了发展有效定量确定I0的方法在近壁NanoPIV测量中的必要性。
此外，从图 6中可以看出，在250nm以下的区域测量速度存在偏大的现象，这部分的误差原因还在进一步研究中。
 |
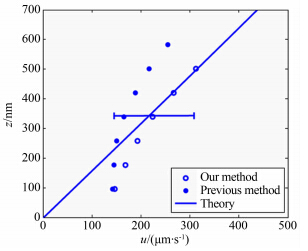| 图 6 测量速度与理论速度的比较Fig. 6 Comparison between the measured velocity data and the theoretical curve |
全内反射显微测量技术的关键在于确定隐失波界面基准光强I0，这是使用该技术对纳米示踪粒子进行准确垂向定位的基础。本文针对此问题，给出了一套确定基准光强I0的方法，并用φ100nm和φ250nm荧光粒子进行亮度测试实验。主要结果：
(1) 首先根据粒子亮度随高度呈指数衰减、粒子浓度Boltzmann分布以及亮度与粒径三次方成正比的理论，给出粒子理论亮度概率分布的数值解。通过实验测量纳米示踪粒子亮度分布。根据实验与理论粒子亮度概率分布相同，确定基准光强I0。
(2) 本实验方法可定量给出不同粒径粒子的I0值。实测φ100nm粒子的I0=880，φ250nm粒子的I0=1020。同样条件下使用较大示踪粒子得到的I0值也较大。
(3) 实验中发现粒径分散性对Imax/I0有影响。φ250nm粒子粒径相对标准偏差s=2%，其Imax/I0=1.3，而φ100nm粒子粒径s=17.5%，其Imax/I0=2.0，因此仅取Imax作为I0将产生高达30%的误差。可见采用本文介绍的新方法来确定I0并进一步进行粒子z向定位是很有必要的。
(4) 从速度测量结果来看，采用本文新方法确定I0得到的速度测量结果和理论曲线明显符合更好。
致谢: 感谢国家自然科学基金(No.11272322和No.11202219)的支持。
| [1] | Prieve D C, Frej N A. Total internal reflection microscopy: a quantitative tool for the measurement of colloidal forces[J]. Langmuir, 1990,6(2):396-403. |
| [2] | Kihm K D, Banerjee A, Choi C K, et al. Near-wall hindered Brownian diffusion of nanoparticles examined by three-dimensional ratiometric total internal reflection fluorescence microscopy (3-D R-TIRFM)[J]. Experiments in Fluids, 2004,37(6):811-824. |
| [3] | Banerjee A, Kihm K D. Experimental verification of near-wall hindered diffusion for the Brownian motion of nanoparticles using evanescent wave microscopy[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2005,72(4 Pt 1):42101. |
| [4] | Huang P, Guasto J S, Breuer K S. Direct measurement of slip velocities using three-dimensional total internal reflection velocimetry[J]. Journal of Fluid Mechanics, 2006,566:447-464. |
| [5] | Bouzigues C I, Tabeling P, Bocquet L. Nanofluidics in the Debye layer at hydrophilic and hydrophobic surfaces[J]. Phys Rev Letters, 2008,101(11):114503. |
| [6] | Yoda M, Kazoe Y. Dynamics of suspended colloidal particles near a wall: Implications for interfacial particle velocimetry[J]. Physics of Fluids, 2011,23(11):111301. |
| [7] | Chan C U, Ohl C D. Total-internal-reflection-fluorescence microscopy for the study of nanobubble dynamics[J]. Phys Rev Letters, 2012, 109:174501. |
| [8] | Hecht E, Zajac A. Optics[M]. Reading Mass: Addison-Wesley, 1974. |
| [9] | Kazoe Y, Yoda M. Measurements of the near-wall hindered diffusion of colloidal particles in the presence of an electric field[J]. Applied Physics Letters, 2011,99(12):124104. |
| [10] | Wang W, Guasto J S, Huang P. Measurement bias in evanescent wave nano-velocimetry due to tracer size variations[J]. Experiments in Fluids, 2011,51(6):1685-1694. |
| [11] | Choi C K, Margraves C H, Kihm K D. Examination of near-wall hindered Brownian diffusion of nanoparticles: Experimental comparison to theories by Brenner (1961) and Goldman et al (1967)[J]. Physics of Fluids, 2007,19(10):103305. |
| [12] | Zheng X, Kong G, Silber-Li Z. The influence of nano-particle tracers on the slip length measurements by microPTV[J]. Acta Mechanica Sinica, 2013,29(3):411-419. |
| [13] | Zheng X, Silber-Li Z. The influence of Saffman lift force on nanoparticle concentration distribution near a wall[J]. Applied Physics Letters, 2009, 95(12): 124105-124105-3. |