二维粒子图像测速技术(2D-PIV:Two Dimension Particle Image Velocimetry)作为非接触、全场、瞬态光学测试手段已广泛应用于实验流体力学,例如对喷流[1]、绕流[2, 3]、分离流等流场的测量。PIV在该类流场测量时光路布置特点是测量平面与来流方向平行或是测量平面内基本无法向速度分量。
PIV技术在一些流向旋涡的发生发展过程及流动结构研究中同样发挥着重要作用,例如翼尖涡[4, 5, 6, 7]、前缘涡[8, 9, 10]、桨尖涡[11]等流动的测量。PIV在该类流场测量中的光路布置特点是测量平面与来流方向垂直或是测量平面内存在法向速度分量。但是该情况下,会出现示踪粒子穿入穿出激光片光平面的情况,经CCD成像后产生透视误差。
实际上,体式PIV(SPIV:Stereoscopic PIV)已经能够从理论上消除透视误差,但是某些特殊流场存在空间狭小、标定困难等问题,不便于采用SPIV。而较为成熟的2D-PIV所需设备相对较少,光路布置简单,十分便于实验的开展。目前,已有较多的国内外研究者采用2D-PIV进行流向旋涡问题的研究,且对透视误差有了一定的了解。
早在1981年,瑞士联邦理工学院Jacquot和Rastogi采用光学方式测量固体位移时就指出离轴角为5°时可造成约10%的透视误差[12]。2000年,美国德拉华大学Prasad[13]在论述基于2台CCD相机的SPIV时分析了基于单台CCD相机的2D-PIV的不足,指出其不能测量垂直于测量平面的速度分量,且在一些流动条件下会存在透视误差。2002年,韩国浦项科技大学(POSTECH)Jong-Hwan和Sang-Joon[14]分别采用2D-PIV和SPIV在水中对一个具有5片前掠扇叶的轴对称风扇进行了测量,通过对比分析估计出了粒子穿出测量平面所产生的透视误差,并指出该误差与穿出平面的速度分量成比例关系。2010年,北京航空航天大学董超[9]等人针对大迎角非对称旋涡进行了SPIV和2D-PIV同步测量,比较了两者测量结果的差异,提出了一种减小透视误差的2D-PIV视场布置方案,成功地将2D-PIV测量中存在的透视误差由原来的14%、18%降到了5%以内。2013年,清华大学戴相录[15]等人分析了二维数字图像相关方法中对固体离面位移引起的测量误差,采用远心镜头进行测量减小了测量误差,并提出了基于理论模型的误差修正方法。由此可见,透视误差由来已久,也出现了一些有效减小和消除该误差的方法。
本文系统地分析了2D-PIV在垂直流向的截面测量时出现透视误差的影响因素,建立了测量平面内的误差模型,找出了理论计算的方法,并通过实验测量进行验证。最后,结合误差模型讨论了该误差对实际测量的影响,提出了3种减小透视误差的方法。 1 2D-PIV基本原理及光路布局要求
PIV技术建立在一个简单的关系之上,即速度是单位时间内运动的距离。粒子以合适的条件投放至流场中,将以一定的跟随性随流体运动。假如在一定时间间隔前后分别获得一张运动粒子(群)的图像,对比两张图像中相同的查问区域,通过互相关算法计算出粒子(群)运动的位移。结合已知的时间间隔,那么粒子(群)的速度矢量就可以得到。
基于该原理,常规2D-PIV擅长测量平行于流向截面内的速度分布。因此理论上光路布局要求激光片光与来流平行即CCD相机轴线与激光片光垂直,图 1为常规2D-PIV光路布局图。
 |
| 图 1 常规2D-PIV光路布局示意图 Fig. 1 Schematic of the traditional 2D-PIV optical layout |
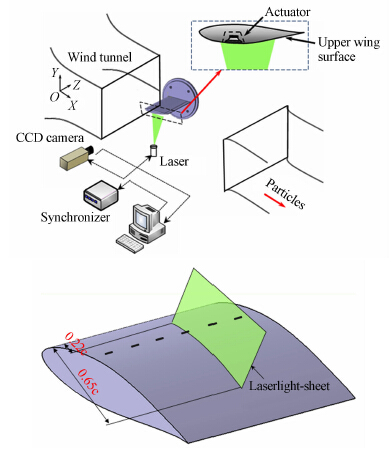
但是,目前国内外文献中采用2D-PIV设备在垂直于流向截面内进行流场测试的例子屡见不鲜[4, 5, 6, 7, 8, 10, 11],例如对流向涡的测量。图 2为2D-PIV用于翼尖涡测量的典型光路布局图,测量平面与流向垂直,此类光路布局中会出现明显的测量误差。
 |
| 图 2 2D-PIV翼尖涡测量的典型光路布局示意图Fig. 2 Schematic of wing tip vortex measurement |
2D-PIV采用图 2所示的光路布局进行测量时,流场中的示踪粒子会穿入穿出激光片光。此时,片光平面附近具有法向位移的粒子(群)投影在焦平面上时将产生横向虚位移,该虚位移会被视做粒子(群)的面内横向运动而处理得到一定的横向速度矢量。图 3为透视误差产生原理示意图。
 |
| 图 3 透视误差原理示意图Fig. 3 The principle schematic diagram of perspective |
设测量平面垂直于流向且气流速度为Uz,一次测量中A、B两个脉冲激光的时间间隔为Δt(s)。测试区域高度为H(m)、宽度为W(m)。相机距拍摄平面的距离为Z(m),如图 3所示。
PIV测量中,假定tA时刻粒子(群)位于CCD相机所聚焦的物平面内偏离视场中心OA的PA处,OAPA=x;Δt时间间隔后即tB时刻粒子(群)沿流向运动Δz距离到达PB处,此时该粒子(群)将被投影到CCD相机所聚焦的物平面内PB′处,OAPB′=x+Δx。Δx即为投影误差所造成的虚位移。该虚位移将被CCD相机通过光学原理成像在A、B两帧图像中,且会被PIV系统的图像处理软件通过互相关算法计算出来。
于是有运动方程:
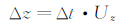
几何关系:
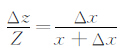
因此:
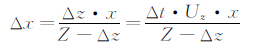
x向速度误差:
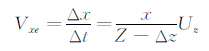
同样,y向速度误差:
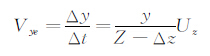
实际上,由于设定的时间间隔Δt非常短,Δz通常小于1mm,ΔzZ,因此以上两式可简化为:
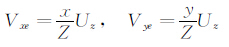
定义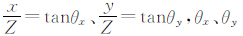 分别为x、y向离轴角。此时,透视误差模型可化为:
分别为x、y向离轴角。此时,透视误差模型可化为:
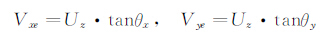
由此可见,透视误差与垂直于测量截面的法向速度和离轴角直接相关。
很明显,法向速度越大粒子运动产生的横向虚位移也就越大,误差就会越大。离轴角决定了在测量平面内不同位置上误差的大小。离轴角越大,x、y的绝对值越大,越偏离视场中心,透视误差也就越大。在同一来流条件下,无论图像尺寸的大小,图像中具有相同离轴角的位置其透视误差大小相同,因此,透视误差在测试平面中呈同心圆分布,且圆心始终位于视场中心。
定义视场系数:
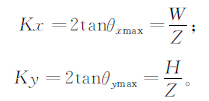
2D-PIV测试中通常采用较小畸变的定焦镜头,CCD具有固定的视场角和视场系数。视场角等于两倍的最大离轴角,在x和y向分别为2θxmax、2θymax。因此,最大透视误差为:
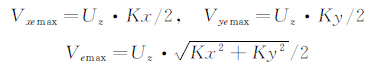
本文实验中所采用的一个焦长60mm定焦镜头,在x向的视场系数为0.15,即CCD镜头距离测量平面1m时,视场宽度为0.15m。根据透视误差模型,使用该镜头测量时在x向产生的最大透视误差约为法向速度Uz的7.5%。因此,2D-PIV测量所产生的最大透视误差与使用的镜头直接相关。 3 实验验证
通过建立的误差模型,可从理论上得到测量截面上的透视误差分布。设计了一种测试透视误差的实验方法,针对各影响因素做了对比测试。
射流风洞出口具有均匀的速度场,气流速度和流向确定且稳定,出口测量截面内湍流度在4‰以内,气流偏角小于0.2°。也就是说,在出口处横向速度分量小于主流的0.35%。在射流风洞出口横截面内,2D-PIV系统测量得到的流场结果中横向速度Vtr明显超过0.35%主流速度的即为透视误差,并与理论值进行对比分析。 3.1 实验设备装置
实验所使用的射流风洞出口尺寸为100mm×80mm,最大风速达35m/s。
实验采用美国TSI公司生产的2D-PIV系统,组件参数详见表 1。
| Components | Model | Parameter |
| laser | Dual Nd:YAG Laser | Power:120mJ/pulse |
| CCD | PIVCAM 14-10 | 1376pixel×1024pixel |
| synchronizer | 610035 | programmable |
| lens | NIKON | Kx=0.15 |
| software | Insight 3G | Version9.1 |
| particles | Glycerin,ethylene glycol | particle diameter≈5μm |
将测量截面选定在风洞出口,与来流垂直,激光片光距出口15mm,测量区域最大为60mm×44.6mm。图像处理采用Insight3G软件,查问域大小为100pixel×100pixel,重叠率为50%。最终结果由40次测量结果平均得到。
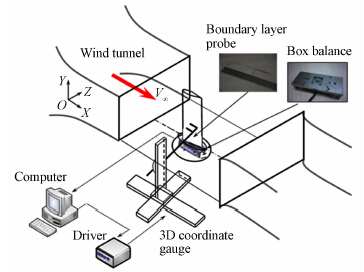
试验台采用光学平台和铝型材搭设,CCD相机可在导轨上前后移动以改变测试距离。整个测试中CCD相机轴线与风洞轴线平行,与激光片光垂直;而激光片光平面与风洞出口截面平行且保持15mm的距离。图 4给出了实验装置照片。
 |
| 图 4 实验装置布局照片Fig. 4 Photograph of experimental setup layout |
根据误差模型,实验主要从以下几个因素进行测试:来流风速V∞、测试距离Z、镜头焦长f。表 2为测试的各影响因素的实验参数。
| Influence factors | Experimental value |
| Incoming flow V∞/(m·s-1) | 12.8,19.4,25.9,32.3 |
| Measurement distance Z/mm | 200,300,400 |
| Lens focus length f/mm | 60,105 |
测量截面内法向速度为透视误差的直接来源。测试时只改变来流速度。其它测量参数为Z=300mm、Δt=10μs、镜头焦长f=60mm。此时,PIV测试区域为45mm×33.5mm。
图 5为不同风速下测试区域内误差分布及与理论误差分布对比情况。从上到下来流风速依次为:12.8,19.4,25.9和32.3m/s。实际测量的误差分布图形状基本与理论误差分布一致,等误差线呈圆环状分布,且圆心位于视场中心。对于不同的风速条件,2D-PIV测量结果中的相同相对位置处的误差会随风速增大而增大。
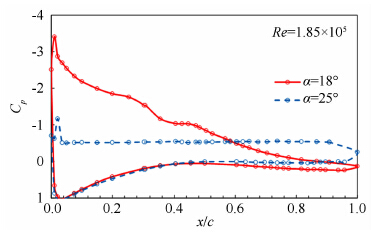 |
| 图 5 来流风速对透视误差的影响Fig. 5 Influence of streamwise velocity |
图 6为测试区域(视场)右下角抽取出速度矢量的2个方向的速度分量Vxe和Vye即透视误差随来流速度的变化曲线,该结果表明透视误差与法向速度成线性比例关系,测量误差随来流风速增大而增大。
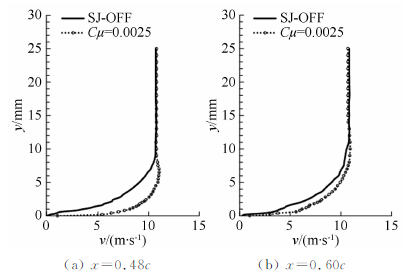 |
| 图 6 透视误差大小随来流风速的变化曲线Fig. 6 The relationship between velocity components from the bottom right corner and normal velocity component |
实测误差分布图中等误差圆环不够规则,主要原因是实际光路布局中激光片光未能与来流保持严格的垂直、CCD相机轴线与片光也未能保持严格的垂直。 3.3 测试距离的影响
保持激光片光位置不变即测试平面固定,调整CCD相机与测试平面的距离,可得到尺寸大小不同的测试区域。其它测量参数为V∞=32.3m/s、Δt=10μs、镜头焦长f=60mm。表 3为各测试距离下视场区域尺寸。
| Measurement distance Z/mm | View field W×H/(mm×mm) |
| 200 | 30×22.3 |
| 300 | 45×33.5 |
| 400 | 60×44.6 |
CCD相机采用定焦镜头,具有固定的视场角(视场系数)。当改变测试距离时,图像尺寸也会随着改变。图 7为3种测试距离时,视场内误差分布图以及与理论误差分布的对比。结果显示无量纲化后视场内误差分布不随测试距离改变而改变。实际上,只要镜头不变,视场内误差分布是一样的。
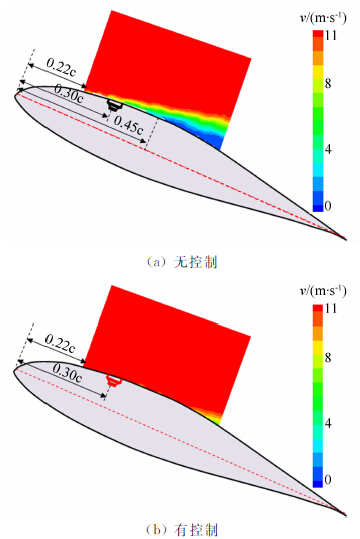 |
| 图 7 测量距离对透视误差的影响Fig. 7 Influence of measurement distance |
对于该镜头,横向视场系数为0.150,纵向视场系数约为0.112。在测试区域内最大透视误差分布在视场的最边缘,最大理论误差为3.02m/s,约为法向速度的9.3%。而实验测量结果显示,截面内边缘处最大横向速度为2.64m/s,约为法向速度的8.2%,这与理论结果接近。
但是,改变拍摄距离可以改变核心流场区域(例如翼尖涡区域)在视场内所占的比例。因此,可以通过增大拍摄距离将核心流场区域布置在误差较小的视场中心区。 3.4 镜头焦长的影响
采用2个焦长不同的镜头进行透视误差测试,以检验视场系数对透视误差的影响,2个镜头参数如表 4所示。
| Focus length/mm | View field coefficient(x & y direction) |
| 60 | 0.150 | 0.112 |
| 105 | 0.081 | 0.060 |
图 8为采用2种镜头时的测量误差分布以及对应的理论误差分布。2种镜头所测量的误差分布图明显不同,测试区域中相对位置相同的地方长焦镜头的测试误差明显要小。
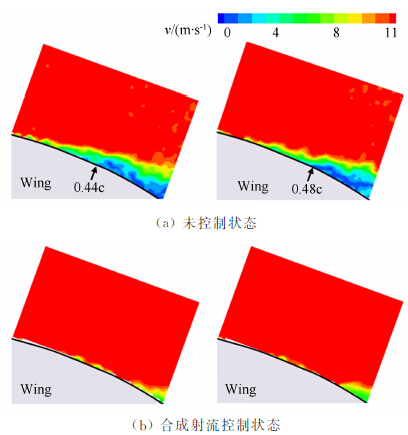 |
| 图 8 CCD镜头对透视误差的影响Fig. 8 The influence of focus length |
相同的测试距离,焦长为105mm的镜头视场明显比60mm焦长的要小,即长焦镜头的视场角、视场系数小,最大误差也就小。反过来,对于相同的测试区域尺寸,长焦镜头需要增大测试距离,因而可以减小透视误差。对于该长焦镜头,测试区域内最大理论误差为Vemax=1.5m/s,约为法向速度的5.0%。因此,一个定焦镜头决定了一种透视误差分布。
无论是测试距离Z还是镜头焦长f,它们直接影响着视场的离轴角θ。通过对PIV测量中3个关键参数进行测试,结果显示理论误差分布与实测误差分布基本一致,说明了误差模型的正确性。特别要指出的是,该模型是基于测量平面与流向垂直的状态建立的。实际上,透视误差只跟垂直于测量平面的法向速度分量有关,而与平行于测量平面的速度分量无关。因此,该模型同样应用于测量平面与流向存在一定夹角时的情况,只需找到法向速度分量即可。 4 透视误差对测量结果的影响及减小措施
在流向涡的2D-PIV测量中,存在透视误差且有些情况下还比较突出,对测量结果会造成明显的影响。主要有3方面:改变流场速度量值大小、改变旋涡形状、改变旋涡的位置。 4.1 改变流场速度量值大小
透视误差的产生使测量平面内出现了最大为9.3%法向速度大小的横向速度,直接改变测量截面内的速度矢量的大小。图 5中的测量误差分布图,理论上测量截面内不存在横向速度分量,而测试时出现了横向速度分量。 4.2 改变旋涡形状
透视误差同时也会改变旋涡的形状。图 9(a)为模拟来流为32.3m/s时的一个流向旋涡,按照误差模型,PIV测量时将得到图 9(b)所示结果,即融入透视误差后的旋涡,速度矢量明显发散,该结果与原始旋涡相比形状发生了改变。
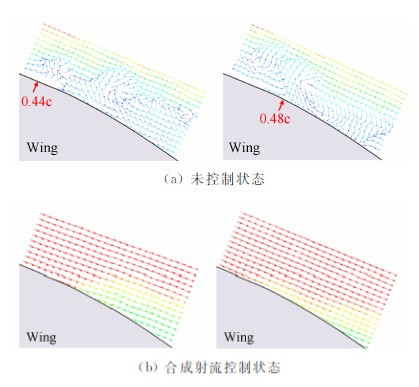 |
| 图 9 透视误差改变旋涡形状示意图Fig. 9 Perspective error change the shape of vortex |
图 10(a)为模拟的另一个流向旋涡,旋涡中心偏离视场中心。对该类流场进行2D-PIV测量时,含透视误差的结果将类似图 10(b)。模拟旋涡中心原始位置为(45,22),融入透视误差后旋涡中心变为(42,16),旋涡位置变化量为(-3mm,-6mm),约占视场尺寸的10%。
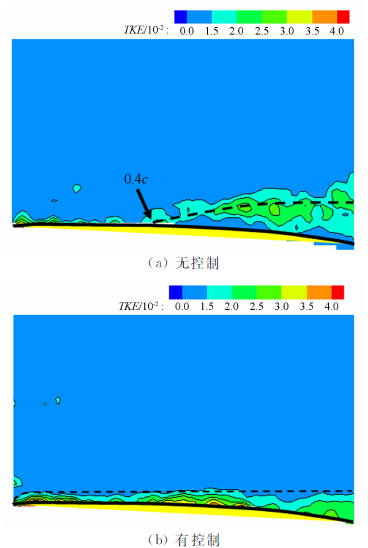 |
| 图 10 透视误差改变旋涡中心位置Fig. 10 Perspective error change the position of vortex |
旋涡偏移的方向与旋涡的旋转方向有关。融入透视误差后旋涡中心将绕视场中心沿着旋涡旋转方向偏移一定的距离。这种偏差在某些情况下将会误导人们对流场的认识,例如采用2D-PIV测量翼尖涡发生发展变化过程时,旋涡中心未能布置在PIV视场的中心,测量得到的翼尖涡涡核位置将偏离它实际的位置。 4.4 减小透视误差措施
截面内存在法向速度时,采用2D-PIV进行测量可采用的减小误差的措施包括:
(1) 在硬件上选择长焦镜头。在满足测试区域尺寸要求情况下,长焦镜头可明显减小透视误差。实验所采用的长焦镜头将最大透视误差由9.3%减小为5%。
(2) 在光路布局上将测试重点区域布置在视场中心。视场中心区域的透视误差小,且旋涡位置偏移误差也小。但该方法会降低流场尺度分辨率。
(3) 在软件处理方面对测试区域内的透视误差进行修正。如果获得测量截面法向速度(一般估算出均值),就可通过误差模型对测量结果进行修正,以减小透视误差的最大量值。 5 结 论
通过研究,可得到如下结论:
(1) 2D-PIV测量截面内存在法向速度时,会出现透视误差,且以视场中心为圆心呈环状分布;
(2) 透视误差的关键影响因素为法向速度分量和离轴角;透视误差的大小与法向速度成比例关系;离轴角决定了透视误差在测量平面内成同心圆分布;
(3) 透视误差对测量结果的影响主要体现在3方面:改变流场速度量值大小、改变旋涡形状、改变旋涡的位置;
(4) 提出的减小透视误差措施,为2D-PIV在垂直流向截面测量应用中的改进提供了指导意见。
| [1] | Lou Huadong. Control of supersonic impinging jets using microjets[D]. Florida State University, 2005. |
| [2] |
田立丰, 易仕和, 赵玉新, 等. 超声速光学头罩流场的PIV研究[J]. 实验流体力学, 2010, 24(1): 26-29. Tian Lifeng, Yi Shihe, Zhao Yuxin, et al. PIV study of supersonic flow around an optical bow cap[J]. Experiments in Fluid Mechanics, 2010, 24(1):26-29. |
| [3] |
解克, 李晓东, 林大楷. 圆柱/翼型干涉流场的试验研究[J]. 飞机设计, 2009, 29(4): 6-12. Xie Ke, Li Xiaodong, Lin Dakai. An experimental investigation of the flow field of rod airfoil interaction[J]. Aircraft Design, 2009, 29(4):6-12. |
| [4] | Zhou Yu, Zhang Hong J. Wing-tip vortex measurement with particle image velocimetry[R]. AIAA 2004-2433. |
| [5] |
顾蕴松, 程克明, 郑新军. 翼尖涡流场特性及其控制[J]. 空气动力学报, 2008, 26(4): 446-451. Gu Yunsong, Cheng Keming, Zheng Xinjun. Flow field characteristics of wing tips vortex and its control[J]. Acta Aerodynamica Sinica, 2008,26(4):446-451. |
| [6] | Steven J Beresh, John F Henfling. Meander of a fin trailing vortex measured using particle image velocimetry[R]. AIAA 2009-406. |
| [7] | Yang Ke, Xu ShengJin. Wing tip vortex structure behind an airfoil with flaps at the tip[R]. Science China, 2011, 54 (4): 743-747. |
| [8] |
刘国政,唐敏中,张伟,等. 80°三角翼流动显示和涡频测量试验研究[J].实验流体力学,2006,20(1):62-66. Liu Guozheng, Tang Minzhong, Zhang Wei, et al. The investigation of a 80-deg sweep delta wing on flow visualization and vortex frequency measurement[J]. Experiments in Fluid Mechanics, 2006,20(1):62-66. |
| [9] |
董超, 邓学蓥, 王延奎, 等. 2DPIV视场布置方案研究[J]. 空气动力学学报, 2010, 28(5): 602-608. Dong Chao, Deng Xueying, Wang Yankui, et al. Investigation to disposition scheme of 2DPIV field of view[J]. Acta Aerodynamica Sinica, 2010, 28(5): 602-608. |
| [10] | Meng Xuanshi, Qiao Zhide. Flow over delta wing with low dorsal fin-piv study[R]. AIAA 2009-541. |
| [11] |
杨永东, 武杰. 悬停旋翼桨尖涡的试验研究[J]. 实验流体力学, 2008, 22(3): 36-40. Yang Yongdong, Wu Jie. Investigation of hovering rotor tip vortex[J]. Experiments in Fluid Mechanics, 2008, 22(3):36-40. |
| [12] | Pierre Jacquot, Pramod K Rastogi. Influence of out-of-plane deformation and its elimination in white light speckle photography[R]. Optics and Lasers in Engineering, 1998, 2: 33-55. |
| [13] | Prasad A K. Stereoscopic particle image velocimetry[R]. Experiments in Fluids, 2000, 29:103-116. |
| [14] | Jong-Hwan Yoon, Sang-Joon Lee. Direct comparison of 2D PIV and stereoscopic PIV measurements [R]. Meas Sci Technol, 2002, 13: 1631-1642. |
| [15] |
戴相录, 谢惠民, 王怀喜. 二维数字图像相关测量中离面位移引起的误差分析[J]. 实验力学, 2013, 28(1): 10-19. Dai Xianglu, Xie Huimin, Wang Huaixi. Analysis of the error caused by off-plane displacement in two-dimensional digital image correlation measurement[J]. Journal of Experimental Mechanics, 2013, 28(1): 10-19. |



