2. 上海理工大学 机器智能研究院,上海 200093
2. Institute of Artificial Intelligence, Shanghai University of Technology and Engineering, Shanghai 200093, China
乒乓球的致胜因素分为速度、力量、旋转、落点、弧线。其中,旋转是乒乓球比赛中最核心的致胜因素。乒乓球的旋转主要源于乒乓球与球拍、球台之间的摩擦。由于它们在碰撞过程中,并不是绝对光滑的接触,而是有摩擦力的作用,故而导致乒乓球所受合力偏离了球的重心而发生旋转。由于乒乓球体积小、质量轻,离心的摩擦力会使其产生较大的旋转速度。这种高速旋转将产生一个与旋转角速度矢量和线速度矢量组成的平面相垂直的马格努斯力,该力量导致整个乒乓球的运动轨迹发生偏移。运动员在击球过程中,需要对乒乓球的旋转进行预判,进而预估乒乓球的落点。运动员对乒乓球落点的预判是基于经验的判断,而对于乒乓球科研而言,需要设计算法找到乒乓球运动轨迹和旋转之间的联系,利用数据对运动员进行更加直观的指导。
目前,对乒乓球旋转与轨迹之间联系的研究主要集中在乒乓球机器人控制领域,若使乒乓球机器人准确地击打乒乓球,就必须准确预测乒乓球的轨迹[1-5]。目前,在乒乓球无旋转的情况下,可以较准确地预测其轨迹。Zhang等[6-7]假设平行于接触平面的2个方向上的速度在碰撞前后呈线性关系,在碰撞平面的法线方向上,利用弹性恢复系数得到了乒乓球碰撞后的速度,然后根据受力情况采用近似的物理模型对乒乓球的运动轨迹进行预测。该方法的优点是预测时间短,可以满足实时性,但参数的不确定性导致不能精确建模,难以推广到旋转球的应用中。
针对有旋转的乒乓球轨迹的预测问题,任艳青等[8-9]较全面地分析了马格努斯力对飞行轨迹的影响。他们设计了一种基于模糊BP神经网络的轨迹预测分类器,该分类器经过离线训练之后可以在一定程度上区分球是否旋转,但是对球的旋转分类很简单,数据量也不够,误差较大。季云峰等[10-11]针对无特殊标记乒乓球的旋转计算问题提出了一种新的计算方法,在假设乒乓球上的商标被准确检测出来的情况下,利用5帧图像中商标的运动轨迹计算乒乓球旋转速度及方向。其核心思想主要是根据3D转2D投影中轨迹会发生变化计算旋转轴的角度,并在后续的优化算法中将5帧图像缩短为连续的4帧图像。
张远辉等[12]利用扩展卡尔曼滤波方法对旋转球的角速度进行在线测量,但是该方法的计算量很大,误差也较大,很难满足测量要求的实时性。张康洁等[13]通过分析旋转乒乓球飞行过程的运动学模型,采用无迹卡尔曼滤波思想构建过程方程和观测方程,利用视觉系统观测到的三维空间位置信息对线速度和角速度进行估计。孙智宇[14]采用Extreme Learning Machines (ELM)算法对乒乓球的旋转进行分类估计,将旋转类型分为上旋、下旋和侧旋3种,在乒乓球的旋转运动轨迹中找到连续10帧图像作为ELM算法的输入,然后创建ELM模式识别网络。该算法在分类准确度和计算时间上有了一定进步,但算法较为简单,分类不够细致,很难应用于真实的对打环境。
目前的旋转轨迹预测算法对旋转的分类较为简单,但在实际的对打过程中,仅对乒乓球的旋转进行简单分类不能满足正常回球需要。针对这一问题,本文通过设计实验获得乒乓球精确的初始位置坐标、精确的初始速率及方向、精确的旋转速率及方向,把这9个初始数据作为神经网络的输入信息,将精确的落点坐标作为输出信息,利用人工神经网络算法探讨输入、输出信息之间的相关性,为精确预测旋转球的轨迹提供理论及实验基础,为后续应用于乒乓球机器人击打旋转球提供参考。
1 实验设计 1.1 实验系统本实验设计的数据采集实验系统包括2台中速摄像机、2台高速摄像机、1台高精度发球机、2台补光灯和1台同步灯,并在乒乓球桌后面摆放一块记分牌和一幅长3.5 m、宽2 m的幕布。整套系统的设计思路是控制发球机发不同类型的旋转球,利用2台中速摄像机拍摄球的整个运动轨迹,利用2台高速摄像机拍摄乒乓球的旋转轨迹,再综合运动轨迹和旋转轨迹的数据信息进行分析。其中:中速摄像机摆放在乒乓球桌的两边,速度为250帧/s,对乒乓球的整个运动轨迹进行拍摄;同步灯在发球机发球的瞬间亮起,以便于后续处理运动轨迹时对2台中速摄像机进行同步。高速摄像机放在乒乓球桌两边,主要拍摄发球机刚发出球的旋转轨迹,速度采用3 000帧/s,利用乒乓球上商标的旋转来确定乒乓球的旋转速度。不同的摆放位置是为了扩大视野,确保至少有1台高速摄像机能清晰地拍摄到乒乓球的商标。拍摄过程中会遇到拍摄不到商标的情况,这种情况比较少见,将其舍弃,重新拍摄。2台补光灯用来对乒乓球的整个运动轨迹进行补光,以方便后续数据的采集,摆放位置以不影响摄像机拍摄为主,覆盖整个乒乓球桌即可。
1.2 实验数据的采集在本实验中,主要是采用SIMI Motion软件对运动轨迹进行分析处理。SIMI Motion软件是一款基于三维录像的、可分析各种形式运动及动作的软件系统,目前被广泛应用于体育运动的技术分析及教学中。它主要是利用多台摄像机同步拍摄物体的运动轨迹,利用多维立体架进行定标,手动标记关节点,可以自动获得物体移动的二维及三维数据,从而进行坐标值、速度、加速度以及标记点之间角度等多种数据的计算。本实验主要利用SIMI Motion软件与2台摄像机同步获得乒乓球的运动轨迹数据。SIMI Motion软件的多维立体架如图 1所示,通过拍摄2台摄像机中的多维立体架,手动标记立体架上的白色圆点,即可完成定标。

|
图 1 SIMI Motion软件多维立体架 Figure 1 Multi-dimensional shelf of SIMI Motion software |
事先对2台中速摄像机进行定标,之后利用同步灯同步2个视频的时间,再利用SIMI Motion软件手动标记确定每帧图片中乒乓球的空间位置,如图 2所示,从而获得乒乓球整个运动轨迹的三维数据。

|
图 2 2台摄像机拍摄运动轨迹 Figure 2 The trajectory of ball movement with two cameras |
获得完整的运动轨迹后计算乒乓球的旋转速度,旋转速度是一个矢量,有大小和方向。
高速摄像机可以拍摄发球机发射乒乓球初始阶段的旋转轨迹。图 3(a)为乒乓球刚出发球机口时的状态,此时记为视频中的第n1帧;图 3(b)为乒乓球旋转1周时的状态,此时记为视频中第n2帧。高速摄像机的帧率为3 000帧/s,从而可以得到乒乓球旋转速度为3 000/(n2-n1)(r/s)。

|
图 3 高速摄像机拍摄乒乓球的旋转轨迹 Figure 3 The rotation of ball movement with high-speed cameras |
旋转方向是通过发球机控制的,发球机通过2个滑轮对乒乓球进行摩擦产生旋转,通过控制上下滑轮的速率和方向控制旋转速度(大小和方向)。本实验将发球机能发出来的所有旋转类型发球都进行了实验,一共有9种旋转类型的发球,依次为上旋、下旋、不转、左旋、右旋、左侧上旋、左侧下旋、右侧上旋、右侧下旋。旋转类型说明如表 1所示。
| 表 1 发球机发球的旋转类型 Table 1 Rotation type of tables tennis from the serve machine |
由表 1可见,由于发球机的局限性,只能发出这9种类型的球,滑轮与水平方向的夹角决定了球的旋转方向,而由于发球机的出球口是水平的,故出球方向是水平的。通过前文所述,可以获得球的速度,而出球口的初始位置已知,因此可以获得精确的9个初始数据,分别为:初始位置x方向的坐标(x),初始位置y方向的坐标(y),初始位置z方向的坐标(z),初始位置x方向的速度(vx),初始位置y方向的速度(vy),初始位置z方向的速度(vz),初始位置x方向的旋转速度(ωx),初始位置y方向的旋转速度(ωy),初始位置z方向的旋转速度(ωz)。坐标系原点设在发球机所在台面的中点,横坐标沿横向台面,纵坐标沿纵向台面,纵坐标垂直于台面。发球机共发了171个有效球,涵盖9种类型的发球,并获得了所有球的9个初始数据及落点数据。因落点都是在台面上,故纵坐标值为0。
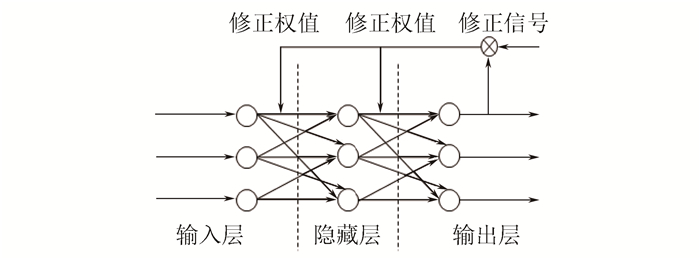
2 人工神经网络模型及结果分析 2.1 人工神经网络简介人工神经网络(Artificial Neural Networks, ANNs)是一种模拟大脑内部神经机理进行信息处理的数学模型,由大量功能简单的神经元以某种拓扑结构连接而成。神经网络示意如图 4所示。
|
图 4 神经网络示意 Figure 4 Schematic of neural network |
神经网络中各个神经元从前一级得到输入,输出给下一级神经元,通过非线性函数的多次复合进行信息处理,同时根据修正信号反向修正权值,降低误差,最终实现信号从输入层到输出层的变换。
2.2 确定输入输出神经元本实验使用MATLAB模式识别函数对不同速度、旋转类型的乒乓球轨迹落点坐标进行预测,输入层神经元节点数维数m=9,为前文所述的9个初始数据,记为
| $ \mathit{\boldsymbol{M}} = \left[ {x\;\;y\;\;z\;\;{v_x}\;\;{v_y}\;\;{v_z}\;\;{\omega _x}\;\;{\omega _y}\;\;{\omega _z}} \right] $ |
输出层神经元节点数维数n=2,为乒乓球的落点横坐标及纵坐标,记为L=[X Y]。乒乓球在落点过程中会有一个临界点,运动方向从向下变为向上,而由于本实验拍摄运动轨迹时采用的摄像机的帧率较高(250帧/s),每2帧之间乒乓球所移动的距离很短,故可将乒乓球处于下降的最后一个时刻(运动方向由向下转为向上之前的时刻)定为乒乓球的落台状态。此时乒乓球的位置记为落点位置,即z=0的点,由于摄像机的帧率足够高,可以确保落台时2帧之间的距离很短,从而可以保证误差较小,因此可以基本确定为乒乓球的落点位置。
乒乓球的旋转类型共有9种。对于每一种旋转类型,设计不同的轨迹发球20种,共计180种。在实验过程中,由于发球机的局限性以及摄像机拍摄等原因会造成一些实验数据的缺失,最终导致获得的有效数据共171组,基本被9种旋转类型数据均分。在171组有效数据中,随机选取70%(即119个数据)作为训练样本,随机选取15%(即26个数据)作为修正样本,剩余的15%(即26个数据)作为测试样本,验证拟合的关联度。
确定输入输出神经元后,接下来要确定隐藏层的节点数,参照经验公式
| $ h = 0.43\;mn + 0.12\;{n^2} + 2.54\;m + 0.77\;n + 0.35 + 0.51 $ |
来计算节点数, 代入m和n的值,并进行四舍五入即可计算出隐藏层节点数为6。
2.3 神经网络拟合算法选择MATLAB神经网络工具箱中的拟合算法,依次对Levenberg-Marquardt、Bayesian Regularization以及Scaled Conjugate Gradient算法进行实验。实验结果表明,Levenberg-Marquardt算法的拟合效果最好,故本文选择Levenberg-Marquardt算法[15-18],拟合步骤如下:
(1) 选取初始权值W。
(2) 输入初始训练样本M1, M2, …, Mq,其中,q=119, 共119组训练数据。
(3) 计算隐节点输出hi=
(4) 计算输出节点的输出l=
(5) 计算所有样本实际输出与期望输出的误差之和,e=∑[(t-l)2/2]。其中,t为期望输出。
(6) 若误差未达到期望值,且向着减小的方向,则μ减小;若误差未达到期望值,且向着增大的方向,则μ增加。计算权值修正量:Δw=[JTJ+μI]-1JTe,I为单位矩阵,J为误差对权值微分的Jacobian矩阵,μ为参数,e为网络误差矢量(由第k步训练过程中计算出的误差之和e值乘以单位矩阵所得);修正网络各层权值:w(k+1)=w(k)+Δw,其中,k为训练步数。
(7) 返回步骤(2),直至满足以下条件之一跳出:误差达到要求;训练步数超过定值;μ值超过给定的最大值。
本文的拟合算法选用Levenberg-Marquardt算法是因为其拟合效果较好,抗噪能力强,拟合时间短,比较适合于本实验,接下来对实验流程进行描述。
2.4 实验步骤本文使用MATLAB中的神经网络工具箱实现神经网络的设计,具体的实验步骤如下:
(1) 采集数据,将输入、输出数据导入数据库。
(2) 对数据进行简单处理,主要包括数据归一化和调整排序等,归一化的变换公式为:
(3) 建立神经网络,设置输入节点、输出节点、隐含层节点及传输函数初始结构。
(4) 将训练次数、训练目标、误差等参数设置好,开始进行训练,并加入修正数据进行权值修正。
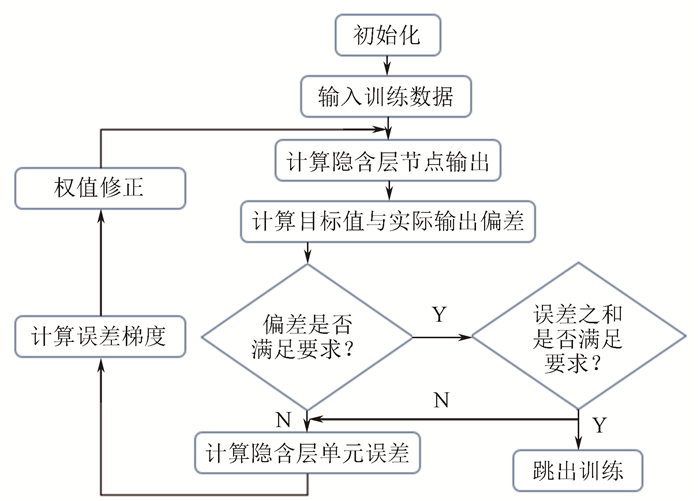
(5) 训练流程如图 5所示,训练结束后输入测试数据进行测试。
|
图 5 训练流程 Figure 5 Training flowchart |
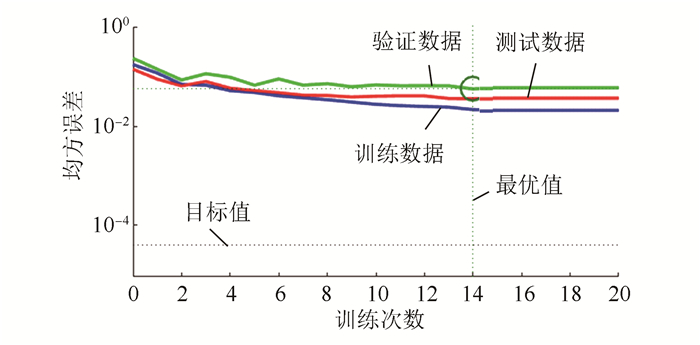
根据上述步骤利用MATLAB神经网络工具箱进行训练,训练结果如图 6所示。可见:当训练次数为14次时出现最小的均方误差,为0.057 159;当训练次数为14次时,竖虚线与3条实线相交,3条实线从上向下依次为验证数据、测试数据和训练数据的均方误差曲线。
|
图 6 均方误差曲线 Figure 6 Mean square error curves |
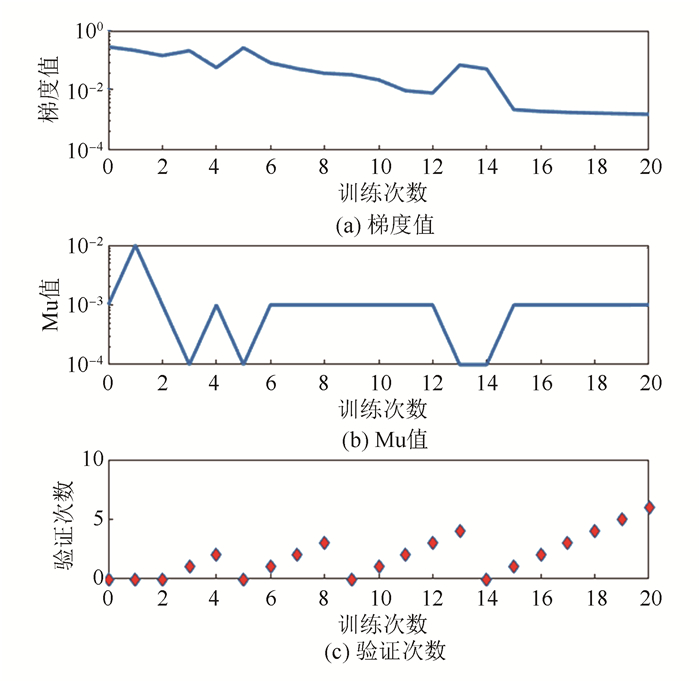
图 7所示为神经网络的训练状态。图 7(a)表示训练梯度的变化,可以看出,梯度值随着训练次数的增加总体呈下降的趋势,当训练次数为20次时,梯度值为0.001 598 8。图 7(b)表示Mu值的变化趋势,本文的拟合算法选择的是Levenberg Marquardt算法,Mu值是该算法中的一个参数,其随着误差变大而增加,直到误差不再增加为止。当训练次数为20时,Mu值为0.001,并保持稳定。图 7(c)表示训练过程中的有效验证次数,可以看出,当训练次数为20时,有效验证次数为6次。
|
图 7 神经网络的训练状态 Figure 7 Training state of network |
图 8所示为拟合结果。图中:虚线代表预期结果,R值代表的是预期结果和拟合结果的相关系数,并且R∈[0, 1]。一般而言,R值越接近1,说明拟合结果与预期结果越接近。在本实验中,训练及测试结果中的R值分别在9.5和9.3以上,这说明初始速度、旋转类型及初始位置坐标与球落点坐标之间存在很大的相关性,本文选择的方法也较为适当。
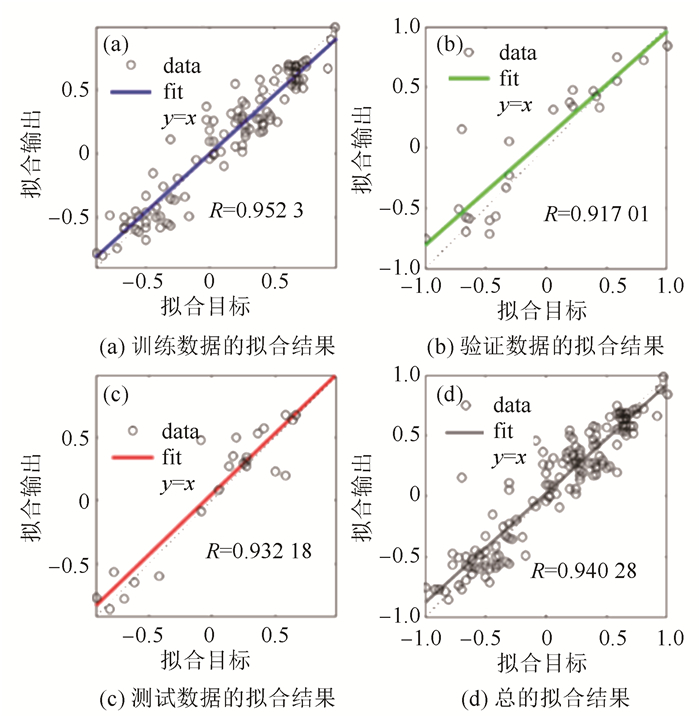
|
图 8 拟合结果 Figure 8 Fitted results |
本文的创新点体现在以下几点:①设计全新实验获得精确的速度、旋转类型及位置坐标信息;②第1次利用精确的速度、旋转数据预测乒乓球的落点信息,之前的研究都是对乒乓球的旋转进行模糊分类预测乒乓球的运动轨迹,但分类太粗糙,对旋转球的真实轨迹预测不理想;③选用合适的拟合算法,拟合效果良好,便于后续研究。作为第1次探讨精确速度、旋转数据对落点影响的实验,本文同样存在一些问题和不足:①数据较为单一,发球机集中在中路发球,轨迹较为类似;②旋转方向类型受限,旋转数据不够全面;③发球机发球旋转速度最高为90 r/s,而运动员最高可击打出的旋转速度为170 r/s。
受设备及环境影响,数据量在短时间内无法扩充。本文的主要目的是证明乒乓球的旋转与运动轨迹之间的相关性很大,这可为后续利用乒乓球轨迹反推旋转作为理论依据。乒乓球旋转是最重要的制胜因素,研究乒乓球的特征必须将旋转加入,笔者希望设计实验验证乒乓球旋转直接影响乒乓球的运动轨迹,故通过其相关性来证明。最终Levenberg-Marquardt拟合相关性达到90%以上,虽然受到数据样本量的困扰,并未达到最理想的效果,但是在一定程度上已经可以证明乒乓球旋转与运动轨迹之间的相关性很大。同时,针对以上不足之处,在后续研究中拟对运动员击打球进行测试,同时设计旋转计算公式,结合图像处理方面的知识完成旋转测速的自动化,以满足更多的实验设计。希望在后续工作中可以完善乒乓球轨迹预测算法,提高预测精度,缩短预测时间,最终能应用于乒乓球机器人,为其击打旋转乒乓球奠定基础。
| [1] |
AKRIA N, YUKI O.Robotic table tennis based on physical models of aerodynamics and rebounds[C]//Robotics and Biomimetics(ROBIO), IEEE International Conference.[s.l.]: [s.n.], 2011: 2348-2354
https://www.researchgate.net/publication/254025486_Robotic_table_tennis_based_on_physical_models_of_aerodynamics_and_rebounds (  0) 0)
|
| [2] |
NAKASHIMA A, TSUDA Y, LIU C, et al.A real-time measuring method of translational/rotational velocity of a table tennis ball[C]//Proceeding of 5th IFAC Symposium on Mechatronic Systems.[s.l.]: [s.n.], 2010: 732-738
(  0) 0)
|
| [3] |
苏虎, 徐德, 陈国栋, 等. 基于两阶段多目标模糊决策的乒乓球机器人击球点选择[J].
控制理论与应用, 2013, 30(5): 597-603 (  0) 0)
|
| [4] |
HUANG Y, XU D, TAN M, et al.Trajectory prediction of spinning ball for ping-pong player robot[C]//2011 IEEE/RSJ Int Conf on Intelligent Robots and Systems.San Francisco: [s.n.], 2011: 3434-3439
https://www.researchgate.net/publication/221066696_Trajectory_prediction_of_spinning_ball_for_ping-pong_player_robot (  0) 0)
|
| [5] |
LIU C, HAYAKAWA Y, NAKASHIMA A.A registration algorithm for on-line measuring the rotational velocity of a table tennis ball[C]//Proceeding of IEEE/RSJ International Conference on Intelligent Robots and Systems.[s.l.]: [s.n.], 2012: 2270-2275
https://www.researchgate.net/publication/241628593_A_registration_algorithm_for_on-line_measuring_the_rotational_velocity_of_a_table_tennis_ball (  0) 0)
|
| [6] |
ZHANG Z, XU D, YU J. Visual measurement and prediction of ball trajectory for table tennis robot[J].
IEEE Transactions on Instrumentation and Measurement, 2010, 59(12): 3195-3205 DOI:10.1109/TIM.2010.2047128 (  0) 0)
|
| [7] |
ZHANG Z, XU D, YU J.Research and latest development of ping-pong robot player[C]//7th World Congress on Intelligent Control and Automation.[s.l.]: [s.n.], 2008: 4881-4886
https://www.researchgate.net/publication/224324457_Research_and_Latest_Development_of_Ping-Pong_Robot_Player (  0) 0)
|
| [8] |
任艳青, 徐德, 谭民. 旋转球与乒乓球台/球拍的反弹模型[J].
控制理论与应用, 2012, 29(11): 1433-1439 (  0) 0)
|
| [9] |
任艳青, 方灶军, 徐德, 等. 基于模糊神经网络的乒乓球旋转飞行轨迹模式分类[J].
控制与决策, 2014, 29(2): 263-269 (  0) 0)
|
| [10] |
季云峰, 施之皓, 任杰, 等. 基于单目视觉伺服系统的高速旋转球体三维速度测定[J].
中国体育科技, 2017, 53(2): 139-144 (  0) 0)
|
| [11] |
季云峰, 陆爱发, 任杰, 等. 基于乒乓球机器人视觉系统的单色乒乓球旋转三维速度测定[J].
上海体育学院学报, 2017, 41(3): 83-88 (  0) 0)
|
| [12] |
张远辉, 韦巍. 在线角速度估计的乒乓球机器人视觉测量方法[J].
浙江大学学报(工学版), 2012, 46(7): 1320-1326 DOI:10.3785/j.issn.1008-973X.2012.07.026 (  0) 0)
|
| [13] |
张康洁, 王奇志. 无迹卡尔曼滤波在旋转乒乓球轨迹预测中的应用[J].
计算机科学, 2014, 41(1): 83-87 DOI:10.3969/j.issn.1002-137X.2014.01.014 (  0) 0)
|
| [14] |
孙智宇.乒乓球轨迹预测与分类研究[D].北京: 北京交通大学, 2015: 33-40
http://cdmd.cnki.com.cn/Article/CDMD-10004-1015611160.htm (  0) 0)
|
| [15] |
陈海英, 郭巧, 徐力. 基于神经网络的人体100 m跑运动能力综合评价[J].
中国体育科技, 2003, 39(2): 1-3 DOI:10.3969/j.issn.1002-9826.2003.02.001 (  0) 0)
|
| [16] |
张鸿燕, 狄征. Levenberg-Marquardt算法的一种新解释[J].
计算机工程与应用, 2009, 45(19): 5-8 DOI:10.3778/j.issn.1002-8331.2009.19.002 (  0) 0)
|
| [17] |
WANG G, WANG C, DU Q, et al. Distributed cooperative control of multiple nonholonomic mobile robots[J].
Journal of Intelligent & Robotic Systems, 2016, 83(3): 525-541 (  0) 0)
|
| [18] |
WANG G, WANG C, DU Q, et al. Distributed adaptive output consensus control of second-order systems containing unknown non-linear control gains[J].
International Journal of Systems Science, 2016, 47(14): 3350-3363 DOI:10.1080/00207721.2016.1139760 (  0) 0)
|
 2018, Vol. 42
2018, Vol. 42











