乒乓球机器人是研究快速视觉感知和运动控制的良好平台。自20世纪80年代Billingsley提出举办乒乓球机器人比赛的倡议以来, 各国先后展开了乒乓球机器人方面的研究[1]。Andersson[2-3]、Acosta等[4], Matsushima等[5-7]先后设计了不同的机器人系统, 成功实现了人机对打。
实现乒乓球机器人的人机对打, 主要需要机器视觉和运动控制的共同配合。先通过机器视觉找到乒乓球的空间位置, 再通过对乒乓球进行动力学分析或经验判断预测乒乓球的运动轨迹, 传达给控制端, 选择一个合适的回球落点, 将乒乓球拍移动到相应位置, 完成击球。在乒乓球运动中, 旋转球是运动员使用最多也是最具特色的一项技术, 是运动员比赛制胜的重要法宝。一直以来很少有人根据旋转运动过程对运动轨迹进行分析, 旋转球基本未应用到乒乓球机器人之中。目前无论是国外还是国内乒乓球机器人, 大多数的预测轨迹工作都是围绕无旋球展开的, 针对旋转球的预测目前只集中在经验学习方法中的模糊预测。Zhang等[8]根据受力情况采用近似的物理模型对乒乓球运动轨迹进行预测, 优点是预测时间短, 可以满足实时性, 但其中参数的不确定性导致不能精确建模, 难以推广到旋转球的应用中。
实际打球过程中, 球拍与乒乓球、球桌与乒乓球之间都有摩擦力的作用, 使得乒乓球所受合力偏离了球的中心而产生旋转。现阶段也有文献对乒乓球的旋转进行探讨, Leung等[9]详细分析了旋转球与球拍和球台碰撞过程, 并创建了一种旋转球与球拍和球台的反弹模型。Akira等[10-12]在分析了旋转球与球台反弹模型的基础上, 提出相应的旋转球的飞行轨迹预测算法, 但这些算法都未针对特定的旋转类型和大小设计。
以上这些算法都是通过对乒乓球进行受力分析预测乒乓旋转球的轨迹, 但该预测只能获得旋转的大概信息, 到目前为止缺乏准确计算无标记乒乓球旋转的算法。有学者在乒乓球上做标记测算旋转速度, Nakashima等[13-15]在球上做标记通过高速视觉对球的旋转进行测算, 但在乒乓球上做标记会增加乒乓球的质量, 对乒乓球的圆度也会产生一定影响, 在比赛中不可能使用添加标记的乒乓球, 故该方法并不能被广泛应用于测算乒乓球旋转中。
到目前为止, 并没有学者提出一个精确的不做标记的方法对球体旋转的三维速度进行测量。本文主要针对球体旋转速度大小及方向问题, 利用球体旋转中的一些特征, 提出一种基于单目摄像机的测量球体三维速度的方法, 并用实验验证算法的有效性。
1 实验准备目前乒乓球机器人的视觉系统一般由多台摄像机共同定位乒乓球的空间位置, 事先对摄像机进行标定, 根据乒乓球的特征对其进行识别跟踪。由于大部分乒乓球机器人的视觉系统都是针对无旋转乒乓球进行识别, 故将乒乓球当成一个白色球体进行识别, 获得其中心的空间坐标。
本文提出一种全新的测算乒乓球旋转速度和方向的方法, 主要利用乒乓球面的商标相对于球的运动计算旋转速度。同样利用高速摄像机作为视觉系统, 高速摄像机的帧率保证能看到连续几帧乒乓球商标即可。在机器人视觉系统中, 如果使用多目摄像机进行乒乓球定位, 会由于定标、环境的影响造成误差多倍放大, 故本文采用的是基于单目摄像机测算旋转速度的方法。由于乒乓球在空中是有旋转的, 故摄像机架在球桌四周皆可, 只要帧率跟上球的旋转速度即可, 一般将摄像机放在裁判席附近。因为在实验中需要识别乒乓球的商标, 所以要确保摄像机能够拍到商标, 故在实验中采用2台摄像机放在乒乓球桌的两边, 并且高度不同。在实验过程中只对可以识别商标的那台摄像机进行算法处理, 故覆盖范围较大, 在大部分情况下可以识别商标, 所以对于前后旋转的乒乓球也可以进行识别, 本文的算法基本适用于任何旋转速度的识别计算。
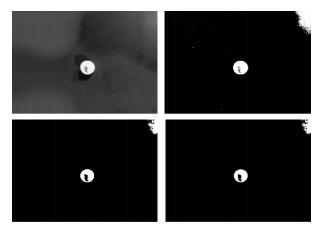
由于本文测算旋转主要依靠乒乓球面的商标, 故选取所拍视频中的一张图像进行处理实验, 经过二值化, 腐蚀和膨胀, 查找轮廓, 以乒乓球中心点作为原点建立坐标系, 可以获得商标中心的坐标(图 1)。在乒乓机器人视觉系统中, 获得几帧图片中乒乓球的商标中心坐标, 再利用这几个中心坐标间的关系测算乒乓球的旋转速度和方向。
|
图 1 获得乒乓球商标中心坐标 Figure 1 The acquisition of the coordinate of table tennis brand's center |
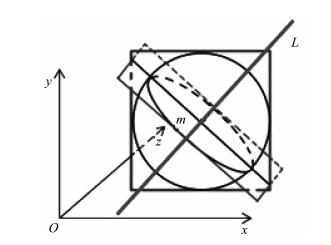
乒乓球在空中的旋转必将绕某一个旋转轴进行旋转, 故乒乓球上任意一点旋转一周必将形成一个圆形。用单目摄像机从某一角度拍, 这个角度不一定是正对旋转轴, 若将商标中心作为标记点, 形成的轨迹在单目视觉中将形成一个椭圆。本文需要基于单目摄像机对旋转乒乓球进行拍摄, 利用转乒乓球的旋转特征计算乒乓球的旋转速度的大小和方向; 先利用乒乓球的旋转建立一个旋转球体模型, 对旋转乒乓球的特征进行分析(图 2)。
|
图 2 乒乓球旋转模型 Figure 2 The model of table tennis rotation |
假设乒乓球在空间坐标系Oxyz中进行旋转, 图 2中的2个圆代表旋转的乒乓球, 其中实线圆代表乒乓球投影在xOy平面形成的圆, 虚线圆代表球体上任意一个截面所形成的圆。2个方框代表 2个圆形所在的截面, 在空间中2个平面相交会产生一条交线, 在图中2个平面相交的交线即为中间那条黑色直线; 而这2个圆形截面的交线, 即为虚线圆的直径, 记为直径m, 属于2个平面交线的一部分。
2.2 乒乓球三维速度分解高速旋转的乒乓球必将沿着某条通过球心的轴转动, 故可将求解高速旋转的乒乓球的三维速度方向问题转化为求解转动轴空间位置问题。现假设此球体旋转方向为沿着虚线圆旋转, 则此球体的转动轴为垂直于虚线圆所在截面的直径m的中垂线所在直线, 即为直线L。
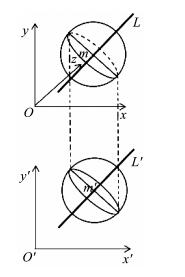
如图 3所示, 将高速旋转的乒乓球投影到xOy平面上, 可以得到球体在新的坐标系x′O′y′的平面图形。此时, 空间坐标中的实线圆保持不变, 而虚线圆将在平面中被投影成一个椭圆。此外, 空间中的转动轴L将被投影到平面x′O′y′中, 成为椭圆长轴m′的中垂线L′。故可将求解旋转乒乓球转动轴L空间位置问题转化为2个问题:① 直线L′在平面x′O′y′的位置; ② 直线L′与平面x′O′y′的夹角。
|
图 3 旋转乒乓球投影 Figure 3 The projection of table tennis rotation |
先解决直线L′在平面x′O′y′位置问题, 可转化为求解椭圆长轴m′与x轴倾角及椭圆中心点坐标问题。对于任意一个椭圆, 都可以用其一般方程
| $A{x^2} + Bxy + C{y^2} + Dx + Ey + 1 = 0$ |
表示, 总共有A、B、C、D、E 5个系数, 即只要找到椭圆上面任何5个点的坐标就可以解出椭圆的一般方程。在乒乓球旋转测定中, 可以利用乒乓球上面的商标中心作为识别对象, 记下5帧图像中商标中心位置即可。假设找到椭圆上任意5个点的坐标(xn, yn), n=1, 2, 3, 4, 5, 则可以得到以下五元一次方程组:
| $\left. \begin{array}{l} Ax_1^2 + B{x_1}{y_1} + Cy_1^2 + D{x_1} + E{y_1} + 1 = 0\\ Ax_2^2 + B{x_2}{y_2} + Cy_2^2 + D{x_2} + E{y_2} + 1 = 0\\ Ax_3^2 + B{x_3}{y_3} + Cy_3^2 + D{x_3} + E{y_3} + 1 = 0\\ Ax_4^2 + B{x_4}{y_4} + Cy_4^2 + D{x_4} + E{y_4} + 1 = 0\\ Ax_5^2 + B{x_5}{y_5} + Cy_5^2 + D{x_5} + E{y_5} + 1 = 0 \end{array} \right\}$ | (1) |
在方程组(1) 中, x、y都是已知数, 未知数是系数A、B、C、D、E, 它们都是一次的, 故解出这个方程组的解是唯一的, 利用5张图像即可求出椭圆轨迹方程。
利用Matlab软件编程求解方程(1) 的解, 获得系数值, 从而得到椭圆一般方程之后, 开始计算椭圆长轴m′与x轴倾角及椭圆中心点坐标。令
| $F\left( {x,y} \right) = A{x^2} + Bxy + C{y^2} + Dx + Ey + 1$ | (2) |
由于椭圆属于中心型曲线, 故中心点坐标(x0, y0)满足
| $\begin{array}{*{20}{c}} {\frac{{\partial F}}{{\partial x}}\left( {{x_0},{y_0}} \right) = 0,}&{\frac{{\partial F}}{{\partial y}}} \end{array}\left( {{x_0},{y_0}} \right) = 0$ | (3) |
代入F(x, y), 有
| $\left. \begin{array}{l} {x_0} = \frac{{BE - 2CD}}{{4AC - {B^2}}}\\ {y_0} = \frac{{BD - 2AE}}{{4AC - {B^2}}} \end{array} \right\}$ | (4) |
即得椭圆中心坐标为(x0, y0)。
假设椭圆长轴m′与x轴倾角为β, 现将原坐标系沿着x轴旋转β角, 令坐标系中任意一点坐标为(x1, y1), 其对应于新坐标系的坐标为(x′1, y′1), 根据解析几何中相关变换, 可以得到如下关系:
| $\left. \begin{align} & {{x}_{1}}=x_{1}^{'}\cos \beta -y_{1}^{'}\sin \beta \\ & {{y}_{1}}=x_{1}^{'}\sin \beta +y_{1}^{'}\cos \beta \\ \end{align} \right\}$ | (5) |
令F(x, y)=0, 将式(5) 代入, 可得
| ${A}'x_{1}^{'2}+{B}'x_{1}^{'}y_{1}^{'}+{C}'y_{1}^{'2}+{D}'x_{1}^{'}+{E}'y_{1}^{'}+1=0$ | (6) |
其中,
| $\left. \begin{array}{l} A' = A{\cos ^2}\beta + B\sin \beta \cos \beta + C{\sin ^2}\beta \\ B' = 2\left( {C - A} \right)\sin \beta \cos \beta + B\left( {{{\cos }^2}\beta - {{\sin }^2}\beta } \right)\\ C' = A{\sin ^2}\beta - B\sin \beta \cos \beta + C{\cos ^2}\beta \\ D' = D\cos \beta + E\sin \beta \\ E' = - D\sin \beta + E\cos \beta \end{array} \right\}$ | (7) |
要求夹角β, 即将坐标轴旋转β角度, 此时x′1y′1的系数B′值为0, 即
| $2\left( {C - A} \right)\sin \beta \cos \beta + B\left( {{{\cos }^2}\beta - {{\sin }^2}\beta } \right) = 0$ | (8) |
利用二倍角公式, 有
| $\left( {C - A} \right)\sin 2\beta + B\cos 2\beta = 0$ | (9) |
化简得
| $\tan 2\beta = \frac{B}{{A - C}}$ | (10) |
即可得到椭圆长轴m′与x轴倾角β的值:
| $\beta = \frac{1}{2}\arctan \left( {\frac{B}{{A - C}}} \right)$ | (11) |
至此, 计算出乒乓球的旋转轴L在平面x′O′y′内的投影L′与x、y轴夹角分别为:
| $\begin{array}{*{20}{c}} {\frac{{\rm{ \mathsf{ π} }}}{2} - \frac{1}{2}\arctan \left( {\frac{B}{{A - C}}} \right),} & {\frac{1}{2}\arctan \left( {\frac{B}{{A - C}}} \right)} \end{array}$ |
接下来解决直线L′与平面x′O′y′夹角, 在单目摄像机视角下, 一个与摄像机视角平面倾角为α的平面中的一个圆会被识别成一个椭圆。其主要原因是将原本平面中圆投射到摄像机视角平面中, 从而导致图像变形, 椭圆的短轴就是因为原本直径投射到新平面下缩短所形成的。
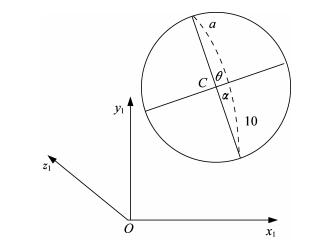
如图 4所示, 假设摄像机视角平面为x1Oy1平面, 则计算机视角平面与圆所在平面的夹角为α, ,投影形成的三角形的三条边长分别为a、b、c, 原本圆的直径为c, 投影到x1Oy1平面上变成椭圆短轴b则有
| $\cos \alpha =b/c$ | (12) |
|
图 4 空间夹角转换关系 Figure 4 Convert relation of spatial angle |
此处的夹角α即为直线L′与平面x′O′y′夹角, 三角形的边长b和c即为椭圆的长轴和短轴, 记椭圆长轴为a′, 短轴为b′, 可得
| $\alpha = \arccos \left( {b'/a'} \right)$ | (13) |
故可将问题转化为求解椭圆长轴a′和短轴b′问题。根据前文计算结果, 可知椭圆中心坐标为(x0, y0), 假设一条直线过椭圆中心点与x轴夹角为φ, 则这条直线的参数方程为
| $\left. \begin{array}{l} x = {x_0} + t\cos \varphi \\ y = {y_0} + t\sin \varphi \end{array} \right\}$ | (14) |
式中:t为参数; φ为直线与x轴夹角。
令F(x)=0, 将式(14) 代入, 可得
| $\begin{array}{l} \left( {A{{\cos }^2}\varphi + B\sin \varphi \cos \varphi + C{{\sin }^2}\varphi } \right){t^2} + \\ \quad \quad \left[ {\left( {2A{x_0} + B{y_0} + D} \right)} \right.\cos \varphi + \\ \quad \quad \left. {\left( {B{x_0} + 2C{y_0} + E} \right)\sin \varphi } \right]t + H = 0 \end{array}$ | (15) |
式中,
| $H = Ax_0^2 + B{x_0}{y_0} + Cy_0^2 + D{x_0} + E{y_0} + 1$ | (16) |
将前文算出的中心坐标值代入式(16), 可得
| $H = \frac{{{B^2} - 4AC + A{E^2} + C{D^2} - BDE}}{{{B^2} - 4AC}}$ | (17) |
假设根据式(15) 求解得方程的两根为t1、t2, 由参数|t|的几何意义可知, 经过对称中心点(x0, y0)的弦的长度为
| $\left| {{t_1} - {t_2}} \right| = \sqrt {{{\left( {{t_1} + {t_2}} \right)}^2} - 4{t_1}{t_2}} $ | (18) |
易知
| ${t_1} + {t_2} = 0$ | (19) |
故可得
| $\left| {{t_1} - {t_2}} \right| = 2\sqrt { - {t_1}{t_2}} $ | (20) |
由韦达定理可得
| ${t_1}{t_2} = \frac{H}{{A{{\cos }^2}\varphi + B\sin \varphi \cos \varphi + C{{\sin }^2}\varphi }}$ | (21) |
故可得
| $\begin{array}{l} \left| {{t_1} - {t_2}} \right| = \\ \quad \quad 2\sqrt {\frac{{ - H}}{{A{{\cos }^2}\varphi + B\sin \varphi \cos \varphi + C{{\sin }^2}\varphi }}} \end{array}$ | (22) |
由式(22) 可求得倾角为φ的以(x0, y0)为中点的弦的长度, 因为椭圆的长轴、短轴分别是其弦中最长和最短的两根弦, 当Acos2 φ+Bsin φcos φ+Csin2 φ取得极值时, 对应的弦即为椭圆的长轴和短轴。
令G=Acos2 φ+Bsin φcos φ+Csin2 φ, 则
| $\begin{array}{l} G = \frac{{A\left( {\cos 2\varphi + 1} \right)}}{2} + \frac{{B\sin 2\varphi }}{2} + \\ \quad \quad \frac{{C\left( {1 - \cos 2\varphi } \right)}}{2} \end{array}$ | (23) |
经化简, 可得
| $\begin{array}{l} G = \left( {A + C} \right)/2 + \\ \quad \quad \frac{{\sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}{2}\sin \left( {2\varphi + \arctan \frac{{A - C}}{B}} \right) \end{array}$ | (24) |
易知
| $ - 1 \le \sin \left( {2\varphi + \arctan \frac{{A - C}}{B}} \right) \le 1$ | (25) |
故可得
| $\left. \begin{array}{l} {G_{\max }} = \frac{{A + C}}{2} + \frac{{\sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}{2}\\ {G_{\min }} = \frac{{A + C}}{2} + \frac{{\sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}{2} \end{array} \right\}$ | (26) |
由此可求得椭圆的长轴a′和短轴b′长度如下:
| $\left. \begin{array}{*{35}{l}} {a}'=2\sqrt{\frac{-2H}{A+C-\sqrt{{{\left( A-C \right)}^{2}}+{{B}^{2}}}}} \\ {b}'=2\sqrt{\frac{-2H}{A+C+\sqrt{{{\left( A-C \right)}^{2}}+{{B}^{2}}}}} \\ \end{array} \right\}$ | (27) |
根据式(13)、(17)、(27) 可得直线L′与平面x′O′y′夹角α的计算公式如下:
| $\alpha = \arccos \sqrt {\frac{{A + C - \sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}{{A + C + \sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}} $ | (28) |
根据式(28), 计算出乒乓球的旋转轴L与空间坐标系z轴夹角为:
| $\frac{\pi }{2} - \arccos \sqrt {\frac{{A + C - \sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}{{A + C + \sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}} $ | (29) |
至此, 计算出乒乓球旋转轴与空间3个轴的夹角, 即算出乒乓球旋转速度的三维方向。
2.4 求解旋转速度大小精确地计算速度大小的方法是先计算任意2帧图像中同一点运动的弧线的距离, 然后除以2帧图像相隔时间, 即得到球体转速大小。其计算量会相对较大, 在高速旋转球体上, 可以将两点间的弧线距离近似为两点间的直线距离, 从而可以大幅度降低计算量, 缩短计算时间。本文选取了椭圆上的5个点, 即同一个点连续5帧的运动轨迹。为了降低误差, 将选取这5个点中每相邻2点之间距离的平均值。
根据前文可知, 椭圆上任意5个点的坐标为(xn, yn), n=1, 2, 3, 4, 5, 记球体旋转速度大小为v, 每2帧之间间隔时间为t, 物体实际大小与图像中像素大小比值为k, 则得出
| $v = \frac{{k\sum\limits_{n = 1}^4 {\sqrt {{{\left( {{x_{n + 1}} - {x_n}} \right)}^2} + {{\left( {{y_{n + 1}} - {y_n}} \right)}^2}} } }}{{4t}}$ | (30) |
式(30) 可以计算出的v为选取坐标点的线速度, 可以根据线速度v计算球体旋转的角速度。球体是绕旋转轴进行旋转的, 本文所选取的点的运动轨迹是垂直于旋转轴的一个圆, 但是这个圆不一定会经过球心, 所以不能简单地利用球体的半径计算角速度。
本文计算角速度利用所选取点运动轨迹圆的半径, 而在单目视觉中, 该半径即为椭圆轨迹的长轴a′。故利用式(28) 和式(30) 可算得球体旋转的角速度计算公式为:
| $\omega = \frac{{\sum\limits_{n = 1}^4 {\sqrt {{{\left( {{x_{n + 1}} - {x_n}} \right)}^2} + {{\left( {{y_{n + 1}} - {y_n}} \right)}^2}} } }}{{8t\sqrt {\frac{{ - 2H}}{{A + C - \sqrt {{{\left( {A - C} \right)}^2} + {B^2}} }}} }}$ | (31) |
为了验证设计算法的正确性, 本文利用摄像机拍摄视频进行实验验证。将2台摄像机摆放在乒乓球桌两边, 用一个智能发球机进行发球, 发球的旋转速度事先调试、测试好, 控制在60 r/s, 再利用2个摄像机同时进行拍摄。摄像机的帧率采用100帧/s, 最终用拍摄到乒乓球商标的视频进行实验验证。
2台摄像机放在球桌两边, 且高度有一点差异, 便于确保有一台摄像机可以拍摄到乒乓球的商标运动轨迹, 再针对拍摄的视频进行算法代入, 从而进行实验验证。拍摄的视频截图如图 5所示, 经过二值化、去噪、腐蚀膨胀、查找轮廓灯一系列图像处理操作, 可找出乒乓球的商标中心坐标。

|
图 5 图像处理 Figure 5 Image processing |
经过一系列图像处理操作之后可以找到乒乓球的商标相对于乒乓球中心点的坐标, 根据模型验证, 选取连续5帧图像的商标中心坐标为:(67, -25), (31, -58), (2, -64), (-30, -58), (-61, -35), 代入椭圆一般方程, 用Matlab计算可得:
| $\left. \begin{array}{l} A = 1.7948{{\rm{e}}^{ - 4}}\\ B = 9.1191{{\rm{e}}^{ - 6}}\\ C = 2.0961{{\rm{e}}^{ - 4}}\\ D = 3.4943{{\rm{e}}^{ - 4}}\\ E = - 2.2000{{\rm{e}}^{ - 3}} \end{array} \right\}$ | (32) |
利用上面模型可以算出中心坐标为(-1.107, -2.645), 此外夹角如下:
| $\beta = {8.42^ \circ }$ | (33) |
| $\alpha = {22.76^ \circ }$ | (34) |
由于选择坐标系中心点尽量靠近坐标轴, 故理想中的β值为0°, 测量中可能会由于中心不准有一定误差, 在可接受范围内。
根据实际测量数据, 摄像机镜头中心离地面距离112.5 cm, 球体中心离地面87.5 cm, 镜头中心离球体中心距离为62.5 cm, 根据实际数据可测得摄像机拍摄平面与球体平面夹角α计算公式如下:
| $\alpha = \arcsin \frac{{112.5 - 87.5}}{{62.5}}$ | (35) |
可计算出:
| $\alpha = {23.58^ \circ }$ | (36) |
至此, 可以验证算法中关于求解乒乓球旋转三维速度方向问题基本正确。
再利用上面角速度模型可以计算出角速度为:
| $\omega = 61.1{\rm{r}}/{\rm{s}}$ | (37) |
角速度与实际测量角速度之间的误差为:
| $\eta = \frac{{61.1 - 60}}{{60}}$ | (38) |
即
| $\eta = 1.83\% $ | (39) |
角速度计算误差控制在1.83%, 基本可以验证本算法对于乒乓球旋转速度计算的正确性。至此, 在误差允许的范围内, 已用对照实验验证了本算法的正确性。
以上是针对一般情况下的实验验证, 特殊情况分为2种情况:① 当M轴与摄像机的主光轴是平行的, 这时形成的运动轨迹将不是一个椭圆, 此时算出的轨迹方程将会是一个圆的轨迹方程; 再利用公式可以算出此时L线与摄像机光轴的角度为90°, 即垂直。② 当商标处于旋转轴上时, 商标相对于球体中心的坐标是不变的, 此时获得的5个x、y坐标是一样的, 代入方程组中有无穷多解, 这种情况下无法获得轨迹方程。这是最特殊的情况, 此时L线与摄像机光轴线是平行的, 即夹角为0°, 这应特别加以说明。
3 结论及展望本文利用乒乓球商标的运动轨迹参数方程, 根据一些空间转换关系获得乒乓球旋转的三维速度及大小, 并用实验验证了算法的有效性。在后续研究中, 主要从以下2个方面进行深入:① 算法中轨迹点的数量要减少, 尽量尝试用更少的点进行旋转速度计算, 从而降低对摄像机拍摄视频的要求; ② 在图像处理算法上深入学习研究, 争取提高图像识别精度, 减少处理时间, 满足机器人视觉系统的实时性要求。
| [1] |
Zhang Z, Xu D, Yu J.Research and latest development of ping-pong robot player[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing:IEEE, 2008:4881-4886
( 0) 0)
|
| [2] |
Andersson R L.
A robot ping-pong player:Experiment in real time intelligent control[M]. Cambridge, CA: MIT Press, 1988: 11-19.
( 0) 0)
|
| [3] |
Andersson R L. Aggressive trajectory generator for a robot ping-pong player[J].
IEEE Control System Magazine, 1989, 9(2): 15-21 DOI:10.1109/37.16766 ( 0) 0)
|
| [4] |
Acosta L, Rodrigo J, Mendez J A, et al. Ping-pong player prototype, a PC-based, low-cost, ping pong robot[J].
IEEE Robotics and Automation Magazine, 2003, 10(4): 44-52 DOI:10.1109/MRA.2003.1256297 ( 0) 0)
|
| [5] |
Matsushima M, Hashimoto T, Trkeuchi M, et al. A learning approach to robotic table tennis robotics[J].
IEEE Transactions on Robotics and Automation, 2005, 21(4): 767-771 DOI:10.1109/TRO.2005.844689 ( 0) 0)
|
| [6] |
Matsushima M, Hashimoto T, Miyazaki F.Learning to the robot table tennis task-ball control and rally with a human[C]//Proceedings of IEEE Conference on System, Man and Cybernetics.Washington D C, USA:IEEE, 2003:2962-2969
( 0) 0)
|
| [7] |
Miyazaki F, Matsushima M, Takeuchi M.
Learning todynamically manipulate:a table tennis robot controls a ball and rallies with a human being[M]. Advance in Robot Control.Berlin, Germany: Springer Berlin Heidelberg, 2006: 317-341.
( 0) 0)
|
| [8] |
Zhang Zhengtao, Xu De, Yu Junzhi. Visual measurement and prediction of ball trajectory for table tennis robot[J].
IEEE Transactions on Instrumentation and Measurement, 2010, 59(12): 3195-3205 DOI:10.1109/TIM.2010.2047128 ( 0) 0)
|
| [9] |
Leung H, Wang H Q, Cao C X.An improved locally weighted regression for a converter re-vanadium prediction modeling[C]//The 6th World Congress on Intelligent Control and Automation.Dalian:[s.n.], 2006:1515-1519
( 0) 0)
|
| [10] |
Huang Yanlong, Xu De, Tan Min, et al.Trajectory prediction of spinning ball for ping-pong player robot[C]//2011 IEEE/RSJ Int Conf on Intelligent Robots and Systems.San Francisco:[s.n.], 2011:3434-3439
( 0) 0)
|
| [11] |
Chen Xiaopeng, Tian Ye, Huang Qiang, et al.Dynamic model based ball trajectory prediction for a robot ping-pong player[C]//The 2010 IEEE Int Conf on Robotics and Biomimetics.Tianjin:[s.n.], 2010:603-608
( 0) 0)
|
| [12] |
Akira N, Yosuke K, Yuki O, et al.Modeling of rebound phenomenon between ball and racket rubber[C]//ICROSSICE Int Joint Conf.Fukuoka:[s.n.], 2009:2295-2300
( 0) 0)
|
| [13] |
Nakashima A, Yuki Ogawa.Robotic table tennis based on physical models of aerodynamics and rebounds[C]//Conference:Robotics and Biomimetics(ROBIO), IEEE International Conference, 2011:2348-2354
( 0) 0)
|
| [14] |
Nakashima A, Tsuda Y, Liu C, et al.A real-time measuring method of translational/rotational velocity of a table tennis ball[C]//Proceeding of 5th IFAC Symposium on Mechatronic Systems, 2010:732-738
( 0) 0)
|
| [15] |
Liu C, Hayakawa Y, Nakashima A.A registration algorithm for on-line measuring the rotational velocity of a table tennis ball[C]//Proceeding of IEEE/RSJ International Conference on Intelligent Robots and Systems, 2011:428-438
( 0) 0)
|
 2017, Vol. 41
2017, Vol. 41


