乒乓球是我国的“国球”,也是我国的传统优势项目。随着乒乓球运动的不断发展,以及国际间竞争的日趋激烈,我国乒乓球项目的世界领先地位也时刻面临着来自其他国家的严峻挑战。因此,须加强关于乒乓球训练方法和理论的研究,不断革新乒乓球技术,强化青少年乒乓球后备人才培养[1]。
乒乓球作为一项具有较高精细性、技巧性的技能类对抗项目,具有球速和转速较快、反应时间较短等特点,对乒乓球运动员有着复杂的技术及战术要求。技术是战术的基础,只有具备强大而稳定的技术水平,才能形成灵活多变的战术[2-3]。技术动作的合理、规范是运动员达到高水平层次和实现比赛制胜的重要基础,不合理、不规范的技术动作不仅会影响运动员的技战术组合衔接,还会提升其运动训练伤病的发生率。青少年(尤其是启蒙阶段)乒乓球运动员正处于技术动作的认知、形成及固定阶段,培养科学、规范、稳定的技术动作显得尤为重要[4-5]。加强对青少年乒乓球运动员(以下简称“青少年运动员”)训练的投入,有利于保障后备人才的不断输送,保持我国乒乓球项目的世界领先地位。
随着科学技术的日新月异与乒乓球运动的不断发展,传统青少年运动员技术动作训练方法存在的弊端逐渐显现,具体表现为:主观性和经验性较为突出,缺乏定量化、科学化的训练监控与指导等[6-9]。科学合理的技术动作训练与监控方法能有效促进运动员竞技水平的提高,预防和减少运动伤病的发生,进一步提高后备人才培养的质量。因此,国家体育总局相关领导强调要充分发挥“科技助力奥运”的作用,通过大数据、动作捕捉和人工智能等现代科技手段攻破运动训练过程中的技术难题,提高运动训练过程的科学性。其中,动作捕捉技术运用计算机图形学原理,通过空间内布置的多个摄像头以图像形式跟踪、测量和记录人体主要关节点的三维空间运动轨迹,已被广泛应用于影视制作、机械控制、模拟训练与教学、人体姿态研究和人机工程学等领域[10-16]。
基于此,运用高速动作捕捉技术,在采集国家队优秀乒乓球运动员(以下简称“国家队运动员”)和青少年运动员基本技术动作的空间特征数据基础上,构建国家队运动员基本击球动作模型;运用动态时间规整(Dynamic Time Warping,DTW)算法,将青少年运动员的击球动作曲线与之进行相似度比较,结合击球质量数据分析青少年运动员击球动作的合理性及不足,从而将传统的经验式教学与科学化、定量化的指导方法相结合,以克服现有训练监控手段存在的不足,为更有效地提高基本技术动作的合理性、促进专业技术动作的形成与固定奠定基础。
2 研究方法 2.1 德尔菲法运用德尔菲法就选取哪些主要关节点进行击球动作的合理性评价进行了3轮专家咨询与评判。综合各轮专家咨询与评判的结果,选取权重比例较大(> 75%)的关节点,为后续击球动作各关节点空间位移和角度数据的采集及击球动作合理性分析提供依据。
2.2 实验法 2.2.1 实验内容实验内容包括2个部分:高速动作捕捉数据采集和击球质量数据采集。前者主要采集运动员击球动作的空间特征数据(各主要关节点的空间运动轨迹时序曲线),后者主要采集击球的速度、转速和落点。在进行动作捕捉数据采集实验的同时采集每次击球动作的球速、转速和落点数据。
2.2.2 实验对象(1)国家队运动员。为构建优秀乒乓球运动员击球动作模型,选取了15名乒乓球国家二队优秀运动员,均为国家级运动员,平均年龄17.3岁,右手横拍,弧圈结合快攻打法,身体各关节无伤病情况。
(2)青少年运动员。为诊断青少年运动员击球动作的合理性,选取10名中国乒乓球学院少年班运动员,平均年龄15.1岁,右手横拍,弧圈结合快攻打法,身体各关节无伤病情况。
2.2.3 实验仪器与设备通过红外高速动作捕捉系统采集运动员击球过程中身体各主要关节点的空间位置、关节角度和重心变化等(采样频率:120帧/s)。采用Miro R111型高速摄像机测量乒乓球击球旋转速度,采用SPEEDSTER测速仪测量击球速度。
2.2.4 实验设备布置实验设备布置如图 1所示。
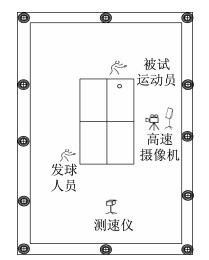
|
| 图 1 实验设备布置示意 Figure 1 Experimental equipments layout |
在图 1中,外围矩形框上的黑色实心圆为实验场地布置的12个红外高速摄像头,2名运动员分别为被试运动员和发球人员。要求发球人员以多球的形式给被试运动员发反手拉上旋弧圈球。为提高实验结果的可靠性,整个实验过程中发球人员固定为同一人,原地定点发球,并尽量使多个发球的速度、落点和旋转等基本保持一致。
2.2.5 人体骨骼模型和贴点人体骨骼模型如图 2所示。在实验前,将23个标记点按图 2中人体骨骼模型主要关节点的位置对被试运动员进行贴点。
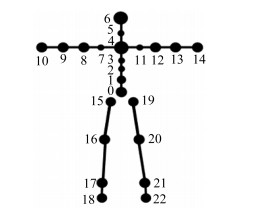
|
| 图 2 人体骨骼模型 Figure 2 Human skeleton model |
在高速动作捕捉实验过程中,采集相对于空间坐标系的运动员主要关节点和重心的空间位置坐标,坐标原点位于球网右侧的地面上,其标定如图 3所示。
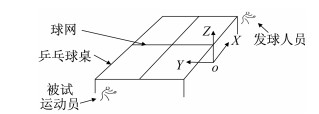
|
| 图 3 空间坐标系标定 Figure 3 Calibration of spatial coordinate system |
参照人体坐标系描述人体关节点运动的关节角度,以髋关节作为人体的根关节点(图 2中编号为0的人体髋关节点),其他关节以其父关节点为关节中心。
3 基于DTW算法的击球动作曲线相似度比较 3.1 DTW算法曲线相似度比较的基本原理DTW算法通过动态规划的思路,寻找并求解输入样本参数和参考模版之间最短距离相对应的规整函数,实现样本和模板之间的最优匹配。DTW算法解决了需要比较的2段时间序列长度可能并不相等的曲线相似性匹配问题。近年来,DTW算法被广泛应用于数据挖掘、语音识别和动作识别等领域[17-19]。
在乒乓球击球过程中,不同运动员在做相同类型技术动作时,其击球动作的快慢和动作结构特征不同[17],击球过程中各关节点的时间序列长度也不同。因此,国家队运动员击球动作模型构建和青少年运动员击球动作合理性诊断等的曲线相似度比较均采用DTW算法进行最优匹配。
3.2 基于DTW算法的击球动作曲线相似度计算公式基于DTW算法的击球动作曲线相似度比较,是把不同乒乓球运动员的击球动作时间序列进行延长或缩短,对特征参数(关节点的空间位置或关节角度)的序列模式重新进行时间上的调整,然后再对2个时间序列的相似度进行比较,从而得出最佳匹配结果[20]。通过计算不同曲线上2个点的欧氏距离比较不同乒乓球运动员击球动作各关节点轨迹曲线的相似度[21],具体计算公式如下。
以乒乓球运动员A和B的击球动作曲线(分别为曲线P和曲线Q)的相似度计算数据为例,如图 4所示。
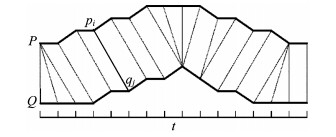
|
| 图 4 击球动作曲线采样 Figure 4 Sampling diagram of striking action curve |
曲线P和Q上任意2点pi和qj间的欧氏距离
| $ {\rm{dis}}\left( {{p_i}, {q_j}} \right) = \frac{{{r^2}}}{{{r^2} + {p_i} - {q_j}}} $ | (1) |
2条曲线P和Q的相似度
| $ {\rm{ \mathsf{ σ} }}\left( {P, Q} \right) = \left( {\mathop \sum \limits_{\begin{array}{*{20}{c}} {{p_i} \in P}\\ {{q_j} \in Q} \end{array}} {\rm{dis}}\left( {{p_i}{\rm{}}, {q_j}} \right) + \mathop \sum \limits_{\begin{array}{*{20}{c}} {{q_j} \in Q}\\ {{p_i} \in P} \end{array}} {\rm{dis}}\left( {{q_j}{\rm{}}, {p_i}} \right)} \right)/\left( {m + n} \right) $ | (2) |
其中,i和j分别为曲线P和Q的采样点编号,i=[1, m], j=[1, n],
通过高速动作捕捉系统采集乒乓球运动员不同击球动作过程中各主要关节点的空间位置和关节角度数据,从中任意选取2条击球动作曲线用于相似度比较。
3.3.2 击球动作曲线的平移和拉伸由于乒乓球运动员身高及其击球动作快慢的差异,不同乒乓球运动员在做相同类型的技术动作时,其身体同一关节点的空间轨迹曲线长短不一,击球动作曲线的起始点也可能不重合。为减少这种差异对曲线相似度计算结果的影响,对击球动作曲线进行平移和拉伸处理。
击球动作曲线平移的作用在于,将不同乒乓球运动员击球动作曲线的起点均移至空间坐标系的原点位置,以排除不同乒乓球运动员间身高差异对曲线相似度比较结果的影响。选取平移前曲线上任意点P,假设击球动作曲线起始点为P0,P点平移后对应的点为P′,曲线平移的计算公式为Xi'= Xi-X0,Yi′= Yi-Y0,Zi′= Zi-Z0,其中,Xi、Yi、Zi为击球动作曲线上任意点P的坐标,Xi′、Yi′、Zi′为击球动作曲线上任意点P经曲线平移后的新坐标P',X0、Y0、Z0为击球动作曲线起始点P0的坐标。
击球动作曲线拉伸的作用在于将不同乒乓球运动员击球动作曲线的时间轴统一为相同长度(曲线的宽度一样),以消除不同乒乓球运动员击球动作的快慢对曲线相似度比较结果的影响。曲线拉伸的算法是将较窄曲线上点的时间坐标乘以2条曲线宽度的比例系数(≥1)。
曲线平移和拉伸的整体意义在于消除不同运动员个体差异对动作曲线相似度比较结果的影响,以提高计算结果的精度,使击球动作合理性诊断结果更贴合实际。以反手拉上旋弧圈球中右膝关节X方向的位移曲线为例,击球动作曲线数据平移前后的结果如表 1所示。
| 表 1 右膝关节X方向位移数据的平移 Table 1 Displacement data translation of the right knee joint in X direction |
根据击球动作曲线相似度计算公式,计算出2条击球动作曲线的相似度。根据计算结果,对2条曲线对应关节点运动轨迹的相似度进行评价。
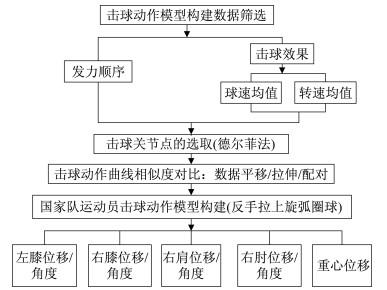
4 青少年运动员击球动作合理性评价 4.1 国家队运动员击球动作模型构建 4.1.1 模型构建流程① 实验中分别采集15名国家队运动员训练状态下反手拉上旋弧圈球上台的5次击球动作数据。②根据高速动作捕捉系统采集的击球过程中各关节点的发力顺序数据,从每个运动员反手拉上旋弧圈球的5次击球动作中,选取发力顺序合理、击球效果最好的(球速和转速均在15位国家队运动员击球球速和转速的均值之上)1次作为后期击球动作建模的数据。③根据德尔菲法选取的影响基本击球动作合理性评价相关关节点(表 2),整理出各关节点X、Y、Z方向的空间位移和角度数据。
| 表 2 影响击球动作合理性评价的相关关节点选取 Table 2 Selection of relevant key joints for the rationality evaluation of striking action |
运用DTW算法进行不同乒乓球运动员击球动作曲线相似度计算,筛选出与15名国家队运动员击球动作轨迹最接近的曲线,作为国家队运动员击球动作模型构建的基础。具体流程如图 5所示。
|
| 图 5 国家队运动员击球动作模型构建流程 Figure 5 Construction flowchart of striking action model of national elite players |
选取反手拉上旋弧圈球技术动作进行国家队运动员击球动作模型构建[22]。据表 2数据,以影响击球动作合理性评价权重比例最高(92.3%)的右肩关节为例,构建国家队运动员反手拉上旋弧圈球动作模型。
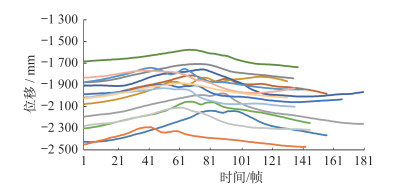
(1)绘制15位国家队运动员反手拉上旋弧圈球过程中右肩关节X方向位移曲线,如图 6所示。由图 6可知,国家队运动员在完成反手拉上旋弧圈球时,右肩关节X方向位移曲线的波动主要为-2 300~ -1 700 mm。从时间帧数上看,击球动作的周期最长为187帧,其他多数分布在135~151帧。
|
| 图 6 15名国家队运动员反手拉上旋弧圈球右肩关节X方向位移曲线 Figure 6 Original displacement curves of 15 national elite players'right shoulder joint in X direction when pulling topspin ball with backhand |
(2)将15名国家队运动员的关节运动曲线进行平移和拉伸,运用基于DTW算法的击球动作曲线相似度计算公式,分别计算每名乒乓球运动员右肩关节X方向运动轨迹曲线与其他14名乒乓球运动员同一关节点X方向位移曲线(共14条)的相似度,共计15组曲线相似度比较数据样本。以反手拉上旋弧圈球时右肩关节X方向位移曲线为例,15名国家队运动员击球动作曲线两两比较的相似度数据如表 3所示。
| 表 3 15名国家队运动员反手拉上旋弧圈球动作曲线两两比较的相似度 Table 3 Curve similarity of 15 national elite players when pulling topspin ball with backhand |
(3)将曲线两两比较得到的15组相似度数据,运用SPSS软件计算出每组曲线相似度数据的标准差(SD),结果如表 4所示(按标准差升序排列)。
| 表 4 右肩关节X方向位移曲线相似度标准差(升序) Table 4 Standard deviation of displacement curve similarity of the right shoulder joint in X direction (ascending) |
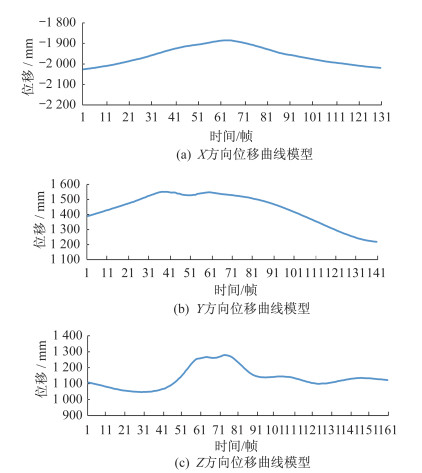
(4)选取表 4中曲线相似度标准差最小的ID=13(SD=0.077)所对应的曲线,作为国家队运动员反手拉上旋弧圈球右肩关节X方向位移动作模型,如图 7(a)所示。
|
| 图 7 右肩关节X、Y、Z方向位移曲线模型 Figure 7 Displacement curve model of the right shoulder joint in X, Y, Z direction |
由图 7(a)可知,国家队运动员反手拉上旋弧圈球时,右肩关节X方向位移曲线波峰、波谷的波动范围为-2 020~-1 880 mm。引拍阶段右肩关节位置逐渐前移,击球后右肩关节又逐渐恢复至初始状态,其X方向位移曲线变化符合击球动作中右肩关节的前后位移变动方向。
同理,可以构建国家队运动员反手拉上旋弧圈球过程中右肩关节在Y、Z方向的位移动作模型,分别如图 7(b)、(c)所示。如图 7(b)所示,国家队运动员反手拉上旋弧圈球时,右肩关节Y方向位移曲线的波动范围为1 210~1 550 mm。在引拍与挥拍击球阶段,右肩关节Y方向位移曲线上升,还原阶段Y方向位移曲线逐渐下降,说明在反手拉上旋弧圈球时,右肩关节的Y方向位移变动方向为先向左后向右,其变化过程符合击球动作中右肩关节的左右位移变动方向。如图 7(c)所示,国家队运动员反手拉上旋弧圈球时,右肩关节Z方向位移曲线的波动范围为1 047~1 278 mm,曲线中段波峰有一定的波动。在引拍阶段,右肩关节Z方向的位移下降,挥拍击球阶段位移上升,说明在击球过程中右肩关节的纵向位移变化顺序为由低到高,其变化过程符合反手拉上旋弧圈球的重心转换发力顺序。右肩关节在X、Y、Z方向角度变化的动作模型构建与X、Y、Z方向位移动作模型的构建类似。
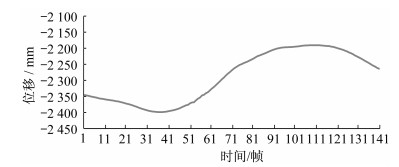
同理,可以构建国家队运动员反手拉上旋弧圈球过程中其他关节(左膝关节、右膝关节和右肘关节)在X、Y、Z方向位移和角度变化的动作模型,以及身体重心变化模型。以身体重心X方向为例,其位移曲线模型如图 8所示。国家队运动员反手拉上旋弧圈球时,身体重心X方向位移曲线波动范围为-2 400~-2 190 mm。引拍阶段运动员身体重心逐渐向后移动调整相对应的击球位置,挥拍击球阶段重心由后向前移,还原阶段重心逐渐回归初始准备状态,其变化过程符合反手拉上旋弧圈球击球过程中重心转换的发力顺序。
|
| 图 8 身体重心X方向位移曲线模型 Figure 8 Displacement curve model of the body gravity center in X direction |
在构建国家队运动员击球动作模型的基础上,以反手拉上旋弧圈球技术动作为例,从10名青少年运动员被试中随机选取1名,对其击球动作合理性进行案例分析。同样以权重较高的右肩关节为例,对青少年运动员反手拉上旋弧圈球技术动作的合理性进行评价。为更清晰地描述击球动作合理性评价的结果,将击球动作的合理性评价结果分为5个等级(表 5)。
| 表 5 击球动作合理性程度等级划分 Table 5 Grade division for the rationality of striking action |
青少年运动员与国家队运动员击球质量(球速和转速均值)比较结果(表 6)显示,两者球速的差异较小,转速的差异较大。结合击球质量数据,根据青少年运动员击球动作曲线与模型的相似度比较结果对其击球动作的合理性进行诊断分析[23-25]。
| 表 6 青少年运动员与国家队运动员击球质量比较 Table 6 Comparison of striking quality between young and national elite players |
(1)关节位移变化合理性分析。将青少年运动员反手拉上旋弧圈球的右肩关节位移曲线(X、Y、Z方向)与国家队运动员反手拉上旋弧圈球的右肩关节位移模型(X、Y、Z方向)分别进行曲线相似度比较发现:青少年运动员反手拉上旋弧圈球时,右肩关节在X方向位移曲线与对应国家队运动员击球动作模型的相似度为62.85%,合理性程度较低;Y方向位移曲线与模型的相似度为81.20%,Z方向位移曲线与模型的相似度为81.87%,均比较合理。
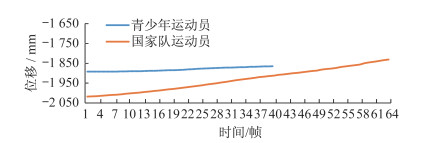
为进一步分析青少年运动员反手拉上旋弧圈球动作的合理性,将青少年运动员反手拉上旋弧圈球的右肩关节位移曲线和国家队运动员对应关节点的位移模型均按击球动作的三阶段(引拍、挥拍击球和还原)进行划分,并按3个阶段进行曲线与模型相似度比较(表 7)发现,青少年运动员在X方向击球动作的三阶段中,引拍阶段X方向的位移曲线合理性程度较低(66.61%)。为分析原因,将引拍阶段X方向的2条位移曲线绘制在同一张图上进行比较分析(图 9)发现,引拍阶段青少年运动员右肩关节在X方向由后至前的位移变化趋势明显低于国家队运动员,说明其右肩关节在引拍阶段X方向的位移不够充分,影响重心转换的效果,导致击球质量降低。
| 表 7 青少年运动员右肩关节位移三阶段曲线与模型相似度比较 Table 7 Similarity comparison of three-phase displacement curve of the right shoulder joint between young players and the model |
|
| 图 9 青少年运动员引拍阶段右肩关节X方向位移曲线与模型的比较 Figure 9 Comparison of leading-phase displacement curve of the right shoulder joint in X direction between young players and the model |
(2)关节角度变化合理性分析。将青少年运动员右肩关节角度变化曲线(X、Y、Z方向)与模型进行相似度比较发现:青少年运动员反手拉上旋弧圈球时,右肩关节的X方向角度变化曲线与对应国家队运动员击球动作模型的相似度为78.84%,合理性程度一般;Y方向的角度变化曲线与模型的相似度为83.72%,Z方向的角度变化曲线与模型的相似度为80.33%,合理性程度均较高。
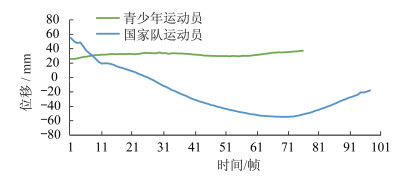
青少年运动员右肩关节角度变化三阶段曲线与模型相似度比较结果如表 8所示。还原阶段Z方向的角度变化合理性程度较低(58.24%)。还原阶段的曲线相似度比较如图 10所示,发现青少年运动员在还原阶段Z方向的角度值无任何明显的旋转变化趋势,说明青少年运动员右肩关节在还原阶段的角度变化完成不够充分,还原不到位。同理,可以完成青少年运动员反手拉上旋弧圈球过程中其他关节点和重心在X、Y、Z方向的位移和角度变化的合理性分析。
| 表 8 青少年运动员右肩关节角度变化三阶段曲线与模型相似度比较 Table 8 Similarity comparison of three-phase angle change curve of the right shoulder joint between the young players and the model |
|
| 图 10 青少年运动员右肩关节还原阶段Z方向角度变化与模型的比较 Figure 10 Comparison of restoring-phase angle change curve of the right shoulder joint in Z direction between young players and the model |
乒乓球运动员击球过程的合理性分析结果及其存在的问题以可视化曲线并结合相关数据反馈给教练员和运动员,从而为乒乓球教练员科学评价运动员的技术动作训练过程提供参考依据,实现对青少年运动员技术动作训练过程的科学、定量化监控,降低训练监控指导过程的盲目性和经验性,提高训练监控过程的科学化水平和训练效果。
5 结论与建议 5.1 结论(1)基于高速动作捕捉技术构建的国家队运动员击球动作模型能有效地对青少年运动员击球动作的合理性进行评价,具有一定的科学性。
(2)将青少年运动员击球过程中各主要关节点运动轨迹和身体重心变换与国家队运动员的动作模型进行比较,可深入探析青少年运动员击球过程中引拍、挥拍击球和还原三阶段各主要关节点运动轨迹和身体重心变换的合理性及其不足,且这一评价结果具有一定的可靠性。
(3)通过对青少年运动员反手拉上旋弧圈球动作的合理性分析发现:该运动员引拍阶段右肩关节带动手臂向前移动的幅度较小,导致引拍不到位;还原阶段右肩关节还原幅度较小,重心稳定性较差。
5.2 建议(1)在引拍阶段, 可通过分解徒手挥拍动作练习,加强右肩关节向左前侧移动的训练,强化其充分引拍的意识;在还原阶段,可采用中弹力带、重力球等负重抗阻专项训练,以强化其击球后右肩关节带动手臂还原至体前初始状态的意识,提高其击球过程中重心转换的稳定性。
(2)在日常的青少年运动员基本技术动作训练过程中,教练员应将数字化训练监控手段与经验式教学相结合,运用国家队运动员击球动作模型对青少年运动员击球动作的合理性进行评价,并结合击球效果找出青少年运动员击球动作存在的问题,为制订具有针对性的个性化训练方案提供依据。
6 不足与展望(1)实验过程所采集的数据均来自训练状态下反手拉上旋弧圈球击球动作,在之后的研究中可尝试构建比赛状态下的击球动作模型,拓展击球动作合理性评价模型的应用范围。
(2)只选取了关节点的空间位置和关节角度等运动学指标构建运动员击球动作的合理性评价模型,后续可进一步选取关节点运动的速度、加速度、角速度和角加速度等其他运动学指标,构建合理性评价模型。
(3)仅以青少年运动员反手拉上旋弧圈球为例对其击球动作的合理性进行分析与评价,后续可扩大击球动作合理性实例分析的运动员数量和击球动作的种类,使击球动作的合理性评价更具实践价值。
作者贡献声明:
冯喆:提出论文主题,指导实验设计;
肖毅:设计论文框架,统计分析数据,撰写、修改论文;
曹梓威:指导实验,核实实验数据;
邓婕:查找文献,搜集、处理实验数据。
| [1] |
唐炜.中国竞技乒乓球运动面临的挑战与机遇[D].北京: 北京体育大学, 2014: 18-25
http://cdmd.cnki.com.cn/Article/CDMD-10043-1015537302.htm (  0) 0)
|
| [2] |
田麦久, 刘大庆.
运动训练学[M]. 北京: 人民体育出版社, 2012: 221-222.
(  0) 0)
|
| [3] |
刘建和.
乒乓球教学与训练[M]. 北京: 人民体育出版社, 2008: 182-186.
(  0) 0)
|
| [4] |
马仁风. 浅谈儿童少年乒乓球运动员的基本功训练[J].
哈尔滨体育学院学报, 2004(1): 90-92 DOI:10.3969/j.issn.1008-2808.2004.01.039 (  0) 0)
|
| [5] |
李文. 简析少儿乒乓球运动基础训练的方法[J].
青少年体育, 2013(3): 78-79 DOI:10.3969/j.issn.2095-4581.2013.03.033 (  0) 0)
|
| [6] |
刘凌鸿. 青少年乒乓球训练的细节问题与强化方法探索[J].
青少年体育, 2018(6): 108-109 DOI:10.3969/j.issn.2095-4581.2018.06.064 (  0) 0)
|
| [7] |
张涛. 不同年龄段青少年乒乓球运动员的训练方法研究[J].
价值工程, 2017, 36(30): 212-214 (  0) 0)
|
| [8] |
沈文丽. 青少年乒乓球多球训练方法研究[J].
河南教育学院学报(自然科学版), 2012(1): 88-90 DOI:10.3969/j.issn.1007-0834.2012.01.029 (  0) 0)
|
| [9] |
屈子路, 叶冬清. 中国乒乓球运动研究综述[J].
广州体育学院学报, 2018, 38(1): 98-103 DOI:10.3969/j.issn.1007-323X.2018.01.022 (  0) 0)
|
| [10] |
刘江, 曾辽原. 利用混合动作捕捉方法辅助排球运动技术标准化的研究[J].
北京体育大学学报, 2014(5): 133-138 (  0) 0)
|
| [11] |
朱怡婕. 基于动作捕捉的汽车座椅坐姿自动化装配方法研究[J].
自动化与仪器仪表, 2020(1): 126-129 (  0) 0)
|
| [12] |
何天宇, 罗奇. 运动捕捉技术及其在体育运动中的应用研究综述[J].
电子测量技术, 2019, 42(3): 140-146 (  0) 0)
|
| [13] |
KRUK E V D, REIJNE M M. Accuracy of human motion capture systems for sport applications; state-of-the-art review[J].
European Journal of Sport Science, 2018, 18(6): 806-819 DOI:10.1080/17461391.2018.1463397 (  0) 0)
|
| [14] |
THOMAS G, GADE R, MOESLUND T B, et al. Computer vision for sports:Current applications and research topics[J].
Computer Vision and Image Understanding, 2017, 159: 3-18 DOI:10.1016/j.cviu.2017.04.011 (  0) 0)
|
| [15] |
李兆波, 陶庆, 康金胜, 等. 基于动作捕捉技术的人体上肢运动舒适性评价[J].
工程设计学报, 2018, 25(3): 338-345 DOI:10.3785/j.issn.1006-754X.2018.03.013 (  0) 0)
|
| [16] |
娄康, 朱志宇, 葛慧林. 基于目标运动特征的红外目标检测与跟踪方法[J].
南京理工大学学报, 2019, 43(4): 455-461 (  0) 0)
|
| [17] |
周驰, 李智, 徐灿. 基于DTW算法的空间目标结构识别研究[J].
计算机仿真, 2019, 36(9): 98-102 DOI:10.3969/j.issn.1006-9348.2019.09.021 (  0) 0)
|
| [18] |
蒋津君, 姚家新, 孟庆华. 乒乓球正手中远台拉冲技术的生物力学特征分析[J].
天津体育学院学报, 2016, 31(6): 506-514 (  0) 0)
|
| [19] |
唐东阳, 曾藕元, 谢虎. 乒乓球击球时间的划分依据及其作用研究[J].
辽宁体育科技, 2013, 35(1): 24-26 DOI:10.3969/j.issn.1007-6204.2013.01.009 (  0) 0)
|
| [20] |
黄刘松, 储岳中, 张学锋. 基于加速度传感器的乒乓球击球动作识别[J].
传感器与微系统, 2016, 35(1): 56-58 (  0) 0)
|
| [21] |
郭岩, 罗珞珈, 汪洋, 等. 一种基于DTW改进的轨迹相似度算法[J].
国外电子测量技术, 2016, 35(9): 66-71 DOI:10.3969/j.issn.1002-8978.2016.09.016 (  0) 0)
|
| [22] |
陈铸. 浅述乒乓球击球的基本原理[J].
课程教育研究, 2017(13): 215-216 DOI:10.3969/j.issn.2095-3089.2017.13.208 (  0) 0)
|
| [23] |
李莉. 乒乓球技术动作协调性和合理性浅析[J].
体育科技, 2002(2): 38-40 (  0) 0)
|
| [24] |
毛旭江, 杨红春, 潘慧炬, 等. 我国优秀跳高运动员黄海强起跳过程蹬摆动作及合理性分析[J].
南京体育学院学报(自然科学版), 2013, 12(5): 66-69 DOI:10.3969/j.issn.1671-5950.2013.05.012 (  0) 0)
|
| [25] |
滑冰. 基于三维图像的羽毛球运动合理性判断方法研究与仿真[J].
科学技术与工程, 2017, 17(10): 231-235 DOI:10.3969/j.issn.1671-1815.2017.10.040 (  0) 0)
|
 2020, Vol. 44
2020, Vol. 44


