2. 华东师范大学未来城市实验室,上海 200241;
3. 华东师范大学地理科学学院,上海 200241
2. Future City Lab, East China Normal University, Shanghai 200241, China;
3. School of Geographic Science, East China Normal University, Shanghai 200241, China
位序规模法则作为城市规模分布领域影响最为深远的经验规律,被广泛地应用于中国[1-3]以及国外[4-6]的城市体系研究中。许多学者对不同国家的城市规模分布是否符合位序规模法则进行了验证[7-9],不乏研究质疑城市规模分布在位序—规模双对数坐标系下的线性假设[10, 11]。随着研究深入,上尾城市中最大城市与其他城市以及城市规模线性分布①的关系得到了越来越多的关注。典型的是城市首位律的研究[12],一个国家的最大城市规模被发现经常超过第二大城市的两倍以上,或者远大于排序靠前的几个城市,在城市体系中的规模地位超乎寻常的高。后续研究从人口规模[13]、国土面积[13, 14]、政治体制[15]、贸易开放度[16]、经济发展水平[17]等国家特征角度为城市首位现象的产生寻找原因。另一个研究方向把城市规模线性分布视作整体,探究最大城市真实规模偏离其线性分布拟合理论预测值的现象[18],尤其是偏下塌陷的特征[19-21]。这类研究较多来自中国,并被认为是长期以来大城市人口与户籍控制政策造成的[22]。最新研究发现,这种最大城市规模塌陷的现象并不是中国特有的,而是一个全球范围内广泛存在的现象,可能的原因在于集聚不经济的存在以及一定时期内大城市技术经济和管理能力的限制[3]。
开展最大城市规模塌陷研究具有重要的现实意义。最大城市规模往往被看作是一个国家经济是否集聚的表现。最大城市规模不足被看作是集聚经济不够,过大又会与集聚不经济联系。联合国[23]预测,人口超过1000万的特大城市(megacities)的数量将由2018年的33个增长为2030年的43个;人口向着大城市集中带来了愈发严峻的挑战,诸如大量城市贫困人口的出现、交通拥堵和上升的环境污染水平,如何缓解大城市病始终是实践中被关注的问题。在城市人口众多的我国尤其如此,存在着是否要控制超大城市规模的争论以及如何优化城市规模的现实需求。深化最大城市规模与其他城市及城市规模线性分布关系的研究有助于更深入地理解最大城市规模的性质乃至于整体城市规模分布的形成机制,为在发展实践中应对日趋严重的大城市病带来启发性解决思路。
在已有的研究中,关于城市首位律现象的探索较为丰富,但这类研究只涉及最大城市与其他个别城市关系,具有一定偶然性和不确定性。相比较而言,对最大城市规模塌陷即低于城市规模线性分布理论预测值的研究更具有整体性和系统性,是一个值得继续探索的方向。这类研究目前不多,主要局限于最大城市规模塌陷现象描述和形成机制的猜测,对塌陷程度的测度、机制和影响因素的深入分析尤其是定量分析涉及很少,研究区域也主要局限于中国,对世界其他国家关注很少。为了弥补已有研究不足,本文基于欧盟委员会联合研究中心的人口和建成区数据,识别了1975—2015年全球范围内具有统一定义的实体城市地域,在此基础上,第一次对全球超过100个国家城市规模分布中的最大城市规模塌陷现象进行了系统地量化测度,并从最大城市自身层面因素尤其是集聚经济和集聚不经济的角度对背后的作用机制进行了检验。
2 文献综述及理论假说 2.1 文献综述城市规模分布的位序规模法则自Auerbach[24]提出以来,在相当长的一段时间内被广泛接受。但是当将越来越多的国家纳入研究范围后,线性分布的假设被发现在大多数情况下并不成立[7-9],它可能只是对数正态分布的一部分[18, 25],而整体分布可能是对数正态—帕累托分布[26-28]或者双帕累托对数正态分布[29, 30]。
与位序规模法则关注整体城市规模分布不同,城市规模分布的一端即上尾城市尤其是最大城市与其他城市的关系也得到了研究的关注。其中一支文献研究城市首位律即最大城市与其他城市的规模关系。Jefferson[12]将最大城市的人口规模远大于其他城市的现象定义为城市首位律,其中的最大城市也被称为首位城市。关于城市首位现象的原因,Mehta[13]发现其与国家人口数量以及国土面积显著相关。Linsky[14]认为,城市首位律现象通常发生在范围小和密度高、人均收入低、出口导向型和农业经济、殖民历史和人口快速增长的国家。政治因素中,一般认为民主程度越高的国家,首位度越低[15, 31],但对曾经被殖民过的国家来说结论相反[32]。经济因素中,贸易开放度高的国家对于本地市场的依赖度更低,因此首位度更低,但已有研究中结论并不统一[15, 16, 33];国家经济发展水平与首位度存在倒U型关系[8, 17, 34],即随着经济不断发展,城市首位程度先上升后下降。
研究最大城市与其他城市关系的另一支文献则把城市规模线性分布视作一个整体,探索最大城市真实规模与其理论预测值的偏离现象。Berry[18]将城市规模分布类型分为首位分布、位序规模分布以及处于两者中间的过渡阶段,其中首位分布与过渡分布都存在最大城市人口规模超过位序规模分布的理论值的特征。也有一些研究关注到了最大城市规模较线性分布理论预测值偏小的现象。周一星[19]最早发现,当采用不固定截距的位序规模分布分析时,中国最大城市的真实值显著低于其理论值。张欣炜和宁越敏[20]使用六普数据研究中国大都市区时发现,规模最大的几个都市区的人口都小于位序规模法则的理论值,魏守华等[21]对中国2000—2010年县级以上城市的研究也佐证了这一发现。对于最大城市规模偏小的原因,Li和Lu[22]将其归咎为中国改革开放以来限制大城市鼓励小城市发展的政策以及户籍制度。与前述研究只关注中国不同,孙斌栋等[3]发现了最大城市规模偏小现象的普遍性,并称之为最大城市塌陷现象,以中国和美国为代表的国家城市规模分布以及世界城市规模分布都存在最大城市规模塌陷的特征,并推测集聚不经济的存在以及一个时代的技术、经济和管理水平约束可能是最大城市偏离线性分布的重要原因。
综上所述,现有关于最大城市与其他城市关系的研究主要集中于城市首位律现象,对最大城市规模塌陷即低于城市规模线性分布理论预测值的研究已有所涉及,但主要局限于中国的研究,对世界其他国家涉及较少;而且主要局限于最大城市规模塌陷现象描述,对塌陷程度的测度、机制和影响因素分析尤其是定量分析关注较少;城市首位律研究对机制的探索较为系统,为最大城市塌陷机制的进一步分析提供了很好了参考,但主要聚焦于国家尺度的影响因素,对最大城市个体层面的因素和机制没有涉及。对最大城市规模塌陷的研究对于洞悉城市规模分布性质与规律具有重要理论意义,对于国家城市化战略选择也具有重要的启发价值,弥补已有研究不足构成了本文的初衷。
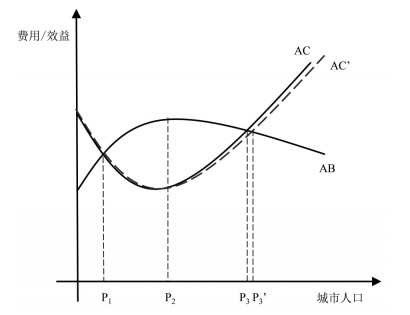
2.2 理论假说在开展实证研究之前,首先基于巴顿[35]的成本收益模型提出本文的假说。如图 1所示,AB和AC分别代表城市居民的平均收益和平均成本。P1代表城市的最低人口规模,这时城市内个体的平均收益和平均成本相同。P2是对于城市内个体而言的最佳城市规模,此时的个体平均净收益最高。P3代表城市的最大规模,这时迁入城市的收益为0,因此不会有新的个体进入城市。个体在城市中获得的收益AB,在城市规模较低时(在P2之前),是随城市规模增加而不断上升的,这是因为共享、匹配、学习等集聚经济机制的存在。然而当规模增长到一定程度后(城市规模大于P2),规模继续增加会导致城市中个体的平均收益开始降低。个体承担的成本AC,在城市规模增长到一定程度后(超过P2),将随城市规模增加而上升,通勤成本、住房成本、环境污染以及人们的压力是主要成本来源。
|
图 1 随城市规模变化的个人成本收益曲线 Fig.1 Individual Cost-benefit Curves that Vary with City Size |
本文据此提出个体净收益(AB减去AC)与城市规模增长之间的关系假说,①在一定城市规模以内(如P1和P2之间),个体净收益越高,城市吸引力越大,城市规模增长率也越高;②当城市规模足够大时(如超过P2后),由于规模越大个体净收益越低,城市规模增长率也越低,从而城市的增长率可能低于城镇体系中其他城市的增长率,出现实际值低于理论值的塌陷现象;③地铁等先进交通工具的应用可以降低集聚不经济而减轻城市的塌陷,但当城市规模继续增长,将可能超出地铁等交通工具的承载力,从而加剧城市的规模塌陷。总之,集聚不经济的存在以及一定时期内大城市技术经济和管理能力的限制,导致最大城市规模低于其城市规模分布理论预期值,从而产生最大城市规模塌陷现象。本文这一假说延续了已有文献的观点[3]。
如图 1所示,虚线部分表示当城市出现地铁之后成本收益曲线的变化情况。当城市拥有地铁后,地铁可以通过减少通勤等成本来减少个体的成本,降低集聚不经济,从而提高了城市的最大规模(P3'相对P3右移),这会使城市继续获得增长空间而减少塌陷。但是如果城市规模继续增长,当超过地铁给城市新增的承载力,塌陷程度还会进一步增强。
3 方法与数据 3.1 城市识别与数据来源在城市规模分布的跨国研究中,不同国家的城市定义和城市人口门槛并不相同,这会带来不可比的问题[8]。为此,我们借助建成区和人口栅格数据并运用统一的门槛标准对所有国家的实体城市进行识别。城市识别所用的建成区和人口数据来自于欧盟委员会联合研究中心发布的全球人类定居区图层(https://ghsl.jrc.ec.europa.eu/),最小栅格单元为一平方公里,国家边界数据主要来自哥伦比亚大学的全球行政区划数据(https://gadm.org/data.html)。
已有的实体城市定义通常对最小识别栅格单元内的人口密度、建成区面积指标进行规定。在识别出符合规定的栅格单元后,将相邻的栅格单元连接起来作为一个空间实体。进一步将空间实体内所包含的人口进行加总,把人口规模大于一定门槛值的空间实体定义为城市[36, 37]。但是这一识别方法存在人口密度或者城市人口规模门槛设定的主观性和随意性,缺少客观标准。而且,用设定人口门槛的城市进行城市规模分布分析会难以观察城市规模分布整体态势[10]。为了弥补这些不足,参考联合国人居署等多个国际组织提出的标准[38],本文城市识别过程如下:首先,识别出所有建成区面积占比超过50% 的最小栅格单元;然后将识别出来的相邻单元合并定义出实体城市的边界;最后,使用人口栅格数据与实体城市边界进行匹配得到所有城市样本的人口规模。为了保证得到无人口门槛值的城市规模分布,在整个识别过程中,我们并不对城市的人口规模与建成区面积设置门槛进行限制。
3.2 最大城市规模塌陷的测度城市规模分布形态的相关研究已经证明,城市规模分布下尾部分即规模较小一端城市是偏离线性分布的,这意味着,在我们使用位序规模法则进行城市规模相关研究时,对于位序规模法则线性假设的适用范围的关注是重要且有意义的。本文运用城市规模分布形态研究的最新成果,在识别城市规模分布最优拟合分布类型的基础上,对最大城市理论规模进行预测,再进一步测度最大城市实际规模相对于理论规模的偏离,以此来识别最大城市相对于整个城市体系而言的特殊性。
按照分布形式从简单到复杂的顺序,我们使用的城市规模分布函数类型依次是:对数正态分布(lognormal distribution,简称LN)、帕累托分布(pareto distribution,简称pareto)、对数正态—帕累托分布(composite lognormal-pareto distribution,简称CLP)以及双帕累托尾部—对数正态分布(two-pareto tail-lognormal distribution,简称TPLN)。
最大城市规模塌陷的具体计算过程如下。首先,运用最大似然法对每个国家的城市规模分布进行四种函数类型的参数拟合;在得到结果后,通过比较最大似然值得到拟合程度最好的函数类型;接着根据这一拟合最优函数的参数计算出一个国家最大城市规模的理论拟合值②,最后计算最大城市理论规模与实际规模的比值来反映最大城市的塌陷程度。具体地,当该比值大于1时,说明最大城市实际规模低于理论值,出现了真实意义上的塌陷;当该比值等于或小于1时,意味着最大城市实际规模与整体城市规模分布相适应或者偏大,不存在真实塌陷。但不管怎样,该值越大意味着实际规模比理论规模小的可能性越大,在本文中被定义为塌陷程度越高。
由于进行城市规模分布的参数识别通常对样本量有一定要求,稳定的城市规模分布需要足够数量的城市,因此只将那些城市数量大于20的国家纳入我们的研究样本中,最终1975年、1990年、2000年以及2015年分别有95、104、116以及119个国家被纳入研究样本。
3.3 最大城市规模塌陷的影响因素识别模型本文采用面板双向固定效应模型对塌陷的影响因素以及机制进行识别和检验。公式如下:
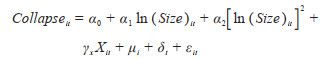
|
(1) |
Collapse代表国家最大城市的塌陷程度,Size为一个国家内最大城市的人口规模,i、t分别表示国家和年份,X为控制变量,μi是不随时间变化的国家固定效应,δt代表时间固定效应;εit为误差项。
城市层面的控制变量包括最大城市是否有地铁以及是否为国家首都。地铁会支撑城市获得更大的规模,从而对最大城市规模塌陷带来影响。地铁数据来自Gonzalez-Navarro和Turner[39]关于城市在1975—2010年间是否有地铁存在的信息,虽然数据的最后一个时间点与城市人口数据的2015年并不一致,但这已经是我们能找到的最好的数据。首都城市位置数据来源于北京大学城市与环境学院地理数据平台(http://geodata.pku.edu.cn)。国家层面的控制变量借鉴了城市首位律的文献,包括人均GDP、城镇化率、国家总人口、贸易开放度及政治体制。人均GDP、城镇化率、国家总人口以及贸易开放度的数据都来自世界银行数据库。政治制度的控制变量来自Polity Ⅳ(2018)的政体指数。
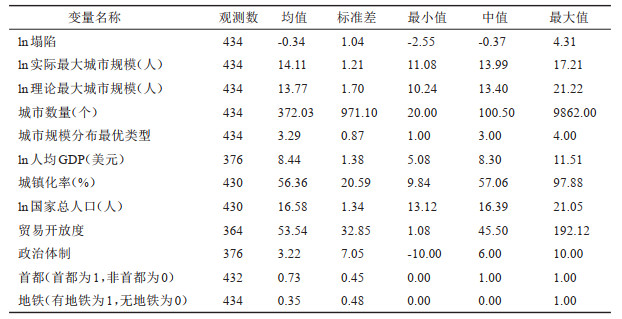
3.4 变量描述性统计表 1列举了本文所有变量的描述性统计信息。塌陷程度最高的是2015年的中国,最低的是1975年的菲律宾。对全部国家样本而言,塌陷值取对数后的平均值和中位数都小于0,这说明超过半数以上国家的最大城市并不存在真实塌陷。全世界最大的城市位于2015年的日本,人口规模达到2985万。1975年阿联酋的最大城市在所有国家最大城市中规模最小,只有6.5万人。理论上的国家最大城市的规模最小值是2.8万人,最大值是16.4亿。最优分布类型有四种,1—4分别代表LN、Pareto、CLP和TPLN。
| 表 1 变量描述性统计 Tab.1 Descriptive Statistics of Variables |
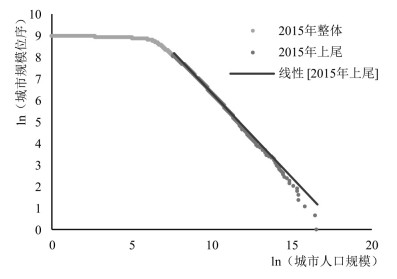
首先,举例展示国家最大城市规模塌陷现象。为了减少政府干预等因素对于最大城市塌陷现象的影响,这里选择市场化程度相对较高的美国为例。以2015年为例,美国城市规模分布类型符合双帕累托尾部—对数正态分布,该年美国的上尾城市人口门槛为1980人,对超过这一门槛的城市进行拟合。如图 2所示,人口规模排名靠前的城市对于线性分布的偏离现象十分明显。1975年、1990年和2000年美国城市规模分布同样存在这一现象。根据我们前面的假说,可能的原因在于,这些城市规模较大的城市由于集聚不经济也较大,规模增长相比其他规模的城市更慢,而且随着规模增长其增长率逐年减缓,最终偏离了线性分布,发生了塌陷。
|
图 2 2015年美国城市规模分布及上尾塌陷 Fig.2 US City Size Distribution and Upper-Tail Collapse in 2015 |
接着使用2015年国家最大城市规模排名前10的国家,观察1975年至2015年这些国家最大城市的规模塌陷情况。发现在1975年有四个最大城市的规模是真实塌陷的,即城市规模理论拟合值大于实际值。而到了2000年和2015年,最大城市规模塌陷的国家数量增加到了8个。同时,从1975年到2015年,排名前10国家的最大城市规模塌陷平均程度也是逐年增高的。
最后,观察所有数据可得的100多个国家的最大城市规模在这四个时间段的塌陷程度。结果显示,约三分之二的国家其最大城市并不是真实塌陷的,但是所有国家最大城市规模塌陷程度的平均值随时间在不断变大。从1975年到2015年,真实塌陷(即真实规模小于理论规模)国家的数量由30个增长为43个③,最大城市塌陷的国家占所有样本比重也由31.6% 增长到36.1%。
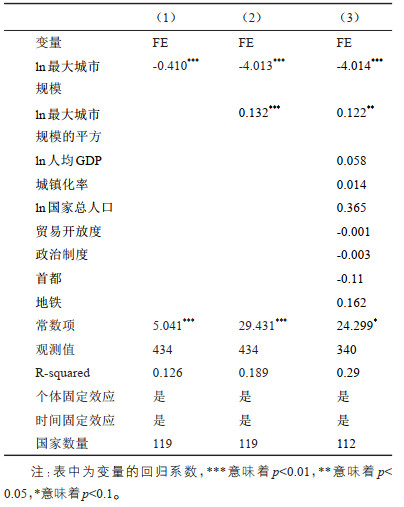
4.2 最大城市规模与塌陷程度的非线性关系根据前面假说,城市在到达一定规模后进一步增长的速度低于整体城市规模增长水平可能是导致城市规模塌陷的直接原因,而背后的机制在于城市内部集聚不经济逐渐超过了集聚经济。为了检验这一假说,接下来使用个体时间双固定效应模型对最大城市规模塌陷程度与其规模之间的关系进行探究。结果显示(表 2),在只考虑最大城市规模对数作为自变量时,塌陷程度与最大城市规模都是负相关的,最大城市规模越大,塌陷程度越低;而在加入最大城市规模对数二次项后,二次项的系数显著为正,一次项系数显著为负,这说明塌陷程度与最大城市规模之间存在非线性U型关系,即最大城市的塌陷程度随着最大城市规模的增加先降低后增加。这表明,最大城市的实际规模并不是可以无限扩张的,随着规模不断增加,由于当前时代的技术经济与管理能力的限制,集聚不经济力量的增加会快于集聚经济,从而最终抑制最大城市的增长。而城市体系中的绝大多数城市并未接近规模增长的天花板,因此其城市规模仍可以不断增长,最大城市与整体城市规模分布之间出现的这一增长差异也就导致了当最大城市规模达到一定门槛值后,随规模增长塌陷程度的不断增加。在加入其他控制变量后,上述结果不变。
| 表 2 最大城市规模对塌陷程度的非线性影响:固定效应回归结果 Tab.2 The Non-Linear Impact of the Biggest City Size on Collapse Extent: FE Results |
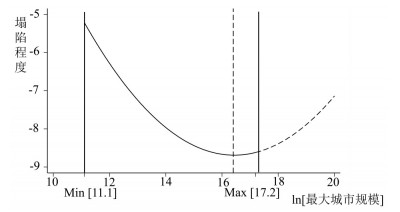
基于模型(3)对最大城市塌陷程度与最大城市规模二者的U型关系进行可视化(图 3)。总的来看,U型关系在整个首位城市规模的范围内得到了展现,随着最大城市规模不断增加,其塌陷程度先降低后增加。拐点处的首位城市规模的对数值为16.45,对应现实的城市规模为1394万。基于模型(2)算出的拐点处城市规模约为400万。这可能意味着400万到1394万人口是城市集聚经济和集聚不经济的一个转折点区间。在这一区间规模以下的城市,城市内部的集聚经济力量占主导,但主导程度随规模增加不断降低;但当城市规模超过这一区间,量变引起质变,最大城市内部的集聚不经济力量开始占据主导地位,最大城市规模增长率相对整体城市规模分布明显下降,因此这时城市规模继续上升会提高最大城市的塌陷程度。
|
图 3 塌陷程度与最大城市规模的U型关系 Fig.3 The U-shaped Relationship Between Collapse Degree and Maximum City Size |
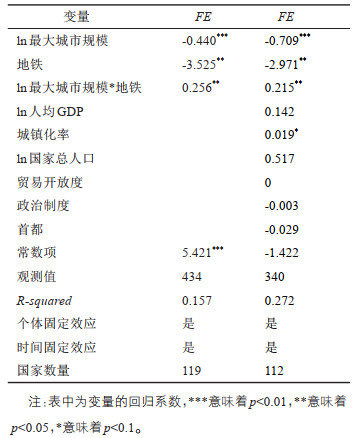
根据假说,最大城市规模与塌陷程度之间的U型关系是由于集聚经济与集聚不经济二者的相对强弱决定的。当最大城市规模足够大了之后,由于交通技术以及城市管理水平等因素的限制,对快速增加的集聚不经济的缓解能力有限,其规模增长速度慢于城镇体系中其他城市,因此其规模塌陷程度会随之增加,其规模已经越来越接近目前技术经济条件下的天花板。交通技术的发展是推动城市空间扩张以及城市规模增长的重要力量,城市内部应用更好的交通技术可以通过降低交通成本减少集聚不经济对城市规模增长的抑制性影响。为了验证这一假说,接下来将城市是否拥有地铁作为反映交通技术的变量,城市拥有地铁被认为具有更高的交通技术水平。个体时间双固定效应结果显示(表 3),地铁的系数显著为负,同时最大城市规模与地铁的交互项显著为正。这表明,地铁可以减弱集聚不经济带来的成本上升,从而增加城市的增长潜力,缓解塌陷现象;但随着城市规模的持续增加,地铁给城市带来的增长潜力会被抵消和耗尽,集聚不经济再度占据上风,塌陷日趋明显。这一结果支持了前面提出的假说。
| 表 3 塌陷程度与最大城市规模关系的机制检验 Tab.3 The Mechanism Test of the Relationship Between Collapse Extent and Biggest City Size |
基于全球人口数据和建成区数据,本文识别了1975—2015年全球范围内具有统一定义的实体城市,测度了国家最大城市人口规模对于城市规模线性分布的塌陷程度,在全球范围内验证了最大城市规模塌陷现象的存在,并使用计量方法对塌陷程度的影响因素以及机制进行了检验与分析,结论如下:
(1)最大城市规模塌陷现象并不是中国独有的,全世界范围内有约三分之一的国家其最大城市是塌陷的,即最大城市实际规模低于根据国家城市规模分布拟合推算出来的理论值,且最大城市的塌陷程度逐年增加。最大城市规模大的国家,塌陷程度更高,2015年最大城市规模排名前10的国家中有8个国家的最大城市表现为真实的塌陷。
(2)塌陷程度与最大城市规模之间的关系呈U型,即随着最大城市规模的不断增加,塌陷程度先下降后增加。这一现象是集聚经济与集聚不经济相对强弱的外在表现,当城市规模较小时,集聚经济机制起主导作用,最大城市规模增长相对整体城市规模分布而言更快,因此其塌陷程度随城市规模增加而降低;但当最大城市增长到一定规模后,集聚不经济相对于集聚经济逐渐占据主导地位,最大城市规模增长相对于整体城市规模分布而言相对滞后,其塌陷程度随着规模的增长而增强。
(3)地铁等新交通技术的应用有助于塌陷程度降低,但最大城市规模越大,影响作用越弱。交通技术的改善可以通过减弱城市内部的集聚不经济程度,从而促进城市规模增长,减弱塌陷现象。但随着最大城市规模持续增加,单一交通方式的引进对于城市的影响会不断削弱,因此最大城市规模塌陷程度还会进一步提升。
本文可能的理论贡献在于,第一次对国家最大城市规模偏离城市线性分布而塌陷的现象进行了长时段、大样本的系统测度,从城市层面集聚经济和集聚不经济的角度探究塌陷的原因,并使用最大城市是否存在地铁这一条件对理论假设进行检验,从而尝试为城市规模分布理论贡献新的知识。本文发现支持了关于最大城市规模塌陷的原因假说,即集聚不经济的存在以及一定时期内大城市技术经济和管理能力的限制,导致最大城市规模低于其城市规模分布理论预期值。本文结论的现实启示在于,应当认识到城市规模不是无限扩张的,而是受制于集聚不经济的制约,而这又与所处时代的交通技术等因素相关。因此,在当前的新型城镇化实践中,为了发挥最大城市等中心城市的集聚经济效应和区域引领作用,增强城市交通技术水平以提高其承载力是重要的保障措施之一。
本文存在三点不足。一是对最大城市规模塌陷这一现象的产生原因,主要从城市领域的独特性出发,其结论不具有一般性,无法用以解释词频、图书销售量、姓氏频率等其它领域中出现的类似现象。二是在城市研究领域内,本文仅从集聚经济与集聚不经济角度对最大城市规模塌陷现象进行了解释,但这只是诸多原因中的一种,未来可以从城市间关系或城市内部的其他角度进一步开展研究。三是,本文只选择了国家作为研究单元,对于研究尺度对于塌陷程度测度的影响考虑不足。
注释:
① 文中提到的线性分布以及对于线性分布的偏离,所指的都是在位序-规模双对数图中的现象,包括但不限于Pareto、CLP以及TPLN分布的上尾帕累托分布部分以及LN分布的上尾部分。
② 在最大城市理论规模的拟合中,对于整体城市规模分布符合Pareto、CLP以及TPLN分布类型的国家而言,最大城市的理论规模计算的是线性分布部分的预测值。对于LN分布而言,计算的则是整体分布的预测值,但是LN分布的上尾部分也基本是线性分布,且符合这一类型的国家数量很少。为了简化表述,文中对于塌陷程度的相关表述统一为最大城市相对于线性分布的偏离。
③ 以下国家在2015年时,最大城市的真实规模小于理论规模:澳大利亚、比利时、巴西、加拿大、智利、中国、捷克共和国、德国、阿尔及利亚、西班牙、芬兰、法国、英国、匈牙利、印度尼西亚、印度、伊朗、伊拉克、以色列、意大利、日本、哈萨克斯坦、韩国、利比亚、墨西哥、马其顿、荷兰、波兰、罗马尼亚、俄罗斯、苏丹、塞内加尔、索马里、塞尔维亚、斯洛伐克、瑞士、特立尼达和多巴哥、土耳其、乌克兰、美国、乌兹别克斯坦、委内瑞拉、南非。
致谢: 感谢匿名审稿人对本文提出的宝贵意见!| [1] |
余吉祥, 周光霞, 段玉彬. 中国城市规模分布的演进趋势研究——基于全国人口普查数据[J]. 人口与经济, 2013(2): 44-52. [Yu Jixiang, Zhou Guangxia, Duan Yubin. The trend of city size distribution in China: Based on census data[J]. Population & Economics, 2013(2): 44-52.] |
| [2] |
唐为. 中国城市规模分布体系过于扁平化吗?[J]. 世界经济文汇, 2016(1): 36-51. [Tang Wei. Is China's city size distribution system too flat?[J]. World Economic Papers, 2016(1): 36-51.] |
| [3] |
孙斌栋, 王言言, 张志强, 等. 中国城市规模分布的形态和演化与城市增长模式——基于Zipf定律与Gibrat定律的分析[J]. 地理科学进展, 2022, 41(3): 361-370. [Sun Bindong, Wang Yanyan, Zhang Zhiqiang, et al. The form and evolution of city size distribution and urban growth model in China: An analysis based on Zipf's Law and Gibrat's Law[J]. Progress in Geography, 2022, 41(3): 361-370.] |
| [4] |
Soo K T. Zipf's Law for cities: A cross-country investigation[J]. Regional Science and Urban Economics, 2005, 35(3): 239-263. DOI:10.1016/j.regsciurbeco.2004.04.004 |
| [5] |
Soo K T. Zipf, Gibrat and geography: Evidence from China, India and Brazil[J]. Papers in Regional Science, 2014, 93(1): 159-181. DOI:10.1111/j.1435-5957.2012.00477.x |
| [6] |
Cottineau C. MetaZipf. A dynamic meta-analysis of city size distributions[J]. Plos One, 2017, 12(8): e0183919. DOI:10.1371/journal.pone.0183919 |
| [7] |
Carroll G R. National city-size distributions: What do we know after 67 years of research?[J]. Progress in Human Geography, 1982, 6(1): 1-43. DOI:10.1177/030913258200600101 |
| [8] |
Rosen K, Resnick M. The size distribution of cities: An examination of the Pareto law and primacy[J]. Journal of Urban Economics, 1980, 8(2): 165-186. DOI:10.1016/0094-1190(80)90043-1 |
| [9] |
Nitsch V. Zipf zipped[J]. Journal of Urban Economics, 2005, 57(1): 86-100. DOI:10.1016/j.jue.2004.09.002 |
| [10] |
Eeckhout J. Gibrat's law for (all) cities[J]. American Economic Review, 2004, 94(5): 1429-1451. DOI:10.1257/0002828043052303 |
| [11] |
Malevergne Y, Pisarenko V, Sornette D. Testing the Pareto against the lognormal distributions with the uniformly most powerful unbiased test applied to the distribution of cities[J]. Physical Review E, 2011, 83: 036111. DOI:10.1103/PhysRevE.83.036111 |
| [12] |
Jefferson M. The law of the primate city[J]. Geographical Review, 1939, 29(2): 226-232. DOI:10.2307/209944 |
| [13] |
Mehta S. Some demographic and economic correlates of primate cities: A case for revaluation[J]. Demography, 1964(1): 136-147. |
| [14] |
Linsky A S. Some generalizations concerning primate cities[J]. Annals of The Association of American Geographers, 1965, 55(3): 506-510. DOI:10.1111/j.1467-8306.1965.tb00531.x |
| [15] |
Ades A F, Glaeser E L. Trade and circuses: Explaining urban giants[J]. The Quarterly Journal of Economics, 1995, 110(1): 195-227. DOI:10.2307/2118515 |
| [16] |
Krugman P, Livas E R. Trade policy and the Third World metropolis[J]. Journal of Development Economics, 1996, 49(1): 137-150. DOI:10.1016/0304-3878(95)00055-0 |
| [17] |
El-Shakhs S. Development, primacy, and systems of cities[J]. Journal of Developing Areas, 1972, 7(1): 11-36. |
| [18] |
Berry B J L. City-size distributions and economic development[J]. Ekistics, 1962, 13(76): 90-97. |
| [19] |
周一星. 城市体系规模结构分析的两个误区[J]. 城市规划, 1995(2): 13-16. [Zhou Yixing. Two misunderstandings in the analysis of the scale structure of the urban system[J]. City Planning Review, 1995(2): 13-16.] |
| [20] |
张欣炜, 宁越敏. 中国大都市区的界定和发展研究——基于第六次人口普查数据的研究[J]. 地理科学, 2015, 35(6): 665-673. [Zhang Xinwei, Ning Yuemin. The definition and development of metropolitan areas in China based on the data from the 6th national census[J]. Scientia Geographica Sinica, 2015, 35(6): 665-673.] |
| [21] |
魏守华, 孙宁, 姜悦. Zipf法则与Gibrat法则在中国城市规模分布中的适用性[J]. 世界经济, 2018, 41(9): 96-120. [Wei Shouhua, Sun Ning, Jiang Yue. The applicability of Zipf's Law and Gibrat's Law to city size distribution in China[J]. The Journal of World Economy, 2018, 41(9): 96-120.] |
| [22] |
Li P, Lu M. Urban Systems: Understanding and predicting the spatial distribution of China's population[J]. China & World Economy, 2021, 29(4): 35-62. |
| [23] |
United Nations, Department of Economic and Social Affairs, Population Divi-sion (2018). The World's Cities in 2018—Data Booklet (ST/ESA/ SER. A/417)[Z/OL]. (2019-04-11)[2023-12-29]. https://digitallibrary.un.org/record/3799524.
|
| [24] |
Auerbach F. Das gesetz der belvolkerungskoncertration[J]. Petermanns Geographische Mitteilungen, 1913, 59: 74-76. |
| [25] |
Parr J B, Suzuki K. Settlement populations and the lognormal distribution[J]. Urban Studies, 1973, 10(3): 335-352. DOI:10.1080/00420987320080471 |
| [26] |
Levy M. Gibrat's law for (All) cities: Comment[J]. American Economic Review, 2009, 99(4): 1672-1675. DOI:10.1257/aer.99.4.1672 |
| [27] |
Ioannides Y, Skouras S. US city size distribution: Robustly Pareto, but only in the tail[J]. Journal of Urban Economics, 2013, 73(1): 18-29. DOI:10.1016/j.jue.2012.06.005 |
| [28] |
Calderín-Ojeda E. The distribution of all French communes: A composite parametric approach[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 450: 385-394. DOI:10.1016/j.physa.2016.01.018 |
| [29] |
Reed W J. The Pareto, Zipf and other power laws[J]. Economics Letters, 2001, 74(1): 15-19. DOI:10.1016/S0165-1765(01)00524-9 |
| [30] |
Giesen K, Zimmermann A, Suedekum J. The size distribution across all cities - Double Pareto lognormal strikes[J]. Journal of Urban Economics, 2010, 68(2): 129-137. DOI:10.1016/j.jue.2010.03.007 |
| [31] |
Davis J C, Henderson V. Evidence on the political economy of the urbanization process[J]. Journal of Urban Economics, 2003, 53(1): 98-125. DOI:10.1016/S0094-1190(02)00504-1 |
| [32] |
Candau F, Gbandi T. Trade and institutions: Explaining urban giants[J]. Journal of Institutional Economics, 2019, 15(6): 1017-1035. DOI:10.1017/S1744137419000328 |
| [33] |
Karayalcin C, Yilmazkuday H. Trade and cities[J]. The World Bank Economic Review, 2015, 29(3): 523-549. DOI:10.1093/wber/lhu002 |
| [34] |
魏守华, 方聪波. 经济发展水平、政治中心分布与城市首位度[J]. 现代经济探讨, 2021(9): 1-11. [Wei Shouhua, Fang Congbo. Level of economic development, distribution of political centers and urban primacy[J]. Modern Economic Research, 2021(9): 1-11.] |
| [35] |
Button K J. Urban Economics Theory and Policy[M]. London: MacMillan, 1976: 91-107.
|
| [36] |
Rozenfeld H D, Rybski D, Gabaix X, et al. The area and population of cities: New insights from a different perspective on cities[J]. American Economic Review, 2011, 101(5): 2205-2225. DOI:10.1257/aer.101.5.2205 |
| [37] |
Florczyk A J, Corbane C, Ehrlich D, et al. GHSL Data Package 2019[M]. Luxembourg: Publications Office of the European Union, 2019.
|
| [38] |
OECD, European Commission, FAO, et al. Applying the Degree of Urbanisation: A Methodological Manual to Define Cities, Towns and Rural Areas for International Comparisons[M]. Paris: Brussels, 2021.
|
| [39] |
Gonzalez-Navarro M, Turner M A. Subways and urban growth: Evidence from earth[J]. Journal of Urban Economics, 2018, 108: 85-106. DOI:10.1016/j.jue.2018.09.002 |