随着港口对陆港的布局建设、多式联运的发展、港口供应链各方主体联盟或协同等,均使得港口作为物流运输网络中关键节点的通达能力和便利水平显著提升,高效的港口连通性对货物流转的效率具有直接影响,是货主/托运人选择出海口和航运企业规划航线的重要参考依据。分析港口连通性及其影响因素的时空差异,有助于港口部门根据自身情况合理规划港口建设布局,加强同港口供应链各环节的互动和联系,对提升区域港口经济发展具有重要的现实意义。
目前,有关连通性的研究多集中在道路交通、城市地理和区域经济等领域,而对航运和港口连通性或可达性的研究相对较少,且主要从航运和港口间相互关系的角度研究,采用的方法可分为四类。第一类研究主要借助复杂网络的度、中心性和路径长度等指标,从海运网络视角分析港口连通性,如Jiang等[1]、Beatriz等[2]运用复杂网络指标分别测算21世纪海上丝绸之路(MSR)、加纳利群岛的港口连通能力。通过模拟航运网络中节点受攻击失效时网络的度、中心性和路径长度等指标变化,分析其对网络连通性的影响[3-7]。第二类研究主要基于港口具有货物运输的属性构建港口连通性模型,如考虑港口货物运输能力和时间[8],综合内陆腹地、内贸支线和国际航运三方面[9],基于多式联运中港口连通能力[10],基于复杂网络六项指标[11]构建港口连通性模型。第三类研究主要借助自动识别系统(AIS)和地理信息系统(GIS)等航运大数据测算港口连通性,如Peng等基于货物运输网络,借助AIS数据分析港口活动的连通影响[12]、港口受攻击时网络的鲁棒性[13]、轴辐式结构中枢纽港的重要性[14]。基于港口在MSR网络中地位和通达性等指标借助GIS分析港口竞争力[15, 16]和优势度[17]。第四类研究主要采用运输时间、成本和距离等评价指标从地理空间视角测算港口连通性,如石伟等[18]提出最小累积成本距离和加权Voronoi图的可达性评价指数,Thill等[19]、韩增林等[20]借助GIS技术通过修正引力模型,分别分析港口对多式联运货物运输可达性和港口的内陆空间可达性格局。此外学者研究了海运网络和港口的连通可靠性[21-23],港口与腹地间的空间可达性[24, 25],内陆货物经港口运输的便利水平[26, 27]。
综上,目前同时考虑港口面向内陆腹地、内贸支线和外贸运输以整条货物运输链的视角对港口连通性的研究较少,且对影响港口连通性的因素探讨仍未涉及。基于此,本文从以下两方面进行分析:①基于港口引力和地理区位,运用修正的引力模型和区位优势方法,建立港口内陆、内贸和外贸连通强度模型;继而从港口供应链视角,结合港口内陆/内贸/外贸连通性三个层面构建港口连通性模型。②将空间计量经济学引入港口连通性影响因素的分析中,由于港口连通性受众多因素影响,各因素间相互联系共同作用,使得不同区位港口连通性差异显著,空间相关性、异质性等作用不可忽略,因此,本文采用空间计量模型对中国环渤海港口连通性的影响因素进行测度。该研究有助于港口明确在港口供应链中的地位、通达水平及制约连通性提升的因素,对制定港口发展策略具有重要的现实意义。
2 研究方法、区域及数据来源 2.1 研究方法 2.1.1 港口连通性模型本文同时考虑港口与内陆(与内陆腹地城市间)、内贸(与内贸支线网络中其他港口间)和外贸(与海外贸易伙伴间)通达和便利程度,以修正的引力模型和区位条件为基础,测算港口引力连通强度和区位连通强度,构建港口内陆/内贸/外贸连通强度模型,最后以动态熵权TOPSIS(DE-TOPSIS)法构建港口连通性模型。
(1)港口连通强度
港口区位优势和交通便利程度越高,对货主、航运公司等吸引力越大。本文从引力和区位连通强度两方面表征港口连通强度,构建港口内陆/内贸/外贸连通强度模型。
引力连通强度。引力模型是广泛应用的测算空间联系强度的模型,基本形式为 Fij= αijMiMjdij-r,质量 Mi、距离 dij和引力系数 αij,由于港口连通能力受多种复杂的综合因素影响,不能简单的用单一指标衡量,因此,本文采用基于复合指标的质量(与港口连通相关的多指标体系构建港口连通质量)、距离(基于时间—空间距离、货币—时间成本和价值构建时空经济距离)和引力连通系数(调整引力常量,修正引力系数),测算港口引力连通强度。
1)质量修正:采用与港口连通性相关的复合指标构成港口连通质量,全面反映港口连通强度。依据选取指标的科学性(能客观反映港口的可达水平和便利程度)、系统性(指标间有一定的层次性和逻辑关系)、目的性(既能测算连通性,又可探究其影响差异)和可操作性(可量化,数据可获得、真实、可靠),结合港口内外通达的特点,本文从五个方面选取:物流贸易规模体现港口的运营状况和连通水平,城市经济支持度是港口提升吸引力的保障,集疏运能力反映连通内外货物节点的便利水平,网络连通度反映港口的中心性和地位,地理交通区位是结合空间地理、空间经济学,体现港口空间和时间的交通便利性,从而构建包含指标层的港口连通质量指标体系(表 1)。
| 表 1 港口连通质量指标体系 Tab.1 Index System of Port Connectivity Quality |
部分指标解释:港口地理交通区位,由于本文综合考虑港口内陆、内贸和外贸连通性三个层面,因此,指标选择应包含内陆(距腹地城市交通时间:主港区到城市行政中心的平均交通时间)、内贸(距渤海湾主要港口航运时间:环渤海内贸支线网络中,通过天津、青岛和大连港的货物吞吐量和中转量较多,且这些港口的航线数量及地理区位等均有较大优势,因此,选择作为主要港口计算与其他港口的海运时间进而衡量各个港口的地理交通区位的优劣)和外贸(距新加坡港航运时间:由于中国国际贸易中超过2/3贸易量的贸易伙伴分布在东南亚、南亚、非洲和欧洲地区,且海运线路主要是传统中欧航线,马六甲海峡是必经之地,而新加坡港作为扼守海峡东端的进出口,且目前作为世界第二大集装箱吞吐量港口,在中国国际海运运输中具有至关重要的作用,因此,选择新加坡港作为中国港口外贸连通性的关键节点,评价港口对外贸易的地理交通区位的优劣)。客货运周转量含公路、铁路和水运和航空运输。港口网络连通度指渤海湾港口组成的沿海内贸集装箱航运网络的连通性;紧密度为该港与衔接港口间最短距离之和;平均路径长度为该港与衔接港口最短距离所经过的边数均值;集聚系数为该港与衔接港口间实际存在的边数占可能的最大边数的比例。
2)距离修正:随着交通工具的发展,地区间要素流动加快,“时空压缩”现象明显,货币成本和时间价值越来越被重视,综合考虑不同运输方式的空间、时间、货币成本和时间价值构成时空经济距离 dij=∑lλl(ηltldlml)1/3 ,其中λl= Hl/∑lHl为第l种方式权重,Hl为货运量;ηl,tl,dl,ml分别为运输单位TEU时间价值、最短运输时间、距离和单位距离货币成本。
3)引力系数修正:引入引力常量调节系数a,构造引力连通系数 αij= G ×(1 + a),G 为引力常量(取1),a= (Mi2 + Mj2)/(Mi + Mj)2,Mi,Mj分别为i,j地区连通质量。
因此,基于引力模型修正的港口引力连通强度为:
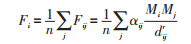
|
(1) |
对内陆、内贸和外贸引力连通强度:j = 1, 2, ∙∙∙, n 分别为内陆城市、内贸支线港口和海外地区数量;αij分别为港口对内陆、港口间和港口对海外地区的引力连通系数;Mi为港口连通质量;Mj分别为内陆城市出口额、港口外贸量和海外地区进口额;dij分别为港城间、港口间和港口与海外地区间时空经济距离;r 为距离衰减因子,取2。
区位连通强度。港口区位优势对港口通达性和交通便利程度影响较大,本文采用交通时间测算港口区位连通强度Pij= βijTij,其中 βij= Mj/∑jMj为区位连通系数,Mj为进/出口额;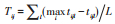
因此,港口区位连通强度为:
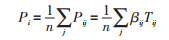
|
(2) |
对内陆、内贸和外贸区位连通强度:βij分别为港口对内陆、港口间和港口对海外地区的区位连通系数;Mj含义同上;tijl分别为港城间、港口间和港口与海外地区间交通时间。
综上,同时考虑港口引力和区位连通强度,分别构建港口内陆/内贸/外贸连通强度模型:
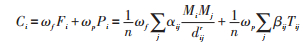
|
(3) |
式中:Ci为港口内陆/内贸/外贸连通强度;ωf, ωp为引力和区位连通强度权重;其他符号含义同上。
(2)港口连通性模型建立
根据长时间序列港口连通性的动态过程,以各港内陆、内贸和外贸连通强度为指标,采用DE-TOPSIS法构建港口连通性模型,同时考虑指标当前值和增量,具体步骤为:
1)计算指标信息熵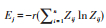
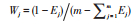
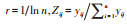
2)构建指标同趋势化矩阵Aij(tk)=[aij(tk)]n×m,对Aij(tk)静态和动态增量加权:
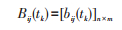
|
(4) |
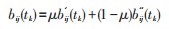
|
(5) |
式中: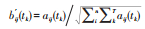
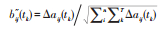
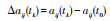
3)计算各时刻各港与最优/劣解距离:

|
(6) |
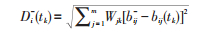
|
(7) |
式中:Wjk为指标 j 在 tk时刻权重,最优/劣解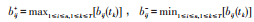
4)计算各时刻各港连通性Ci(tk)= Di-(tk)/(Di+(tk)+ Di-(tk))。
5)引入时间熵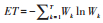
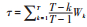
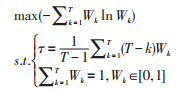
|
(8) |
⑥ 根据时序加权平均算子计算各港连通性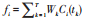
为全面分析各港不同时期连通性差异的影响机理,根据港口连通质量指标体系的要素层,由于港口地理交通区位在不同时期变化较小,故不予考虑,从而选取港口物流贸易规模(WLGM)、腹地支持度(FDZC)、集疏运能力(JSY)和网络连通度(WLLT)4项为自变量,首先通过ArcGIS软件OLS检验变量多重共线性,显示所有年份方差膨胀因子VIF 均小于7.5,共线性程度不高,因此,本文选取上文4项为自变量(数据为重新通过DE-TOPSIS测算的各港要素层4项要素的连通性值),港口综合连通性(C,数据为根据各港内贸/内陆/外贸连通强度通过DE-TOPSIS测算的港口连通性值)为因变量。由于本文采用的是空间面板数据,本文从全域(环渤海港口群)和局域(群内各港口)两个层次进行研究。
首先,从整体衡量4项自变量对所有港口连通性在空间分布上的影响情况,仅考虑自变量空间相关性(因变量和误差项的滞后),不考虑空间异质性,全域层面采用空间面板滞后模型(SLM)和空间面板误差模型(SEM)。SLM模型反映变量是否具有扩散效应(或溢出效应),体现因变量的空间滞后,其对数形式:
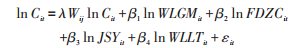
|
(9) |
式中:λ 为空间回归系数;Wij为空间权重矩阵;β 为各因素影响系数;εij为随机误差项。SEM模型反映邻近地区误差冲击对本地影响,体现误差项的空间滞后,其对数形式:
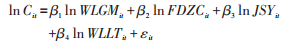
|
(10) |
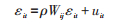
|
(11) |
式中:ρ 为空间误差系数;uit为残差扰动项;其他参数含义同上。
其次,基于港口个体视角,考虑港口的不同地理区位影响时,衡量4项自变量对各个港口的连通性差异影响情况,不仅考虑了自变量的空间相关性,同时考虑了空间异质性,即考虑不同区位港口的实际情况分析其影响因素,更加符合实际。局域层面采用GWR模型揭示自变量对不同区域港口连通性影响的时空差异。GWR模型考虑研究对象的空间位置影响,反映参数在空间分布上的差异,设第 i 个港口主港区地理坐标(αi, βi),构建GWR模型:
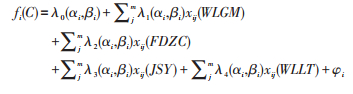
|
(12) |
式中:λ0为截距,λj,(j = 1, 2, ∙∙∙, m)为解释变量的回归系数,m 为解释变量个数;xij为第 i 港第 j 个解释变量值;φi为随机误差。
2.2 研究区域及数据来源根据2006年中国交通部发布的《全国沿海港口布局规划》和2015年国务院批复的《环渤海地区合作发展纲要》,选取辽宁沿海的大连、营口、锦州、丹东、盘锦和葫芦岛港,京津冀沿海的天津、唐山、秦皇岛和黄骅港,山东沿海的青岛、烟台、日照、威海、潍坊、滨州和东营港。内陆地区选取辽宁省、河北省、北京市、天津市和山东省等港口直接经济腹地;内贸区域为环渤海内贸支线港口;外贸地区根据MSR主要航线,选取东亚(日韩)、东南亚、南亚、西亚、东非、北非、南欧、西北欧和大洋洲9个地区。
本文以进入21世纪航运快速发展的2002年为起始年,以2006、2012和2017年为时点。数据主要有3类:一是港口连通质量指标数据来源于《中国港口年鉴》、国民经济与社会发展统计公报及航运公司网站等;二是内陆数据来源于《中华人民共和国道路技术标准》、《国际集装箱汽车运输费收规则》、《铁路线路设计规范》、《铁道部铁路货物运价规则》,路网根据中国公路和货运铁路网地图集,全国地理信息资源目录服务系统;三是内贸和外贸数据来源于BLM-Shipping航运软件、船讯网、世界贸易组织网站等。
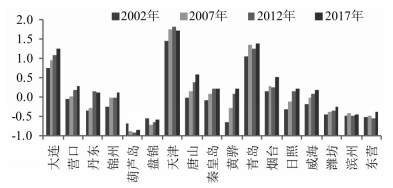
3 结果分析 3.1 港口连通性分析 3.1.1 港口连通质量首先对表 1中港口连通质量指标进行Bartlett球型检验KMO检验,结果适合做因子分析,根据特征值法提取公因子,计算历年各港连通质量(图 1)。
|
图 1 港口连通质量 Fig.1 Quality of Port Connectivity |
由图 1知,环渤海各港连通质量差异较大,天津、青岛和大连港历年的连通质量均最强,由于这些港口城市经济发展水平高,集疏运设施完善,且近年来大力布局内陆港,发展多式联运,不断开通中欧班列,使得港口连通质量的指标值均优于其他港口;葫芦岛和盘锦始终最小,其他港口连通质量有不同程度的差异,基本与港口连通质量的指标优劣相一致。
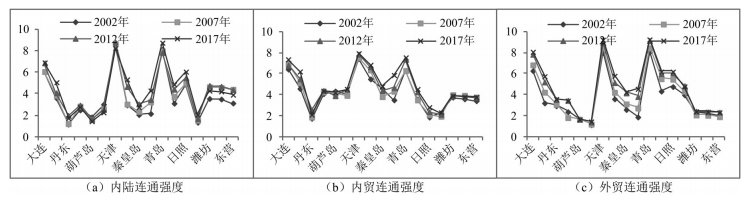
3.1.2 港口连通强度本文设定 ωf, ωp为0.65和0.35,测算不同时期港口内陆、内贸和外贸连通强度(图 2)。
|
图 2 港口连通强度 Fig.2 Strength of Port Connectivity |
由图 2知,天津、青岛和大连的连通强度始终最强,且远高于其他港口,内陆以天津和青岛最强,城市经济实力强,内陆腹地范围大,集疏运体系完善;内贸以天津和大连最强,这两个港口的地理区位较好且拥有较强的基础设施提供货物中转,外贸以青岛和天津最强,航线数量最多,对外建立的外贸联系较频繁。其余港口分析:内陆最强为日照和唐山,由于距内陆城市近,且邻近大型枢纽港,区位优势明显,最弱为威海和丹东,与内陆城市交通距离远,区位优势不明显,难以吸引充足货源,导致与内陆经济联系弱。黄骅、唐山和烟台增速较快,2002—2017年年平均增长率分别为6.61%、5.39%和3.78%,黄骅作为冀东南和山西等地运距最短的出海口,便利的交通优势和区位条件,使得内陆货源不断积聚;内贸以唐山最强,作为区域型港,目前已开通多条内贸航线,与天津航线“双向互通”促进外贸货物中转联运,开启了零担货物拼箱海运新模式,且与国内沿海港口开通定期班轮,是“北煤南运”、“南气北运”的重要港口;外贸最强为烟台和日照,盘锦和葫芦岛最弱,与港口连通质量结果一致,由于自身条件差,区位优势不明显,对船舶挂靠的吸引力较弱,难以与海外地区建立联系;为提升港口竞争力,2018年潍坊、滨州和东营进行三港整合,组建渤海湾港,以实现资源集约高效利用,优化完善港口功能。
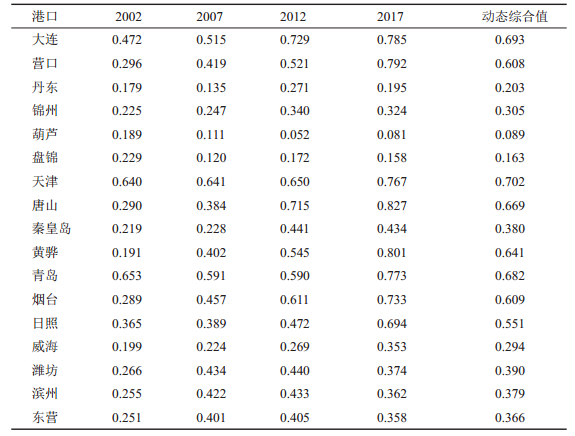
3.1.3 港口连通性同时考虑连通强度的静态和动态增量,取μ = 0.5,计算各港连通性;取时间度τ = 0.3,运用Lingo求解得时间权Wk=(0.105, 0.16, 0.264, 0.47),进而得港口动态综合连通性(表 2)。
| 表 2 港口综合连通性 Tab.2 Values of Port Comprehensive Connectivity |
根据表 2,从横向看,随着时间推移连通性呈增大趋势,且综合值基本位于2012—2017年间,说明该时期连通性最具有代表性,能反映港口的连通水平。从纵向看,各港连通性差异较大,与港口连通质量变化相似,反映了不同区位的港口连通性不同。为更直观刻画港口连通性分布特征,借助ArcGIS空间分析模块做进一步分析。
3.1.4 港口连通性格局特征根据历年港口连通性值及动态综合值,港口连通性空间分布格局如图 3。

|
图 3 港口连通性空间分布格局 Fig.3 The Spatial Pattern of Port Connectivity |
根据港口连通性分布特征,天津、青岛和大连连通性最高,连通国内外货物运输的能力具有绝对优势,分布在京津冀、山东半岛和辽东半岛的核心位置;连通性较差的港口分布在地理位置偏远、区位优势不明显地区,且自身经济水平较低导致的集疏运设施、路网密度、航线数量等较差对货主和航运公司的吸引力较小,如丹东、盘锦和东营等;总体连通性分布具有“核心—边缘”特征。由长时间变化知,最明显的特征是天津、青岛增速放缓,在2002—2007,2007—2012和2012—2017年间年平均增长率年仅为0.02%,0.22%和2.94%、-1.53%,2.47%和2.07%,而黄骅、营口、烟台增速达5.27%,3.58%和3.62%、3.08%,2.54%和4.94%、4.21%,3.83%和3.06%,且分布在核心港周围,可见“边缘挑战”现象显现,可达性强的多门户港口并存的格局也逐渐明显,这些港口借助核心港的辐射带动作用,提供转运服务和零担货物拼箱的功能不断提升,使得连通性稳步增强。
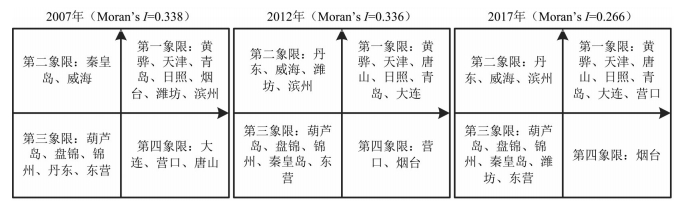
3.2 港口连通性影响因素分析 3.2.1 空间相关性检验首先整体考察各港连通性是否存在空间相关性,采用GeoDa测算历年的Global Moran's I指数分别为- 0.056、0.264、0.202和0.189,P值为0.445、0.028、0.04和0.047,显示2002年没有通过5%显著性检验,其他年份均存在空间正相关性(下文选取2007、2012和2017年),说明环渤海港口连通性具有相互依赖和影响的特征,邻近区域港口连通性对当地港口具有空间溢出效应,结果符合下文空间计量回归建模要求。其次采用Local Moran's I指数与Moran I散点图检验港口间连通性关联的程度和集聚特征,如图 4、图 5所示。
|
图 4 港口连通性Moran散点图 Fig.4 Moran Scatter Plot of Port Connectivity |
|
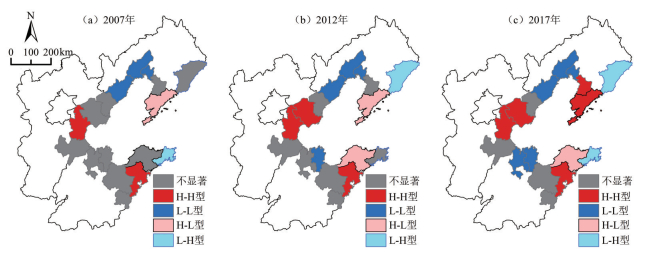
图 5 港口连通性LISA集聚图 Fig.5 Significant Areas of Local Moran's I for Port Connectivity |
由图 4知:第一、三象限连通性存在正空间相关(高高、低低集聚),具有同质性,第二、四象限存在负空间相关(低高、高低集聚),具有异质性。落在第一、三象限的散点数占总数比分别为70.6%、64.7%和76.5%,再次说明连通性存在空间正相关性,高高和低低集聚占主导地位,表明该区域连通性分布格局不均衡;由散点图演变趋势知,港口象限位置变动不明显,2017年第一、三象限散点总数最多,说明各港间差异减小。
由LISA集聚图知,2007和2012年形成两个高值集聚区:以天津为核心的京津冀地区和以青岛为核心的山东半岛,2017年增加了以大连和营口为核心的辽宁半岛,这些港口软、硬实力雄厚,对邻近地区辐射带动作用强,逐步形成门户港口。低值区有两个:渤海湾东北侧的盘锦、葫芦岛和西南侧的滨州、东营,由于基础设施、区位交通条件、经济发展水平及距枢纽港较远等使得综合实力弱,难以吸引充足的货源,与外界联系较少。
综合全局和局部空间相关性结果,环渤海港口连通性具有一定的空间相关性,港口间具有空间溢出效应,下文进一步通过空间计量模型分析连通性影响因素的时空差异。
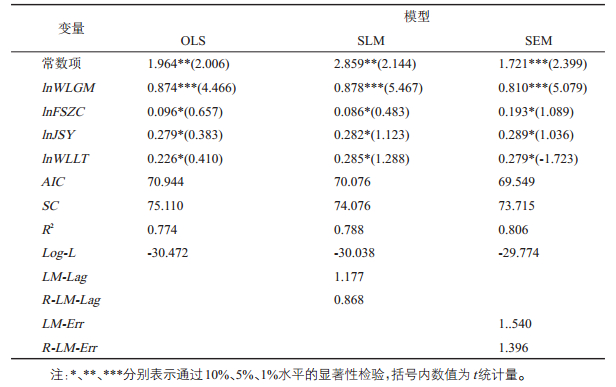
3.2.2 全域层面分析采用SLM和SEM模型分析各因素对港口连通性的总体影响,同时给出OLS回归,通过对比说明最适合的回归模型,各模型回归结果如表 3。
| 表 3 OLS、SLM和SEM模型回归结果 Tab.3 Regression Results of OLS, SLM and SEM Model |
首先从总体上看,空间计量模型的拟合优度R2和Log likelihood值均较大,AIC和SC均较小,表明SLM和SEM模型均优于OLS;同时各模型均通过了10%的显著性检验,进一步表明模型是合理的,各模型变量系数差异较小,反映估计结果的稳健性。
其次对比SLM和SEM模型,从拉格朗日乘子及其稳健性检验判断,LM-Err和R-LM-Err值均比LM-Lag和R-LMLag值大,说明SEM模型更能解释各因素对连通性的影响差异。
最后各因素系数均为正,说明其对连通性有正向作用,尤其物流贸易规模,系数在1%水平上显著为正,表明增大港口贸易量,连通性提升效果显著,根据上文物流贸易规模由集装箱、货物吞吐量和航线数量等指标体现,增加航线数量使港口对外联系增强;其余3个因素对连通性影响程度不同,集疏运能力体现港口对内陆腹地的货物吸引强度、货物运至港口的便利程度和效率等;网络连通度体现港口在内贸支线网络中的地位及可达性水平;腹地城市支持度是港口连通性的基础,腹地不仅为港口提供货源,同时给予资金、政策等支持。
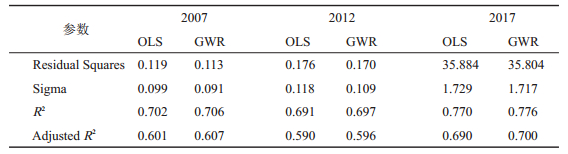
3.2.3 局域层面分析为明确地理区位对港口连通性的影响差异,采用GWR模型从个体层面进行分析,空间权重采用Guass函数,最优带宽采用交叉验证法CV和AIC信息准则,通过ArcGIS计算回归系数,并与OLS比较(由于GWR模型是在OLS的基础上考虑了研究对象的地理位置,即空间效应,能更清晰地解释变量对连通性影响的空间差异):
由表 4知,GWR模型的拟合优度R2更高,Residual Squares和Sigma均略有下降,标准化残差范围分别为[-1.25, 1.68]、[-2.38, 1.11]和[-1.57, 1.87],均通过残差检验,且残差的Global Moran's I为0.003、-0.067、-0.035,P值为0.291、0.214、0.298,呈随机分布,通过相关性检验,说明GWR模型拟合效果更好(下文以距最近的2017年进行说明)。由于GWR模型对各港影响因素都有特定的系数,统计各系数如表 5所示。
| 表 4 OLS与GWR回归参数结果比较 Tab.4 Results Comparison Between OLS and GWR Model |
| 表 5 GWR模型回归系数统计 Tab.5 Statistics of Regression Coefficients in GWR Model |
结果显示各系数均为正,说明各因素均对连通性有正向作用,影响大小为WLGM>JST>WLLT>FDZC;不同分位点回归系数有差异,反映各因素存在空间异质性,进一步说明GWR模型更适合测度不同区位港口连通性的空间差异,将各港回归系数更直观以ArcGIS图像化显示(图 6)。
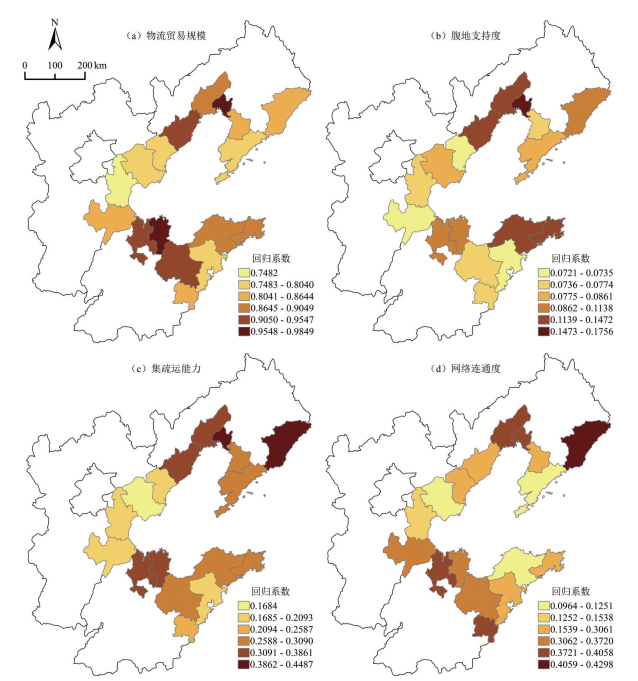
|
图 6 GWR模型回归系数空间分布 Fig.6 Spatial Distribution of Regression Coefficients in GWR Model |
(1)物流贸易规模:与港口连通性正相关,物流贸易是港口运营和发展的基础,增大贸易量对提升连通性作用较大。从系数空间分布看,丹东、渤海北侧和西南侧影响最大,津冀和山东半岛影响较小,分布呈核心—边缘格局,即以山东半岛的青岛、津冀地区的天津和唐山、辽宁半岛的大连和营口为核心,由内向外影响逐渐增大,说明综合实力强的港口连通性也较强,符合“马太效应”,实力弱的港口在增大货运量、增加航线数量等方面较为迫切。
(2)腹地支持度:与港口连通性正相关,但回归系数最小,说明腹地支持度对连通性影响较小,由于港口位于城市边缘,且腹地多交叉,直接影响效果并不显著。从系数空间分布看,影响最大的地区分布在辽宁沿海、威海和烟台,津冀地区和山东半岛西南侧影响较小,由于环渤海西南地区城市经济发展水平较高,加大腹地支持度对连通性的提升效果已经较小,而东北地区城市支持度仍是制约港口连通性提升的重要因素。
(3)集疏运能力:与港口连通性正相关,集疏运能力体现港口对外界陆运和海运的通达能力。从系数空间分布看,高值分布在辽宁半岛的边缘港口和山东半岛的东营和滨州,低值分布在津冀地区,随着天津、青岛等大型枢纽港建设内陆港、中欧班列不断开通和海铁联运货运量持续增加,港口连通性显著提高,东北地区港口仍较多受制于集疏运设施的限制,应加大与东北腹地建立贸易联系、完善港区交通基础设施。
(4)网络连通度:回归系数为正,对港口连通性有正向作用,体现港口在内贸海运网络中的地位和中心性。从系数空间分布看,山东半岛大部分港口处于高值区,辽宁半岛和津冀处于低值区,由于环渤海内贸海运货物主要在东三省与京津冀之间流转,二者间的直接联系较多,而山东沿海港口由于地理位置因素参与力度相对较小。
4 结论与讨论本文从引力和区位优势的视角,基于港口面向内陆、内贸和外贸连通性三个层面,构建连通性模型,并借助空间计量模型探索了中国环渤海港口连通性及其影响因素的时空差异,主要结论如下:
(1)环渤海港口内陆、内贸、外贸和综合连通性均差异较大:内陆连通性天津和青岛最高,丹东和威海最低,黄骅和唐山增速较快;内贸连通性天津和大连最强,唐山连通性上升较快;外贸连通性天津和青岛最高,盘锦、葫芦岛最弱;综合连通性天津、青岛和大连最强,具有绝对优势,盘锦、丹东等最弱。
(2)环渤海港口连通性格局具有“多核心—边缘”分布特征,即以天津为核心的京津冀地区、以青岛为核心的山东半岛和以大连为核心的辽宁半岛,且黄骅、营口、烟台等连通性增速较快,“边缘挑战”现象和多门户港口并存的格局基本形成。
(3)环渤海各港连通性存在一定的空间相关性和空间溢出效应,总体上各港连通性差异逐渐缩小,空间计量回归结果显示,各因素均对连通性具有促进作用,物流贸易规模影响最显著,且对港口影响的分布符合“马太效应”,腹地支持度影响最小,对辽宁沿海港口的制约较明显,集疏运能力是港口内外通达的重要因素,津冀港口的集疏运优势明显,网络连通度对山东半岛港口影响较大,可加强与东北沿海港口的海运联系。
随着“一带一路”倡议、“北极丝绸之路”、中欧班列开通及中日韩自贸区建设等为我国环渤海港口发展带来了机遇;一方面港口部门应结合制约连通性提升的影响因素,加快集疏运体系建设,改善港口区位环境,增大城市支持力度,另一方面,在跨区域或省域港口资源整合的背景下,优化完善港口功能,加快与内陆腹地建立陆港,提高多式联运能力,加强同沿海、海外地区的联系;另外根据港口连通性测算结果,环渤海港口应以实际地理区位进行组团发展提升连通性,即京津冀地区港群、山东半岛港群和辽宁半岛港群,实现群内港口优劣互补,协同发展,进而提高环渤海经济圈的整体连通性。由于港口连通性受众多因素影响,本文港口连通质量指标的选取仍需完善;由于各因素会随时间变化,应进一步探讨影响因素的时间差异特征。
| [1] |
Jiang L P, Jia Y, Zhang C, et al. Analysis of topology and routing strategy of container shipping network on "Maritime Silk Road"[J]. Sustainable Computing:Informatics and Systems, 2019, 21(3): 72-79. |
| [2] |
Beatriz T, Rubén H, Héctor R D. Container port competitiveness and connectivity:The Canary Islands main ports case[J]. Transport Policy, 2015, 38: 40-51. DOI:10.1016/j.tranpol.2014.11.001 |
| [3] |
吴迪, 王诺, 于安琪, 等. "丝路"海运网络的脆弱性及风险控制研究[J]. 地理学报, 2018, 73(6): 1133-1148. [Wu Di, Wang Nuo, Yu Anqi, et al. Vulnerability and risk management in the Maritime Silk Road container shipping network[J]. Acta Geographica Sinica, 2018, 73(6): 1133-1148.] |
| [4] |
吴迪, 王诺, 吴暖, 等. 主航道中断背景下集装箱海运网络的脆弱性及其对中国的影响[J]. 地理研究, 2017, 36(4): 719-730. [Wu Di, Wang Nuo, Wu Nuan, et al. The impact of main channel interruption on vulnerability of container shipping network and China container shipping[J]. Geographical Research, 2017, 36(4): 719-730.] |
| [5] |
王诺, 董玲玲, 吴暖, 等. 蓄意攻击下全球集装箱海运网络脆弱性变化[J]. 地理学报, 2016, 71(2): 293-303. [Wang Nuo, Dong Lingling, Wu Nuan, et al. The change of global container shipping network vulnerability under intentional attack[J]. Acta Geographica Sinica, 2016, 71(2): 293-303.] |
| [6] |
杨翠香, 胡志华. 中国与海上丝绸之路的连通性分析[J]. 上海大学学报(自然科学版), 2018, 24(3): 1-9. [Yang Cuixiang, Hu Zhihua. Analysis of the connectivity between China and the Maritime Silk Road[J]. Journal of Shanghai University (Natural Science Edition), 2018, 24(3): 1-9.] |
| [7] |
严南南, 陆珉, 宗康. 海上丝绸之路航线网络的连通性建模与仿真研究[J]. 华中师范大学学报(自然科学版), 2017, 51(5): 655-662. [Yan Nannan, Lu Min, Zong Kang. Research on connectivity modeling and simulation for route network of Maritime Silk Road[J]. Journal of Central China Normal University (Natural Science Edition), 2017, 51(5): 655-662.] |
| [8] |
Jiang J L, Lee L H, Chew E P, et al. Port connectivity study:An analysis framework from a global container liner shipping network perspective[J]. Transportation Research Part E, 2015, 73: 47-64. DOI:10.1016/j.tre.2014.10.012 |
| [9] |
Wang G W Y, Zeng Q C, Li K, et al. Port connectivity in a logistic network:The case of Bohai Bay, China[J]. Transportation Research Part E, 2016, 95: 341-354. DOI:10.1016/j.tre.2016.04.009 |
| [10] |
Peter W de Langen, Kristina S. Intermodal connectivity as a port performance indicator[J]. Research in Transportation Business & Management, 2013, 8(3): 97-102. |
| [11] |
潘静静, 王晓峰. 复杂网络视角下的港口连通性建模及应用[J]. 深圳大学学报理工版, 2017, 34(5): 544-550. [Pan Jingjing, Wang Xiaofeng. Port connectivity model based on complex network and its application[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(5): 544-550.] |
| [12] |
Peng P, Jessie P H, Yang Y, et al. Global oil traffic network and diffusion of influence among ports using real time data[J]. Energy, 2019, 172(1): 333-342. |
| [13] |
Peng P, Cheng S F, Chen J H, et al. A fine-grained perspective on the robustness of global cargo ship transportation networks[J]. Journal of Geographical Sciences, 2018, 28(7): 881-899. DOI:10.1007/s11442-018-1511-z |
| [14] |
Peng P, Yang Y, Cheng S F, et al. Hub-and-spoke structure:Characterizing the global crude oil transport network with mass vessel trajectories[J]. Energy, 2019, 168(1): 966-974. |
| [15] |
Peng P, Yang Y, Lu F, et al. Modelling the competitiveness of the ports along the Maritime Silk Road with big data[J]. Transportation Research Part A, 2018, 118(C): 852-867. |
| [16] |
杨忍, 牟乃夏, 彭澎, 等. "海上丝绸之路"沿线重要港口竞争力评价[J]. 地球信息科学学报, 2018, 20(5): 623-631. [Yang Ren, Mou Naixia, Peng Peng, et al. Evaluation on competitiveness of important ports along 21st-Century Maritime Silk Road[J]. Journal of Geo-information Science, 2018, 20(5): 623-631.] |
| [17] |
牟乃夏, 廖梦迪, 张恒才, 等. "海上丝绸之路"沿线重要港口区位优势度评估[J]. 地球信息科学学报, 2018, 20(5): 613-622. [Mou Naixia, Liao Mengdi, Zhang Hengcai, et al. Evaluation on location advantages of the ports along the Maritime Silk Road[J]. Journal of Geo-information Science, 2018, 20(5): 613-622.] |
| [18] |
石伟, 苏奋振, 周成虎, 等. 南沙岛礁及周边港口可达性评价模型研究[J]. 地理学报, 2014, 69(10): 1510-1520. [Shi Wei, Su Fenzhen, Zhou Chenghu, et al. Research on accessibility model of Nansha Islands and surrounding seaports[J]. Acta Geographica Sinica, 2014, 69(10): 1510-1520. DOI:10.11821/dlxb201410010] |
| [19] |
Thill J C, Lim H. Intermodal containerized shipping in foreign trade and regional accessibility advantages[J]. Journal of Transport Geography, 2010, 18(4): 530-547. DOI:10.1016/j.jtrangeo.2010.03.010 |
| [20] |
韩增林, 尚颜颜, 郭建科, 等. 东北地区港口内陆空间可达性综合测度[J]. 地球科学进展, 2017, 32(5): 502-512. [Han Zenglin, Shang Yanyan, Guo Jianke, et al. Comprehensive assessment of inland spatial accessibility of the Northeast seaports[J]. Advances in Earth Science, 2017, 32(5): 502-512.] |
| [21] |
吕靖, 王爽. 基于不确定理论的原油海运网络连通可靠性研究[J]. 运筹与管理, 2018, 27(5): 85-94. [Lv Jing, Wang Shuang. Connectivity reliability of maritime transportation network for crude oil based on uncertainty theory[J]. Operations Research and Management Science, 2018, 27(5): 85-94.] |
| [22] |
王爽, 吕靖, 赖成寿. 基于Vine Copula的原油海运网络中节点连通可靠性研究[J]. 交通运输系统工程与信息, 2018, 18(4): 32-37. [Wang Shuang, Lv Jing, Lai Chengshou. Connectivity reliability of nodes in the maritime transportation network of crude oil based on vine copulas[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(4): 32-37.] |
| [23] |
Wang S, Yang D, Lu J. A connectivity reliability-cost approach for path selection in the maritime transportation of China's crude oil imports[J]. Maritime Policy & Management, 2018, 45(5): 567-584. |
| [24] |
Ferrari C, Parola F, Gattorna E. Measuring the quality of port hinterland accessibility:The Ligurian case[J]. Transport Policy, 2011, 18(2): 382-391. DOI:10.1016/j.tranpol.2010.11.002 |
| [25] |
Chen S L, Jeevan J, Cahoon S. Malaysian container seaport-hinterland connectivity:Status, challenges and strategies[J]. The Asian Journal of Shipping and Logistics, 2016, 32(3): 127-137. DOI:10.1016/j.ajsl.2016.09.001 |
| [26] |
Guo L Q, Yang Z Z. Evaluation of foreign trade transport accessibility for Mainland China[J]. Maritime Policy & Management, 2018, 45(1): 34-52. |
| [27] |
Wei H R, Sheng Z H. Logistics connectivity considering import and export for Chinese inland regions in the 21st-Century Maritime Silk Road by dry ports[J]. Maritime Policy & Management, 2018, 45(1): 53-70. |