2. 西北工业大学 动力与能源学院,西安 710072;
3. 陕西省航空发动机内流动力学重点实验室,西北工业大学,西安 710072;
4. 先进航空发动机协同创新中心,北京 100191
2. School of Power and Energy, Northwestern Polytechnical University, Xi'an 710072, China;
3. Shanxi Key Laboratory of Internal Aerodynamics in Aero-Engine, Northwestern Polytechnical University, Xi'an 710072, China;
4. Collaborative Innovation Center for Advanced Aero-Engine, Beijing 100191, China
等离子体激励器在航空航天工程中的应用都是基于等离子体的固有特性.其中, Joule热和周期性静电力是最广泛采用的效应. Joule加热也被称为Ohm加热或电阻加热, 该现象是运动的带电粒子之间随机碰撞并将其一部分动能转化为热能的结果.在稳定状态下, 释放的能量与电流的平方成正比, 与介质的电导率成反比q=σ·E2=I2/σ, 这就是著名的Joule第一定律.由于电导率取决于电离气体的状态, 导致量化时存在较大不确定性.从实验数据来看, 等离子体鞘内阴极产生的Joule热约占直流放电(direct current discharge, DCD)总能量输入的6%[1].与传统高速航空飞行器的热传导和热对流相比, 其传递到流场的能量是很微小的, 但当其作用于边界层底层时, 对改变位移厚度是非常有效的.但是, DCD用于流动控制仅限于低气压的环境下.
形成Debye屏蔽长度的电子-正离子间的静电力由Coulomb定律确定, 其与带电粒子之间的距离成反比.在电极附近, 大量移动的电子将首先附着到阴极, 形成等离子体鞘层, 使得电荷分离.尽管瞬时静电力非常强, 与核键量级相当, 但在介质阻挡放电(dielectric barrier discharge, DBD)的一个交流周期内的时均静电力只有几N/cm3, 这与高Reynolds数下的高速气流动压力相比是非常微小的[2-3].尽管如此, 大量重离子与中性粒子碰撞, 形成了能被检测到的类似喷流的气流运动, 称之为“电子风”[4-5].值得注意的是, Joule热和电子风只存在于等离子体鞘内, 在工程应用中, 其厚度一般为电极表面上几个微米厚.
等离子体在外加磁场的作用下将产生Lorentz力和Hall效应[6].前者是由电磁场中移动的带电粒子产生的, 其方向与电流密度和磁通密度垂直, J×B.后者是由等离子体中带电粒子的旋转加速产生的.带电粒子在垂直于磁场轴的平面内旋转u⊥=ω×r, 其中, ω=|q|B/m为Larmor频率, r=mu⊥/|q|B为Larmor半径, q为粒子所带电荷,m为粒子质量.由于电子与离子单位质量的巨大差异, 两者的轨迹并不相同.在这种情况下, 离子的Larmor半径将大于电子的半径, 而其Larmor频率将低于电子.这种差异造成Hall电势, 导致Hall电流, 这就是磁流体动力(magnetohydrodynamic, MHD)发电机[7]的关键机制.
通过辐射产生等离子体也被称为通过光学手段产生等离子体, 它基本上是一个自由转换的反向过程, 电子或离子通过吸收或发射光子以获得或释放它们的动能, 称之为轫致辐射.辐射产生等离子体通常是通过具有足够强度的单频微波或激光来击穿像空气一类的透明气体介质, 从而产生自由电子[8-9].要达到这个目的, 须利用透镜将激光束能量通量进行汇聚.电离过程沿着光束路径传播, 并伴随着波的吸收和加热.当加热的气体膨胀时, 就形成像爆炸一样的激波向四面八方传播.该爆炸波的传播可以利用Chapman-Jouguet条件进行评估.这一发现为远程能量沉积的等离子体动力学研究和应用开辟了新的途径[10-11].
航天飞行的离子推进器以及再入时的热防护是最具可行性的应用方向.这方面等离子体的应用已经得到认可, 并且持续的研究和开发工作至今仍在继续.下面将讨论等离子体在流动控制、改善点火和燃烧稳定性等方面的应用与创新.
1 等离子体建模等离子体激励器适用于从稀薄流到连续流的气体动力学范围.实际应用中的电离过程主要是由电子撞击产生.直流放电(DCD)的电离过程包括电子二次辐射和级联过程.在交变电场中, 过程是相同的, 但会伴随着随机的微放电, 因此对其开展基础物理过程的研究将面临巨大的挑战.此外, 部分电离的等离子体中包含了超过数百种量子化的亚稳态化学物质, 这就有必要建立可用于分析不均匀介质化学非平衡的物理模型.
在稀薄气体中, 计算模拟必须在Lagrange框架下进行.目前大多数稀薄气体模拟方法都是将单元颗粒法(particle in cell, PIC)与直接模拟Monte Carlo方法(direct simulation Monte Carlo, DSMC)[12]相结合.在全PIC-DSMC模拟中, 所有带电粒子和中性粒子都被宏观假设的粒子追踪, 也就是说, 每个宏观粒子代表了数十亿至数万亿具有相同特征的稀薄等离子体的真实粒子, 被跟踪的宏观粒子总数仍可以轻易超过百万个.基本控制方程是带电粒子动力学的经典Newton-Lorentz方程, 相应的电场分布由电磁学中净电荷密度(n±)的Poisson方程来确定:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{u}}_i} = \frac{{{\text{d}}{\mathit{\boldsymbol{x}}_i}}}{{{\text{d}}t}}} \\ {{m_i}\frac{{{\text{d}}{\mathit{\boldsymbol{u}}_i}}}{{{\text{d}}t}} = q(\mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{u}}_i} \times \mathit{\boldsymbol{B}})} \\ {\;\;\;\;\;{\nabla ^2}\varphi = \frac{e}{\varepsilon }({n_ - } - {n_ + })} \end{array}\ $ |
宏观粒子模拟所需的巨大计算资源不仅要满足PIC-DSMC算法严格的计算稳定性准则, 而且必须满足Debye屏蔽长度在时间和空间上精确的分辨率要求.数值精度还会受到来自大量采样宏观粒子统计噪声的影响.尽管如此, 这种技术已经成功应用于深空探测和卫星台站的离子推进器.简而言之, Lagrange方法在模拟稀薄气体等离子体动力学时对计算资源具有极高的要求.因此高性能并行计算技术的持续改进是必不可少的.
最严格的等离子体建模是基于量子化学和量子物理学的.根据化学动力学理论, 任何复杂的化学反应都可以通过质量作用规律分解为多个单步基元反应[13].在微观尺度上, 化学反应必须通过化学动力学或量子化学物理学来模拟.在该方法中, 包括电离在内的所有化学反应都可以表示为容许的基元反应的集合.对于有限速率或者非平衡化学反应, 正逆反应速率用非平衡化学反应系数来描述.化学反应速率由Arrhenius经验公式决定, 该公式假设反应速率常数强烈依赖于温度.非平衡化学反应的总体速率是正向和逆向化学反应的动态平衡.化学反应体系的质量守恒方程可写为
| $ \frac{{\partial {\rho _i}}}{{\partial t}} + \nabla \cdot [{\rho _i}(\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{u}}_i})] = \frac{{{\rm{d}}{w_i}}}{{{\rm{d}}t}} $ |
其中, 第i种物质的速度为ui, u为混合气体的平均速度.而守恒方程右边源项可写成与该物质相关的第j个化学反应式中反应物(ν′i, j)和生成物的化学当量系数(ν″i, j)、正向(kf, j)和逆向反应速率(kb, j)的函数[13-14]
| $ \begin{array}{l} \frac{{{\rm{d}}{w_i}}}{{{\rm{d}}t}} = {M_i}\sum\limits_{j = 1}^J {\left( {{{\nu ''}_{i, j}} - {{\nu '}_{i, j}}} \right)} \left\{ {{k_{{\rm{f}}, j}}\prod\limits_{k = 1}^{{N_{k{\rm{f}}}}} {{{\left( {\frac{{{\rho _k}}}{{{M_k}}}} \right)}^{{{\nu '}_{k, j}}}} - } } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;{k_{{\rm{b}}, j}}\prod\limits_{k = 1}^{{N_{k{\rm{b}}}}} {{{\left( {\frac{{{\rho _k}}}{{{M_k}}}} \right)}^{{{\nu ''}_{k, j}}}}} } \right\} \end{array} $ |
其中, Mi表示第i种物质的分子量, J表示共有J个化学反应, k表示在第j个化学反应中所包含的第k种物质, 其所对应的分子量为Mk, 密度为ρk, 作为反应物时的化学计量系数为ν′k, j, 作为生成物时的化学计量系数为ν″k, j. Nkf, Nkb分别表示第j个化学反应式中所具有的反应物、生成物的种类数.在大多数等离子体应用中, 主要的化学反应分为4类:电子-分子, 原子-分子, 分解和合成过程. Elisson等[4]对介质阻挡放电(DBD)进行了深入研究.他们通过143个基元反应确定了30种物质在微放电中的电离过程.在最近一项Bogdanov等[15]的工作中, 通过576步涉及振动激发的氮氧、臭氧、正负离子, 以及氧化物、氮化物的化学反应, 来研究空气等离子体的化学-物理动力学.然而, 化学动力学方法的薄弱环节就在于非常有限的验证数据库和繁琐且刚性的计算程序.
最近, Surzhikov等[16]通过经典漂移-扩散理论开发了一种不同于化学动力学理论的有效替代电离模型.为了分析可追踪观测范围内的非弹性碰撞动力学, 带电粒子被简化为电子、正负离子的气体介质.他们的方法是扩展磁流体动力学(MHD)理论中多流体等离子体模型.与推导等离子体动力学多流体模型的共同点是, 它们都是采用气体动力学理论与时域Boltzmann方程和Maxwell方程组结合的方法.虽然在这个过程中, 失去了对电离气体化学成分的详细描述, 但其后将通过电子碰撞对电离极其有效的分析能力而获得修正.
从气体动力学理论出发, 通过二元碰撞近似推导出电子、正负离子的动量输运方程, 便可得到电子、正负离子的速度[14, 16]
| $ {n_{\rm{e}}}{\mathit{\boldsymbol{u}}_{\rm{e}}} = - {d_{\rm{e}}}\nabla {n_{\rm{e}}} - {\mu _{\rm{e}}}{n_{\rm{e}}}(\mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{u}}_{\rm{e}}} \times \mathit{\boldsymbol{B}}) $ |
| $ {n_ + }{\mathit{\boldsymbol{u}}_ + } = - {d_ + }\nabla {n_ + } + {\mu _ + }{n_ + }(\mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{u}}_ + } \times \mathit{\boldsymbol{B}}) $ |
| $ {n_ - }{\mathit{\boldsymbol{u}}_ - } = - {d_ - }\nabla {n_ - } - ({\mu _ - }{n_ - }\mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{u}}_ - } \times \mathit{\boldsymbol{B}}) $ |
强制扩散系数de, d+, d-和带电粒子迁移率μe, μ+, μ-的定义及其关系由Einstein关系式给出[16].
涉及量子力学的复杂化学物理的电子碰撞电离和耗散过程将通过多流体多温度模型的非弹性碰撞模型来模拟.在没有外加磁场的情况下, 模型方程为[14]:
| $ \begin{array}{l} \frac{{\partial {n_{\rm{e}}}}}{{\partial t}} - \nabla \cdot ({n_{\rm{e}}}{\mu _{\rm{e}}}\mathit{\boldsymbol{E}} + {d_{\rm{e}}}\nabla {n_{\rm{e}}}) = \alpha (\left| E \right|)|{\mathit{\Gamma }_{\rm{e}}}| - \beta {n_ + }{n_{\rm{e}}} - \nu {}_{\rm{a}}{n_{\rm{e}}} + {\kappa _{\rm{d}}}{n_{\rm{n}}}{n_{\rm{e}}}\\ \;\;\;\;\frac{{\partial {n_ + }}}{{\partial t}} + \nabla \cdot ({n_ + }{\mu _ + }\mathit{\boldsymbol{E}} - {d_ + }\nabla {n_ + }) = \alpha (\left| E \right|)|{\mathit{\Gamma }_{\rm{e}}}| - \beta {n_ + }{n_{\rm{e}}} - {\beta _{\rm{i}}}{n_ + }{n_ - }\\ \;\;\;\;\;\;\;\;\;\;\frac{{\partial {n_ - }}}{{\partial t}} - \nabla \cdot ({n_ - }{\mu _ - }\mathit{\boldsymbol{E}} + {d_ - }\nabla {n_ - }) = \nu {}_{\rm{a}}{n_{\rm{e}}} - {\kappa _{\rm{d}}}{n_{\rm{n}}}{n_ - } - {\beta _{\rm{i}}}{n_ + }{n_ - } \end{array} $ | (1) |
在空气电子撞击非弹性碰撞模型中(式(1)), 所有比例系数的具体数值都是已知的.其中, α为Townsend相似法则所描述的离解系数, Γe为电子数密度通量.离子-电子复合系数β=2×10-7 cm3/s, 离子-离子复合系数βi=1.6×10-7 cm3/s, 电子附着频率νa=108/s, 脱离系数的最大值κd=8.6×10-10 cm3/s. nn代表中性粒子数密度, 通常作为常数2.69×1019/cm3处理.非弹性碰撞模型已经成为电子碰撞电离的标准模型, 所有系数都可以通过实验中放电电流数据来验证[2, 14, 16].该模型的缺点就像MHD理论一样, 是由多流体和多温度方程引起的, 无法区分不同的亚稳态物质.
2 等离子体控制基于等离子体所特有的热效应以及电磁力作用, 以等离子体激励器为基础的主动流动控制方法在亚声速到高超声速领域都得到了广泛的研究.基于等离子体热激励的控制研究, 主要集中在超声速流场中的激波调控、湍流转捩触发以及射流掺混等方面; 基于其静电力作用的控制研究, 则在亚声速流动分离控制中获得了显著的效果; 而基于磁场力的控制研究, 则更多地集中于应用从外加磁场来增强相应的等离子体控制效果; 应用远程能量沉积的控制方法, 则主要集中于高超声速钝体减阻、降低热流密度、飞行姿态控制等方面.下面将从等离子体的这4种基本特性出发, 详细介绍其在流动控制应用中的控制原理及效果.
2.1 热激励器流动控制低密度空气下直流放电(DCD)有一个明显的特点就是宏观稳定.正常的辉光放电电流只有10-5~10-3A.在较高压力下非均匀场中的气体击穿明显取决于电极的几何形状以及电晕放电的极性[17-18].电晕放电发生在高度不均匀的电场中, 这是由于电极半径r比电极之间的间隙距离d小得多.对于平行排布的电极而言, 极限比d/r=5.83, 当比值大于该值时, 放电从电晕放电过渡并产生火花.在接近大气压的情况下, 击穿很可能导致电弧产生.电极间电弧电势通常从几百伏降至几十伏.辉光放电到电弧放电的过渡是难以预测的.在辉光放电中, 电子的供给主要来自正离子轰击阴极而形成的二次发射.在电弧放电中, 电子的另一个重要来源是阴极的热离子发射.过渡态放电或火花放电可以在很宽的电流范围内发生.
众所周知DCD的结构包括阴极表面的阴极鞘层以及在其之上连接到阳极的阳极柱区.阳极柱的详细结构引人瞩目, 但在流动控制应用中, 电极总是并排分布的.从实验观察结果来看, 如图 1所示, 其显著特征就是明亮的阴极鞘层辉光.图中阴极位于阳极的左侧, 强烈的辉光亮度反映出阴极具有较高的电流密度.阴极层实际上是等离子体鞘, 其中发生阴极压降和集中的Joule加热.

|
| 图 1 平板上并排电极的DCD, p=5.0 Torr(665 Pa), I=100.0 mA Fig.1 DCD with side-by-side electrodes on flat plate, p=5.0 Torr(665 Pa), I=100.0 mA |
为了放大流动控制中Joule加热所引起的扰动, DCD布置于高超声速平板流动的前缘位置, 其控制效果可由有黏-无黏流动相互作用而增强.当向外偏转的边界层撞击到无黏性外部来流时, 就会激发有黏-无黏流动相互作用, 引发一系列压缩波.这种现象的典型例子就是超声速流动中的激波-边界层相互作用以及激波冲击.在高超声速流动中, 前缘无分离流动可以由经典涡和Mach波相互作用理论描述.尖锐前缘所发生的有黏-无黏流相互作用是由超声速边界层的位移厚度引起的, 即所谓的压力或Mach波扰动[19].由Mach波引起的压力扰动是超声速流动中特有的现象, 并提高了下游物面压力.事实上, 根据边界层理论, 位移厚度的增长率在尖锐前缘处是奇异的, 类似于爆炸波.总而言之, 前缘处边界层位移厚度的增长率是十分重要的.
高超声速Mach波相互作用是边界层位移厚度纵向曲率变化导致的.根据经典的边界层理论, 与无黏流场相当的物面边界是在原始物面上加上边界层的位移厚度.因此小扰动高超声速相似参数κ可写为
| $ \kappa = {M_\infty }({\alpha _{\rm{b}}} + \frac{{{\rm{d}}{\delta ^*}}}{{{\rm{d}}x}}) $ |
其中, αb为线性化常数.在零攻角的尖锐平板前缘, 结合常用的近似边界层位移厚度, 高超声速相似性参数可写为
| $ \kappa = {M_\infty }(\frac{\delta }{x}) = \frac{{M_\infty ^3\sqrt {{C_\infty }} }}{{\sqrt {\mathit{R}{\mathit{e}_x}} }} = \bar \chi $ |
其中, C∞=(μ∞/μ)/(T/T∞)为气体黏性与温度线性关系系数.将高超声速相似性参数χ代入斜激波方程, 就可获得平板上Mach波相互作用导致的下游表面压力变化.根据χ值是大于还是小于3, 可将表面压力扰动进一步分为强扰动和弱扰动.
前缘的强弱压力扰动分布可分别表示为[19]
| $ \frac{{{p_{\rm{w}}}}}{{{p_\infty }}} = 0.514\bar \chi + 0.759 $ |
| $ \frac{{{p_{\rm{w}}}}}{{{p_\infty }}} = 1 + 0.31 + 0.05{\bar \chi ^2} $ |
其中, pw表示壁面压力.压力扰动产生沿流向的压升, 其值与距前缘距离的平方根成反比.对于弱压力扰动作用, 流动偏转小, 边界层仍然以x1/2的速度增长.通过Joule加热在尖锐前缘附近产生局部小扰动, 扰动经过有黏-无黏流相互作用得到放大从而改变流场结构.
结合数值模拟和实验观察, 图 2给出了DCD激励器在平板尖锐前缘附近产生的诱导斜激波[20].有黏-无黏流相互作用是在Mach数为5.15的高超声速流场中通过164 W的低功率输入产生的.前缘斜激波下游由DCD产生的第二道激波强度要弱得多, 但仍然可以在纹影图像以及计算所得的密度等值线图中看到.阴极处的电极加热和Joule加热使得边界层位移厚度突然增长, 诱导有黏-无黏流相互作用.随后表面一系列压缩波汇聚成一道斜激波.在阴极前缘附近产生的压缩波诱导下游表面压力升高, 这就构成一种有效的高超声速流动控制技术.这将是一个真正的空气动力学-电磁学相互作用的领域[20].

|
| 图 2 DCD在平板前缘处诱导产生斜激波, Ma=5.15 Fig.2 DCD induced oblique shock over a sharp leading edge plate, Ma=5.15 |
虚拟前缘肋板[20-21]以及可变唇口[22-23]等概念已经通过在高超声速平板尖锐前缘附近安装DCD激励器产生Joule加热, 诱导有黏-无黏流相互作用来放大边界层位移厚度突增的方法加以证实.
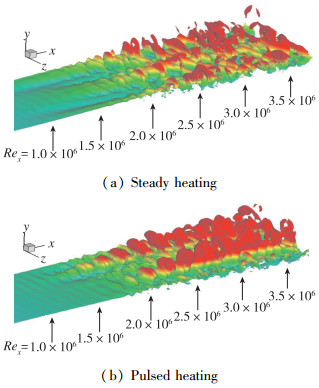
Yan等[24]进行了稳态和脉动热激励下流体不稳定性的数值模拟, 计算采用了高分辨率, 3阶迎风Roe格式.利用沿展向有限分布的稳定/不稳定扰动来产生流向涡. 图 3(a)显示了在稳态热激励下涡在下游的衰减.然而, 脉冲式热激励导致连续的涡流破碎, 并且涡流扰动幅值在下游处增加, 如图 3(b)所示.这种扰动传播模式与线性稳定性分析一致.数值结果显示热激励所产生的三维扰动产生了与流向一致的发夹涡结构.在图 3(b)显示了发夹涡结构, 其y和z坐标的拉伸尺度不均匀, Reynolds数Rex≈2.0×106.从涡量的等值面可以看出, 发源于壁面的发夹涡根部是由一对沿流向对齐的反向旋转旋涡构成的.旋涡主要由x分量组成, 但在边界层中z分量占主导地位.发夹涡结构被认为是湍流中的一种基本结构, 可以增加下游的动量交换.总之, DCD激励器可用于产生热激励, 从而应用于层流-湍流转捩的触发.
|
| 图 3 热激励下游发夹涡结构 Fig.3 Hairpin vortexes downstream of thermal bump |
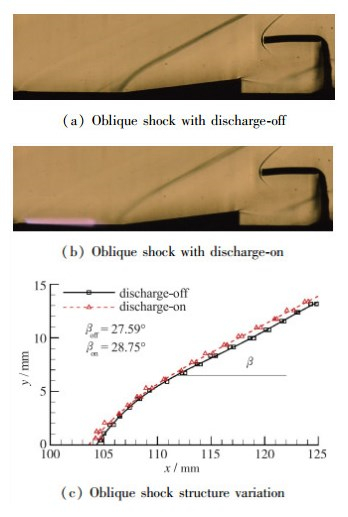
Yan等[25]利用DCD在近壁面边界层内产生稳定的流向电弧, 在Ma=2.5的流场中对斜激波进行控制, 如图 4所示, 基于其热效应的影响, 可实现对激波强度、位置及激波角度的有效控制.这就为DCD激励器实现进气道口部激波系调控提供可能.
|
| 图 4 DCD流向电弧斜激波控制(Ma=2.5, 斜面角度б=7°) Fig.4 Streamwise arc of DCD shock control (Ma=2.5, compression ramp angle б=7°) |
基于等离子体热激励流动控制的研究中, 多种激励器被应用于航空航天领域中最常见的激波诱导边界层分离的控制当中, 其中使用最为广泛的包括直流放电(DCD), 纳秒介质阻挡放电(nano-second DBD, NSDBD), 等离子体合成射流(plasma synthetic jet, PSJ)等激励器.其中DCD激励器由于等离子体的加热, 使得边界层增厚, 导致激波诱导的分离区增加; 而在NSDBD流动控制中, 其对流场的影响主要体现在两个方面: (1)对边界层的加热, (2)近壁面形成涡结构.对边界层的加热使得分离区增大, 而近壁面涡结构的形成, 促进了主流区与边界层之间的动量交换, 可以有效抑制分离区; 而脉冲PSJ激励器, 可以在边界层内同时加入能量与动量, 迫使分离区以激励器频率前后移动, 虽仍未达到完全抑制分离区的目的, 却实现了分离区脉动频率的有效控制, 这就可以有效规避飞行器机体的共振频率.同样基于等离子体的热效应, 当等离子体以不同的形式加入到流场当中时, 其所达到的控制效果也存在较大差别, 因此, 对于特定流动控制问题, 就须根据等离子体流动控制的基本原理, 设计最为合理的等离子体激励方式, 以达到最佳的控制效果.
2.2 静电力流动控制周期交流电(alternating current, AC)产生的电子碰撞电离与直流(direct current, DC)场产生的区别不大.两者基本的电离过程都是Townsend放电机理, 但它们放电形式却存在较大差异. DBD是由一个暴露在外的金属导体和一个电介质封装电极串联构成, 放电主要表现为流光、细丝或微放电, 并在时间和空间上具有随机性[4-5].电极间隙中的流光或微放电是强电场中由初级电子雪崩所形成的弱电离通道, 在空间和时间上都是随机的, 且持续时间只有纳秒量级.空间电荷总是自身产生电场, 使其不同于电晕放电.当微放电从阳极到阴极开始时, 它被称为阴极导向或正极化流光, 否则称为阳极导向或负流光.然而, 电子雪崩在到达电极之前就变成了流光, 就像在微波炉中一样, 流光同时流向两个电极.在周期交流电发生击穿时, 放电随时间和空间的随机出现和消失, 因此只能用高速高分辨率摄像机才能捕捉到.
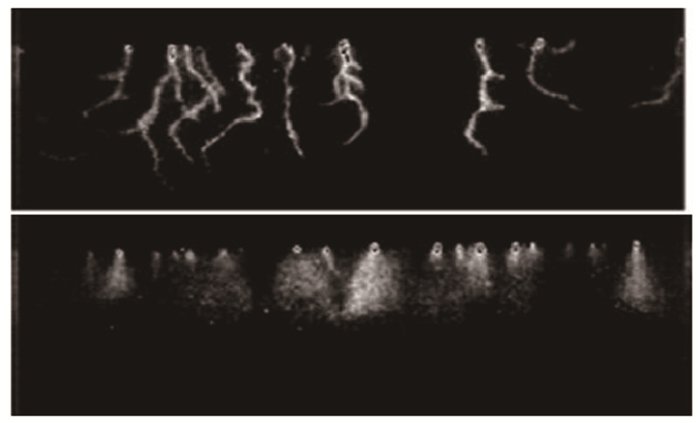
Enloe等[5]采用高速图像强化技术, 在每个AC周期获得了清晰的DBD微放电结构.在AC循环中, 微放电在外露和封装电极之间交替发生.在AC正循环阶段, 外露的金属电极作为阳极, 电介质作为阴极.在这种情况下, 随机微放电从金属电极开始, 称之为正电晕放电, 随后在到达电介质之前, 在电子雪崩过程中转换成流光.在AC负循环阶段, 起始的电晕放电要转变为微放电, 就必须对抗电子漂移运动或电场进行传播, 因此, 流光比正循环时更具扩散性, 如图 5所示.目前, DBD的这种多个随机周期性的微放电过程和动态结构远超出了现有数值模拟的能力.
|
| 图 5 正向/负向传播的流光 Fig.5 Positive and negative propagating streamers |
DBD电极表面上电荷的累积将降低电极间的电场强度. DBD这种独特的自我限制功能可以防止其在大气压下转变为电弧.该特征实际上是由电极上累积的电荷, 以及界面上等离子体和电介质之间的相对介电常数的巨大差异引起的.这种特征可以从等离子体和电极之间不连续的界面边界条件来证实[3].根据时域Maxwell方程, 在没有外加磁场情况下, 仅须电场的界面边界条件.等离子体与电极之间界面处的边界条件须满足跳跃的电位移D, 其必须与表面电荷ρe, s保持平衡[26], 即
| $ \mathit{\boldsymbol{\hat n}} \cdot ({\mathit{\boldsymbol{D}}_{\rm{d}}} - {\mathit{\boldsymbol{D}}_{\rm{p}}}) = {\rho _{{\rm{e, s}}}} $ | (2) |
下标p和d表示位于等离子体介质内或电极表面上的电位移D.根据边界条件方程(2), 垂直于等离子体和电介质界面的不连续电位移必须由局部表面电荷密度来平衡.尽管完全电导体中电流和电荷数密度可能是无限大, 但是在介质表面的特性大小仍可以定义为
| $ {\rho _{{\text{e}},{\text{s}}}} = e\int {({n_ + } - {n_{\text{e}}} - {n_ - }){\text{d}}\mathit{\Delta }} $ |
这是在与介质交界面垂直的无限小距离Δ上对带电粒子数密度的积分, 单位为C/cm2.无论介质表面上发生任何物理化学过程, 都必须满足这个要求.对于全局中性和各向同性的等离子体, 电场强度E可以从电势函数导出E=-▽φ.将该式代入电荷平衡条件式(2)中, 并引出电场强度与电位移的构成关系D=εE, 可得
| $ \frac{{\partial {\varphi _{\rm{p}}}}}{{\partial n}} = \frac{{{\varepsilon _{\rm{d}}}}}{{{\varepsilon _{\rm{p}}}}}\frac{{\partial {\varphi _{\rm{d}}}}}{{\partial n}} + \frac{e}{{{\varepsilon _{\rm{p}}}}}\smallint ({n_ + } - {n_{\rm{e}}} - {n_ - }){\rm{d}}\mathit{\Delta } $ | (3) |
式(3)中的εp, εd分别表示等离子体和电介质的相对电容率.对于弱电离等离子体εp的值为1, 而电介质的相对介电常数εd却有较大的不同, 其材料从聚苯乙烯到橡胶变化时, 值最高可达7.0.事实上, 式(3)也明确揭示了DBD防止放电过渡到电弧这一突出特性.介质表面电荷积累以及介质材料相对于等离子体的相对介电常数之间的差异大大减小了电极间隙的电场强度.更为重要的是, 防止DBD过渡到电弧的这种自我限制特性是满足时域Maxwell方程不连续界面边界条件所产生的直接结果.
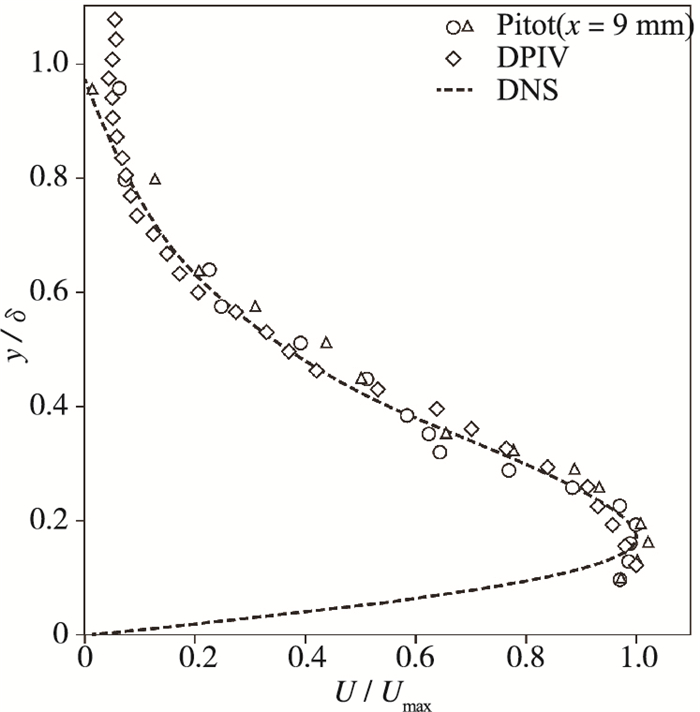
当DBD用于流动控制时, 电极对于电子和离子的吸引和排斥必须根据AC循环的电极极性进行周期性和交替切换.在该动态过程中, 等离子体鞘层中重离子与部分电离空气的中性粒子发生碰撞, 并转移一部分动量而形成所谓的电子风[4, 27], 其表现为垂直于DBD固体表面的类似于壁面喷射流的速度分布. 图 6中的结果显示了粒子图像测量法(particle image velocimetry, PIV)和Pitot压力探针测量的实验结果以及直接数值模拟结果[27].实验数据显示单个不对称电极配置的DBD在等离子体鞘内诱导速度约10 m/s, 实验中其估算的厚度约为几微米且深埋在边界层内.边界层对引入到紧邻固体表面的最内层的扰动具有很高的灵敏度, DBD的近壁面射流为流体提供动能, 加速中性流体以克服表面逆压梯度, 从而促使剪切层附着于固体表面.因此, DBD所形成的电子风就为流体动力学分叉问题(例如流动分离, 涡流破碎等)的控制提供了可能[14].
|
| 图 6 静止空气中的DBD诱导壁面射流 Fig.6 Wall jet of DBD in still air |
Nishihara等[28]开展了为数不多的DBD高速流动控制应用研究.将纳秒脉冲DBD激励器放置在Mach数为5的自由流中的圆柱体模型上, 放电连接在100 kHz的交流电中, 激励器的能量为7.3~7.8 mJ/脉冲.由氮发光谱所确定的等离子体温度为(340±30)K, 该值与大气中DBD的典型值相符.实验利用相位固定的纹影捕获单个纳秒放电中弓形激波的位置偏移和结构.由于诱导波的相互作用, 圆柱上游稳定的弓形激波驻点距离增加了25%.该观察结果与Ziemer实验[29]中施加外部磁场的所得结果类似.
在所有实验观测中, 如果等离子体鞘的尺寸与边界层内层相当, 那么DBD激励器用于空气动力学分叉点流动控制最为有效.换言之, DBD控制的有效性被限制在流速比电子风高出大约一个量级的流场或是低Reynolds数环境下[30].使用等离子体进行有效流动控制的基本条件是对主流产生扰动, 与DCD相似, 但DBD不受低密度或低压条件的限制.还应该注意到, DBD时间平均静电力在电流的正相和负相之间是净平衡的, 因此其强烈依赖于所施加的交流电压波形.
根据Coulomb定律和等离子体动力学的Poisson方程, 给定点的DBD周期性静电力是分离的净电荷数密度与电场强度矢量的乘积[3]:
| $ \mathit{\boldsymbol{F}} = e({n_ + } - {n_ - } - {n_{\rm{e}}})\mathit{\boldsymbol{E}} $ | (4) |
式(4)的力矢量方向必须遵循电场矢量E和正离子与负离子以及电子的净数密度的组合.电场强度可以由电势的负梯度给出(E=-▽φ).在三维公式中, 周期性静电力有3个分量:
| $ \mathit{\boldsymbol{F}} = e({n_{\rm{e}}} + {n_ - } - {n_ + })\nabla \varphi $ | (5) |
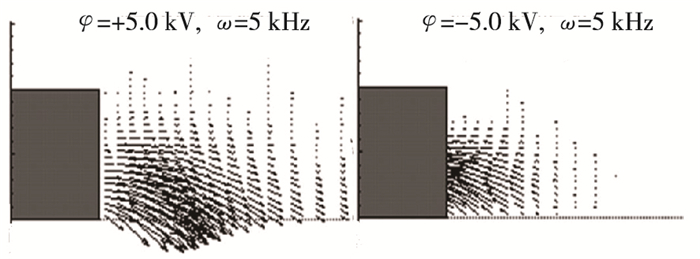
从式(5)可以看出, DBD中周期性静电力的方向由电场电位梯度和净带电粒子密度的组合符号决定.电荷分离仅发生在等离子体鞘层或电极间隙内, 电子较大的迁移率导致在该区域中具有更高的离子数密度.现有电离动力学模型表明, 带正电的离子数密度也远大于带负电的离子数密度[3, 15], 故鞘层区域的净电荷密度主要是负的, (ne+n--n+)<0.因此, 周期性静电力的方向由外加电场电位梯度的符号决定.在AC正循环阶段, 电势从外露电极到电介质表面逐渐减小, 电势梯度或电场强度在外露电极向外的方向上为负, ▽φ<0, 因此方程(5)中的力为正, 静电力的x分量是从外露电极指向电介质覆盖的电极.在AC负循环阶段, DBD产生的合力将改变方向, 电势沿着外露电极到电介质方向逐渐增加, 因此电势梯度为正, ▽φ>0.在此AC循环中, 电荷分离导致的感应静电力指向外露电极, 如图 7所示.因此, DBD由电荷分离所引起的周期性静电力在AC负循环周期时会改变方向.实质上, 在一个完整交流周期中, 由DBD产生的非平衡周期性静电力是方向相反的力的净合力.这个结论已经被实验充分证实, 即DBD产生的周期性静电力是推-拉力[5]. DBD的时间积分力的大小由交流电压波形控制.基于此, 仅保持正相的整流交流电压将大大增强静电力和电子风, 但是如何在极性转换之间中和电介质上的净电荷还是个未解决的问题[3, 14].
|
| 图 7 电势值为±5.0 kV时DBD激励的力场分布 Fig.7 Force field of DBD at peak vales of electrical potential φ=±5.0 kV |
磁场通常可以根据Biot-Savart定律使电流流经电磁螺线管而产生, 或通过铁磁体、稀土等材料的合金组成永磁体而获得.永磁体要保持磁性, 通常具有较低的磁通密度, 最大值不超过0.5 T.但是, 在接近Curie温度(400 K左右)的热环境中, 其磁场强度将迅速降低, 这严重制约了其实际应用范围.尽管如此, 磁场仍对带电粒子产生垂直于其运动方向的力, 从而产生Lorentz加速度和Hall效应.研究表明横向磁场可以有效增强电磁场-气动力相互作用和电推进[31].外加磁场的作用改变了仅由静电力驱动的带电粒子动力学特征.由于电场和磁场的正交关系, 磁化等离子体的带电粒子速度总是分解为平行和垂直于磁场的两部分.根据Ohm定律, 带电粒子所引起漂移速度分量与E×B的方向一致.
外加磁场中的等离子体产生了很多新奇现象.首先, 对带电粒子的约束力产生了强磁场中的等离子体约束.磁化等离子体的另一个重要特征是横向电磁波.在低频谱中, Alfven波占主导, 其他情况下可从电离气体控制方程的特征值中导出总共8个声-电磁波[32-33].该电磁波彼此垂直且同步振荡, Poynting理论表明, 能量垂直于波传播方向进行传递.其中一些波的传播速度远远超过声速.
第一个使用外加磁场进行流动控制的实验是在并排分布的DCD上进行的[1, 23].实验在嵌入电极的平板表面上施加了横向磁场, 实验结果提供了对电磁场-气动力相互作用(对控制效果的放大或抑制)的直接评估.通过假定介质电导率对施加的磁场具有弱依赖性, 有效的Hall参数β(电子平均自由程和Larmor半径之比β=eB/mν=λe/rb)近似为1.3.横向于磁场线的电流为Jx=σ(Ex-βEy)/(1+β2).在-0.2 T~+0.2 T的磁场强度下, 通过1.2 kV电压维持了50.0 mA左右的放电电流.
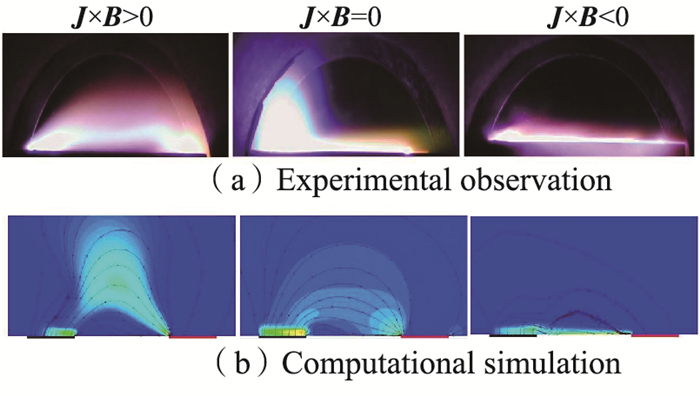
图 8给出了外加磁场Bz=0.0, ±0.2 T时的直流放电照片.横向磁场确实对放电产生强烈的影响:外加磁场对DCD的主要作用是抑制或消除电极上的可见放电.在无外加磁场时(B=0), 在阴极上方以及电极之间的绝缘体表面上的DCD是十分明显的, 如图 8中间照片所示.当Lorentz力指向平板下方时(J×B<0), 放电被压向平板表面, 抑制其离开电极表面.相反, 当Lorentz力指向平板上方时(J×B>0), 其将驱使等离子体远离电极表面.同时, 由于Lorentz力驱使电子远离电极而使得放电在电极上方更为均匀, 外加横向磁场基本上改变电磁场-气动力相互作用的放电区域.
|
| 图 8 外加磁场-0.2 T<Bz<+0.2 T时DCD Fig.8 Side-by-side DCD in externally applied magnetic fields -0.2 T < Bz < +0.2 T |
图 8同时也给出了利用漂移-扩散等离子体模型(方程(1))在相同实验条件下所得的计算结果, 其与实验条件设置几乎一致, 只是为了保证数值的稳定性, 计算须在较低的磁通密度下进行, 其计算结果通过实验中的观测得到了验证.图中也显示了电子速度矢量展示的在外加横向磁场下电子的位移轨迹.在电极边缘上的局部高梯度区域苛刻的计算条件下, 最小网格点的空间间距必须减小到1.67×10-3 cm, 计算的网格点也须加倍.网格细化后得到的数值结果呈现出对电磁场-气动力相互作用的基本特征捕获的略微改进, 表明已经满足网格密度的无关性要求.
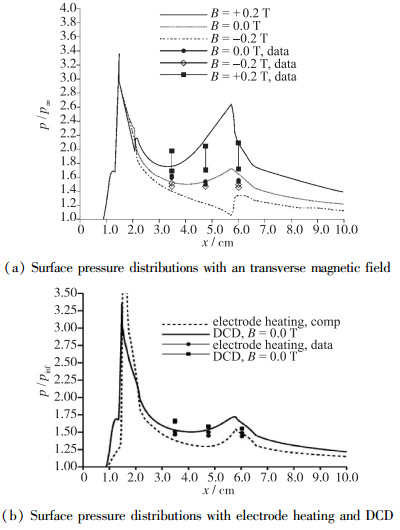
在DCD虚拟前缘肋板模型中施加横向磁场来改善其在高速流动控制中的效果, 如图 9(a)所示.在高超声速MHD风洞中进行了一系列的实验以及相关数值模拟[20, 23], 通过实验证实了外加磁场通过Lorentz力作用可以控制表面压力分布, 并清楚地显示了在虚拟前缘肋板上压力的增加.计算结果通常高于实验测量的压力值, 而且由于外加磁场下不稳定的DCD, 实验数据也表现出非常大的分散性.尽管如此, 流场在Joule热和Lorentz力的共同作用下, 有黏-无黏流的相互作用得到增强, 在相同电场强度下, 相比于单纯的电极加热-气动力相互作用(见图 9(b)), 其在流场中所引起的压升增加了42.8%.在有Lorentz力抑制带电粒子向外运动的工况下(J×B<0), 使用漂移-扩散模型的计算结果与实验数据之间的差异变得更加明显.为捕捉电极尖点放电效应而形成的陡峭梯度, 须增加计算量以保证在有外加磁场时计算的稳定性.使用漂移-扩散模型的数值模拟结果较好地捕获了相反极性下有外加磁场时的基本特性.
|
| 图 9 虚拟前缘肋板在外加磁场下电磁场-气动力的相互作用得到增强Ma=5.15, E=1.2 kV, I=50 mA Fig.9 Amplified electromagnetic-aerodynamic interactions over a virtual leading edge strake by an externally applied transverse magnetic field, Ma=5.15, E=1.2 kV, I=50 mA |
作为磁镜和离子发生器限制器的特殊磁约束是在运动的带电粒子上施加一个流向磁场.其基本机理是基于带电粒子在磁场中旋转运动与其受力相互垂直, 这就不会在闭合的热力学系统中产生功.在均匀的电场中, 等离子体的动能在变化的磁场中保持不变.磁场增加所导致的更大回转速度是通过沿着磁力线速度分量的减少来平衡的.因此, 带电粒子进入增强的磁场时将会减速甚至发生反射.磁镜已应用于离子推进器中来限制电离室内电子的产生.同样的原理也适用于Tokamak控制热核聚变, 在这种情况下, 等离子体被限制为圆环状.
磁场在MHD现象中起着非常重要的作用, 不同强度磁场对带电粒子运动起到截然不同的作用.最好的方法是从Faraday感应定律推导磁输运方程, 来了解磁化等离子体的基本原理:
| $ \frac{{\partial \mathit{\boldsymbol{B}}}}{{\partial t}} + \nabla \times \mathit{\boldsymbol{E}} = {\bf{0}} $ | (6) |
当电流仅由空间中变化的磁场通量密度所引起时, 可表示为μJ=▽×B.根据广义Ohm定律[34]得到▽×J=σ[▽×E+▽×(u×B)], 代入式(6), 磁通量密度输运方程可改写为
| $ \frac{{\partial \mathit{\boldsymbol{B}}}}{{\partial t}}{\rm{ }} - \nabla \times (\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{B}}) = - \frac{{\nabla \times \left( {\nabla \times \mathit{\boldsymbol{B}}} \right)}}{{\sigma \mu }} $ | (7) |
通过矢量变换▽×(▽×B)=▽·(▽·B)-▽(▽·B)以及磁场的Gauss定律▽·B=0, 方程(7)可写为
| $ \frac{{\partial \mathit{\boldsymbol{B}}}}{{\partial t}} - \nabla \times (\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{B}}) = - \frac{{{\nabla ^2}\mathit{\boldsymbol{B}}}}{{\sigma \mu }}{\rm{ }} $ | (8) |
方程右边项的物理意思是表示基于Faraday感应定律所导致的磁扩散. 1/(σμ)表示电导率和磁导率乘积的倒数, 被称为磁黏度, 与流体动力学中分子运动黏度对应.对于大多数等离子体工程应用, 例如电推进、基于等离子激励器的流动控制、远程能量沉积等, 对流所导致的磁场变化率(▽×(u×B))是很微小的, 此时扩散机制占主导[14].
| $ \frac{{\partial \mathit{\boldsymbol{B}}{\rm{ }}}}{{\partial t}} = - (\frac{1}{{\mu \sigma }}{\rm{ }}){\nabla ^2}\mathit{\boldsymbol{B}} $ |
另一极端情况是强磁场完全支配带电粒子的运动.实验观察到高导电粒子只能沿着磁力线自由移动, 无法穿过磁力线.事实上, Bittencourt[35]已经利用Stokes定理(其将表面积分与线积分联系起来)进行了证明, 根据公式(8), 垂直于控制面与磁通密度的速度将消失:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\int {\mathit{\boldsymbol{B}}(r, t) \cdot {\rm{d}}\mathit{\boldsymbol{s}} = 0} $ | (9) |
方程(9)是Alfven[36]得到的导电流体中磁场线被冻结的数学表达.换句话说, 等离子体的带电粒子被锁定在磁场线上, 并跟随磁力线一起偏转和转动.这种独特的磁场现象只适用于具有无穷大电导率的等离子体或在极强磁场下, 所需磁场的强度目前只能由超导技术产生.
DBD被认为是层流-湍流转捩控制最具前景的手段.然而, 其在流体动力学不稳定性中同时引入热和速度扰动, 就与Morkovin的感受性理论相矛盾, 而且高强度层流-湍流旁路转捩并不是单一特征值问题[37].这种矛盾就否定了DBD用于防止层流-湍流转捩的可能.我们知道湍流是一种具有强非定常、非线性的三维流动现象, 其随机的涡结构具有宽广的空间和频谱尺度.最重要的是, 多尺度湍流漩涡或涡包结构是从整个剪切层厚度到Kolmogorov尺度连续变化的.流体的随机特征具有特定的形式, 每种形式都具有特定的连续能谱, 并在高波数的小涡中耗散消失.从随机强脉动涡结构的角度来看, 湍流运动可以通过包括涡流和主流之间相互作用的涡旋动力学来描述.因此, 可以在等离子体上施加强磁场来抑制旋涡的扩散或减小脉动强度.由此, 外部施加的磁场可以通过抑制涡流的脉动来减少湍流运输.这种湍流控制的创新理念是流体动力学中最具挑战性的问题, 它在四十多年前就被提出来了, 但只进行了一些初步的探索实验研究[38].
2.4 远程能量沉积通过聚焦激光束达到高辐射能量密度来实现气体击穿的方式进行流动控制.这种相对较新的辐射电离过程于20世纪60年代中期被发现[8-9].在微波光学焦点处, 气体吸收远程微波能量源所释放的辐射能量可以产生爆炸一样的效果.该过程是由初始电子引起光致电离, 接着是由轫致辐射供能产生级联反应.对于流动控制而言, 通过吸收和反射激光能量, 电磁波引发的爆炸波沿着从光源到光学焦点的路径传播.在超声速飞行器上游特定位置处加入能量, 将产生爆炸波并使气体温度升高, 从而降低来流Mach数, 减少激波阻力.该爆炸波也发生改变, 来减少由于冲击激波与弓形激波相互作用而引起的冲击热流.
Adelgren等[11]实现了脉冲激光能量沉积.热释放产生低Mach数区域, 并导致复杂的激波相互作用.单频电磁波(Nd:YAG激光)的能量相当低(283 mJ /10 ns), 但可将其聚焦在约为(3±1) mm3的焦点上, 远程沉积的激光能量可保持在10 Hz.从Edney Ⅳ型斜激波与弓形激波相互作用中观察到峰值压力降低30%.
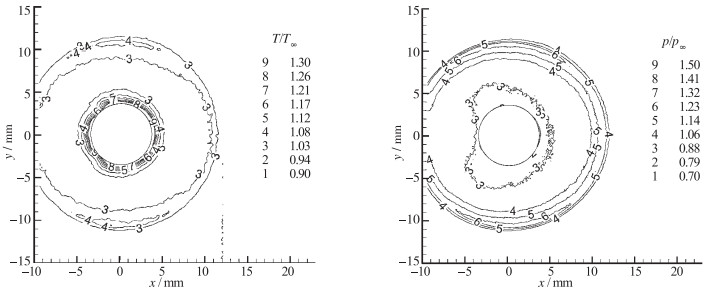
将远程辐射能量沉积应用于可靠点火或增强的燃烧稳定性等方面具有很好的前景.根据燃烧动力学理论, 如果外部供应能量源超过特定化学反应的能量势垒, 化学反应链将被启动或维持.根据Yan等[10]的实验, 图 10给出了远程微波能量沉积经过20 μs后的温度和压力等值线分布, 其中脉冲能量为145 mJ, 脉宽为10 ns.图中清楚地描绘了通过辐射电离而产生的爆炸波从焦点向外传播过程, 局部升高的压力和温度也清楚地表明了能量的加入.爆炸波以超声速传播, 超过了所有吸气式发动机内流中燃油-空气的混合速度.不可否认, 这需要巨大的微波功率, 但是可以通过添加合适的颗粒材料来消除.
|
| 图 10 微波能量沉积下的温度和压力等值线, T∞=293 K, ρ∞=1.20, E=145 mJ/10 ns, 10 ns为激光脉宽 Fig.10 Temperature and pressure contours of microwave energy deposition T∞=293 K, ρ∞=1.20, E=145 mJ/10 ns, laser pulse duration is 10 ns |
从非弹性碰撞导致基本能量转移角度来看, 等效电场强度E/N可用于电离碰撞之间能量增益的度量.对于非平衡等离子体产生过程, 等效电场强度通常由Townsend度量(Td=10-17 V·cm2).发现通过脉冲过程产生的等离子体是最有效的, 且更为稳定, 由于采用了小于10-3的占空比来避免放电不稳定性.为比较不同非平衡等离子体的点火时间, 进行了一系列放电实验, 发现表面微波放电具有最宽的测量范围100 Td<E/N<200 Td.放电的等效电场强度越高, 燃烧诱导时间越短[39].
使用等离子体点火并保持燃烧稳定性的另一优点在于电离气体内在的力扩散机制.典型化学反应的经典描述可由Damköhler数给出, 其定义为化学反应速率与传质扩散速率之间的比值.该比值与动力学反应常数, 物质浓度或扩散系数和反应元素的界面面积成正比.对于稳定的燃烧过程, 反应速率相对于扩散速率具有相同的量级或更快一些.相对于普通扩散, 等离子体或电离介质通过静电力具有额外且显著的强制扩散机制, 所以理论上等离子体可以通过额外的扩散机制来提高燃烧稳定性.
基于近期的研究成果, 通过远程脉冲辐射电离产生能量沉积可能为点火助燃增强燃烧稳定性开辟一条新的研究途径.总之, 这个研究领域可能为等离子体动力学开辟了新的前沿.
3 结论作为宇宙中最丰富的介质, 等离子体的基础研究应该始终坚持, 从照明、通讯到深空探测的电推进等等, 都具有很大的应用潜力.除了极少数例外情况外, 还必须认识到, 在航空航天工程中, 这一工质的应用还十分有限, 基于等离子体流动控制的有效性可以通过空气动力学相互作用或外加的磁场来增强.
在等离子体研究方面任何有意义的进展, 必然是在多学科框架下, 涉及量子跃迁的原子/分子尺度上进行的.从量子物理化学理论来认知电离过程是相当有限的.未来为实现应用的任何进步或创新都须建立在实验数据库开发和高性能计算模拟之上.
致谢: 第二和第三作者对国家自然科学基金的资助(资助号:11672242)表示感谢.| [1] |
Shang J S, Huang P G, Yan H, et al. Computational electrodynamic simulation of direct current discharge[J]. Journal of Applied Physics, 2009, 105(2): 023303. DOI:10.1063/1.3066185 |
| [2] |
Boeuf J P, Pitchford L C. Electrohydrodynamic force and aerodynamic flow acceleration in surface dielectric barrier discharge[J]. Journal of Applied Physics, 2005, 97(10): 103307. DOI:10.1063/1.1901841 |
| [3] |
Shang J S, Roveda F, Huang P G. Electrodynamic force of dielectric barrier discharge[J]. Journal of Applied Physics, 2011, 109(11): 113301. DOI:10.1063/1.3585853 |
| [4] |
Eliasson B, Kogelschatz U. Nonequilibrium volume plasma chemical processing[J]. IEEE Transactions on Plasma Science, 1991, 19(6): 1063-1077. DOI:10.1109/27.125031 |
| [5] |
Enloe C L, McLaughlin T E, Van Dyken R D, et al. Mechanisms and responses of a single dielectric barrier plasma actuator:plasma morphology[J]. AIAA Journal, 2004, 42(3): 589-594. DOI:10.2514/1.2305 |
| [6] |
Hall E H. On a new action of the magnet on electric currents[J]. American Journal of Mathematics, 1879, 2(3): 287-292. DOI:10.2307/2369245 |
| [7] |
Rosa R J. Magnetohydrodynamic energy conversion[M]. Washington: Hemisphere Publishing, 1987.
|
| [8] |
Meyerand Jr R G, Haught A F. Gas breakdown at optical frequencies[J]. Physical Review Letters, 1963, 11(9): 401-403. DOI:10.1103/PhysRevLett.11.401 |
| [9] |
Raizer Y P. Breakdown and heating of gases under the influence of a laser beam[J]. Soviet Physics Uspekhi, 1966, 8(5): 650-673. DOI:10.1070/PU1966v008n05ABEH003027 |
| [10] |
Yan H, Adelgren R, Boguszko M, et al. Laser energy deposition in quiescent air[J]. AIAA Journal, 2003, 41(10): 1988-1995. DOI:10.2514/2.1888 |
| [11] |
Adelgren R G, Yan H, Elliott G S, et al. Control of Edney Ⅳ interaction by pulsed laser energy deposition[J]. AIAA Journal, 2005, 43(2): 256-269. DOI:10.2514/1.7036 |
| [12] |
Verboncoeur J P. Particle simulation of plasmas:review and advances[J]. Plasma Physics and Controlled Fusion, 2005, 47(5A): A231-A260. DOI:10.1088/0741-3335/47/5A/017 |
| [13] |
Clarke J F, McChesney M. The dynamics of real gases[M]. Washington: Butterworths, 1964.
|
| [14] |
Shang J J S. Computational electromagnetic-aerodyna-mics[M]. Hoboken: IEEE, 2016.
|
| [15] |
Bogdanov E A, Kudryavtsev A A, Kuranov A L, et al. 2D simulation and scaling of DBD plasma actuator in air[C]. 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno: AIAA, 2008.
|
| [16] |
Surzhikov S T, Shang J S. Two-component plasma model for two-dimensional glow discharge in magnetic field[J]. Journal of Computational Physics, 2004, 199(2): 437-464. DOI:10.1016/j.jcp.2004.02.019 |
| [17] |
Raizer Y P. Gas discharge physics[M]. Berlin: Springer-Verlag, 1991.
|
| [18] |
Moreau E. Airflow control by non-thermal plasma actua-tors[J]. Journal of Physics D:Applied Physics, 2007, 40(3): 605-636. DOI:10.1088/0022-3727/40/3/S01 |
| [19] |
Hayes W D, Probstein R F. Hypersonic flow theory[M]. New York: Academic Press, 1959.
|
| [20] |
Shang J S, Surzhikov S T. Magnetoaerodynamic actuator for hypersonic flow control[J]. AIAA Journal, 2005, 43(8): 1633-1652. DOI:10.2514/1.6625 |
| [21] |
Borghi C A, Carraro M R, Cristofolini A, et al. Magnetohydrodynamic interaction in the shock layer of a wedge in a hypersonic flow[J]. IEEE Transactions on Plasma Science, 2006, 34(5): 2450-2463. DOI:10.1109/TPS.2006.883377 |
| [22] |
Shang J S. Electrostatic-aerodynamic compression in hypersonic cylindrical inlet[J]. Communications in Computational Physics, 2008, 4(4): 838-859. |
| [23] |
Shang J S, Kimmel R L, Menart J A, et al. Hypersonic flow control using surface plasma actuator[J]. Journal of Propulsion and Power, 2008, 24(5): 923-934. DOI:10.2514/1.24413 |
| [24] |
Yan H, Gaitonde D. Effect of thermally induced perturbation in supersonic boundary layers[J]. Physics of Fluids, 2010, 22(6): 064101. DOI:10.1063/1.3432513 |
| [25] |
Yan H, Liu F, Xu J, et al. Study of oblique shock wave control by surface arc discharge plasma[J]. AIAA Journal, 2018, 56(2): 532-541. DOI:10.2514/1.J056107 |
| [26] |
Kong J A. Electromagnetic wave theory[M]. New York: John Wiley & Sons, 1986.
|
| [27] |
Corke T C, Post M L, Orlov D M. SDBD plasma enhanced aerodynamics:concepts, optimization and applications[J]. Progress in Aerospace Sciences, 2007, 43(7/8): 193-217. |
| [28] |
Nishihara M, Takashima K, Rich J W, et al. Mach 5 bow shock control by a nanosecond pulse surface dielec-tric barrier discharge[J]. Physics of Fluids, 2011, 23(6): 066101. DOI:10.1063/1.3599697 |
| [29] |
Ziemer R W. Experimental investigation in magneto-aerodynamics[J]. ARS Journal, 1959, 29(9): 642-647. DOI:10.2514/8.4856 |
| [30] |
Corke T C, Enloe C L, Wilkinson S P. Dielectric barrier discharge plasma actuators for flow control[J]. Annual Review of Fluid Mechanics, 2010, 42: 505-529. DOI:10.1146/annurev-fluid-121108-145550 |
| [31] |
Goebel D M, Katz I. Fundamentals of electric propulsion:ion and hall thrusters[M]. New York: John Wiley & Sons, 2008.
|
| [32] |
Jeffrey A, Taniuti T. Non-linear wave propagation[M]. New York: Academic Press, 1964.
|
| [33] |
Brio M, Wu C C. An upwind differencing scheme for the equations of ideal magnetohydrodynamics[J]. Journal of Computational Physics, 1988, 75(2): 400-422. DOI:10.1016/0021-9991(88)90120-9 |
| [34] |
Mitchner M, Kruger C H. Partially ionized gases[M]. New York: John Wiley & Sons, 1973.
|
| [35] |
Bittencourt J A. Fundamentals of plasma physics[M]. Oxford: Pergamon Press, 1986.
|
| [36] |
Alfven H. Cosmical electrodynamics[M]. Oxford: Clarendon Press, 1950.
|
| [37] |
Reshotko E. Boundary-layer stability and transition[J]. Annual Review of Fluid Mechanics, 1976, 8: 311-349. DOI:10.1146/annurev.fl.08.010176.001523 |
| [38] |
Sonju O K, Kruger C H. Experiments on Hartmann channel flow in plasmas[J]. Physics of Fluids, 1969, 12(12): 2548-2552. DOI:10.1063/1.1692393 |
| [39] |
Starikovskaia S M. Plasma assisted ignition and combus-tion[J]. Journal of Physics D:Applied Physics, 2006, 39(16): R265-R299. DOI:10.1088/0022-3727/39/16/R01 |




