相比圆形射流, 非圆形(如椭圆矩形三角形等)射流能够更有效地卷吸周围流体, 这意味着更有效地混合[1], 这种性质使非圆形射流在过程工业中有着重要应用(比如燃烧器, 混合器等), 因此在过去几十年中被广泛地研究[1-3].
作为一种典型的非圆形射流, 三角形射流的流动与混合特性受到了国内外众多学者的研究. Quinn[4-5]采用热线测量正三角形和等腰三角形孔口射流, 给出了平均速度场和脉动速度场的特征, 与圆形射流进行了对比, 发现三角形射流具有更好的湍流混合效果.进一步, Xu等采用PIV技术, 详细对比了三角形射流与圆形射流场区涡结构的形成与演化规律[3].三角形射流能够增强混合的主要机理在于非均匀的曲率, 以及方位涡与流向涡之间的相互作用, 引起涡环的自诱导变形[1].由于自诱导作用, 小曲率半径的涡环将以更快的速度向下游传递, 也将更快地扩散.由于涡环的最小曲率半径出现在长轴平面, 而最大曲率半径出现在短轴平面, 因此短轴以更快的速度发展, 导致在距离出口一定位置处, 产生“轴变换”现象[6-13], 即随着这种流动向下游发展, 它们的横截面平均流场呈现类似于喷嘴的形状, 但是围绕中心轴连续地以射流喷嘴特征角度旋转.这种“轴变换”在椭圆矩形等非圆形射流中是一种普遍存在的现象.
Gutmark等[6],Schadow等[14]及Koshigoe等[15]先后在冷态和反应流中研究了三角形和方形射流的混合和燃烧效果, 在射流出口尖角附近产生小尺度湍流, 而在平边处则产生大尺度相干结构, 燃烧实验中也对应发现了小尺度火焰和大尺度火焰.他们建议, 喷嘴尖角产生的小尺度湍流与喷嘴平边产生的大尺度运动相结合, 对于一些燃烧应用是有益的.
很多学者也将三角形射流与其他非圆形射流进行了对比研究. Mi等[2, 16]对包括三角形在内的9种孔口射流中心线速度统计特性进行了详细系统直接的对比.他们指出实验无法将进流条件与实验误差完全区分开, 因此直接对比不同实验设施产生的实验结果存在困难.而射流进流条件, 比如喷嘴类别[17-21],Reynolds数[22-23]等, 对射流下游甚至是远场自相似区都起着重要作用.同样地, 前人也指出了测量结果对设备的依赖性[8, 24]. Mi等研究发现射流初始非轴对称性能够在近场区引起平均速度衰减和湍流度的增加, 意味着卷吸量的增加.在8种非圆形射流中, 等腰三角形射流的卷吸量最大, 这与Miller等[25]的模拟结果一致.但是, Quinn[5],Azad等[26]的实验结果却表明等边三角形的卷吸率高于等腰三角形.因此为了确认顶角角度对三角形射流的影响规律, 需要开展不同顶角的等腰三角形射流流动特性研究.
虽然已经对三角形射流进行了一些研究, 但是主要局限于平均速度场和脉动速度场的分析, 对不同顶角的三角形射流近场区的涡结构运动特征, 以及多尺度湍流统计量的影响缺少研究.这些问题的解决, 对三角形射流的实际工程应用有重要价值.因此本文对喷嘴等效直径相同出口Reynolds数均为15000的3种等腰三角形孔口射流(顶角分别为30, 60和90°)以及圆形孔口射流进行流场显示与速度场测量, 系统研究了等腰三角形射流的涡结构平均速度场脉动速度场和湍动能谱等的演变规律.
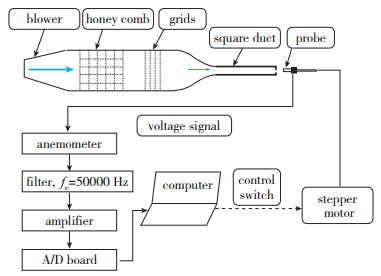
1 实验介绍本文采用的射流实验装置如图 1所示.射流实验装置主要由变频器风机整流箱喷嘴热线探头热线风速仪三相位移电机和计算机等器件组成.通过基于LabVIEW程序的计算机来控制变频器, 再通过变频器控制风机电压, 使风机产生出口流量和风速可定的恒温气流.风机出口连接了一个2 m长的整流箱, 内部装设金属网格和蜂窝状格栅, 平行于主流的长段蜂窝格栅可以减少流体的卷曲, 金属网格能够降低湍流度, 并减少湍流边界层对速度的影响, 气流通过栅格之后湍流度将大幅降低, 流动状态更加稳定, 也能够提高测量的精度.热线探头固定在三维坐标架上, 所测流场范围为x/De=0~50.所有实验在同一台射流装置上进行, 该装置放置在一个独立实验室中, 实验操作时的室内温差要控制在±2℃内, 同时, 实验室可以确保测量不受外界声音和振动的干扰.实验室空间体积为l×w×h=6 m×3 m×3 m, 射流装置与地面平行放置于实验室中部.房高与射流出口直径比为l/De=300, 房间横截面积与射流出口面积比约为57300, 射流出口距地面1.5 m(150De), 距墙壁4 m(400De).
|
| 图 1 射流实验装置 Fig.1 Schematic diagram of jet experiment |
实验采用单热线测量射流流向速度分量, 热线探头为直径2.5 μm的Wollaston线, 长度约为1 mm, 探头接于恒温热线风速仪, 过热系数为1.5.电压信号经过滤波放大后, 由一块12-bit A/D转换板采集入计算机, 实验设置的采样频率为50000 Hz, 采样时间为120 s, 热线标定在射流出口处的势核区中进行.标准风速由连接于数字微压计的标准Pitot管测量得到, 数字微压计量程为0~50 m/s. Pitot管与热线探头对称地放置于射流出口处, Pitot管直径为2 mm, 热线探头支架直径为1 mm, 两者横截面积与射流出口横截面积比约为1.25%, 为避免标定时Pitot管或热线探头相互影响, 两者距离不小于8 mm.热线标定速度范围为所测流场最大风速的2倍.标定曲线采用3阶多项式.实验过程中, 当热线测量值漂移大于0.2 m/s时, 即停止实验, 重新标定.需要指出的是, 高频噪音对小尺度的影响非常大, 因此本文应用Mi等[27, 29]及徐敏义等[28]提出的数字迭代滤波方法有效地将信号中的高频噪音滤除.
本实验研究等腰三角形自由射流, 如图 2(a)所示. x轴沿腔体轴心线,指向射流出口方向, z轴方向位于三角形顶角方向, y轴平行于三角形底边.喷嘴出口采用45°倒角向外突扩的形式.圆形喷嘴直径为10 mm.三角形喷嘴的顶角分别为30, 60和90°, 它们的等效直径De=10 mm, 如图 2(b)所示.需要注意的是, 此圆管横截面积与孔口面积的比值很小(γ≈4.5), 因此与传统γ值很大(例如文献[4]中, γ≈22.8) 的孔口射流相比, 出口条件可能明显不同, 但是本孔口γ值更接近实际工程应用.射流出口Reynolds数Re(≡UjDe/υ)=15000, 其中Uj为出口平均速度, De为等效直径, υ为流体运动黏性.在x/De=20位置处, 主要统计量的最大不确定度范围为:平均轴向速度U≈±0.5%, RMS速度<u2>1/2≈±1.5%, 湍动能耗散率ε≈±8.5%.

|
| 图 2 喷嘴示意图(单位:mm) Fig.2 Schematic diagram of nozzles(unit: mm) |
为了更好地研究射流近场区流场结构的发展规律, 本文采用大连理工大学研发的航华烟线仪对Re=15000条件下的圆形与三角形射流进行了流场显示.将一根直径为0.1 mm的304不锈钢丝悬挂在射流出口, 钢丝上涂抹石蜡油和柴油的混合液.大容量电容放电加热钢丝上的液滴产生烟雾,并使用一台佳能5DII相机拍摄烟雾.烟线仪使用AT MEGA单片机及人机交互界面对放电电流以及拍照时间进行精确控制.
2 结果与讨论 2.1 瞬时流场特性图 3为圆形和三角形射流的近场区流场结构.从图中可以看出, 在射流出口处, 存在明显的涡结构, 这是因为剪切层结构不稳定, 形成持续脱落的大尺度涡结构, 存在很大的速度梯度, 随着射流的发展会发生卷吸掺混.三角形射流存在比圆形射流更明显的涡结构, 这是由于三角形出口顶角处射流产生的小尺度涡快速向下游传递和扩散, 并与底边产生的大尺度涡相结合的作用.对比3种三角形射流, 随着顶角的不断变小, 射流的不对称性更加明显, 涡结构的三维性更强, 说明顶角的减小增强了射流小尺度涡结构的传递和扩散能力, 更利于射流的卷吸和掺混.

|
| 图 3 圆形和等腰三角形出口处(x/De=0.05) 烟线流场显示 Fig.3 Smoke-flow visualizations of jets at exiting |
图 4显示了圆形射流和三角形射流中心线平均速度Um/Uc.从图中可以看出, 0 < x/De < 10范围内, 三角形射流中心线衰减比圆形射流更快.这是由于三角形射流出口处形成强烈的涡结构, 导致中心速度极速衰减.随着射流向下游发展, 三角形射流中心线速度特性逐渐趋近圆形射流中心线速度特性.三角形射流中心线的速度衰减随顶角的减小递增, 因为顶角越小, 形成的涡结构尺度越大, 卷吸周围流体能力越强, 因此中心线速度衰减越快.

|
| 图 4 圆形和三角形射流中心线平均速度分布 Fig.4 Centreline evolutions of velocity decay for the jets |
当射流发展到x/De > 10, 平均速度衰减的线性特征明显, 从图中可以看出圆形和三角形射流Um/Uc的斜率基本保持不变, Um/Uc值都会在远场区(x/De > 10) 单调递增.不同射流的衰减率会逐渐变成一条直线, 这个直线区域称之为自相似区, 是速度稳定发展的区域.因此, 这个区域的数据被拟合成线性回归方程:
| $ \frac{{{U_{\rm{m}}}}}{{{U_{\rm{c}}}}} = B\frac{{x - {x_u}}}{{{D_{\rm{e}}}}} $ | (1) |
其中, B为速度衰减率, De为喷嘴的等效直径, xu为轴线绝对位置的零点.
表 1给出了圆形和不同顶角等腰三角形射流的平均速度衰减率.同时, 表 1也给出了Mi等[2]和Azad等[26]的相关实验结果.比较发现, 三角形射流的衰减率略高于圆形射流, 意味着三角形射流在远场区的扩散率较大.但不同顶角的等腰三角形射流的扩散率基本相同, 并且本文的实验结果与Mi等的结果一致.
| 下载CSV 表 1 不同形状喷嘴平均速度衰减特性 Tab.1 Mean streamwise centreline velocity decay parameters on jet centreline for jets |
图 5显示了三角形射流和圆形射流中心线上的湍流度, 它是衡量射流混合程度强弱的重要指标.湍流度越大, 射流与周围流体掺混能力越强.从图中可以发现, 随着对流和扩散现象的发生, 射流湍流度在射流近场区(0 < x/De < 8) 迅速增长, 湍流度明显增高, 反映了三角形射流与周围流体发生卷吸和掺混作用增强.随着三角形顶角的增加, 三角形射流在近场区(x/De=8) 射流湍流度存在一个明显的峰值, 表明近场区卷吸形成的大尺度涡结构破碎成小尺度涡结构, 引起强烈的湍流脉动.

|
| 图 5 圆形和三角形中心线湍流度分布 Fig.5 Centreline evolutions of turbulence intensity of jets |
随着射流向下游发展至远场区(x/De > 20), 矩形射流湍流度趋于常数, 保持在0.20~0.24范围内, 并且与圆形射流的湍流度一致.这一现象的出现表明湍流度已经进入自相似流动阶段, 但与平均速度场相比, 湍流度进入自相似阶段较远.
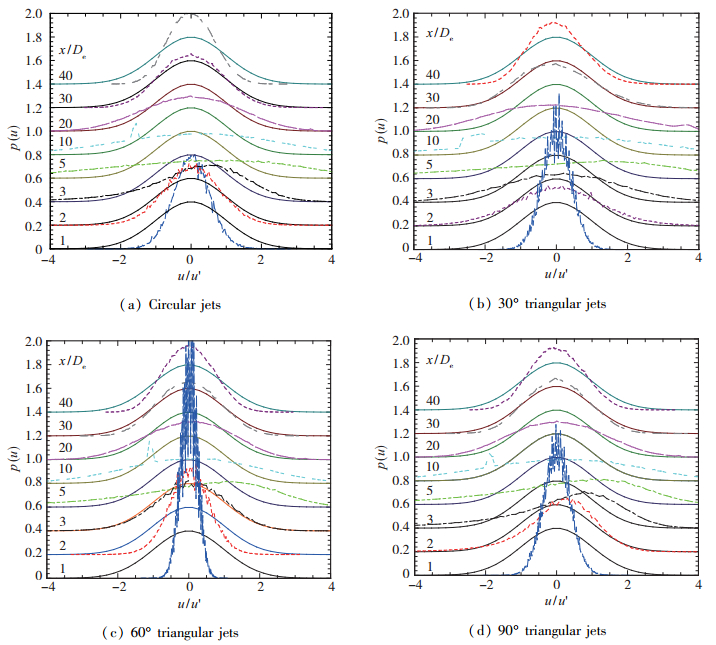
2.4 概率密度函数图 6显示了圆形和等腰三角形喷嘴射流中心线的概率密度函数p(u)的分布情况, x轴方向的脉动速度分量u的统计量可以通过概率密度函数(probability density function, PDF)表达出来:
| $ \left\langle {{u^m}} \right\rangle = \int_{ - \infty }^\infty {{u^m}} p\left( u \right){\rm{d}}u $ | (2) |
|
| 图 6 圆形和三角形的概率密度函数分布图 Fig.6 Centreline evolutions of p(u) in jets |
同时将Gauss概率密度函数
| $ G(u) = {\rm{exp}}\left[ {\frac{{ - \left( {\frac{u}{{u'}}} \right)}}{2}} \right]{\left( {2\pi } \right)^{ - 1}} $ |
作为参考.
从图中可以看出, 在不同的出口条件下, x/De=1时, p(u)近似于G(u).但是在3 < x/De < 5范围内, 三角形射流和圆形射流的p(u)偏离Gauss分布.这是由于近场区卷吸的涡结构在5De下游处破裂成小尺度涡结构, 引起强烈的湍流脉动.随着x/De的进一步增加, 由于三角形射流和圆形射流与环境流体的充分混合, 中心线的p(u)重新趋于Gauss函数分布, 但由于射流持续卷吸环境中的静止流体, 所以p(u)不可能变为标准Gauss分布.
为了量化p(u)与Gauss函数的关系, 采用偏斜因子Su≡<u3>/(<u2>3/2)和平坦因子Fu≡<u4>/(<u2>2), 分别表示速度测量结果的概率密度函数的对称性和平坦程度.计算得到的Su和Fu都是基于高采样量的统计分析, 高采样量才能保证概率密度函数实现收敛.本文的各个图像都是每组采样数50000, 采样时间为120 s, 即采样量为6000000, 符合高采样量的要求.
图 7给出了圆形和三角形喷嘴射流中心线方向的偏斜因子Su和平坦因子Fu的变化规律.从图中可以看出, 在0 < x/De < 10时, 三角形和圆形射流都存在一个局部峰值, 出现在射流的势流核尾段附近, 这是由于卷吸形成的大尺度涡结构破碎成小尺度涡结构, 导致湍流脉动增强, 这也对应了p(u)明显偏离Gauss函数的分布.三角形射流的Fu的最大值(近似Su的最小值)出现在x/De≈2.6处, 圆形射流的最大值出现在x/De≈3.6处.随着射流向下游发展(x/De > 10), 三角形射流和圆形射流的Su和Fu函数分别趋于0.1和2.9, 与Gauss分布的Su=0和Fu=3非常接近, 但这种微小的差别是由于射流持续卷吸环境中的静止流体, 存在湍流间歇性.

|
| 图 7 圆形和等腰三角形偏斜因子与平坦因子沿中心线的变化 Fig.7 Centreline evolutions of skewness and flatness in jets |
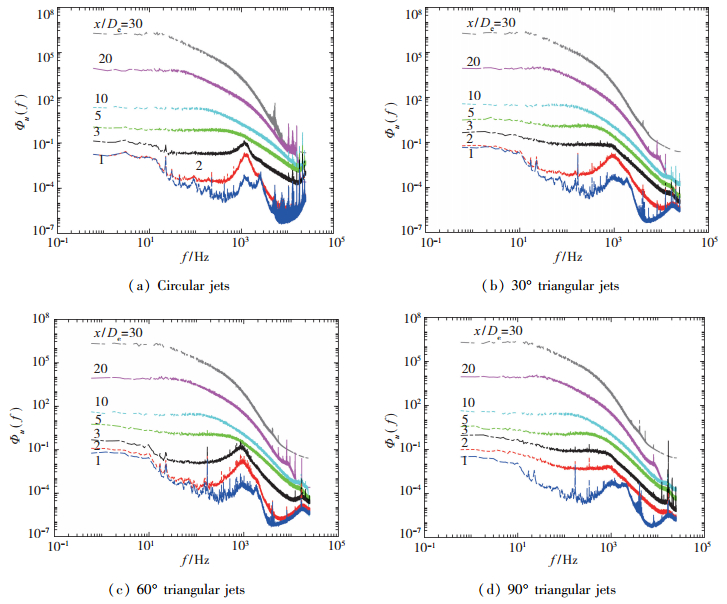
图 8显示了圆形和矩形喷嘴射流的中心线能量频谱Φu(f), 即
| $ \left\langle {{u^2}} \right\rangle = \int_0^\infty {{\mathit{\Phi }_u}} {\rm{d}}f $ |
|
| 图 8 圆形和等腰三角形中心线频谱分布图 Fig.8 Centreline spectra distributions of different jets |
图中显示了在1 < x/De < 30中心线上圆形和等腰三角形射流的一维湍动能谱Φu(f)演化规律, 反映了流向脉动速度湍动能<u2>在不同湍流尺度上的能量分布特性.从图中可以看出, 圆形射流和三角形射流在近场区存在明显的峰值, 三角形射流和圆形射流对应的频率分别约为1900和1300 Hz, 这表明射流剪切层中形成持续脱落的大尺度涡结构, 射流剪切层失稳, 形成了大尺度涡环结构, 引起脉动速度周期性变化, 对应的无量纲脱落频率F*=fDe/Uc=0.5.同时圆形射流的峰值较三角形形射流更明显, 表明圆形射流的周期性更强, 而三角形射流的三维性更强.随着射流向下游发展, 涡环结构破碎成小尺度涡结构, 因此当x/De > 5时, 湍动能谱峰值消失.
图 9为圆形射流和三角形射流在x/De=30处的湍流能谱分布, 可以发现湍动能从含能区(低频)经过惯性区传递到耗散区(高频).从图 9(a)中可以看出, 这些频谱在惯性区(20≤f≤300 Hz)呈现幂律分布, 即Φu(f)∝f-m.然而幂指数m低于Kolmogorov提出的5/3, 而接近于1.5, 这是由于本文的Reynolds数较小. 图 9(b)展示了m=1.5以及m=5/3时的补偿频谱.这种现象也在其他文献中发现, 如Mi等[2, 31]和Burattini等[30]在渐缩圆形射流实验中也观察到m≈1.5的现象.因此可以认为喷嘴形状对幂指数的影响较弱.

|
| 图 9 圆形和三角形射流在x/De≈30处中心线频谱图 Fig.9 Centreline spectra of jets obtained at x/De≈30 |
相比于圆形射流, 首次发现三角形射流的能谱在含能区(低频)较高, 而在耗散区(高频)较低, 这符合能量守恒原理.同时表明三角形射流的湍流大尺度混合较强, 而湍流小尺度混合较弱.
2.6 湍流尺度特性图 10显示的是圆形和三角形射流中心线上湍流积分尺度Taylor尺度和Kolmogorov尺度沿中心线的变化规律.积分尺度Taylor尺度和Kolmogorov尺度分别用来表示湍流结构的大尺度小尺度和最小尺度的特征.本文的积分长度尺度L是由积分时间尺度基于Taylor冻结湍流假设粗略估计得来的, 关系式如下
| $ L = {U_{\rm{c}}}T = {U_{\rm{c}}}\int_0^{{\tau _0}} {\left\langle {u\left( t \right)u\left( {t + \tau } \right)} \right\rangle } {\left\langle {{u^2}} \right\rangle ^{ - 1}}{\rm{d}}\tau $ | (3) |
τ0对应自相关函数

|
| 图 10 圆形和三角形中心线上特征尺度沿中心线的变化规律 Fig.10 Centreline evolutions of turbulent L/De, λ/De and η/De for jets |
图 10(a)展示了不同射流的L/De的结果, 可以看出, 圆形与三角形射流的积分尺度差异较为明显.三角形射流积分尺度大于圆形射流, 表明三角形射流具有更大的含能尺度, 随着射流向下游发展, 差别逐渐减小.从图 10(b)(c)可以看出, 在射流中下游, λ/De和η/De的值随x轴呈线性增长, 三角形射流Taylor尺度和Kolmogorov尺度均高于圆形射流, 这与积分尺度的规律一致, 但是随着尺度的减小, 这种差别逐渐减小, 说明喷嘴形状对湍流大尺度统计量影响较大, 而对湍流小尺度统计量影响较小.进一步表明大尺度湍流特性会对出口条件的改变更为敏感, 这是因为出口条件对下游射流发展的任何影响都是由初始的涡结构通过大尺度运动传递的, 它们与外围流体的相互作用及自身分解, 在远场形成小尺度涡结构并与环境流体相互作用.
3 结论本文采用烟线流场显示和热线风速仪技术, 对3种等腰三角形(顶角分别为30, 60和90°)以及圆形孔口射流进行流场显示与速度场测量,分析了三角形射流中心线上平均速度频谱湍流尺度等变化规律, 主要得出以下结论:
(1) 相比于圆形射流, 三角形喷嘴射流近场区涡结构更大, 卷吸能力更强.随着三角形顶角减小, 中心线衰减率和湍流度更大, 涡结构三维性更强, 意味着近场区的卷吸和掺混能力更强, 但对远场中心线的速度湍流度影响较小.
(2) 通过对三角形和圆形射流概率密度函数湍流能谱Taylor尺度和Kolmogorov尺度等统计量的分析, 发现湍流小尺度运动受出口形状的影响较小, 较湍流大尺度运动更早地发展到自相似状态.
| [1] | Gutmark E J, Grinstein F F. Flow control with noncircular jets[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 239-272. DOI:10.1146/annurev.fluid.31.1.239 |
| [2] | Mi J, Nathan G. Statistical properties of turbulent free jets issuing from nine differently-shaped nozzles[J]. Flow, Turbulence and Combustion, 2010, 84(4): 583-606. DOI:10.1007/s10494-009-9240-0 |
| [3] | Xu M Y, Zhang J P, Mi J C, et al. PIV measurements of turbulent jets issuing from triangular and circular orifice plates[J]. Science China:Physics, Mechanics & Astronomy, 2013, 56(6): 1176-1186. |
| [4] | Quinn W R. Mean flow and turbulence measurements in a triangular turbulent free jet[J]. International Journal of Heat and Fluid Flow, 1990, 11(3): 220-224. DOI:10.1016/0142-727X(90)90040-I |
| [5] | Quinn W. Measurements in the near flow field of an isosceles triangular turbulent free jet[J]. Experiments in Fluids, 2005, 39(1): 111-126. DOI:10.1007/s00348-005-0988-2 |
| [6] | Gutmark E, Schadow K C, Parr T P, et al. Noncircular jets in combustion systems[J]. Experiments in Fluids, 1989, 7(4): 248-258. |
| [7] | Ho C M, Gutmark E. Vortex induction and mass entrainment in a small-aspect-ratio elliptic jet[J]. Journal of Fluid Mechanics, 1987, 179: 383-405. DOI:10.1017/S0022112087001587 |
| [8] | Hussain F, Husain H S. Elliptic jets. Part 1. Characteristics of unexcited and excited jets[J]. Journal of Fluid Mechanics, 1989, 208: 257-320. DOI:10.1017/S0022112089002843 |
| [9] | Husain H S, Hussain F. Elliptic jets. Part 2. Dynamics of coherent structures:pairing[J]. Journal of Fluid Mechanics, 1991, 233: 439-482. DOI:10.1017/S0022112091000551 |
| [10] | Krothapalli A, Baganoff D, Karamcheti K. On the mixing of a rectangular jet[J]. Journal of Fluid Mechanics, 1981, 107: 201-220. DOI:10.1017/S0022112081001730 |
| [11] | Quinn W R, Militzer J. Experimental and numerical study of a turbulent free square jet[J]. Physics of Fluids, 1988, 31(5): 1017-1025. DOI:10.1063/1.867007 |
| [12] | Sfeir A. Investigation of three-dimensional turbulent rectangular jets[J]. AIAA Journal, 1979, 17(10): 1055-1060. DOI:10.2514/3.61277 |
| [13] | Tsuchiya Y, Horikoshi C. On the spread of rectangular jets[J]. Experiments in Fluids, 1986, 4(4): 197-204. DOI:10.1007/BF00717815 |
| [14] | Schadow K C, Gutmark E, Parr D M, et al. Selective control of flow coherence in triangular jets[J]. Experiments in Fluids, 2004, 6(2): 129-135. |
| [15] | Koshigoe S, Gutmark E, Schadow K C. Wave structures in jets of arbitrary shape. Ⅲ. Triangular jets[J]. Physics of Fluids, 1988, 31(6): 1410-1419. DOI:10.1063/1.867016 |
| [16] | Mi J, Nathan G J, Luxton R E. Centreline mixing characteristics of jets from nine differently shaped nozzles[J]. Experiments in Fluids, 2000, 28(1): 93-94. DOI:10.1007/s003480050012 |
| [17] | Deo R C, Nathan G J, Mi J. The influence of nozzle-exit geometric profile on statistical properties of a turbulent plane jet[J]. Experimental Thermal and Fluid Science, 2007, 32(2): 545-559. DOI:10.1016/j.expthermflusci.2007.06.004 |
| [18] | Deo R C, Nathan G J, Mi J C. Comparison of turbulent jets issuing from rectangular nozzles with and without sidewalls[J]. Experimental Thermal and Fluid Science, 2007, 32(2): 596-606. DOI:10.1016/j.expthermflusci.2007.06.009 |
| [19] | Mi J, Nobes D S, Nathan G J. Influence of jet exit conditions on the passive scaler field of an axisymmetric free jet[J]. Journal of Fluid Mechanics, 2001, 432: 91-125. |
| [20] | Mi J, Nathan G J, Nobes D S. Mixing characteristics of axisymmetric free jets from a contoured nozzle, an orifice plate and a pipe[J]. Journal of Fluids Engineering:Transactions of the ASME, 2001, 123(4): 878-883. DOI:10.1115/1.1412460 |
| [21] | Xu G, Antonia R. Effect of different initial conditions on a turbulent round free jet[J]. Experiments in Fluids, 2002, 33(5): 677-683. DOI:10.1007/s00348-002-0523-7 |
| [22] | Deo R C, Mi J, Nathan G J. The influence of Reynolds number on a plane jet[J]. Physics of Fluids, 2008, 20(7): 075108 DOI:10.1063/1.2959171 |
| [23] |
杜诚, 徐敏义, 米建春. 雷诺数对圆形渐缩喷嘴湍流射流的影响[J].
物理学报, 2010, 59(9): 6331-6338. Du C, Xu M Y, Mi J C. Effect of exit Reynolds number on a turbulent round jet[J]. Acta Physica Sinica, 2010, 59(9): 6331-6338. DOI:10.7498/aps.59.6331 |
| [24] | Dowling D R, Dimotakis P E. Similarity of the concentration field of gas-phase turbulent jets[J]. Journal of Fluid Mechanics, 1990, 218: 109-141. DOI:10.1017/S0022112090000945 |
| [25] | Miller R S, Madnia C K, Givi P. Numerical simulation of non-circular jets[J]. Computers & Fluids, 1995, 24(1): 1-25. |
| [26] | Azad M, Quinn W R, Groulx D. Mixing in turbulent free jets issuing from isosceles triangular orifices with different apex angles[J]. Experimental Thermal and Fluid Science, 2012, 39: 237-251. DOI:10.1016/j.expthermflusci.2012.01.028 |
| [27] | Mi J, Xu M, Du C. Digital filter for hot-wire measurements of small-scale turbulence properties[J]. Measurement Science and Technology, 2011, 22(12): 125401 DOI:10.1088/0957-0233/22/12/125401 |
| [28] |
徐敏义, 杜诚, 米建春. 圆形射流中心线上小尺度湍流的统计特性及其受高频噪声的影响[J].
物理学报, 2011, 60(3): 376-384. Xu M Y, Du C, Mi J C. Centreline statistics of the small-scale turbulence of a circular jet and their dependence on high frequency noise[J]. Acta Physica Sinica, 2011, 60(3): 376-384. |
| [29] | Mi J, Deo R C, Nathan G J. Fast-convergent iterative scheme for filtering velocity signals and finding Kolmogorov scales[J]. Physical Review E:Statistical Nonlinear and Soft Matter Physics, 2005, 71(6): 066304 DOI:10.1103/PhysRevE.71.066304 |
| [30] | Burattini P, Antonia R A, Danaila L. Similarity in the far field of a turbulent round jet[J]. Physics of Fluids, 2005, 17(2): 025101 DOI:10.1063/1.1833414 |
| [31] | Mi J, Antonia R A. Effect of large-scale intermittency and mean shear on scaling-range exponents in a turbulent jet[J]. Physical Review E:Statistical Nonlinear and Soft Matter Physics, 2001, 64(2): 026302 DOI:10.1103/PhysRevE.64.026302 |



