采用固定模板插值得到的高阶有限差分格式来计算包含间断的非线性问题时, 会出现虚假振荡, 即Gibbs现象, 随着网格加密这些振荡并不会减小, 这给实际的计算带来了很大问题, 数值不稳定会最终导致错误的解. 1987年以前, 主要用两种方法来消除间断处的数值振荡[1].第一种是加入人工黏性, 最早提出这种方法的是Jameson等[2]; 第二种是应用限制器, 这种方法是Harten[3]首次提出的总变差递减格式, 即TVD格式.
TVD格式具有很好的单调保持的特性, 但是在间断和局部极值点处会降低精度, 数学上已经证明TVD格式最多能达到2阶精度, 而且某些TVD格式的耗散过大. 1987年, Harten等[4]改进了TVD格式, 提出总变差有界性质的高阶精度高分辨率本质无振荡的格式, 简称ENO格式. ENO格式是第一个自相似的一致高阶精度格式, 对于分段光滑函数是本质无振荡的.在重构过程中ENO格式根据Newton差商的大小来自适应地选择扩展模板, 以达到一致高阶的精度, 并且在间断和局部极值点附近具有本质无振荡的性质.这种基于单元平均的有限体积形式的ENO格式在向三维情形推广上遇到了困难, 随后Shu等[5, 6]发展了基于通量的有限差分ENO格式. 1994年, Liu等[7]基于ENO格式发展了WENO格式, 即加权ENO格式. WENO格式把ENO格式重构过程中计算的Newton差商和模板都利用了起来, 然后把各个候选模板以凸组合的方式进行非线性加权. 1996年, Jiang等[8]改进了Liu等[7]的WENO格式, 提出了一种基于子模板上重构多项式的光滑测试因子.假设有k个侯选子模板, Jiang等[8]设计的WENO格式在光滑区具有2k-1阶精度, 在间断处具有k阶精度. Jiang等[8]设计的WENO格式比Liu等[7]的WENO格式在光滑区精度要高, 这也是迄今为止使用范围最广的一种WENO格式, 是后来很多研究者发展WENO格式的基础.
WENO格式能够很好地模拟包含激波等间断的复杂流体动力学问题, 但是用WENO格式模拟激波噪声问题并不理想, 主要原因是格式的分辨率不够理想, 耗散性比较高.
1992年, Lele[9]首先系统研究了高阶精度中心紧致有限差分格式, 通过Taylor分析的方法得到格式的精度, 通过Fourier分析方法得到格式的分辨率, 从而得到格式的色散性和耗散性.紧致格式的主要优点是对短波分量具有高分辨率特性, 而且在相同的模板下与非紧致格式相比具有更高阶的精度.最近, Liu等[10]基于Lele[9]的网格中心型中心紧致格式, 提出了一类中心对称型的线性紧致格式(central compact schemes, CCS格式), 该格式被应用于均匀各向同性湍流的模拟, 并在较少的网格点上取得了很好的结果.
中心型紧致差分格式的一个缺点是无法捕捉激波, 原因是格式的形式是完全中心对称的, 数值耗散为零, 因此该类格式只能用于亚声速流动的模拟, 而无法用于模拟包含激波的流动问题.为了能够精确模拟超声速等包含激波的问题, Zhang等[11]在基于Lele[9]的网格中心型中心紧致格式的基础上, 对插值格式引入了非线性加权技术, 得到了具有捕捉间断能力的高阶非线性紧致格式.
由于Liu等[10]的CCS格式比Lele[9]的网格中心型中心紧致格式的数值误差更小, 而且分辨率更高, 所以基于CCS格式应用Zhang等[11]高阶非线性插值技术发展了一类高阶精度非线性紧致差分格式, 使得这类格式既能捕捉激波又适合于噪声计算的高阶精度、高分辨率和低耗散计算方法.
1 非线性紧致格式为了求解1阶导数, Lele[9]提出了两类格式, 一类是网格结点型中心紧致格式(cell-noded central compact schemes, CNCS格式), 另一类是网格中心型中心紧致格式(cell-centered central compact schemes, CCCS格式).基于Lele的CCCS格式, 通过耦合网格结点和网格中心的函数值以及1阶导数值, 我们设计了一类新的线性紧致格式, 即CCS格式.选取图 1的网格模板, 网格结点处的1阶导数值由下面的格式来得到:
| $ \begin{align} & \beta {{{{f}'}}_{j-2}}+\alpha {{{{f}'}}_{j-1}}+{{{{f}'}}_{j}}+\alpha {{{{f}'}}_{j+1}}+\beta {{{{f}'}}_{j+2}}= \\ & a\frac{{{f}_{j+\frac{1}{2}}}-{{f}_{j-\frac{1}{2}}}}{\Delta x}+b\frac{{{f}_{j+1}}-{{f}_{j-1}}}{2\Delta x}+c\frac{{{f}_{j+\frac{3}{2}}}-{{f}_{j-\frac{3}{2}}}}{3\Delta x}+ \\ & d\frac{{{f}_{j+2}}-{{f}_{j-2}}}{4\Delta x}+e\frac{{{f}_{j+\frac{5}{2}}}-{{f}_{j-\frac{5}{2}}}}{5\Delta x}. \\ \end{align} $ | (1) |

|
| 图 1 中心紧致格式的模板 Fig.1 Stencil of the CCS schemes |
CCS格式同时利用了网格结点和网格中心处的值, 利用到了模板范围内所有网格点信息, 所以CNCS格式和CCCS格式是CCS格式的两种特例. CCS格式中的系数关系可以通过Taylor级数展开式(1) 来得到, 详见文献[10].其中CCS后缀的第一个字母表示格式类型, 分别用字母E, T, P作为后缀来表示显式、三对角、五对角格式, 数字表示格式的阶数.
CCS-T6和CCS-E6格式可以写成如下统一的形式:
| $ \begin{align} & \alpha {{{{f}'}}_{j-1}}+{{{{f}'}}_{j}}+\alpha {{{{f}'}}_{j+1}}=a\frac{{{f}_{j+\frac{1}{2}}}-{{f}_{j-\frac{1}{2}}}}{\Delta x}+b\frac{{{f}_{j+1}}-{{f}_{j-1}}}{2\Delta x}+ \\ & c\frac{{{f}_{j+\frac{3}{2}}}-{{f}_{j-\frac{3}{2}}}}{3\Delta x}. \\ \end{align} $ |
其中系数关系分别为:
| $ a=\frac{9-20\alpha }{6}, b=\frac{-9+62\alpha }{15}, c=\frac{1+12\alpha }{10}. $ |
当α=0时, 得到CCS-E6格式; 当
对导数的差分格式选取的组合方式为:内点格式采用CCS-T6格式, 边界点处采用显式中心差分CCS-E6格式.
在网格中心处的值通过Zhang等[11]的高阶WENO插值的方法得到.
在3个子模板S0, S1, S2上的插值逼近分别为:
| $ \begin{align} & \hat{f}_{j+\frac{1}{2}}^{\left( 0 \right)}=\frac{3}{8}{{f}_{j-2}}-\frac{5}{4}{{f}_{j-1}}+\frac{15}{8}{{f}_{j}}, \\ & \hat{f}_{j+\frac{1}{2}}^{\left( 1 \right)}=-\frac{1}{8}{{f}_{j-1}}+\frac{3}{4}{{f}_{j}}+\frac{3}{8}{{f}_{j+1}}, \\ & \hat{f}_{j+\frac{1}{2}}^{\left( 2 \right)}=\frac{3}{8}{{f}_{j}}+\frac{3}{4}{{f}_{j+1}}-\frac{1}{8}{{f}_{j+2}}. \\ \end{align} $ |
在全模板
| $ \begin{align} & {{{\hat{f}}}_{j+\frac{1}{2}}}=\sum\limits_{r=0}^{k-1}{{{d}_{r}}}\hat{f}_{j+\frac{1}{2}}^{\left( r \right)}= \\ & \frac{3}{128}{{f}_{j-2}}-\frac{5}{32}{{f}_{j-1}}+\frac{45}{64}{{f}_{j}}+\frac{15}{32}{{f}_{j+1}}-\frac{5}{128}{{f}_{j+2}}. \\ \end{align} $ |
从而可以得到线性权值为
| $ {{d}_{0}}=\frac{1}{16}, {{d}_{1}}=\frac{5}{8}, {{d}_{2}}=\frac{5}{16}. $ |
光滑测试因子为:
| $ \begin{align} & I{{S}_{0}}=\frac{13}{12}{{\left( {{f}_{j-2}}-2{{f}_{j-1}}+{{f}_{j}} \right)}^{2}}+\frac{1}{4}{{\left( {{f}_{j-2}}-4{{f}_{j-1}}+3{{f}_{j}} \right)}^{2}}, \\ & I{{S}_{1}}=\frac{13}{12}{{\left( {{f}_{j-1}}-2{{f}_{j}}+{{f}_{j+1}} \right)}^{2}}+\frac{1}{4}{{\left( {{f}_{j-1}}-{{f}_{j+1}} \right)}^{2}}, \\ & I{{S}_{2}}=\frac{13}{12}{{\left( {{f}_{j}}-2{{f}_{j+1}}+{{f}_{j+2}} \right)}^{2}}+\frac{1}{4}{{\left( 3{{f}_{j}}-4{{f}_{j+1}}+{{f}_{j+2}} \right)}^{2}}. \\ \end{align} $ |
光滑测试因子和非线性权之间的关系为:
| $ {{\omega }_{r}}=\frac{{{\alpha }_{r}}}{\sum\limits_{s=0}^{2}{{{\alpha }_{s}}}}, {{\alpha }_{r}}=\frac{{{d}_{r}}}{{{\left( \varepsilon +I{{S}_{r}} \right)}^{2}}}, r=0, \cdot \cdot \cdot, 2. $ |
其中,ε为小量, 目的是防止分母为零, 一般取值为ε=10-6.
所以最终的WENO插值格式为
| $ {{\hat{f}}_{j+\frac{1}{2}}}={{\omega }_{0}}\hat{f}_{j+\frac{1}{2}}^{\left( 0 \right)}+{{\omega }_{1}}\hat{f}_{j+\frac{1}{2}}^{\left( 1 \right)}+{{\omega }_{2}}\hat{f}_{j+\frac{1}{2}}^{\left( 2 \right)}. $ | (2) |
综合CCS有限差分格式(1)和非线性WENO插值格式(2), 得到了一类新的非线性紧致格式(nonlinear CCS格式, 简称NLCCS格式).
2 数值验证空间离散采用5阶NLCCS格式, 时间离散采用3阶TVD Runge-Kutta格式, 计算了如下一系列的算例.
2.1 一维Euler方程 2.1.1 Sod激波管问题在初始时给定一个间断面, 随着时间增长各个物理量会发生变化, 这其中包含激波膨胀波接触间断等.计算区域取为-5≤x≤5, 计算网格采用100个点, 初始间断位于x=0处, 左右两边参数为
| $ \left( \rho, u, p \right)=\left\{ \begin{align} & \left( 1.0, 0.0, 1.0 \right), \ \ \ \ \ \ \ \ -5\le x\le 0 \\ & \left( 0.125, 0.0, 0.1 \right), \ \ \ \ \ 0<x\le 5 \\ \end{align} \right.\cdot $ |
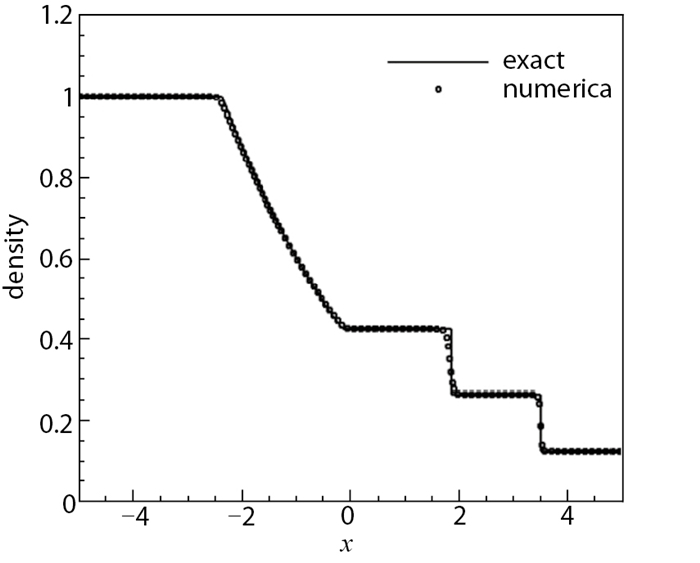
计算到无量纲时间t=2.0并考察计算结果. 图 2给出了高阶非线性NLCCS格式的计算结果, 可以看出, 这类格式的计算结果在激波、膨胀波及接触间断附近都能达到基本无波动, 计算结果与精确解符合得很好.
|
| 图 2 Sod问题(N=100) Fig.2 Sod problem(N=100) |
该问题的初始条件为
| $ \left( {\rho, u, p} \right) = \left\{ \begin{array}{l} \left( {0.445, 0.698, 3.528} \right), \;\;\;\;\; - 5 \le x \le 0\\ \left( {0.5, 0.0, 0.571} \right), \;\;\;\;\;\;\;\;\;\;\;\;0 < x \le 5 \end{array} \right. \cdot $ |
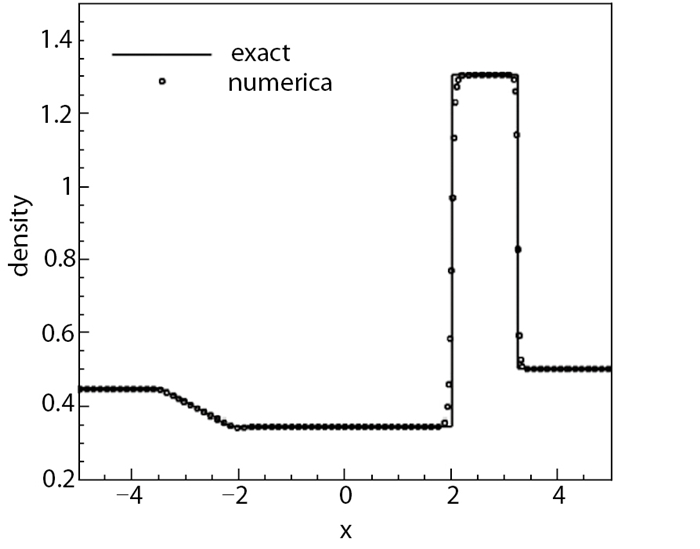
计算区域取为-5≤x≤5, 计算网格采用100个点, 初始间断位于x=0处, 取t=1.3时刻的计算结果并比较. 图 3给出了高阶非线性NLCCS格式的计算结果, 可以看出, 这类格式的计算结果在激波、膨胀波及接触间断附近都能达到基本无波动, 计算结果与精确解符合得很好.
|
| 图 3 Lax问题(N=100) Fig.3 Lax problem(N=100) |
Shu-Osher问题描述的是一个运动Mach数为3的激波和正弦波的相互干扰, 从而诱发出高频扰动, 被看作是激波与湍流相互作用的简化模型.该问题流场中含有明显的细致结构, 对于考察计算格式对流场细节和广谱范围内的分辨率十分合适, 一直是格式验证的标准算例.初始条件为
| $ \begin{array}{*{20}{c}} {\left( {\rho, u, p} \right) = }\\ {\left\{ \begin{array}{l} \left( {3.85714, 2.629369, 10.33333} \right), \;\;\;\;\; - 5.0 \le x \le - 4.0\\ \left( {1 + 0.2\sin \left( {5x} \right), 0.0, 1.0} \right), \;\;\;\;\;\;\;\;\;\;\;\;\; - 4.0 < x \le 5.0 \end{array} \right..} \end{array} $ |
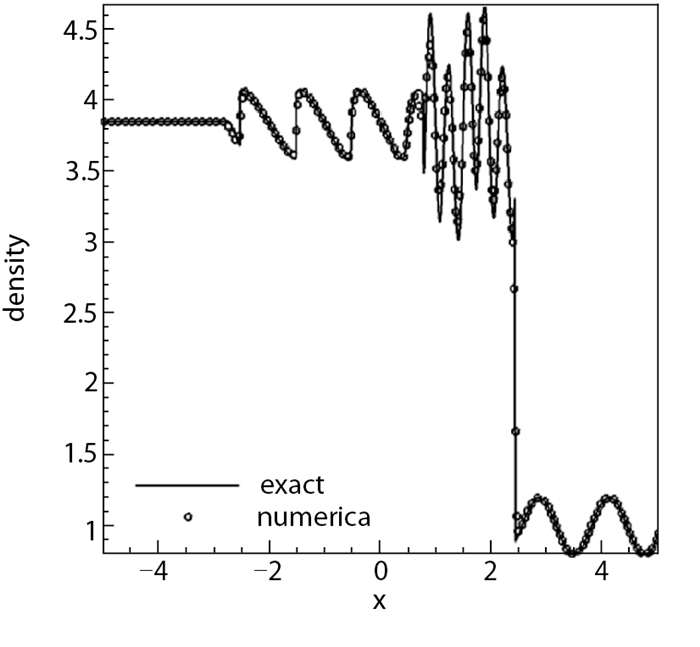
计算区域取为-5≤x≤5, 计算网格采用400个点, 初始间断位于x=-4处, 取t=1.8时刻的计算结果并比较.采用4000个网络点的5阶WENO格式的计算结果作为该问题的精确解. 图 4给出了高阶非线性NLCCS格式的计算结果, 可以看出, 这类格式的计算结果在激波、膨胀波及接触间断附近都能达到基本无波动, 计算结果与精确解符合得很好.
|
| 图 4 Shu-Osher问题(N=100) Fig.4 Shu-Osher problem(N=100) |
双冲击波问题包括了强激、波接触间断和膨胀波之间的相互作用, 对计算格式的稳定性要求比较高.其初值为
| $ \left( {\rho, u, p} \right) = \left\{ \begin{array}{l} \left( {1.0, 0.0, 1000} \right), \;\;\;\;\;\;\;0 \le x < 0.1\\ \left( {1.0, 0.0, 0.01} \right), \;\;\;\;\;\;\;\;0.1 \le x < 0.9\\ \left( {1.0, 0.0, 100} \right), \;\;\;\;\;\;\;\;\;0.9 \le x \le 1.0 \end{array} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdot $ |
两端采用反射边界条件, 计算终止时间为t=0.038, 网格点数取400.
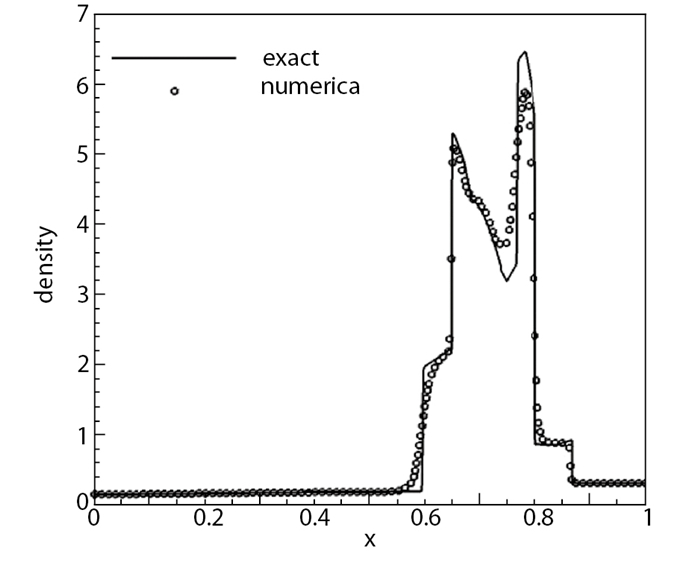
采用4000个网格点的5阶WENO格式的计算结果作为该问题的精确解. 图 5给出了高阶非线性NLCCS格式的计算结果, 可以看出, 这类格式的计算结果在激波、膨胀波及接触间断附近都能达到基本无波动, 计算结果与精确解符合得很好.
|
| 图 5 双冲击波问题(N=100) Fig.5 Two interacting blast waves(N=100) |
双Mach反射问题描述的是Mach数为10的强运动斜激波以与x轴方向呈60°的方向入射, 入射点在(1/6, 0), 计算区域取[0,4]×[0,1].激波波前静止空气的密度为1.4, 压力为1, 波后按激波关系给定初始条件.下边界在[1/6, 4]的区域给定壁面边界条件, 其他边界区域按照激波运动所在的位置, 分别给定波前或波后的值.初始条件为
| $ \left( {\rho, u, v, p} \right) = \left\{ \begin{array}{l} \left( {1.4, 0.0, 0.0, 1.0} \right), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;波前\;\;\;\\ \left( {8.0, 7.145, \;\; - 4.125, 116.5} \right), \;\;\;\;\;波后\;\;\;\; \end{array} \right. \cdot $ |
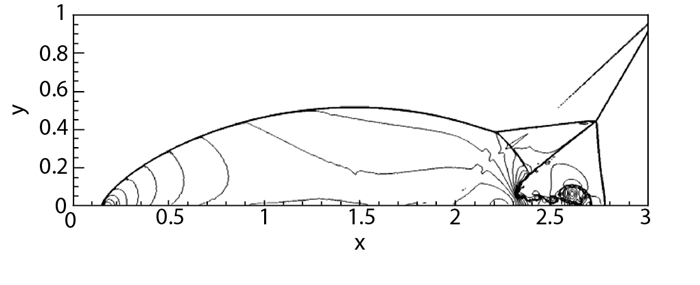
本文采用480×120的均匀网格计算截止到无量纲时间t=0.2的时刻. 图 6给出了高阶非线性NLCCS格式的计算结果, 取密度1.731到20.92共30条等值线做图.可以看出, 这类格式的计算结果在激波、膨胀波及接触间断附近都能达到基本无波动.
|
| 图 6 激波双Mach反射(N=480×120) Fig.6 Double Mach reflection(N=480×120) |
Mach数为3的强运动激波沿着带有台阶的风洞向右传播.台阶高度为0.2, 前缘位置在0.6, 计算域为[0,3]×[0,1].初始条件为
| $ \left( {\rho, u, v, p} \right) = \left( {1.4, 3.0, 0.0, 1.0} \right). $ |
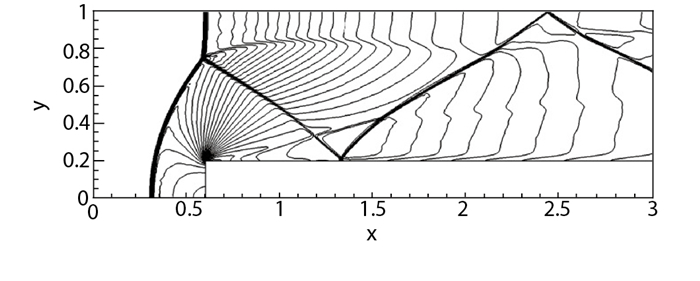
左右边界为开边界, 其余边界取壁面反射条件.本文采用240×80的均匀网格计算截止到无量纲时间t=4的时刻. 图 7给出了高阶非线性NLCCS格式的计算结果, 取密度0.2568到6.607共30条等值线作图.可以看出, 这类格式的计算结果在激波、膨胀波及接触间断附近都能达到基本无波动.
|
| 图 7 前台阶问题(N=240×80) Fig.7 Forward facing step problem(N=240×80) |
Rayleigh-Taylor不稳定性问题描述的是上下两层不同密度和压力的流体形成的接触间断问题, 其初始条件如下:
| $ \begin{array}{c} \left( {\rho, u, v, p} \right) = \\ \left\{ \begin{array}{l} \left( {2, 0, - 0.025a{\rm{cos}}\left( {8{\rm{\pi }}x} \right), 2y + 1} \right), \;\;\;\;0 \le {\rm{y}} < 0.5\\ \left( {1, 0, - 0.025a{\rm{cos}}\left( {8{\rm{\pi }}x} \right), y + 1.5} \right), \;\;\;\;0.5 \le {\rm{y}} \le 1 \end{array} \right.. \end{array} $ |
比热比常数取为γ=5/3, 控制方程在二维Euler方程的右端增加源项S=(0, 0, ρ, ρv).左右边界为壁面反射条件, 上下边界取如下固定值:
| $ \left( {\rho, u, v, p} \right) = \left\{ \begin{array}{l} \left( {1, 0, 0, 2.5} \right), \;\;\;\;{\rm{上边界}}\\ \left( {2, 0, 0, 1} \right), \;\;\;\;\;\;\;{\rm{下边界}} \end{array} \right.\;\;\;\;\;\;. $ |
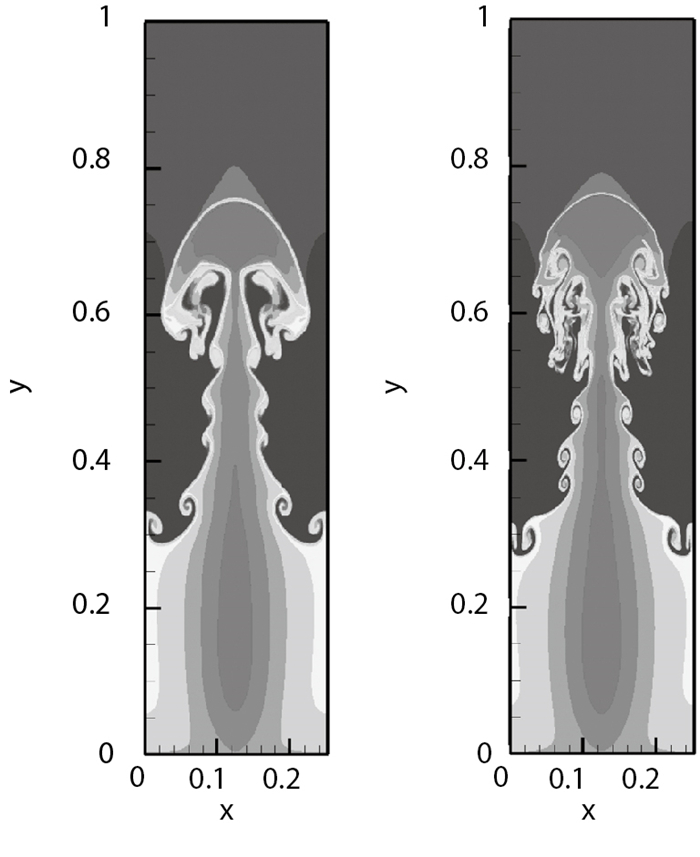
计算域为[0,0.25]×[0,1].本文采用240×960和480×1920的两套均匀网格计算截止到无量纲时间t=1.95的时刻. 图 8给出了高阶非线性NLCCS格式的计算结果, 取密度0.952269到2.14589共15条等值线作图.可以看出, 这类格式的计算结果在接触间断附近都能达到基本无波动, 并且对流场中的细微结构分辨率远远高于5阶WENO格式.
|
| 图 8 Rayleigh-Taylor不稳定性问题 Fig.8 Rayleigh-Taylor instability problem |
本问题在文献[12, 13]中有详细的分析和描述.以下简要说明计算的初始条件和边界条件.在x=0处有一道激波, 激波前后条件为
| $ \begin{array}{c} \left( {\rho, u, v, p} \right) = \\ \left\{ \begin{array}{l} \left( {1, 0.714286, - 1.2, 0} \right), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x\;{\rm{ > }}\;{\rm{0}}\\ \left( {1.34161, 1.08095, - 0.894444, 0} \right), \;\;\;\;\;\;\;x \le {\rm{0}} \end{array} \right.\;\;. \end{array} $ |
计算域取为[-30,10]×[-20,20].
在(xv, yv)=(4, 0) 处施加一个速度扰动涡:
| $ \left\{ \begin{array}{l} \tilde u = - {M_v}{{\rm{e}}^{\frac{{1 - {r^2}}}{2}}}\left( {y - {y_v}} \right)\\ \tilde v = {M_v}{{\rm{e}}^{\frac{{1 - {r^2}}}{2}}}\left( {x - {x_v}} \right) \end{array} \right.. $ |
波前的密度和压力施加扰动后的值取为
| $ \left\{ \begin{array}{l} \rho = {\left[{1-\frac{{\gamma-1}}{2}M_v^2\exp \left( {1-{r^2}} \right)} \right]^{\frac{1}{{\gamma - 1}}}}\\ p = \frac{{{\rho ^\gamma }}}{\gamma } \end{array} \right.. $ |
其中涡强度Mv=1.0, Reynolds数Re=800, Mach数M=1.0.
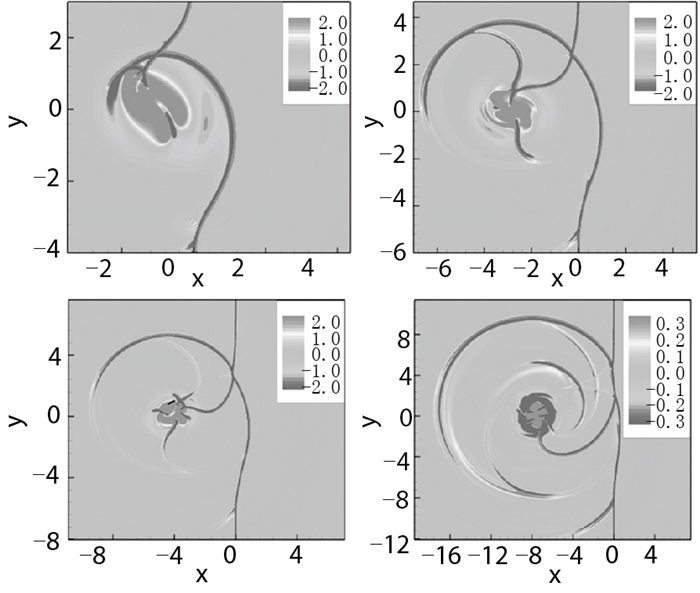
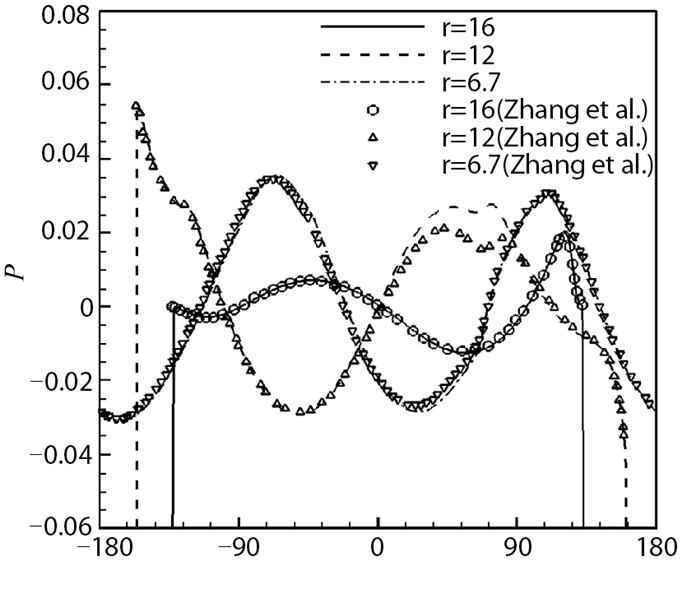
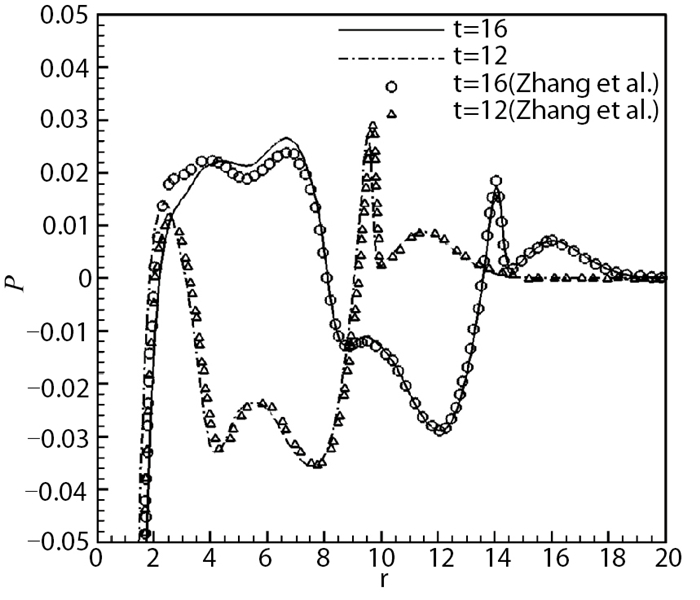
左右边界为开边界, 上下边界取周期边界条件.本文采用1000×1000的拉伸网格计算截止到无量纲时间t=16的时刻. 图 9给出了几个典型时刻的高阶非线性NLCCS格式计算的数值阴影图. 图 10为沿3个不同半径处的声压分布图, 图 11为在两个不同时刻的声压分布图.可以看出, 这类格式的计算结果在激波、压缩波附近都能达到基本无波动, 并且对流场中的旋涡等细微结构以及激波噪声的分辨率高于5阶WENO格式.
|
| 图 9 激波与强旋涡相互作用问题几个典型时刻的数值阴影图 Fig.9 Representative time of numerical shadow graph for the interaction of shock and strong vortex |
|
| 图 10 沿3个不同半径处的声压分布图 Fig.10 Three different circumferential distributions of the sound pressure |
|
| 图 11 在两个不同时刻的声压分布图 Fig.11 Two different radial distributions of the sound pressure |
本问题在文献[14]中有详细的分析和描述.以下简要说明计算的初始条件和边界条件.整个剪切层在初始时刻是等压的, 并且总的焓值也处处相等.计算域取为直角坐标系下的矩形[0,200]×[-20,20].初始时刻可以把计算域分成5个部分, 表 1给出了各个区域具体的流动参数.
| 下载CSV 表 1 初始时刻流场的物理参数 Tab.1 Physical parameters of initial flow field |
上边界条件取激波波后的值, 即取(3)区的值.下边界条件取为滑移壁面边界条件.出口处用远场特征边界条件.
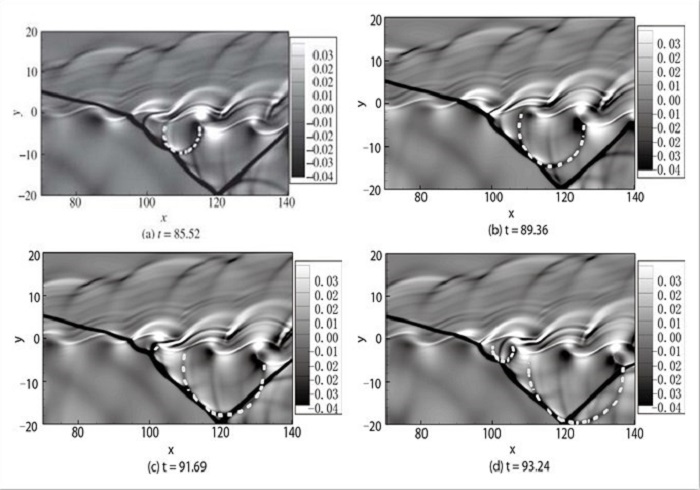
图 12为一个演化周期中几个典型时刻的胀量图, 其中虚线标记的是剪切层下层流体中被追踪的两道声波.由于流体以超声速向下游传播, 声波也随着流体向下游方向对流, 并且声波的辐射半径在逐渐增大.可以明确看到声波的产生源在涡与小激波相互作用的位置, 剪切层的涡列穿过激波, 每个涡与激波发生干扰时, 根据这种激波噪声产生和传播的机制, 在噪声源处向外辐射出一道道的声波.
|
| 图 12 声波的产生和传播 Fig.12 Generations and radiations of acoustic wave |
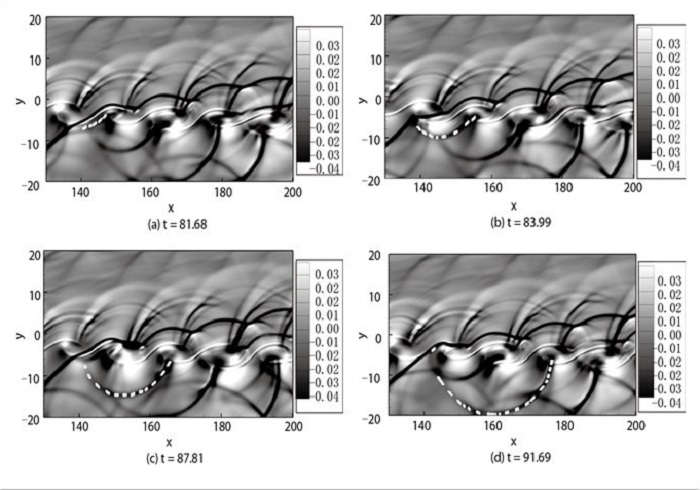
图 13为选取一个演化周期中几个典型时刻的胀量图, 其中虚线标记的是剪切层下层流体中的一道声波.由于流体以超声速向下游传播, 声波也随着流体向下游方向对流, 并且声波的辐射半径在逐渐增大.当t=91.69时, 噪声源处产生了第二道声波, 可以明确看到声波的产生源在旋涡之间的鞍点处, 即辫子区的位置.在剪切层的涡列穿过激波时, 涡对与激波发生干扰, 在涡对之间的鞍点处激波透过剪切层, 同时在鞍点处激波被辫子区的旋臂所阻碍, 激波与辫子区的相互干扰使得激波强度变弱, 部分激波穿过剪切层, 还有一部分激波没有穿过剪切层, 而是在鞍点处以声波的形式发生泄漏.这说明了强激波与剪切层相互作用中也存在激波泄漏机制, 在鞍点处激波泄漏并向外辐射声波.根据这种激波噪声产生和传播的机制, 当剪切层穿过激波时, 在噪声源处向外辐射出一道道的声波, 同时可以看到,当声波传播到下壁面时反射回内场, 声波再次与激波和剪切层相互干扰.
|
| 图 13 声波的产生和传播 Fig.13 Generations and radiations of acoustic wave |
NLCCS格式是在我们发展的的线性紧致格式(CCS格式)基础上设计的, 主要思路是采用非线性WENO插值的方法来得到网格中心处的值.数值验证包括一维Euler方程、二维Euler方程, 以及二维Navier-Stokes方程.一系列数值算例表明NLCCS格式是既能捕捉激波又适合于噪声计算的高阶精度高分辨率和低耗散计算方法, 适合于气动声学和湍流等多尺度问题的数值模拟.
| [1] |
Shu C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[R]. NASA/CR-97-206253 ICASE Report 97-65, 1997.
|
| [2] |
Jameson A, Schmidt W, Turkel E. Numerical solutions of the Euler equations by finite volume methods using Runge-Kutta time stepping schemes[R]. AIAA 1981-1259, 1981.
|
| [3] |
Harten A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 49(3): 357-393. DOI:10.1016/0021-9991(83)90136-5 |
| [4] |
Harten A, Engquist B, Osher S, et al. Uniformly high order accurate essentially non-oscillatory schemes Ⅲ[J]. Journal of Computational Physics, 1987, 71(2): 231-303. DOI:10.1016/0021-9991(87)90031-3 |
| [5] |
Shu C W, Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1988, 77(2): 439-471. DOI:10.1016/0021-9991(88)90177-5 |
| [6] |
Shu C W, Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes Π[J]. Journal of Computational Physics, 1989, 83: 32-78. DOI:10.1016/0021-9991(89)90222-2 |
| [7] |
Liu X D, Osher S, Chan T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115(1): 200-212. DOI:10.1006/jcph.1994.1187 |
| [8] |
Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228. DOI:10.1006/jcph.1996.0130 |
| [9] |
Lele S K. Compact finite difference schemes with spectral-like resolution[J]. Journal of Computational Physics, 1992, 103(1): 16-42. DOI:10.1016/0021-9991(92)90324-R |
| [10] |
Liu X L, Zhang S H, Zhang H X, et al. A new class of central compact schemes with spectral-like resolution I: linear schemes[J]. Journal of Computational Physics, 2013, 248: 235-256. DOI:10.1016/j.jcp.2013.04.014 |
| [11] |
Zhang S H, Jiang S F, Shu C W. Development of nonlinear weighted compact schemes with increasingly higher order accuracy[J]. Journal of Computational Physics, 2008, 227(15): 7294-7321. DOI:10.1016/j.jcp.2008.04.012 |
| [12] |
Inoue O, Hattori Y. Sound generation by shock-vortex interactions[J]. Journal of Fluid Mechanics, 1999, 380: 81-116. DOI:10.1017/S0022112098003565 |
| [13] |
Zhang S H, Zhang Y T, Shu C W. Multistage interaction of a shock wave and a strong vortex[J]. Physics of Fluids, 2005, 17(116101): 1-13. |
| [14] |
刘旭亮, 张树海. 二维激波与剪切层相互作用的直接数值模拟研究[J]. 力学学报, 2013, 45(1): 61-75. Liu X L, Zhang S H. Direct numerical simulation of the interaction of 2D shockwave and shear layer[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(1): 61-75. DOI:10.6052/0459-1879-12-106 (in Chinese) |
| [15] |
Liu X L, Zhang S H, Zhang H X, et al. A new class of central compact schemes with spectral-like resolution Π: hybrid weighted nonlinear schemes[J]. Journal of Computational Physics, 2015, 284: 133-154. DOI:10.1016/j.jcp.2014.12.027 |



