激波与界面相互作用具有丰富的物理现象和重要的学术价值.如激波在界面的反射和折射都是长期研究的传统课题; 强冲击波作用金属自由界面会引起微喷射[1]; 激波作用扰动界面会引起扰动的Richtmyer-Meshkov(R-M)不稳定性增长[2-3]. R-M不稳定性会诱导物质间的湍流混合, 在超燃、惯性约束聚变等重大工程领域具有重要作用, 一直是国际研究的热点.
由于成本低、易诊断等优点, 激波管在R-M不稳定性及湍流混合机理方面的实验研究得到广泛应用.利用激波管对R-M不稳定性的研究多集中在一维平面激波冲击具有扰动界面的问题, 如平面激波冲击正弦界面[5-6]、斜界面[7-9]、气泡[10-11]、气柱[12-13]等; 而对激波波形结构产生界面扰动的问题研究较少.激波形状直接与压力梯度的方向相关, 当压力梯度方向和密度方向不在同一方向时, 由于∇ρ×∇p≠0的斜压机制生成涡量, 从而引起界面的变形.激波在圆柱绕射过程发生两次Mach反射, 演化成两对三波点、两对滑移线、两对弯曲反射波的复杂波形结构[14], 波阵面压力梯度方向具有较大的变化, 在两对滑移线之间的局部流场具有较强的非均匀性[15].这些非均匀特征引起的界面变形同绕柱后激波的波形和Mach数相关[16-17].由于激波波形以及波后局部复杂流场引起的界面变形同传统研究的正弦、斜界面模态不同, 这类界面变形具有较强的局部特征和复杂的形状, 在反射激波二次冲击后, 界面R-M不稳定性发展表现出不同的演化特征.相对激波一次冲击, 界面受反射激波二次冲击后的演化特征更加复杂.描述反射激波冲击下随机扰动增长的Mikaelian模型h=CAt[u]t, C=0.28, 式中h为混合区宽度, C为增长系数, At为Atwood数,[u]为界面跃迁速度, t为时间, 表明混合区宽度呈线性增长[18]; Ukai等[19]的数值模拟结果显示, 不同维数和界面模态增长系数C的值差别较大; 刘金宏等[17]的实验结果表明复杂结构界面的混合区宽度增长是非线性的.反射激波在界面的复杂动力学过程, 以及作用后混合区涡量的演化特征, 是影响混合区演化的主要因素.
现实中材料的非均匀性会造成激波结构的变化, 研究波形结构导致的界面变形以及变形界面的R-M不稳定性具有现实意义; 另一方面, 可以利用复杂激波波形结构产生界面扰动, 增强界面R-M不稳定性的发展, 实现材料的增混.利用激波管加载, 纹影和激光片光散射的测试方法, 实验研究波后滑移线引起的平面界面的变形, 以及不同演化特征的变形界面在反射激波冲击下的R-M不稳定性.
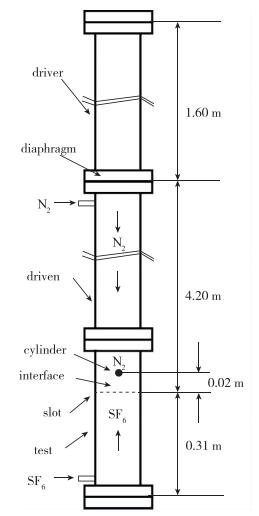
1 实验方法 1.1 实验装置图 1为激波管研究不同气体界面R-M不稳定性演化规律的结构图.激波管竖直安装, 内截面为100 mm×100 mm, 由驱动段driver(长度1.6 m)、被驱动段driven(膜片与界面的距离4.2 m)和实验段test(实验气体SF6, 高度0.31 m)构成, 距离界面0.02 m处安装钢性圆柱体, 驱动段和被驱动段间的隔膜用于产生压力差, 实验时隔膜瞬间破碎后往被驱动段传播激波, 激波在圆柱绕射、对碰后冲击界面, 由此研究复杂激波引起的界面变形以及反射激波冲击下的界面R-M不稳定性.与文献[4]的实验和测试方法相同, 该实验采用重气体SF6从激波管尾部充入, 轻气体N2从上部充入, 富余气体在狭缝(slot)流出, 由此生成N2/SF6动态稳定的初始平面界面; 采用高速纹影、激光片光散射的测试方法记录界面的演化过程.
|
| 图 1 实验装置示意图 Fig.1 Shock tube facility |
如表 1所示, 共开展了4次实验.入射激波Mach数Ma=u/a0, u为入射激波速度, 由激波到达压力传感器的时间间隔和传感器间距得到, a0为激波波前声速. 表 1中a0, ρ和T分别为激波波前的声速、密度和温度, D为图 1中圆柱的直径.圆柱中心与初始界面的距离均为20 mm, 实验气体SF6, 初始高度均为310 mm.
| 下载CSV 表 1 实验初始条件 Tab.1 Initial conditions of the experiment |
平面激波在圆柱障碍物绕射后发生对碰, 在圆柱背风面形成较为复杂的波系和流场结构[14-15], 绕射激波的演化同激波Mach数和气体参数相关. 图 2为Ma=1.24平面激波在直径10 mm圆柱体绕射后的波形演化, 其中s为入射波与圆柱中心的距离, 激波在圆柱体上Mach反射时, 入射波(IS)、第1个Mach杆(MS1)和第1个反射波(RS1)都在第1个三波点(TP1)相交, 在RS1和MS1间存在滑移线SL1, 并与TP1相交; MS1对碰后, 产生新的TP2和SL2.可见, 平面激波在圆柱绕射后, 既存在多种波系结构, 波后流场也存在速度间断的两对滑移线, 这些结构伴随激波传播而发生变化, 通过调整圆柱与界面的距离可研究波形结构对界面变形的作用. Mach反射波后滑移线存在滑移速度和密度间断, 会引起小尺度的二次混合现象[20], 滑移线作用下界面如何变形却鲜有研究.激波在圆柱绕射后会产生两对滑移线结构, 由此设计图 1实验, 研究滑移线引起的界面变形.

|
| 图 2 激波在圆柱的绕射过程的纹影图 Fig.2 Schlieren pictures of shock wave diffracted over a cylinder |
如图 2所示, 平面激波在圆柱绕射后结构发生了显著变化, 这类激波冲击平面界面会引起界面的复杂变形.通过改变圆柱与界面的距离和圆柱直径D, 界面变形形态与文献[16-17]的实验结果不同, 说明界面的变形同激波冲击界面时的波形结构和波后流场密切相关.
图 3是纹影测试方法得到的界面演化图, 其中, I为初始界面; P为滑移线SL的顶点; TC为CR在界面的透射波; RS为底部固壁反射波; TW为横波; a, b为竖直线.以Run-3实验为例, 入射激波到达初始界面为0时刻; -0.01 ms时刻, 激波在圆柱绕射后发生对碰, 冲击界面时演化成两对三波点TP, 两对对滑移线SL和两对弯曲反射波CR的复杂波形结构; 0.16 ms时刻, 弯曲的反射波CR部分透射后发展为斜激波, 上部分发展成横波TW; 滑移线与界面相交, 界面运动过程中交点间距保持不变; 滑移线外的界面没有发生明显的变形, 滑移线内部的滑移速度场致使界面发生变形; 滑移线两侧流体由于切向速度差存在K-H不稳定性, 滑移线横向变宽.对Run-1实验而言, 由于圆柱直径小于Run-3实验, 绕射激波较早发生对碰, 两对滑移线的顶点均在界面上方, 沿着第二对滑移线产生较大的“凹坑”变形. 图 4为激光片光散射测试得到的界面演化图像, 其中λ为扰动长度, 这种测试是对流场截面的显示, 能够清晰显示界面结构, 消除了纹影测试的积分效应. 图 4清晰地显示了界面变形主要发生在滑移线内部, 以及由于滑移线与界面相交位置的不同导致中心区域变形的差异.

|
| 图 3 绕柱后的激波冲击下界面变形纹影图 Fig.3 Schlieren pictures of interface evolution by diffracted incident shock wave |

|
| 图 4 绕柱后的激波冲击下界面变形的片光图 Fig.4 Laser sheet pictures of interface evolution by diffracted incident shock wave |
如图 3所示, 激波冲击界面后0.15 ms时刻, 透射激波波形结构较为平整, 透射波TC衰减为声波, 由于平面激波的稳定性, 透射激波整形为一维平面激波.若移除图 1中的圆柱, 平面激波正冲击平面界面时, 界面能够很好的保持平面性而不发生变形[5, 17], 说明图 1实验方法得到的初始界面具有很好的平面性, 图 3和图 4中的实验界面变形均是由复杂波形和波后非均匀流场造成的.
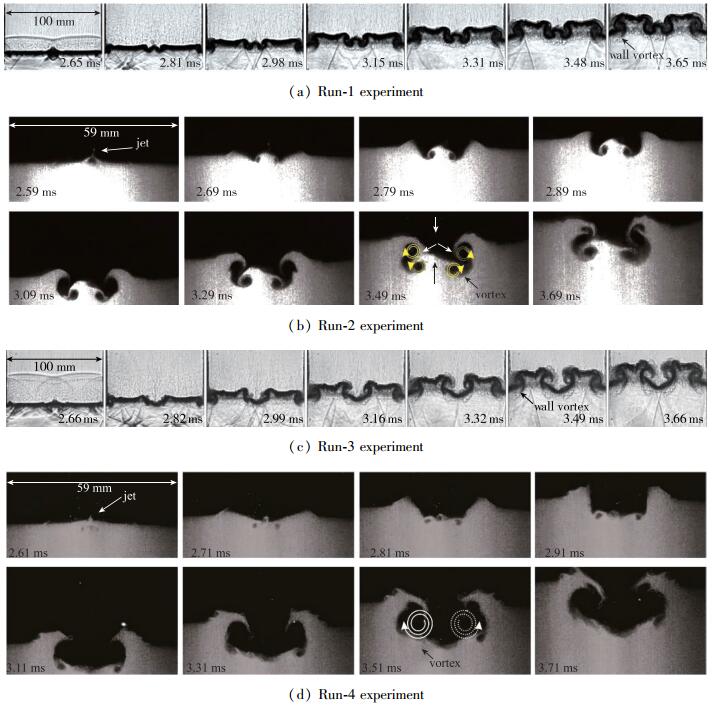
2.3 反射激波冲击变形界面的R-M不稳定性如图 3所示, 透射激波运动到底部固壁后产生向上传播的反射波RS, 由于平面激波的稳定性可以认为RS为一维平面正激波.反射波RS与变形界面相遇时, 会引起界面的R-M不稳定性增长.与传统的变形界面不同, 表 1实验的变形界面存在滑移结构. 图 5为反射激波冲击后界面的演化图: Run-1和Run-2是同类实验, Run-3和Run-4是同类实验, 只是测试方法不同, 纹影测试给出波系结构, 而片光散射测试给出清晰的界面演化.
|
| 图 5 反射激波冲击后界面的演化图 Fig.5 Interface evolution by reshock waves |
如图 5所示, 在Run-1和Run-2实验中, 反射激波冲击后“缺口”内界面演化成向上运动的“尖钉”结构, 外界面演化成向下运动的“气泡”结构, “尖钉”和“气泡”相撞后, 混合区演化成两对涡结构, 这两对涡主导混合区的演化.边界层/反射波/界面/固壁之间相互作用, 在壁面产生壁面涡.而Run-3和Run-4实验, 外界面产生的涡量占主导作用, 混合区演化成一对主控涡的“气泡”结构.
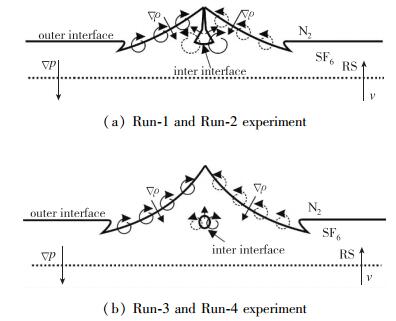
2.4 结果分析 2.4.1 反射波与界面的相互作用如图 6所示, 反射波RS由SF6向上传入N2, N2密度低阻抗小, RS在界面反射稀疏波向下传播, 透射激波向上传播; RS与界面具有一定夹角, 由于斜压效应, 反射激波冲击后在界面生成正涡(虚线)和负涡(实线).如图 6(a)所示, 对Run-1和Run-2实验, 外界面左侧产生负向涡量(实线), 右侧产生正向涡量(虚线), 两边的涡致使界面扰动发生向下翻转, 产生“气泡”结构; 内界面产生与外界面相反的涡量, 界面向上增长, 产生“尖钉”结构; 内外界面涡量的相互作用, 最终演化成图 5(b)中两对主控的涡结构.如图 6(b)所示, 对Run-3和Run-4实验, 内界面较小且远离外界面, 反射激波冲击内界面产生的涡量对外界面影响较小; 界面的变形主要受外界面产生的一对涡主导, 演化成图 5(d)所示的“气泡”结构; 内界面在主控涡的作用下破碎, 成为外界面的扰动.
|
| 图 6 反射波冲击界面产生涡量示意图 Fig.6 Drawing of structure of vortex at interface by reshock |
如图 7所示, 定义混合区宽度

|
| 图 7 混合区宽度定义图 Fig.7 Drawing of mixing zone width |
h=d1-d2
式中, d1, d2分别为扰动边缘和扰动中心与底部固壁的距离.
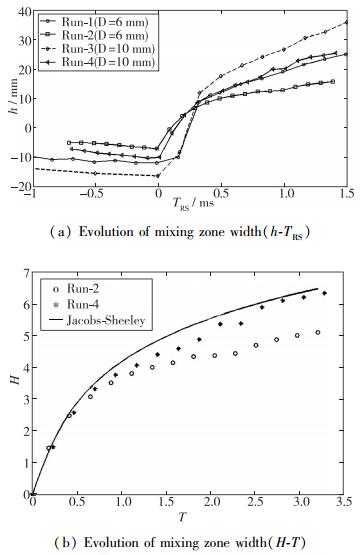
图 8(a)为实验得到h随时间的发展图, TRS为时间, 定义反射激波到达变形界面时为零时刻:纹影测试具有积分效应, 由于边界层的影响, 同类实验得到的混合区宽度增长明显高于激光片光散射测试结果, 误差较大; Run-2和Run-4实验是对流场截面信息的测试, 具有较高的精度.如图 8(a)所示, 对Run-2和Run-4实验数据:界面受入射激波第一次冲击下, 扰动增长缓慢; TRS=0时, 界面受反射激波第二次冲击后, 扰动由负变正, 扰动倒置, 扰动增长较快; 扰动幅度和波长较大的Run-4实验扰动增长高于Run-2实验.为更好地研究反射激波冲击下界面扰动的增长规律, 对混合区宽度和时间进行无量纲处理.定义混合区宽度无量纲量为H= 2π(h-h0)/λ, h为总混合宽度, h0为反射激波到达界面时的混合宽度, λ为扰动长度, 实验中λ的定义见图 4.时间无量纲量为T=v0TRS/λ, v0为混合宽度初始增长速率. 图 8(b)为H关于T的演化图.
|
| 图 8 混合区宽度增长 Fig.8 Growth of the mixing zone width |
激波冲击小扰动界面的扰动振幅增长的Jacobs-Sheeley涡量模型[21]
a(t)=sinh-1[2kv0t/π+sinh(ka0)]/k
式中, a为振幅; 波数k=2π/λ; v0为振幅的初始增长速率; t为时间; a0为激波刚过界面时的振幅.影响扰动增长的主要参量为λ, t和v0, 总的混合宽度h=2a.对ka0为小量时可将Jacobs-Sheeley涡量模型近似为
h=h0+λ[sinh-1(4v0TRS/λ)]/π
或
| $ H=2\sinh^{-1}(4T) $ | (1) |
式中, h0为反射激波冲击界面前混合宽度, 对Run-2实验h0=-7 mm, 对Run-4实验h0=-10 mm; λ为扰动波长, 对Run-2实验λ=28 mm, 对Run-4实验λ=35 mm; v0为反射激波扫过界面时扰动增长率, 由实验测试得到.对Run-2实验v0=65 mm/ms, 对Run-4实验v0=82 mm/ms; TRS为时间, 反射激波到达界面时为零时刻. 图 8(b)所示:反射激波冲击早期, Run-2实验和Run-4实验与式(1)比较吻合; 对Run-2实验(图 5(b)), “尖钉”和“气泡”发生碰撞, 混合区演化成两对主控的涡核, 抑制了混合区宽度h的增长, 在T~1.0以后, 无量纲H增长明显低于Run-4实验和式(1);对Run-4实验(图 5(d)), 混合区演化成一对主控的涡核结构, 滑移线SL2内界面的演化对混合区影响较小, 无量纲后混合宽度H与式(1)较吻合.
3 结论本文利用高速纹影和激光片光散射的测试方法, 实验研究了绕柱激波波后滑移线导致的界面变形, 以及反射激波冲击变形界面的R-M不稳定性演化特征.实验结果表明: (1)激波在圆柱绕射对碰后, 激波波阵面存在两对三波点、两对弯曲反射波和两对波后滑移线结构, 这类激波冲击平面界面会引起界面的变形, 其中波后滑移线起主要作用; (2)滑移线与界面相交后, 交点无横向运动, 而界面仅在滑移线内部发生变形, 第2对滑移线内界面的变形同滑移线顶点和界面相对位置相关; (3)反射激波冲击下两对滑移线内变形界面产生的涡量方向相反, 对混合区宽度增长具有一定的抑制作用; (4)当第1对滑移线内界面产生的涡明显占优时, 混合区演化成一对主控涡, 第2对滑移线内界面产生较强涡时, 混合区演化成两对主控涡结构; (5)本文研究的反射激波冲击下的界面R-M不稳定性, 除了不同介质存在密度强间断, 在同种介质内滑移线两侧流体也存在密度弱间断, 反射激波冲击下界面产生的涡量和滑移线产生的涡量的相互作用需要借助高精度数值和PIV实验进行深入研究.
致谢: 感谢国家自然科学基金(11772309, 11472253), 科学挑战专题(TZ2016001), 冲击波物理与爆轰物理重点实验室基金(9140C670801150C67292)项目的资助.| [1] |
Walsh J M, Shreffler R G, Willig F J. Limiting conditions for jet formation in high velocity collisions[J]. Journal of Applied Physics, 1953, 24(3): 349-359. DOI:10.1063/1.1721278 |
| [2] |
Richtmyer R D. Taylor instability in shock acceleration of compressible fluids[J]. Communications on Pure and Applied Mathematics, 1960, 13(2): 297-319. DOI:10.1002/(ISSN)1097-0312 |
| [3] |
Meshkov E E. Instability of the interface of two gases accelerated by a shock wave[J]. Fluid Dynamics, 1969, 4(5): 101-104. |
| [4] |
罗喜胜, 翟志刚, 司廷, 等. 激波诱导下的气体界面不稳定性实验研究[J]. 力学进展, 2014, 44(1): 260-290. Luo X S, Zhai Z G, Si T, et al. Experimental study on the interfacial instability induced by shock waves[J]. Advances in Mechanics, 2014, 44(1): 260-290. (in Chinese) |
| [5] |
Collins B D, Jacobs J W. PLIF flow visualization and measurements of the Richtmyer Meshkov instability of an air/SF6 interface[J]. Journal of Fluid Mechanics, 2002, 464(1): 113-136. |
| [6] |
刘金宏, 邹立勇, 柏劲松, 等. 激波冲击下air/SF6界面的Richtmyer-Meshkov不稳定性[J]. 爆炸与冲击, 2011, 31(2): 135-140. Liu J H, Zou L Y, Bai J S, et al. Richtmyer-Meshkov instability of shock-accelerated air/SF6 interfaces[J]. Explosion and Shock Waves, 2011, 31(2): 135-140. (in Chinese) |
| [7] |
McFarland J, Reilly D, Creel S, et al. Experimental investigation of the inclined interface Richtmyer-Meshkov instability before and after reshock[J]. Experiments in Fluids, 2014, 55(1): 1640. DOI:10.1007/s00348-013-1640-1 |
| [8] |
Reilly D, McFarland J, Mohaghar M, et al. The effects of initial conditions and circulation deposition on the inclined-interface reshocked Richtmyer-Meshkov instabili-ty[J]. Experiments in Fluids, 2015, 56: 168. DOI:10.1007/s00348-015-2035-2 |
| [9] |
刘金宏, 黄文斌, 谭多望, 等. 激波冲击下air/SF6斜界面不稳定性实验研究[J]. 实验流体力学, 2010, 24(6): 27-31. Liu J H, Huang W B, Tan D W, et al. Experimental study of instability of shock accelerated air/SF6 inclined interfaces[J]. Journal of Experiments in Fluid Mecha-nics, 2010, 24(6): 27-31. (in Chinese) |
| [10] |
Layes G, Jourdan G, Houas L. Distortion of a spherical gaseous interface accelerated by a plane shock wave[J]. Physical Review Letters, 2003, 91(17): 174502. DOI:10.1103/PhysRevLett.91.174502 |
| [11] |
Zhai Z G, Si T, Luo X S, et al. On the evolution of spherical gas interfaces accelerated by a planar shock wave[J]. Physics of Fluids, 2011, 23(8): 084104. DOI:10.1063/1.3623272 |
| [12] |
Zou L Y, Huang W B, Liu C L, et al. On the evolution of double shock-accelerated elliptic gas cylinders[J]. Journal of Fluid Engineering, 2014, 136(9): 091205. |
| [13] |
Shankar S K, Kawai S, Lele S K. Two-dimensional viscous flow simulation of a shock accelerated heavy gas cylinder[J]. Physics of Fluids, 2011, 23(2): 024102. DOI:10.1063/1.3553282 |
| [14] |
Glazer E, Sadot O, Hadjadj A, et al. Velocity scaling of a shock wave reflected off a circular cylinder[J]. Phy-sical Review E, 2011, 83(6): 066317. DOI:10.1103/PhysRevE.83.066317 |
| [15] |
Tsai I N, Huang J C, Tsai S S, et al. Unsteady relativistic shock-wave diffraction by cylinders and sph-eres[J]. Physical Review E, 2012, 85(2): 026317. DOI:10.1103/PhysRevE.85.026317 |
| [16] |
刘金宏, 邹立勇, 曹仁义, 等. 绕射激波和反射激波作用下N2/SF6界面R-M不稳定性实验研究[J]. 力学学报, 2014, 46(3): 475-479. Liu J H, Zou L Y, Cao R Y, et al. Experimentally study of the Richtmyer-Meshkov instability at N2/SF6 flat interfaces by diffracted incident shock waves and reshock[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 475-479. DOI:10.6052/0459-1879-13-355 (in Chinese) |
| [17] |
刘金宏, 邹立勇, 廖深飞, 等. 绕射激波和反射激波冲击下的Richtmyer-Meshkov不稳定性[J]. 中国科学:物理学力学天文学, 2014, 44(11): 1203-1212. Liu J H, Zou L Y, Liao S F, et al. The Richtmyer-Meshkov instability by diffracted incident shock waves and re-shock[J]. Scientia Sinica Physica:Mechanica & Astronomica, 2014, 44(11): 1203-1212. (in Chinese) |
| [18] |
Mikaelian K O. Turbulent mixing generated by Rayleigh-Taylor and Richtmyer-Meshkov instabilities[J]. Physica D:Nonlinear Phenomena, 1989, 36(3): 343-357. DOI:10.1016/0167-2789(89)90089-4 |
| [19] |
Ukai S, Balakrishnan K, Menon S. Growth rate predic-tions of single-and multi-mode Richtmyer-Meshkov instability with reshock[J]. Shock Waves, 2011, 21(6): 533-546. DOI:10.1007/s00193-011-0332-0 |
| [20] |
Rikanati A, Sadot O, Ben-Dor G, et al. Shock-wave Mach-reflection slip-stream instability:a secondary small-scale turbulent mixing phenomenon[J]. Physical Review Letters, 2006, 96(17): 174503. DOI:10.1103/PhysRevLett.96.174503 |
| [21] |
Jacobs J W, Sheeley J M. Experimental study of incompressible Richtmyer-Meshkov instability[J]. Physics of Fluids, 1996, 8(2): 405-415. DOI:10.1063/1.868794 |



