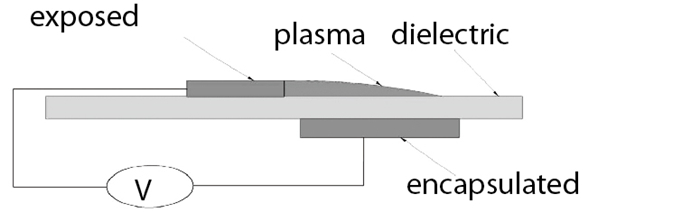
流动控制是流体力学的一个重要分支, 主要目的是改善物体受力状态, 进而获得改善升阻特性拓宽稳定工作范围等效果.介质阻挡放电(dielectric barrier discharge, DBD)[1]等离子体激励器进行分离流控制具有可靠性强无需移动部件尺寸小重量轻频带宽响应快等优势,是近年来流动控制研究的一个热点.如图 1所示, 等离子体激励器由两片电极和隔离它们的电介质层组成, 其进行流动控制的基本原理是等离子体在电磁场的作用下与飞行器绕流相互作用, 进行动量和能量转移, 改变边界层流场的结构和物理特性, 从而抑制边界层分离, 获得增升减阻等控制效果.近年来美俄等发达国家航空领域普遍关注DBD等离子体激励器, 开展了等离子体激励器流动分离控制边界层流动控制减弱气动噪声控制圆柱绕流流动分离等方面的研究[2-4].
|
| 图 1 等离子体激励器示意图 Fig.1 Schematic diagram of the plasma actuator |
动量效应是等离子体气动激励诱导流动的一个主要因素, 一般将等离子体气动激励等效成一个体积力源项来模拟其动量效应.目前常用的等离子体气动激励建模仿真方式有如下4种:基于唯相学描述的仿真方法基于集成电路模型描述的电特性仿真方法基于物理原理的耦合求解等离子体-流体方程组仿真方法粒子群-Monte Carlo模拟方法.
本文采用计算流体力学方法, 将等离子体对中性气体的作用模型化为体积力矢量, 求解带体积力源项的Navier-Stokes方程, 数值模拟多对等离子体激励器在NACA0015翼型过失速状态下的控制作用, 为等离子体激励的应用提供可靠的模拟方法.
1 等离子体激励器模型根据Suzen等[5]的分析方法, 可将电势Φ分为两部分:外加电场产生的电势
| $ \nabla \cdot \left( {{\varepsilon }_{\rm{r}}}\nabla \phi \right)=0. $ | (1) |
等离子体中电荷产生的诱导电势
| $ \nabla \cdot \left( {{\varepsilon }_{\rm{r}}}\nabla \varphi \right)=-{{\rho }_{\rm{c}}}/{{\varepsilon }_{0}}. $ | (2) |
其中,ρc为静电荷密度, ε0为真空介电常数, εr为相对介电常数.根据文献[5]
| $ \varphi =-{{\rho }_{\rm{c}}}\lambda _{\rm{d}}^{2}/{{\varepsilon }_{0}}. $ |
代入式(2) 可得到等离子体内电荷密度的方程:
| $ \nabla \cdot \left( {{\varepsilon }_{\rm{r}}}\nabla {{\rho }_{\rm{c}}} \right)={{\rho }_{\rm{c}}}/\lambda _{\rm{d}}^{2}. $ | (3) |
λd为Debye长度, 表征静电屏蔽尺度.
上述方程的计算域和边界条件如下:外加电势
| $ {{\rho }_{\rm{c}, \omega }}\left( x, t \right)=\rho _{\rm{c}}^{\max }G\left( x \right)f\left( t \right). $ |
| $ G\left( x \right)=\exp \left[-{{\left( x-\mu \right)}^{2}}/\left( 2{{\sigma }^{2}} \right) \right]. $ |
其中,位置参数μ为最大电荷密度位置, 取下电极最左端, 尺度参数σ=0.3.
等离子体产生的电场强度为
| $ \mathit{\boldsymbol{E}} = - \nabla \mathit{\Phi }. $ |
求解方程(1) 可得到外电势, 求解方程(3) 可得到等离子体的电荷密度.等离子体对流动的宏观作用可以等效为体积力, 表示为净电荷受到的电场力:
| $ {\mathit{\boldsymbol{f}}_{\rm{B}}} = {\rho _{\rm{c}}}\mathit{\boldsymbol{E}} = - {\rho _{\rm{c}}}\nabla \mathit{\Phi }. $ |
由此模型获得的体积力幅值与外加电压相关, 其变化周期与电源频率相关, 周期在10-4s量级, 而流动的响应时间为10-2s量级, 故认为计算中体积力的作用是定常的.
2 控制方程及数值方法流体运动遵循3个基本方程:连续方程动量方程能量方程.由于着眼于等离子体激励对流动的作用, 将等离子体产生的作用模型化为等价的作用于流体的体积力.二维情形控制方程可以表示为
| $ \frac{\partial }{\partial t}\iiint_{V}{\mathit{\boldsymbol{W}}\rm{d}\mathit{V}+\iint_\mathit{S}{\mathit{\boldsymbol{F}}}}=\mathit{\boldsymbol{Q}}. $ |
式中, V为以S为封闭边界的任意控制体, n为边界的外法向量, 流场状态变量W的表达式为
| $ \mathit{\boldsymbol{W}}={{\left( \rho, \rho u, \rho v, \rho E \right)}^{\rm{T}}}. $ |
源项矢量表示为
| $ \mathit{\boldsymbol{Q}}={{\left( 0, {{f}_{x}}, {{f}_{y}}, {{f}_{v}} \right)}^{\rm{T}}}. $ |
其中, F=(ƒx, ƒy)T为电场对等离子体作用的体积力, ƒv=ƒxu+ƒyv为体积力做功.
本文采用商用软件FLUENT求解定常Navier-Stokes方程, 在计算中, 等离子激励器所产生的作用被模型化为体积力, 通过FLUENT的用户自定义函数(UDF)定义为体积力源项加入到控制方程中.求解采用S-A湍流模型, 基于压力的SIMPLE格式, 扩散项采用2阶差分格式, 对流项采用2阶迎风格式, 离散后得到的代数方程组采用Gauss-Seidel迭代方法求解, 求解方程的收敛准则为连续方程无量纲残差小于10-5, 其他方程的残差小于10-3.
3 等离子体激励平板射流DBD激励器参数如下:上电极宽度1mm, 下电极宽度2mm, 上下电极水平方向间距1.5mm, 下电极埋深0.2mm, 电极厚度0.03mm.空气的相对介电常数εr1=1.0, 绝缘材料相对介电常数为εr2=1.0. Debye长度为0.001m, 电荷密度最大值为
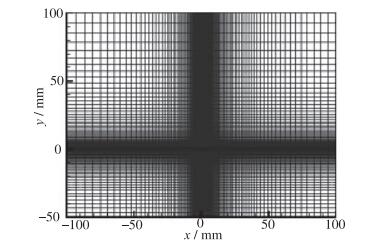
|
| 图 2 平板计算网格 Fig.2 Grids for the flat plate |
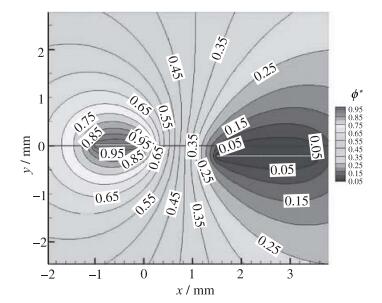
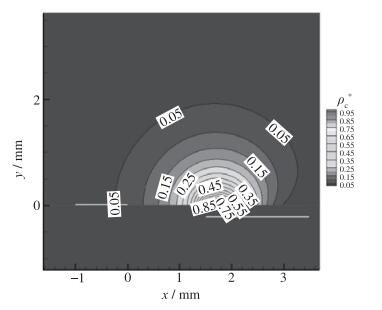
图 3和图 4为等离子体激励器上下电极附近无量纲电势分布和电荷密度分布.可以看出上下电极间隙处电势变化较为剧烈, 电势梯度较大.电荷集中分布在下电极上方和上下电极间隙处, 下电极上方电荷密度最大, 向外逐渐减少.
|
| 图 3 平板等离子体激励电势分布 Fig.3 Electric potential of flat plate under plasma actuation |
|
| 图 4 平板等离子体激励电荷密度分布 Fig.4 Charge density distributions around flat plate under plasma actuation |
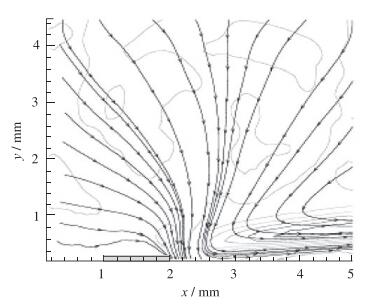
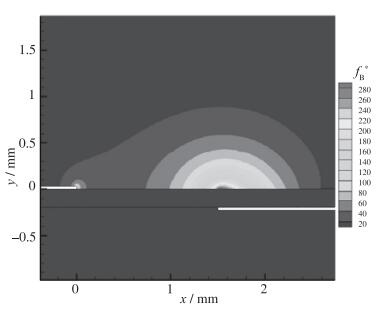
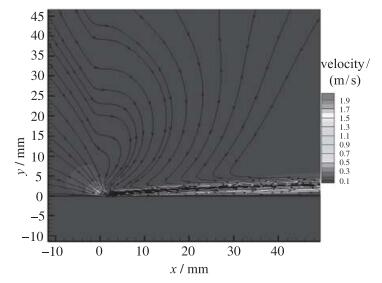
图 5为求解电势方程和电荷密度方程得到的等离子体激励器附近无量纲体积力分布, 将其引入流动控制方程求解.来流条件为静止大气, 一个标准大气压. 图 6为计算获得的等离子体激励器诱导的平板射流, 约在x=5mm处诱导速度最大, 其值约为1.9m/s. 图 7为文献[8]中实验测得DBD等离子体气动激励诱导的平板壁面射流, 实验测得在x=4mm处诱导速度最大, 其值约为2m/s.由此可见该体积力模型可被用于进行相关的DBD等离子体激励器的数值模拟.
|
| 图 5 等离子体激励的无量纲体积力分布 Fig.5 Dimensionless body force contours of plasma actuation |
|
| 图 6 等离子体激励的平板上方诱导流场 Fig.6 Induced flow field over flat plate under plasma actuationx |
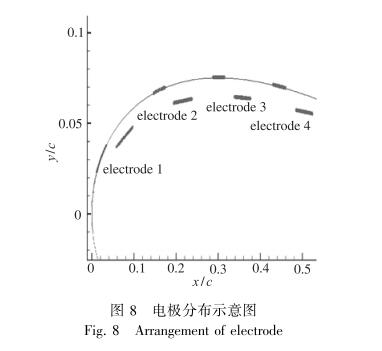
选取NACA0015翼型作为研究对象进行计算分析.在翼型上表面布置4对电极(如图 8所示)来研究等离子激励器对翼型绕流的作用.上电极宽度为3mm, 下电极宽度为4mm, 上下电极流向间距为2mm, 下电极上边缘与翼型表面距离为1mm, 上下电极厚度均为0.04mm, 每对电极之间的距离为5mm.
|
| 图 8 电极分布示意图 Fig.8 Arrangement of electrode |
由于在翼型上表面粘贴了电极, 它在效果上相当于一个粗糙带, 因而可能会对流动产生一些附加影响.为了排除粗糙带效应, 需要对干净翼面和粗糙翼面的流动进行比较分析.
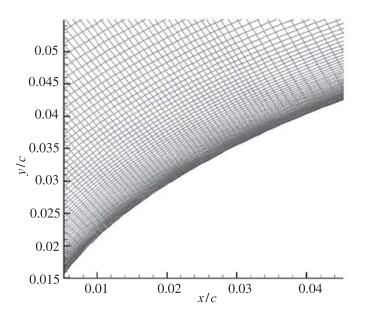
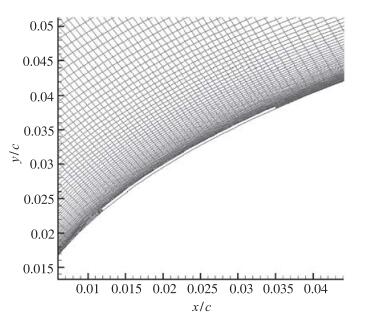
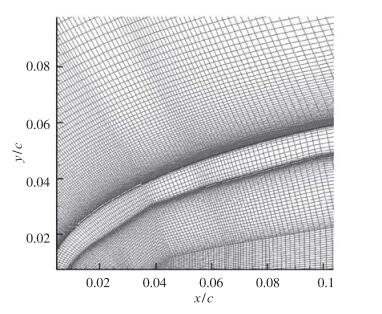
对于干净翼面的外流场计算, 网格采用C型拓扑, 远场边界距翼面为20倍弦长, 网格点数为906×181.对于贴有电极的粗糙翼面, 则需在电极侧面区域另辟一块薄层网格. 图 9、图 10给出了干净翼面与粗糙翼面上电极附近的网格.由于外电势需要在整个计算域(翼型内外)求解, 翼型内同样需要生成网格. 图 11为翼型前半段内外计算网格, 图 12为翼型前缘电极附近网格图, 在电极附近网格进行了加密.
|
| 图 9 干净翼面局部网格 Fig.9 Local grids of clean airfoil |
|
| 图 10 粗糙翼面电极附近网格 Fig.10 Local grids of rough airfoil |

|
| 图 11 计算域翼型附近网格 Fig.11 Grids nearby airfoil |
|
| 图 12 计算域电极附近网格 Fig.12 Grids nearby electrode inside and outside airfoil |
选取等离子体外加激励为正弦交流电, 电压峰峰值Vp-p=20kV, 电荷密度最大值为
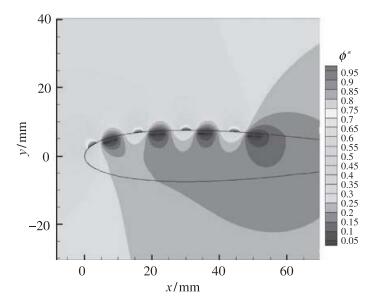
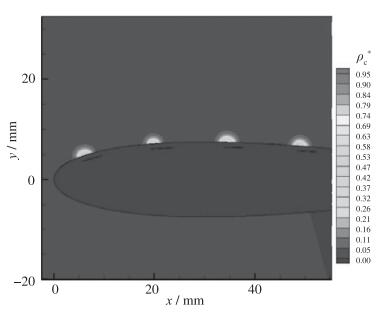
图 13给出了计算获得的静止大气中的电势无量纲分布图. 4组激励器为并联关系, 对于同一组激励器, 电场强度从上电极的高电势指向下电极的低电势, 电极间隙附近, 电势梯度较大.电荷密度方程在空气区域求解, 图 14给出了4组电极附近的电荷密度无量纲分布, 翼型表面对应下电极区域电荷密度呈Gauss分布.
|
| 图 13 翼型内外电势分布 Fig.13 Contours of electric potential inside and outside airfoil |
|
| 图 14 翼型外的电荷密度分布 Fig.14 Charge density contours outside airfoil |
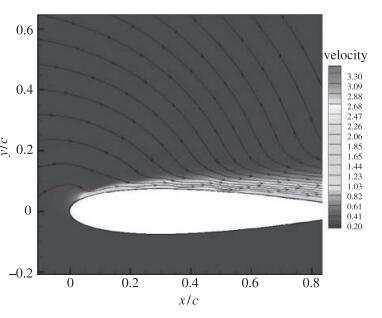
首先研究在来流速度为零的静止大气中等离子体激励对翼型周围空气的激励作用.翼型弦长取为0.1m. 图 15为基准激励强度下等离子体激励的速度分布, 可以看出由于多条电极蠕动加速效果, 射流的最大速度位置在最后一对电极下电极上方, 最大速度约为3.4m/s.
|
| 图 15 翼型表面等离子体诱导流动 Fig.15 Flow field induced by plasma actuation near airfoil surface |
对于有来流的情形, 取翼型弦长为0.1m, 来流速度V∞=17.4m/s, 基于弦长的Reynolds数为Re=1.2×105, 迎角取为α=17°. 表 1给出了计算获得干净翼面和粗糙翼面以及激励后的翼型升力阻力系数.可以看出, 电极导致的粗糙带影响使翼型升力略低于干净翼型, 对阻力影响很小.基准激励后翼型升力系数增加26%, 阻力系数减小11%, 5倍激励强度下升力系数增加76%, 阻力系数减小41%.由此可见等离子体激励有增升减阻的效果.等离子体激励器的强度对升阻系数有重要影响.
| 下载CSV 表 1 激励前后翼型升力系数和阻力系数 Tab.1 Lift and drag coefficients of airfoil with and without plasma actuation |
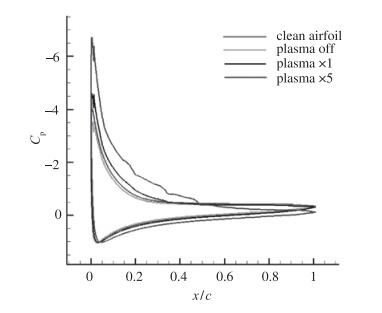
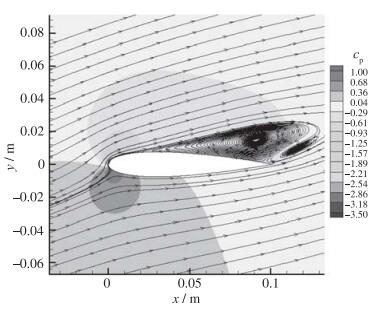
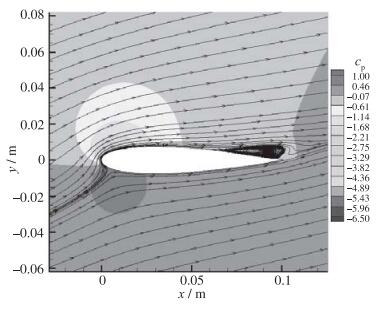
图 16为计算获得的干净翼面和粗糙翼面以及激励后的翼面压力分布, 可以看出, 干净翼面和粗糙翼面压力分布基本相同, 电极粗糙带效果仅仅使上翼面吸力峰有所下降, 而等离子体激励使压力分布曲线有显著变化, 尤其是5倍基准强度的情形, 上翼面负压大面积增大, 前缘负压峰值显著提高. 图 17和图 18为无激励和5倍基准强度激励下的流场图谱, 由图可见激励后翼型流动分离推迟, 分离区减小, 5倍基准激励强度下, 翼型分离点从18%弦长处推迟至60%弦长处.可见等离子体激励对流动分离有控制作用, 同时等离子体激励强度越大, 对流动分离的抑制作用越明显.
|
| 图 16 激励前后翼型表面压力分布 Fig.16 Pressure distributions over airfoil surface with and without actuation |
|
| 图 17 无激励流场 Fig.17 Flow field without plasma actuation |
|
| 图 18 5倍基准激励强度流场 Fig.18 Flow field with actuation of five-time baseline intensity |
等离子体激励器在翼型上表面产生的物面射流为分离区的气体注入动量, 从而对气流产生加速效果, 增加了其抵抗逆压梯度的能力, 从而抑制了流动分离.随着激励强度的增加, 这种加速效果越发明显, 流动分离得到明显的控制.
5 结论本文求解带源项的N-S方程, 数值模拟了等离子体激励器诱导静止大气中平板上的射流NACA0015翼型上的射流, 及等离子体激励对NACA0015翼型分离流的控制作用.计算分析表明, 多条电极等离子体激励器可有效控制NACA0015翼型大迎角分离流动, 可以得到增升减阻的效果.激励强度越大, 流动分离控制效果越好.考虑到增大电压从而增大激励强度所需的成本, 实际采用等离子体激励控制时应该根据实际需要适当地选择激励强度.
| [1] |
Roth J R, Sherman D M, Wilkinson S P. Boundary layer flow control with a one atmosphere uniform glow discharge surface plasma[R]. AIAA 1998-0328, 1998.
|
| [2] |
孙宗祥. 等离子体减阻技术的研究进展[J]. 力学进展, 2003, 33(1): 87-94. Sun Z X. Research progress of plasma drag reduction technology[J]. Advances in Mechanics, 2003, 33(1): 87-94. DOI:10.6052/1000-0992-2003-1-J2001-095 (in Chinese) |
| [3] |
李应红, 吴云, 宋慧敏, 等. 大气压等离子体流动控制实验[J]. 空军工程大学学报(自然科学版), 2006, 7(3): 1-3. Li Y H, Wu Y, Song H M, et al. Atmospheric pressure plasma flow control experiment[J]. Journal of Air Force Engineering University (Natural Science Edition), 2006, 7(3): 1-3. (in Chinese) |
| [4] |
刘万刚, 李一滨. 应用等离子体实现主动流动控制的实验研究[J]. 弹箭与制导学报, 2006, 26(2): 110-111. Liu W G, Li Y B. Plasma is applied to implement active flow control experimental study[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(2): 110-111. (in Chinese) |
| [5] |
Suzen Y B, Huang P G, Jacob J D. Numerical simulations of plasma based flow control applications[R]. AIAA 2005-4633, 2005.
|
| [6] |
Enloe C L, McLaughlin T E, VanDyken R D, et al. Plasma structure in the aerodynamic plasma actuator[R]. AIAA, 2004-844, 2004.
|
| [7] |
张来平, 赫新, 常兴华, 等. 复杂外型静动态混合网格生成技术研究新进展[J]. 气体物理, 2016, 1(1): 42-61. Zhang L P, He X, Chang X H, et al. Recent progress of static and dynamic hybird grid generation techniques over complex geometries[J]. Physics of Gases, 2016, 1(1). (in Chinese) |
| [8] |
Suzen Y B, Huang P G. Simulations of flow separation control using plasma actuators[R]. AIAA 2006-877, 2006.
|