大型飞机具有大展弦比结构和轻质特性, 导致其气动/结构间的耦合效应显著增强.这种耦合效应对飞机的性能有重要影响, 必须进行CFD/CSD耦合计算.一方面, 机翼是为飞机提供升力的主要气动部件, 除了要满足全机的升力要求外, 还应保证阻力尽量小.机翼的升阻力特性主要受其气动外形影响, 结构变形引起的机翼气动外形的改变将显著影响机翼的升阻力特性.另一方面, 机体结构在气动载荷作用下发生变形, 导致操纵面安定面位置的变化, 从而引起全机操纵性和稳定性的改变.基于上述原因, 大型飞机设计过程需要优化设计结构的刚度, 保证气动结构的耦合效应不会引起飞机性能的恶化.但是直接调用CFD/CSD耦合分析方法将使优化设计的计算量及优化时间大幅度增加.
随着现代飞行器日益复杂, 优化设计及多学科优化设计逐渐成为航空航天领域的研究热点[1-5], 能够近似表达真实函数的代理模型方法逐渐得到重视, 并成为优化设计研究的关键技术[6-8].如今, 代理优化方法逐渐发展成为和传统的梯度优化方法无梯度优化方法具有相同功能的通用优化算法[9], 并成功应用于不同领域工程问题的优化设计.
近年来, Kriging模型已广泛应用于气动优化设计中.国外在运用Kriging模型进行气动优化设计方面已有大量研究. Jeong等[10]发展了一种结合Kriging模型和遗传算法的气动优化算法, 进行了二维翼型设计和多段翼型襟翼位置的优化设计. Kanazaki等[11]利用Kriging模型进行了多段翼型缝道参数的多目标优化设计.国内夏露等[12]将Kriging自适应代理模型与优化算法结合应用到翼型减阻优化问题中.许瑞飞等[13]将改进的Kriging代理模型应用于RAE2822翼型的减阻优化设计中.苏伟等[14]将Kriging模型与遗传算法相结合, 建立了一种代理遗传算法.
从目前已有文献看出, 对Kriging模型的应用多集中在气动外形优化设计中.本文基于Kriging代理模型结合改进的粒子群算法建立了序列优化算法, 以RAE2822翼型优化标准算例[15]验证本文的序列优化算法, 并对大型飞机巡航状态下的全机结构弯曲刚度和扭转刚度进行了优化设计.
1 Kriging代理优化方法 1.1 Kriging方法Kriging方法是一种半参数化的插值技术, 包含了回归部分和非参数部分, 其中非参数部分是对随机分布的描述. Kriging方法预测某一点时, 通过最小化预测值的误差方差对该点周围信息加权处理.因此, Kriging方法通常可以视为最优线性无偏估计.通常Kriging方法可以写为如下形式[16]
| $y(\boldsymbol{x}) = F(\boldsymbol{\beta }, \boldsymbol{x}) + z(\boldsymbol{x}) = {\boldsymbol{f}^{\rm{T}}}(\boldsymbol{x}) \cdot \boldsymbol{\beta } + z(\boldsymbol{x})$ |
其中, F(β, x)为Kriging方法的回归项, 以多项式的形式在设计空间中提供全局近似, β为多项式的回归系数; z(x)为Kriging方法的非参数部分, 是服从正态分布N(0, σ2)的随机过程, 其协方差为
| ${\rm{Cov}}[z\left( {{\boldsymbol{x}_i}} \right), z\left( {{\boldsymbol{x}_j}} \right)] = {\sigma ^2}\left[{{R_{ij}}\left( {\boldsymbol{\theta }, {\boldsymbol{x}_i}, {\boldsymbol{x}_j}} \right)} \right]$ |
其中, Rij(θ, xi, xj)为关于训练样点xi和xj的相关函数, θ为相关函数的参数.相关函数R与样本点的空间相对位置有关, 其具体形式为
| $\boldsymbol{R}(\boldsymbol{\theta }, {\boldsymbol{x}_i}, {\boldsymbol{x}_j}) = \prod\limits_{k = 1}^n {{R_k}\left( {{\theta _k}, {d_k}} \right)}, {d_k} = \left| {x_i^k-x_j^k} \right|$ |
其中, n为设计空间的维数, xik和xjk分别为样本点xi和xj的第k个分量.相关函数Rk(θk, dk)有多种形式, 本文采用Gauss函数,即
| ${R_k}({\theta _k}, {d_k}) = {\rm{exp}}(-{\theta _k}d_k^2)$ |
作为相关函数的核函数. Kriging模型非参数部分的方差σ2和相关函数中的参数θ可以通过最大似然估计方法求出.
1.2 取样方法设计空间内的样本信息是构建代理模型的基础.分布均匀的样本点不仅能够更全面地提供设计空间的信息, 也能避免因样本不均匀引起代理模型精度降低的问题.常用的取样方法有Sobol取样方法均匀设计方法(uniform design, UD). Latin超立方取样方法(Latin hypercube sampling, LHS)和本文采用的改进的Latin超立法取样方法(improved Latin hypercube sampling, ILHS).
针对LHS方法存在设计空间中分布的均匀性不稳定问题, 研究人员提出了一些改进方法, 其中以实现样本间最优距离为目标的ILHS方法[17]能够更好地保证样本点在设计空间中分布的均匀性.
对于n维设计空间中取样规模为n0的问题来说, 设计空间的体积为n0n, 平均每个样本占据的超立方体空间的体积为n0n/n0, 因此设计空间中两个样本点间的平均距离应该是超立方体的边长
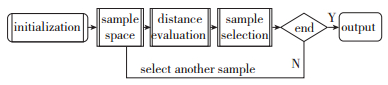
|
| 图 1 ILHS方法取样流程 Fig.1 Flow chart of ILHS |
当已经选择了l个样本点以后, 下一个样本点的位置大约有(n0-l)n种可能, 遍历这些样本点需要花费大量的时间, 这成为影响ILHS方法计算效率的主要原因.为提高ILHS方法的计算效率, 实际操作中可以将每一维度的样本点可能位置(n0-l)重复p次, 用缩减的子空间S1替代子空间S0.当重复次数p达到一定数值时, 缩减后的子空间S1也足够反映新样本点的基本特征.
1.3 粒子群优化算法(particle swarm optimization, PSO)初始的粒子群算法需要根据问题的不同, 对粒子飞行过程的参数设定不同的取值; 同时需要对粒子的飞行速度加以限制, 才能避免经过若干次迭代后粒子速度急剧增大到不合理的水平.
通过对粒子群算法迭代过程的深入研究, Clerc等[18]将收缩因子引入初始粒子群算法中, 通过收缩因子控制优化过程中粒子的飞行速度.引入收缩因子的粒子群算法有不同的形式, 其中比较简洁的形式为
| $\begin{array}{c} v_i^{k + 1} = \chi \left[{v_i^k + {\eta _1}\left( {p_i^k-x_i^k} \right) + {\eta _2}\left( {g_i^k-x_i^k} \right)} \right]\\ x_i^{k + 1} = x_i^k + v_i^{k + 1}\\ \chi = \frac{2}{{\left| {(\eta -2) -\sqrt {{\eta ^2} -4\eta } } \right|}} \end{array}$ |
其中, vik表示第i个粒子在第k次迭代时的速度, pik为当前粒子所经过的最优位置, gk表示所有粒子的历史最好位置; η1和η2为区间[0, ϕ]内均匀分布的伪随机数, η=η1+η2, 此处取η1=η2=2.05.飞行速度表达式右端的3项分别表示粒子的飞行惯性自我认知和社会经验.
改进后的粒子群算法能够提高粒子群算法的收敛性, 是当前粒子群算法的主流版本.
1.4 优化加点准则代理模型在样本点比较集中的区域具有较高的精度, 能够较为准确地预测目标函数; 在样本点少的地方, 模型的预测精度较低.因此, 当Kriging模型建立后, 在优化设计中采用该模型可能无法找到问题的全局最优, 这是由于建立的代理模型在预测点附近本身存在不确定性, 如果Kriging模型精度很低, 则会给优化设计带来很大误差.因此为了在优化设计中提高模型的预测精度, 可以通过保证目标函数预测值的不确定性最小的方法提高代理模型的预测精度, 这里采用EI(expected improvement)函数以加强样本点在非线性区域的分布.
该方法是一种同时考虑预测均值和预测不确定性的加点准则:以最小化的优化问题为例, 相对于当前已有样本点的最小值ymin, 在设计点x处的响应值的提高I(x)=max[ymin-ŷ(x), 0]也服从正态分布, 其期望为
| $E\left[{I\left( \mathit{\boldsymbol{x}} \right)} \right] = \left\{ {\begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;, \;\;\;\;\sigma \left( \mathit{\boldsymbol{x}} \right) = 0\;}\\ {\left[{{y_{\min }}-\hat y\left( \mathit{\boldsymbol{x}} \right)} \right]\mathit{\Phi }\left[{\frac{{{y_{\min }}-\hat y\left( \mathit{\boldsymbol{x}} \right)}}{{\sigma \left( \mathit{\boldsymbol{x}} \right)}}} \right] + \sigma \left( \mathit{\boldsymbol{x}} \right)\phi \left[{\frac{{{y_{\min }}-\hat y\left( \mathit{\boldsymbol{x}} \right)}}{{\sigma \left( \mathit{\boldsymbol{x}} \right)}}} \right]\;\;\;\;\;, \;\;\;\;\sigma \left( \mathit{\boldsymbol{x}} \right) > 0} \end{array}} \right.$ |
其中, Φ和ϕ分别表示标准正态分布的累计分布函数和概率密度函数.
根据上式, 在响应值提高I(x)较大或者预测不确定性σ(x)较大的位置, 预测值提高I(x)的期望E[I(x)]就越大, 设计空间中E[I(x)]最大的点就是新的训练样本点. EI准则表达式的两项分别反映优化方法的局部搜索能力和全局搜索能力, 过多的全局搜索将减低优化算法的收敛速度.可以引入权重函数调节全局搜索和局部搜索的程度, 使优化算法能够兼顾全局和局部的搜索能力, 即
| $E\left[{I\left( \mathit{\boldsymbol{x}} \right)} \right] = \left\{ {\begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;, \;\;\;\sigma \left( \mathit{\boldsymbol{x}} \right) = 0\;}\\ {\omega \left[{{y_{\min }}-\hat y\left( \mathit{\boldsymbol{x}} \right)} \right]\mathit{\Phi }\left[{\frac{{{y_{\min }}-\hat y\left( \mathit{\boldsymbol{x}} \right)}}{{\sigma \left( \mathit{\boldsymbol{x}} \right)}}} \right] + \left( {1 - \omega } \right)\sigma \left( \mathit{\boldsymbol{x}} \right)\phi \left[{\frac{{{y_{\min }}-\hat y\left( \mathit{\boldsymbol{x}} \right)}}{{\sigma \left( \mathit{\boldsymbol{x}} \right)}}} \right]\;\;, \;\;\;\sigma \left( \mathit{\boldsymbol{x}} \right) > 0} \end{array}} \right.$ |
其中, ω为条件算法搜索能力的权函数, ω越大算法的局部搜索能力越强.
使用该方法进行样本添加的终止条件为
| $\max \left\{ {E\left[{I\left( {\rm{x}} \right)} \right]} \right\} \le \varepsilon $ |
当代理模型给出预测值的期望的提高量小于某个阈值时停止.
2 气动优化设计方法的验证2015年AIAA应用空气动力学专委会给出了4个气动优化设计的标准算例, 本文以基于Kriging模型的代理优化算法优化其中第2个算例.此算例的原始外形为RAE2822翼型, 以降低跨声速飞行阻力为优化目标(Cd最小), 同时考虑升力俯仰力矩和机翼面积的约束(升力CL=0.824, 俯仰力矩Cm≥=-0.1, 机翼面积大于基准翼型面积).整个优化问题可以描述为:
| $\begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\min \;{C_{\rm{d}}}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{C_{\rm{L}}} = 0.824}\\ {\;\;\;\;\;\;{C_{\rm{m}}} \ge-0.100}\\ {\;\;\;\;\;\;A > {A_{{\rm{baseline}}}}} \end{array}$ |
为了便于使用三维CFD程序分析翼型的气动特性, 将翼型的网格沿展向延拓为三维网格.基准外形物面附近的对称面网格分布情况如图 2所示, 翼型周向共有305个网格点, 物面法向网格共有65层, 首层网格高度为1×10-5c, 总的网格量大约为5 × 104.飞行状态为M=0.734, Re=6.5×106, 升力系数CL=0.824时对应的攻角为α=2.693°, 阻力系数CD=0.0188.
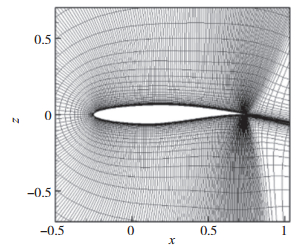
|
| 图 2 基准状态物面附近网格分布情况 Fig.2 Grid distribution around baseline shape |
利用自由变形方法(free form deformation, FFD)方法作为翼型的参数化方法, 翼型周围控制体及控制点的位置分布如图 3所示.控制体上展向有两层共28个控制点, 翼型前后缘位置对应的4个控制点为固定控制点, 展向的两层控制点同步变形, 因此独立的设计变量共有10个.改变设计变量的位置给出不同的物面形状, 通过径向基函数(radial basis function, RBF)网格变形方法得到相应的空间网格.
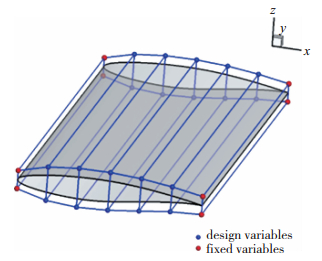
|
| 图 3 FFD控制体及设计变量的位置分布 Fig.3 Distribution of FFD control volume and design variables |
利用ILHS方法在设计空间内选取60个训练样本, 并计算得到样本点的升阻力及俯仰力矩.以训练样本作为初始样本集, 利用Kriging方法建立目标函数的代理模型.序列优化方法的加点采用EI加点准则, 以静态罚函数方法作为约束处理方法, 利用粒子群优化算法PSO方法训练目标函数的代理模型.每次寻优过程PSO种群规模为1500, 更新代数为150. 图 4给出了优化过程中阻力系数的收敛过程, 经过200次左右的加点, 最小阻力系数基本保持不变.
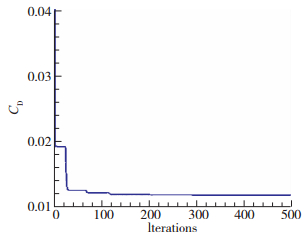
|
| 图 4 优化过程阻力系数收敛曲线 Fig.4 Convergence curve of drag coefficient during optimization |
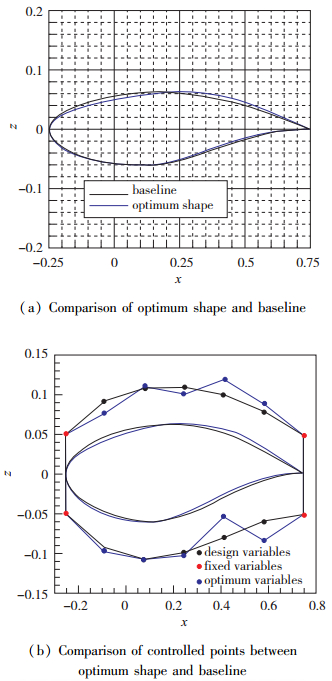
优化后的翼型与对应控制点的变化如图 5所示.优化结果计算得到的阻力系数CD=0.0115, 升力系数CL=0.8237, 俯仰力矩系数Cm=-0.0951, 优化翼型的截面面积为0.0779, 与基准外形的截面面积相同.与基准外形相比, 优化后的翼型阻力系数下降39%, 升力系数和力矩系数满足约束条件.与基准外形相比, 优化外形的上表面形状发生了较大变化.
|
| 图 5 优化后外形及对应控制点位置变化 Fig.5 Comparisons of shape and controlled points positions between baseline and optimum shape |
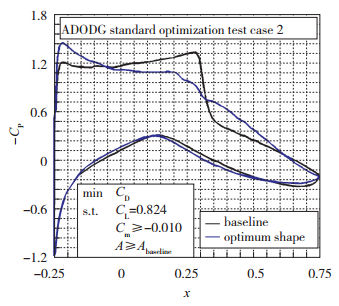
优化前后翼型表面压力的分布情况见图 6, 优化前后翼型下表面的压力分布变化不大, 主要变化发生在翼型上表面:优化后外形激波强度大大减弱, 降低了飞行时的激波阻力; 优化后的外形前缘吸力峰值大幅增加, 弥补了激波强度减弱引起的升力损失.
|
| 图 6 优化前后表面压力分布的比较 Fig.6 Comparison of surface pressure between baseline and optimum shape |
优化后的翼型弯度和厚度都有所减小, 翼型上表面的激波强度减弱, 大幅降低了跨声速飞行的激波阻力.通过对翼型的优化验证表明, 本文基于Kriging模型的序列优化算法具有较强的寻优能力, 能够处理带有多约束的优化设计问题.
3 大型飞机结构刚度优化设计 3.1 问题的描述大型飞机的气动/结构间存在明显的耦合效应, 这种耦合效应对飞机的性能有重要的影响.一方面, 机翼是为飞机提供升力的主要气动部件, 除了要满足全机的升力要求外, 还应保证阻力尽量小.机翼的升阻力特性主要受机翼的气动外形影响, 结构变形引起的机翼气动外形的改变将显著影响机翼的升阻力特性.另一方面, 机体结构在气动载荷作用下发生变形, 导致操纵面安定面位置的变化, 从而引起全机操纵性和稳定性的改变.由于上述原因, 大型飞机设计过程需要合理控制结构的刚度, 保证气动结构的耦合效应不会引起飞机性能的恶化.
本文对大型飞机巡航状态下的全机结构弯曲刚度和扭转刚度进行了优化设计, 使优化后的结构在气动载荷的作用下产生变形时, 尽量减小飞机的飞行阻力, 同时保证结构变形不会导致全机升力系数的降低及纵向静稳定性的恶化.
飞机巡航状态为H=1.05×104 m, 飞行Mach数M=0.85, Reynolds数Re=5.53×107, 来流攻角为α=1.94°.设计优化问题可以描述为
| $\begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\min \;\;{C_{\rm{D}}}}\\ {s.t.\;\;\;{C_{\rm{L}}} \ge 0.4101}\\ {\;\;\;\;\;\;\;{x_{\rm{f}}} \ge 0.479} \end{array}$ |
其中, xf为优化后的机体结构达到静平衡后的全机焦点位置.
3.2 初始样本的设计优化的设计变量为飞机结构的弹性模量和剪切模量, 原始结构的弹性模量和剪切模量分别为E0=7.00×107 Pa, G0=2.69×107 Pa.优化过程中弹性模型和剪切模量上下浮动的变化范围为50%.
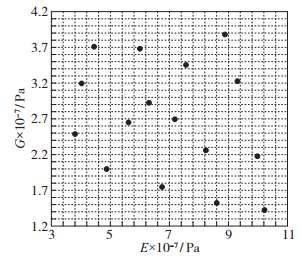
利用改进ILHS方法在设计空间内选择16个点作为刚度优化的初始样本, 初始样本在设计空间的分布如图 7所示, 16个样本点相对均匀地分布在整个二维设计空间.
|
| 图 7 ILHS方法选择的初始样本点分布 Fig.7 Distributions of initial samples selected by ILHS |
利用CFD/CSD耦合分析方法计算初始样本点的气动特性, 得到了这些样本点的升力系数阻力系数及全机焦点相对位置等气动特性, 初始样本点的气动数据如表 1所示.
| 下载CSV 表 1 初始样本的气动特性 Tab.1 Aerodynamic characteristics of initial samples |
利用初始样本点的数据建立Kriging代理模型, 用本文的序列优化方法对问题进行优化.优化过程中加点准则选择EI准则, 用静态罚函数方法处理优化问题的约束.粒子群方法种群规模为200, 优化代数为300.
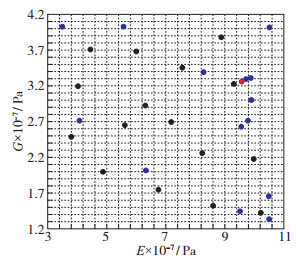
经过19次加点, 最终得到优化后的满足优化设计要求的结构刚度. 图 8给出了设计空间中样本点的最终分布情况.其中黑色的是ILHS方法选择的初始样本点, 蓝色的是序列优化方法通过EI准则添加的样本点, 红色的是最优解对应的样本点.在优化加点的初始阶段, EI方法选取的样本点大多分布在设计空间边界附近, 随着迭代次数的增多, EI准则的样本点逐渐逼近最优解的位置.
|
| 图 8 序列优化的加点后的样本点分布 Fig.8 Distribution of samples after adding samples with optimization algorithm |
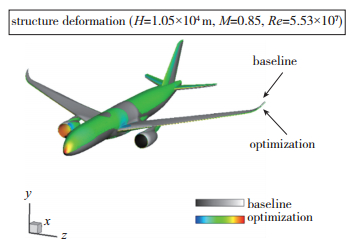
优化后的结构弹性模量和剪切模量分别为E=9.58×107 Pa, G=3.28×107 Pa, 与基准方案相比分别提高了36.8%和45.3%, 优化后的方案提高了结构的弹性模量和扭转模量. 图 9给出了优化前后巡航状态静平衡位置的比较, 优化方案的机翼和后机身的结构变形都小于基准方案的结构变形. 表 2给出了优化前后全机气动特性对比.
|
| 图 9 最优方案和基准方案结构变形情况 Fig.9 Comparison of deformation between baseline and optimization |
| 下载CSV 表 2 优化前后全机气动特性的比较 Tab.2 Comparison of aerodynamic characteristics between baseline and optimization |
由表 2可知, 优化后结构达到静平衡状态时, 全机阻力系数降低了2.7%左右, 焦点向后移动了约7%CA的距离, 进一步提高了全机的纵向静稳定域度, 其中CA代表平均气动弦长.
机翼是为飞机提供升力的关键气动部件, 在气动载荷的作用下机翼的弹性结构发生弯曲和扭转.机翼在气动载荷作用下通常发生负扭转, 引起机翼有效攻角的减小, 从而降低机翼上产生的升力; 此外, 气动载荷引起机翼上弯, 引起机翼上反角的变化, 这也会影响机翼的升阻力特性.
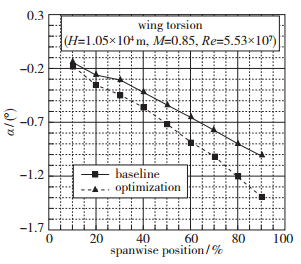
机翼变形不大的情况下, 机翼气动载荷的变化主要受扭转变形引起的有效攻角影响.基准方案和优化方案机翼各截面扭转角变化如图 10所示, 优化方案增大了机翼的弹性模量和扭转模量, 提高了结构的抗弯抗扭刚度, 减小了机翼的弯曲和扭转变形.基准方案在90%展长的截面相对刚性外形产生-1.40°的扭转角, 而优化方案同样位置的截面扭转角为-1.01°, 有效攻角大约提高了0.30°.
|
| 图 10 优化前后机翼截面扭转角的比较 Fig.10 Twist angles comparisons between baseline and optimization |
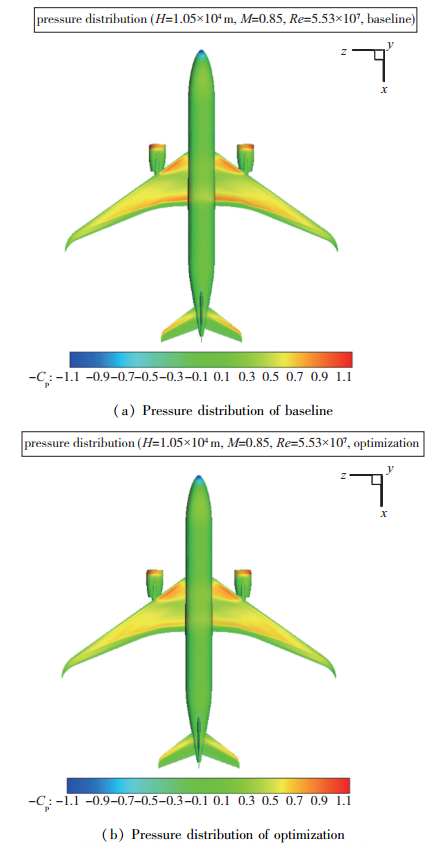
优化前后机翼上表面的压力系数分布情况如图 11所示.两种方案上表面压力系数的分布形态相似:在机翼后缘附近有一道强度较弱的激波, 其强度在展长方向由内向外逐渐减弱; 在发动机短舱与机身间的机翼内段的前缘附近也有一道激波, 优化方案波前低压区范围比基准方案有所增加.
|
| 图 11 优化前后飞机表面压力系数分布情况 Fig.11 Distributions of aircraft surface pressure between baseline and optimization |
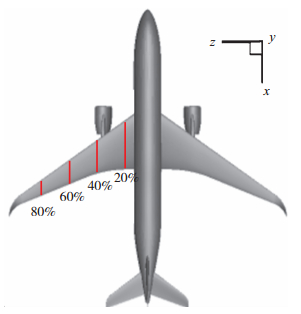
为了进一步比较优化前后两种方案机翼气动载荷的变化情况, 在机翼展向选取了4个不同的站位, 比较变形后两种方案不同站位上压力系数的分布情况.这4个站位分别位于机翼半展长20%,40%,60%和80%的位置上, 站位在机翼上的具体位置如图 12所示.
|
| 图 12 机翼不同站位的位置分布示意图 Fig.12 Wing section positions along span |
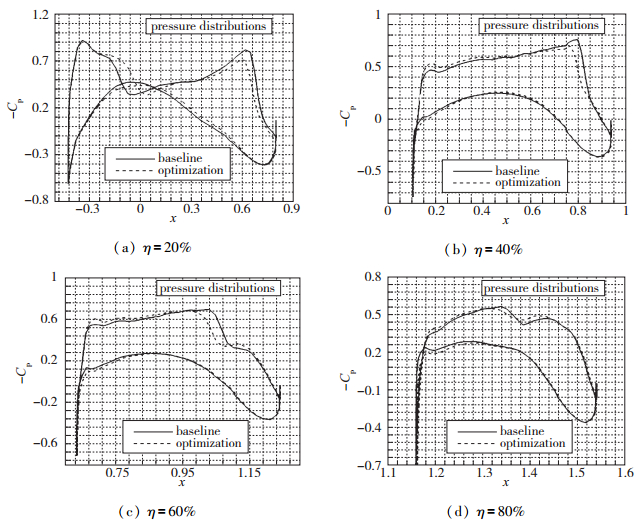
图 13中给出了优化前后不同位置的截面压力系数分布情况, 从中能够更清楚地看出优化前后机翼上气动载荷的变化情况.在展长20%的截面上, 机翼前缘附近的激波向后移动6%CA, 增大了前缘附近低压区的范围, 后缘附近的激波强度有所减弱; 在展长40%的站位上, 前缘附近的激波消失, 优化方案后缘的激波强度有所减弱, 激波位置略微向前移动; 在展长60%的站位上, 压力系数呈现出典型的超临界翼型的特点, 机翼中间靠后的位置和后缘各有一道激波, 两道激波前各有一段相对平坦的压力平台, 与基准方案相比, 优化方案的第1道激波大约向前移动4%CA, 波前压力平台的吸力也略有增加.在展长80%的站位上, 机翼上激波强度大大降低.
|
| 图 13 优化前后机翼截面压力系数分布 Fig.13 Distributions of wing section pressures |
本文通过ILHS取样方法, 提高设计样本在设计空间中分布的均匀性及取样结果的稳定性, 对用改进的粒子群方法作为寻优方法, 利用最大化期望提高准则(EI)作为序列优化算法的加点准则, 基于Kriging代理模型进行全机结构刚度的优化设计, 得到以下结论:
(1) 本文采用基于Kriging模型的序列优化方法, 利用气动优化设计的标准算例进行了验证, 表明该方法能够处理复杂目标函数的全局优化问题.
(2) 对大型飞机的结构刚度进行了优化, 结构弹性模量和剪切模量分别提高了36.8%和45.3%, 减小了飞机弹性变形的扭转角, 在保证升力系数及纵向稳定性能不恶化的前提下, 降低了巡航状态的飞行阻力.
(3) 本文基于Kriging代理模型结合加点准则和优化算法的序列优化方法, 可有效减少计算量, 适用于飞行器的结构优化设计.
| [1] | Balesdent M, Bérend N, Dépincé P, et al. A survey of multidisciplinary design optimization methods in launch vehicle design[J]. Structural and Multidisciplinary Optimization, 2012, 45(5): 619-642. DOI:10.1007/s00158-011-0701-4 |
| [2] | Deaton J D, Grandhi R V. A survey of structural and multidisciplinary continuum topology optimization:post 2000[J]. Structural and Multidisciplinary Optimization, 2014, 49(1): 1-38. DOI:10.1007/s00158-013-0956-z |
| [3] | Martinez-Val R, Perez E. Aeronautics and astronautics:recent progress and future trends[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2009, 223(12): 2767-2820. DOI:10.1243/09544062JMES1546 |
| [4] | Yao W, Chen X, Luo W, et al. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles[J]. Progress in Aerospace Sciences, 2011, 47(6): 450-479. DOI:10.1016/j.paerosci.2011.05.001 |
| [5] | Sobieszczanski-Sobieski J, Haftka R T. Multidisciplinary aerospace design optimization:survey of recent develop-ments[J]. Structural Optimization, 1997, 14(1): 1-23. DOI:10.1007/BF01197554 |
| [6] | Othman N, Kanazaki M. Surrogate model of aerodynamic model toward efficient digital flight[J]. Procedia Engineering, 2015, 99: 703-712. DOI:10.1016/j.proeng.2014.12.592 |
| [7] | Razavi S, Tolson B A, Burn D H. Review of surrogate modeling in water resources[J]. Water Resources Research, 2012, 48(7): 7401 |
| [8] | Moon K, Mavris D N. Modeling and simulation for damage analysis of intelligent, self-reconfigurable ship fluid systems in early design phase[J]. Simulation Modelling Practice and Theory, 2011, 19(9): 1983-2006. DOI:10.1016/j.simpat.2011.05.010 |
| [9] | Keane A, Nair P. Computational approaches for aerospace design:the pursuit of excellence[M]. New Jersey:John Wiley & Sons, 2005. |
| [10] | Jeong S, Murayama M, Yamamoto K. Efficient optimization design method using Kriging model[R]. AIAA 2004-118, 2004. |
| [11] | Kanazaki M, Tanaka K, Jeong S, et al. Multi-objective aerodynamic exploration of elements' setting for high-lift airfoil using Kriging model[R]. AIAA 2006-1471, 2006. |
| [12] |
夏露, 王丹. 基于Kriging自适应代理模型的气动优化方法[J].
航空计算技术, 2013, 43(1): 13-17. Xia L, Wang D. Aerodynamic optimization method based on Kriging adaptive surrogate model[J]. Aeronautical Computing Technique, 2013, 43(1): 13-17. |
| [13] |
许瑞飞, 宋文萍, 韩忠华. 改进Kriging模型在翼型气动优化设计中的应用研究[J].
西北工业大学学报, 2010, 28(4): 504-510. Xu R F, Song W P, Han Z H. Application of improved Kriging-model-based optimization method in airfoil aerodynamic design[J]. Journal of Northwestern Polytechnical University, 2010, 28(4): 504-510. |
| [14] |
苏伟, 高正红, 夏露. 一种代理遗传算法及其在气动优化设计中的应用[J].
西北工业大学学报, 2008, 26(3): 303-307. Su W, Gao Z H, Xia L. An effective surrogate-assisted genetic algorithm for airfoil aerodynamic optimization design[J]. Journal of Northwestern Polytechnical University, 2008, 26(3): 303-307. |
| [15] | Tesfahunegn Y A, Kozeil S, Gramanzini J R, et al. Application of direct and surrogate-based optimization to two-dimensional benchmark aerodynamic problems:a comparative study[C]. Florida:AIAA Sci Tech 2015, 2015. |
| [16] | Lophaven S N, Nielsen H B, Sondergaard J. DACE-a matlab Kriging toolbox, version 2.0[DB/OL].[2016-12-05]. http://www.compute.dtu.dk/english/Resultat?&qt=dtupublicationquery&fr=1&sw=dace&tab=3#tabs. |
| [17] | BeachkofskiB, Grandhi R. Improved distributed hypercube sampling[R]. AIAA 2002-1274, 2002. |
| [18] | Clerc M, Kennedy J. The particle swarm:explosion, stability and convergence in a multi-dimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73. DOI:10.1109/4235.985692 |



