湍流边界层流动是一种非常基础的流动现象, 广泛存在于飞行器的内流和外流之中.虽然流动形式简单, 但从物理的角度来看, 湍流边界层流动仍然是基础研究和数值建模的关注点所在.人们为了方便研究边界层, 根据边界层的速度分布规律, 将边界层细分为几个区域.其中根据黏性的影响可以划分为近壁面区(z+ < 50)和外层(z+≥50), 近壁面区可以再次划分为黏性底层(z+ < 5)和缓冲层(5≤z+≤30), 以及部分对数层.
早期国外的学者们开展了各具特色的实验对湍流边界层进行了具体的研究, 打开了对湍流边界层内部结构认知的大门[1-6].随着计算机技术的发展, 使用计算机对湍流边界层进行数值模拟成为了一种新型的研究方法. Kim等[7]在1979年使用大涡模拟(large-eddy simulation, LES)方法对湍流边界层进行数值模拟, 宣告了数值模拟方法在流体研究中进入应用阶段.湍流边界层中的三维压力场、涡量场、速度场等都能通过数值模拟得到, 研究人员通过这些流场信息对三维的流场结构进行更深入的研究, 也得到了更深的理解.除了大涡模拟方法外, 常用的方法还有直接数值模拟(direct numerical simulation, DNS)方法和Reynolds平均N-S方法(Reynolds average Navier-Stokes, RANS). DNS方法直接求解最小尺度流动, 得到的信息最全面也最准确, Shadloo等[8]综述了国外湍流边界层的DNS研究进展.虽然DNS获得的结果更加准确, 但是随着Reynolds数的增加, 分辨最小尺度流动所需要的计算网格以及计算量将变得难以承受. RANS方法只求解与壁面尺度相当的大尺度流动, 其余尺度均以模型代替, 从而大大减少了计算量, 但同时也损失了大量的流场细节信息并且模型依赖于边界. LES方法介于两者之间, 对各向同性的小尺度涡进行建模, 称为亚格子模型, 保留了大部分尺度范围的流动且计算量适中.
Lenormand等[9-10]对Re = 3 000, Ma分别为0.5和1.5的亚声速和超声速槽道流动进行了大涡模拟研究.他们利用不同的亚格子模型进行可压缩槽道流动大涡模拟数值计算, 并与实验值或者DNS结果进行了对比分析. Mossi等[11]研究了2阶中心格式加人工黏性或者非线性的Roe-TVD格式在槽道流动大涡模拟中的应用, 对比发现Roe-TVD格式的耗散要远大于DSM模型耗散, 矩阵形式的人工黏性耗散与DSM相当, 标准形式的人工黏性耗散要更大一些. Spyropoulos等[12]使用不同阶数迎风有限差分格式对Ma = 2.25沿空间发展的超声速边界层流动进行了大涡模拟研究, 发现低阶格式计算得到壁面摩擦力要比高阶格式低20%.利用空间离散格式的数值耗散来代替SGS模型, 称为隐式大涡模拟(implicit large-eddy simulation, ILES). Yan等[13]使用ILES分别研究了Ma为2.88和4条件下的绝热和等温壁面边界层流动, 经过Van-Driest变换后的平均流向速度分布在黏性底层和对数层, 符合理论规律.流向Reynolds应力除了壁面附近外符合良好, 得到的湍流Prandtl数与实验值0.89非常一致. Urbin等[14]开展了Ma = 3的绝热壁面边界层流动, 细致研究了黏性底层、对数层和边界层外部区域对于网格分辨率的需求, 结果强调了可以通过ILES来代替SGS作用. Kawai等[15]对于可压缩平板边界层流动提出了一种简单的依赖网格的动态壁面模型. Hadjadj等[16]通过数值的方式研究了壁面温度对壁面附近湍流流动的影响, 但SGS模型的影响暂未考虑. Ben-Nasr等[17]使用高阶中心分裂格式和3种不同的SGS模型模拟了Ma = 2的边界层流动.与标准的激波捕捉WENO格式相比, 高阶中心分裂格式能有效地避免数值耗散.网格加密能让所有SGS模型更加准确地捕捉壁面附近的湍流流动.所有模型均能正确预测流动的动态特性, 但壁面附近的温度分布差异明显.对于分辨率良好的LES, 由于脉动速度梯度带来的SGS耗散主导了总的SGS耗散. Montecchia等[18]使用能够捕捉各向异性的SGS模型对高Reynolds数壁面湍流进行大涡模拟研究, 发现该种模型对网格分辨率的敏感性不高, 达到同等精度情况下网格要比各向同性模型所需求的少1个量级.张涵信[19]指出只有无黏部分的计算精度是高阶的, 真正的黏性流的计算精度才是高阶的, 否则过大的数值耗散将会掩盖真实的物理耗散.
本文工作旨在对比几种常用的SGS模型在亚声速槽道流大涡模拟中的预测效果.计算结果与实验值和DNS值较为符合, 但对于不同的具体物理量各个模型表现有好有坏, 不能一概而论.
1 控制方程 1.1 基本方程槽道流动服从质量、动量和能量守恒规律, 可以由经典的N-S方程组来描述, 采用的守恒形式的无量纲N-S方程组如下, 重复下标代表求和.
| $ \begin{array}{*{20}{c}} {\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}} \right) = 0}\\ {\frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) + \frac{{\partial p}}{{\partial {x_i}}} + {f_i}{\delta _{i1}} = \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}}}\\ {\frac{{\partial E}}{{\partial t}} + \frac{{\partial \left( {E + p} \right){u_j}}}{{\partial {x_j}}} + {f_1}{u_1} = \frac{\partial }{{\partial {x_j}}}\left( {{\sigma _{ij}}{u_i}} \right) - \frac{\partial }{{\partial {x_j}}}{q_j}} \end{array} $ | (1) |
其中,t和xi分别表示时间和空间坐标, fiδi1为流向方向的体积力项.密度ρ,温度T和压力p满足理想气体状态方程
| $ p = \frac{1}{{\gamma {M^2}}}\rho T $ |
总能E的表达式为
| $ E = \frac{p}{{\gamma - 1}} + \frac{1}{2}{u_j}{u_j} $ |
黏性应力σij的表达式为
| $ {\sigma _{ij}} = \frac{{\mu \left( T \right)}}{{\mathit{Re}}}{S_{ij}} $ |
黏性系数μ与温度相关, 通过Sutherland公式进行计算
| $ \mu \left( T \right) = {\mu _0}{\left( {\frac{T}{{{T_0}}}} \right)^{1.5}} \cdot \left( {\frac{{{T_0} + S}}{{T + S}}} \right) $ |
式中T0 = 273.15 K, 对于空气μ0 = 1.716 08×10-5Pa·s, Sutherland常数S = 110.4 K.
应变率张量Sij定义为
| $ {S_{ij}} = \frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_k}}}{{\partial {x_k}}} $ |
热通量qj表示为
| $ {q_j} = \frac{{ - \mu }}{{\left( {\gamma - 1} \right)\mathit{RePrM}_0^2}}\frac{{\partial T}}{{\partial {x_j}}} $ |
无量纲化参数
为了节省计算资源, 期望在有限的空间内模拟时间上不断发展的槽道湍流流动, 故在流向和展向采用周期性边界条件, 因此要维持流向方向的均匀性, 须在流向方向上添加额外均匀的体积力f1来保证质量流量不变, 用公式表示为
| $ \frac{\partial }{{\partial t}}\int_0^2 {\left\langle {\rho {u_1}} \right\rangle {\rm{d}}z} = 0 $ |
〈·〉表示平行于壁面的均匀方向上的平均, z = 0和z = 2分别表示下壁面和上壁面.
1.2 大涡模拟控制方程 1.2.1 滤波方程LES的控制方程是通过对N-S方程组进行滤波得到的.任意流动变量f可分解为
| $ \bar f = \int_\mathit{\Omega } {{G_\Delta }\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\xi }}} \right)f\left( \mathit{\boldsymbol{\xi }} \right){\rm{d}}\mathit{\boldsymbol{\xi }}} $ |
GΔ为满足
对于可压缩湍流, 为了形式上与不可压缩方程相似, 引入了密度加权的滤波定义
| $ \tilde f = \frac{{\overline {pf} }}{{\bar \rho }} $ |
任意变量可以分解为
| $ \begin{array}{*{20}{c}} {\frac{{\partial \bar \rho }}{{\partial t}} + \frac{{\partial \bar \rho {{\tilde u}_j}}}{{\partial {x_j}}} = 0}\\ {\frac{{\partial \bar \rho {{\tilde u}_i}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\bar \rho {{\tilde u}_i}{{\tilde u}_j} + \frac{{\partial \bar \rho }}{{\partial {x_i}}} - \frac{{\partial {{\hat \sigma }_{ij}}}}{{\partial {x_j}}} + {f_1} = }\\ { - \frac{\partial }{{\partial {x_j}}}{\tau _{ij}} + \frac{\partial }{{\partial {x_j}}}\left( {\overline {{\sigma _{ij}}} - {{\hat \sigma }_{ij}}} \right)} \end{array} $ |
τij和
| $ {\tau _{ij}} = - \bar \rho \left( {\widetilde {{u_i}{u_j}} - {{\tilde u}_i}{{\tilde u}_j}} \right)\\ {{\hat \sigma }_{ij}} = \frac{\mu }{{\mathit{Re}}}\left( {\frac{{\partial {{\tilde u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\tilde u}_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {{\tilde u}_k}}}{{\partial {x_k}}}} \right) $ |
选择的基本变量不同, 能量方程滤波后得到的SGS项也不同, 本文选择Vreman采用的
| $ \hat E = \frac{{\bar p}}{{\gamma - 1}} + \frac{1}{2}\bar \rho {{\tilde u}_j}{{\tilde u}_j} $ |
这样滤波后得到能量方程形式与公式(1)相同.
| $ \begin{array}{*{20}{c}} {\frac{{\partial \hat E}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\hat E + \bar p} \right){{\tilde u}_j} - \frac{\partial }{{\partial {x_j}}}\left( {{{\hat \sigma }_{ij}}{{\tilde u}_i}} \right) + \frac{{\partial {{\hat q}_j}}}{{\partial {x_j}}} + {f_1}{{\tilde u}_1} \approx }\\ { - \frac{1}{{\gamma - 1}}\frac{{\partial \left( {\overline {p{u_j}} - \bar p{{\tilde u}_j}} \right)}}{{\partial {x_j}}} - {{\tilde u}_j}\frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}} \end{array} $ |
滤波后的通量为
| $ {{\hat q}_j} = \frac{{ - \mu }}{{\left( {\gamma - 1} \right)\mathit{RePrM}_0^2}}\frac{{\partial \tilde T}}{{\partial {x_j}}} $ |
至此得到的密度加权滤波方程组左端与原N-S方程组形式相同, 右端是因为滤波多出来的SGS项, LES的目的就是对这些项进行建模从而封闭方程.
滤波后的理想气体状态方程为
| $ \bar p = \frac{{\bar \rho \tilde T}}{{\gamma {M^2}}} $ |
滤波后的动量方程出现了
| $ O\left( {\frac{\partial }{{\partial {x_j}}}\left( {{{\bar \sigma }_{ij}} - {{\hat \sigma }_{ij}}} \right)} \right) \approx \left. {\frac{1}{{100}}O\frac{\partial }{{\partial {x_j}}}{\tau _{ij}}} \right) $ |
根据这个结果,
(1) Smagorinsky model(SM)
在Boussinesq的涡黏假设基础上, 经典Smagorinsky模型可以表述为
| $ {\tau _{ij}} - \frac{1}{3}{\tau _{kk}}{\delta _{ij}} = - {\mu _{\rm{t}}}{S_{ij}}\left( {\tilde u} \right) $ |
涡黏系数μt的计算方式为
| $ {\mu _{\rm{t}}} = \bar \rho {\left( {{C_{\rm{s}}}\Delta } \right)^2}\left| {S\left( {\tilde u} \right)} \right|,{\left| {S\left( {\tilde u} \right)} \right|^2} = \frac{1}{2}{S_{ij}}\left( {\tilde u} \right){S_{ij}}\left( {\tilde u} \right) $ |
特征长度尺度为Δ = (ΔxΔyΔz)1/3, 其中Δx, Δy, Δz分别为x, y, z这3个方向的网格尺度.一般情况下,SM模型常数Cs在不可压缩均匀各向同性湍流中取0.18, 但是该常数依赖于具体的流动, Deardorff建议在槽道流中取Cs = 0.1[9].
在壁面附近涡黏系数应该衰减为零, 但是SM只依赖于大尺度流动, 在壁面附近仍不为零, 所以需要额外的衰减函数, 强制其在壁面附近衰减为零, 一般采用如下形式的Van Driest衰减函数来修正CsΔ.
| $ {\left( {{C_{\rm{s}}}\Delta } \right)^{{\rm{new}}}} = \left( {1 - {{\rm{e}}^{ - {z^ + }/a}}} \right) \cdot {\left( {{C_{\rm{s}}}\Delta } \right)^{{\rm{old}}}} $ |
z+为到壁面的无量纲距离, a为常数取为25.
(2) dynamic Smagorinsky model(DSM)
经典SM模型中的一个自由参数是需要预先给定的, 而不同流动状态下该值的最佳选择是有差异的, 针对这个问题, Germano等[20]提出了动态Smagorinsky模型, 随着流场动态地调整Cs的值.
| $ C_{\rm{s}}^2 = - \frac{1}{2}\frac{{{L_{ij}}{M_{ij}}}}{{{M_{mn}}{M_{mn}}}} $ |
其中
| $ {L_{ij}} = {\left( {u_i^{\rm{r}}u_j^{\rm{r}}} \right)^{\rm{t}}} - u_i^{{\rm{rt}}}u_j^{{\rm{rt}}} $ |
| $ {M_{ij}} = {\left( {{\Delta ^{\rm{t}}}} \right)^2}\left| {{S^{{\rm{rt}}}}} \right|S_{^{ij}}^{{\rm{rt}}} - {\left( {{\Delta ^{\rm{r}}}} \right)^2}{\left( {\left| {{S^{\rm{r}}}} \right|S_{^{ij}}^{\rm{r}}} \right)^{\rm{t}}} $ |
上标r和t分别表示网格滤波和测试滤波, 网格滤波即推导LES控制方程时的滤波过程. Δr和Δt分别表示网格滤波尺度和测试滤波尺度, 一般有Δt/Δr = 2.
实际计算中, 为了计算的稳定, 须在均匀方向上进行平均, 即
| $ C_{\rm{s}}^2 = - \frac{1}{2}\frac{{\left\langle {{L_{ij}}{M_{ij}}} \right\rangle }}{{\left\langle {{M_{mn}}{M_{mn}}} \right\rangle }} $ |
(3) wall-adapting local eddy-viscosity model(WALE)
WALE模型基于速度梯度的不变量来计算涡黏系数[21], 公式定义如下
| $ {\mu _{\rm{t}}} = \bar \rho {\left( {{C_{\rm{w}}}\Delta } \right)^2}\frac{{{{\left( {S_{ij}^dS_{ij}^d} \right)}^{3/2}}}}{{{{\left( {{{\tilde S}_{ij}}{{\tilde S}_{ij}}} \right)}^{5/2}} + {{\left( {S_{ij}^dS_{ij}^d} \right)}^{5/4}}}} $ |
其中
| $ S_{ij}^d = \frac{1}{2}\left( {\tilde g_{ij}^2 + \tilde g_{ji}^2} \right) - \frac{1}{3}{\delta _{ij}}{{\tilde g}_{kk}} $ |
| $ {{\tilde g}_{ij}} = \frac{{\partial {{\tilde u}_i}}}{{\partial {x_j}}},\tilde g_{ij}^2 = {{\tilde g}_{ik}}{{\tilde g}_{kj}} $ |
| $ {{\tilde S}_{ij}} = \frac{1}{2}\left( {\frac{{\partial {{\tilde u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\tilde u}_j}}}{{\partial {x_i}}}} \right) $ |
Cw为WALE模型常数, 默认取0.5.
(4) coherent structures model(CSM)
相干结构模型使用速度梯度张量的函数动态地确定Cs值, 该函数基于如下假设:对于具有良好分辨率的DNS网格, SGS耗散在小尺度的相干涡中心处很小, 解析的尺度和SGS之间的能量传递位于该相干涡周围[22].公式定义如下
| $ C_{\rm{s}}^2 = {C_{{\rm{csm}}}}{\left| {{F_{{\rm{cs}}}}} \right|^{3/2}} $ |
| $ {F_{{\rm{cs}}}} = \frac{{\tilde Q}}{{\tilde E}} $ |
| $ \tilde Q = - \frac{1}{2}\frac{{\partial {{\tilde u}_j}}}{{\partial {x_i}}}\frac{{\partial {{\tilde u}_i}}}{{\partial {x_j}}},\tilde E = \frac{1}{2}\frac{{\partial {{\tilde u}_j}}}{{\partial {x_i}}}\frac{{\partial {{\tilde u}_j}}}{{\partial {x_i}}} $ |
式中,Ccsm为模型常数, 取默认值1/30, Fcs为相干结构函数,且-1≤Fcs≤1.
1.2.3 亚格子热通量模型类比亚格子应力的建模方法, 热通量的模化也建立在涡黏假设基础之上, 公式如下
| $ \frac{1}{{\gamma - 1}}\frac{{\partial \left( {\overline {\rho {u_j}} - \bar p{{\tilde u}_j}} \right)}}{{\partial {x_j}}} = - \frac{{{\mu _{\rm{t}}}}}{{\left( {\gamma - 1} \right)\mathit{P}{\mathit{r}_{\rm{t}}}M_0^2}}\frac{{\partial \tilde T}}{{\partial {x_j}}} $ |
亚格子Prandtl数Prt取常值0.9.
2 数值方法 2.1 时间推进时间推进采用显式的3步Runge-Kutta(RK3)方法, 对于任意变量W有
| $ \frac{{\partial W}}{{\partial t}} + H\left( W \right) = 0 $ |
RK3可表示为
| $ {W_1} = {W^n} + {\gamma _1} \cdot \Delta t \cdot H\left( {{W^n}} \right),{H_1} = H\left( {{W_1}} \right) + {\chi _1}\left( {{W_0}} \right) \\{W_2} = {W_1} + {\gamma _2} \cdot \Delta t \cdot {H_1},{H_2} = H\left( {{W_2}} \right) + {\chi _2}{H_1} $ |
| $ {W^{n + 1}} = {W_2} + {\gamma _3} \cdot \Delta t \cdot {H_2} $ |
其中,Δt为时间推进的步长, γ1, γ2, γ3, χ1, χ2是由Lowery和Reynolds推荐的常数.
2.2 空间离散本文计算所采用的程序代码基于廖飞发展的格心有限差分方法, 将自由度从格点转移至格心, 使得内外边界条件处理更加简洁, 2阶精度时与有限体积法完全等价.该套方法中, 空间离散分为3步:插值、求Riemann通量、求导[23-24].该方法已在激波湍流问题中有了初步的应用[25].
第1步插值是将原始变量或者守恒变量从网格中心向网格面上进行插值.采用迎风格式时, 不同迎风方向得到的值一般不同, 左迎风模板得到的值称为左值, 右迎风模板得到的值称为右值.本文计算采用的是邓小刚提出的线性耗散紧致格式[26](dissipative compact scheme, DCS)应用到格心有限差分法上的插值格式, 3阶的DCS插值格式(DCS3)表达式为
| $ \begin{array}{l} \frac{1}{6}\left( {1 + \alpha } \right)Q_{i - 1/2}^{\rm{L}} + Q_{i + 1/2}^{\rm{L}} + \frac{1}{6}\left( {1 - \alpha } \right)Q_{i + 3/2}^{\rm{L}} = \\ \;\;\;\frac{2}{3}\left( {{Q_i} + {Q_{i + 1}}} \right) - \frac{\alpha }{3}\left( {{Q_{i + 1}} - {Q_i}} \right) \end{array} $ |
| $ \begin{array}{l} \frac{1}{6}\left( {1 - \alpha } \right)Q_{i - 1/2}^{\rm{R}} + Q_{i + 1/2}^{\rm{R}} + \frac{1}{6}\left( {1 + \alpha } \right)Q_{i + 3/2}^{\rm{R}} = \\ \;\;\;\frac{2}{3}\left( {{Q_i} + {Q_{i + 1}}} \right) + \frac{\alpha }{3}\left( {{Q_{i + 1}} - {Q_i}} \right) \end{array} $ |
式中,上标L, R分别表示左值和右值, α是个自由参数, 用来调节迎风特性, α = 0对应着4阶中心紧致插值格式, α = 1对应传统的3阶紧致迎风插值格式, α在[0, 1]中取值且越大耗散越大.
通过网格中心向网格面上插值得到面上的左右值后, 第2步就是求面上的Riemann通量, 一般是通过通量差分裂格式来完成, 本文选择常用的经典Roe格式, 该格式使用广泛, 这里就不再详述.
获得网格面上的通量之后, 最后一步就是求网格中心的通量导数, 这一步是通过面上的通量向中心进行差分进行的.本文采用4阶中心紧致差分格式来求网格中心通量导数, 具体形式如下
| $ \frac{1}{{22}}{{Q'}_{i - 1}} + {{Q'}_i} + \frac{1}{{22}}{{Q'}_{i + 1}} = \frac{{12}}{{11}}\left( {{Q_{i + 1/2}} - {Q_{i - 1/2}}} \right) $ |
对内外边界的处理采用虚网格的方式, 故物理边界使用与内场一致的格式, 无需额外的边界格式.
2.3 体积力项如前面指出的, 流向采用了周期性边界条件, 需要额外的均匀体积力来驱动流动以保持质量流量守恒, 对动量方程在xy平面上平均后沿壁面方向进行积分, 得到
| $ \frac{\partial }{\partial }{Q_{\rm{m}}} = \frac{1}{{\mathit{Re}}}{L_y}\left[ {\left\langle \mu \right\rangle \frac{{\partial \left\langle {{u_1}} \right\rangle }}{{\partial z}}} \right]_{{\rm{low}}}^{{\rm{up}}} - {L_y}{L_z}{f_1} $ |
其中,〈·〉表示在xy平面上的平均操作, Ly, Lz分别为槽道的宽度和高度, up和low分别代表上下壁面, Qm为通过yz截面的质量流量.因为槽道流动平均后的流场是对称的, 所以
| $ \left\langle \mu \right\rangle \frac{{\partial \left\langle {{u_1}} \right\rangle }}{{\partial z}}\left| {_{{\rm{up}}}} \right. = - \left\langle \mu \right\rangle \frac{{\partial \left\langle {{u_1}} \right\rangle }}{{\partial z}}\left| {_{{\rm{low}}}} \right. $ |
从而
| $ \frac{\partial }{{\partial t}}{Q_{\rm{m}}} = - {L_y}{L_z}{f_1} - \frac{{2{L_y}}}{{\mathit{Re}}}\left\langle \mu \right\rangle \frac{{\partial \left\langle {{u_1}} \right\rangle }}{{\partial z}}\left| {_{{\rm{low}}}} \right. $ |
因为流动从层流转变为湍流过程中
| $ f_1^{n + 1} = f_1^n + \frac{{\Delta t}}{{{L_y}{L_z}}}\left[ {\alpha \left( {{Q^{n + 1}} - {Q_0}} \right) + \beta \left( {{Q^n} - {Q_0}} \right)} \right] $ |
Q0, Qn, Qn+1分别表示初始时刻、当前时刻以及下一时刻的质量流量, α = 2/Δt, β = -0.2/Δt, Qn+1可由当前时刻流量的1阶预测近似得到
| $ {Q^{n + 1}} = {Q^n} - \Delta t{g^n} $ |
| $ {g^n} = {L_y}{L_z}{f^n} + \frac{{2{L_y}}}{{\mathit{Re}}}\left\langle {{\mu _n}} \right\rangle \frac{{\partial \left\langle {u_1^n} \right\rangle }}{{\partial z}}\left| {_{{\rm{low}}}} \right. $ |
体积力在能量方程中以f1u1的形式出现, 前人的工作表明只有用f1ub来代替f1u1时计算才能是稳定的, ub为体平均速度.
2.4 边界条件壁面采用等温无滑移边界条件, 公式表示为
| $ T = {T_{\rm{w}}},{u_k} = 0,k = 1,2,3 $ |
壁面温度是无量纲化控制方程时采用的特征温度,故Tw = 1.流向和展向采用周期性边界条件, 公式表示为
| $ f\left( {x, \cdots , \cdots } \right) = f\left( {x + {L_x}, \cdots , \cdots } \right) $ |
| $ f\left( { \cdots ,y, \cdots } \right) = f\left( { \cdots ,y + {L_y}, \cdots } \right) $ |
初始速度场是在层流速度分布的基础上,叠加幅度为平均速度大小的10%的随机脉动
| $ {U_1}\left( {t = 0} \right) = {U_{1\max }}\left( {1 - {{\left( {z - 1} \right)}^2}} \right)\left( {1 + \varepsilon } \right) $ |
| $ {U_2}\left( {t = 0} \right) = 0 $ |
| $ {U_3}\left( {t = 0} \right) = 0 $ |
ε = 0.1g为相对扰动量, g为[-1, 1]内的随机数. U1max为中心线上的平均速度, 取为1.5,则入口处的体平均速度刚好为1.
使用均匀的密度场初始化密度, 温度场则使用层流的温度分布进行初始化.
| $ T\left( {t = 0} \right) = 1 + \frac{{\left( {\gamma - 1} \right)\mathit{PrM}_0^2}}{3}{U_{1\max }}\left( {1 - {{\left( {z - 1} \right)}^4}} \right) $ |
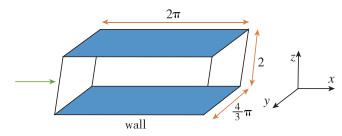
本文研究的对象为等温壁面亚声速槽道湍流, 参照的数据来源于Niederschulte等[27]完成的实验和Kim等[28]的DNS结果. 图 1给出了计算域的设置, x, y, z分别为流向、展向和壁面法向方向.基于体平均速度、槽道半高和壁面黏性系数的参考Reynolds数取为3 000.基于体平均速度和壁面声速的参考Mach数取为0.5.
|
| 图 1 计算域示意图 Fig.1 Schematic of computational domain |
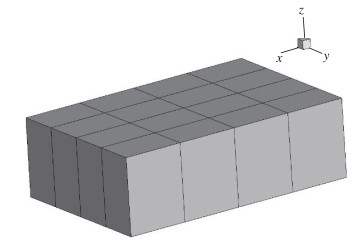
在采用周期性边界的方向上, 计算域长度的选择须满足一定的条件, 参考Lenormand等的文献[9-10], 计算域各方向长度选择为Lx = 2π, Ly = 4π/3, Lz = 2.流向和展向采用均匀网格, 壁面法向方向在壁面附近加密网格, x, y, z方向网格点为41×65×119, 无量纲网格尺度为Δx+≈27, Δy+≈12, 壁面Δzw+≈0.5, 中心线Δzc+≈6.3.网格量以及各方向尺度选择与文献中较密的一套网格保持一致.为提高计算速度, 程序使用MPI并行方式, 计算域须剖分为多块, 图 2为分块示意图, 只在流向和展向进行剖分, 图 3给出了xz平面上的网格分布, 除在壁面附近加密外, 其余区域近乎为均匀网格.
|
| 图 2 计算域分块示意图 Fig.2 Diagram of domain blocks |

|
| 图 3 xz平面网格(壁面处局部加密) Fig.3 Meshes in xz plane(refined at wall) |
计算选择了以下几种方式:
(1) DCS3(α = 0.001)不加模型(记为DCS3);
(2) DCS3(α = 0)加SM模型(记为SM);
(3) DCS3(α = 0)加DSM模型(记为DSM);
(4) DCS3(α = 0)加WALE模型(记为WALE);
(5) DCS3(α = 0)加CSM模型(记为CSM).
须指出的是, 第1种方式不使用SGS模型, 但是迎风格式自身的耗散可以起到类似SGS模型的作用, 可以认为是ILES.时间推进统一使用3步Runge-Kutta显式方法, 时间步长均为Δt = 0.003.
3.2 结果及分析计算从随机扰动的层流初场开始, 须经历一段时间的发展成为完全的湍流流动后, 所得到的数据才是有意义的.判断流场是否发展为真实的湍流流动的重要依据之一就是阻力系数的变化, 湍流边界层摩擦阻力系数明显高于层流边界层, 计算刚开始一段时间阻力系数在层流边界层相应值附近抖动, 经过一段时间的发展, 阻力系数平衡位置开始逐渐增加到湍流边界层对应的阻力系数水平, 认为在这之后流场已经是完全发展的湍流场了, 数据也在这之后进行收集.结果中的平均操作是在时间和空间均匀方向即xz平面上进行的.
Dean[29]研究了不同Reynolds数下槽道湍流的平均参数, 并给出了中心线平均速度和壁面阻力系数关于Reynolds数的关系式
| $ \left\langle {{u_{\rm{c}}}} \right\rangle = 1.28{\left( {2\mathit{Re}} \right)^{ - 0.0116}} $ |
| $ {C_{\rm{f}}} = 0.073{\left( {2\mathit{Re}} \right)^{ - 0.25}} $ |
本文计算的Reynolds数为3 000, 对应该关系式得到的中心线平均速度和壁面阻力系数分别为1.157和8.29×10-3.
表 1给出了不同模型计算得到的中心线平均速度、壁面摩擦速度、摩擦力系数、中心线温度与壁面温度之比以及中心线密度与壁面密度之比.中心线平均速度和壁面阻力系数第2行给出了与参考值的相对误差.对于中心线平均速度来说, 所有结果与公式参考值误差均在1%之内, 再具体来看, CSM结果最为接近, WALE其次, 其余3个结果误差相近.而对于壁面阻力系数, WALE的误差最大, 约9%, DCS3的误差最小, 约3%.误差从大到小顺序为WALE > SM > DSM > CSM > DCS3.由于壁面摩擦速度与壁面阻力系数均与壁面速度梯度相关, 不同模型计算的壁面摩擦速度大小关系与壁面阻力系数大小关系一致, 即DCS3 > CSM > DSM > SM > WALE.
| 下载CSV 表 1 平均流动参数 Tab.1 Mean flow quantities |
不同模型下中心线温度和密度与壁面温度和密度的比值差异很小并且值都很接近1, 说明在本文计算条件下, 流动的压缩性较弱.
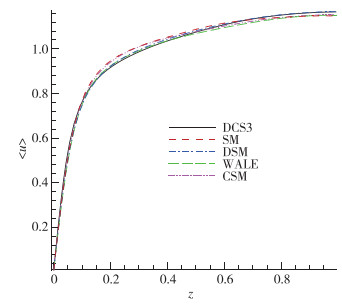
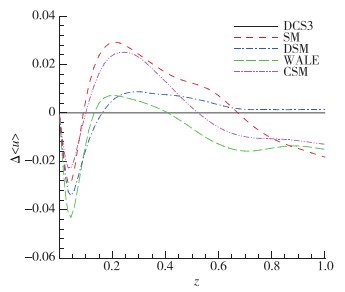
图 4给出了壁面法向的流向平均速度, 从原始的速度图来看, 不同模型下的结果十分相近, 图 5选取DCS3曲线为参照, 从壁面到z = 0.1附近所有曲线偏离值从零变为负并在z = 0.05附近达到负极值, z = 0.1附近偏离值均由负转正, 并在z = 0.2达到正极值, 之后偏离值开始下降, 除DSM外, 其余曲线均在中心线附近降到负值, 比参照值略低.
|
| 图 4 平均流向速度 Fig.4 Mean streamwise velocities mean streamwise |
|
| 图 5 平均流向速度差值(以DCS3为参考) Fig.5 Differences in mean streamwise velocities (referenced by DCS3) |
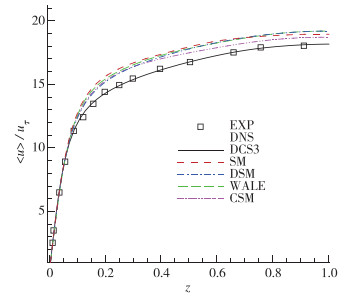
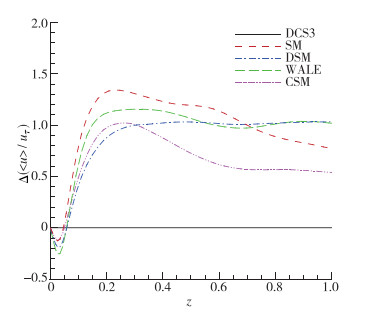
图 6通过壁面摩擦速度进行无量纲化后与Niederschulte的实验值和Kim的DNS结果进行对比发现, DCS3的结果符合得非常好. 图 7选取DCS3曲线为参照, 在z = 0.05的壁面附近区域偏离值均为负, 之后均为正, z = 0.2附近偏离值最大, 最大相对偏离量约10%, 不同曲线最大偏差的大小关系为SM > WALE > CSM > DSM.峰值之后到中心线附近SM和CSM曲线逐渐向参照值靠近, DSM和WALE曲线则保持与参照值相同的趋势, 偏离量基本不变.总体的偏差可以用均方根来刻画, 大小关系SM(0.959)> WALE(0.910)> DSM(0.894)> CSM(0.6713).出现这样结果的原因在于4种模型在壁面附近耗散较DCS3大, 导致得到的平均速度梯度在壁面附近偏小, 从而摩擦速度偏小. Lenormand等[9]的计算结果中SM曲线与本文类似, 除壁面附近外, 平均流向速度均高于参照值, 但与本文区别在于其偏差明显更大.本文SM模型得到的摩擦速度为6.042×10-2, 而文献中对应值为5.852×10-2, 偏小的摩擦速度导致了无量纲化后偏大的值. Mossi等[11]使用DSM模型计算得到的壁面阻力系数为7.37×10-3, 本文则为7.87×10-3.本文的计算网格和参数与上述文献一致, 唯一区别在于空间离散格式: Lenormand使用4阶显式的中心格式, 而Mossi则使用的2阶中心格式, 本文使用的4阶紧致中心格式.推测使用精度更高、频谱特性更好的格式, SM和DSM的耗散可能更小, Mossi一系列的计算表明, 不论是亚声速还是超声速条件下, 额外引入的耗散越小, 得到的壁面阻力系数则越大.
|
| 图 6 摩擦速度无量纲化后的流向平均速度 Fig.6 Mean streamwise velocities dimensioned with friction velocities |
|
| 图 7 无量纲的平均速度差值(以DCS3为参考) Fig.7 Differences in dimensionless mean streamwise velocities (referenced by DCS3) |
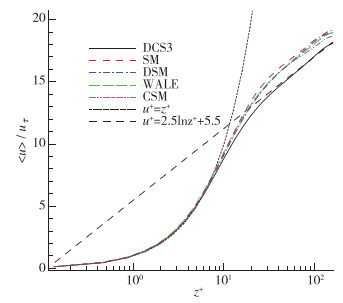
图 8中曲线u+ = z+对应的是黏性底层速度的理论分布, 而u+ = 2.5lnz++5.5对应对数层速度理论分布.由图中结果可以看到, 各曲线均符合黏性底层的线性分布规律, 但在对数层, 只有DCS3曲线与理论公式符合, 其他曲线均在理论分布之上, 但依然符合对数分布趋势.
|
| 图 8 边界层速度分布 Fig.8 Profiles of mean velocities in boundary layer |
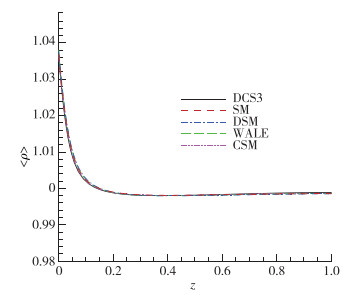
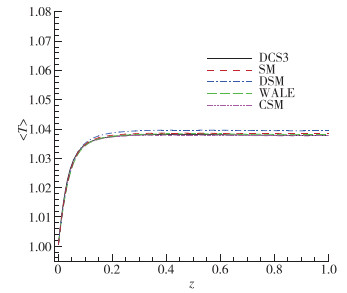
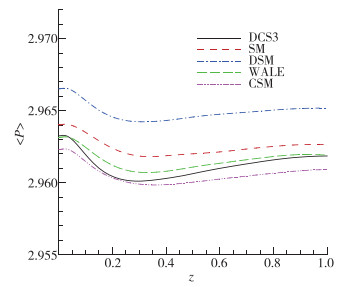
图 9~11给出了平均密度、温度和压力在壁面法向方向的分布.不同模型计算的3个物理量差异非常小, 最大相对误差也不超过0.2%.从结果来看, 热力学量对亚格子模型并不敏感, 不适合作为评价模型优劣的判据.另外从平均压力的分布图来看, 压力沿壁面的最大相对变化只在0.1%左右, 说明在本文的计算条件下, 压力沿壁面法向几乎不变, 接近层流边界层中的情形.在Lenormand等[9]的亚声速槽道流计算结果中, 不同模型计算得到的热力学量与本文类似, 差异不明显.
|
| 图 9 平均密度剖面 Fig.9 Profiles of mean densities |
|
| 图 10 平均温度剖面 Fig.10 Profiles of mean temperatures |
|
| 图 11 平均压力剖面 Fig.11 Profiles of mean pressures |
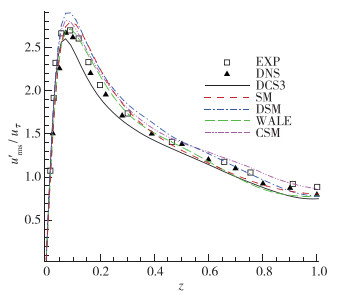
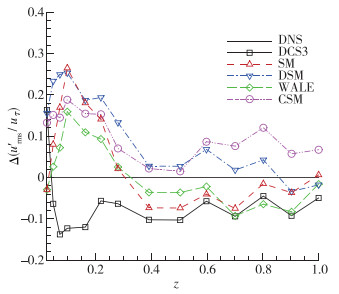
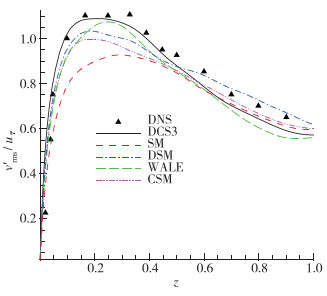
图 12所示为壁面法向方向流向速度脉动的变化曲线, 图 13以DNS结果为参照, 给出了不同结果的偏离值随法向位置的变化.结合两幅图可以看到, z = 0.1峰值附近所有曲线相较参照值偏离最大, DCS3偏低, 其余均偏高, 峰值处偏离量大小关系为SM > DSM > CSM > WALE > DCS3.峰值过后, 各曲线的偏差均快速减小, 在z = 0.4~0.5区域内保持平稳, z > 0.5范围内除了CSM其余曲线均在波动中向参照值靠近.总体的偏差均方根大小关系为DSM(0.148)> CSM(0.115)> SM(0.113)> DCS3(0.097)> WALE(0.074).
|
| 图 12 流向速度脉动 Fig.12 Fluctuating velocities in streamwise direction |
|
| 图 13 流向速度脉动差值(以DNS为参考) Fig.13 Differences in streamwise fluctuating velocities (referenced by DNS) |
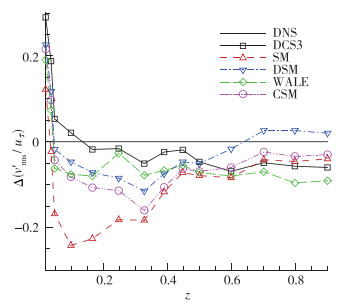
图 14为不同模型得到的展向速度脉动随法向位置的变化, 图 15则为以DNS结果为参照的偏离量在法向的分布情况.壁面附近z < 0.05区域所有曲线相较DNS均偏高, 其余区域除了DSM在中心线附近偏高外, 所有曲线均低于参照值.除了SM曲线在z = 0.1达到最大偏差外, 其余曲线均在壁面附近偏差最大, 最大偏差大小关系有DCS3 > SM > DSM > CSM > WALE.总体的偏差均方根大小为SM(0.136)>DCS3(0.101)>CSM(0.100)>WALE(0.087)> DSM(0.086).
|
| 图 14 展向速度脉动 Fig.14 Fluctuating velocities in spanwise direction |
|
| 图 15 展向速度脉动差值(以DNS为参考) Fig.15 Differences in spanwise fluctuating velocities (referenced by DNS) |
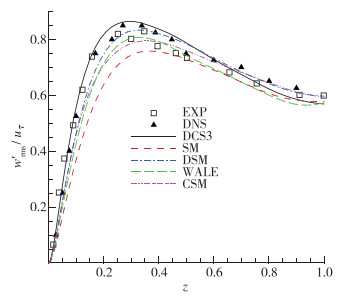
图 16所示为壁面法向方向速度脉动随法向位置的变化, 实验值与DNS值在峰值附近差异明显并且实验值有明显抖动, 实验中存在的噪声和高频非湍流压力振荡可能是主要原因[9].壁面到峰值前, 除DCS3之外其他曲线均低于实验值与DNS值; 峰值附近DCS3曲线略微偏高, 其余曲线均在DNS值之下, 峰值大小关系为DCS3 > DSM > WALE > CSM > SM; 中心线附近DSM和CSM曲线与DNS结果吻合得很好, 其余曲线明显偏低.
|
| 图 16 壁面法向速度 Fig.16 Fluctuating velocities in wall-normal direction |
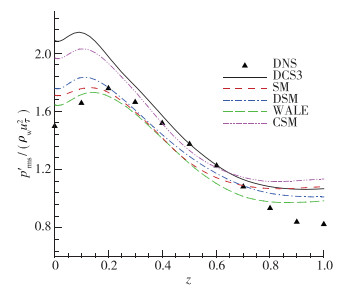
压力脉动随壁面距离的变化如图 17所示.所有曲线在壁面附近和中心线附近与参考值差异明显, 均高于参考值, 峰值位置偏前.壁面附近DCS3曲线偏离参考值最大而WALE曲线最接近.峰值后到中心线之间位置各曲线之间差异变小, 基本符合参考值变化趋势.
|
| 图 17 压力脉动 Fig.17 Fluctuating pressures |
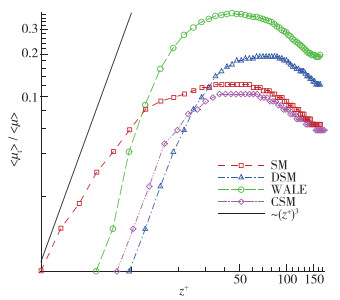
Garnier等[30]指出网格分辨率良好的情况下, SGS模型给出的涡黏系数在壁面附近应满足μt~(z+)3的关系, 否则壁面附近的耗散会过强, 结果之一就是壁面速度梯度计算偏差增大, 从而壁面摩擦速度和阻力系数预测不准. 图 18是4种SGS模型给出的涡黏系数随到壁面的无量纲距离的变化, 图中黑色斜线是满足μt~(z+)3关系的参考线.可以看到, DSM和CSM在壁面附近与参考线斜率一致, SM明显斜率偏小, WALE斜率偏大.比较SM和WALE在壁面附近的值(平移将两条曲线第1个点重合), 有WALE > SM, 同理对于DSM和CSM, 有DSM > CSM.再结合Garnier的观点, 壁面附近模型耗散大小关系有WALE > SM > DSM > CSM, 而计算得到的摩擦速度和阻力系数大小关系为WALE < SM < DSM < CSM.意味着模型在壁面附近的耗散越大, 预测的摩擦速度和阻力系数就越小.
|
| 图 18 涡黏系数随壁面无量纲距离的变化 Fig.18 Eddy viscosity variation with dimensionless distance from the wall |
本文基于格心有限差分方法, 使用4阶紧致中心格式, 分别采用了5种不同的SGS模型即DCS3(隐式), SM, DSM, WALE和CSM, 对Ma = 0.5, Re = 3 000的亚声速槽道湍流进行大涡模拟计算, 分析对比各项结果后有如下结论:
(1) 对于流场平均温度、平均密度等热力学量以及平均流向速度来说, 不同模型的结果差异很小, 说明这些量对模型的敏感性较低, 不适合作为判别模型优劣的标准.
(2) 与壁面速度梯度相关的壁面摩擦速度、阻力系数不同模型结果差异明显, 且模型在壁面处耗散越大, 壁面摩擦速度和阻力系数越小.如果只关注壁面摩擦速度和阻力系数, 弱耗散的DCS3迎风格式与参考结果最接近.
(3) 对于与速度相关的脉动量来说, 壁面和脉动峰值附近误差最为明显, 而中心线附近误差一般较小; 显式亚格子模型计算得到流向速度脉动峰值均比DNS值高, 展向和壁面法线方向速度脉动峰值处则均偏低.这一定性结果与文献[9-10]中的亚声速和超声速槽道大涡模拟计算得到的结果是一致的.
(4) 考虑显式的4种SGS模型在壁面附近的涡黏系数分布, DSM和CSM满足壁面附近μt~(z+)3的分布规律, 而SM斜率偏小, WALE斜率则偏大, 导致SM和WALE在壁面附近表现出更大的耗散, 壁面摩擦速度和阻力系数也更小.
| [1] |
Corrsin S, Kistler A L. Free-stream boundaries of turbulent flows[R]. Technical Report TN-1244, 1955.
|
| [2] |
Grant H L. The large eddies of turbulent motion[J]. Journal of Fluid Mechanics, 1958, 4(2): 149-190. DOI:10.1017/S0022112058000379 |
| [3] |
Runstadler P W, Kline S J, Reynolds W C. An experimental investigation of the flow structure of the turbulent boundary layer[R]. Report MD-8, 1963.
|
| [4] |
Kline S J, Reynolds W C, Schraub F A, et al. The structure of turbulent boundary layers[J]. Journal of Fluid Mechanics, 1967, 30(4): 741-773. DOI:10.1017/S0022112067001740 |
| [5] |
Kim H T, Kline S J, Reynolds W C. The production of turbulence near a smooth wall in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1971, 50(1): 133-160. DOI:10.1017/S0022112071002490 |
| [6] |
Offen G R, Kline S J. Combined dye-streak and hydrogen-bubble visual observations of a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1974, 62(2): 223-239. DOI:10.1017/S0022112074000656 |
| [7] |
Kim J, Moin P. Large eddy simulation of turbulent channel flow: ILLIAC 4 calculation[R]. NASA-TM-78619, 1979.
|
| [8] |
Shadloo M S, Hadjadj A, Hussain F. Statistical behavior of supersonic turbulent boundary layers with heat transfer at M = 2[J]. International Journal of Heat and Fluid Flow, 2015, 53: 113-134. DOI:10.1016/j.ijheatfluidflow.2015.02.004 |
| [9] |
Lenormand E, Sagaut P, Phuoc L T. Large eddy simulation of subsonic and supersonic channel flow at moderate Reynolds number[J]. International Journal for Numerical Methods in Fluids, 2000, 32(4): 369-406. DOI:10.1002/(ISSN)1097-0363 |
| [10] |
Lenormand E, Sagaut P, Phuoc L T, et al. Subgrid-scale models for large-eddy simulations of compressible wall bounded flows[J]. AIAA Journal, 2000, 38(8): 1340-1350. DOI:10.2514/2.1133 |
| [11] |
Mossi M, Sagaut P. Numerical investigation of fully developed channel flow using shock-capturing schemes[J]. Computers & Fluids, 2003, 32(2): 249-274. |
| [12] |
Spyropoulos E T, Blaisdell G A. Large-eddy simulation of a spatially evolving supersonic turbulent boundary-layer flow[J]. AIAA Journal, 1998, 36(11): 1983-1990. DOI:10.2514/2.325 |
| [13] |
Yan H, Knight D, Zheltovodov A A. Large-eddy simulation of supersonic flat-plate boundary layers using the monotonically integrated large-eddy simulation (MILES) technique[J]. Journal of Fluids Engineering, 2002, 124(4): 868-875. DOI:10.1115/1.1516578 |
| [14] |
Urbin G, Knight D. Large-eddy simulation of a super-sonic boundary layer using an unstructured grid[J]. AIAA Journal, 2001, 39(7): 1288-1295. DOI:10.2514/2.1471 |
| [15] |
Kawai S, Larsson J. A dynamic wall model for large-eddy simulation of high Reynolds number compressible flows[J]. CTR Annual Research Briefs, 2010, 25-37. |
| [16] |
Hadjadj A, Ben-Nasr O, Shadloo M S, et al. Effect of wall temperature in supersonic turbulent boundary layers:a numerical study[J]. International Journal of Heat and Mass Transfer, 2015, 81: 426-438. DOI:10.1016/j.ijheatmasstransfer.2014.10.025 |
| [17] |
Ben-Nasr O, Hadjadj A, Chaudhuri A, et al. Assessment of subgrid-scale modeling for large-eddy simulation of a spatially-evolving compressible turbulent boundary layer[J]. Computers & Fluids, 2017, 151: 144-158. |
| [18] |
Montecchia M, Brethouwer G, Johansson A V, et al. Taking large-eddy simulation of wall-bounded flows to higher Reynolds numbers by use of anisotropy-resolving subgrid models[J]. Physical Review Fluids, 2017, 2(3): 034601. DOI:10.1103/PhysRevFluids.2.034601 |
| [19] |
张涵信. 关于CFD高精度保真的数值模拟研究[J]. 空气动力学学报, 2016, 34(1): 1-4. Zhang H X. Investigations on fidelity of high order accurate numerical simulation for computational fluid dy-namics[J]. Acta Aerodynamica Sinica, 2016, 34(1): 1-4. (in Chinese) |
| [20] |
Germano M, Piomelli U, Moin P, et al. A dynamic subgrid-scale eddy viscosity model[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(7): 1760-1765. DOI:10.1063/1.857955 |
| [21] |
Ducros F, Nicoud F, Poinsot T. Wall-adapting local eddy-viscosity models for simulations in complex geome-tries[C]. Proceedings of the 6th ICFD Conference on Numerical Methods for Fluid Dynamics, 1998: 293-299.
|
| [22] |
Kobayashi H, Ham F, Wu X. Application of a local SGS model based on coherent structures to complex geome-tries[J]. International Journal of Heat and Fluid Flow, 2008, 29(3): 640-653. DOI:10.1016/j.ijheatfluidflow.2008.02.008 |
| [23] |
Liao F, Ye Z Y, Zhang L X. Extending geometric conservation law to cell-centered finite difference methods on stationary grids[J]. Journal of Computational Physics, 2015, 284: 419-433. DOI:10.1016/j.jcp.2014.12.040 |
| [24] |
Liao F, Ye Z Y. Extending geometric conservation law to cell-centered finite difference methods on moving and deforming grids[J]. Journal of Computational Physics, 2015, 303: 212-221. DOI:10.1016/j.jcp.2015.09.032 |
| [25] |
洪正, 叶正寅. 各向同性湍流通过正激波的演化特征研究[J]. 力学学报, 2018, 50(6): 1356-1367. Hong Z, Ye Z Y. Study on evolution characteristics of isotropic turbulence passing through a normal shock wave[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(6): 1356-1367. (in Chinese) |
| [26] |
毛枚良, 邓小刚. 高阶精度线性耗散紧致格式的渐近稳定性[J]. 空气动力学学报, 2000, 18(2): 165-171. Mao M L, Deng X G. Boundary schemes and asymptotic stability for high-order dissipative compact schemes[J]. Acta Aerodynamica Sinica, 2000, 18(2): 165-171. DOI:10.3969/j.issn.0258-1825.2000.02.006 (in Chinese) |
| [27] |
Niederschulte M A, Adrian R J, Hanratty T J. Measurements of turbulent flow in a channel at low Reynolds num-bers[J]. Experiments in Fluids, 1990, 9(4): 222-230. DOI:10.1007/BF00190423 |
| [28] |
Kim J, Moin P, Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number[J]. Journal of Fluid Mechanics, 1987, 177: 133-166. DOI:10.1017/S0022112087000892 |
| [29] |
Dean R B. Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow[J]. Journal of Fluids Engineering, 1978, 100(2): 215-223. DOI:10.1115/1.3448633 |
| [30] |
Garnier E, Adams N, Sagaut P. Large eddy simulation for compressible flows[M]. London: Springer, 2009.
|



