2. 香港科技大学土木与环境工程系,香港 999077;
3. 工业装备与结构分析国家重点实验室,辽宁大连 116024
2. Department of Civil & Environmental Engineering, the Hong Kong University of Science & Technology, Hong Kong 999077, China;
3. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian 116024, China
后向(背向)台阶流动通常是指沿固体壁面发展的边界层在一个突然出现的台阶拐点与壁面分离, 并最终贴附于台阶下游壁面的流动形式.该流动是一种典型的分离流, 在自然界及工业界中广泛存在, 如沙丘背面, 截面发生突变的管道和燃烧室等.研究分析背向台阶流动的基本规律, 了解不同参数对流动现象及重新贴附距离、壁面换热系数等重要特征参数的影响, 具有显著意义.
边界层发生分离以后, 流动的强烈剪切作用会形成剪切层.因K-H不稳定性, 大尺度涡结构在剪切层中产生并发展. Eaton等[1]指出, 在发生分离初期(x<2H, H为台阶高度), 后向台阶剪切层与自由剪切层非常相似, 其无量纲特征频率为fθ/Uo≈0.012, 其中, f为频率, θ为剪切层动量缺损厚度, Uo为来流速度. Chun等[2-3]发现涡结构在剪切层中发生配对融合现象, 其频率沿剪切层逐渐减小, 至再附点附近降为fH/Uo≈0.2, 此后f变化减缓.该运动形式通常被称为台阶模态(step mode), 波动模态(wake mode)或涡脱模态(shedding mode).此外, Hasan[4]发现后向台阶流场内还存在一个特征频率为涡脱模态的1/5~1/12的摆动运动, 剪切层被周期性一分为二, 通常称作剪切层摆动频率(flapping). Spazzini等[5]通过流动显示及实时壁面切应力测量发现, 该摆动会在台阶下方形成一个低频变化的旋涡.
在现有的分离流控制手段中, 使用布置在分离点附近的合成射流是一种较常见的方式. Chun等[2]发现当激励频率fAH/Uo>0.8时, 分离区长度有所增加, 而fAH/Uo<0.8时, 分离区长度减小, 当fAH/Uo≈0.2时, 分离区长度最小. Yoshioka等[6-7]发现当fAH/Uo≈0.2时, Reynolds切应力的生成项达到最大, 使剪切层垂直于流向的动量传输能力达到最强, 从而使得分离区长度达到最小值.使用合成射流对后向台阶流场在扰动下的特性进行了初步研究[8-9], 发现不同频率扰动下流场特征参数改变存在显著区别, 靠近剪切层摆动频率的低频激励与其他频率区别最为明显.因此, 有必要对不同频率下流场的运动特性进行进一步详细分析.
snapshot POD方法可将由PIV获得的原始数据分解为互相正交的多个模态流速的叠加, 通过分析含能较高的数个主要流动模态, 可以得出该条件下流场的主要运动形式. Kostas等[10]使用该方法分别分析了无激励后向台阶流动的二维速度场和涡量场, 发现其大尺度涡旋结构存在相似性并存在于低阶模态当中. Buchmann等[11]分别使用快照POD及DMD方法分析了大迎角机翼表面的分离流动, 发现这两种方法可以得到相似的各尺度涡旋结构, 并分别对应数个模态.
通过对比各POD模态的时间常数, 可以获得各模态间的动态关系. Oberleithner等[12]用这一方法分析了圆形喷口流动在合成射流作用下的运动, 发现数个主要模态之间的相图关系近似于Lissajous图形, 因此能够确定其属于同一个协同振荡运动, 描述了相同周期的旋涡发展过程. Liné等[13]用该方法分析了二维混合流动, 发现了两个模态的相图近似于椭圆, 并分析了相点密度随模态系数的分布关系, 得到了与模拟相符的结论.
因此, 本文主要通过以上方法对PIV采集的不同频率激励下后向台阶流场特征运动进行分析, 获得了含激励流场的低阶模型.本文首先介绍实验设备并简述各分析方法的原理, 然后对得到的结果进行讨论, 最后进行总结.
1 实验方法 1.1 流场及激励装置本实验使用一座下吹式风洞提供来流, 该风洞由一台3 kW离心式风机驱动空气, 流经扩散段、静压箱以及收缩比为9:1的收缩段进入实验段.收缩段出口截面为0.3 m×0.3 m矩形, 出口风速Uo=5.7 m/s, 湍流度<2.0%.
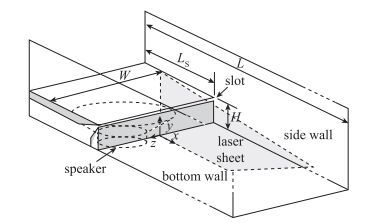
实验段及其附属设备如图 1所示.实验段全长0.72 m, 宽0.3 m, 底板为铝制, 左右均有高0.4 m的亚克力挡板, 一侧挡板为透明, 另一侧挡板及底板喷涂哑光黑色.在距实验段入口0.24 m处有一高度为H=0.025 m的后向台阶, 台阶转角尖端留有1 mm宽度狭缝, 狭缝方向与台阶平面夹角为45°.狭缝底端连接长×宽×高为0.22 m×0.28 m×0.02 m的立方体谐振腔、谐振腔下方安装有直径0.22 m, 阻抗8 Ω, 最大功率150 W的低音扬声器.以台阶立面与底板交界线中心为原点建立实验直角坐标系, 其中x轴与台阶立面垂直并平行于底板中线,y轴与底板垂直指向正上方.
|
| 图 1 后向台阶实验段 Fig.1 Schematics of test rig |
实验通过DSP数字信号处理开发板TI TMS320C6713DSK产生一定频率和幅值的正弦信号, 经过功率放大器后驱动低音扬声器, 使扬声器的振膜产生周期性运动以改变谐振腔体积, 从而在狭缝处产生周期性喷射/抽吸的零质量合成射流.实验中选择的激励频率为fA =10, 40, 80 Hz, 分别简称为低频、中频及高频激励.激励频率对应的无量纲化Strouhal数St=fAH/Uo分别为0.04, 0.18, 0.35, 分别对应剪切层摆动频率, 涡脱频率及更高频运动.实验中使用的激励强度为无量纲系数u′A/Uo=0.9, 其中u′A为无来流时由激励器产生的射流喷气阶段速度的均方根值, 通过在射流出口中央架设单丝热线探头测得.
1.2 烟线流动显示烟线流动显示技术可以显示并拍摄流动结构的瞬时变化情况, 帮助直观地察看流动状态.实验中在台阶背部x=0, z=0处沿y方向布置一根直径d=0.1 mm的304不锈钢线, 在Uo=5.7 m/s来流下其Reynolds数Uod/v=32, 并在线上使用刷子涂抹石蜡油作为发烟油.在实验段侧面架设一台佳能5D-Ⅱ相机用于拍摄流场, 并在流场上方合适位置架设佳能600EX-RT相机闪光灯提供瞬时照明.本实验使用航华SW2型烟线仪控制发烟、照明和拍摄动作, 其内置的4 400 μF电容在每次拍摄前预先完成充能.通过DSP输出与激励信号相差固定相位的拍摄触发脉冲信号, 该触发信号通过光电隔离系统传输给烟线仪, 烟线仪在接到拍摄触发信号后, 经过设定的延时控制烟线的发烟、闪光灯的闪光和相机的快门拍照.这样就可以拍摄出拍摄时刻呈固定相位关系的流动显示图像, 以观察流场的周期性变化情况.该技术的详细描述可见文献[14].
1.3 PIV及相位平均实验采用Lavision 2D PIV系统测量台阶中央z=0平面的流动速度分布, 对植物油进行加压雾化, 作为示踪粒子, 并于风洞扩散段注入.粒子直径约1 μm.使用脉冲持续时间4 ns的Litron Laser激光源通过偏光装置对台阶中央z=0平面进行照明, 其输出功率为200 mJ, 采用Lavision Highspeedstar高速相机对流场进行拍摄.为了尽量反映激励周期内更多相位状态的流动状态, 使用拍摄频率为49 Hz, 每实验条件拍摄2 000帧, 每帧包含间隔150 μs的一对图像, 图像像素为1 024 pixel×1 024 pixel.后期计算使用系统配属的Davis 8.1软件, 分析使用24 pixel×24 pixel的方形网格, overlap值设定为50%, 向量后处理采用中值、填充、平滑方式.
当采用固定拍摄频率49 Hz对固定频率激励下的流场进行PIV拍摄时, 得到的瞬时速度场分别对应于激励周期中49个不同相位.将对应各相位的速度场分别进行平均, 即可得到相位平均速度场.本实验中相位平均共使用1 960帧, 并将每个相位对应的40帧进行平均得到相位平均速度场.
1.4 snapshot POD方法本征正交分解法(proper orthogonal decomposi-tion, POD)是一种用于提取离散数据特征信息的数学方法, 其目的是把多维随机过程进行低维近似描述并提取复杂随机过程的本质特征.其基本思想是将随机量分解为由自身特征所确定的一组基函数来表示, 基函数的确定原则为在每一次分解的过程中使得最低阶的模式上含能最多.该方法通常用于将一段时间内的流场变化状态加以分解, 以识别其包含的主要运动形式的变化规律.
当对一组在M个空间点分别于N个相同时间点采集得到的数据进行POD分解时, 使用经典POD方法将得到M个模态, 并对应M组分解信号[15].当运用采集空间点数量M较大的采集方法时(例如PIV), 通常POD方法对应的计算量过大, 且得到的模态中大部分含能极小, 不包含流场重要运动特征.因此对于该类数据, 可以使用snapshot POD方法进行分解.该方法由Sirovich[16]提出, 其得到的模态与经典POD方法相同, 但仅求解N个模态及对应的N组分解信号.当运用该方法分解N远小于M的采集数据时, 可以大幅降低计算量及分解数据量, 且不影响对含能较高的主要模态及对应运动的分析.
使用snapshot POD方法进行分解时, 首先需要建立M×N阶数据矩阵, 矩阵中每个元素对应在每一特定位置(共M个)及时间采样点(共N个)测得的数据.实验中通过二维PIV对流场特定区域流速进行采集, 因此分别建立矩阵U(p, t)及V(p, t), 其中p∈1~M, t∈1~N, 分别对应每点的流向及切向瞬时速度.
去除各点数据的时间平均值可得到脉动流速:
| $\mathit{\boldsymbol{u}}\left( {p,t} \right) = \mathit{\boldsymbol{U}}\left( {p,t} \right) - \frac{1}{N}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{U}}\left( {p,{t_i}} \right)} $ |
| $\mathit{\boldsymbol{v}}\left( {p,t} \right) = \mathit{\boldsymbol{V}}\left( {p,t} \right) - \frac{1}{N}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{V}}\left( {p,{t_i}} \right)} $ |
使用去除时间平均值后的数据求出互相关矩阵R(τ=0).在经典POD方法中R为M×M矩阵, 而在snapshot POD方法中为N×N矩阵:
| $\mathit{\boldsymbol{R = }}\frac{{{\mathit{\boldsymbol{u}}^\prime }\mathit{\boldsymbol{u + }}{\mathit{\boldsymbol{v}}^\prime }\mathit{\boldsymbol{v}}}}{N}$ |
求解互相关矩阵R的N组特征值λn(n∈1~N)及对应特征向量φn, 它们分别对应分解后的第n阶模态:
| $\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{\varphi }}_n} = {\lambda _n}{\mathit{\boldsymbol{\varphi }}_n}$ |
对各阶模态的特征向量进行归一化, 并使用其计算归一化后的M维空间系数ψnx, ψny:
| $\mathit{\boldsymbol{\varphi }}_n^* = {\mathit{\boldsymbol{\varphi }}_n}/\sqrt {\sum\limits_{i = 1}^N {\mathit{\boldsymbol{\varphi }}_n^2\left( i \right)} } $ |
| $\mathit{\boldsymbol{\psi }}_n^x = \mathit{\boldsymbol{u\varphi }}_n^*/\sqrt {N{\lambda _n}} $ |
| $\mathit{\boldsymbol{\psi }}_n^y = \mathit{\boldsymbol{v\varphi }}_n^*/\sqrt {N{\lambda _n}} $ |
此时有
再使用其计算N维时间系数anx, any:
| $\mathit{\boldsymbol{a}}_n^x = {\mathit{\boldsymbol{u}}^\prime }\mathit{\boldsymbol{\psi }}_n^x$ |
| $\mathit{\boldsymbol{a}}_n^y = {\mathit{\boldsymbol{v}}^\prime }\mathit{\boldsymbol{\psi }}_n^y$ |
通过模态的空间与时间系数, 可求得对应该阶模态的速度场(M×N矩阵):
| ${\mathit{\boldsymbol{u}}_n} = \mathit{\boldsymbol{\psi }}_n^x\mathit{\boldsymbol{a}}_n^{x\prime }$ |
| ${\mathit{\boldsymbol{v}}_n} = \mathit{\boldsymbol{\psi }}_n^y\mathit{\boldsymbol{a}}_n^{y\prime }$ |
一般将分解得到的N个模态按照其对应特征值λn由大到小, 即对应含能由多到少进行排列, 越靠前的模态在整体中占比重越大.对靠前的部分模态进行分析, 可以得到流场中的主要运动形式.该方法的matlab编程及应用可参考文献[17-18].
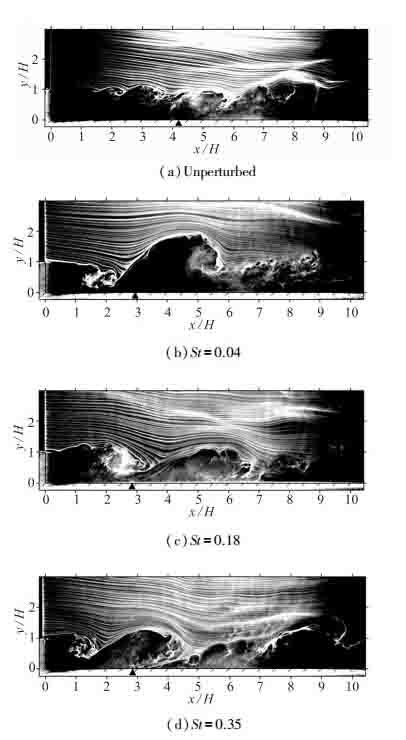
2 实验结果及讨论 2.1 烟线流动显示流场在不同激励频率下的流动状态可以使用烟线流动显示技术进行初步观察, 如图 2所示.其中有激励流场烟线显示图片的拍摄时刻均为激励正弦信号90°处, 黑色实心三角形代表剪切层的时均贴附位置.图中可见白色流线由x/H=0, y/H>1处发生并向下游发展, 而下方区域为回流区, 其中没有可见流线.这两个区域之间的交界线标志着流场剪切层在当前时刻的发展状况.在无激励条件下(图 2(a)), 由K-H不稳定性引起的大尺度旋涡在剪切层上形成与发展, 剪切层逐渐向下弯曲, 在x/H=6附近贴附于台阶表面.在低频激励下(图 2(b)), 剪切层迅速向下弯曲并在x/H=2处就与壁面接触, 流动贴附后的壁面附近(x/H=2~6) 出现了较大尺度的分离涡旋结构, 而贴附前剪切层中涡旋的尺度并未受到明显影响.随着激励频率提升至中高频(图 2(c)(d)), 贴附后壁面附近涡旋结构的尺度逐渐减小, 而贴附前剪切层中涡旋的尺度逐渐增大, 在高频下(图 2(d))可以观察到剪切层中涡旋与激励的明显对应关系, 称为“合拍”(lock-in)现象.这说明低频和高频激励对流场的影响产生的现象有着明显区别, 为了分析原因, 须对不同频率下流场的运动使用PIV进行详细记录和研究分析.
|
| 图 2 不同激励频率下流场烟线流动显示 Fig.2 Visualizations for different perturbed frequencies |
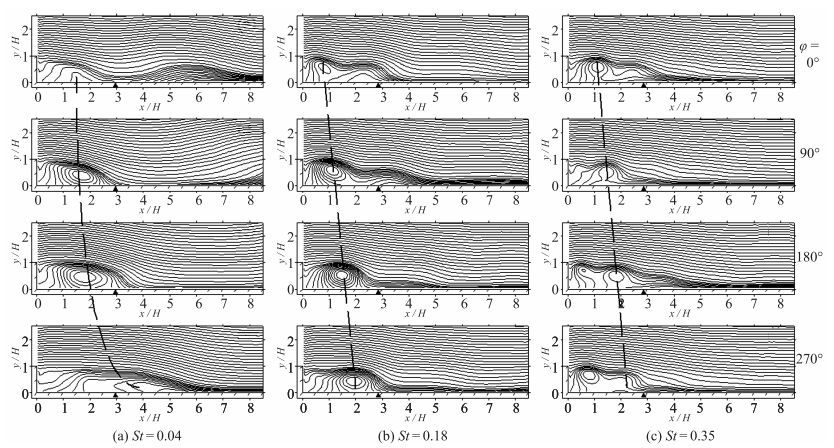
通过对激励周期不同相位下的相位平均速度场进行分析, 如绘制流线等, 可以得到流场随激励周期的变化规律, 进而分析激励对流场的影响作用方式.各激励频率下与激励正弦信号相位差分别为0, 90, 180及270°的相位平均流线, 如图 3所示, 黑色实心三角形代表剪切层的时均贴附位置.可以观察到不同条件下回流区旋涡的位置均随激励相位呈周期性变化, 说明激励对其产生了显著影响.各相位下回流区旋涡中心所在位置的变化可以反映出旋涡在激励影响下发展的规律, 低频St=0.04激励下回流区旋涡的中心所在位置连线为一条曲线, 这说明低频激励下回流区旋涡在激励周期0~ 90°范围内沿流向运动速度较慢, 在90~270°范围内沿流向运动速度逐渐加快.中高频激励下该连线近似为一条直线, 说明在中高频激励下回流区旋涡沿流向运动的速度在激励周期内近似不变.这一现象说明St=0.04附近的低频激励对流场的作用效果与中高频存在明显区别, 提示低频激励对流场的作用原理可能与中高频激励存在差别.
|
| 图 3 各激励频率下相位平均流线(只代表流向, 流线密度不代表流速) Fig.3 Phase averaged streamlines for different perturbed frequencies |
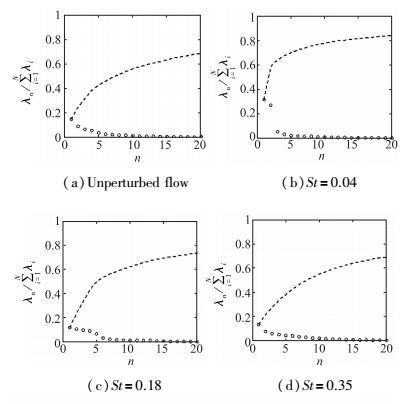
分别使用snapshot POD方法对不同激励条件下PIV测得的流动进行分解, 得到的前20阶模态特征值λ1~λ20, 如图 4所示.其中空心圆点代表该阶模态归一化后特征值
|
|
图 4 各条件下前20阶POD模态含能 |
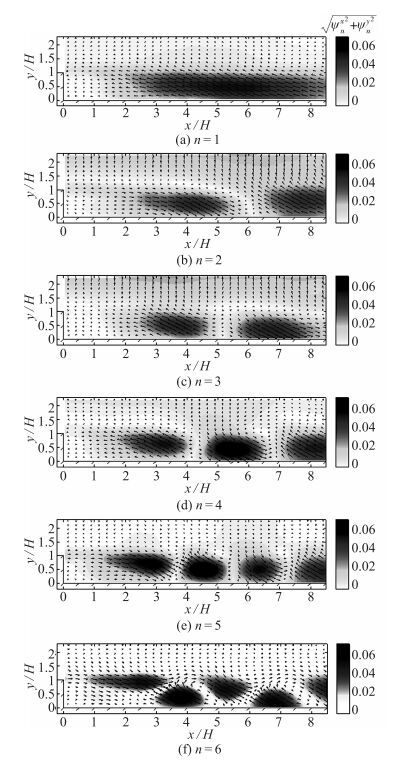
在已知模态的含能及相位关系的基础上, 分析低阶模态的空间系数ψnx, ψny, 可以得到其表征的空间运动形式.无激励流场的前6阶模态的空间系数分布如图 5所示, 图中灰度表示该点的脉动速度大小.可见无激励流场的低阶脉动运动均位于y/H=1平面以下.第1阶模态在实验可视范围内仅包含1块脉动速度较高的区域, 随着阶数逐渐增大, 可见的区域数量逐渐增多, 2~3阶可见2块, 4阶可见3块, 5阶可见4块, 6阶可见5块.这说明在前6阶内越低阶的模态所描述的运动形式尺度越大.除1阶模态外, 其他模态在相邻的高脉动速度区域内流向都是近似相反的, 说明其是由两块区域间的旋涡产生的.此外, 除第6阶模态较为特殊外, 其他阶模态高速区域的垂向位置都几乎相同.
|
| 图 5 无激励流场前6阶模态的空间特征.箭头为ψnx, ψny的矢量分布, 背景灰度对应矢量长度 Fig.5 Spatial functions for modes 1~6 of unperturbed flow |
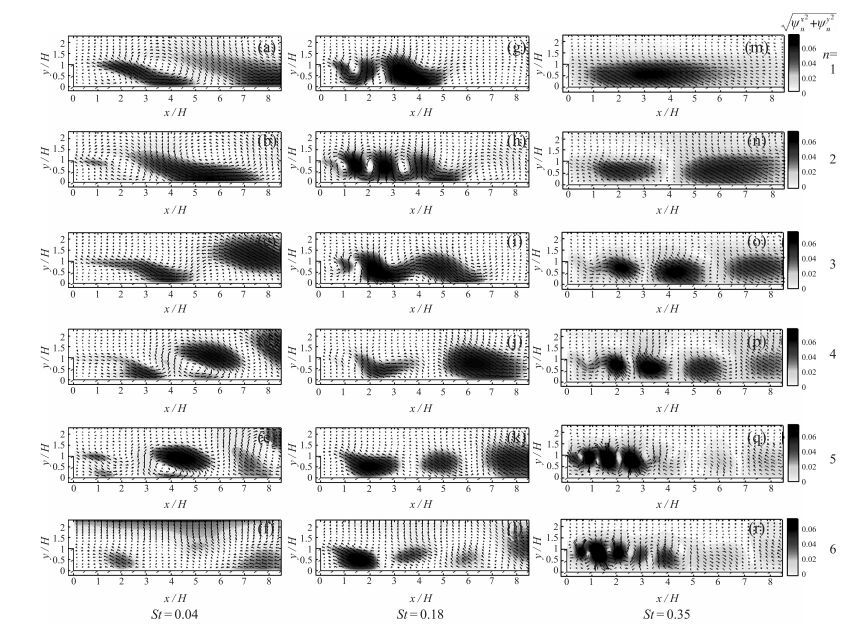
进一步分析各频率激励下低阶模态的空间特征, 如图 6所示.在低频(St=0.04) 激励条件下(图 6(a)~(f)), 占总含能59%的前两阶模态(图 6(a)(b))中高速区域均为剪切层区域, 在两阶模态中其流向位置明显不同, 即这两阶模态描述了剪切层位置的往复摆动过程.这说明剪切层位置的摆动是低频激励下的最主要运动形式.观察3~5阶模态(图 6(c)~(e))的空间特征可见, 除剪切层部分外, 流场中还存在着逐渐远离台阶底面的高脉动速度区域, 这说明剪切层的摆动运动在贴附后造成了沿台阶底面向后滚动且尺度逐渐增大的涡旋结构, 使得y/H>1的流场也受到影响而发生震荡.该现象只存在低频激励下的流场中.
|
| 图 6 不同频率激励下流场前6阶模态的空间特征 Fig.6 Spatial functions for modes 1~6 of different perturbed frequencies |
在激励频率提升至中频St=0.18时(图 6(g)~(l)), 前4阶模态(图 6(g)~(j))中的高脉动速度区域形状与其他模态出现了明显的区别.剪切层中多块高脉动速度区域之间表现出了显著的互相影响效果, 甚至互相连接.这说明该条件下剪切层中旋涡的强度明显较高, 使得多块脉动动能较高的区域之间出现了显著的掺混现象.这符合其他研究者观察到的, 涡结构在剪切层中发生配对融合现象的结果, 同时说明使用St≈0.2的频率进行激励可以使得该种运动显著增强.这种现象在模态5, 6(图 6(k)(l))中已不再显著出现, 说明使用前4阶模态近似概括此现象动态特征是合适的.在该条件下并未看到覆盖整个剪切层的模态, 说明剪切层的运动在该条件下不是主要运动形式.
当激励频率提升至高频St=0.35时(图 6(m)~(r)), 第1阶模态的空间特征与其他模态明显不同, 只存在一片范围较大的高脉动速度区域, 这与无激励条件下的第1阶模态类似, 表现了覆盖全剪切层的速度脉动.因此认为激励并未对该阶模态产生显著影响. 2~6阶模态表现了旋涡沿流向逐渐传播的运动形式, 是该条件下激励造成的主要影响.
2.4 低阶模态间相位关系为分析不同频率激励作用下含能较大的主要模态间的关系, 计算前5阶模态的N维模态时间系数:
| ${\mathit{\boldsymbol{a}}_n}\left( i \right) = \mathit{\boldsymbol{a}}_n^x\left( i \right) + \mathit{\boldsymbol{a}}_n^y\left( i \right)$ |
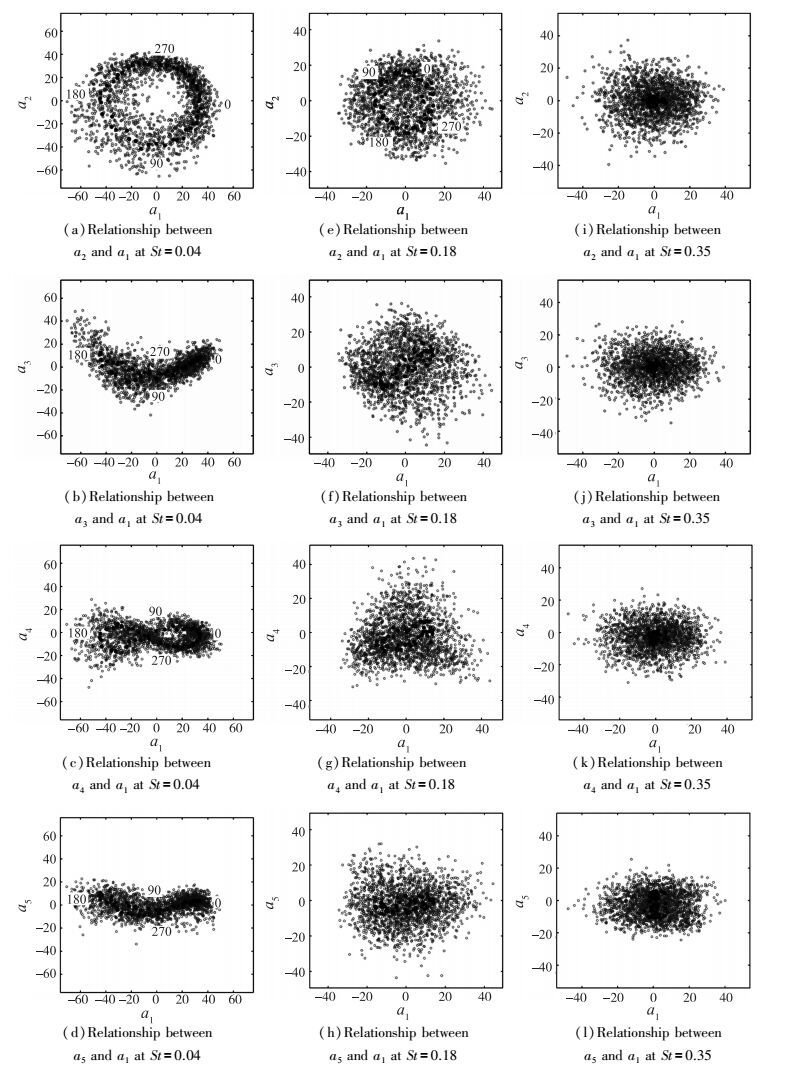
其中i∈1~N, 并分别以a1(i)为横坐标, 绘制在采样时间内a2(i)~a5(i)与a1(i)的相对关系, 即模态2~5与模态1的相位关系, 见图 7.每个子图中包含2 000个空心圆点, 对应PIV拍摄2 000帧时的相位.各条件下模态相位点的分布各不相同, 其中部分模态相点的分布显示出特殊的形状.为更清晰地观察相点随时间的分布, 并找出其与激励周期之间的对应规律, 使用相位平均方法, 将1 960个相点对应至49个相位之上并进行平均, 得到相位平均后的时间系数
|
|
图 7 前5模态时间系数an=anx+any(空心)及相位平均后 |
分析相点曲线图形可知, 低频激励下第1, 2阶模态的曲线近似圆形, 表示其周期同等于激励周期且相位相差90°, 因此这两个模态描述流场中同一由正弦激励引起的运动, 即剪切层的往复摆动.当激励器出口速度为0时(0°, 180°), 第2阶模态系数a2为0;当激励器出口抽吸速度最大(90°)时a2最小, 而出口喷射速度最大(270°)时a2最大.同样, 分析3~5阶模态与1阶模态的关系曲线可知其频率均为激励频率的2倍, 其中第4阶模态与第1阶模态起始相位差近似为0, 因此曲线近似于8字型.
当激励频率提升至中频St=0.18时(图 7(e)~(h)), 仍能看出相位平均后的相点近似于连续曲线, 但相点明显变得更杂乱, 相位平均前的相点分布范围也距曲线更远.这表示模态运动与激励的相关性较低频低, 随机性较强.其中, 第1, 2阶模态的曲线仍近似圆形, 说明其周期同等于激励周期且相位相差90°, 共同描述旋涡在剪切层中传播的运动过程.
当激励频率提升至高频St=0.35时(图 7(i)~(l)), 相位平均后的相点均分布于原点附近, 这说明该条件下每个主要模态中激励的影响较其他条件更弱, 即高频激励并未在流场中产生大规模的改变.
2.5 使用低阶模态重构流场由上节分析可知, 激励对流场内大尺度运动的影响主要集中体现于含能较大的低阶模态当中.因此, 尝试使用部分低阶模态的相位平均后的时间系数
|
|
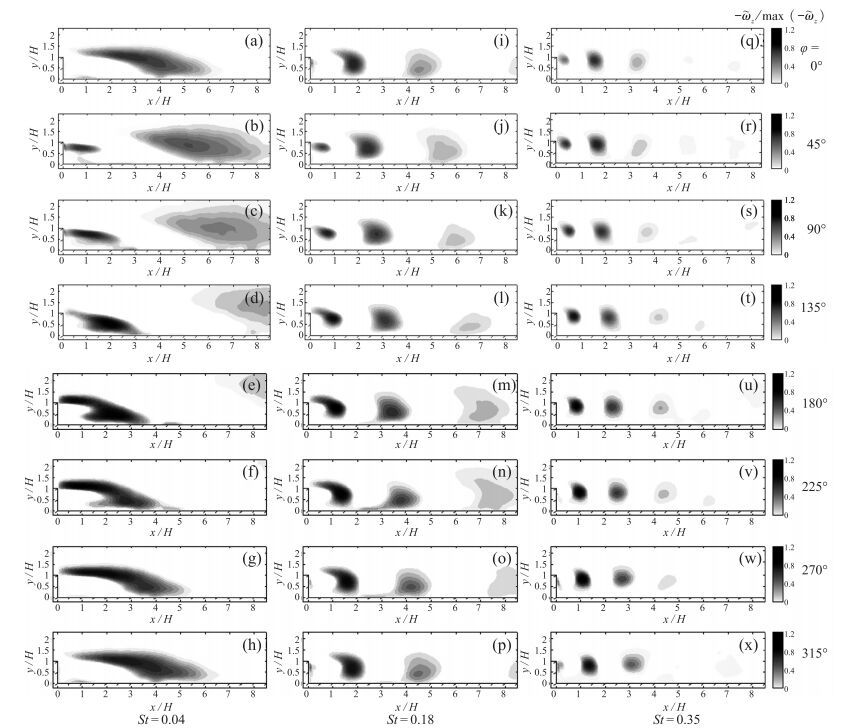
图 8 使用低阶模态还原脉动涡量场 |
低频激励条件下(St=0.04), 旋涡在激励器开始抽吸时(45°, 图 8(b))于台阶顶角产生, 并随抽吸进一步增大(图 8(b)~(d)).当抽吸过程结束时(180°, 图 8(e)), 旋涡贴附于台阶底面, 使得整个剪切层都受到激励影响而改变.随着激励器的喷射过程(图 8(e)~(h)), 剪切层形状逐渐发展并沿流向运动, 与壁面的接触位置逐渐后移, 并形成沿壁面向后滚动的大尺度旋涡结构.这一结构在下一周期(图 8(a)~(d))中仍然可见, 并快速向下游移动, 其速度显著加快, 这与在2.2节中观察相位平均流线所得到的结论相同.即在低频激励下, 激励主要对分离剪切层产生影响, 使得剪切层沿流向大幅度摆动, 并形成下游的大尺度旋涡结构.这一运动在实验激励强度下占总动能的59%以上, 并可用两个正交模态进行近似描述.符合之前相关研究得出的低频激励主要影响剪切层摆动的结论.
当激励频率提升至中频St=0.18时(图 8(i)~(p)), 旋涡在流向的尺度明显变小, 不再覆盖整个剪切层, 而是在剪切层中形成并沿剪切层向后传播.前一激励周期形成的旋涡在下一激励周期才于时均贴附点附近与台阶底面接触, 然后沿台阶底面继续向下游运动, 在接触后尺度并未如低频条件下一样显著增大.这说明中频激励产生的脉动运动主要为在剪切层中生成和传播的旋涡.同时, 在该条件下未看到覆盖剪切层的涡旋结构, 可以说明剪切层的位置改变在该条件下并不是主要的运动形式.
在高频激励St=0.35下(图 8(q)~(x)), 旋涡同样在剪切层中形成并沿剪切层向后传播, 其尺度较中频条件下更小.这说明激励频率超过了激励剪切层中旋涡的最佳频率, 使得响应减小并被更快耗散掉, 造成该条件下激励的影响较其他条件弱.
3 结论在对后向台阶流场进行合成射流激励并研究不同激励频率对流场发展影响的过程中, 通过对流场参数的测量及流动状态的显示, 注意到流场在St≈0.04的低频激励条件下与St≥0.18的中、高频条件下表现完全不同.为了详细分析这一现象的成因及实质, 将通过PIV方法测得的流速分布数据进行POD分解, 对含脉动动能较大的主要模态间的关系采用相位平均手段进行分析, 并试图使用数个主要模态对流场在激励下的主要脉动运动形式进行还原.结果表明, 流场在各条件下的主要运动形式均可用5个以内的低阶模态加以基本概括.模态间的相位关系可以使用相图进行分析, 在低频激励下的模态相图近似于Lissajous图形, 可以表示模态间的周期及相位关系.通过分析还原得到的各相位涡量场变化, 证实低频激励主要影响剪切层整体摆动且响应较大, 而中高频激励主要影响剪切层内旋涡的生成与发展.这与之前研究中的流场参数变化及显示结果吻合.因此, 使用snapshot POD分解法寻找复杂流场中主要运动形式, 并使用低阶模态为其建立简化模型的方法是合适的, 而后向台阶流场在激励作用下的特性仍需要通过更多的方法及分析进行进一步研究.
致谢: 本文研究得到国家自然科学基金项目11572078及973项目2014CB744100的资助.| [1] | Eaton J K, Johnston J P. A review of research on subsonic turbulent flow reattachment[J]. AIAA Journal, 1981, 19(9): 1093-1100. DOI:10.2514/3.60048 |
| [2] | Chun K B, Sung H J. Control of turbulent separated flow over a backward-facing step by local forcing[J]. Experiments in Fluids, 1996, 21(6): 417-426. DOI:10.1007/BF00189044 |
| [3] | Chun K B, Sung H J. Visualization of a locally-forced separated flow over a backward-facing step[J]. Experiments in Fluids, 1998, 25(2): 133-142. DOI:10.1007/s003480050217 |
| [4] | Hasan M A. The flow over a backward-facing step under controlled perturbation:laminar separation[J]. Journal of Fluid Mechanics, 1992, 238: 73-96. DOI:10.1017/S0022112092001642 |
| [5] | Spazzini P G, Iuso G, Onorato M, et al. Unsteady behavior of back-facing step flow[J]. Experiments in Fluids, 2001, 30(5): 551-561. DOI:10.1007/s003480000234 |
| [6] | Yoshioka S, Obi S, Masuda S. Organized vortex motion in periodically perturbed turbulent separated flow over a backward-facing step[J]. International Journal of Heat and Fluid Flow, 2001, 22(3): 301-307. DOI:10.1016/S0142-727X(01)00092-3 |
| [7] | Yoshioka S, Obi S, Masuda S. Turbulence statistics of periodically perturbed separated flow over backward-facing step[J]. International Journal of Heat and Fluid Flow, 2001, 22(4): 393-401. DOI:10.1016/S0142-727X(01)00079-0 |
| [8] | Li Z Y, Bai H L, Gao N. Response of turbulent fluctuations to the periodic perturbations in a flow over a backward facing step[J]. Theoretical and Applied Mechanics Letters, 2015, 5(5): 191-195. DOI:10.1016/j.taml.2015.08.002 |
| [9] |
李卓越, 高南, 白宏磊. 零质量射流对后向台阶分离流场影响的实验研究[C]. 2015中国力学大会, 上海, 2015.
Li Z Y, Gao N, Bai H L. The forced flapping motion of a separated shear layer over a backward facing step[C]. The Chinese Congress of Theoretical and Applied Mechanics-2015, Shanghai, 2015(in Chinese). |
| [10] | Kostas J, Soria J, Chong M S. A comparison between snapshot POD analysis of PIV velocity and vorticity data[J]. Experiments in Fluids, 2005, 38(2): 146-160. DOI:10.1007/s00348-004-0873-4 |
| [11] | Buchmann N A, Kitsios V, Atkinson C, et al. Investigation of coherent structures and dynamics using POD and DMD of a separated airfoil subjected to ZNMF jet forcing[A].//Instability and Control of Massively Separated Flows[M]. Berlin:Springer International Publishing, 2015:33-38. |
| [12] | Oberleithner K, Sieber M, Nayeri C N, et al. Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown:stability analysis and empirical mode construction[J]. Journal of Fluid Mechanics, 2011, 679(7): 383-414. |
| [13] | Liné A, Gabelle J C, Morchain J, et al. On POD analysis of PIV measurements applied to mixing in a stirred vessel with a shear thinning fluid[J]. Chemical Engineering Research and Design, 2013, 91(11): 2073-2083. DOI:10.1016/j.cherd.2013.05.002 |
| [14] | Liu X H, Gao N. An improved smoke-wire visualization technique for flow with relatively high velocities[C]. Proceedings of the 4th International Conference on Experimental Fluid Mechanics, Beijing, 2014:12-15. |
| [15] | Holmes P, Lumley J L, Berkooz G. Turbulence, coherent structures, dynamical systems and symmetry[M]. Cambridge:Cambridge University Press, 1998:1-382. |
| [16] | Sirovich L. Turbulence and the dynamics of coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571. DOI:10.1090/qam/1987-45-03 |
| [17] | Chen H, Reuss D L, Hung D L, et al. A practical guide for using proper orthogonal decomposition in engine research[J]. International Journal of Engine Research, 2013, 14(4): 307-319. DOI:10.1177/1468087412455748 |
| [18] | Chen H, Reuss D L, Sick V. On the use and interpretation of proper orthogonal decomposition of in-cylinder engine flows[J]. Measurement Science & Technology, 2012, 23(8): 755-766. |



