2. 中航工业直升机设计研究所, 江西景德镇 333001;
3. 西北工业大学翼型叶栅空气动力学国防科技重点实验室, 陕西西安 710072
2. AVIC China Helicopter Research and Development Institute, Jingdezhen 333001, China;
3. National Key Laboratory of Science and Technology on Aerodynamic Design and Research, Northwestern Polytechnical University, Xi'an 710072, China
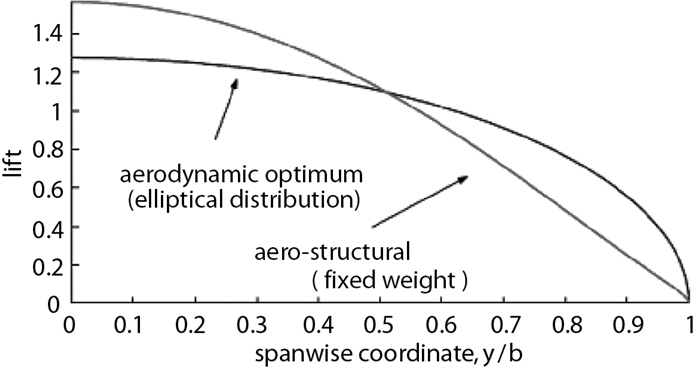
多学科优化设计的模型比单学科更接近真实的系统, 具有充分挖掘系统性能潜力的优势,在近年来获得了国内外的高度重视.对于飞行器设计来说, 气动与结构的耦合优化设计能够获得比单学科更好的结果, 并能带来设计理念的变化.比如, 气动学科认为亚音速机翼展向环量分布呈椭圆形时升阻比最大, 在以航程为设计目标, 经过气动与结构的多学科优化设计后, 实际最优环量分布如图 1所示[1].可见在考虑了结构特性之后, 机翼的最佳环量并非气动学科的最优环量分布.因此多学科优化设计对传统的飞行器如运输机等的设计及无成熟的设计经验可循的新概念飞行器如超音速飞行器[1, 2]、桁架支撑飞行器[3]等的设计都具有重要意义, 国外许多著名研究机构如NASA,DLR,ONERA等和许多著名大学如斯坦福大学,密歇根大学,纽约州立大学,多伦多大学等都对其开展了广泛和深入的研究, 极大地推动了气动/结构多学科优化设计的发展.
|
| 图 1 不同优化方法优化结果的环量分布比较 Fig.1 Lift distributions of results optimized by different methods |
在飞行器的气动/结构优化设计中, 各学科分析方法的精度极大地影响了优化设计结果的质量、可信度和效率.因此在飞行器设计特别是详细设计阶段, 采用高精度的分析方法进行多学科优化设计是非常有必要的.采用高精度的分析工具将带来计算量剧增、优化效率急剧下降的问题.例如在CFD/CSD(computational fluid dynamics/computational structural dynamics)耦合多学科优化设计中, 在PC机上一次静气动弹性分析通常至少需要十数小时, 而优化设计动辄需要数百甚至数千次的CFD,CSD分析, 因此提高优化设计效率成为包括飞行器气动/结构耦合优化设计在内的基于高精度分析方法的所有多学科优化设计面临的共同问题.巨大的计算量成为限制基于CFD/ CSD的多学科优化设计在飞行器设计中的大量应用的关键因素, 制约了我国飞行器设计水平的进一步提高.
近年来国内在基于高精度分析方法的气动结构多学科优化设计方面开展了一些研究工作, 但主要集中于应用现有成熟优化设计方法与学科评估软件进行集成应用, 以各种代理模型为基础开展优化设计[4-6].在气动与结构特性评估方法方面,则采用了一般的松耦合静气动弹性分析方法, 缺少创新的方法.
针对以上问题, 本文拟开展飞行器气动/结构多学科优化设计, 采用高精度的学科分析方法, 通过具体分析飞行器气动与结构的关系, 构建创新的设计方法来提高优化设计效率, 突破长期以来基于高精度学科分析方法的气动/结构多学科优化设计由于效率低而很难在工程中广泛应用的障碍, 推动我国飞行器设计水平的进步.
1 飞行器气动结构特性分析方法 1.1 气动与结构特性分析方法采用N-S方程进行气动特性分析, 在三维Descartes坐标系下, 守恒型的N-S方程可写为
| $ \frac{{\partial Q}}{{\partial t}} + \frac{{\partial E}}{{\partial x}} + \frac{{\partial F}}{{\partial y}} + \frac{{\partial G}}{{\partial z}} = \frac{1}{{Re}}\left( {\frac{{\partial R}}{{\partial x}} + \frac{{\partial S}}{{\partial y}} + \frac{{\partial T}}{{\partial z}}} \right). $ |
本文采用有限体积方法求解N-S方程, 空间离散格式为SLAU格式[7], 湍流模型为SA模型, 时间推进方式为LU-SGS方法.为了提高计算效率, 采用了并行计算多重网格等措施加速收敛.
对于多自由度系统, 忽略结构阻尼, 其受迫振动的运动微分方程为
| $ \mathit{\boldsymbol{M\ddot x}}\left( t \right) + \mathit{\boldsymbol{Kx}}\left( t \right) = \mathit{\boldsymbol{f}}\left( t \right). $ | (1) |
其中,M, K分别表示与气动计算无关的结构质量矩阵刚度矩阵;x(t)表示待求的结构变形矢量;f(t)表示作用在结构上的气动力矢量, 也就是从气动计算中传递过来的气动力.正是气动力把CFD和CSD两个系统联系起来.对于静气动弹性, 结构变形与时间无关, 因此方程(1) 变为
| $ \mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{K}}^{ - 1}}\mathit{\boldsymbol{f}}\left( t \right) = \mathit{\boldsymbol{Cf}}. $ |
其中,C为结构柔度矩阵.对于结构方程采用有限元方法进行离散求解.
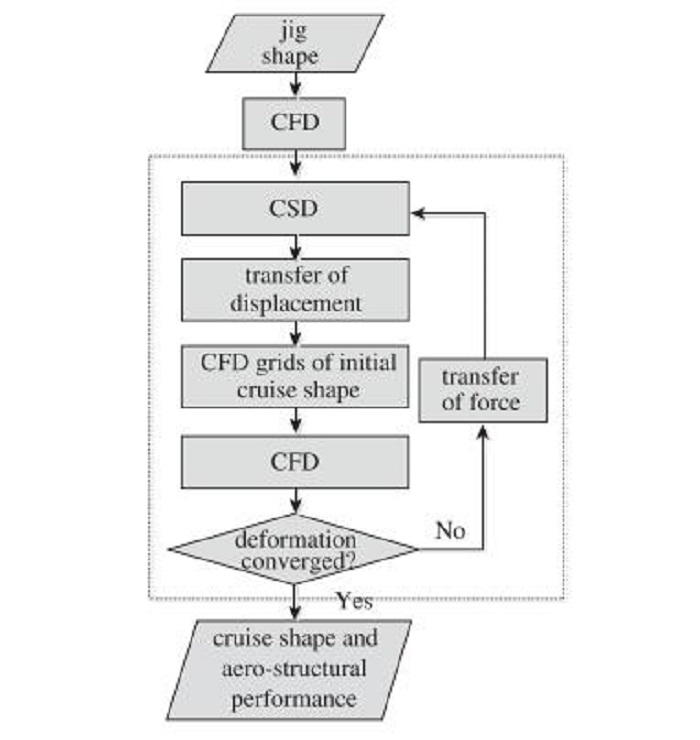
1.2 飞行器气动/结构特性分析方法一般的气动/结构耦合多学科优化设计均以型架外形为优化设计对象, 通过静气动弹性分析获得飞行器的气动与结构特性.由于需要反复调用气动与结构分析模块, 因此效率低.典型的CFD/CSD松耦合静气动弹性分析的流程如下:
(1) 对型架外形进行CFD分析, 获得其气动载荷.
(2) 将气动力、重力和发动机推力转换到型架外形结构有限元模型上.
(3) 进行结构变形计算, 获得结构网格点的位移, 对该位移进行插值, 构建初始巡航外形CFD表面网格点, 根据表面网格生成新的空间网格.
(4) 进行CFD分析, 获得巡航外形对应的气动特性.
(5) 判断变形是否收敛.如果不收敛, 则将气动载荷插值传递到型架外形有限元模型, 返回(3);否则退出.
该流程如图 2所示.
|
| 图 2 CFD/CSD松耦合静气动弹性分析流程图 Fig.2 Flowchart of loosely-coupled static aeroelastic analysis |
我们的目标是提高巡航构型的气动与结构性能.考虑到对飞行器巡航外形进行型架外形修正可在得到型架外形的同时获得巡航外形的结构特性(应力分布及相对于型架外形的应变)这个特点, 提出新的设计思路:直接以巡航构型为设计对象(巡航外形由几何外形参数化方法给出, 与一般的气动单学科的优化设计一致), 对其进行参数化与多学科优化设计.这样, 对于给定的巡航外形, 其气动特性可以直接获得, 不再需要经过反复迭代.只需要再获得巡航外形的结构特性, 就可以对巡航外形进行优化设计.
首先考虑最简单的Aly所提出的型架外形修正方法.该方法直接将巡航外形的气动力与重力反向作用在巡航外形的有限元模型上, 通过结构分析获得变形后的外形, 即为型架外形.同时也可获得结构的应力、应变, 但此应力、应变与实际相差较大, 具体表现为如果我们对采用该方法获得的型架外形进行静气动弹性分析, 会发现所得的外形与原来的巡航外形并不重合, 且应力、应变与前面修正时获得的不一致.
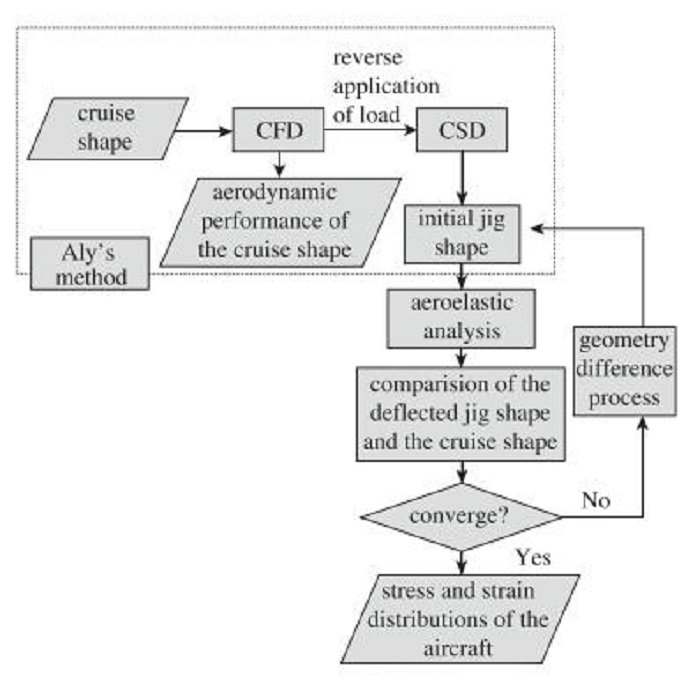
为了获得精度较高的结构特性, 可以采用经过改进的高精度常规型架外形修正方法(conventional jig shape correction, CJSC)[8], 流程如下:
(1) 经过气动计算获得巡航外形气动载荷, 将气动力重力和发动机推力反向作用到结构模型上进行结构变形计算, 获得初始型架外形.
(2) 对获得的型架外形进行静气动弹性分析.
(3) 比较变形后的型架外形与巡航外形的差别.如两者的差别不满足某一收敛准则,将该差量经过处理反馈叠加到型架外形上, 更新型架外形, 转(2);否则退出.
该流程如图 3所示.
|
| 图 3 改进的型架外形修正方法 Fig.3 Improved jig shape correction method |
通常在气动/结构多学科优化设计中, 气动与结构特性评估只需要一次静气动弹性分析即可完成, 上述过程需要反复调用静气动弹性分析模块, 显然达不到减小计算量提高效率的目的.
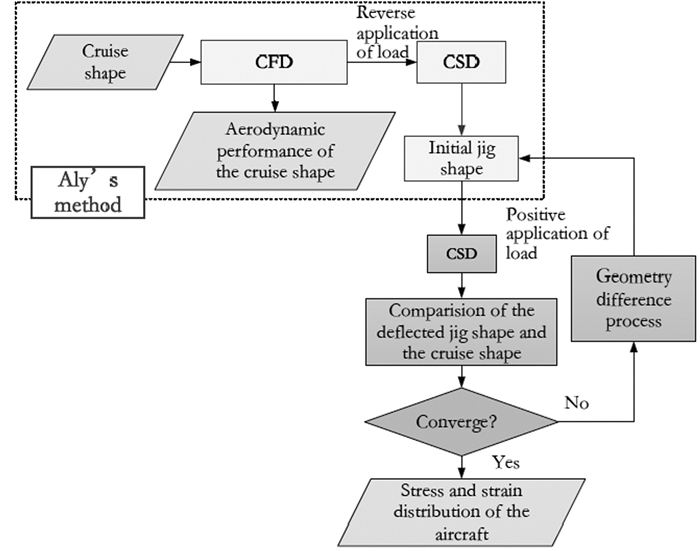
注意到以上流程中, 在达到收敛状态时, 作用在型架外形有限元模型上的气动力其实就是巡航外形的气动力.据此我们提出改进的飞行器气动/结构特性评估方法, 命名为结构模型反迭代方法(reverse iteration of structural model, RISM)[9].其流程如下:
(1) 经过气动计算获得巡航外形气动载荷, 将气动力、重力和发动机推力反向作用到结构模型上, 进行结构变形计算, 获得初始型架外形.
(2) 将巡航外形的气动载荷等加载到型架外形的结构模型上, 进行结构变形计算.
(3) 比较变形后的型架外形与巡航外形的差别.如两者的差别不满足某一收敛准则, 将该差量经过处理反馈叠加到型架外形上, 更新型架外形, 转(2);否则退出.
该流程如图 4所示.经过这个流程可以同时获得飞行器的气动特性最大应力与最大变形.
|
| 图 4 结构模型反迭代方法流程图 Fig.4 Flowchart of RISM |
从以上过程可以看出, 整个过程只需要进行一次气动特性评估, 有限元分析则需要反复调用.由于一般优化中有限元分析的时间相比CFD分析的时间可以忽略不计, 而一般的松耦合静气动弹性分析一般需要进行5~10次的气动特性分析, 因此本方法相比于传统的静气动弹性分析可以将飞行器气动与结构特性分析效率提高4倍以上.在松耦合静气动弹性分析中, 飞行器型架外形有限元网格不更新, 计算结构变形后的有限元网格的目的是插值获得变形后的气动外形及相应的气动载荷, 并将新的气动载荷传递给有限元模型.因此, 在松耦合静气动弹性分析过程中,CFD网格与有限元模型中的节点载荷反复更新; 在RISM方法中, CFD网格与气动载荷始终不变, 型架外形有限元网格则不断更新,以寻找与该巡航外形和气动载荷匹配的型架外形.
设巡航外形有限元网格坐标矢量为Xc, 巡航外形与型架外形之间的有限元网格坐标差为U.型架外形在巡航外形气动载荷作用下的应变也就是U, 而型架外形的有限元网格坐标矢量为Xc-U.型架外形变形的控制方程可写为
| $ \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{X}}_{\rm{c}}}, \mathit{\boldsymbol{U}}} \right)\mathit{\boldsymbol{U - F}} = 0. $ | (2) |
其中K(Xc, U)为型架外形的结构刚度矩阵, 由巡航外形的有限元网格坐标矢量Xc,应变U和材料属性等决定; F为气动载荷与重力的合力.
方程(2) 为关于U的非线性代数方程, 可采用松弛迭代方法进行计算.首先采用Aly的方法获得U的初始U0, 然后采用式(3) 进行迭代:
| $ {\mathit{\boldsymbol{U}}_{k + 1}} = \left( {1 - \mathit{\boldsymbol{\omega }}} \right){\mathit{\boldsymbol{U}}_k} + \mathit{\boldsymbol{\omega K}}{\left( {{\mathit{\boldsymbol{X}}_{\rm{c}}}, {\mathit{\boldsymbol{U}}_k}} \right)^{ - 1}}\mathit{\boldsymbol{F}}. $ | (3) |
其中k=0, 1, …; ω为松弛因子, 其取值范围为(0, 1).
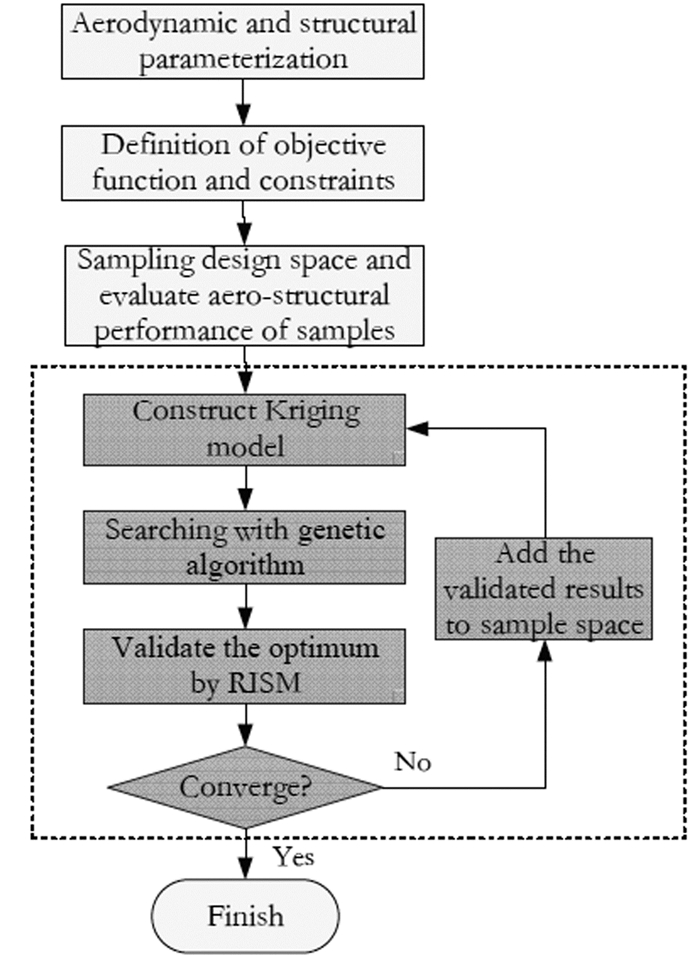
2 气动结构耦合多学科优化设计框架由于CFD/CSD耦合计算的计算量非常大, 因此本文采用基于代理模型的优化设计方法来提高优化效率.采用Latin超立方取样, 获得较为均匀的样本空间, 采用RISM方法获得样本的气动与结构特性.代理模型选取当前被广泛应用的Kriging模型.利用遗传算法对所建立的代理模型进行搜索, 搜索结果采用RISM方法分析校核并加入样本集, 重新进行训练和搜索直到校核的目标特性不再变化.该流程如图 5所示.
|
| 图 5 气动结构多学科优化设计框架 Fig.5 Framework of aero-structural multi-disciplinary optimization |
以某无人机为例, 对本文建立的气动结构特性分析方法进行验证.该无人机巡航状态时的平均质量为1136kg, 飞行速度为0.6M, 飞行高度为20km, 半展长为8.0m, 展弦比为17.6, 巡航升力系数为0.55.采用双梁结构, 前后梁分别位于当地弦长的15%和65%处, 并布置了长桁与肋板.
在文献[6]中, CFD网格的表面网格与有限元网格并不重合, 必须进行流固耦合数据传递, 因此会引入误差.为了研究RISM方法本身的精度, 将CFD表面网格的点提取出来直接作为有限元模型的表面网格点.对应的CFD网格与有限元模型如图 6和图 7所示.

|
| 图 6 CFD网格 Fig.6 CFD grids |

|
| 图 7 机翼结构模型 Fig.7 Wing structural model |
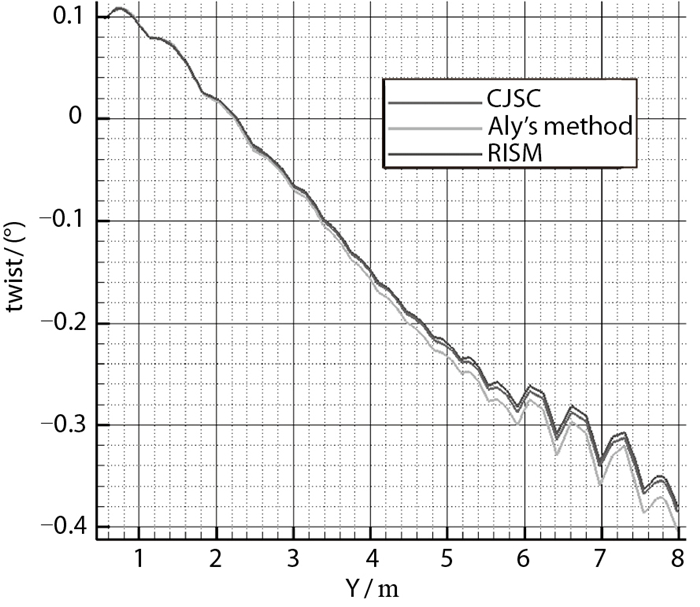
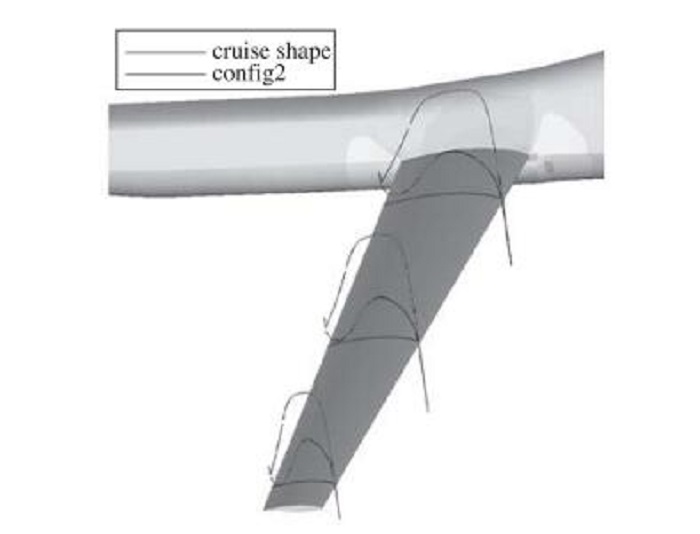
采用RISM方法对该无人机在巡航状态下的气动与结构特性进行分析.采用两种方法对RISM方法进行了验证.首先采用CJSC方法对该外形进行型架外形修正, 获得新的巡航外形(外形1);其次对采用RISM方法获得的型架外形进行静气动弹性分析, 获得变形后的型架外形(外形2). 表 1给出了不同方法评估的飞行器结构特性与质量. 表 2给出了不同方法计算的型架外形机翼翼尖扭转角. 图 8给出了对应外形的机翼沿展向扭转角分布. 表 3给出了不同外形的气动特性. 图 9为巡航外形与外形2的剖面压力分布比较.
| 下载CSV 表 1 不同方法计算的UAV结构性能 Tab.1 Structural performance of the UAV predicted by different methodologies |
| 下载CSV 表 2 不同方法计算的型架外形机翼翼尖扭转角 Tab.2 Wing tip twist angle of jig shape predicted by different methods |
|
| 图 8 不同方法计算的型架外形机翼剖面扭转角分布 Fig.8 Wing twist angles of jig shape predicted by different methods |
| 下载CSV 表 3 不同外形气动特性比较 Tab.3 Aerodynamic characteristics of different configurations |
|
| 图 9 不同外形剖面压力分布与云图比较 Fig.9 Pressure contours and sectional pressure distributions of different configures |
从表 1可见, RISM方法预测的型架外形与CJSC方法最大位移仅相差0.005m, RISM计算的最大应力比改进的型架外形修正方法大了2.5%.相比之下, Aly的方法最大应力比CJSC方法小了7.2%.几种方法计算的型架外形的质量均相差不多.在型架外形翼尖扭转角预测方面, RISM方法与CJSC方法仅相差0.0052°, 基本可忽略. Aly的方法与CJSC相比则达到0.0185°.不同方法最后获得变形后的型架外形气动特性均相差不大.
由于在气动结构多学科优化设计中, 飞行器的质量与阻力通常用来构造目标函数, 因此是最重要的.最大应力与应变用于构造约束条件, 相比较而言, 有一定的误差影响不大.由于RISM方法计算的质量与阻力均十分准确, 最大应力误差稍大一点, 但对优化设计影响不大, 故RISM方法适合于高精度的气动/结构多学科优化设计.
3.2 气动结构多学科优化设计对该无人机进行多学科优化设计过程中,以无人机的机翼为设计对象, 气动分析时考虑机身影响, 结构分析时仅对机翼进行分析.后文如不做特殊说明均指该无人机右半模型.
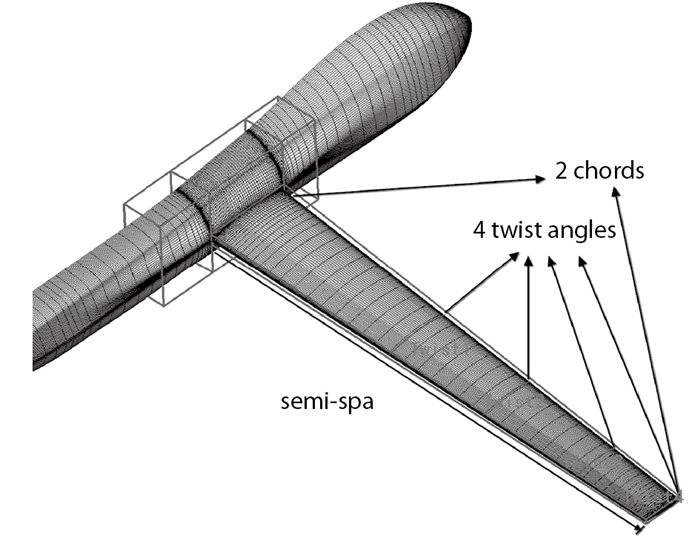
采用自由变形参数化方法[10, 11]对机翼的平面形状和4个剖面的扭转角进行了优化设计, 选取的剖面位置如图 10所示.平面形状设计变量包括根弦长、梢弦长、半展长.机翼有限元模型沿展向分为3段, 取每段的蒙皮厚度、前梁和后梁的梁缘条面积为设计变量, 共9个结构设计变量.设计变量共计16个.
|
| 图 10 几何外形参数化示意图 Fig.10 Parameterization of wing configuration |
以航程为优化设计目标, 计算公式如下:
| $ R = \frac{V}{C}\frac{L}{D}\ln \left( {\frac{{{W_1}}}{{{W_2}}}} \right). $ |
其中,R为航程, V为巡航速度, C为动力系统比燃油消耗, L/D为升阻比, W1和W2为巡航开始和结束时的飞行器重量.这里W1取为12357.8N, W2由空机重量等构成.优化的实质是降低机翼结构重量, 增加燃油重量W1-W2.飞行器巡航飞行时实际的升阻比随重量变化而变化, 为简单起见, 这里取为飞行器平均重量11132.8N时对应的升阻比, 且假定C为常量, 则最大化航程实际上等价于最大化L/Dln(W1/W2).
优化中计算升力系数的机翼参考面积固定为7.27m2, 此时对应的巡航升力系数为0.55.约束条件取为保持升力不变(即固定升力系数), 最大应力不超过95MPa, 对外露翼面积范围也应进行限制.固定升力系数是通过CFD计算过程中不断调整迎角达到的.该优化设计的优化模型如下所示.
| $ \begin{array}{l} {\rm{maximize}}:\;\;\;\;F = \frac{L}{D}\ln \left( {\frac{{{W_1}}}{{{W_2}}}} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{C_{\rm{L}}} = 0.55.\\ {\rm{subject}}\;{\rm{to}}:\;\;\;\;\;6.3{{\rm{m}}^2} < {S_{{\rm{wing}}}} < 6.7{{\rm{m}}^2}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\delta _{\max }} < 95{\rm{MPa}}. \end{array} $ |
其中,L与D分别为巡航的升力与阻力, Swing为右半机翼外露部分投影面积, δmax为机翼最大von Mises应力.
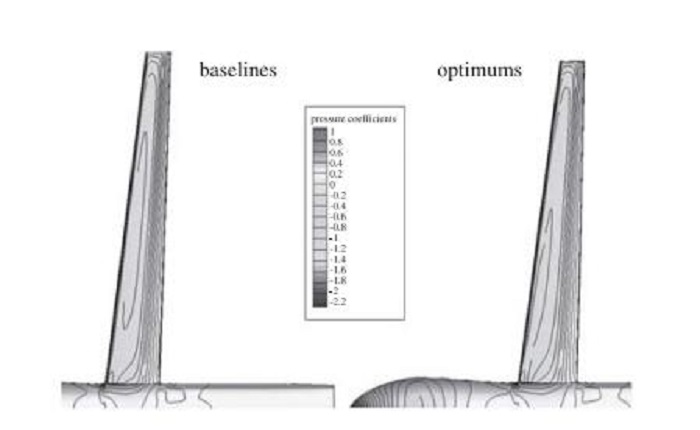
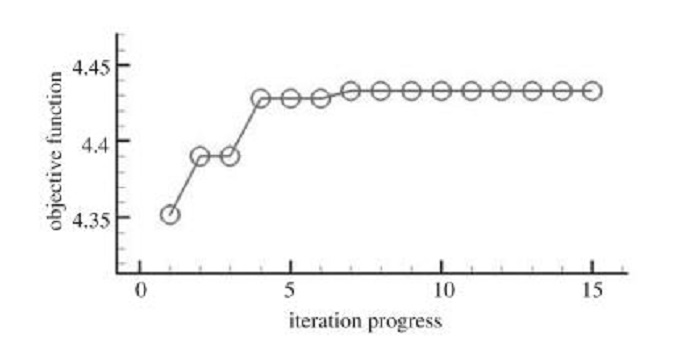
初始样本数取为280个, 优化时进行了15次校核, 故总的计算量为295次RISM气动/结构特性分析.优化前后相关变量的变化见表 4.对优化结果采用3.1节的方法进行了验证, 结果见表 5.优化前后机翼应力分布比较如图 11所示.优化前后机翼的上表面压力云图比较如图 12所示.平面形状比较如图 13所示, 收敛过程如图 14所示.由图可知, 优化后机翼翼根弦长增加, 展弦比减小, 导致了机翼最大应力有所减小.
| 下载CSV 表 4 优化结果 Tab.4 Optimization results |
| 下载CSV 表 5 优化结果校核 Tab.5 Optimization results validation |

|
| 图 11 优化前后机翼应力分布比较 Fig.11 Von Mises stresses before and after optimization |
|
| 图 12 优化前后表面压力云图比较 Fig.12 Pressure contour comparisons before and after optimization |

|
| 图 13 优化前后平面形状比较 Fig.13 Planform comparisons before and after optimization |
|
| 图 14 优化过程收敛曲线 Fig.14 Convergence history of the optimization |
可见, 优化后全机阻力减小0.00021, 机翼重量减轻4.35kg, 且该减轻的重量用于增加燃油装载量, 使得航程最终增加了4.67%.优化结果满足了所有的约束条件, 优化取得了良好的效果.
4 结论本文提出了一种新的气动结构多学科优化设计方法, 经过验证, 其气动与结构特性计算效率比传统的松耦合静气动弹性分析方法提高了4倍以上.对某无人机的优化设计也证明了其有效性.研究表明该方法是一种具有广阔应用前景的飞行器详细设计阶段的多学科优化设计方法.
| [1] |
Martins J R, Alonso J J, Reuther J J. High-fidelity aerostructural design optimization of a supersonic business jet[J]. Journal of Aircraft, 2004, 41(3): 523-530. DOI:10.2514/1.11478 |
| [2] |
Allison D L, Morris C C, Schetz J A, et al. A multidisciplinary design optimization framework for design studies of an efficient supersonic air vehicle[R]. AIAA 2012-5492, 2012.
|
| [3] |
Meadows N A, Schetz J A, Kapania R K, et al. Multidisciplinary design optimization of medium-range transonic truss-braced wing transport aircraft[J]. Journal of Aircraft, 2012, 49(6): 1844-1856. DOI:10.2514/1.C031695 |
| [4] |
粟华, 谷良贤, 龚春林. 基于高拟真度模型的高超声速飞行器静气动弹性优化[J]. 航空动力学报, 2013, 28(8): 1836-1842. Su H, Gu L X, Gong C L. Static aeroelastic optimization of hypersonic aircraft based on high-fidelity model[J]. Journal of Aerospace Power, 2013, 28(8): 1836-1842. (in Chinese) |
| [5] |
左英桃, 王晓鹏, 陈云, 等. 一种高效的CFD/CSD耦合飞行器多学科设计优化方法[J]. 航空动力学报, 2014, 29(12): 2898-2904. Zuo Y T, Wang X P, Chen Y, et al. An efficient method for multidisciplinary design optimization of aircraft based on CFD/CSD coupling[J]. Journal of Aerospace Power, 2014, 29(12): 2898-2904. (in Chinese) |
| [6] |
朱华光, 刘莉, 龙腾, 等. 机翼气动结构多学科设计优化研究[J]. 北京理工大学学报, 2011, 31(10): 1147-1152. Zhu H G, Liu L, Long T, et al. Research of wings aero-structural multidisciplinary design optimization[J]. Transactions of Beijing Institute of Technology, 2011, 31(10): 1147-1152. (in Chinese) |
| [7] |
Fu L, Gao Z H, Xu K, et al. A multi-block viscous flow solver based on GPU parallel methodology[J]. Computers & Fluids, 2014, 95: 19-39. |
| [8] |
Huang W, Lu Z L, Guo T Q, et al. Numerical method of static aeroelastic correction and jig-shape design for large airliners[J]. Science China Technological Sciences, 2012, 55(9): 2447-2452. DOI:10.1007/s11431-012-4936-0 |
| [9] |
Zuo Y T, Gao Z H, Chen G, et al. Efficient aero-structural design optimization: coupling based on reverse iteration of structural model[J]. Science in China Seies E: Technological Sciences, 2015, 58(2): 307-315. DOI:10.1007/s11431-014-5744-5 |
| [10] |
王丹, 白俊强, 黄江涛. FFD方法在气动优化设计中的应用[J]. 中国科学:物理学力学天文学, 2014, 44(3): 267-277. Wang D, Bai J Q, Huang J T. The application of FFD method in aerodynamic optimization design[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2014, 44(3): 267-277. (in Chinese) |
| [11] |
白俊强, 徐家宽, 黄江涛, 等. 多区域自由变形技术在短舱安装位置减阻设计中的应用研究[J]. 空气动力学学报, 2014, 32(5): 682-687. Bai J Q, Xu J K, Huang J T, et al. Drag reduction design of install position of nacelle based on multi-zone FFD technology[J]. Acta Aerodynamica Sinica, 2014, 32(5): 682-687. DOI:10.7638/kqdlxxb-2012.0185 (in Chinese) |



