压缩拐角是高超声速飞行器上典型的结构, 如超燃冲压发动机前体等[1], 其上有激波/边界层干扰、边界层转捩、Görtler涡等经典流动现象, 会对飞行器气动热及气动性能产生重要影响, 因此是高超声速领域重要的、基础的实验模型.对高超声速条件下压缩拐角流动的实验研究可以追溯到20世纪50年代[2].众多研究人员也通过数值计算手段分析了压缩拐角流动在不同工况下的流动分离、压力分布、热流分布以及Görtler涡特性等[3-7].除了实验和计算方面, 研究人员也从理论或者半经验的参数总结方面对压缩拐角流动进行了研究[8-10].
压缩拐角流动中, 给定拐角角度及实验工况时, 边界层会因逆压梯度而导致流动分离, 从而导致在分离泡上有弯曲的剪切层产生.弯曲的剪切层会诱导离心不稳定性, 从而诱导压缩拐角上Görtler涡的形成. 1964年该现象最早由Childs等通过油流的方法观察到[11].此后De La Chevalerie等研究了不同的平板长度与前缘形状对斜坡上热流分布的影响[12], Ishiguro等通过温敏漆(temperature sensi-tive paint, TSP)及压敏漆(pressure sensitive paint, PSP)技术在激波风洞中研究了不同激波-激波相互作用类型对压缩拐角斜坡上Görtler涡特性及热流、压力分布的影响[13]. Yang等[14]采用TSP及PSP技术研究了双压缩拐角上Görtler涡特性及变攻角对Görtler涡特性的影响.
TSP是一种非接触式光学测量技术, 可定量测量模型表面全局的温度和热流参数, 从而辨别出流动现象[15-16], 如层流/湍流边界层转捩、激波/边界层干扰、近壁面驻涡等.与单点式热流传感器相比具有成本低、可进行全局测量、空间分辨率高等优势.
本文搭建了TSP系统, 开发了数据后处理程序, 对TSP涂层进行了标定, 调研并选用合适的热流计算方法, 并利用TSP技术对Görtler涡进行可视化, 研究了层流边界层条件下, 压缩拐角坡面角度和Reynolds数对Görtler涡特性以及热流分布的影响.
1 温敏漆(TSP)测试技术温敏漆测量的原理是基于发光分子的热猝灭效应.温敏漆涂层中, 发光分子散布在聚合物载体中, 当受紫外光源激发时, 受激发的分子会变成不稳定的激发态, 在之后回复基态的过程中会发出1个波长较长的光子, 但是此过程受温度影响, 当温度升高时, 更多激发态的分子由于内部作用不发光而直接回复到基态, 此过程称为热猝灭.可用以下关系式来表达温度比与光强比之间的关系, 常用多项式来表达[17].
| $ \frac{I}{{{I}_{\text{ref}}}}~=f\left( \frac{T}{{{T}_{\text{ref}}}} \right) $ |
式中, T为测点温度, Tref为参考温度, I为测点光强, Iref为参考温度所对应的参考光强.
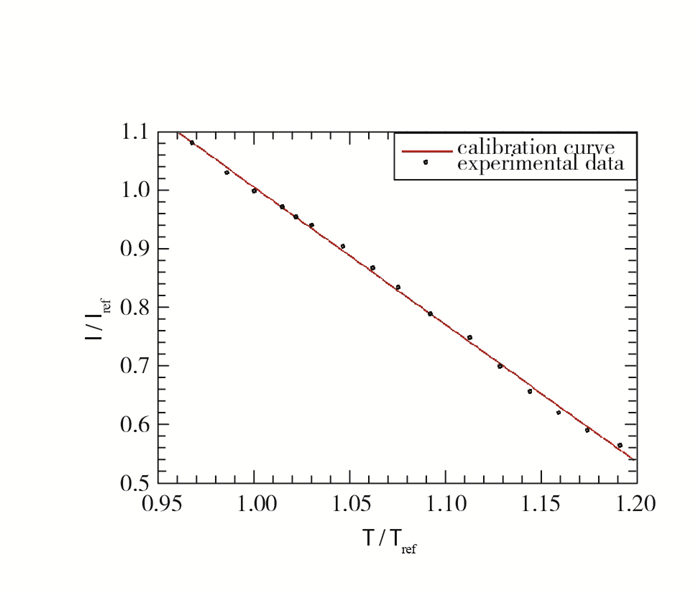
1.1 温敏漆标定及喷涂方法本研究所使用的温敏漆为单组分温敏漆, 其激发波长为365 nm, 光致发光波长峰值为500 nm.本实验使用的温度标定为静态标定, 标定片尺寸为50 mm×50 mm, 喷涂TSP涂层厚度为20 μm, TSP涂层厚度由膜厚仪测得.标定的温度范围从283.15~353.15 K(即10~80 ℃), 每隔5 ℃进行一次测量. 图 1为光强比-温度比的标定曲线, 参考温度为293.15 K(20 ℃), 使用一次多项式拟合, 得到标定曲线方程为
|
| 图 1 标定曲线 Fig.1 Curve of calibration |
| $ \frac{I}{{{I}_{\text{ref}}}}=-2.347\frac{T}{{{T}_{\text{ref}}}}+3.353 $ |
使用喷笔喷涂TSP涂料, 喷笔口径为0.2 mm.实验研究发现, TSP涂层厚度会对温度灵敏度有一定影响[18], 为减小误差, 本研究TSP涂层厚度与静态标定实验时厚度一致, 均为20 μm.在TSP喷涂到模型上之前, 要在模型表面喷涂白色丙烯酸涂料作绝热层, 厚度为0.1 mm, 涂层厚度同样使用膜厚仪测得.白色绝热层有两个作用, 一是白色增加反光, 使TSP涂料的光致发光能很大程度上被反射, 相机接收到的信噪比高[19]; 另一方面, 金属模型导热快, 若直接喷涂, 会使模型表面热流迅速损失, 模型表面温升低, 造成信噪比下降[14, 20-21].总的来说, 绝热层是为了增强信噪比.
1.2 温敏漆辅助设备根据温敏漆的特性, 选取了光源与滤光片.光源采用波长为365 nm的LED光源, 灯头有两个, 总功率为80 W.滤光片选用了460 nm长波通滤光片, 相机选用12位CCD相机, 分辨率为2 456 ×2 048, 连续模式下帧频为11帧/s.
1.3 实验过程及数据后处理在模型安装到试验段后, 将一个K型热电偶粘贴到模型底部, 用来测量模型的初始温度.实验前, 要记录对应初始温度的wind-off图像用作参考图像; 风洞运行时, 记录wind-on图像.另须在风洞运行前记录LED灯不打开时的dark图像, 在做光强比计算时将dark图像减掉以进行暗噪声补偿.计算光强比的公式如下所示.之后将光强比带入到标定曲线中得到温度比, 再与初始温度相乘则可得到模型壁面温度[22].
| $ \frac{I}{{{I}_{\text{ref}}}}=\frac{{{I}_{\text{wind-on}}}-{{I}_{\text{dark}}}}{{{I}_{\text{wind-off}}}-{{I}_{\text{dark}}}}\text{ }\!\!~\!\!\text{ } $ |
式中,I/Iref为光强比, Iwind-on为风洞运行过程中的光强, Iwind-off为风洞未运行状态下的光强, Idark为暗环境中的光强.
由温度反算热流, 有不同的数据处理方法.使用最多的是基于一维半无穷假设的Cook-Felderman方法, 已经大量应用于测量热流的风洞实验中[23], 但该方法须满足一维半无穷假设, 假设边界条件是无穷的, 在常规高超声速风洞使用时一般认为须使用绝热材料如电木、尼龙等才满足要求, 对本实验模型则适用. Liu等通过将Laplace变换使用在热传导方程中, 改进了热流计算方法, 使其可以在有效厚度模型上使用, 但方法复杂, 计算量大[24].此外, 为计算高导热材料表面喷涂绝热层的实验模型的表面热流, Liu等还提出基于一维定常假设、与时间无关的热流计算方法, 并在Purdue大学静风洞中进行了实验验证, 计算方法简单, 但须测得模型温度随时间的变化, 较难准确测量, 较常用的做法是在一段时间内将模型温度看成某一个定值, 故该方法准确率低, 还须进一步改进[22].对本实验研究较为适用的方法是Liu等[25-26]提出的基于离散Fourier定律的算法, 适用于高导热率材料上覆盖薄有机物绝热层的实验模型, 计算方法如下
| $ \begin{align} &{{q}_{\text{s}}}\left( t \right)\cong \frac{{{k}_{\text{p}}}}{L}{{\theta }_{\text{ps}}}\left( t \right)- \\ &\ \ \ \ \ \ \ \ \ \ \ \ \sqrt{\frac{{{k}_{\text{p}}}{{\rho }_{\text{p}}}{{c}_{\text{p}}}}{\text{ }\!\!\pi\!\!\text{ }}}\left[ \frac{{{\theta }_{\text{ps}}}\left( t \right)}{\sqrt{t}}+\frac{1}{2}\int{\frac{{{\theta }_{\text{ps}}}\left( t \right)-{{\theta }_{\text{ps}}}\left( \tau \right)}{{{\left( t-\tau \right)}^{3/2}}}~\text{d}\tau }~ \right] \\ \end{align} $ |
其中, θps(t)=T(t, L)-Tin,表示t时刻TSP涂层表面的温升, qs(t)表示t时刻的热流, T(t, L)表示t时刻涂层表面温度, Tin表示风洞运行前模型的初始温度. kp, ρp, cp分别表示绝热层的热传导系数、密度以及比热容.
| $ \varepsilon =\text{ }\sqrt{{{k}_{\text{p}}}{{\rho }_{\text{p}}}{{c}_{\text{p}}}/{{k}_{\text{b}}}{{\rho }_{\text{b}}}{{c}_{\text{b}}}}\ll 1~ $ |
式中, ε为热系数之比, kb, ρb, cb分别表示基底材料的热传导系数、密度以及比热容.本论文中, 基底材料为碳钢, kb=45 W/(m·K); ρb=7 800 kg/m3, cb=440 J/(kg·K), 作为绝热层的白漆的相关参数为kp=0.18 W/(m·K); ρp=1 300 kg/m3, cp=1 565 J/(kg·K).
计算得ε=0.043 9≪1, 满足该热流计算方法使用条件.
使用计算机进行计算时须将方程进行离散, 离散后的方程如下
| $ \begin{align} &{{q}_{\text{s}}}\left( t \right)\cong \frac{{{k}_{\text{p}}}}{L}{{\theta }_{\text{ps}}}\left( {{t}_{n}} \right)- \\ &\ \ \ \ \ \ \ \ \ \ \ \ 2\text{ }\sqrt{\frac{{{k}_{\text{p}}}{{\rho }_{\text{p}}}{{c}_{\text{p}}}}{\text{ }\!\!\pi\!\!\text{ }}}\sum\limits_{i=1}^{n}{\frac{{{\theta }_{\text{ps}}}\left( {{t}_{i}} \right)-{{\theta }_{\text{ps}}}\left( {{t}_{i-1}} \right)}{\sqrt{{{t}_{n}}-{{t}_{i}}~}+\text{ }\sqrt{{{t}_{n}}-{{t}_{i-1}}}}~} \\ \end{align} $ |
本研究使用的风洞设备为国防科大Ma=6.0低噪声风洞, 见图 2.运行方式为吹吸式, 使用干燥洁净空气作为气源.风洞系统包括上游的高压储气罐、加热器、稳定段、方形喷管、试验段、真空系统以及辅助系统.设计总温可调节范围为420~650 K, 最高可运行总压为3 MPa, 可实现单位Reynolds数调节范围为1.3×106~3.8×107/m[27].试验段采用直连式, 尺寸为260 mm×260 mm×700 mm.运行时间与风洞运行总压相关, 在3 MPa总压条件下, 运行时间可超过10 s[28].

|
| 图 2 低噪声风洞实物图 Fig.2 Hypersonic low-noise wind tunnel |
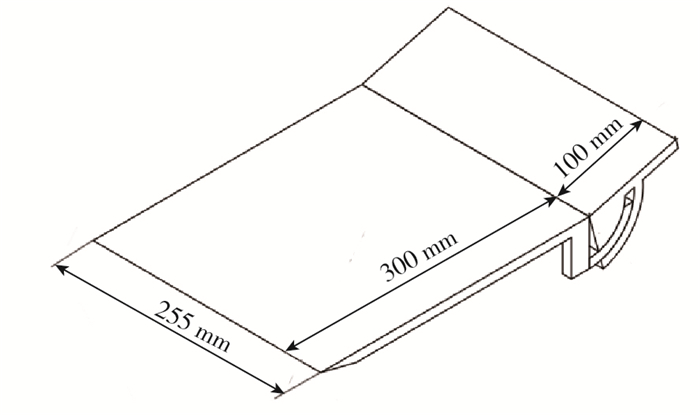
实验模型为压缩拐角,如图 3所示.压缩拐角平板部分长度为300 mm, 斜坡部分长度为100 mm.平板部分前缘为尖前缘, 尖前缘角度为10°.为保证压缩拐角上流动的二维性, 平板及斜坡部分宽度为255 mm, 比风洞试验段的宽度小5 mm, 拐角的角度依靠平板部分和斜坡板部分连接处的导轨以及斜坡板背面的支撑杆来调节, 可实现0~45°的角度调节, 本实验采用了10°和15°两种拐角角度.
|
| 图 3 实验模型示意图 Fig.3 Dimension of compression ramp model |
平板部分长300 mm, 本论文中最大单位Rey-nolds数为8.05×106/m.根据之前在本风洞中进行的长度为400 mm的平板边界层转捩实验, 采用基于纳米示踪的平面激光散射(nano-tracer planar laser scattering, NPLS)技术观察到, 当单位Reynolds数达到3×107/m时, 仍未发生边界层转捩[29], 所以本实验拐角前来流为层流.
3 实验结果与分析 3.1 Görtler涡特性分析图 4是Görtler涡结构及引起的热流条带示意图,在来流层流的条件下, 由于对涡的相向旋转, 左侧右旋的涡与右侧左旋的涡会将涡两侧的气流拉向涡对中间, 涡对对两侧气流的拉扯作用叫做“上洗”, 造成壁面温度的降低; 而两涡之间形成的流动滞止行为称为“下洗”, 造成壁面温度的升高.当涡对在压缩拐角斜坡上产生时, “上洗”和“下洗”气流会使壁面产生低、高热流条带结构[14]. 图 5和6可观察到热流的条带结构, 且热流条带的宽度可反映出Görtler涡的波长.

|
| 图 4 Görtler涡结构及引起的热流条带原理示意图[13] Fig.4 Schematic of Görtler vortex structure and the induced heat flow strip |
|
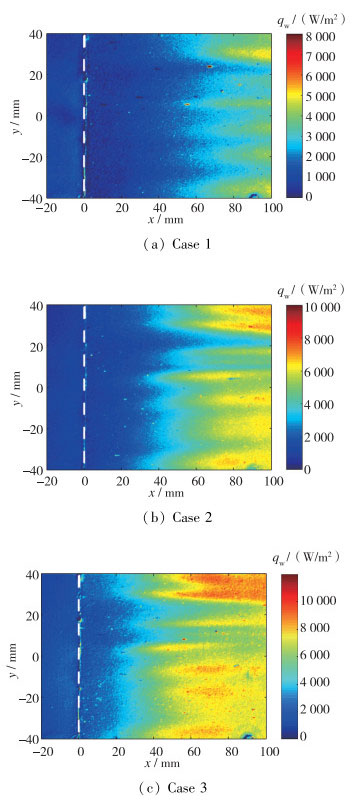
| 图 5 10°压缩拐角热流分布(流动方向从左到右) Fig.5 Heat flux distributions of 10° compression ramp |
|
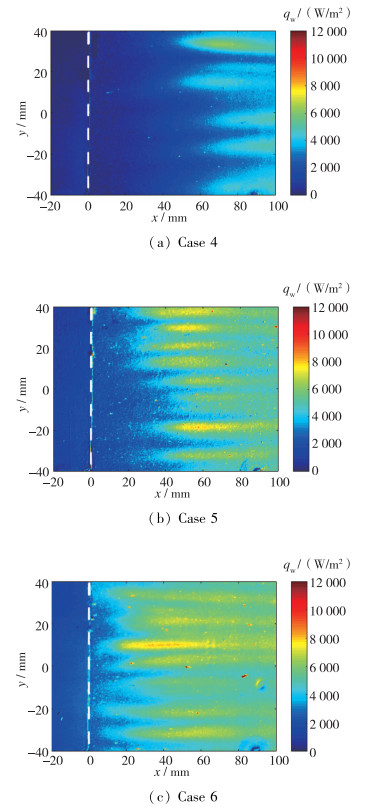
| 图 6 15°压缩拐角热流分布图(流动方向从左到右) Fig.6 Heat flux distributions of 15° compression ramp |
本研究的实验状态及风洞运行参数见表 1.
| 下载CSV 表 1 实验状态及参数 Tab.1 Experimental conditions |
图 5为10°压缩拐角在不同Reynolds数下的热流分布图, 流动方向从左到右.图中变色虚线表示拐角处. x轴沿斜坡方向, 起始点x=0 mm处表示拐角处; y方向为展向, y=0 mm位置表示模型中心线. 图 5(a)状态1总压0.3 MPa, 总温425 K, Reynolds数为3.45×106/m; 图 5(b)状态2总压0.55 MPa, 总温425 K, Reynolds数为6.32×106/m; 图 5(c)状态3总压0.7 MPa, 总温425 K, Reynolds数为8.05×106/m.
统计图 5中3个不同Reynolds数状态下, 斜坡上热流陡升位置, 将结果表示在表 2中.由表 2可知, 随Reynolds数的增加, 热流陡升的位置前移, 向拐角方向靠近, 即Görtler涡开始出现的位置随Reynolds数的增加向拐角方向靠近.这是由于Görtler涡开始出现的位置处于流动再附点附近[14, 31], 而随Reynolds数的增大, 分离区减小, 再附点向拐角处靠近, 因而Görtler涡开始出现的位置随Reynolds数的增大向拐角处靠近.
| 下载CSV 表 2 10°斜坡板热流陡升位置 Tab.2 Position of the peak of heat flux |
前文已分析得出, 热流条带的宽度与Görtler涡的波长相等, 视场范围内热流条带的数量等于Görtler涡的数量.将图 5中Görtler涡的条数进行统计, 并由此计算出平均波长, 结果见表 3.由表可知, 随Reynolds数的增大, Görtler涡波长减小.原因是Görtler涡的波长与再附前的边界层厚度有关, 约为再附前边界层厚度的2倍[30], 而边界层厚度与Reynolds数的均方根值成反比.
| 下载CSV 表 3 Görtler涡统计结果 Tab.3 Paraments of Görtler vortex |
图 6为15°压缩拐角的热流分布图, 图 6(a), (b), (c)分别为状态4, 5, 6, 具体参数见表 1.可以发现, 热流条带更加清晰, 可能拐角角度增大时, Görtler涡强度增大, 使其引起的高、低温度差更加显著, 由此热流条带更加明显.
将图 5和图 6中的热流分布结果进行对比, 可以发现: 10°压缩拐角状态1, 2, 3对应的热流开始陡升的平均位置大致为x=60, 40, 25 mm; 而15°压缩拐角状态4, 5, 6对应的热流开始陡升的平均位置大致为x=50, 30, 14 mm.即单位Reynolds数相同时, 对于15°压缩拐角, 热流条带开始出现位置比10°时提前, 而Görtler涡是引起该热流条带的原因, 因此可得, 对于拐角角度增大时, Görtler涡起始位置前移.将Görtler涡起始位置做统计, 见表 4, 由于Görtler涡开始出现的位置处于流动再附点附近, 拐角角度增大, 分离区减小, 再附点向拐角方向靠近, 使Görtler涡出现开始的位置前移.
| 下载CSV 表 4 10°和15°斜坡Görtler涡起始位置 Tab.4 Initial position of Görtler vortex |
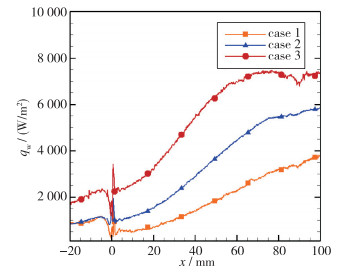
将展向(即y方向)的热流值进行平均, 做出平均热流沿流向的分布曲线,如图 7~8所示, 图中采用不同颜色和线型表示不同的状态.横坐标轴表示沿流向坐标, x=0 mm位置为拐角处, 方向指向下游为正, 纵坐标表示平均热流值.
|
| 图 7 10°压缩拐角平均热流沿流向分布 Fig.7 Average heat flow along the flow direction in 10° compression corners |
|
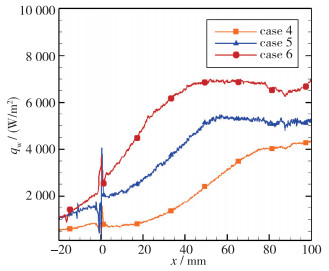
| 图 8 15°压缩拐角平均热流沿流向分布 Fig.8 Average heat flow along the flow direction in 15° compression corners |
由图 7可知, 对10°压缩拐角, 状态1和状态2热流曲线随流向为单调上升趋势, 即在测量区域内, 未出现热流峰值, 可能是由于小拐角、低Reynolds数下, 分离区大, 在观测区域内未发生流动再附.状态3有热流峰值出现, 且两状态在热流峰值之后, 热流随流向位置下降较平缓, 结合热流分布图(见图 5(c))可知, 此热流下降平缓位置为Görtler涡较为明显的区域, 热流峰值位置为再附点位置.热流峰值处存在一个“喉道”, 即边界处最薄区域, 造成此处热流最大[30].之后边界处从此处开始重新发展, 边界层为层流, 所以至边界层转捩之前, 热流沿流向降低.
如图 8, 对15°压缩拐角, 状态4沿流向热流单调上升, 显示在数据测量区域内未发生流动再附.状态5,6热流沿流向有峰值出现, 且出现热流峰值后, 热流下降平缓, 结合热流分布图(见图 5(b), (c)), 可得热流下降平缓区域为Görtler涡较明显区域.而状态3的热流在x=83 mm左右位置之后发现热流的升高, 可能是发生了边界层转捩现象.状态4未发现热流峰值, 状态5热流峰值位置约为x=52 mm, 状态6热流峰值位置约为x=50 mm, 可得热流峰值位置随Reynolds数的增加而前移, 即向靠近拐角方向移动.
将15°拐角与10°拐角热流峰值位置进行比较.对单位Reynolds数8.05×106/m时, 10°压缩拐角热流峰值位置约为x=73 mm, 而15°压缩拐角热流峰值位置约为x=50 mm.通过比较可发现, 对相同的Reynolds数, 拐角角度增加, 热流峰值向靠近拐角方向移动.
4 总结(1) 搭建了TSP系统, 并采用基于离散Fourier定律的热流算法, 得到了高超声速压缩拐角流动中表面热流分布图, 对Görtler涡进行了可视化.
(2) 得出Görtler涡展向方向的特性:给定拐角角度时, 随Reynolds数的增加, Görtler涡变得细密, 即在测量范围内, Görtler涡条数增加, 波长减小.给定Reynolds数时, 随拐角角度增加, Görtler涡在观测范围内条数增加, 波长减小.
(3) 得到Görtler涡流向特性: Reynolds数增加或者拐角角度增加, 会使热流陡升的位置向拐角处靠近, 即Görtler涡起始位置前移, 向拐角处靠近.
(4) 得到展向平均热流随流向变化规律:拐角角度相同时, 随Reynolds数的增加, 热流峰值位置前移, 且热流值增加; Reynolds数相同时, 拐角角度增加, 热流峰值位置前移.
(5) 流向热流曲线在峰值后下降平缓区域, 为Görtler涡明显区域.
| [1] |
Borg M P, Schneider S P. Effect of freestream noise on roughness-induced transition for the X-51A forebody[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1106-1116. DOI:10.2514/1.38005 |
| [2] |
Bogdonoff S M, Hammitt A G. Fluid dynamic effects at speeds from M=11 to 15[J]. Journal of the Aeronautical Sciences, 1956, 23(2): 108-116. DOI:10.2514/8.3516 |
| [3] |
Needham D A, Stollery J L. Hypersonic studies of incipient separation and separated flows[C]. Separated Flows, AGARD Conference Proceedings, 1966: 97-119.
|
| [4] |
Mallinson S G, Cai S L, Mudford N R. High-enthalpy, hypersonic compression corner flow[J]. AIAA Journal, 1996, 34(6): 1130-1137. DOI:10.2514/3.13203 |
| [5] |
Marini M. Analysis of hypersonic compression ramp laminar flows under sharp leading edge conditions[J]. Aerospace Science and Technology, 2001, 5(4): 257-271. DOI:10.1016/S1270-9638(01)01109-9 |
| [6] |
Egorov I, Neiland V, Shredchenko V. Three-dimensional flow structures at supersonic flow over the compression ramp[C]. 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando: AIAA, 2011: 730-738. https://www.researchgate.net/publication/269129478_Three-Dimensional_Flow_Structures_at_Supersonic_Flow_over_the_Compression_Ramp
|
| [7] |
Ren J, Fu S. Secondary instabilities of Görtler vortices in high-speed boundary layer flows[J]. Journal of Fluid Mechanics, 2015, 781: 388-421. DOI:10.1017/jfm.2015.490 |
| [8] |
Bushnell D M, Weinstein L M. Correlation of peak heating for reattachment of separated flows[J]. Journal of Spacecraft and Rockets, 1968, 5(9): 1111-1112. DOI:10.2514/3.29432 |
| [9] |
Hung F T, Barnett D O. Shockwave-boundary layer interference heating analysis[C]. 11th Aerospace Sciences Meeting, Washington: AIAA, 1973: 10-12. https://arc.aiaa.org/doi/10.2514/6.1973-237
|
| [10] |
Katzer E. On the lengthscales of laminar shock/boundary-layer interaction[J]. Journal of Fluid Mechanics, 1989, 206: 477-496. DOI:10.1017/S0022112089002375 |
| [11] |
Childs M E, Hijman R, Miller D S. Mach 8 to 22 studies of flow separations due to deflected control surfaces[J]. AIAA Journal, 1964, 2(2): 312-321. DOI:10.2514/3.2289 |
| [12] |
De La Chevalerie D A, Fonteneau A, De Luca L, et al. Görtler-type vortices in hypersonic flows:the ramp prob-lem[J]. Experimental Thermal and Fluid Science, 1997, 15(2): 69-81. DOI:10.1016/S0894-1777(97)00051-4 |
| [13] |
Ishiguro Y, Nagai H, Asai K, et al. Visualization of hypersonic compression corner flows using temperature-and pressure-sensitive paints[C]. 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno: AIAA, 2007. https://www.researchgate.net/publication/260584903_Visualization_of_Hypersonic_Compression_Corner_Flows_Using_Temperature-_and_Pressure-Sensitive_Paints
|
| [14] |
Yang L, Zare-Behtash H, Erdem E, et al. Investigation of the double ramp in hypersonic flow using luminescent measurement systems[J]. Experimental Thermal and Fluid Science, 2012, 40: 50-56. DOI:10.1016/j.expthermflusci.2012.01.032 |
| [15] |
Jiao L R, Peng D, Liu Y Z. Lifetime-based PSP and TSP measurements on rotating blades with high rotation rate[C]. 33rd AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Denver: AIAA, 2017. https://www.researchgate.net/publication/318142178_Lifetime-Based_PSP_and_TSP_Measurements_on_Rotating_Blades_with_High_Rotation_Rate
|
| [16] |
尚金奎, 衷洪杰, 赵民, 等. TSP转捩探测技术在民机风洞试验中的应用研究[J]. 空气动力学学报, 2016, 34(3): 341-345, 353. Shang J K, Zhong H J, Zhao M, et al. Application of TSP transition detection technique for a civil aircraft[J]. Acta Aerodynamica Sinica, 2016, 34(3): 341-345, 353. DOI:10.7638/kqdlxxb-2015.0106 (in Chinese) |
| [17] |
Liu T S, Sullivan J P. Pressure and temperature sensitive paints[M]. Berlin Heidelberg: Springer, 2005.
|
| [18] |
杨雷超, 王喜超.高超声速流动中温度敏感涂料测温技术研究[C].高等学校工程热物理第二十届全国学术会议, 青岛, 2014. Yang L C, Wang X C. Surface temperature measurement using temperature-sensitive paint in hypersonic flows[C]. National Academic Conference on Engineering Thermophysics, Qingdao, 2014(in Chinese). http://cpfd.cnki.com.cn/Article/CPFDTOTAL-GJGC201405004022.htm |
| [19] |
张扣立, 常雨, 孔荣宗, 等. 温敏漆技术及其在边界层转捩测量中的应用[J]. 宇航学报, 2013, 34(6): 860-865. Zhang K L, Chang Y, Kong R Z, et al. Temperature sensitive paint technique and its application in measurement of boundary layer transition[J]. Journal of Astronautics, 2013, 34(6): 860-865. DOI:10.3873/j.issn.1000-1328.2013.06.017 (in Chinese) |
| [20] |
Goldfeld M A, Mosharov V E, Radchenko V N, et al. Problems of investigation of boundary layer transition by temperature sensitive paint in impulse wind tunnel IT-302[C]. 17th International Conference on the Methods of Aerophysical Research, Novosibirsk, 2014. http://www.itam.nsc.ru/users/libr/eLib/confer/ICMAR/2014/pdf/Goldfeld%20et%20al_191.pdf
|
| [21] |
Bhandari P. Evaluation and improvement of temperature sensitive paint data reduction process through analysis of tunnel data[D]. Maryland: University of Maryland, 2012. https://drum.lib.umd.edu/handle/1903/13564
|
| [22] |
Swanson E O. Boundary-layer transition on cones at angle of attack in a Mach-6 quiet tunnel[D]. Lafayette: Purdue University, 2008. https://core.ac.uk/display/4967299
|
| [23] |
Cook W J, Felderman E J. Reduction of data from thin-film heat-transfer gages:a concise numerical technique[J]. AIAA Journal, 1966, 4(3): 561-562. DOI:10.2514/3.3486 |
| [24] |
Liu T S, Montefort J, Stanfield S, et al. Analytical inverse heat transfer method for temperature-sensitive-coating measurement on a finite base[J]. International Journal of Heat and Mass Transfer, 2018, 118: 651-662. DOI:10.1016/j.ijheatmasstransfer.2017.11.020 |
| [25] |
Liu T S, Ward C A, Rubal J, et al. Heat-flux measurements with temperature-sensitive paint in a Mach-6 quiet tunnel[J]. Journal of Spacecraft & Rockets, 2013, 50(2): 282-293. |
| [26] |
Liu T S, Cai Z M, Lai J H, et al. Analytical methods for determination of heat transfer fields from temperature sensitive paint measurements in hypersonic tunnels[C]. 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando: AIAA, 2009. https://arc.aiaa.org/doi/abs/10.2514/6.2009-736
|
| [27] |
刘小林.高超声速低噪声风洞技术及相关试验研究[D].长沙: 国防科学技术大学, 2015. Liu X L. The hypersonic low noise wind tunnel technique and relative experimental studies[D]. Changsha: National University of Defense Technology, 2015(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1017835529.htm |
| [28] |
冈敦殿.低噪声条件下超声速/高超声速边界层转捩及钝舵绕流实验研究[D].长沙: 国防科学技术大学, 2017. Gang D D. Low noise experimental investigation on supersonic/hypersonic boundary layer transition and flow over blunt fins[D]. Changsha: National University of Defense Technology, 2017(in Chinese). |
| [29] |
杨跃. Mach数6高超声速平板边界层转捩流动显示实验研究[D].长沙: 国防科学技术大学, 2016. Yang Y. Hypersonic flat plate boundary layer transition experimental studies of flow visualization at Mach 6[D]. Changsha: National University of Defense Technology, 2016(in Chinese). |
| [30] |
Roghelia A, Olivier H, Egorov I, et al. Experimental investigation of Görtler vortices in hypersonic ramp flows[J]. Experiments in Fluids, 2017, 58(10): 139-152. DOI:10.1007/s00348-017-2422-y |
| [31] |
Roghelia A, Chuvakhov P V, Olivier H, et al. Experimental investigation of Görtler vortices in hypersonic ramp flows behind sharp and blunt leading edges[C]. 47th AIAA Fluid Dynamics Conference, Denver: AIAA, 2017.
|



