Reynolds数是飞行的一个十分重要的参数, 常规飞行器一般飞行Reynolds数在106量级或更高.低速飞行器若在高空及临近空间大气密度较低的环境下飞行, 如临近空间太阳能无人机和飞艇, 或是本身尺寸较小, 如微小型飞行器等, 则飞行Rey-nolds数将处于104~105量级, 与之相应的螺旋桨推进器也将面临相同或更低的Reynolds数范围.航空领域将Reynolds数在104~105量级定义为飞行器低Reynolds数范围[1].研究和飞行实验发现, 飞行器在低Reynolds数下飞行, 升阻比大幅降低, 相应螺旋桨效率也大幅下降, 其气动特性还表现出非定常、非线性以及流动结构稳定性差等现象[2-3].
虽然低Reynolds数流动在空气动力学领域是一个分支, 但由于以往在低Reynolds数环境下的飞行器较少, 工程应用需求不足, 加之低Reynolds数流动较常规Reynolds数流动复杂, 所以国内外针对飞行器低Reynolds数空气动力学理论方面的研究相对较少且很不系统.低Reynolds数空气动力学经典理论仍存在很多不足, 对与之相关的大量复杂气动问题还无法给出合理有效的解释, 低Reynolds数空气动力学基础理论仍存在不少空白点, 主要面临4个方面的问题.
(1) 低Reynolds数下飞行器气动性能大幅降低, 非线性效应突出
低Reynolds数下翼型最大升力系数与升阻比特性严重恶化, 升阻比甚至仅为常规情形的1/10左右.对于高空低速长航时飞行器和微小型飞行器而言, 其航时、航程、爬升率、机动能力等均与升阻比密切相关, 若受低Reynolds数效应影响升阻比下降20%~30%, 则相应的总体设计性能也将下降20%~30%.安定面的特征尺度相较主翼更小, 更容易受到低Reynolds数效应的影响.另一方面, 低Reynolds数气动特性更容易出现非定常和非线性效应, 从而对飞行器稳定性造成不利影响.同时由于操纵面都安装在机翼和安定面的后缘, 受层流分离等低Reynolds数效应的影响, 其操纵效率下降, 舵效不足常规Reynolds数时的一半甚至反效.这些因素将会使飞行器的气动性能大幅降低, 甚至严重影响飞行安全.
(2) 低Reynolds数经典基础理论存在不足
低Reynolds数基础理论及流动机理研究的奠基性和开创性工作可以追溯到20世纪60年代Gaster[4]和Horton[5]提出的经典层流分离泡模型, 他们首次系统提出了层流分离泡理论, 并指出正是由于层流分离泡的存在, 光滑机翼低Reynolds数气动特性急剧变坏, 升阻性能急剧下降.但随后的某些研究表明层流分离存在很强的非定常特性, 低Reynolds数分离流动实质上可能是一种非定常流动.此外随攻角和Reynolds数变化, 层流分离泡外部形态和内部结构会发生改变, 相应的力学特性也会产生本质的差异, 对于这些现象经典理论无法给出合理的解释, 低Reynolds数空气动力学经典理论仍存在很多不确定性.
(3) 低Reynolds数下许多特殊现象的流动机理无法合理解释
低Reynolds数下飞行器气动特性将会产生非常严重的非线性效应.就翼型而言, 对称翼型在0°攻角附近升力线斜率不再保持2π, 升力系数随攻角变化曲线会出现平台甚至反向, 造成小攻角气动特性的非线性, 从而可能引起操纵的非线性或反效[6].此外, Reynolds数由高到低变化, 翼型气动特性出现二次恶化现象, 首先阻力快速升高, 在某一临界Reynolds数下, 阻力进一步升高的同时升力快速降低, 导致气动特性最终的恶化[7].但这些气动特性的变化规律还难以从流动机理上去揭示它们的作用机制, 已成为限制低Reynolds数飞行器性能的重要问题之一.
(4) 数值模拟和风洞实验准确预测低Reynolds数下气动特性存在困难
Reynolds数处于104~105量级, 流场中可能存在层流边界层、层流分离、转捩、湍流边界层和湍流分离.流动容易受来流湍流度、背景噪声和表面粗糙度的影响, 使得其流态、流动结构和气动特性发生很大变化.低Reynolds数流动本身稳定性较差, 易受外界各种因素的干扰, 这给风洞实验和数值模拟预测低Reynolds数气动特性带来很大困难.同时, 低Reynolds数条件下的动压低, 作用在模型上的气动力小, 难于在风洞中精确测量, 对于风洞实验条件和测试设备的能力提出严苛要求.这些因素导致不同风洞获得的低Reynolds数实验结果差异较大[8]. Selig等[9]对比了不同研究机构采用不同风洞、支撑方式和测试设备获得的低Reynolds数升阻极曲线实验结果, 表明随着Reynolds数降低实验数据之间差异很大.数值模拟方面受特征矩阵刚度[10]、方程性质[11]、数值方法[12-13]、低Reynolds数转捩模型[14-15]和湍流模型[16]发展程度的限制, 精确预测低Reynolds数气动特性也存在较大困难.
以临近空间低速飞行器和高性能微小型飞行器为代表的低Reynolds数飞行器是当前和未来新型飞行器研究领域的重要热点, 具有突出的战略价值和广泛的应用前景.然而上述这些基础理论问题研究的不足, 给低Reynolds数飞行器总体、气动、动力、飞控等设计和分析工作带来了极大挑战, 严重制约了该类飞行器的性能甚至影响其研制成败.因此深入研究飞行器低Reynolds数流动特点和气动特性, 分析其中存在的各种复杂效应及其相互作用机制, 揭示其深层次的流动机理, 不仅有助于丰富和完善经典低Reynolds数流动分离基础理论, 对提高低Reynolds数流动机理的认识水平具有显著的科学意义, 还将为相关低Reynolds数空气动力学工程和飞行器型号应用提供理论和技术支撑, 具备突出的工程价值.
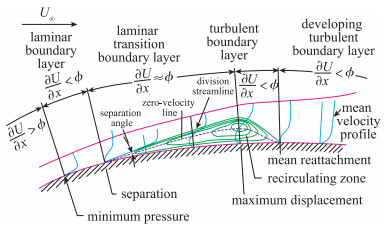
1 低Reynolds数层流分离经典理论20世纪60年代, Gaster[4]通过在平板上方安装辅助翼型, 在平板上形成不同强度的逆压梯度的方式, 形成层流分离现象并加以研究. Horton[5]进一步描述了经典二维层流边界层分离泡的结构(见图 1):低Reynolds数下层流边界层在逆压梯度的作用下产生分离而离开物面, 层流流动在空间发生转捩演化成为湍流, 将外层高能量的气流引入边界层从而产生再附, 形成层流分离泡, 分离泡再附点后流动逐渐发展为湍流边界层.
|
| 图 1 低Reynolds数层流分离泡结构示意图 Fig.1 Sketch of laminar separation bubble at low Re |
按照层流分离泡的位置和长度可分为短分离泡和长分离泡.对翼型而言, 短泡发生在翼型前缘附近, 长度为弦长的百分之几; 长泡发生在翼型后部, 长度占翼型弦长的百分之十几至百分之几十. Horton认为层流分离泡中短泡稳定性较好, 而长泡稳定性较差[5].
20世纪80年代以Mueller为代表的学者对层流分离现象开展了大量的风洞实验研究[17], 发现低Reynolds数下的长分离泡是由短分离泡在特定临界Reynolds数条件下发生“破裂”而形成的.另外的一些实验结果显示在较小攻角时首先形成长层流分离泡, 随后随攻角增加长层流分离泡位置不断前移, 长度逐渐缩小, 最终演变为前缘位置附近的短层流分离泡[18].目前对于长分离泡和短分离泡之间的演化规律和形成机制还存在不一致的认识.由于短层流分离泡长度很小, 而长层流分离泡尺寸较大, 长度可以扩展到翼型上的很大范围, 它的存在对飞行器低Reynolds数性能会产生更为严重的影响.
2 低Reynolds数层流分离非定常流动特征低Reynolds数流动经典理论认为长层流分离泡较短, 分离泡更容易出现不稳定, 但流动主要还是定常结构.之后一些学者的实验观测[19]和数值计算[20]发现了这种流动的非定常现象, 但受当时研究手段的局限, 其非定常特性难以得到深入探索.近些年来, 随着数值模拟和风/水洞等实验方法的精度、时/空间分辨率的提高, 针对层流分离非定常流动特性的研究获得了迅速的发展.
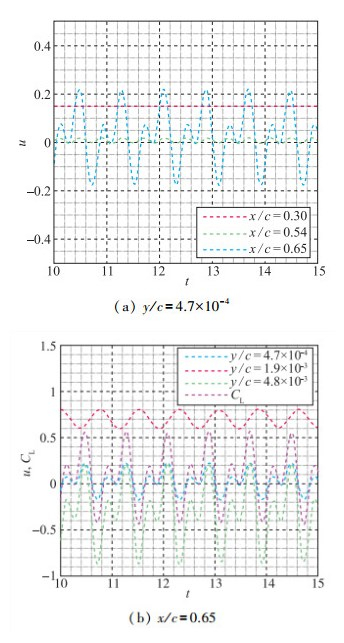
数值模拟[21]和水洞实验[22]研究都表明低Reynolds流动存在很强的非定常效应. 图 2给出了数值模拟翼型不同弦向位置(x/c)和距物面不同法向距离(y/c)点处流场的流向速度u和翼型升力系数CL随时间的变化曲线, 其数值均以翼型弦长和远场来流速度为参考量进行无量纲化.从图 2中可见在分离点之前(x/c=0.3), 流动基本为定常, 而分离点之后位置(x/c=0.54, 0.65), 流向速度分量产生周期性脉动.速度脉动幅值会随着弦向位置后移和距物面法向距离增大而增加, 同时升力系数也呈现周期性变化的规律.
|
| 图 2 Re=6×104, α=4°翼型上表面不同站位流向速度及升力系数非定常曲线 Fig.2 Unsteady lift coefficients and flow velocity plots at different locations at Re=6×104, α=4° |
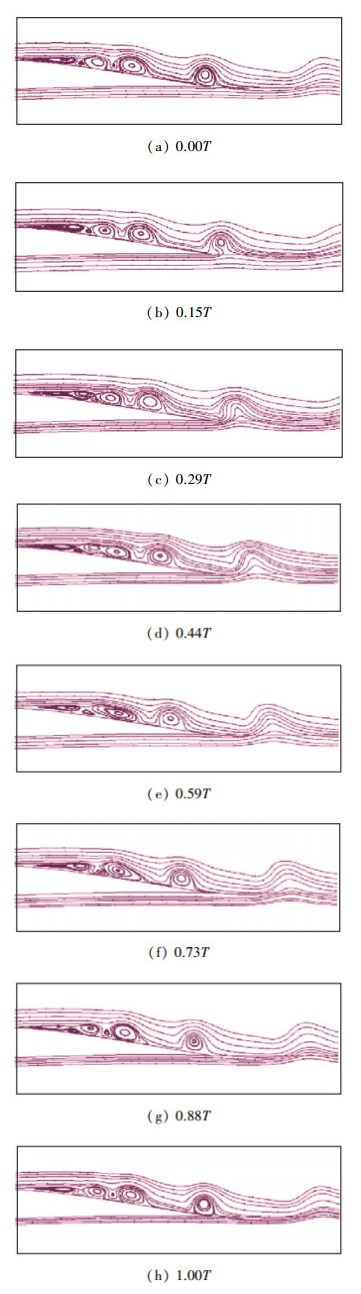
图 3给出了一个升力系数变化周期内流场流线变化, 其中T表示升力系数的变化周期.该图显示了一个升力系数脉动周期内, 非定常分离涡的形成、运动、对并和脱落的过程. 0.00T~0.29T, 一个分离涡离开翼面, 同时从分离点形成的层流分离涡层, 在靠近壁面二次涡的作用下形成两个分离涡. 0.29T~0.73T, 由前面壁面二次涡作用形成的两个分离涡并没有彼此远离, 而是发生对并, 从两个较弱的涡合成一个较强的分离涡. 0.73T~1.00T, 前次对并形成的较强分离涡在来流的作用下逐渐向后缘运动.这种对并现象在Pauley等[23]平板层流分离泡数值模拟中同样出现.有关层流分离泡非定常特性的详细分析与讨论见文献[21].
|
| 图 3 翼型一个升力系数变化周期内流线(Re=6×104, α=4.0°)[21] Fig.3 Re=6×104, α=4.0°, unsteady streamlines during one airfoil lift coefficient period[21] |
图 4给出了翼型攻角为3.5°时, 水洞粒子图像测速法流动显示实验获得的不同时刻(0.0T, 0.35T, 0.7T)流线分布[22], 图 4还显示低Re下翼型的层流分离区存在一系列脱落的层流分离旋涡, 他们在分离点附近不断生成, 沿流向持续运动、对并、脱落, 流动结构与稳定的经典层流分离泡结构迥异.
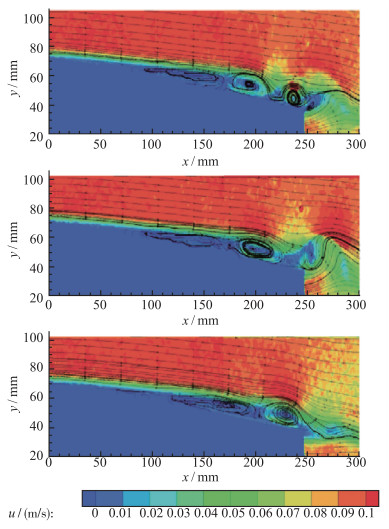
|
| 图 4 水洞粒子图像测速法实验显示不同时刻层流分离流动结构(Re=4×104, α=3.5°)[22] Fig.4 Laminar separation flow structures at different times by particle image velocity(PIV) experiment in water tunnel[22] |
对图 3、图 4两个非定常流场进行时间平均, 分别选取对8个速度脉动周期的流场结果进行时均化, 得到的平均流场流线见图 5.显示其非定常的周期性脱落涡消失, 代之以位置和形状都固定的层流分离泡, 即Gaster和Horton所描述的层流分离泡, 这同经典层流分离泡理论是一致的.
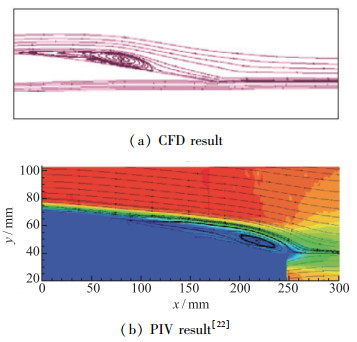
|
| 图 5 翼型时均化流动结构 Fig.5 Time-average flow structures on airfoils |
在低Reynolds数翼型层流分离现象中, 占主导作用的是层流边界层的分离, 以及层流分离涡的形成、对并、移动和脱落等一系列较大尺度旋涡结构的复杂作用过程.低Reynolds数下经典理论所描述的层流分离泡, 是周期性的层流分离形成层流分离涡, 再通过对并等复杂过程不断沿流向脱落的非定常过程的时均化结果.由于非定常流动的平均特性可反映流动的主要特征, 因此时均化模型是低Reynolds数非定常分离流动有效的理论分析模型.
3 低Reynolds数后缘层流分离泡经典理论认为根据尺寸和位置, 低Reynolds数层流分离泡可分为长泡和短泡.但在研究翼型低Reynolds数层流分离流动的过程中, 发现了一种不同于经典层流分离泡的时均化层流分离泡新模型——后缘层流分离泡[22, 24, 25], 如图 6所示.
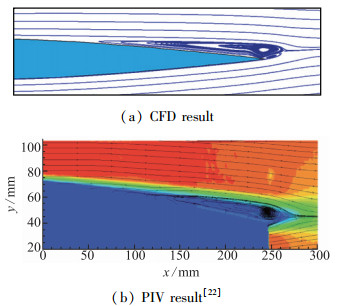
|
| 图 6 SD8020翼型后缘层流分离泡结构(Re=4×104) Fig.6 Trailing-edge laminar separation bubbles on SD8020 airfoil (Re=4×104) |
后缘层流分离泡同样广泛存在于低Reynolds数流场当中, 后缘层流分离泡结构同经典层流分离泡存在显著不同.
首先, 时均化后缘层流分离泡的典型特征为存在分离点、主分离涡、主涡诱导的二次分离涡和后缘分离涡, 如图 7(a)所示, 后缘分离泡始终停留在后缘上方, 不随攻角变化, 不存在经典层流分离泡的再附点.而经典层流分离泡其典型特征为存在分离点、再附点、主分离涡和主涡诱导的二次分离涡, 如图 7(b)所示.且随攻角增加, 其分离点、再附点和分离涡位置均前移, 尽管非定常分离区增加, 但时均化分离泡长度则可能减小.
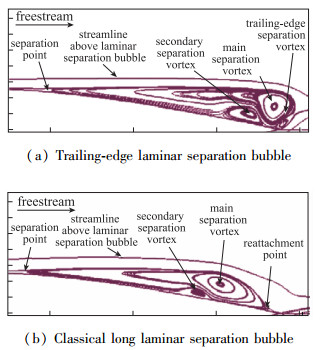
|
| 图 7 时均化后缘层流分离泡和经典层流分离泡结构[22, 24] Fig.7 Time-average trailing-edge laminar separation bubble and classical laminar separation bubble |
其次, 对应时均化后缘分离泡的非定常结构不同于经典层流分离泡, 它的强非定常区域较小, 只是在后缘附近呈现强非定常, 而经典层流分离泡对应的强非定常区域较大, 相应地造成对应两种不同流动结构翼型表面的非定常压力系数量值和脉动频率均存在显著差异, 其中后缘层流分离泡压力分布积分后的升力系数远小于经典层流分离泡升力系数[22, 24].
再次, 两种流动结构所对应的非定常Strouhal数也存在突变, 如图 8所示, 低Reynolds数下翼型流动结构在小攻角下为后缘分离泡, 在某一攻角突然演化为经典层流分离泡, 流场的脉动频率突然降低.
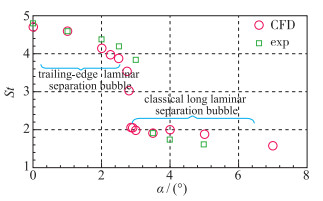
|
| 图 8 不同攻角下非定常升力系数Strouhal数 Fig.8 Strouhal number of unsteady lift coefficient at different angles of attack |
后缘层流分离泡是低Reynolds数流动研究中的新发现, 这种分离泡结构对气动特性的影响强于经典层流分离泡结构.后缘层流分离泡的发现以及模型的提出是对低Reynolds数经典层流分离理论的重要扩充.
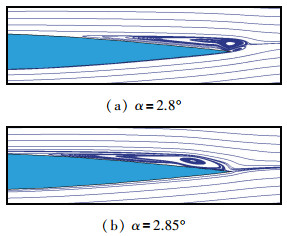
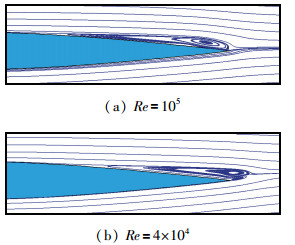
4 低Reynolds数非线性效应及其流动机理研究发现后缘层流分离泡和经典层流分离泡均普遍存在于低Reynolds数流场中, 且两种层流分离泡流动结构之间并不是孤立存在的, 它们会随翼型、Reynolds数、攻角的不同, 以及蒙皮振动、表面粗糙度等激励因素的不同而相互演化, 甚至发生突变.如: Reynolds数不变而翼型攻角增加, 分离泡结构由后缘层流分离泡突变为经典层流分离泡(见图 9); 攻角不变而Reynolds数降低, 分离泡结构由经典层流分离泡演化为后缘层流分离泡(见图 10).正是由于这两种时均化层流分离泡的产生和相互演化, 导致了复杂的低Reynolds数效应, 这是低Reynolds数流动中很多特殊现象产生的本质所在.
|
| 图 9 SD8020翼型不同攻角下流动结构(Re=4×104) Fig.9 Flow structures on SD8020 airfoil at different angles of attack(Re=4×104) |
|
| 图 10 SD8020翼型不同Reynolds数下流动结构(α=2.0°) Fig.10 Flow structures on SD8020 airfoil at different Reynolds numbers (α=2.0°) |
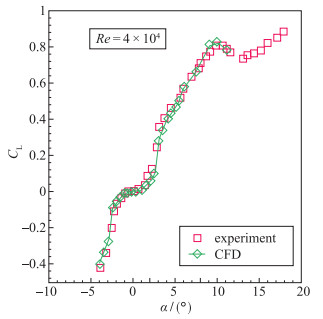
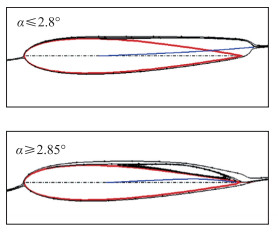
翼型在低Reynolds数小攻角下, 升力线斜率不再保持2π, 升力系数随攻角变化会出现非线性效应[6], 如图 11所示.这种现象的流动机理在于攻角的变化造成翼型上表面的后缘层流分离泡向经典层流分离泡的突变, 如图 9所示的SD8020翼型由攻角2.8°增加到2.85°的状态.
|
| 图 11 SD8020翼型升力系数非线性变化曲线 Fig.11 Nolinear lift coefficients plots on SD8020 airfoil |
由于后缘层流分离泡会使翼型的等效弯度降低, 翼型在此攻角范围内(α≤2.8°), 升力系数增长缓慢, 升力线斜率显著小于2π.而当攻角增加到2.85°时, 时均化分离泡结构演化为经典层流分离泡, 翼型等效弯度增加, 如图 12所示, 造成在该攻角附近升力系数快速变大和升力线斜率大于2π[24].后缘层流分离泡与经典长层流分离泡之间的演化是造成低Reynolds数翼型小攻角非线性效应的根本原因.
|
| 图 12 SD8020翼型等效外形示意图(Re=4×104)[24] Fig.12 Sketch of the equivalent airfoil shapes on SD8020 (Re=4×104)[24] |
上节研究结果显示翼型低Reynolds数下随攻角的增加, 其流动结构将会产生突变, 由后缘层流分离泡转变为经典层流分离泡, 进而导致了翼型升力系数随攻角的非线性效应.然而在固定攻角下, 逐渐降低流动的Reynolds数, 其流动结构同样会发生突变, 造成翼型气动特性随Reynolds数的突变.
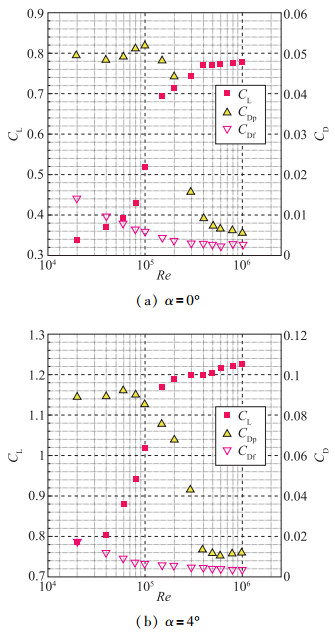
图 13为FX63-137翼型, Reynolds数从1.0×106下降至4.0×104过程中, 0°和4°攻角下的升阻力系数随Reynolds数的变化曲线[7].其中翼型阻力系数CD可分为由壁面黏性切应力造成的摩擦阻力系数CDf及压强分布引起的压差阻力系数CDp. 图 13显示, Reynolds数从1.0×106下降至5.0×105时, 翼型的升力系数略微降低, 阻力系数略微上升, 翼型气动特性随Reynolds数变化不显著.但当Reynolds数降至3.0×105时, 阻力系数首先开始快速升高, 其中压差阻力系数的增速较摩擦阻力系数要快得多, 当Reynolds数下降至1.5×105时, 压差阻力已经成为阻力系数的主要组成部分.而此时升力系数仍保持缓慢下降, 直至Reynolds数继续下降至1.0×105, 升力系数开始迅速下降, 升力特性急剧恶化.
随Reynolds数的下降, 不同翼型升力系数和阻力系数发生急剧变化的临界Reynolds数不同, 对应FX63-137翼型, 其中阻力系数剧增的Reynolds数在3.0×105左右, 而升力系数剧降的Reynolds数大致为1.5×105.由此可知随Reynolds数下降, 翼型气动特性的恶化是分步的.首先当Reynolds数降低至某一临界值时, 阻力系数开始快速增加, 此时升力系数变化不大; Reynolds数继续降至第2临界值时, 升力系数迅速下降, 阻力系数继续缓慢增长, 此时气动特性最终恶化, 该现象称为翼型低Reynolds数气动特性的二次恶化效应.
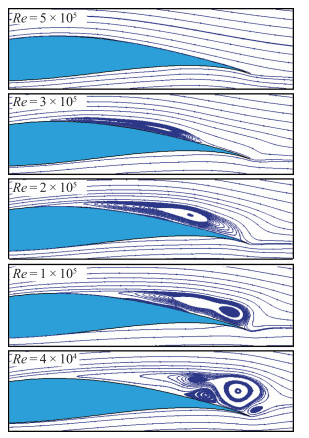
通过分析不同Reynolds数下翼型的流动结构, 可以揭示其气动特性变化规律的影响.以4°攻角为例, 图 14给出了翼型气动特性降低所对应的流动结构演化规律[7]. Reynolds数从5.0×105降低至2.0×105, 翼型上表面的经典层流分离泡从无到有, 分离区长度不断增加, 再附点最终延伸至后缘位置, 分离泡尺度增大导致翼型压差阻力快速上升, 这与图 13(b)中阻力变化特性相契合.当Reynolds数从2.0×105继续降至4.0×104, 翼型上表面分离泡后部逐渐隆起, 分离泡主涡位置向后缘移动, 逐渐由经典层流分离泡转变为后缘层流分离泡, 分离泡尺度增大, 气流从下表面向上卷起的分离涡结构使流动不存在分离再附现象.正是由于两种分离泡结构之间差异及演化, 导致了图 13(b)中翼型升力系数的急剧降低.
|
| 图 14 FX63-137翼型不同Reynolds下时均化流动结构(α=4.0°)[7] Fig.14 Time-average flow structures on FX63-137 airfoil at different Reynolds numbers(α=4.0°)[7] |
由此可知, 翼型气动特性二次恶化效应的流动机理在于随Reynolds数下降经典层流分离泡和后缘层流分离泡的产生及相互之间的演化. Reynolds数下降过程中, 经典层流分离泡的出现和增长造成了阻力系数的突增和气动特性的一次恶化, 后缘层流分离泡的出现导致升力系数的剧降和气动特性的最终恶化, 即二次恶化.翼型低Reynolds数条件下气动特性最终恶化的根源不是经典层流分离泡的产生, 而是后缘层流分离泡的出现.
5 总结与展望在科学技术的发展史上, 许多理论都经历了一个不断完善和发展的过程, 低Reynolds数流动理论的进步也正在经历这一过程.低Reynolds数经典层流分离理论在低Reynolds数流动领域无疑起到了奠基性的作用, 其时均层流分离泡概念仍是指导低Reynolds数流动研究的基础和工具.然而随着研究的不断深入, 经典理论也需拓展和完善.实际上低Reynolds数流动是一种非定常流动, 不存在经典理论描述的层流分离泡, 它是非定常流时均化的结果; 低Reynolds数流场存在两种不同特征的流动分离, 以时均化概念则表征为经典层流分离泡和后缘层流分离泡, 这两种不同的分离结构会随攻角和Reynolds数变化而相互演化.正是这两种不同流动结构的形成和相互演化, 决定了低Reynolds数流动的本质.
低Reynolds数经典理论认为当层流边界层发生分离并离开壁面后, 流动在空间将发生转捩.虽然前人针对层流转捩效应已经发展了不同的数值模拟和实验研究方法, 同时已经开展了大量的研究工作, 但对低Reynolds数流动的转捩机制并没有完全认识清楚.一般来说转捩机制主要可以分为自然转捩、旁路转捩和分离诱导转捩3种类型, 人们往往将低Reynolds数的转捩机制归结为分离诱导转捩.由于层流分离和分离诱导转捩的并存及相互影响使得低Reynolds数转捩流动的机理研究非常复杂, 截至目前, 大量的文献都仅是提出分离诱导转捩的术语或概念, 真正对低Reynolds数条件下的转捩机制开展机理性研究的工作还基本空缺.正是由于这部分机理研究工作的不足, 造成低Reynolds数流动转捩位置以及再附后的流动特性难以准确预测, 相关工作有待进一步深入展开.
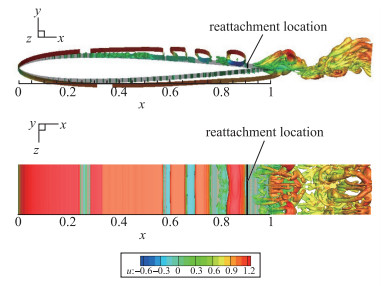
低Reynolds数经典理论认为层流分离泡引入空间能量使流动再附后逐渐形成湍流边界层.然而近期的大涡模拟结果显示[26], 低Reynolds数非定常层流分离流动中存在复杂的三维涡系结构, 如图 15所示, 其中Q不变量以无量纲速度u着色。图 15显示首先层流边界层在逆压梯度的作用下从分离点离开物面, 并产生规则的非定常二维展向分离涡结构, 这种规则的展向分离涡结构不断沿弦向向下游移动, 期间依然近似保持较为规则的二维展向结构, 直至到达时均化再附点位置附近, 这种规则的展向大尺度二维层流分离涡突然发生破碎演变成一系列复杂的较小尺度的三维涡系, 包含一系列复杂的流向涡和发卡涡.从流动结构看, 这种复杂流动不是传统意义上的湍流边界层, 其厚度要远大于湍流边界层, 类似于湍流分离.该结果与经典层流分离泡理论中关于再附点后形成湍流边界层的看法不一致, 也与RANS数值模拟的结果不同, 该区域的流动结构本质是什么, 有待进一步地深入研究.
|
| 图 15 SD8020翼段LES非定常三维模拟Q不变量瞬态结果(Re=4.0×104, α=3.0°) Fig.15 Instantaneous iso-surfaces of Q-criterion on SD8020 airfoil by LES unsteady simulation(Re=4.0×104, α=3.0°) |
| [1] |
Lissaman P B. Low-Reynolds-number airfoils[J]. Annual Review of Fluid Mechanics, 1983, 15: 223-239. DOI:10.1146/annurev.fl.15.010183.001255 |
| [2] |
李锋, 白鹏, 石文, 等. 微型飞行器低雷诺数空气动力学[J]. 力学进展, 2007, 37(2): 257-268. Li F, Bai P, Shi W, et al. Low Reynolds number aerodynamics of micro air vehicles[J]. Advances Mechanics, 2007, 37(2): 257-268. DOI:10.6052/1000-0992-2007-2-J2006-134 (in Chinese) |
| [3] |
李锋, 白鹏, 叶川, 等. 临近空间太阳能飞行器关键基础力学问题研究[J]. 中国科学:物理学力学天文学, 2015, 45(12): 124708. Li F, Bai P, Ye C, et al. Study about key dynamic problems of near space solar power aircraft[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2015, 45(12): 124708. (in Chinese) |
| [4] |
Gaster M. The structure and behaviour of laminar separation bubbles[R]. AGARD CP-4, 1966:813-854.
|
| [5] |
Horton H P. Laminar separation bubbles in two and three dimensional incompressible flow[D]. London:University of London, 1968. https://qmro.qmul.ac.uk/jspui/handle/123456789/1508
|
| [6] |
Selig M S, Guglielmo J J, Broern A P, et al. Experimentson airfoils at low Reynolds numbers[R]. AIAA 1996-0062, 1996.
|
| [7] |
刘强, 刘强, 白鹏, 等. 不同雷诺数下翼型气动特性及层流分离现象演化[J]. 航空学报, 2017, 38(4): 22-34. Liu Q, Liu Q, Bai P, et al. Aerodynamic characteristics of airfoil and evolution of laminar separation at different Reynolds numbers[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(4): 22-34. (in Chinese) |
| [8] |
Olson D A, Katz A W, Naguib A M, et al. On the challenges in experimental characterization of flow separation over airfoils at low Reynolds number[J]. Experiments in Fluids, 2013, 54(2): 1470. DOI:10.1007/s00348-013-1470-1 |
| [9] |
Selig M S, McGranahan B D. Wind tunnel aerodynamic tests of six airfoils for use on small wind turbines[R]. AIAA 2004-1188, 2004.
|
| [10] |
李寿佛. 刚性常微分方程及刚性泛函微分方程数值分析[M]. 湘潭: 湘潭大学出版社, 2010, 22-31. Li S F. Numerical analysis for stiff ordinary and functional differential equations[M]. Xiangtan: Xiangtan University Press, 2010, 22-31. (in Chinese) |
| [11] |
Anderson J D Jr. Computational fluid dynamics:the basics with applications[M]. New York: McGraw-Hill, 1995.
|
| [12] |
Rogers S E, Kwak D, Kiris C. Steady and unsteady solutions of the incompressible Navier-Stokes equations[J]. AIAA Journal, 1991, 29(4): 603-610. DOI:10.2514/3.10627 |
| [13] |
Weiss J M, Smith W A. Preconditioning applied to variable and constant density flows[J]. AIAA Journal, 1995, 33(11): 2050-2057. DOI:10.2514/3.12946 |
| [14] |
Langtry R B, Menter F R. Correlation-based transition mo-deling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2894-2906. DOI:10.2514/1.42362 |
| [15] |
Choudhry A, Arjomandi M, Kelso R. A study of long separation bubble on thick airfoils and its consequent effects[J]. International Journal of Heat and Fluid Flow, 2015, 52: 84-96. DOI:10.1016/j.ijheatfluidflow.2014.12.001 |
| [16] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [17] |
Mueller T J, Batill S M. Experimental studies of separation on a two-dimensional airfoil at low Reynolds numbers[J]. AIAA Journal, 1982, 20(4): 457-463. DOI:10.2514/3.51095 |
| [18] |
Selig M S. The design of airfoils at low Reynolds numbers[R]. AIAA 1985-0074, 1985.
|
| [19] |
Mcghee J, Walker B S, Millard B F. Experimental results for the Eppler 387 airfoil at low Reynolds numbers in the Langley low-turbulence pressure tunnel[R]. NASA-TM-4062, 1988.
|
| [20] |
Lin J C, Pauley L L. Low-Reynolds-number separation on an airfoil[J]. AIAA Journal, 1996, 34(8): 1570-1577. DOI:10.2514/3.13273 |
| [21] |
白鹏, 崔尔杰, 周伟江, 等. 翼型低雷诺数层流分离泡数值研究[J]. 空气动力学学报, 2006, 24(4): 416-424. Bai P, Cui E J, Zhou W J, et al. Numerical simulation of laminar separation bubble over 2D airfoil at low Rey-nolds number[J]. Acta Aerodynamica Sinica, 2006, 24(4): 416-424. (in Chinese) |
| [22] |
白鹏, 李锋, 詹慧玲, 等. 翼型低Re数小攻角非线性非定常层流分离现象研究[J]. 中国科学:物理学力学天文学, 2015, 45(2): 024703. Bai P, Li F, Zhan H L, et al. Study about the non-linear and unsteady laminar separation phenomena around the airfoil at low Reynolds number with low incidence[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2015, 45(2): 024703. (in Chinese) |
| [23] |
Pauley L L, Moin P, Reynolds W C. The structure of two-dimensional separation[J]. Journal of Fluid Mechanics, 1990, 220: 397-411. DOI:10.1017/S0022112090003317 |
| [24] |
白鹏, 崔尔杰, 李锋, 等. 对称翼型低雷诺数小攻角升力系数非线性现象研究[J]. 力学学报, 2006, 38(1): 1-8. Bai P, Cui E J, Li F, et al. Study of the nonlinear lift coefficient of the symmetrical airfoil at low Reynolds number near the 0° angle of attack[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 1-8. (in Chinese) |
| [25] |
Bai P, Li F, Liu Q, et al. Evolution of the non-linear and unsteady low Reynolds number laminar separation bubble around the airfoil with small angle of attack[R]. AIAA 2016-4337, 2016.
|
| [26] |
Zhu Z B, Bai P, Jiao Z H. Large eddy simulation of low Reynolds number flow past the SD7003 airfoil[C]. 3rd International Retreat on Vortical-flow and Aerodynamics. Beijing, 2016.
|