圆柱绕流减阻问题在航空航天飞行器涡轮机械海上舰船以及建筑工程等方面具有广泛的工程应用前景[1].从Prandtl创立边界层理论开始, 人们的注意力就集中在型体方面, 即探索物体的流线型.对于光滑表面圆柱体的绕流, 由于边界层的分离, 在圆柱体前后产生了压力差, 构成圆柱体阻力的绝大部分.由此结果出发, 可以设想是否可以控制边界层的分离, 以达到减阻的目的.最直接的方法即是对柱体修形.
日本横须贺国防研究院Igarashi对带狭缝圆柱的流场特性进行了一系列相关的实验测量工作[2-6]. 1985年Igarashi发表了不同截面形状的圆柱在风洞中进行的实验研究成果[3], 在风洞中, 对直径d=34 mm, 狭缝比s/d=0.08和0.185的开缝圆柱在Reynolds数1.38×104~5.2×104范围内进行了实验. Igarashi认为开缝圆柱绕流流场可分为3种不同的流动型态: 0≤β≤40°(β为缝隙与来流夹角), 尾流受到自引入现象的控制; 40° < β < 60°, 缝隙对流动的影响甚微; 60°≤β≤90°, 流动由边界层“吹吸”现象主导; 特别地, 当80°≤β≤90°, 在开缝圆柱缝隙两端, 交替产生“吹吸”现象, 同时伴随着旋涡的周期性脱落, 这种情况造成基部压力骤降, 阻力变大.随后Igarashi测试了不同截面形状的钝体在圆形管道中的涡流溢放效果[5-6], 发现狭缝比s/d=0.1的开缝圆柱的涡流溢放性能优于梯形柱体, 开缝圆柱具有低阻线形, 其Strouhal数和Reynolds数的线形关系非常好, 在工业流量测量方面具有潜在的运用价值.
2000年英国纽卡斯尔大学的Olsen等在风洞中进行了缝隙大小和圆柱外轮廓形状对Strouhal数和阻力系数影响的研究[7]. Olsen等的研究结果认为90°开缝圆柱在60 < Re < 1000时, 涡流溢放频率大于基准圆柱.且Olsen等明确指出90°开缝圆柱能够增强涡流溢放的强度.
在本课题组已有的研究基础上, 本文通过PIV测量全流场, 借助频谱分析POD分析等方法, 重点关注缝隙倾斜角β=90°, 狭缝比s/d=0.15的开缝圆柱绕流流场, 并且揭示其相干结构及物理机制.
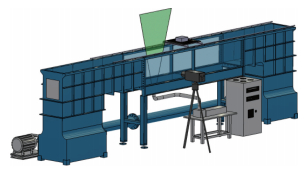
1 实验模型与研究方法本文涉及的实验测量工作均在开放式循环水槽中进行, 该水槽配备了拖曳台车六分量测力天平和1套完整的非介入式粒子成像测速设备(particle image velocimetry, PIV), 如图 1所示.
|
| 图 1 实验平台 Fig.1 Experiment platform |
本文须对开缝圆柱绕流的瞬态流场进行分析, 因此建立了时序PIV系统, 具体参数见表 1.选用的激光器为半导体准连续Nd:YAG激光器, 工作频率为40 kHz, 波长为532 nm, 最大输出功率为15 W. PIV相机选用高速CMOS相机, 分辨率为200万像素, 满幅最大触发频率为1 kHz, 测量窗口任意可调.本文实验中的PIV系统采用丹麦DANTEC公司的Dynamic Studio软件, 系统误差在1%以内.
| 下载CSV 表 1 PIV系统相关参数 Tab.1 Relative parameters of PIV system |
实验模型选用直径d=40 mm, 缝隙宽度s=6 mm, 轴向有效长度l=440 mm的开缝圆柱, 具体参数见表 2.
| 下载CSV 表 2 开缝圆柱尺寸参数 Tab.2 Geometrical parameters of slit cylinder |
为保证PIV实验测量的精度, 模型外径公差控制在±0.2 μm, 并进行黑色阳极氧化处理, 减少激光反射, 如图 2所示.

|
| 图 2 实验模型 Fig.2 Experimental model |
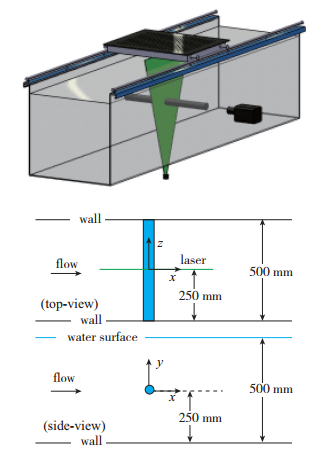
实验时, 实验模型柱体水平安装于水槽中央, 采用底部中央激光打光, 高速相机在侧面采集原始图像, 如图 3所示, 实验堵塞比低于8%.
|
| 图 3 实验模型及激光切面安装位置 Fig.3 Positions of experimental model and laser |
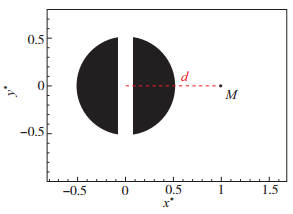
为理解开缝圆柱缝隙的“吹吸”作用对圆柱绕流流场的影响, 本文设置距离圆柱中心下游1d处[8]单点M为监控点, 如图 4所示.
|
| 图 4 监控点M位置示意图 Fig.4 Position of monitoring point M |
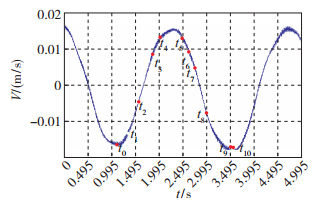
通过监控点M处流体介质法向速度分量V划分开缝圆柱缝隙内部及近尾迹场的流场演化周期, 如图 5所示.
|
| 图 5 单点M法向速度分量V的变化规律 Fig.5 Normal velocity variation of monitoring point M |
图 6为水流速度v=0.075 m/s(基于圆柱直径的Reynolds数Red=3000) 工况下, 一个完整周期内开缝圆柱缝隙内部及近尾迹场的流场演化过程.
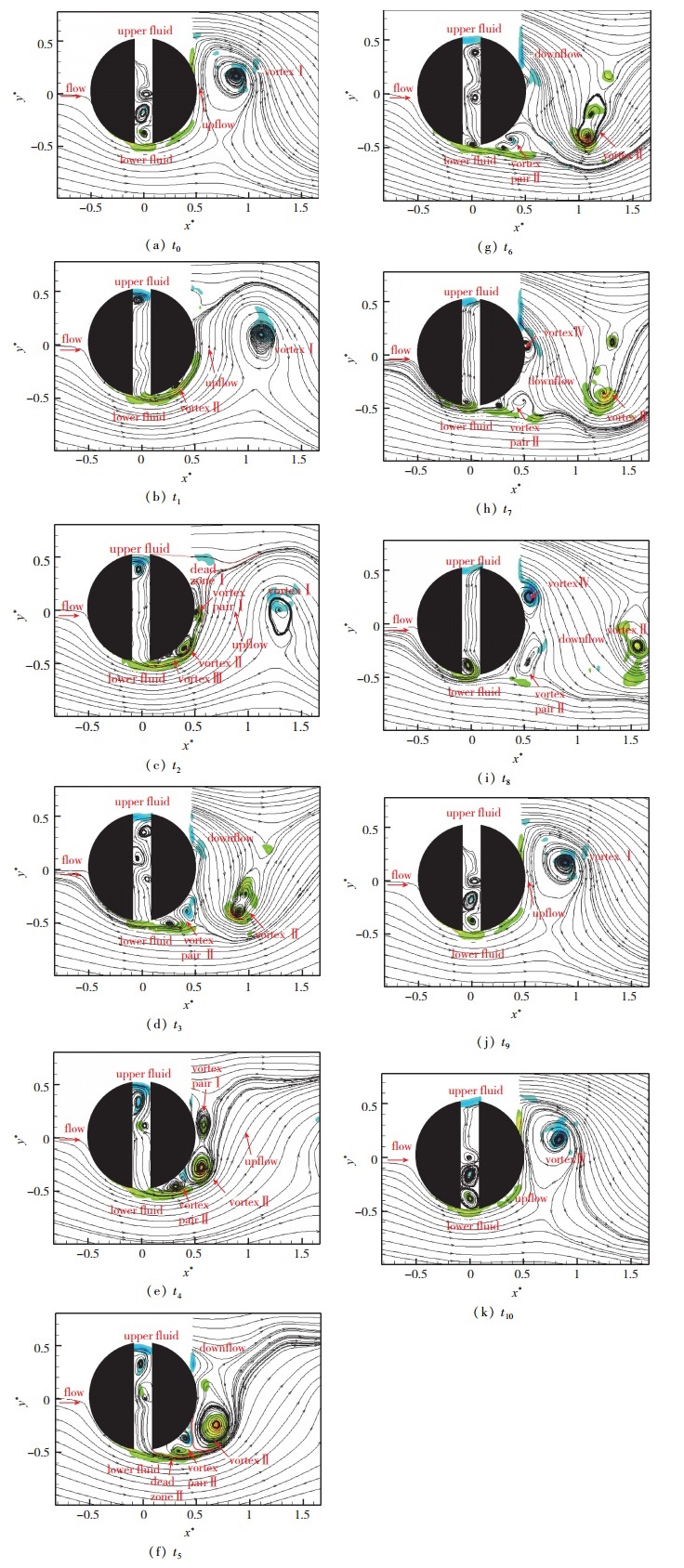
|
| 图 6 Red=3000时, 缝隙及近区尾流流场 Fig.6 Inner flow and near wake at Red=3000 |
t0时刻, 圆柱下游距离圆柱中心上方一侧的旋涡(记为旋涡Ⅰ)随着上冲尾流和上侧主流开始加速脱落, 此时, 经前端圆柱壁面加速分流后的上侧来流从缝隙上端口开始被“吸入”, 由于初始被吸入缝隙内的流体介质能量较缝隙下端口主流能量更弱, 故被“吸入”的流体介质以涡旋的结构积聚在缝隙下端口.
t1时刻, 随着缝隙内部流体介质持续“吸入”, 积聚在缝隙下端口的流体介质不再维持明显的涡旋结构, 由下侧主流“一搓”吹出端口并使得后半圆柱壁面发生流体分离, 产生逆时针旋涡(记为旋涡Ⅱ).
t2时刻, 伴随着缝隙内流体及下侧主流能量的持续输入, 后半圆柱下壁面分离点前移并产生一个新的逆时针旋涡(记为旋涡Ⅲ).旋涡Ⅱ受旋涡Ⅲ挤压逐渐后移, 能量逐渐提高.由于上冲尾流受上侧主流及旋涡Ⅱ挤压后移, 死区Ⅰ变大, 涡对Ⅰ整体涡旋结构变大, 其后半圆柱上壁面流体附着点也沿后半圆柱壁面后移.
t3时刻, 旋涡Ⅰ继续随上冲尾流向后脱落, 旋涡Ⅱ与涡对Ⅰ发生明显的耦合作用, 死区Ⅰ逐渐消失.旋涡Ⅲ经下侧主流和旋涡Ⅱ的“冲搓”作用, 发展成马蹄涡结构的涡对(记为涡对Ⅱ).
t4时刻, 旋涡Ⅱ完全“吞噬”涡对Ⅰ并向后方移动, 逐渐脱离后半圆柱壁面, 死区Ⅰ完全消失, 上侧主流发展成下冲尾流.涡对Ⅱ继续吸收缝隙内部流体及下侧主流能量输入而发展, 在此, 本文将涡对Ⅱ与下侧主流及下冲尾流之间构成的区域定义为死区(记为死区Ⅱ).
t5时刻, 与t0时刻类似, 旋涡Ⅱ随着下冲尾流和下侧主流开始加速脱落, 此时, 经前端圆柱壁面加速分流后的下侧主流从缝隙下端口被“吸入”, 由于初始被吸入缝隙内的流体介质能量较缝隙上端口主流能量更弱, 故被“吸入”的流体介质以涡旋的结构积聚在缝隙上端口.
t6时刻, 随着缝隙内部流体介质持续被“吸入”, 积聚在缝隙上端口的流体介质不再维持明显的涡旋结构, 由上侧主流“一搓”吹出端口并且使得后半圆柱壁面发生流体分离, 产生顺时针旋涡(记为旋涡Ⅳ)(由于PIV数据采集区域的限制导致旋涡Ⅳ无法直接观测, 但结合t1时刻旋涡Ⅱ的形成机理及开缝圆柱流场结构周期性对称性的特点, 这里本文直接指出旋涡Ⅳ的存在及特性).
t7时刻, 伴随着缝隙内流体及上侧主流能量的持续输入, 后半圆柱上壁面分离点前移并产生一个新的顺时针旋涡(记为旋涡Ⅴ).旋涡Ⅳ受旋涡Ⅴ挤压逐渐后移, 能量逐渐提高.由于下冲尾流受下侧主流及旋涡Ⅳ挤压后移, 死区Ⅱ变大, 涡对Ⅱ整体涡旋结构变大, 其后半圆柱上壁面流体附着点也沿后半圆柱壁面后移.
t8时刻, 旋涡Ⅱ继续随下冲尾流向后脱落, 旋涡Ⅳ与涡对Ⅱ发生明显的耦合作用, 死区Ⅱ逐渐消失, 随后旋涡Ⅴ经上侧主流和旋涡Ⅳ的“冲搓”作用, 发展成马蹄涡结构的涡对(记为涡对Ⅲ).
t9时刻, 旋涡Ⅳ完全“吞噬”涡对Ⅱ并向后方移动逐渐脱离后半圆柱壁面, 死区Ⅱ完全消失, 下侧主流发展成上冲尾流.涡对Ⅲ继续吸收缝隙内部流体及下侧主流能量输入而发展, 相同的, 本文将涡对Ⅲ与下侧主流及下冲尾流之间构成的区域定义为死区Ⅲ.
t10时刻, 流场情况与t0时刻一致, 开缝圆柱缝隙内部流动完成一个演化周期.
至此, 得到如下结论:
在有势力作用下圆柱周围存在一个与圆柱尾缘脱落涡强度相等方向相反的涡, 亦称绕形环流.在环流与来流叠加作用下, 开缝圆柱缝隙上下端口产生速度差异.再由Bernoulli定理可得, 缝隙上下端口的速度差异导致了上下端口的压力差异, 从而随着开缝圆柱尾缘旋涡周期性脱落, 开缝圆柱缝隙内部出现周期性“吹吸”现象.
再者, 缝隙内部“吹吸”方向发生变换的起始阶段, 缝隙内流体介质以涡旋结构积聚在“吹出”端口.直至缝隙内积聚的能量足以克服来流时, 缝隙内流体介质从相应端口“吹出”并导致后半圆柱壁面流体分离, 产生旋涡.该旋涡历经附着壁面发展与另一侧壁面产生的旋涡对耦合直至随来流加速脱落这一系列过程.
3 实验结果分析本征正交分解方法是研究复杂空间-时间变化问题的有效工具, 在研究圆柱绕流流场时有独到的实用性.通过分析前几阶模态的分布规律即可推导出支配全流场发展的大尺度逆序结构的演化发展规律, 因此POD方法提供了分析海量实验数据的一种有效途径.例如Ma等[9], Venturi[10], Konstantinidis等[11]均采用POD方法研究了圆柱绕流问题.
因此, 为了进一步探究决定开缝圆柱绕流流场特性的主要相干结构及不同Reynolds数下开缝圆柱绕流流场之间的差异, 采用POD方法从连续几个完整周期内的开缝圆柱绕流流场中提取开缝圆柱绕流流场主要的相干结构, 进而探究Reynolds数对于开缝圆柱流场特性的作用机理.
3.1 POD方法分析开缝圆柱绕流流场图 7为不同Reynolds数下各阶模态湍动能占比关系.可以发现其分布有比较明显的收敛性.根据各阶模态形态所占湍动能能量量级可以将前6阶模态分为3部分, 其中1, 2阶模态(两者占有相同量级的湍动能)对脉动流场贡献最大, 其次是3, 4阶模态(两者占有相同量级的湍动能), 再者是5, 6阶模态(两者占有相同量级的湍动能), 前3部分共占有超过90%的湍动能, 这就决定了前6阶模态形态是开缝圆柱绕流流场中最主要的相干结构.下文以此为依据研究前6阶模态形态[12-13], 从前6阶模态形态中探究不同Reynolds数下开缝圆柱绕流流场中潜在的性质.
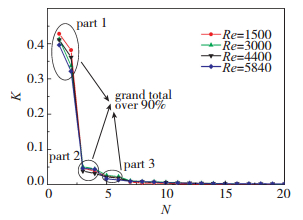
|
| 图 7 不同Reynolds数下各阶模态湍动能占比关系 Fig.7 Each mode′s fraction of energy in different Reynolds numbers |
下文选取Red=3000, 对圆柱绕流流场数据进行POD分析, 并对前6阶模态形态进行细致的研究. 图 8是1, 2阶模态流场结构, 可以发现较明显的沿圆柱中轴线对称且旋向交替的涡街结构.
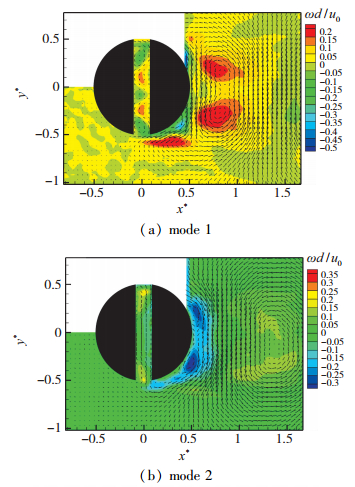
|
| 图 8 1, 2阶模态流场结构(Red=3000) Fig.8 Flow constructions of mode 1 and mode 2 (Red=3000) |
图 9为1, 2阶模态展开系数之间的关系, 可以发现模态展开系数a1与a2具有相同的周期性, 在时间域上仅存在相位之间的差异.
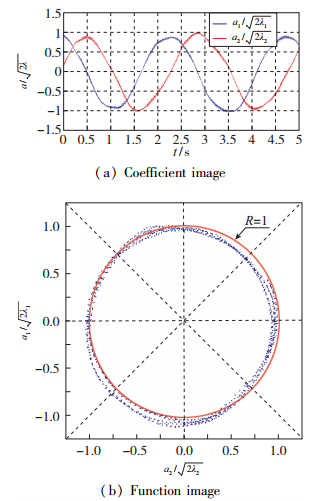
|
| 图 9 1, 2阶模态展开系数之间的关系 Fig.9 Correlation between coefficients a1 with a2 |
本文利用信号处理中的快速Fourier变换(fast Fourier transformation, FFT)将时间域上的模态展开系数a1信息转变为频率域上信号强度信息, 如图 10(a)所示, 其波峰对应的频率即为开缝圆柱绕流涡街脱落频率. 图 10(b)是传统的利用单点位置速度周期性变化信息得到的涡街脱落频率.比较图 10(a)与图 10(b), 可以发现, 两种方法得到的结果具有一致性.因此, 再结合模态展开系数和模态流场结构叠加特性, 本文得出1, 2阶模态共同控制着圆柱绕流流场中涡街相继脱落.与Liu等[14]对沟槽圆柱后尾迹以及Shi等[15]对近壁方柱后尾迹的POD分析结论一致.
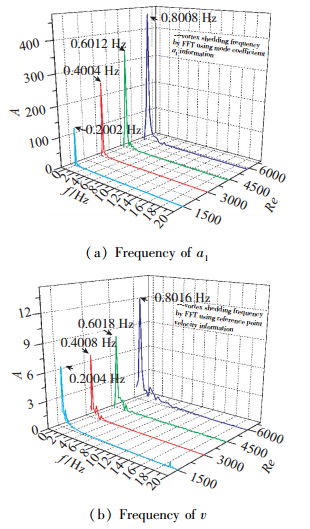
|
| 图 10 两种方法测得的脱落涡频率 Fig.10 Vortex frequencies by two different methods |
图 11为3, 4阶模态流场结构, 可发现较明显的沿圆柱中心线对称的涡街交替结构.为说明3, 4阶模态流场结构在原始流场中的作用, 统计了单一涡旋结构随时间发展情况, 结果如图 12所示.
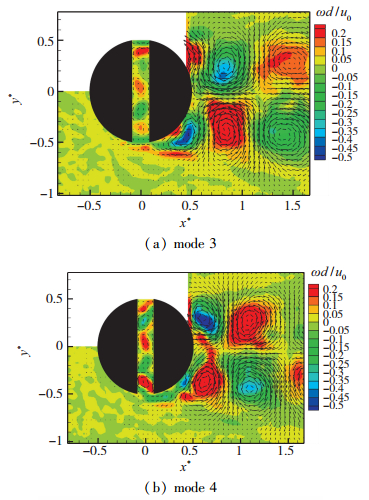
|
| 图 11 3, 4阶模态流场结构(Red=3000) Fig.11 Flow constructions of mode 3 and mode 4 (Red=3000) |
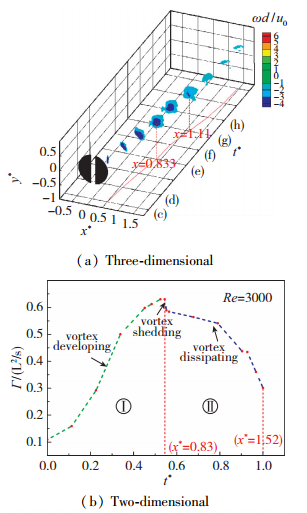
|
| 图 12 涡旋结构随时间发展 Fig.12 Developments of vortex structure |
可以看出, 单一涡旋结构在空间上(以涡心位置为基准)几乎水平向后移动发展, 在时间上(以环量大小为基准)可分为涡旋结构缓慢离开柱体时旋涡能量逐渐增大(Ⅰ)和涡旋结构脱离主体时旋涡能量逐渐消散(Ⅱ)两部分, 其中旋涡脱离位置为x*=0.83(Red=3000).因此, 3, 4阶模态形态对开缝圆柱绕流流场起着控制脱落旋涡沿流向方向能量运输的作用.
图 13是分别利用前4及前6阶模态形态重构的流场与原始流场之间的差异(以(Ⅰ)过程中旋涡环量为统计背景).可以明显看出, 利用前6阶模态形态重构的流场在旋涡能量上与原始流场中的旋涡能量相差无几, 利用前4阶模态形态重构的流场在旋涡能量上随时间发展趋势与原始流场中的旋涡能量发展趋势相当, 但两者旋涡能量上存在明显的差异.因此, 5, 6阶模态形态在(Ⅰ)过程中存在一定的影响.
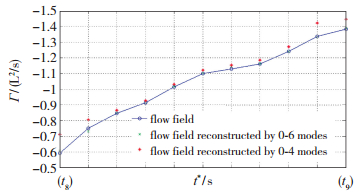
|
| 图 13 模态形态重构与原流场之间的差异 Fig.13 Differences between flow field reconstruction with original flow field |
图 14是5, 6阶模态流场结构, 可以观察到明显的同向涡旋结构, 这在第2节开缝圆柱流场特性分析图 6中e时刻和i时刻中的流场结构相对应, 也因此可以看出同向涡旋结构之间的相互耦合, 必定导致旋涡脱落位置处的旋涡能量的变化. 图 15统计了不同Reynolds数下因同向涡旋结构相互作用导致的旋涡脱落位置处旋涡能量变化差异. 图 15纵坐标为5, 6阶模态形态对于旋涡脱落位置处旋涡能量衰减百分比.可以明显看出, 5, 6阶模态形态同向旋涡的相互作用, 使得主要的脱落旋涡在能量上存在衰减(以统计旋涡脱落位置处旋涡能量为基准), 且这种衰减作用随着Reynolds数的增大而减小.
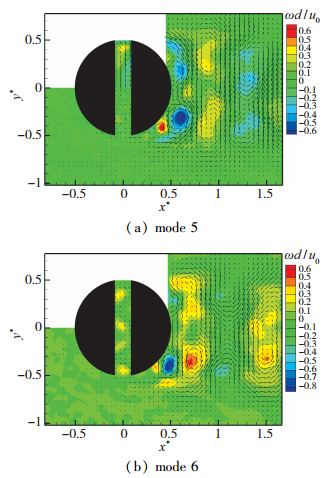
|
| 图 14 5, 6阶模态流场结构(Red=3000) Fig.14 Flow constructions of mode 5 and mode 6 (Red=3000) |
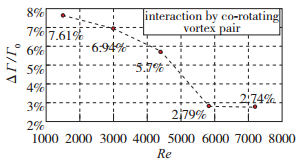
|
| 图 15 不同Reynolds数下同向旋涡结构相互作用 Fig.15 Interaction by co-rotating vortex pair in different Reynolds numbers |
本文采用PIV流场测试技术观察了开缝圆柱的近场区流场特性, 探究缝隙对其流场的影响, 并采用POD方法探究开缝圆柱绕流流场各阶相干结构及作用机理, 得到以下结论:
(1) 实验Reynolds数范围内, 流体流经开缝圆柱时, 在环流与来流叠加作用下, 开缝圆柱缝隙上下端口产生速度差异, 这种差异导致了近壁面区边界层的“吸入”和“吹出”效应, 从根本上改变了圆柱绕流近区尾流的结构.
(2) 应用POD方法对开缝圆柱绕流流场相干结构进行分析时, 得出前6阶模态形态是最主要的相干结构.
(3) 第1和2阶模态形态控制着圆柱绕流流场中涡街相继脱落.利用1或2阶模态系数即可得到脱落涡频率.
(4) 第3和4阶模态形态对开缝圆柱绕流流场起着控制脱落旋涡沿流向方向能量运输的作用.
(5) 第5和6阶模态形态中的同向旋涡作用在旋涡缓慢脱离柱体这一过程中,对主旋涡能量起着一定的衰减作用.
| [1] | Konstantinidis E, Balabani S. Symmetric vortex shedding in the near wake of a circular cylinder due to streamwise perturbations[J]. Journal of Fluids and Structures, 2007, 23(7): 1047-1063. DOI:10.1016/j.jfluidstructs.2007.03.002 |
| [2] | Igarashi T. Flow characteristics around a circular cylinder with a slit:1st report, flow control and flow patterns[J]. Bulletin of the JSME, 1978, 21(154): 656-664. DOI:10.1299/jsme1958.21.656 |
| [3] | Igarashi T. Fluid flow around a bluff-body used for a Karman vortex flowmeter[C]. Proceedings of International Symposium on Fluid Control and Measurement FLUCOME86, Tokyo, 1985, 1017-1022. |
| [4] | Igarashi T. Flow characteristics around a circular cylinder with a slit:2nd report, effect of boundary layer suction[J]. Bulletin of JSME, 1982, 25(207): 1389-1397. DOI:10.1299/jsme1958.25.1389 |
| [5] | Igarashi T. Performance of new type vortex shedder for vortex flowmeter[C]. Proceedings of the 6th Triennal International Symposium on Fluid Control, Measurement and Visualization FLUCOME, Sher-brooke, 2000, 13-17. |
| [6] | Igarashi T. Flow resistance and Strouhal number of a vortex shedder in a circular pipe[J]. JSME International Journal series B:Fluids and Thermal Engineering, 1999, 42(4): 586-595. DOI:10.1299/jsmeb.42.586 |
| [7] | Olsen J F, Rajagopalan S. Vortex shedding behind modified circular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 86(1): 55-63. DOI:10.1016/S0167-6105(00)00003-9 |
| [8] |
马力群, 冯立好. 放置于驻点的合成射流控制圆柱涡脱落模式的实验研究[J].
中国科学:技术科学, 2013, 42(2): 208-219. Ma L Q, Feng L H. Experimental investigation on control of vortex shedding mode of a circular cylinder using synthetic jets placed at stagnation points[J]. Scientia Sinica:Technological Sciences, 2013, 42(2): 208-219. |
| [9] | Ma X, Karniadakis G E, Park H, et al. DPIV-driven flow simulation:a new computational paradigm[J]. Proceedings of the Royal Society of London A:Mathematical, physical and Engineering Sciences, the Royal Society, 2003, 459: 547-565. DOI:10.1098/rspa.2002.0981 |
| [10] | Venturi D. On proper orthogonal decomposition of randomly perturbed fields with applications to flow past a cylinder and natural convection over a horizontal plate[J]. Journal of Fluid Mechanics, 2006, 559: 215-254. DOI:10.1017/S0022112006000346 |
| [11] | Konstantinidis E, Balabani S, Yianneskis M. Bimodal vortex shedding in a perturbed cylinder wake[J]. Physics Fluids, 2007, 19(1): 011701 DOI:10.1063/1.2432152 |
| [12] | Feng L H, Wang J J. Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point[J]. Journal of Fluid Mechanics, 2010, 662: 232-259. DOI:10.1017/S0022112010003174 |
| [13] | Feng L H, Wang J J, Pan C. Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control[J]. Physics of Fluids, 2011, 23(1): 014106 DOI:10.1063/1.3540679 |
| [14] | Liu Y Z, Shi L L, Yu J. TR-PIV measurement of the wake behind a grooved cylinder at low Reynolds number[J]. Journal of Fluids and Structures, 2011, 27(3): 394-407. DOI:10.1016/j.jfluidstructs.2010.11.013 |
| [15] | Shi L L, Liu Y Z, Wan J J. Influence of wall proximity on characteristics of wake behind a square cylinder:PIV measurements and POD analysis[J]. Experimental Thermal and Fluid Science, 2010, 34(1): 28-36. DOI:10.1016/j.expthermflusci.2009.08.008 |



