2. 中国科学院大学数学科学学院,北京 100049;北京航空航天大学数学与系统科学学院,北京 100191;
3. 北京航空航天大学数学与系统科学学院,北京 100191
2. School of Mathematical Sciences, UCAS, Beijing 100049, China; School of Mathematics and Systems Science, Beihang University, Beijing 100191, China;
3. School of Mathematics and Systems Science, Beihang University, Beijing 100191, China
Euler方程的高精度高分辨率数值方法主要有3种:有限差分方法[1-14], 有限体积方法[15-20]和有限元方法(例如间断有限元法[21-23]).有限差分法简单高效, 只在每个方向上做一维变量/通量重构, 在简单区域问题上使用方便, 但是处理复杂区域比较困难.有限体积法[20]和有限元法[23]适合复杂区域, 但须要重构每个网格单元上变量的高维分布或计算多个自由度, 这使得这两种方法和有限差分法相比在计算量上有很大的增加.
我们发现, 传统有限体积法及其变种方法[24-25]中计算量占比很大的高维重构在后来计算中被用到的仅仅是边界Gauss积分点处的变量值, 单元内部的高维重构似乎并非必需.因此在本文中, 考虑仅在网格单元边上进行重构, 目的是发展计算量小且有高精度高分辨率特性的方法.我们设计了一致矩形和非结构三角形网格边上的一维重构, 由此提出了计算二维Euler方程的降维重构算法.对于矩形网格容易证明该算法是守恒的, 它的激波间断捕捉能力和WENO差分方法[2-4]相当, 计算效率略差, 但比WENO有限体积方法[20, 26]大为提高.该算法的主要思想是在一个网格单元上, 从微分型控制方程出发, 利用网格边上多个解点处的通量导数信息来推进解点处的解.当网格是一致矩形网格时, 可用一维WENO[2-4]有限差分法计算沿边方向的通量导数, 边内部解点的法向导数用插值方式计算.当网格是非结构三角形网格时, 我们只用三角形单元各边上几个解点来重构本边的多项式.对于边端点解点处的通量导数用共享端点的边重构加权来计算, 而对于边内部解点处的法向通量导数则用插值方式计算.算例表明, 该算法在一致矩形网格上可达到3阶精度, 在三角形网格上可达到2阶精度, 可以计算有强激波的无黏流动问题, 且有较高的计算效率.
1 二维双曲守恒律的降维重构算法考虑二维双曲守恒律组
| $ {u_t} + {f_x}\left( u \right) + {g_y}\left( u \right) = 0 $ | (1) |
的数值求解.这里下标表示偏导数.降维重构算法在图 1中矩形或三角形网格边上设置的解点(边内部解点用

|
| 图 1 (左)和三角形网格(右) Fig.1 Rectangular grids (left) and triangular grids (right) |
在图 1(左)所示的均匀矩形网格单元ei, j上, 每条边上均匀分布K个解点, 其中两个为端点.解点处的解变量u, 通量f, g以及通量导数都是连续的.根据式(1), 解点变量的演化须计算该点的通量导数fx(u), gy(u).对于x方向j+1/2网格线上解点m处的通量导数f(u)x可以按照一维有限差分WENO方法来逼近, 即
| $ {\left( {{f_x}} \right)_{m,j + 1/2}} \approx \frac{{{{\hat f}_{m + 1/2,j + 1/2}} - {{\hat f}_{m - 1/2,j + 1/2}}}}{{{h_x}}} $ | (2) |
其中,hx=Δx/(K-1).类似地, y方向网格线上解点的gy(u)按照y方向的一维有限差分WENO方法获得.这样, 边顶点解点处的fx(u)和gy(u)信息是完整的.但边内部解点处的通量导数信息并不完整, 如x方向边内部解点m处缺少导数信息gy(u), 这时, 我们通过x方向4个顶点解点处的通量导数的加权组合得到内部解点的通量导数值, 对于y方向边上缺失的fx(u)类似处理.下面以x方向边为例详述.
以网格单元每条边有K=3个解点的情形为例.对于x方向边的中间解点处的gy(u)信息, 可采用x方向边4个顶点处通量导数的线性组合来获得, 即由顶点(i-3/2, j+1/2), (i-1/2, j+1/2), (i+1/2, j+1/2)和(i+3/2, j+1/2)向中间解点m处进行O(Δx4)阶精度的Lagrange插值, 结果为
| $ \begin{array}{l} {\left( {{g_y}} \right)_{m,j + 1/2}} = - \frac{1}{{16}}{\left( {{g_y}} \right)_{i - 3/2,j + 1/2}} + \frac{9}{{16}}{\left( {{g_y}} \right)_{i - 1/2,j + 1/2}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{9}{{16}}{\left( {{g_y}} \right)_{i + 1/2,j + 1/2}} - \frac{1}{{16}}{\left( {{g_y}} \right)_{i + 3/2,j + 1/2}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{2}\left[ { - \frac{1}{8}{{\left( {{g_y}} \right)}_{i - 3/2,j + 1/2}} + \frac{3}{4}{{\left( {{g_y}} \right)}_{i - 1/2,j + 1/2}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{3}{8}{{\left( {{g_y}} \right)}_{i + 1/2,j + 1/2}}} \right] + \frac{1}{2}\left[ { - \frac{1}{8}{{\left( {{g_y}} \right)}_{i + 3/2,j + 1/2}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{3}{4}{{\left( {{g_y}} \right)}_{i + 1/2,j + 1/2}} + \frac{3}{8}{{\left( {{g_y}} \right)}_{i - 1/2,j + 1/2}}} \right] \end{array} $ | (3) |
从式(3)第2个等号可以看出中间解点的y方向通量导数是上风偏斜(第1个方括号项)和下风偏斜插值(第2个方括号项)的代数平均.对于一些问题用中心型插值(3)会产生数值振荡.更加稳定的方法是采用上风偏斜和下风偏斜插值的非线性加权组合.类似于Jiang-Shu WENO[2, 27]的非线性加权的思想, 我们将中间解点处的通量导数用上风(L)和下风(R)子模板的凸组合
| $ {\left( {{g_y}} \right)_{m,j + 1/2}} = \beta \left( {{g_y}} \right)_{m,j + 1/2}^{\rm{L}} + \left( {1 - \beta } \right)\left( {{g_y}} \right)_{m,j + 1/2}^{\rm{R}} $ | (4) |
其中, 非线性权β采用以下方法计算(优化系数为C0=C1=0.5)
| $ {\beta _k} = \frac{{{\alpha _k}}}{{{\alpha _0} + {\alpha _1}}},{\alpha _k} = \frac{{{C_k}}}{{{{\left( {I{S_k} + \varepsilon } \right)}^2}}},\varepsilon = {10^{ - 6}},k = 0,1 $ | (5) |
其中ISk为子模板上二次重构多项式在区间[xi-1/2, xi+1/2]上按Jiang-Shu定义算的光滑度指示子, 具体给出(这里省略下标j+1/2)
| $ \begin{array}{l} I{S_0} = {\left[ {{{\left( {{g_y}} \right)}_{i + 1/2}} - {{\left( {{g_y}} \right)}_{i - 1/2}}} \right]^2} + \frac{{13}}{{12}}\left[ {{{\left( {{g_y}} \right)}_{i + 1/2}} - } \right.\\ \;\;\;\;\;\;\;\;{\left. {2{{\left( {{g_y}} \right)}_{i - 1/2}} + {{\left( {{g_y}} \right)}_{i - 3/2}}} \right]^2},\\ I{S_1} = {\left[ {{{\left( {{g_y}} \right)}_{i + 3/2}} - {{\left( {{g_y}} \right)}_{i + 1/2}}} \right]^2} + \frac{{13}}{{12}}\left[ {{{\left( {{g_y}} \right)}_{i + 3/2}} - } \right.\\ \;\;\;\;\;\;\;\;{\left. {2{{\left( {{g_y}} \right)}_{i + 1/2}} + {{\left( {{g_y}} \right)}_{i - 1/2}}} \right]^2} \end{array} $ | (6) |
利用类似的方法可得到y方向边内部解点处的通量导数.
对于每边3个解点K=3情形, 将守恒律(1)应用每一个解点(is, js)
| $ {\left( {\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}}} \right)_{{i_s},{j_s}}} = 0 $ | (7) |
可以对每条网格线的解点进行循环求解.
事实上, 式(7)在网格边的端点解点上, 就是传统的有限差分WENO法; 在网格边的中间解点上, 一个方向的通量导数是按照一维WENO方法得到的, 另一方向的通量导数是按照插值方式获得的, 这是降维重构法的特点.由于子模板3个顶点向边中间解点的插值引入了O(Δx3)插值误差, 因此凸组合(4)的精度阶介于3~4之间.由于每个解点两侧有唯一的数值通量, 故该方法是守恒的.但要注意, 算法稳定的时间步长正比于解点之间的间距hx.
1.2 三角形网格上的降维重构算法如图 1(右)的三角形网格, 记Uk, s为边s上解点k处的解, 我们用简单的Lagrange多项式重构边s上的解变量分布
| $ {\mathit{\boldsymbol{U}}_s}\left( \xi \right) = \sum\limits_{k = 1}^K {{L_{k,s}}\left( \xi \right){\mathit{\boldsymbol{U}}_{k,s}}} ,\xi \in \left[ {0,1} \right] $ | (8) |
其中, Lk, s(ξ)为边s上点k处的一维Lagrange插值函数, ξ为边的参数坐标.对于每边均匀分布3个解点的情形, 式(8)可用3点Newton插值多项式表示
| $ \begin{array}{l} {\mathit{\boldsymbol{U}}_s}\left( \xi \right) = {\mathit{\boldsymbol{U}}_{2,s}} + \left( {{\mathit{\boldsymbol{U}}_{3,s}} - {\mathit{\boldsymbol{U}}_{1,s}}} \right)\left( {\xi - \frac{1}{2}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;2\left( {{\mathit{\boldsymbol{U}}_{1,s}} - 2{\mathit{\boldsymbol{U}}_{2,s}} + {\mathit{\boldsymbol{U}}_{3,s}}} \right){\left( {\xi - \frac{1}{2}} \right)^2} \end{array} $ | (9) |
其中, 下标1, 2, 3分别对应参数坐标ξ=0, 1/2, 1.这里规定从顶点全局小编号到大编号方向为ξ的正向.
网格顶点全局编号v处的通量导数用围绕此顶点的所有边l的一维重构Ul(ξ)的局部坐标导数(dUl(ξ)/dξ)v的组合来近似
| $ \begin{array}{l} {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}}} \right)_v} = {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \mathit{\boldsymbol{U}}}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial x}}} \right)_v} = {\mathit{\boldsymbol{A}}_v}{\left( {\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial x}}} \right)_v}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {\mathit{\boldsymbol{A}}_v}\sum\limits_{l = 1}^{{N_v}} {\beta _l^x\frac{{\cos {\theta _l}}}{{{d_l}}}{{\left( {\frac{{{\rm{d}}{\mathit{\boldsymbol{U}}_l}}}{{{\rm{d}}\xi }}} \right)}_v}} ,\\ {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}}} \right)_v} = {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \mathit{\boldsymbol{U}}}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial y}}} \right)_v} = {\mathit{\boldsymbol{B}}_v}{\left( {\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial y}}} \right)_v}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {\mathit{\boldsymbol{B}}_v}\sum\limits_{l = 1}^{{N_v}} {\beta _l^y\frac{{\sin {\theta _l}}}{{{d_l}}}{{\left( {\frac{{{\rm{d}}{\mathit{\boldsymbol{U}}_l}}}{{{\rm{d}}\xi }}} \right)}_v}} \end{array} $ | (10) |
Fy, Gx类似计算.其中
| $ \beta _l^x = \frac{{\left| {\frac{1}{{\Delta {x_l}}}} \right|}}{{\sum\limits_{s = 1}^{{N_v}} {\left| {\frac{1}{{\Delta {x_s}}}} \right|} }},\beta _l^y = \frac{{\left| {\frac{1}{{\Delta {y_l}}}} \right|}}{{\sum\limits_{s = 1}^{{N_v}} {\left| {\frac{1}{{\Delta {y_s}}}} \right|} }} $ | (11) |
数值实验显示用式(11)计算间断问题会发散.为改善稳定性, 我们用类似WENO的非线性权, 其中优化权仍取式(11), 光滑指示子用边l的一维重构多项式(9)在ξ∈[0, 0.5]区间上的积分, 取光滑指示子
| $ \begin{array}{*{20}{c}} {I{S_l} = \sum\limits_{j = 1}^2 {\int_0^{0.5} {{{\left( {\Delta \xi } \right)}^{2j - 1}}{{\left[ {\frac{{{{\rm{d}}^j}{U_l}\left( \xi \right)}}{{{\rm{d}}{\xi ^j}}}} \right]}^2}{\rm{d}}\xi } } ,}\\ {l = 1, \cdots ,{N_v}} \end{array} $ | (12) |
经过计算得到具体的光滑指示子为
| $ \begin{array}{l} I{S_l} = \frac{1}{4}\left[ {\left( {{U_{3,l}} - {U_{1,l}}} \right) + 4\left( {{U_{3,l}} - } \right.} \right.\\ \;\;\;\;\;\;\;{\left. {\left. {2{U_{2,l}} + {U_{1,l}}} \right)} \right]^2} \end{array} $ | (13) |
于是式(10)中的权用如下的非线性权计算
| $ \begin{array}{l} \bar \beta _l^x = \frac{{\alpha _l^x}}{{\sum\limits_{s = 1}^{{N_v}} {\alpha _s^x} }},\alpha _l^x = \frac{{\beta _l^x}}{{{{\left( {I{S_l} + \varepsilon } \right)}^2}}}\\ \bar \beta _l^y = \frac{{\alpha _l^y}}{{\sum\limits_{s = 1}^{{N_v}} {\alpha _s^y} }},\alpha _l^y = \frac{{\beta _l^y}}{{{{\left( {I{S_l} + \varepsilon } \right)}^2}}} \end{array} $ | (14) |
用式(10)可计算顶点解点处的全部通量导数Fx, Fy, Gx, Gy, 但中间解点m处只有通量切向导数是可计算的, 如(
设n =(nx, ny)为当前边s的法向矢量, 则边两个顶点解点的通量法向导数为
| $ \left\{ \begin{array}{l} {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial n}}} \right)_k} = {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}}} \right)_k}{n_x} + {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial y}}} \right)_k}{n_y}\\ {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial n}}} \right)_k} = {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial x}}} \right)_k}{n_x} + {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}}} \right)_k}{n_y} \end{array} \right.,k = {v_1},{v_2} $ | (15) |
边中间解点m处的通量法向导数用顶点的代数平均来近似
| $ \begin{array}{l} {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial n}}} \right)_m} = \frac{1}{2}\left[ {{{\left( {\left. {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial n}}} \right|} \right)}_{{v_1}}} + {{\left( {\left. {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial n}}} \right|} \right)}_{{v_2}}}} \right] + O\left( {d_s^2} \right)\\ {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial n}}} \right)_m} = \frac{1}{2}\left[ {{{\left( {\left. {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial n}}} \right|} \right)}_{{v_1}}} + {{\left( {\left. {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial n}}} \right|} \right)}_{{v_2}}}} \right] + O\left( {d_s^2} \right) \end{array} $ | (16) |
由于边s的切向
| $ \begin{array}{l} {\left( {{{\mathit{\boldsymbol{\tilde F}}}_x}} \right)_m} = {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial n}}} \right)_m}{n_x} + {\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \xi }}} \right)_m}\frac{{{\xi _x}}}{{{d_s}}}\\ {\left( {{{\mathit{\boldsymbol{\tilde G}}}_y}} \right)_m} = {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial n}}} \right)_m}{n_y} + {\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \xi }}} \right)_m}\frac{{{\xi _y}}}{{{d_s}}} \end{array} $ | (17) |
其中ds为单元边长,因此得到边s上所有解点k处的半离散格式
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{U}}_{k,s}}}}{{{\rm{d}}t}} + {\left( {{{\mathit{\boldsymbol{\tilde F}}}_x} + {{\mathit{\boldsymbol{\tilde G}}}_y}} \right)_{k,s}} = 0 $ | (18) |
式(18)用3阶TVD-RK方法[28-29]时间推进求解.
2 数值结果 2.1 二维标量方程考虑二维线性标量对流方程的初边值问题
| $ \left\{ \begin{array}{l} {u_t} + {u_x} + {u_y} = 0\\ u\left( {x,y,0} \right) = \sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2}\left( {x + y} \right)} \right)\\ \left( {x,y} \right) \in \left[ { - 2,2} \right] \times \left[ { - 2,2} \right] \end{array} \right. $ | (19) |
其精确解为[30]
| $ u\left( {x,y,t} \right) = \sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2}\left( {x + y - 2t} \right)} \right) $ |
边界上采用周期边界条件.计算区域的边长为无量纲量,用图 2中两种不同的计算网格来进行比较.以CFL=0.5计算到时间t=2. 图 3(a)和(b)分别显示用图 2(a)和(b)两种类型网格的计算结果,可见差别不大.

|
| 图 2 两种三角形网格, 网格尺度l=1/450 Fig.2 Two different triangular grids with grid size l=1/450 |

|
| 图 3 线性问题(19)的计算结果 Fig.3 Numerical results of Eq.(19) |
| $ \left\{ \begin{array}{l} {u_t} + {\left( {\frac{{{u^2}}}{2}} \right)_x} + {\left( {\frac{{{u^2}}}{2}} \right)_y} = 0\\ u\left( {x,y,0} \right) = 0.3 + 0.7\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2}\left( {x + y} \right)} \right)\\ \left( {x,y} \right) \in \left[ { - 2,2} \right] \times \left[ { - 2,2} \right] \end{array} \right. $ | (20) |
其精确解为
| $ u\left( {x,y,t} \right) = 0.3 + 0.7\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2}\left( {x + y - 2u\left( {x,y} \right)t} \right)} \right) $ |
边界上采用周期边界条件.以CFL=0.45计算到时间t=0.5, 此时间断解尚未形成. 表 1给出矩形网格上的误差与收敛阶, 可见精度可以达到3阶以上. 表 2给在三角形网格上的误差收敛阶, 可见只有2阶精度.
| 下载CSV 表 1 Burgers方程在矩形网格上的精度阶 Tab.1 Convergence rate for the solution of the Burgers equation (20) on rectangular grids |
| 下载CSV 表 2 Burgers方程在三角形网格上的精度阶 Tab.2 Convergence rate for the solution of the Burgers equation (20) on triangular grids |
考虑二维可压缩流Euler方程组
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{U}}_t} + {\mathit{\boldsymbol{F}}_x} + {\mathit{\boldsymbol{G}}_y} = 0\\ \mathit{\boldsymbol{U}} = {\left( {\rho ,\rho u,\rho v,E} \right)^{\rm{T}}}\\ \mathit{\boldsymbol{F}} = {\left( {\rho u,\rho {u^2} + p,\rho uv,u\left( {E + p} \right)} \right)^{\rm{T}}}\\ \mathit{\boldsymbol{G}} = {\left( {\rho v,\rho uv,\rho {v^2} + p,v\left( {E + p} \right)} \right)^{\rm{T}}}\\ E = \frac{p}{{\gamma - 1}} + \frac{1}{2}\rho \left( {{u^2} + {v^2}} \right) \end{array} \right. $ | (21) |
式中, ρ, u, v, p, E, γ分别为流体的密度, x和y方向速度分量、压力、单位体积的总能及气体比热比(γ=1.4).计算3个典型问题.
(1) 前台阶问题[15, 25].在1个单位宽和3个单位长的风洞内, 下壁面从左边起0.6个单位开始, 有高0.2单位的固体台阶一直延伸到风洞右端, 左边为Ma=3.0的进口速度, 上壁面和台阶上为壁面反射条件, 右边为出口条件.计算到t=4. 图 4为三角形网格示意图. 图 5为三角形网格上降维算法在两个不同尺度网格上计算结果的比较.可见随网格加密, 分辨率明显提高. 图 6是K=3直角网格上降维方法和加密1倍网格上有限差分WENO格式计算结果的比较, 可见直角网格降维算法虽然分辨率较低, 但是CPU时间仅为后者的70%.另外, 直角网格降维算法(见图 6(a))的分辨率高于同样网格边长的三角形网格降维重构法结果(见图 5(a)).

|
| 图 4 GMSH生成的三角形网格示意图 Fig.4 Triangular grids generated by GMSH |

|
| 图 5 三角网格降维重构算法, 30条均分密度等值线从0.256 8到6.607,计算时间t=4.0 Fig.5 30 density contours from 0.256 8 to 6.607 at t=4.0 computed by the present algorithm on triangular grids |

|
| 图 6 30条均分密度等值线从0.2568到6.607,t=4.0 Fig.6 30 density contours from 0.2568 to 6.607 at t=4.0 |
(2) 双Mach反射问题[1, 15].取1个单位宽和4个单位长, 计算域大小为[0, 4]×[0, 1], 一个Mach数为10的强激波放置在x=1/6, y=0处, 并与正x轴成60°交角.激波右侧的波前区域的初始流场值为(ρ, u, v, p)=(1.4, 0.0, 0.0, 1.0), 左侧波后区域的流场值用正激波跳跃关系确定.用降维重构方法在不同边长的三角形网格上进行计算, 从图 7的计算结果可见, 该方法可以得到较高的分辨率.

|
| 图 7 降维重构方法, 密度等值线40条从1.88783到20.9144, t=0.2 Fig.7 40 density contours from 1.88783 to 20.9144 at t=0.2 computed by the present algorithm |
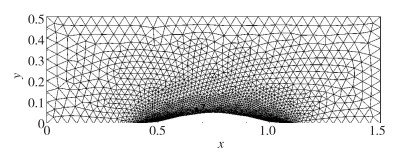
(3) 亚声速流绕过管道中的一个平滑凸起物[31].计算区域为-1.5≤x≤1.5, 0≤y≤0.8.沿全部底壁的光滑凸起为y =0.062 5e-25x2, 图 8为计算区域的三角形网格示意图,入流Mach数为0.5, 迎角0°, 密度ρ=1和声速c=1. 表 3给出了用文献[31]中的办法确定的计算收敛情况, 图 9给出了密度分布, 可见三角形网格上降维重构法具有较高的分辨率.
|
| 图 8 GMSH生成的三角形网格示例, 2629单元 Fig.8 Triangular grids generated by GMSH with 2629 elements |
| 下载CSV 表 3 亚声速流通过一个光滑凸起在三角形网格上的精度阶 Tab.3 Convergence rate for the solution of subsonic flow through a smooth bump on triangular grids |

|
| 图 9 三角形网格上降维重构算法的计算的密度分布, Mach数0.5绕流管道中的突起物(30条等值线, 最大为1.014, 最小为0.954, 网格数=3 689) Fig.9 30 density contours from 0.954 to 1.014 computed by the present algorithm on triangular grids for Ma=0.5 subsonic flow past a bump in a channel |
本文提出了二维矩形网格和三角形网格上求解Euler方程的降维重构方法, 通过对二维问题进行测试, 并和传统的有限差分WENO方法进行比较, 表明矩形网格上降维重构方法可达到3阶精度, 具有较好的分辨率和较高的计算效率.非结构三角形网格上降维重构方法有2阶精度, 且可以计算有间断的流动.
| [1] |
Shu C W, Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes Ⅱ[J]. Journal of Computational Physics, 1989, 83(1): 32-78. |
| [2] |
Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [3] |
Henrick A K, Aslam T D, Powers J M. Mapped weighted essentially non-oscillatory schemes:achieving optimal order near critical points[J]. Journal of Computational Physics, 2005, 207(2): 542-567. |
| [4] |
Borges R, Carmona M, Costa B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227(6): 3191-3211. DOI:10.1016/j.jcp.2007.11.038 |
| [5] |
Adams N A, Shariff K. A high-resolution hybrid compact-ENO scheme for shock-turbulence interaction problems[J]. Journal of Computational Physics, 1996, 127(1): 27-51. |
| [6] |
Pirozzoli S. Conservative hybrid compact-WENO schemes for shock-turbulence interaction[J]. Journal of Computational Physics, 2002, 178(1): 81-117. |
| [7] |
Ren Y X, Liu M E, Zhang H X. A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws[J]. Journal of Computational Physics, 2003, 192(2): 365-386. |
| [8] |
Kim D, Kwon H K. A high-order accurate hybrid scheme using a central flux scheme and a WENO scheme for compressible flowfield analysis[J]. Journal of Computational Physics, 2005, 210(2): 554-583. DOI:10.1016/j.jcp.2005.04.023 |
| [9] |
Banks J W, Aslam T, Rider W J. On sub-linear convergence for linearly degenerate waves in capturing schemes[J]. Journal of Computational Physics, 2008, 227(14): 6985-7002. DOI:10.1016/j.jcp.2008.04.002 |
| [10] |
Balsara D S, Shu C W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy[J]. Journal of Computational Physics, 2000, 160(2): 405-452. DOI:10.1006/jcph.2000.6443 |
| [11] |
Yamaleev N K, Carpenter M H. A systematic methodology for constructing high-order energy stable WENO sche-mes[J]. Journal of Computational Physics, 2009, 228(11): 4248-4272. DOI:10.1016/j.jcp.2009.03.002 |
| [12] |
Hu X Y, Wang Q, Adams N A. An adaptive central-upwind weighted essentially non-oscillatory scheme[J]. Journal of Computational Physics, 2010, 229(23): 8952-8965. DOI:10.1016/j.jcp.2010.08.019 |
| [13] |
Feng H, Hu F X, Wang R. A new mapped weighted essentially non-oscillatory scheme[J]. Journal of Scientific Computing, 2012, 51(2): 449-473. DOI:10.1007/s10915-011-9518-y |
| [14] |
Wang R, Feng H, Huang C. A new mapped weighted essentially non-oscillatory method using rational mapping function[J]. Journal of Scientific Computing, 2015, 67(2): 540-580. |
| [15] |
Woodward P, Colella P. The numerical simulation of two-dimensional fluid flow with strong shocks[J]. Journal of Computational Physics, 1984, 54(1): 115-173. |
| [16] |
Harten A, Osher S. Uniformly high-order accurate nonoscillatory schemes. I[J]. SIAM Journal on Numerical Analysis, 1987, 24(2): 279-309. |
| [17] |
Harten A, Engquist B, Osher S, et al. Uniformly high order accurate essentially non-oscillatory schemes, Ⅲ[J]. Journal of Computational Physics, 1987, 71(2): 231-303. |
| [18] |
Liu X D, Osher S, Chan T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physi-cs, 1994, 115(1): 200-212. |
| [19] |
Wang Q J, Ren Y X, Sun Z S, et al. Low dispersion finite volume scheme based on reconstruction with mini-mized dispersion and controllable dissipation[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(2): 423-431. DOI:10.1007/s11433-012-4987-z |
| [20] |
Hu C Q, Shu C W. Weighted essentially non-oscillatory schemes on triangular meshes[J]. Journal of Computa-tional Physics, 1999, 150(1): 97-127. |
| [21] |
Cockburn B, Lin S Y, Shu C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅲ:one-dimensional systems[J]. Journal of Computational Physics, 1989, 84(1): 90-113. DOI:10.1016/0021-9991(89)90183-6 |
| [22] |
Cockburn B, Shu C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅱ:general framework[J]. Mathematics of Computation, 1989, 52(186): 411-435. |
| [23] |
Cockburn B, Hou S C, Shu C W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV:the multidimensional case[J]. Mathematics of Computation, 1990, 54(190): 545-581. |
| [24] |
Huynh H T. A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods[C]. Proceedings of the 18th AIAA Computational Fluid Dynamics Conference. Miami: AIAA 2007: 4079.
|
| [25] |
Deng X, Xie B, Xiao F. A finite volume multi-moment method with boundary variation diminishing principle for Euler equation on three-dimensional hybrid unstructured grids[J]. Computers & Fluids, 2017, 153: 85-101. |
| [26] |
Titarev V A, Toro E F. Finite-volume WENO schemes for three-dimensional conservation laws[J]. Journal of Computational Physics, 2004, 201(1): 238-260. DOI:10.1016/j.jcp.2004.05.015 |
| [27] |
Shu C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[C]. Advanced Numerical Approximation of Nonlin-ear Hyperbolic Equations[M]. Berlin: Springerverlag, 1998: 325-432.
|
| [28] |
Shu C W. Total-variation-diminishing time discretiza-tions[J]. SIAM Journal on Scientific and Statistical Computing, 1988, 9(6): 1073-1084. DOI:10.1137/0909073 |
| [29] |
Gottlieb S, Shu C W. Total variation diminishing Runge-Kutta schemes[J]. Mathematics of Computation, 1998, 67(221): 73-85. DOI:10.1090/S0025-5718-98-00913-2 |
| [30] |
Zhou T, Li Y F, Shu C W. Numerical comparison of WENO finite volume and Runge-Kutta discontinuous Galerkin methods[J]. Journal of Scientific Computing, 2001, 16(2): 145-171. DOI:10.1023/A:1012282706985 |
| [31] |
Cheng J, Liu T G, Luo H. A hybrid reconstructed discontinuous Galerkin method for compressible flows on arbitrary grid[J]. Computers & Fluids, 2016, 139: 68-79. |



