2. 中国空空导弹研究院,河南洛阳 471000;
3. 北京电子工程总体研究所,北京 100854
2. China Airborne Missile Academy, Luoyang 471000, China;
3. Beijing Institute of Electronic System Engneering, Beijing 100854, China
随着跨帧CCD相机和双脉冲激光器的出现, 亚微秒的时间间隔使其可以记录1 000 m/s量级流动速度的互相关图像, 粒子图像测速(particle image velocimetry, PIV)技术开始应用于超声速流动甚至高超声速流动.但是, PIV技术的分析精度在本质上取决于示踪粒子的密度、大小和运动响应等物理特性, 特别是示踪粒子跟随性对超声速流动中的PIV应用至关重要.示踪粒子跟随性的好坏直接影响高速PIV测量的准确性, 而示踪粒子直径(dp)和气相对流Mach数(Mc)成为了研究PIV粒子跟随性的关键因素.
在PIV实验方面, 美国斯坦福大学的Urban等[1]在试验中发现TiO2粒子的松弛时间大约为3~4 μs, 而Al2O3粒子松弛时间超过20 μs.荷兰代尔夫特理工大学的Scarano等[2]通过分析斜激波后的粒子速度型认为所用的TiO2粒子松弛时间小于2 μs. Ragni等[3]还采用了松弛时间范围0.4~3.7 μs的一系列固态粒子进行了系统研究.这些PIV测试都表明, 亚微米-纳米尺度的示踪粒子都表现出很好的跟随性, 有能力捕捉到超声速流动细节.美国空军技术学院的Huffman等[4]分别比较了PIV和分子标记测速(molecular tagging velocimetry, MTV)技术在超声速轴对称射流中的应用, 结果发现100 nm示踪粒子在平均射流也还有不错的跟随能力.
在大部分超声速流动试验中, 定量分析粒子松弛过程的数学模型仅适用于激波法向Mach数小于1.4的情况, 这为更大激波法向Mach数下的流动分析带来了很多的不确定性.虽然, 日本东北大学的Koike等[5]以及荷兰代尔夫特理工大学的Schrijer等[6]分别提出了一些方法对此进行了修正, 但是试验条件对粒子的气动特性和体密度都有着直接影响.
在气固两相流数值研究方面, 超声速混合层中的强剪切、大梯度流场成为了研究粒子跟随性的良好载体[7], 固体/液体粒子在混合层中的弥散和迁徙运动也成为了研究热点. Chein等[8]对不可压缩的剪切混合层中的粒子扩散运动进行了较详细的综述, 但其对高速可压缩流动混合层中的粒子扩散还研究不足.随时间发展的气固两相混合层因为粒子在涡辫剪切区域的分布呈现一定的倾向性[9-11], 且具有较明显的周期性, 因而研究较多, 而空间发展的超声速混合层研究较少.刘伟[12]等研究了随时间和空间发展的气固两相混合层中的颗粒弥散和浓度分布, 表明Stokes数(St)仍是影响颗粒弥散的主要因素.林建忠等[13-14]对气固两相混合层进行了研究, 结果表明涡的合并与配对会影响粒子在混合层中的分布.樊建人等[15-16]采用拟谱法得到气固两相混合层的三维特征会影响其动量厚度发展的结论, 同时St影响粒子在混合层中的分布.任兆欣等[17]、张会强等[18]研究了超声速混合层中的粒子弥散和激波响应机制, 认为颗粒尺度影响颗粒弥散, 颗粒经过斜激波产生动量和热量响应延迟.
基于以上研究现状, 本文通过理论、试验和数值模拟研究了PIV示踪粒子的运动特性.提出了在Mn > 1.4时的PIV粒子松弛特性分析模型, 并通过高速/低速来流分别布撒PIV粒子, 统计分析了dp和Mc对示踪粒子跟随性的影响, 以及粒子在高速/低速来流中的运动和弥散特性.
1 PIV示踪粒子松弛特性分析模型 1.1 PIV示踪粒子松弛特性建模根据德国纽伦堡大学的Melling[19]对固态粒子在气流中的运动特性分析, 在Basset-Boussinesq-Oseen(BBO)方程中仅须考虑黏性项和惯性项.这时, 粒子速度Up对气相速度U的响应为指数衰减关系:
| $ {{U}_{\text{p}}}\left( t \right)=U\left[1-\exp \left(-\frac{t}{\tau } \right) \right] $ |
式中, τ代表示踪粒子的响应时间:
| $ \tau =\frac{4}{3}\frac{{{\rho }_{\text{p}}}d_{\text{p}}^{2}}{{{\mu }_{\text{f}}}}C_{\text{D}}^{-1}Re_{\text{p}}^{-1} $ |
其中, CD为阻力系数, 粒子Reynolds数Rep则由粒子速度和流动速度之间的相对速度给出:
| $ {Re_{\text{p}}}=\frac{{{\rho }_{\text{p}}}\left| {{U}_{\text{p}}}-U \right|{{d}_{\text{p}}}}{{{\mu }_{\text{f}}}} $ |
μf为气流的动力黏度, 而ρp和dp分别为粒子密度和当量直径.
示踪粒子跨越激波之后将会以指数衰减规律逐渐减速, 并恢复到波后气流速度.假定所有示踪粒子在激波附近区域混合均匀, 由此引入无量纲滑移速度U*:
| $ {{U}^{*}}=\left( {{U}_{\text{p}n}}\left( t \right)-{{U}_{n2}} \right)/\left( {{U}_{n1}}-{{U}_{n2}} \right)={{\text{e}}^{\text{-}\frac{t}{\tau }}} $ |
式中, Upn(t)为粒子法向速度, Un1和Un2分别为激波前后的气流速度.
Dring[20]和Tedeschi等[21]对粒子跨激波的流动现象进行了深入的分析, 而Haertig等[22], Urban等[1]以及Amatucci等[23]将其用于分析粒子惯性运动.但是在大部分超声速流动试验[3, 24-25]中, 小角度尖楔绕流诱发的斜激波法向Mach数都小于1.4. Melling[19]提出了一个近似模型, 认为粒子松弛过程表现为线性关系, 即
| $ \frac{{{x}_{n}}}{{{\xi }_{n}}}\approx \frac{t}{\tau }=-\ln {{U}^{*}} $ |
其中, xn为激波的法向距离, ξn为粒子的法向松弛距离.这个公式在更强激波条件下不大适用.
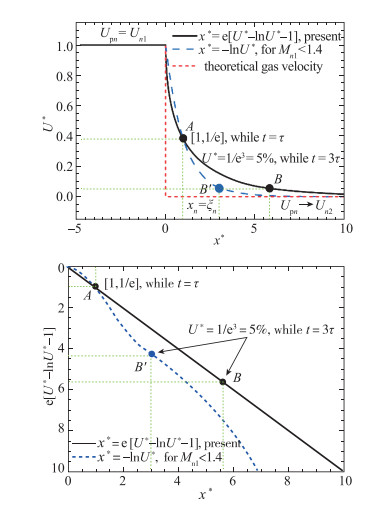
上海交通大学Chen等[26]通过在[0, t]时间间隔内进行积分之后, 引入无量纲松弛距离x*=xn/ξn, 提出了一个新的分析模型:
| $ {{x}^{*}}=\text{e}\left[{{U}^{*}}-\ln {{U}^{*}}-1 \right] $ |
其中, e为自然对数底数, 粒子松弛距离
| $ {{\xi }_{n}}=\tau \left[{{U}_{n1}}-\left( {{U}_{n1}}-{{U}_{n2}} \right)/\text{e} \right] $ |
图 1对两个分析模型进行了比较, 结果发现:粒子在A点之前的运动衰减较快, 之后则由于惯性相对较慢.当粒子速度恢复到波后气流速度的95%(即e-3=5%)时, 粒子松弛距离大约为Melling模型计算值的2倍.这里t/τ是一个描述粒子运动松弛过程的关键参数.
|
| 图 1 粒子跨激波的速度变化曲线 Fig.1 Velocity variations of particles across a shock |
考虑正激波关系式, 可以得到以下公式:
| $ \frac{{{\xi }_{n}}}{{{U}_{n1}}\tau }=\frac{\text{e}\left( \gamma +1 \right)M_{n1}^{2}-2M_{n1}^{2}+1}{\text{e}\left( \gamma +1 \right)M_{n1}^{2}} $ |
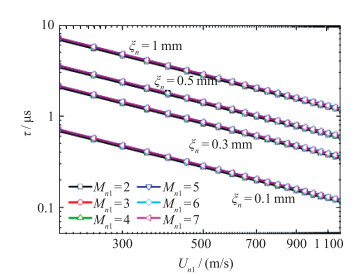
由此, 可以给出激波强度Mn1, 激波前流动速度Un1以及松弛时间τ的相互关系.从图 2可以看出, 激波强度Mn1的影响并不大, 而波前流动速度Un1和粒子松弛时间τ基本成反比.显然, 粒子松弛时间τ越小, 高速流动中PIV测量的可信度越高.
|
| 图 2 粒子运动参数关系 Fig.2 Particle motion parameters |
引入经济学常用的半弹性函数(Wooldridge[27])用于分析以上参数的影响规律, 即
| $ S\left[f\left( x \right) \right]=\frac{{f}'\left( x \right)}{f\left( x \right)}=\frac{\text{d}\left( \ln f\left( x \right) \right)}{\text{d}x}=\frac{\text{d}\left( \log f\left( x \right) \right)}{\text{d}x} $ |
因此, 无量纲滑移速度U*引起无量纲滑移距离x*变化的半弹性函数可以表示为
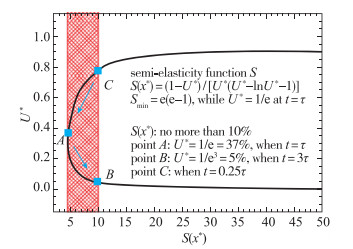
| $ S\left( {{x}^{*}} \right)=\left( 1-{{U}^{*}} \right)/\left[{{U}^{*}}\cdot \left( {{U}^{*}}-\ln {{U}^{*}}-1 \right) \right] $ |
如图 3所示, 当t/τ在0.25~3范围内变化时, 粒子滑移距离x*随粒子滑移速度U*的变化不超过10%.这也表明, 这样的粒子滑移时间可以保证足够的粒子跟随性.这个关系式可以对PIV测量中示踪粒子的选择准则提供非常有价值的技术指导.
|
| 图 3 粒子滑移过程的半弹性函数 Fig.3 Semi-flexible function of a slipping particle |
如果粒子Reynolds数Rep较小(Rep≪1), 粒子阻力系数可以根据Stokes定律给出, 即
| $ {{C}_{\text{D}}}=24/R{{e}_{\text{p}}} $ |
此线性关系只能适用于不可压缩和连续流动, 但是可以反映粒子的基本运动关系, 由此可得到
| $ \tau =\frac{{{\rho }_{\text{p}}}d_{\text{p}}^{2}}{18{{\mu }_{\text{f}}}} $ |
这个方程可以直接给出粒子松弛时间与粒子直径之间的关系.
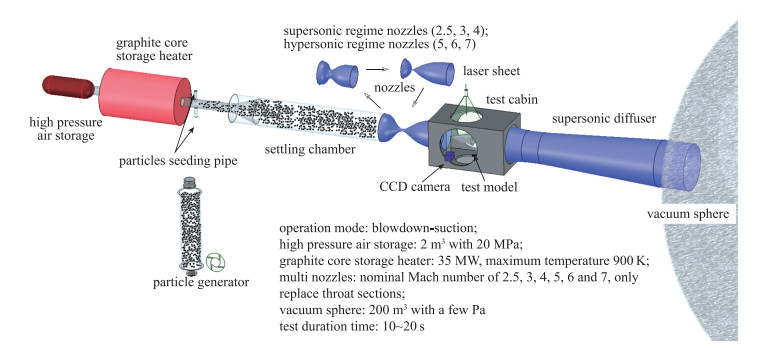
2 高速流动PIV定量化测试 2.1 PIV测试系统和试验工况利用粒子布撒器将示踪粒子均匀地分布在主流中, 当激光光源照射流场时, 粒子将会发生散射, 这样图像采集装置(如CCD相机)就能捕捉到粒子在流场中的位置.通常激光发生器会发射一定时间间隔的两个激光脉冲, 由于同步器的作用, 图像采集装置能够精确地捕捉到两幅清晰的粒子分布图, 这两幅原始图像经过数字化、判读区划分、互相关计算等一系列的后处理过程之后, 就能得到流场的速度分布. 图 4为PIV测试系统工作过程图.
|
| 图 4 高超声速多Mach数风洞和PIV测试系统 Fig.4 Multi-Mach number high-speed wind tunnel and PIV system setup |
在上海交通大学多Mach数风洞, 采用新提出的粒子松驰特性分析模型进行了PIV定量化测试.试验工况如下: M=4高速气流(800 m/s), 测试条件为静压3.1 kPa和静温96.4 K, 气体动力黏度μf=6.4×10-6.根据待测区域的流动速度, PIV时间间隔为500 ns.在此条件下的15°尖劈模型试验中, 尖劈头部诱发一道约27°的斜激波.
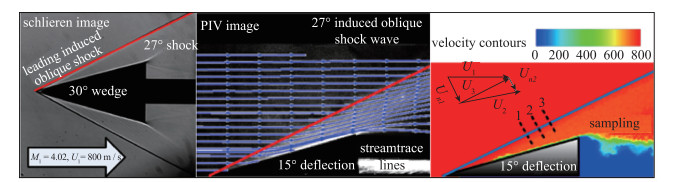
2.2 PIV定量化测试结果对15°尖劈模型进行试验工况下的定量化测量, 可以得到如图 5所示的速度流线图和分布云图.在斜劈的头部, 明显诱导出了一道27°的斜激波.以新提出的示踪粒子松弛模型为基础, 通过进一步分析可以得到速度迟滞特性与松弛距离的变化关系.通过PIV定量化测量试验, 布撒不同尺度的示踪粒子测量其松弛时间, 可以筛选出合理粒径的粒子以满足跟随性要求.
|
| 图 5 M=4流动中粒子跨激波松弛过程 Fig.5 Particle relaxation processes in Mach 4 flows |
图 6表明不同尺寸粒子的松弛过程.很显然, 粒子越小, 粒子松弛距离越短.针对TiO2粒子(密度4.23×103 kg/m3), 要满足t/τ在0.25~3, 采用经过修正的阻力计算模型以后, 示踪粒子粒径至少应该为20~50 nm, 才能够更好地捕捉高速流动.

|
| 图 6 M=4流动中粒子跨激波松弛过程 Fig.6 Relaxation processes downstream an oblique shock in Mach 4 flow |
针对空间发展的超声速气固两相混合层进行粒子跟随性研究, 分别选取Mc=0.20和Mc=0.64的气相载体case1和case2, 来流条件分别与Goebel等[28]的可压缩混合层实验和Hudson等[29-30]的数值计算条件一致, 如表 1所示.文中对流Mach数Mc定义为
| $ {{M}_{\text{c}}}=\left( {{U}_{1}}-{{U}_{2}} \right)/\left( 2\overline{a} \right) $ |
| 下载CSV 表 1 计算参数 Tab.1 Computational parameters |
其中, U1, U2分别为高速和低速来流速度, a为相对声速.计算域为Lx×Ly=0.5 m×0.04 m, 计算网格数量为4×105.入口处上下层来流组成双曲正切型速度分布.为了使边界不影响混合层的发展, 上下边界和出口设置为无反射边界条件.
3.1.2 离散相计算参数选取上海交通大学多Mach数高超声速风洞PIV测试[31-33]所用TiO2纳米粒子作为离散相. TiO2纳米粒子的材料密度为4 230 kg/m3, 摩尔质量为79.9 g/mol. St表征流场特征时间尺度与粒子的松弛时间尺度之比, 在两相流中是重要的无量纲评价参数.可以描述为
| $ St=\frac{{{\tau }_{\text{g}}}}{{{\tau }_{\text{p}}}} $ |
其中, τg=ΔUg/θ0, τp = ρpdp2/18 μg.下标g和p分别指气体和粒子. ΔUg为高速与低速来流速度差, θ0为来流入口的初始混合层厚度, 根据Goebel-Dutton的实验数据, 在此取θ0=0.000 4 m.因此, St进一步表达为
| $ St=\frac{{{\rho }_{\text{p}}}d_{\text{p}}^{2}\Delta {{U}_{\text{g}}}}{18{{\mu }_{\text{g}}}{{\theta }_{0}}} $ |
根据粒子St的不同, 选择St=0.01, 1, 10, 100和500, 对应粒径分别为50 nm, 525 nm, 2 μm, 5 μm和12 μm的PIV示踪粒子作为超声速气固两相混合层的离散相进行研究.
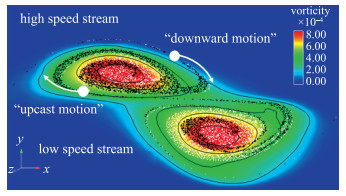
3.2 示踪粒子运动与迁徙特征在超声速气固两相混合层中, St是影响PIV示踪粒子的弥散、跟随特性以及气固两相掺混能力的重要因素.混合层上下层来流不同的速度梯度改变了Mc大小.不同Mc通过大涡拟序结构影响示踪粒子的跟随特性.高速、低速来流不同的特征时间尺度, 影响示踪粒子跟随性和大涡拟序结构中的气-粒掺混特性以及粒子在混合层中的弥散.如图 7所示, 粒子分别从高速来流和低速来流处喷射入超声速混合层, 并在气体的夹裹下围绕涡核做旋转运动.
|
| 图 7 高速/低速来流释放粒子运动示意图 Fig.7 Diagram of particles motion versus high/low speed streams |
超声速混合层的上下层来流的速度、温度差异导致高速和低速来流的特征时间尺度不同, 粒子在混合层中的运动形态也产生差异. 图 7中, 上层高速来流中的黑色着色粒子受剪切黏滞力和离心力等力的作用, 绕涡核做“顺流下卷”运动; 而低速来流的白色着色粒子受气体托运和挤压, 绕涡核做“逆流上抛”运动. “顺流下卷”和“逆流上抛”运动相互补充构成了粒子在涡中的小循环, 并随着空间混合层涡的运动向下游发展.不同的dp和Mc改变了粒子在混合层中的受力状态和运动形态, 直接影响示踪粒子跟随和弥散掺混特性, 影响高速PIV测量的精度.
3.3 Mc=0.20时粒径对粒子跟随性影响不同dp的粒子在Mc=0.20时从混合层的高速/低速入口处分别布撒, 得到的粒子跟随性分布如图 8所示.粒子初始速度与气相保持相等, 初始喷射体积分数为αp=2.55×10-7.为了方便对比, 图 8(a), (c), (e)中都标注了气相的涡量等值线.

|
| 图 8 高速(上)/低速(下)来流入口布撒的粒子在混合层中的运动与分布, Mc=0.20 Fig.8 Motions and distributions of particles ejected from high (upstream) speed and low speed (downstream) in mixing layer, Mc=0.20 |
图 8(a)中dp=50 nm, St=0.01的示踪粒子在混合层中的分布比较均匀, 能够迅速响应周围气体的速度变化.上层高速来流夹裹的粒子“顺流下卷”, 下层低速来流粒子“逆流上抛”, 互相补充填满整个涡区域.粒子在涡核、涡边缘以及涡辫区域的分布差别不大, 跟随性很好.而图 8(b)中dp=525 nm, St=1的粒子分布不如图 8(a)均匀, 但展向最大弥散距离增大.高速来流中的“下卷”粒子在涡核处仍有稀疏分布, 但下层低速来流的“上抛”粒子已经无法到达涡核.高涡量的涡核周围粒子分布稀疏, 但仍有少量粒子分布, 低涡量的涡边缘粒子分布集中, 涡与涡之间的强剪切区域粒子数明显多于其他区域.这时的粒子仍能跟随气体的速度变化, 但粒子的响应时间比St=0.01时要大, 跟随性变差.
图 8(c)中dp=2 μm, St=10的示踪粒子在涡中所受到的离心力显著增大, 粒子的分布更加倾向于远离涡核的区域, 展向的粒子最大弥散距离达到最大.因此, 无论是“顺流下卷”还是“逆流上抛”的粒子几乎无法在低涡量区域存在.粒子在涡核几乎未出现, 而在涡边缘分布集中.粒子在混合层发展的初期随着涡的卷起而运动.随着混合层的发展逐渐充分, 速度变化更为剧烈, 粒子离心力小于惯性力, 不能支配其旋转运动. St=10时粒子的分布带明显变窄, 粒子有最大弥散距离, 跟随性比St=1的粒子差.
图 8(d)中dp=5 μm, St=100的示踪粒子在随混合层运动的过程中惯性力始终起主导作用, 大部分的流场区域离心力已经不足以维持粒子围绕涡核做环绕运动.高速和低速来流区域的粒子几乎不能做“下卷”和“上抛”运动.粒子集中分布在混合层的中心线区域, 不能像小粒子一样在涡中旋转运动.这时粒子跟随性已经很差, 不足以作为PIV测量的示踪粒子使用.
图 8(e)中dp=12 μm, St=500的示踪粒子在超声速混合层的入口处以与气体相同的速度喷射进流场, 惯性力对粒子的运动轨迹起到决定性作用.此时的粒子只在混合层涡量变化剧烈的区域稍有随流运动的倾向, 但不明显, 其展向最大弥散距离最小.混合层内涡的合并和配对只能在特定区域稍微影响粒子的运动轨迹, 粒子对周围气体的速度变化几乎不能响应, 跟随性最差.
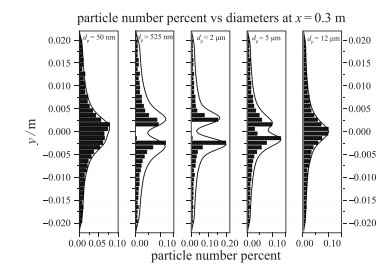
对Mc=0.20的超声速混合层中的示踪粒子进行概率和速度分布统计, 图 9给出了x=0.3 m处的粒子概率分布.由图 9可以看出, 当dp=50 nm时, 混合层中心线附近粒子数最多, 出现概率最大, 约为0.075 0.气相“上抛”和“下卷”使粒子在涡核以及附近聚集.粒径在525 nm~5 μm区间的粒子开始远离涡核等高涡量区域, 富集在涡边缘和涡辫等低涡量区域. dp=2 μm的粒子弥散距离最大, 粒子在低速来流的涡辫区域出现概率最大, 约为0.20.同时, 粒径在50 nm~5 μm区间的粒子分布都呈现“逆流上抛”区域粒子出现概率大于“顺流下卷”区域的特征. dp=12 μm的粒子分布已经几乎不受气体影响. dp=2 μm的示踪粒子倾向性分布最为明显.
|
| 图 9 Mc=0.20, x=0.3 m处粒子概率分布 Fig.9 Particle probabilities at x=0.3 m, Mc=0.20 |
为了探究高对流Mach数下不同粒径粒子的跟随性, 在Mc=0.64的超声速混合层高速/低速来流入口处, 分别布撒粒径dp=50 nm, 525 nm, 2 μm, 5 μm和12 μm的PIV示踪粒子TiO2, 初始布撒体积分数均为αp=2.55×10-7. 图 10为高速和低速来流喷射的粒子在混合层中的运动形态和分布特征.

|
| 图 10 高速(上)/低速(下)来流入口布撒粒子在混合层中的运动与分布, Mc=0.64 Fig.10 Motions and distributions of particles ejected from high speed (upstream) and low speed (downstream) in mixing layer, Mc=0.64 |
不同粒径的粒子靠喷射惯性以及气体的裹挟力初始化其流向的运动, 混合层中涡产生的离心力维持了绕涡核的圆周运动. Mc=0.64时, 由于高速与低速来流的速度差和温度差更大, 涡的卷起和配对相比Mc=0.20时更加剧烈, 从图 10(a)~(e)可以明显看到.如图 10(a), (b)和(c)所示, St=0.01时粒子分布倾向性不明显; St=1时只有涡边缘的低涡量区域富集粒子; St=10时粒子随混合层中涡的旋转已经不明显, 这与小粒径Mc=0.20时粒子的表现相似. Mc=0.64时示踪粒子最大弥散距离随St呈先增大后减小的趋势, 并在St=1时达到最大, 而粒子跟随性在St=1时已表现很差.粒子随高速来流的“顺流下卷”和随低速来流的“逆流上抛”运动趋势更明显和复杂. St≥100的粒子受到的惯性力支配了其运动, 基本不能绕涡核环绕运动, 而只能沿着流向流动, 向超声速混合层出口推进.
相较于Mc=0.20的情形, 粒径对示踪粒子跟随性的影响在Mc=0.64时更敏感. St数大于1的粒子在Mc=0.64时已经不能快速跟随并响应气体速度、温度等物理量的变化, 而这一现象在Mc=0.20下St大于10时才会出现.高对流Mach数下, 对PIV示踪粒子粒径的选择更应该谨慎.在保证足够散射光强的前提下, 尽量选用小粒径粒子来保证良好的跟随性.
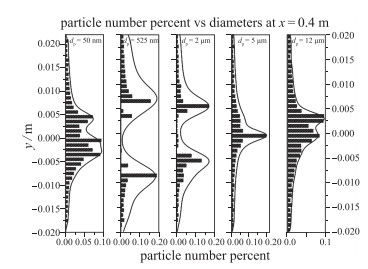
在x=0.4 m处, 对Mc=0.64时的超声速混合层连续相和离散相粒子进行统计, 得到图 11所示的粒子概率分布.粒径50 nm~2 μm区间的粒子, 在x=0.4 m处的概率分布都呈现“低速上抛”区域粒子数略大于“高速下卷”区域的特征. dp=5 μm和dp=12 μm的粒子不能被气相涡卷起, 基本维持布撒入口粒子数分布特征. dp=50 nm的粒子涡边缘和涡核的粒子出现概率基本保持在0.075左右, 倾向性聚集现象不明显, 跟随性良好.而dp=525 nm和dp=2 μm的粒子在涡核处的出现概率几乎为0, 粒子弥散能力强, 跟随性差. dp=5 μm和dp=12 μm的粒子概率分布保持在初始布撒的状态基本不变.
|
| 图 11 Mc=0.64, x=0.4 m处粒子概率分布 Fig.11 Particle probabilities at x=0.4 m, Mc=0.64 |
(1) 新提出的粒子松弛特性分析模型在法向Mach数大于1.4的情形下具有良好的适用性.应用于PIV定量化测量, 认为粒径在20~50 nm之间, 才能够更好地捕捉高速流动;
(2) 相同对流Mach数, 粒径越小, 速度响应越迅速, 掺混能力越强, PIV粒子跟随性越好.不同粒径示踪粒子弥散能力不同, 最大弥散距离随粒径的增大, 先增大再减小, St在[1, 10]区间内的粒子有最大扩散距离;
(3) 相同粒径, 相同PIV示踪粒子初始布撒浓度, Mc=0.64时的粒子跟随性比Mc=0.20情况下差; 较大Mc时粒子跟随性对粒径变化更敏感, 对下层低速来流中的PIV粒子跟随性影响大于上层高速来流
| [1] |
Urban W D, Mungal M G. Planar velocity measurements in compressible mixing layers[J]. Journal of Fluid Mechanics, 2001, 431: 189-222. DOI:10.1017/S0022112000003177 |
| [2] |
Scarano F, Van Oudheusden B W. Planar velocity mea-surements of a two-dimensional compressible wake[J]. Experiments in Fluids, 2003, 34(3): 430-441. DOI:10.1007/s00348-002-0581-x |
| [3] |
Ragni D, Schrijer F, Van Oudheusden B W, et al. Particle tracer response across shocks measured by PIV[J]. Experiments in Fluids, 2011, 50(1): 53-64. DOI:10.1007/s00348-010-0892-2 |
| [4] |
Huffman R, Elliott G. An experimental investigation of accurate particle tracking in supersonic, rarefied, axisymmetric jets[R]. AIAA 2009-1265, 2009. https://experts.illinois.edu/en/publications/an-experimental-investigation-of-accurate-particle-tracking-in-su
|
| [5] |
Koike S, Takahashi H, Tanaka K, et al. Correction method for particle velocimetry data based on the Stokes drag law[J]. AIAA Journal, 2007, 45(11): 2770-2777. DOI:10.2514/1.30962 |
| [6] |
Schrijer F F, Scarano F. Particle slip compensation in steady compressible flows[C]. 7th International Symposium on Particle Image Velocimetry, Rome, 2007. http://www.academia.edu/13042526/Particle_tracer_response_across_shocks_measured_by_PIV
|
| [7] |
Balachandar S, Eaton J K. Turbulent dispersed multiphase flow[J]. Annual Review of Fluid Mechanics, 2010, 42: 111-133. DOI:10.1146/annurev.fluid.010908.165243 |
| [8] |
Chein R Y, Chung J N. Simulation of particle dispersion in a two-dimensional mixing layer[J]. AIChE Journal, 1988, 34(6): 946-954. DOI:10.1002/(ISSN)1547-5905 |
| [9] |
Marcu B, Meiburg E. The effect of streamwise braid vor-tices on the particle dispersion in a plane mixing layer. Ⅰ. Equilibrium points and their stability[J]. Physics of Fluids, 1996, 8(6): 715-733. |
| [10] |
Marcu B, Meiburg E, Raju N. The effect of streamwise braid vortices on the particle dispersion in a plane mixing layer. Ⅱ. Nonlinear particle dynamics[J]. Physics of Fluids, 1996, 8(3): 734-753. DOI:10.1063/1.868858 |
| [11] |
Marcu B, Meiburg E. Three-dimensional features of particle dispersion in a nominally plane mixing layer[J]. Physics of Fluids, 1996, 8(9): 2266-2268. DOI:10.1063/1.869013 |
| [12] |
刘伟, 万国新, 陈景兵, 等. 可压缩气固混合层中离散相与连续相的相互作用研究[J]. 计算力学学报, 2009, 26(1): 8-14. Liu W, Wan G X, Chen J B, et al. Study on the interaction between the continuous and the dispersed phases in compressible gas-solid mixing layer[J]. Chinese Journal of Computational Mechanics, 2009, 26(1): 8-14. (in Chinese) |
| [13] |
林建忠, 石兴, 余钊圣. 二维气固两相混合层中固粒对流场影响的研究[J]. 应用数学和力学, 2000, 21(8): 771-776. Lin J Z, Shi X, Yu Z S. Research on the effect of particle of two-dimensional shear flow[J]. Applied Mathematics and Mechanics, 2000, 21(8): 771-776. (in Chinese) |
| [14] |
林建忠, 石兴. 气固两相混合层流场双向耦合的数值研究[J]. 工程热物理学报, 2001, 22(4): 496-499. Lin J Z, Shi X. Numerical study on the gas-solid two-phase mixing layer by two-way coupling model[J]. Journal of Engineering Thermophysics, 2001, 22(4): 496-499. (in Chinese) |
| [15] |
樊建人, 郑友取, 岑可法. 三维气固两相混合层湍流拟序结构的直接数值模拟[J]. 工程热物理学报, 2001, 22(2): 241-244. Fan J R, Zheng Y Q, Cen K F. Direct numerical simulation in turbulent coherent structures of three-dimensional gas-particle two-phase mixing layer[J]. Journal of Engineering Thermophysics, 2001, 22(2): 241-244. (in Chinese) |
| [16] |
樊建人, 罗坤, 金晗辉, 等. 直接数值模拟三维气固两相混合层中颗粒与流体的双向耦合[J]. 中国电机工程学报, 2003, 23(4): 153-157. Fan J R, Luo K, Jin H H, et al. Direct numerical simulation of the two-way coupling effects between particles and fluid in the three-dimensional particle-laden mixing layer[J]. Proceedings of the CSEE, 2003, 23(4): 153-157. (in Chinese) |
| [17] |
任兆欣, 王兵, 张会强. 超音速拟序旋涡中颗粒的弥散[J]. 工程热物理学报, 2015, 36(9): 1957-1960. Ren Z X, Wang B, Zhang H Q, et al. Dispersion of particles in the supersonic coherent vortex[J]. Journal of Engineering Thermophysics, 2015, 36(9): 1957-1960. (in Chinese) |
| [18] |
张会强, 王赫阳, 王希麟, 等. 两相混合层中颗粒运动的数值模拟[J]. 工程热物理学报, 2000, 21(1): 115-119. Zhang H Q, Wang H Y, Wang X L, et al. Numerical simulation of particle motion in two-phase mixing layer[J]. Journal of Engineering Thermophysics, 2000, 21(1): 115-119. (in Chinese) |
| [19] |
Melling A. Tracer particles and seeding for particle image velocimetry[J]. Measurement Science and Technology, 1997, 8(12): 1406-1416. DOI:10.1088/0957-0233/8/12/005 |
| [20] |
Dring R P. Sizing criteria for laser anemometry particles[J]. Journal of Fluids Engineering, 1982, 104(1): 15-17. DOI:10.1115/1.3240844 |
| [21] |
Tedeschi G, Gouin H, Elena M. Motion of tracer particles in supersonic flows[J]. Experiments in Fluids, 1999, 26(4): 288-296. DOI:10.1007/s003480050291 |
| [22] |
Haertig J, Havermann M, Rey C, et al. Particle image velocimetry in Mach 3.5 and 4.5 shock-tunnel flows[J]. AIAA Journal, 2002, 40(6): 1056-1060. DOI:10.2514/2.1787 |
| [23] |
Amatucci V A, Dutton J C, Kuntz D W, et al. Two-stream, supersonic, wake flowfield behind a thick base. IGeneral features[J]. AIAA Journal, 1992, 30(8): 2039-2046. DOI:10.2514/3.11177 |
| [24] |
Schrijer F F, Scarano F, Van Oudheusden B W. Application of PIV in a Mach 7 double-ramp flow[J]. Experiments in Fluids, 2006, 41(2): 353-363. DOI:10.1007/s00348-006-0140-y |
| [25] |
Ghaemi S, Schmidt-Ott A, Scarano F. Nanostructured tracers for laser-based diagnostics in high-speed flows[J]. Measurement Science and Technology, 2010, 21(10): 105403. DOI:10.1088/0957-0233/21/10/105403 |
| [26] |
Chen F, Liu H, Rong Z. Development and application of nanoparticle tracers for PIV in supersonic and hypersonic flows[R]. AIAA 2012-0036, 2012. http://www.sciencedirect.com/science/article/pii/S1000936117300407
|
| [27] |
Wooldridge J. Introductory econometrics: A modern approach[M]. Michiganz: Cengage Learning, 2012.
|
| [28] |
Goebel S G, Dutton J C, Krier H, et al. Mean and turbulent velocity measurements of supersonic mixing layers[J]. Experiments in Fluids, 1990, 8(5): 263-272. DOI:10.1007/BF00187228 |
| [29] |
Hudson D A, Long L N, Morris P J. Computation of a confined compressible mixing layer[C]. 26th Fluid Dynamics Conference, San Diego, 1995: 1-18. http://www.eng.cam.ac.uk/research_db/publications/groups/dA-T
|
| [30] |
Hudson D A. Numerical simulation of a confined supersonic shear layer[D]. Pennsylvania: The Pennsylvania State University, 1996. http://arc.uta.edu/publications/cp.htm
|
| [31] |
Chen F, Liu H, Rong Z. Development and application of nanoparticle tracers for PIV in supersonic and hypersonic flows[C]. 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, 2012. http://scitation.aip.org/content/aip/proceeding/aipcp/10.1063/1.3651872
|
| [32] |
张亚, 陈方, 刘洪, 等. 高速流动中PIV示踪粒子松弛特性研究[J]. 实验流体力学, 2013, 27(6): 70-75. Zhang Y, Chen F, Liu H, et al. Research on the relaxation characteristics of PIV tracer particles in supersonic flow[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6): 70-75. (in Chinese) |
| [33] |
刘洪, 陈方, 励孝杰, 等. 高速复杂流动PIV技术研究实践与挑战[J]. 实验流体力学, 2016, 30(1): 28-42. Liu H, Chen F, Li X J, et al. Practices and challenges on PIV technology in high speed complex flows[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(1): 28-42. (in Chinese) |




