2. 中国科学院大学工程科学学院,北京 100049
2. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
微纳米流体力学(microfluidics/nanofluidics)是研究微米、亚微米直至纳米尺度下流体的流动及物质输运规律的一门学科[1-2].微纳米流体力学目前与生物医学高度交叉, 近年来兴起的纳米医学(nanomedicine)[3]则是微纳米流体力学做出贡献的一个新突破口.其中研究纳米药物输送等问题[4-5]具有重要的理论及应用价值.在人体复杂生理微环境下, 作为药物输运及治疗功能载体的纳米颗粒,其动力学特征是一个亟需深入研究的重要科学问题.
人体生理微环境以血液、细胞液等各种复杂流体为重要组成部分, 流动介质不再是通常研究的简单流体, 同时复杂生物微环境具有各向异性特征, 边界约束更为复杂, 涉及力学、物理、化学等多种作用及它们之间的复杂耦合过程, 流动过程非定常, 其特征时间、空间尺度也与单纯的微纳尺度流动区别明显[6].在纳尺度, 表征对流与扩散之比的Peclet数往往小于1, 可知扩散是重要的物质输运机制.而复杂生物介质中往往观测到纳米颗粒的扩散与经典扩散理论描述的不一致, 引出反常扩散问题.理论上, 反常扩散源自复杂生物介质微环境中的空间各向异性.
以往常用分数Brown运动(fractional Brownian motion,FBM)基于均方位移(mean squared displacement,MSD)描述反常扩散[7].但近来报道“Brown非Gauss”(anomalous yet Brownian)现象引出了新的挑战[8]:仅依靠非线性MSD无法有效描述反常扩散, 需进一步考察位移概率密度分布(displacement probability density,DPD).而且, 研究DPD非Gauss根源是重要的科学问题[9].实际中, 如肿瘤组织内纳米药物颗粒的输运[6, 10], 不仅需要研究拥挤复杂生物介质中的扩散特征和机理, 还需要研究如何强化它们的扩散.纳米颗粒的反常扩散有可能呈现出乎意料的复杂规律, 比如超扩散和亚扩散行为[11].因此, 本文对纳米颗粒在复杂生物介质中的反常扩散进行综述.这是微纳尺度流体力学的前沿.主要基于现有文献介绍主要的物理模型(第1节)、实验方法(第2节)及最新的实验结果(第3节), 最后给出结论(第4节).
1 理论模型对扩散或者随机热运动现象的研究有悠久的历史, 这些年来建立了经典的理论框架.对扩散最早的研究, 是Fick对物质在薄膜上的扩散现象的探索, 他推导出了宏观的扩散方程, 也就是Fick第二定律[12]:
| $ \frac{\partial }{\partial t}n(x, t)=D\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}n(x, t) $ | (1) |
其中, n表示物质的浓度,D表示物质的扩散系数。而实际观测中, 人们往往从MSD或者DPD两个方面来描述微观颗粒的扩散运动[11].本节主要从理论角度进行综述, 首先分别介绍基于MSD和DPD的理论模型.接下来从受限扩散(confined diffusion)及跳跃扩散(hopping diffusion)的角度介绍针对反常扩散的理论研究进展.
1.1 均方位移均方位移(MSD)是研究微观颗粒扩散运动的一个重要指标, 对于传统的自由扩散而言,MSD随观测时间线性变化, 满足如下关系:
| $ \left\langle {{x}^{2}} \right\rangle =2Dnt $ |
其中,n是与运动维度有关的系数, 对于一维、二维和三维运动, n分别取1,2和3.经典理论工作中推导MSD关系主要有以下两种方法: (1)Smolu- chowski基于连续的无规则自由行走的方法[13]; (2)Langevin基于Newton力学给出的运动方程[14].其中Langevin的方法最为经典, 它假设在介质中运动的颗粒遵循Newton第二定律, 它把周围流体分子的热运动对粒子的影响归结为随机力.在x轴方向的Langevin方程如下:
| $ m\dot{v}=-\gamma v+f+\xi (t) $ |
其中, m是颗粒质量, γ是摩擦系数, ξ(t)是随机力, f是外力.通过这个微分方程,很容易能够求得MSD的表达式[14].
近来, 随着生物医学的发展, 人们对如细胞内等生物复杂环境中的纳米颗粒扩散越来越感兴趣[7].在这类复杂环境中, 颗粒扩散的运动特征和自由扩散的不一样, 这时,MSD往往随时间非线性地变化, 所以经典的模型对此并不适用.因此, 很多新的模型被提出来, 更好地解释了这类反常扩散现象.
分数型Brown运动(FBM)[15]把反常扩散当成是一系列服从幂指数分布规律的Gauss过程的叠加.和以往模型不同的是, FBM是一个非Markov过程.它把扩散的特征用传播因子来表示:
| $ {{P}_{\text{FBM}}}(r, t)={{r}^{-d}}{{P}_{\text{Gauss}}}(\hat{r}), \hat{r}\propto r{{t}^{-\alpha /2}} $ |
其中, ΡGauss是传播因子, d代表维度(d=1, 2, 3),而α是唯一系数.这样, MSD则可以写成:
| $ \left\langle {{r}^{2}}(t) \right\rangle =2dK{{t}^{\alpha }} $ |
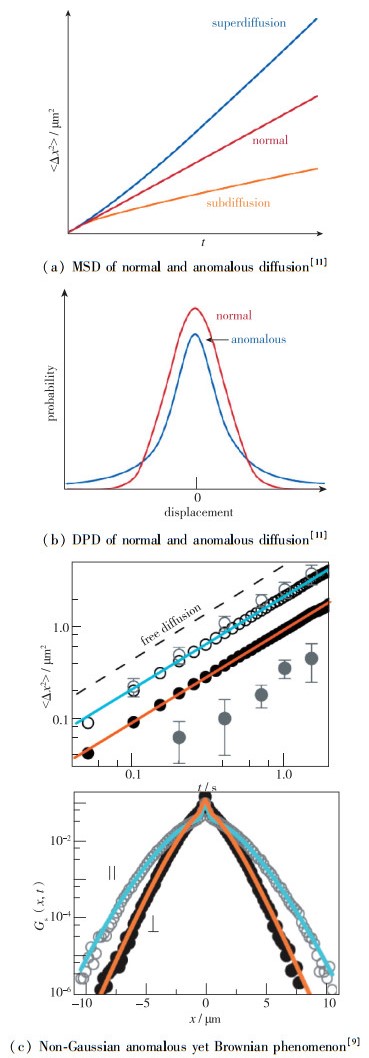
其中, α>1被称为超扩散; α<1被称为亚扩散(图 1(a)).超扩散往往发生在趋化作用的细胞及能自发泳动的微纳马达[16]; 而亚扩散在拥挤的生物微环境中非常普遍.
|
| 图 1 正常扩散和非正常扩散的MSD和DPD,Brown以及非Gauss现象 Fig.1 Typical MSD and DPD of normal and anomalous diffusion, and non-Gaussian anomalous yet Brownian phenomenon |
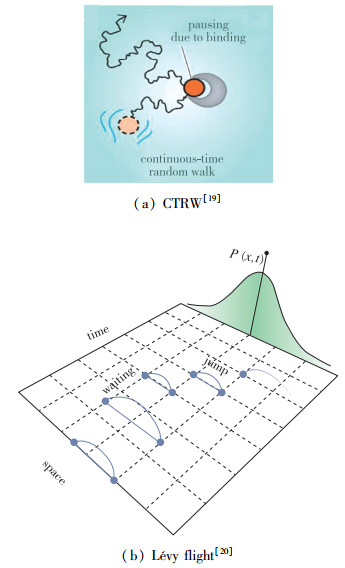
另外一个常用理论模型是连续时间自由行走(continuous time random walk, CTRW)模型[17].这是个适用范围很广的模型.在Einstein模型中, 每两步之间的时间间隔并不是一个内在的性质.而CTRW模型则在假设任意不同的两步仍然是独立的情况下, 假定相邻的两步之间的时间间隔服从一个分布[18].如图 2(a)所示. CTRW常被用来描述生物中观察到的微纳尺度颗粒的扩散特征[19].一种更有意思的情况被称为Lévy跳跃(Lévy flight)[20], 它意味粒子运动到一个点之后会停顿一段时间, 之后会有一个较大幅度的跳跃(图 2(b)).它和CTRW的差别在于:CTRW模型中,粒子在停顿一段时间之后,下一步可能仍然是随机运动; 而Lévy的模型中,粒子在停顿一段时间后,将会有一个位移很大的而且方向有规律的跳跃.
|
| 图 2 CTRW及Lévy跳跃的原理示意图 Fig.2 Schematic diagram of CTRW and Lévy flight |
需要注意的是, FBM仅仅使用一个参数α来描述各类反常扩散, 显然有较大的局限性.仅通过α无法阐明诸多动力学细节.随着研究的深入, 出现了Brown非Gauss的反常现象[6](图 1(c)), 给已有的MSD理论带来了全新的挑战.基于MSD的运动特征必须与基于位移概率分布的统计特征结合起来, 才能完整描述复杂生物介质中纳米颗粒的反常扩散.
1.2 位移概率分布: Gauss及非Gauss模型正常扩散的位移概率分布是呈现Gauss型的. 1905年, Einstein用随机行走理论解释了微观的扩散机理, 推导出了正常扩散的Gauss型位移概率密度分布[18]. Einstein最先通过热动力学把分子扩散的位移概率分布计算出来.他的处理方法是先假设空间上存在着一定的粒子, 然后列出在空间上某一点x经过一段时间后的粒子数等于全空间上每个点在这一小段时间运动到x点的粒子数总和的数学关系式, 再把这个时间设为无穷小的时候, 进行Taylor展开, 便得出了和Fick定律类似的公式, 只要把(1)式中的浓度换成位移概率分布密度P, 即可解出Gauss型的DPD (图 1(b)):
| $ G(x, t)=\frac{1}{\sqrt{4\pi Dt}}{{\text{e}}^{\text{-}\frac{{{x}^{2}}}{4Dt}}} $ |
但是在复杂生物环境中, 最新的研究发现, 位移概率分布呈现近似的指数分布, 尤其是在Brown非Gauss的现象中, 尾部概率分布呈现明显的指数型肥尾分布.此时位移概率分布为(图 1(b)):
| $ G(x, t)=\frac{1}{\lambda (t)}{{\text{e}}^{-\frac{|x|}{\lambda (t)}}} $ |
目前对这个现象的解释和推演主要有3种路径:超统计模型(superstatistics, SUPER)、扩散的扩散系数模型(diffusing diffusivity, DD)及广义的灰度Brown运动模型(generalised grey Brownian motion, GGBM).
SUPER模型主要的想法是认为不同粒子在处于空间上不同位置的时候扩散系数不一样, 那么整体的扩散系数应该是对不同粒子在不同空间环境下的叠加.由于不同空间环境对粒子扩散的影响不同,而且在全空间下,对粒子有相同影响的所有局部空间总和占整个空间的比例有一定的规律,那么不同位置体现的扩散系数应该有一个加权系数, 并用扩散系数的分布函数来描述不同扩散系数所占的比例.这个方法最早由Beck等提出[21-22].这种方法在一定程度上可以解释Brown的MSD和非Gauss的DPD现象.但是扩散系数分布函数的选取并不唯一.目前主要有以下几种选取方式: (1)指数型的扩散系数分布, 也称之为Laplace分布[23]; (2)基于Langevin随机方程给出扩散系数的分布[24]; (3)γ函数形式的扩散系数分布[25].
DD模型引入一系列的扩散系数, 它认为粒子在空间运动中会有着连续变化的扩散系数. Chubynsky等[26]最先提出这个模型, 用来描述在有边界条件下面的随机运动.在这个模型中粒子的扩散系数随着粒子一步一步的移动在不停地变化着, 因而在短时间内有指数型的DPD, 而随着时间的增加DPD逐渐向Gauss型过渡. Chechkin等[27], Matse等[28],Jain等[29-30]进一步研究和发展了DD模型等. Jain等提出了路径积分的概念,而Chechkin等则提出了从属关系的概念并在Fourier空间里面给出了准确的解.尽管两者在数学方法上不相同,但是都得出了和Chubynsky等一样的结论.
GGBM模型则给出了一系列的随机方程.这个模型的核心是把所有的空间上的不均匀性和环境的影响仅仅用一个独立的随机参数的变化来表示.随机方程为
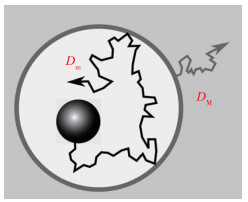
复杂生物介质中存在各向异性的空间结构, 这是其中出现反常扩散的重要原因之一.各向异性空间存在疏密相间结构, 可以将其中的纳米颗粒看作在一定受限空间内进行扩散, 由此发展出了受限扩散模型.受限扩散模型的主要想法是将纳米颗粒的扩散分成两部分: (1)受限区域内的微观扩散; (2)受限区域看成一个整体而发生的宏观扩散. Brown颗粒扩散的MSD可以由这两部分叠加求得.如图 3所示, Brown颗粒在球状区域内部作微观扩散, 对应的均方位移和扩散系数分别为<rm2(t)>及Dm.颗粒不能够穿透这个区域, 而整个球形区域在大尺度流体范围内作宏观扩散, 对应的均方位移和扩散系数为<rM2(t)>及DM.因此总体受限扩散的扩散系数可以表示为[35]:
| $ \begin{align} &\left\langle {{r}^{2}}(t) \right\rangle =\left\langle r_{\text{m}}^{2}(t) \right\rangle +\left\langle r_{\text{M}}^{\text{2}}(t) \right\rangle \\ &=6{{D}_{\text{M}}}t+1.2{{a}^{2}}(1-{{\text{e}}^{-5{{D}_{\text{m}}}t/{{a}^{2}}}}) \\ \end{align} $ |
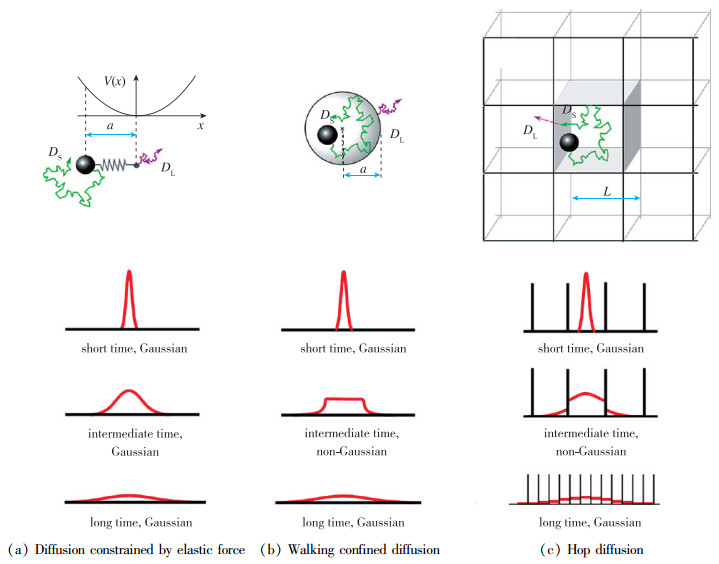
这个模型的运用很广泛.在高聚物物理学方面, 它被用来描述纳米粒子在高聚物溶液里面的运动规律[35].在生物物理中, 它被用来解释突触囊泡在神经元细胞里面的运动[36-37].但是在一些神经元细胞的树突体里面,研究颗粒的运动时,可以把受限扩散模型里面的阻碍认为是近似不动的[38-39]. 图 4(b)中具体给出了受限扩散模型中,粒子DPD随时间变化的3个阶段.
受限扩散还可以进一步采用弹性力受限模型表示[40]. 图 4(a)给出了弹性力受限模型的示意图,以及相应的DPD随时间的变化情况.它把周围环境的影响归纳成一个调和势能的影响, 就如同受到一个弹簧谐振子的牵引.同样地, 这个调和势能的中心点也是在空间中自由移动的.由于这个模型十分简单, 它被广泛地用来描述粒子在各种复杂环境里的运动,例如粒子在高聚物里面的运动[41]、粒子在黏弹性介质里面的运动[40, 42]、Jeffreys流体里粒子的运动[43]以及DNA染色体在细胞内和膜上的运动[44].
1.4 跳跃扩散实际观测中, 常发现纳米颗粒有可能穿透受限扩散模型所描述的微观区域边界, 发生类似跳跃的瞬时长程运动[45].因此, 需要发展障碍模型来进一步描述纳米颗粒穿出微观区域的动力学特征.障碍模型指的是把空间中复杂环境描述成许多的具有不同性质, 且在全空间上会按一定规律反复出现的阻碍物, Brown粒子在空间中的运动有几率碰到阻碍, 也有几率穿过阻碍.当粒子碰到阻碍的时候, 这时候就要改变原来的运动状态. 图 4(c)给出了常用的诠释跳跃扩散的物理模型示意图, 以及相应的DPD随时间的变化情况.纳米颗粒在一个个互相隔离的局部空间中做受限扩散, 但是有一定的概率穿透隔离发生跳跃扩散.显然, 发生跳跃的概率是一个重要的参数.
跳跃扩散[40]指的是把Brown纳米颗粒看作在一个有空间上周期性拓扑几何性质的阻碍结构里运动, 这个结构可以允许Brown粒子有一定的几率渗透过阻碍.跳跃扩散能很好地描述具有Lévy跳跃特征的运动, 也能很好地解释近来发现的Brown非Gauss反常现象中的肥尾非Gauss分布[9].对于二维结构而言, 这个模型广泛地被用来研究蛋白质在细胞膜上面的运动[45-46].但是迄今为止, 该模型还没有能够很好地用到三维的运动上去.
1.5 数值模拟复杂环境中的纳米颗粒扩散现象一般比较难以直接用非常完整的实验展现出来, 数值模拟可以通过合理地构造模型,再在计算机上通过数值计算来模拟出粒子在复杂环境中扩散的情况.对于纳米粒子的扩散, 现在比较流行的方法有Monte Carlo, 分子动力学模拟等.这类方法一般是把环境因素和粒子的特征都抽象到几个数值的参数, 通过引用一定的势能函数, 或者其他判据, 来约束颗粒从既定时刻到下一时刻运动的规律, 在计算机上模拟颗粒运动, 最后统计出运动的特征.
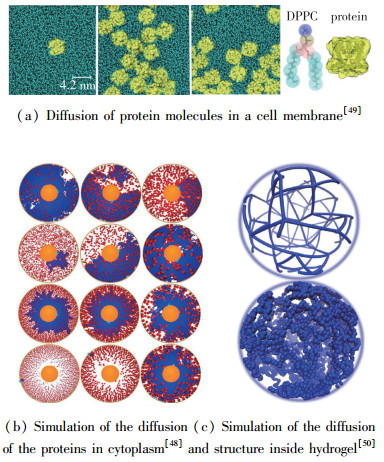
Netz等[47]用Monte Carlo的方法论证了障碍模型对于颗粒在凝胶里面扩散的实用性(图 5(a)).这个模型假设凝胶内的分子链是刚性不动的, 同时设定一个具有周期性边界条件的空间, 里面充满了凝胶分子, 从而组成类似墙壁一样的阻碍, 粒子能在其中运动, 但是不能接触墙壁.首先将粒子随机地放置在形成的空间里面,颗粒走下一步时先产生试探步,假如这一试探步将使得粒子同壁面(凝胶分子)接触,则该步不能用试探步代替,重新随机产生一试探步,如果产生的试探步不会使得粒子同壁面接触,则该步用试探步代替,粒子运动到下一个位置,继续产生新的步数,重复次数到107步,统计结果.模拟的结果显示MSD呈现亚线性而DPD呈现非Gauss, 和实验中凝胶的现象比较符合. Jordan等[36]用Monte Carlo方法去模拟神经元囊泡在神经元细胞里面的运动, 证明了受限扩散模型对细胞内扩散现象的合理性.他同样也是用计算机模拟一块充满了笼子的区域, 颗粒在里面一步一步地运动, 不同的是这里粒子每一步都有一定几率穿过笼子, 而如果粒子碰到了笼子的边缘, 则应该被反弹回去, 计算位置根据反弹的大小来判断, 这与之前的模型不同.
|
| 图 5 典型数值模拟 Fig.5 Typical numerical simulation |
Ghosh等用分子动力学模拟讨论了纳米颗粒在膜上扩散非Gauss现象的起因(图 5(b)).他用软件产生了一个空间, 空间内部随机不重叠地存在其他尺寸较大的物质, 颗粒的运动规律用Lennard-Jones(LJ)势能结合Langevin方程给出.其中可以控制的参量有其他物质的分数比及其尺寸, 总空间的大小, Brown颗粒的大小.有趣的是, 对于一般扩散而言尺寸大的阻碍物质应该对纳米粒子的扩散阻碍要比小尺寸的阻碍物质来得大, 但是在这个模拟中却得出了相反的结论, 小尺寸的阻碍物质在同一分数比的情况下却比大尺寸的阻碍物质来得大[48]. Jeon等则模拟了细胞膜上面蛋白质和磷脂的扩散, 说明了蛋白质在膜上的富集是产生非Gauss现象的主要原因.模拟显示蛋白质富集的两组在MSD上依然呈现线性, 而DPD在短时间内呈现指数型.通过对照可以体现蛋白质富集量对非Gauss现象的出现起着关键的影响[49](图 5(a)).
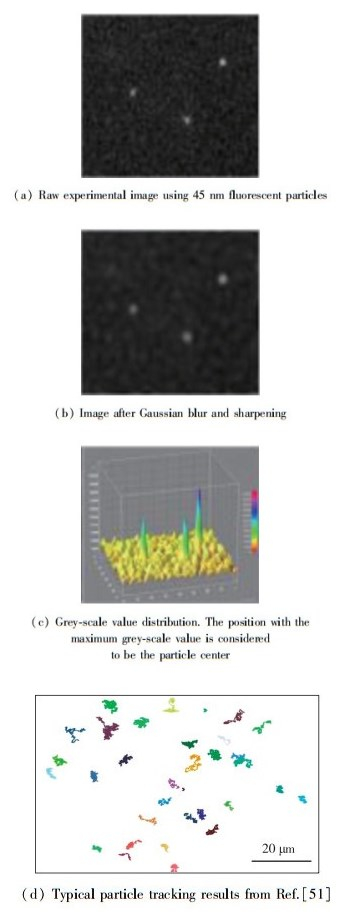
2 实验测量方法 2.1 粒子追踪粒子追踪是先把粒子包裹上荧光物质, 然后用荧光显微镜观测, 再通过摄像机(如EMCCD)转化成电脑图像进行处理.光学观测的核心是显微镜的物镜, 它决定了实际分辨率.在计算机上设定观察的范围, 就可以将观测到的粒子在一定时间内的运动轨迹通过连续多张图片的形式记录下来. 图 6(a)显示了45 nm直径的荧光纳米颗粒的原始图像.
|
| 图 6 粒子追踪的实验图像及其处理过程 Fig.6 Experimental image and the processing method of particle track |
记录下来的图片再用软件进行图像处理.常用的软件包括ImageJ或Matlab.对于荧光纳米颗粒, 我们摸索出了一套实用的处理方法[9, 16].第1步, 用Gaussian blur将图片周边的噪声干扰除去; 第2步, 用contrast sharpen来增强图中纳米粒子的光强度, 锐化处理得到图 6(b)所示结果; 第3步, 画出图像的灰度值等高线, 灰度值最高的地方被认定为粒子所在位置(图 6(c)); 第4步, 进行粒子追踪.这步中计算机将在一定范围内锁定粒子,那么下一张图片在这个范围内出现的粒子被认定为同一个粒子,再把所有图片里的同一个粒子出现的位置记录下来,并把这些位置按时间顺序连接起来就是粒子近似的运动轨迹.在Jiang等[51]的实验中, 粒子追踪技术得到了很好的结果(图 6(d)).
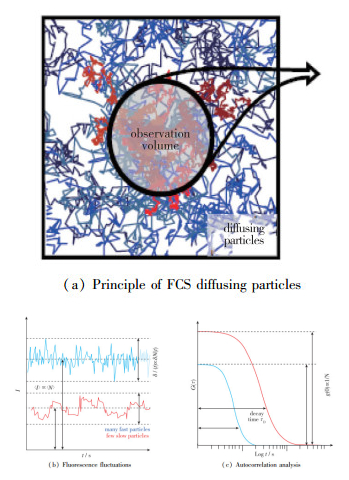
2.2 荧光相关由于纳米颗粒十分小, 即便用显微镜也很难观测它们的运动, 这就需要在粒子外面包裹上荧光物质.荧光物质在一个范围区域内的运动, 会引起这片区域检测到荧光的强度有一个波动, 这个波动的变化可以和粒子的运动特性建立映射关系,从而得到粒子运动的轨迹.
荧光检测实验的设备一般由激光源、CCD摄像机和计算机构成.激光源向样本发射光源, 激发荧光物质发光, 发射的光通过一个滤镜到达CCD, 摄像机把特定区域的经过光电二极管放大的光拍成图片输送到计算机处理.荧光相干光谱(fluorescence correlation spectroscopy,FCS)的原理[53]是通过荧光物质亮度波动信号I和时间t的关系得到自相关函数G(τ),再通过G(τ)的衰减时间推算扩散系数(图 7), 计算公式为τD=Aeff/(4D), 其中τD是衰减时间, Aeff与设备的分子探测效率有关.
3 实验结果实验方法上的改进大大促进了纳米颗粒在复杂生物介质里面反常扩散的研究.这些反常扩散可以分为3种类型:在细胞内部溶液的扩散; 在复杂拥挤环境(如高聚物溶液)里的扩散; 在膜上的扩散. 表 1展示了近年来主要的反常扩散实验研究结果.
| 下载CSV 表 1 复杂生物介质中反常扩散的实验研究小结 Tab.1 Brief summary of experiment researches of anomalous diffusion of nanoparticles in complex biological media |
为了研究细菌内部细胞质的结构, Golding等[55]用显微镜观察了涂上荧光物质的mRNA在E.coli细胞里长达30 min的运动. Weber等[56]同样观测了mRNA在新月细菌里面的扩散情况, 并且用分数型Brown运动去描述mRNA及其蛋白在细胞质溶液里面的亚扩散现象, 同前人在E.coli里面的mRNA运动是一致的. Guigas等[57]在一系列不同哺乳动物的细胞中观测里面的扩散现象, 从而确定不同细胞内部的富集程度, 他指出细胞核内部的物质富集程度比细胞质内的低, 这对研究细胞内部的工作机理有很大意义. Engelke等[58]观测了组成细胞骨架的球状肌动蛋白在细菌里面的运动, 解释了蛋白质在细菌内部运动的机理.
Wong等[59]观测了胶体颗粒在F-actin亚溶液当中的扩散, 发现F-actin形成的网格尺寸对扩散有重要影响, 当网格尺寸和胶体颗粒尺寸相近时, 粒子运动呈现亚扩散, 而当网格尺寸远远大于胶体颗粒时则会呈现正常扩散. Palmer等[60]同样观测了胶体颗粒在蛋白质溶液中的运动, 他发现扩散类型和时间是有很大关系的, 在短时间内扩散呈现正常扩散, 而在长时间尺度下扩散则呈现亚扩散. Weiss等[61]在细胞质溶液里放置了大小不一样的颗粒, 来研究细胞内部蛋白质的分布, 他发现粒子的扩散存在3个时间段, 同时粒子的尺寸会影响粒子MSD的大小和变化趋势.
Gielen等[62]观测MOG蛋白质在神经元细胞膜上的运动情况, 蛋白质同样呈现亚扩散, 同时提出了磷脂双分子组分的扩散解释. Ries等[63]在酵母细胞膜上面观测到了Fus-Mid-GFP蛋白质非常缓慢的正常扩散.
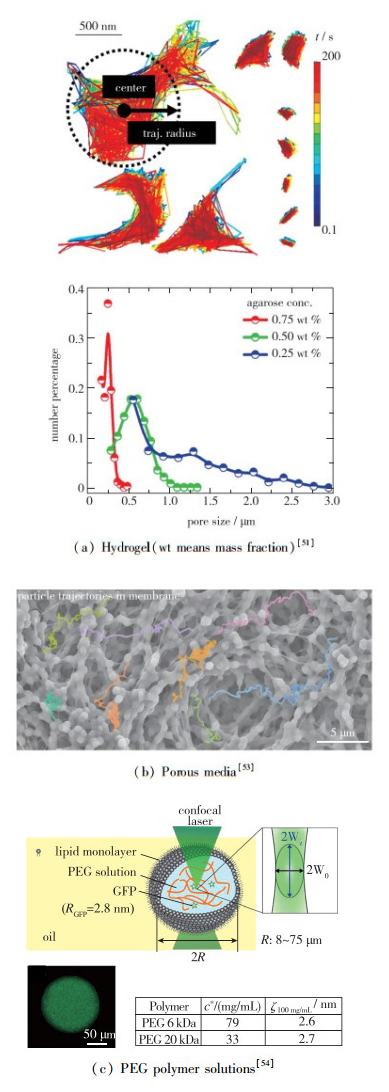
由于凝胶、高聚物、多孔介质和生物体内环境的相似性, 在这些介质里面的扩散成为了热点. Jiang等[51]研究了荧光纳米粒子颗粒在琼脂糖凝胶内部的运动, 他提出可以用纳米粒子的运动轨迹来判断凝胶内部空间孔洞的分布.他先往凝胶内放入多个粒子, 然后用显微镜观测多个粒子的轨迹, 通过粒子的轨迹来判断粒子所在空间的大小, 接着用计算出的空间分布来近似凝胶内孔洞的尺寸分布(见图 8(a)).他分别采用500 nm和200 nm的粒子进行测量, 认为凝胶内部在浓度高的时候呈现Gauss分布, 在浓度低的时候呈现幂分布. Cai等[53]将这个方法扩展到多孔介质, 用纳米粒子的运动来测量细胞膜上的曲折率、复杂程度(见图 8(b)). Watanabe等[54]用高聚物PEG溶液来模拟细胞膜上的环境, 观察荧光蛋白在高聚物溶液中的运动.以往的研究都认为随着高聚物的溶度, 也就是溶液里的拥挤程度的增加, 粒子的扩散速度会减慢, 但是在实验中发现当高聚物形成的笼子尺寸很小的时候, 随着高聚物浓度的增加, 粒子的扩散反而变得更快了(见图 8(c)).
|
| 图 8 纳米颗粒的反常扩散实验研究 Fig.8 Experimental studies of nanoparticle′s anomalous diffusion |
在Newton流体里面纳米颗粒的运动仍然遵循Brown粒子正常扩散的规律, 但是在复杂生物介质里面, 由于其在微观上拥挤复杂的内部环境, 纳米颗粒的运动展现出了新的物理特征, 其中最引人注目的是纳米颗粒的反常扩散.在本文中, 我们从MSD,DPD及受限扩散等多个角度, 系统介绍了各种正常/反常扩散的物理模型, 比较了CTRW和FBM模型分别用跳跃时间分布和Gauss叠加的想法描述反常扩散, 基于受限扩散和跳跃扩散两个模型, 在物理上给出了环境对粒子扩散影响的直观解释.重点介绍了对Brown非Gauss现象的Gauss肥尾解释的SUPER,DD和GGBM模型.在数值模拟方面上, 常用Monte Carlo和分子动力学模拟来重现纳米颗粒在细胞膜等复杂流体的拥挤环境下的扩散.实验观测纳米粒子的扩散方法主要有粒子追踪和荧光相关法.本文对纳米颗粒在高聚物溶液、凝胶等人工多孔介质中, 以及蛋白质、胶体颗粒、DNA等颗粒在生物介质里面的反常扩散研究进行了综述.反常扩散与生物微环境的功能实现有重要的关联, 同时也是流体力学在微纳尺度方向的重要扩展.该问题在微纳尺度流体力学、生物物理等领域是研究的热点, 在理论上和实验上仍有重大挑战,有待进一步深入研究.
致谢 本文作者感谢国家自然科学基金(91543125, 11572335, 11572334)、中科院重大前沿研究项目(QYZDB-SSW-JSC036)、中科院先导B项目(XDB22040403)的资助.| [1] |
Stone H A, Stroock A D, Ajdari A. Engineering flows in small devices:microfluidics toward a lab-on-a-chip[J]. Annual Review of Fluid Mechanics, 2004, 36: 381-411. DOI:10.1146/annurev.fluid.36.050802.122124 |
| [2] |
Schoch R B, Han J, Renaud P. Transport phenomena in nanofluidics[J]. Reviews of Modern Physics, 2008, 80(3): 839-875. DOI:10.1103/RevModPhys.80.839 |
| [3] |
Wagner V, Dullaart A, Bock A K, et al. The emerging nanomedicine landscape[J]. Nature Biotechnology, 2006, 24(10): 1211-1217. DOI:10.1038/nbt1006-1211 |
| [4] |
Daw R, Finkelstein J. Lab on a chip[J]. Nature, 2006, 442(7101): 367. DOI:10.1038/442367a |
| [5] |
Valencia P M, Farokhzad O, Karnik R, et al. Microflu-idic technologies for accelerating the clinical translation of nanoparticles[J]. Nature Nanotechnology, 2012, 7(10): 623-629. DOI:10.1038/nnano.2012.168 |
| [6] |
Koumoutsakos P, Pivkin I, Milde F. The fluid mechanics of cancer and its therapy[J]. Annual Review of Fluid Mechanics, 2013, 45: 325-255. DOI:10.1146/annurev-fluid-120710-101102 |
| [7] |
Höfling F, Franosch T. Anomalous transport in the crowded world of biological cells[J]. Reports on Progress in Physics, 2013, 76(4): 046602. DOI:10.1088/0034-4885/76/4/046602 |
| [8] |
Wang B, Kuo J, Bae S C, et al. When Brownian diffusion is not Gaussian[J]. Nature Materials, 2012, 11(6): 481-485. DOI:10.1038/nmat3308 |
| [9] |
Xue C D, Zheng X, Chen K K, et al. Probing non-Gaussianity in confined diffusion of nanoparticles[J]. The Journal of Physical Chemistry Letters, 2016, 7(3): 514-519. |
| [10] |
施兴华, 张路姚, 李博, 等. 肿瘤及其微环境的力学问题[J]. 力学进展, 2018, 48: 201808. Shi X H, Zhang L Y, Li B, et al. The mechanical problems in tumor and tumor microenvironment[J]. Advances in Mechanics, 2018, 48: 201808. (in Chinese) |
| [11] |
Dix J A, Verkman A S. Crowding effects on diffusion in solutions and cells[J]. Annual Review of Biophysics, 2008, 37: 247-263. DOI:10.1146/annurev.biophys.37.032807.125824 |
| [12] |
Fick A. Ueber diffusion[J]. Annalen der Physik und Chemie, 1855, 170(1): 59-86. DOI:10.1002/(ISSN)1521-3889 |
| [13] |
Von Smoluchowski M. Zur kinetischen theorie der brownschen molekularbewegung und der suspensionen[J]. Annalen der Physik, 1906, 326(14): 756-780. DOI:10.1002/(ISSN)1521-3889 |
| [14] |
Langevin P. Sur la theorie de movement Brownien[J]. C. R. Hebd. Seances Acad, 1908, 146: 530. |
| [15] |
Mandelbrot B B, Van Ness J W. Fractional Brownian motions, fractional noises and applications[J]. SIAM Review, 1968, 10(4): 422-437. DOI:10.1137/1010093 |
| [16] |
Zheng X, Ten Hagen B, Kaiser A, et al. Non-Gaussian statistics for the motion of self-propelled Janus particles:experiment versus theory[J]. Physical Review E, 2013, 88(3): 032304. |
| [17] |
Klafter J, Sokolov I M. First steps in random walks:from tools to applications[M]. Oxford: Oxford University Press, 2011: 45-84.
|
| [18] |
Einstein A. On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat[J]. Annalen der Physik, 1905, 17: 549-560. |
| [19] |
Zhang Y J, Dudko O K. First-passage processes in the genome[J]. Annual Review of Biophysics, 2016, 45: 117-134. DOI:10.1146/annurev-biophys-062215-010925 |
| [20] |
Zaburdaev V, Denisov S, Klafter J. Lévy walks[J]. Reviews of Modern Physics, 2015, 87(2): 483-530. DOI:10.1103/RevModPhys.87.483 |
| [21] |
Beck C, Cohen E G. Superstatistics[J]. Physica A:Statistical Mechanics and its Applications, 2003, 322: 267-275. DOI:10.1016/S0378-4371(03)00019-0 |
| [22] |
Beck C. Superstatistical Brownian motion[J]. Progress of Theoretical Physics Supplement, 2006, 162: 29-36. DOI:10.1143/PTPS.162.29 |
| [23] |
Wang B, Kuo J, Bae S C, et al. When Brownian diffusion is not Gaussian[J]. Nature Materials, 2012, 11(6): 481-485. DOI:10.1038/nmat3308 |
| [24] |
Van Der Straeten E, Beck C. Superstatistical fluctuations in time series:applications to share-price dynamics and turbulence[J]. Physical Review E, 2009, 80(3): 036108. DOI:10.1103/PhysRevE.80.036108 |
| [25] |
Hapca S, Crawford J W, Young I M. Anomalous diffusion of heterogeneous populations characterized by normal diffusion at the individual level[J]. Journal of the Royal Society Interface, 2009, 6(30): 111-122. DOI:10.1098/rsif.2008.0261 |
| [26] |
Chubynsky M V, Slater G W. Diffusing diffusivity:a model for anomalous, yet Brownian, diffusion[J]. Phy-sical Review Letters, 2014, 113(9): 098302. DOI:10.1103/PhysRevLett.113.098302 |
| [27] |
Chechkin A V, Seno F, Metzler R, et al. Brownian yet non-Gaussian diffusion:from superstatistics to subordination of diffusing diffusivities[J]. Physical Review X, 2017, 7(2): 021002. DOI:10.1103/PhysRevX.7.021002 |
| [28] |
Matse M, Chubynsky M V, Bechhoefer J. Test of the diffusing-diffusivity mechanism using near-wall colloidal dynamics[J]. Physical Review E, 2017, 96(4): 042604. DOI:10.1103/PhysRevE.96.042604 |
| [29] |
Jain R, Sebastian K L. Diffusion in a crowded, rearran-ging environment[J]. The Journal of Physical Chemistry B, 2016, 120(16): 3988-3992. DOI:10.1021/acs.jpcb.6b01527 |
| [30] |
Jain R, Sebastian K L. Diffusing diffusivity:a new derivation and comparison with simulations[J]. Journal of Chemical Sciences, 2017, 129(7): 929-937. DOI:10.1007/s12039-017-1308-0 |
| [31] |
Mura A, Taqqu M S, Mainardi F. Non-Markovian diffusion equations and processes:analysis and simula-tions[J]. Physica A:Statistical Mechanics and its Applications, 2008, 387(21): 5033-5064. DOI:10.1016/j.physa.2008.04.035 |
| [32] |
Mura A, Mainardi F. A class of self-similar stochastic processes with stationary increments to model anomalous diffusion in physics[J]. Integral Transforms and Special Functions, 2009, 20(3/4): 185-198. |
| [33] |
Pagnini G, Kober E. Fractional diffusion[J]. Fract Calc Appl Anal, 2012, 5: 117-127. |
| [34] |
Mura A, Pagnini G. Characterizations and simulations of a class of stochastic processes to model anomalous diffu-sion[J]. Journal of Physics A:Mathematical and Theoretical, 2008, 41(28): 285003. DOI:10.1088/1751-8113/41/28/285003 |
| [35] |
Ochab-Marcinek A, Wieczorek S A, Ziębacz N, et al. The effect of depletion layer on diffusion of nanoparticles in solutions of flexible and polydisperse polymers[J]. Soft Matter, 2012, 8(43): 11173-11179. DOI:10.1039/c2sm25925g |
| [36] |
Jordan R, Lemke E A, Klingauf J. Visualization of synaptic vesicle movement in intact synaptic boutons using fluorescence fluctuation spectroscopy[J]. Biophysical Journal, 2005, 89(3): 2091-2102. DOI:10.1529/biophysj.105.061663 |
| [37] |
Yeung C, Shtrahman M, Wu X L. Stick-and-diffuse and caged diffusion:a comparison of two models of synaptic vesicle dynamics[J]. Biophysical Journal, 2007, 92(7): 2271-2280. DOI:10.1529/biophysj.106.081794 |
| [38] |
Gennerich A, Schild D. Fluorescence correlation spectroscopy in small cytosolic compartments depends criti-cally on the diffusion model used[J]. Biophysical Journal, 2000, 79(6): 3294-3306. DOI:10.1016/S0006-3495(00)76561-1 |
| [39] |
Gennerich A, Schild D. Anisotropic diffusion in mitral cell dendrites revealed by fluorescence correlation spectroscopy[J]. Biophysical Journal, 2002, 83(1): 510-522. DOI:10.1016/S0006-3495(02)75187-4 |
| [40] |
Piskorz T K, Ochab-Marcinek A. A universal model of restricted diffusion for fluorescence correlation spectros-copy[J]. The Journal of Physical Chemistry B, 2014, 118(18): 4906-4912. DOI:10.1021/jp502467u |
| [41] |
Rouse P E, Sittel K. Viscoelastic properties of dilute polymer solutions[J]. Journal of Applied Physics, 1953, 24(6): 690-696. DOI:10.1063/1.1721361 |
| [42] |
Knoben W, Besseling N A, Bouteiller L, et al. Dynamics of reversible supramolecular polymers:independent determination of the dependence of linear viscoelasticity on concentration and chain length by using chain stop-pers[J]. Physical Chemistry Chemical Physics, 2005, 7(11): 2390-2398. DOI:10.1039/b503463a |
| [43] |
Raikher Y L, Rusakov V V, Perzynski R. Brownian motion in a viscoelastic medium modelled by a Jeffreys fluid[J]. Soft Matter, 2013, 9(45): 10857-10865. DOI:10.1039/c3sm51956b |
| [44] |
Daumas F, Destainville N, Millot C, et al. Confined diffusion without fences of a G-protein-coupled receptor as revealed by single particle tracking[J]. Biophysical Journal, 2003, 84(1): 356-366. |
| [45] |
Fujiwara T, Ritchie K, Murakoshi H, et al. Phospholip-ids undergo hop diffusion in compartmentalized cell membrane[J]. The Journal of Cell Biology, 2002, 157(6): 1071-1082. DOI:10.1083/jcb.200202050 |
| [46] |
Heinemann F, Vogel S K, Schwille P. Lateral membrane diffusion modulated by a minimal actin cortex[J]. Biophysical Journal, 2013, 104(7): 1465-1475. DOI:10.1016/j.bpj.2013.02.042 |
| [47] |
Netz P A, Dorfmuller T. Computer simulation studies of diffusion in gels:model structures physics today[J]. The Journal of Chemical Physics, 1997, 107(21): 9221-9233. DOI:10.1063/1.475214 |
| [48] |
Ghosh S K, Cherstvy A G, Grebenkov D S, et al. Anomalous, non-Gaussian tracer diffusion in crowded two-dimensional environments[J]. New Journal of Physics, 2016, 18: 013027. DOI:10.1088/1367-2630/18/1/013027 |
| [49] |
Jeon J H, Javanainen M, Martinez-Seara H, et al. Protein crowding in lipid bilayers gives rise to non-Gaussian anomalous lateral diffusion of phospholipids and proteins[J]. Physical Review X, 2016, 6(2): 021006. DOI:10.1103/PhysRevX.6.021006 |
| [50] |
Kamerlin N, Elvingson C. Tracer diffusion in a polymer gel:simulations of static and dynamic 3D networks using spherical boundary conditions[J]. Journal of Physics:Condensed Matter, 2016, 28(47): 475101. DOI:10.1088/0953-8984/28/47/475101 |
| [51] |
Jiang L X, Granick S. Real-space, in situ maps of hydrogel pores[J]. ACS Nano, 2017, 11(1): 204-212. DOI:10.1021/acsnano.6b04468 |
| [52] |
Krieger J W, Singh A P, Bag N, et al. Imaging fluorescence (cross-) correlation spectroscopy in live cells and organisms[J]. Nature Protocols, 2015, 10(12): 1948-1974. DOI:10.1038/nprot.2015.100 |
| [53] |
Cai Y, Schwartz D K. Mapping the functional tortuosity and spatiotemporal heterogeneity of porous polymer membranes with super-resolution nanoparticle tracking[J]. ACS Applied Materials & Interfaces, 2017, 9(49): 43258-43266. |
| [54] |
Watanabe C, Yanagisawa M. Cell-size confinement effect on protein diffusion in crowded poly(ethylene)glycol solution[J]. Physical Chemistry Chemical Physics, 2018, 20(13): 8842-8847. DOI:10.1039/C7CP08199E |
| [55] |
Golding I, Cox E C. Physical nature of bacterial cytoplasm[J]. Physical Review Letters, 2006, 96(9): 098102. DOI:10.1103/PhysRevLett.96.098102 |
| [56] |
Weber S C, Spakowitz A J, Theriot J A. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm[J]. Physical Review Letters, 2010, 104(23): 238102. DOI:10.1103/PhysRevLett.104.238102 |
| [57] |
Guigas G, Kalla C, Weiss M. The degree of macromolecular crowding in the cytoplasm and nucleoplasm of mammalian cells is conserved[J]. FEBS Letters, 2007, 581(26): 5094-5098. DOI:10.1016/j.febslet.2007.09.054 |
| [58] |
Engelke H, Heinrich D, Rädler J O. Probing GFP-actin diffusion in living cells using fluorescence correlation spectroscopy[J]. Physical Biology, 2010, 7(4): 046014. DOI:10.1088/1478-3975/7/4/046014 |
| [59] |
Wong I Y, Gardel M L, Reichman D R, et al. Anomalous diffusion probes microstructure dynamics of entangled F-actin networks[J]. Physical Review Letters, 2004, 92(17): 178101. DOI:10.1103/PhysRevLett.92.178101 |
| [60] |
Palmer A, Mason T G, Xu J Y, et al. Diffusing wave spectroscopy microrheology of actin filament networks[J]. Biophysical Journal, 1999, 76(2): 1063-1071. DOI:10.1016/S0006-3495(99)77271-1 |
| [61] |
Weiss M, Elsner M, Kartberg F, et al. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells[J]. Biophysical Journal, 2004, 87(5): 3518-3524. DOI:10.1529/biophysj.104.044263 |
| [62] |
Gielen E, Vercammen J, Sýkora J, et al. Diffusion of sphingomyelin and myelin oligodendrocyte glycoprotein in the membrane of OLN-93 oligodendroglial cells studied by fluorescence correlation spectroscopy[J]. Comptes Rendus Biologies, 2005, 328(12): 1057-1064. DOI:10.1016/j.crvi.2005.09.008 |
| [63] |
Ries J, Schwille P. Studying slow membrane dynamics with continuous wave scanning fluorescence correlation spectroscopy[J]. Biophysical Journal, 2006, 91(5): 1915-1924. DOI:10.1529/biophysj.106.082297 |