2. 大连理工大学工程力学系,辽宁大连 116024
2. Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024
激波是一个重要的物理现象, 表现为一个曲面或曲线间断[1].一方面, 激波是有害的.对于高亚声速或低超声速飞行器而言, 激波会产生很大的波阻, 从而降低飞行器气动性能.对于高超声速飞行器而言, 激波作用于飞行器表面时会造成强的边界层分离以及严重气动热问题, 这些都会对飞行器结构产生很大影响.另一方面, 激波又是有益的.例如激波可以用来增加吸气式超燃冲压发动机的压力, 以及提升乘波体构型的升力.
对数值模拟而言, 激波的求解十分重要又困难.计算激波一个最直接的办法就是使用激波装配法, 即将激波面看作一个间断, 使其两侧的物理量满足Rankine-Hugoniot(R-H)关系式.这种方式在计算流体力学初期作为一种重要的研究手段被广泛应用于高超声速流动的数值计算中[2-3].作为一种精确的激波数值计算方法, 目前很多研究学者开始利用该方法构造全场一致高精度计算方法[4-5].但是, 激波装配方法由于网格拓扑结构的限制很难应用于具有内嵌激波等复杂波系的实际问题[6].近年来, 由于非结构网格技术的逐渐成熟, 国内外一些研究人员将该激波装配方法与非结构网格技术相结合, 获得了不错的计算效果, 特别是对于含有内嵌激波等复杂结构的超声速流动能够很好地模拟[7-10].
这些提出的激波装配方法都还不能实现自动激波或接触间断的形成, 也不能判断它们之间是如何相交的.对于定常流动来说, 可以利用激波捕捉提供激波的初始位置, 通过逐步迭代消除初始误差.但是对于流动结构在计算过程中可能发生变化的非定常流来说, 这种操作方式就显得比较局限了.为了解决这个问题, 须处理好两个方面的问题:一个是激波辨识方法, 另外一个是对新生激波进行记录, 同时删除很弱的激波[11].当然, 激波辨识方法也不能完全解决激波装配中遇到的问题, 但至少是向实际应用迈出了重要的一步.
目前, 国内外关于激波辨识方法的研究有很多[12-17].这些方法可以分为两类[18]:一种是考虑垂直于激波阵面的法向Mach数, 另一种是将数值解匹配到Riemann解问题中.前一种方法是基于原始变量梯度垂直于激波阵面的假设.一个点垂直于激波阵面的Mach数如果等于1, 则可以认为该处位于激波上.这种方法很容易实施, 但是往往这种方法辨识的不仅是激波还有其他类型的间断.所以往往一些复杂的滤波或阈值限制需要和这种方法一起使用.而且, 阈值的选择好坏往往会对辨识出来的激波有很大影响.后一种方法是在每一个单元内考虑一个一维非定常流动的Riemann问题.这种方法的好处是不仅可以分辨激波也可以分辨接触间断.
从某种程度而言, 这两种方法都是一维的.前者是通过找到激波法向确定激波位置; 后者是匹配一维Riemann问题的解.在特征线理论中, 激波可以看作是同族特征线的收敛.根据这个定义, 文献[18]发展了一种新的激波辨识方法, 该方法在二维问题的辨识中展现了良好的性能以及效率.随后将对其进行详细介绍.
然而, 这些激波辨识方法都是基于流场数据进行显示的一种方法, 很难直接应用于激波装配方法中, 特别是基于网格面元的装配方法中.在激波显示技术中, 激波辨识是在流场计算结果上进行的, 它们之间是一种单向的关系, 即通过计算结果导出激波位置.但是在激波装配中, 激波辨识和激波计算是双向耦合的, 困难程度大大增加.因此, 本文在这些关于激波辨识研究的基础上进行改造, 发展出适合激波装配方法使用的激波辨识方法.
1 计算方法近年来, 刘君等[19-21]利用非结构动网格技术发展了一套应用于格心型有限体积方法的激波装配技术, 并在相关问题中得到了应用, 表现出了良好的性能.在此只对其激波装配的思想进行介绍, 而有限体积法相关的内容可以查看文献[22].
1.1 激波装配方法 1.1.1 激波点标识为了直观地对本文中的激波装配方法进行介绍, 我们考虑如图 1所示的一个含有激波的二维流场.在使用计算程序进行流动计算前, 首先采用三角形单元对全场进行离散, 离散后的网格节点被标记为普通节点(O)和激波节点(S)两种.激波节点和普通节点相比, 在激波节点上存在两组或多组参数, 而在普通节点上有且只有一组参数.

|
| 图 1 节点属性定义 Fig.1 Definition of properties of grid nodes |
值得说明的是:对于定常问题, 可以利用捕捉方法得到一个初场, 然后通过一些相关辨识技术得到初始激波位置.将符合位置条件的网格节点标记为激波点, 经过迭代收敛过程后, 最终得到稳定的流场.对于非定常问题, 在计算过程中有时候存在激波的生成及湮灭, 所以在计算过程中须使用更加准确的激波辨识方法.为此, 本文发展了一套适用于激波装配的激波辨识方法, 相关的内容在下一部分进行介绍.
1.1.2 激波参数确定由于本文采用的捕捉方法为格心型有限体积法, 因此须通过格心参数平均得到格点参数.对于普通节点来讲, 只须将与该节点相邻的所有单元进行加权平均即可得到位于该节点的流动参数.而对于激波节点来说, 由于其包含两组流动参数, 一组为上游流动参数, 一组为下游流动参数.因此在通过单元格心参数来确定格点参数之前须判断相邻单元位于激波上游还是下游.在激波节点的标记完成后, 将所有节点都属于激波节点的面元标记为激波面元.激波面元可以看作是激波阵面的离散, 这些面元可以将流动区域分割成两个部分, 一部分为低压区, 位于激波上游; 一部分为高压区, 位于激波下游.通过比较激波面元两侧单元熵sL和sR的大小判断标识上下游单元.熵大的单元属于下游单元, 熵小的单元属于上游单元.在上下游单元确定之后, 激波节点上游参数Vu=(ρu, uu, pu)T和下游参数Vd=(ρd, ud, pd)T可以通过下式进行确定:
| $ {\mathit{\boldsymbol{V}}_{\rm{u}}} = \frac{{\sum\limits_{k = 1}^N {{\alpha _{1k}}{\mathit{\boldsymbol{U}}_{1k}}} }}{{\sum\limits_{k = 1}^N {{\alpha _{1k}}} }}, {\mathit{\boldsymbol{V}}_{\rm{d}}} = \frac{{\sum\limits_{k = 1}^N {{\alpha _{2k}}{\mathit{\boldsymbol{U}}_{2k}}} }}{{\sum\limits_{k = 1}^N {{\alpha _{2k}}} }} $ |
其中, U表示单元格心参数, N为与激波节点S相邻的单元个数; αk=χ/|R|表示第k个相邻单元的权系数.如图 2所示, R为从第k个单元的单元格心到激波节点S的向量; 考虑流动影响范围的有限性, 所以引入了参数χ, 并且定义:

|
| 图 2 激波节点参数确定 Fig.2 Determination of states on shock nodes |
| $ \chi = \left\{ \begin{array}{l} 0, \;\;M{a_{\tau k}} \le-1\\ 1, \;\;M{a_{\tau k}} >-1 \end{array} \right. $ |
其中, Maτk=V2k·τ/a2k为下游第k个单元流动速度沿激波面元切向的Mach数,
同时, 我们也可以通过激波面元法向确定出激波点的法向n:
| $ \mathit{\boldsymbol{n}} = \frac{{\sum\limits_{k = 1}^N {\alpha {' _k}{\mathit{\boldsymbol{n}}_k}} }}{{\sum\limits_{k = 1}^N {\alpha {' _k}} }} $ |
其中, N表示与激波节点S相邻的激波面元格式, nk为第k个激波面元的法向方向, 并且该方向由上游指向下游; α′k=χ/|R′|表示第k个相邻面元的权系数, χ的定义与上文相同, R′为从面元中心到激波节点S的距离矢量.
通过上述计算方法将单元格心参数平均到格点上, 得到激波节点上的上下游参数Vu和Vd.对于上游流动区域来说, 其位于间断的上游, 流动信息由上游单元通过间断流向下游.在激波坐标系下, 上游流动为超声速流动, 因此处于下游的间断不会对上游单元产生影响.也就是说, 在激波上游使用捕捉方法获得的流动信息是准确的, 即上游流动参数Vu不需要重新确定.由于下游流动区域位于间断下游, 熵、涡量以及向前运动的声波等信息都是从间断传播过来的, 所以使用捕捉方法得到的下游区域的流动计算结果都不是正确的, 即下游流动参数Vd需要重新确定.
对于激波节点而言, 描述激波前后流动参数的R-H关系式被应用于求解新的下游参数V′d.定义w为激波运动速度大小, 其方向沿激波节点法向n.根据上游参数可以得到在激波坐标系下的上游流动Mach数:
| $ M{a_{{\rm{u, rel}}}} = \frac{{{\mathit{\boldsymbol{V}}_{\rm{u}}}\cdot\mathit{\boldsymbol{n}}-w}}{{{a_{\rm{u}}}}} $ |
其中, au表示上游区域的声速.根据Mau, rel以及上游参数, 我们可以得到
| $ \left\{ \begin{array}{l} p{' _{\rm{d}}} = \frac{{p{' _{\rm{u}}}\left[{2\gamma Ma_{{\rm{u, rel}}}^2-\left( {\gamma-1} \right)} \right]}}{{\gamma + 1}}\\ \rho {' _{\rm{d}}} = \frac{{\rho {' _{\rm{u}}}\left( {\gamma + 1} \right)Ma_{{\rm{u, rel}}}^2}}{{\left( {\gamma -1} \right)Ma_{{\rm{u, rel}}}^2 + 2}}\\ \frac{{\rho {' _{\rm{d}}}{{(\mathit{\boldsymbol{V}}{' _{\rm{d}}}\cdot\mathit{\boldsymbol{n}} -{\mathit{\boldsymbol{V}}_{\rm{u}}}\cdot\mathit{\boldsymbol{n}} + {a_{\rm{u}}}M{a_{{\rm{u, rel}}}})}^2}}}{{\gamma p{' _{\rm{d}}}}} = \frac{{\left( {\gamma -1} \right)Ma_{{\rm{u, rel}}}^2 + 2}}{{2\gamma Ma_{{\rm{u, rel}}}^2 - \left( {\gamma - 1} \right)}} \end{array} \right. $ | (1) |
在二维情况下, 沿激波法向总共有包括下游流动状态的3个参数和1个激波运动速度4个参数需要确定, 而方程(1)只能提供3个方程.因此, 要想确定所有参数仍须另外提供一个方程.通过分析, 我们可以知道尽管下游区域内流动相对激波法向而言是亚声速的, 但是反向移动的声波还是携带部分流动信息由下游向上游间断处传播.根据特征线理论, 反向传播的Riemann变量J=2a/(γ-1)-u·n从下游向上游传播过程不发生变化. Riemann变量J由于没有受到间断的影响, 我们可以假设通过激波捕捉方法得到的Riemann变量J也是正确的.因此, 可以获得另外一个方程:
| $ J = \frac{{2\sqrt {\gamma \frac{{p{' _{\rm{d}}}}}{{\rho {' _{\rm{d}}}}}} }}{{\gamma-1}}-\mathit{\boldsymbol{u}}{' _{\rm{d}}}\cdot\mathit{\boldsymbol{n}} = \frac{{2{a_{\rm{d}}}}}{{\gamma-1}} - {\mathit{\boldsymbol{u}}_{\rm{d}}}\cdot\mathit{\boldsymbol{n}} $ | (2) |
可以看出, 方程(2)左侧随Mau, rel线性变化.因此采用Newton公式可以很容易地求解出来流Mach数在激波法向的相对分量Mau, rel.一旦Mau, rel确定, 其他4个未知参数都可以相继得到.
1.1.3 激波通量计算在格心型有限体积方法中, 须求解各个单元界面的流动通量.对于普通面元来说, 通过各种通量计算方法在单元界面上进行通量分解, 进而求出各个单元的通量值.而对于激波面元来说, 流过激波面元的通量计算方法要更为简单.由前文分析可知, 对于激波上游而言, 其流动相对于激波面为超声速的.激波间断位于单元下游, 可以视为上游单元的超声速出口, 因此从上游流过激波面元的通量可以表示为:
| $ {\mathit{\boldsymbol{F}}_u} = {\left[\begin{array}{l} {a_1}\\ {a_1}{\mathit{\boldsymbol{V}}_x} + p{\mathit{\boldsymbol{n}}_x}\\ {a_1}{\mathit{\boldsymbol{V}}_y} + p{\mathit{\boldsymbol{n}}_y}\\ {a_1}{\mathit{\boldsymbol{V}}_z} + p{\mathit{\boldsymbol{n}}_z}\\ {a_1}E + p{a_2} \end{array} \right]_{\rm{u}}} $ |
其中, a1=ρ(V-w·n)·n, a2=V·n, E=V·V/2+p/ρ(γ-1). w为激波面元运动速度值, 其大小可以通过1.1.2节中的激波节点运动速度平均得到.
根据通量守恒, 由激波间断流入下游区域的通量Fd应该在数值上等于Fu.
1.1.4 网格点运动1.1.2节中在确定激波节点下游流动参数的同时也确定了激波点的运动速度.本文采用非结构动网格技术描述激波节点的运动.根据计算的激波点速度w以及激波点法向n可以确定在此时间步内节点运动的位移为w·n·Δt.如图 3所示, 图中实线代表T=t时刻的计算网格, 虚线代表T=t+Δt时刻的计算网络.在激波节点的运动确定后, 通过弹簧近似方法确定其他普通网格节点在新时刻的位置, 从而得到新时刻的计算网格.

|
| 图 3 网格节点运动示意图 Fig.3 Sketch of the present shock-fitting technique |
对于二维定常流动而言存在两类特征线: C+和C-.定义θ+ν和θ-ν分别为沿特征线C+和C-的Riemann不变量, 则θ+ν和θ-ν会分别收敛于C+和C-.其中, θ为流动速度变量, ν为Prandtl-Meyer函数.这样输送方程就可以定义为:
| $ \frac{\partial }{{\partial \xi }}\left( {\theta + \nu } \right) = 0, \;\;\;\frac{\partial }{{\partial \eta }}\left( {\theta-\nu } \right) = 0 $ | (3) |
其中ξ和η分别表示沿C+和C-方向的坐标.设Ma为当地Mach数, 方程(3)可以写成:
| $ \begin{array}{l} \frac{{\sqrt {M{a^2}-1} \cos \theta + \sin \theta }}{{Ma}}\frac{{\partial \left( {\theta + \nu } \right)}}{{\partial x}} + \\ \frac{{\sqrt {M{a^2}-1} \sin \theta-\cos \theta }}{{Ma}}\frac{{\partial \left( {\theta + \nu } \right)}}{{\partial y}} = 0, \\ \frac{{\sqrt {M{a^2} - 1} \cos \theta - \sin \theta }}{{Ma}}\frac{{\partial \left( {\theta - \nu } \right)}}{{\partial x}} + \\ \frac{{\sqrt {M{a^2} - 1} \sin \theta + \cos \theta }}{{Ma}}\frac{{\partial \left( {\theta - \nu } \right)}}{{\partial y}} = 0 \end{array} $ | (4) |
方程(4)可以看作: Riemann不变量θ+ν沿着x方向的传播速度为(
| $ \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) = \left[\begin{array}{l} (\sqrt {M{a^2}-1} \cos \theta \pm \sin \theta )/Ma\\ (\sqrt {M{a^2}-1} \cos \theta \pm \left( {-\sin \theta } \right))/Ma \end{array} \right] $ | (5) |
利用方程(5), 我们可以通过求解下面的流线方程得到特征线.
| $ \frac{{\rm{d}}}{{{\rm{d}}\tau }}\left[\begin{array}{l} x\\ y \end{array} \right] = \left[\begin{array}{l} (\sqrt {M{a^2}-1} \cos \theta \pm \sin \theta )/Ma\\ (\sqrt {M{a^2}-1} \cos \theta \pm \left( {-\sin \theta } \right))/Ma \end{array} \right] $ | (6) |
其中, τ表示虚拟时间参数.
线性方程组(6)可以写成一个矢量形式:
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{x}}}}{{{\rm{d}}\tau }} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{b}} $ | (7) |
方程(7)的解可以写成如下形式:
| $ \mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{x}}_0} + {C_1}{{\rm{e}}^{\left( {{\lambda _1}\tau } \right){\mathit{\boldsymbol{r}}_1}}} + {C_2}{{\rm{e}}^{\left( {{\lambda _2}\tau } \right){\mathit{\boldsymbol{r}}_2}}} $ |
其中, x0为不动点. λi和ri分别表示矩阵A的特征值和特征向量. Ci为积分常数.
求解方程(7), 相应的准线方程可以写成如下形式:
| $ {\mathit{\boldsymbol{x}}_{{\rm{cr}}}}\left( t \right) = {\mathit{\boldsymbol{x}}_0} + t{\mathit{\boldsymbol{r}}_i} $ |
其中, t为一个自由参数, 下标i=1, 2, 分别对应于准线1和2.
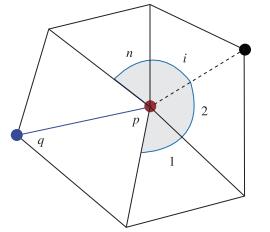
基于特征线理论的激波辨识方法在激波装配中使用的问题可以描述为:如图 4所示, 对于已知激波面qp, 假设点p是激波终点, 则以p为搜寻起点, 判断与其相邻的网格单元中是否含有激波.
|
| 图 4 激波节点搜寻示意图 Fig.4 Sketch of searching new shock points |
根据上面讨论的内容, 具体操作过程可以分为以下几个步骤进行:
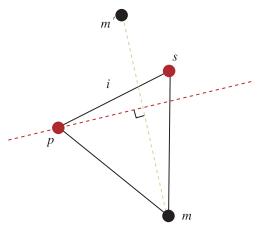
(1) 如图 5所示, 与搜寻始点p相邻的三角形的另外两个节点分别为m和s, 该单元记为△pms.在△pms的3个顶点处分别求解Riemann不变量的传播速度f(x).
|
| 图 5 新的激波点判断 Fig.5 Determining of new shock points |
(2) 利用步骤(1)中得到的传播速度, 可以获得方程(7)的右端项Ax+b.
(3) 求解线性常微分方程组(7), 可以得到双曲方程对应的准线.在求解方程组(7)时, 通常须确定不动点的坐标x0, 再根据准线斜率, 获得准线方程.然而对于本文中的特殊问题而言, 由于点p为已知的激波点, 那么根据定义, 准线必然通过点p, 因此可以利用点p的坐标代替不动点x0.
(4) 根据步骤(3)中获得的准线方程, 就可以判断该准线是否通过目标单元△pms.如果该准线通过这个单元, 如图 5所示(红色虚线表示准线), 则表明有一条间断通过该单元.更进一步, 我们还须利用激波前后的关系式确定这条准线是否为激波.假设点m为离准线较远的点, 则须求解m关于准线的镜像点m′.用Man表示任一点(m或m′)参数沿法向的Mach数.如果m和m′满足关系式: (Man)L>1, (Man)R < 1或者(Man)R>1, (Man)L < 1, 则可以认为该准线表示为一条激波.
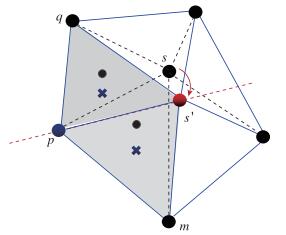
(5) 通常, 准线并不会与网格界面完全重合, 为此须进行简单的网格变形.具体操作是:将s在准线上进行投影, 得到点s′.移动s到s′, 与s相连的网格发生变形, 将新网格在旧网格上进行线性插值即可获得新网格的物理参数, 如图 6所示.对于运动激波来说, R-H关系式只有在激波坐标系下才能满足.因此, 要想使用上述的方法准确判断激波位置, 我们首先须确定激波运动速度Vs.
|
| 图 6 网格变形和插值 Fig.6 Mesh deformation and interpolation |
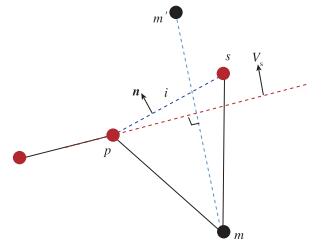
(6) 根据步骤(1)~(5)的计算方法确定激波(此时激波运动速度视为零), 设为ps, 如图 7所示.
|
| 图 7 激波运动速度确定 Fig.7 Determining of shock velocities |
(7) 利用ps两侧流动参数以及面元法向, 求解R-H关系式, 可以获得激波运动速度V′s.
(8) 在激波坐标系下(运动速度V′s), 重复步骤(1)~(5), 再次确定准线.
(9) 重复步骤(7)~(8), 得到最终的准线方程以及激波运动速度Vs.
2 算例验证在超声速风洞中, 气流遇到模型(例如一个楔), 会产生一道斜激波.该问题包含两个状态, 一是气流在斜楔作用下形成运动激波的状态, 另一个是运动激波最后形成稳定的斜激波的状态.前一个属于非定常流动, 后一个属于定常流动.
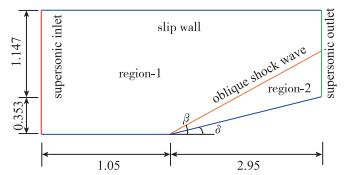
2.1 定常激波首先, 我们考虑定常过程.如图 8所示, 计算区域包括region-1和region-2两个区域, 边界条件以及计算区域尺寸在图 8中进行了标记. region-1内流动参数分别为:密度ρ=1, 压强为p=0.714 3, 水平流动速度u=3. region-2区域参数根据斜激波条件(激波角β=27.5°)进行确定.
|
| 图 8 激波运动速度确定 Fig.8 Determining of shock velocities |
由于region-1和region-2两个区域内参数满足斜激波关系, 计算区域内流动参数不发生变化, 为定常状态.使用前文提到的激波辨识方法对计算区域内的斜激波进行辨识.
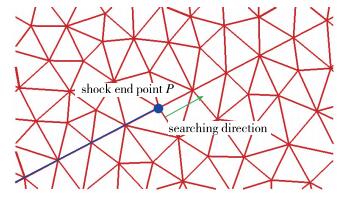
如图 9所示, 假设P为已知激波的终点.按照前文介绍的激波辨识方法, 以P为搜寻起点, 对与P相连的所有网格节点进行判断.如果存在新的激波点, 则对记录激波数组进行扩展, 同时将新搜索到的激波点定义为新的激波终点, 继续进行搜索.如果在P的周围找不到新的激波点, 则终止搜索.
|
| 图 9 定常激波:搜寻示意图 Fig.9 Steady shock: sketch of searching new shock points |
由于本算例中包含唯一的一个斜激波, 以P为搜索起点进行搜索时, 我们可以看到搜索过程沿着图 9中绿色箭头所示方向, 搜索到达超声速出口边界上的网格节点时搜索终止.位于斜激波上的激波点全部被找到.根据辨识得到的激波节点, 使用激波装配方法进行模拟, 计算结果如图 10(b)所示.两个区域的交界面为一个激波, 激波厚度为零, 在激波附近没有数值震荡现象出现.
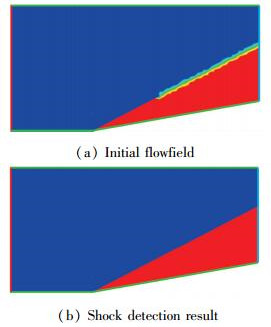
|
| 图 10 计算结果 Fig.10 Computational solutions |
仍然以2.1中问题为例, 模拟超声速流动受斜楔作用形成斜激波的动态过程.为了验证辨识方法的有效性, 本文设定了3种不同情境:
case-1:从计算开始就启动激波辨识程序;
case-2:计算前200步使用激波捕捉方法进行计算, 201步开始启动激波辨识程序;
case-3:计算前200步使用激波装配方法进行计算, 201步开始启动激波辨识程序.
通过计算可以看出:
对于case-1, 在计算进行5步后, 流动时间达到时, 沿着斜楔壁面形成一条运动激波.虽然此时激波还是十分微弱, 但是激波辨识程序还是将该激波迅速辨识出来, 如图 11(a)所示.由于初始辨识的激波需要和网格相匹配, 激波形状并不规则.若干步后, 流动时间到达时, 辨识出来的激波节点运动到达新的位置, 同时在计算过程中彼此相互调整.此时激波形状已经较为光滑.激波节点的运动带动其他网格节点的运动, 网格发生变形, 如图 11(b)所示.随着计算的进行, 网格质量变得越来越差, 此时须结合网格重构技术来对内部网格进行调整, 如图 11(c)所示. 图 11(d), (e), (f)表示流场的收敛过程, 随着时间推进, 激波运动速度逐渐趋近于零, 非定常的运动激波逐渐变成静止的定常激波.
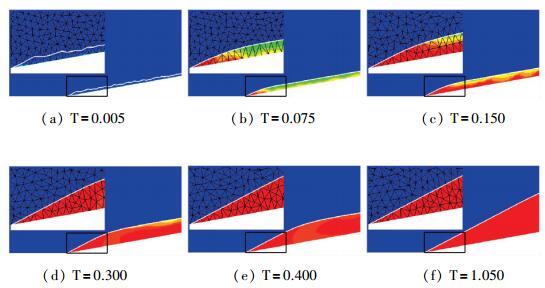
|
| 图 11 Case-1:激波探测结果 Fig.11 Case-1: shock detection results |
对于case-2, 计算进行到200步时, 流动物理时间达到.由于此前使用的激波捕捉方法进行计算, 计算区域内没有任何节点被定义为激波, 网格节点并未发生任何变形, 如图 12(a)所示.在201步时开始启动激波辨识程序, 在204步, 一部分激波节点被辨识出来, 如图 12(b)所示(白线表示激波).随着计算进行, 到209步, 此时流动物理时间达到, 此时越来越多的激波点被标记出来.直到223步, 流动物理时间达到, 全部的激波节点被标记出来, 如图 12(d)所示.标记出来的激波不是非常规则, 部分激波点的位置较为靠近激波上游.但是, 随着流场的发展, 标记出来的激波彼此相互调整, 激波形状也越来越光滑, 如图 12(e), (f)所示.

|
| 图 12 Case-2:激波探测结果 Fig.12 Case-2: shock detection results |
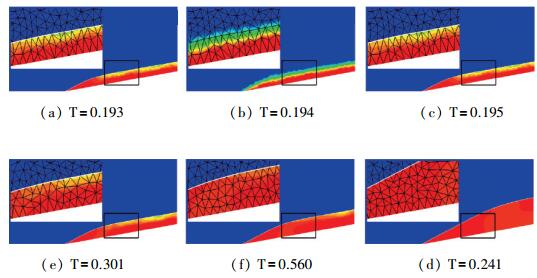
对于case-3, 在200步之前使用装配方法进行计算.在第200步时, 人为删除所有对激波点的标记, 此时流场云图如图 13(b)所示.从201步时重新启动激波辨识程序, 对流场内存在激波节点进行判断.相较case-2而言, 在case-3中, 由于之前是使用激波装配进行计算的, 流场计算精度要更高一些.同时, 由于在激波装配中, 网格面是与激波阵面相匹配的, 因此在202步时, 如图 13(c)所示, 所有的激波点都被准确地辨识出来. 图 13(d), (e), (f)表示被重新标识后的激波开始继续运动, 流场慢慢收敛.
|
| 图 13 Case-3:激波探测结果 Fig.13 Case-3: shock detection results |
case-1的应用表明本文使用的激波辨识方法能够快速准确地对动态激波进行辨识标记, 证明了该方法的有效性.通过case-2和case-3的应用和对比, 说明了流场精度以及网格和激波阵面的匹配情况对于激波辨识有着严重影响.激波辨识建立在流场计算结果之上, 因此误差越大, 对于激波的分辨也就越不容易.但是, 通过case-2的使用也从另一方面说明, 即使在流场计算结果非常差的情况下, 使用本文的激波辨识方法还是能够快速地将流场中存在的激波较为准确地辨识出来.
3 结论基于特征线理论辨识激波的方法是一种精确而有效的辨识方法.本文将其应用到激波装配技术中, 用于激波初始位置的确定.从给出的结果来看, 无论是定常激波还是非定常激波都能够快速有效地辨识出来, 为激波装配方法的应用提供了便利.本文使用的方法目前还只是在二维问题中得到使用和验证, 如何将该方法向三维中推广将是我们下一部分的研究内容.
致谢: 本文工作是在国家自然科学基金No. 9154117的资助下完成的, 在此表示感谢.| [1] |
Wu Z N, Xu Y Z, Wang W B, et al. Review of shock wave detection method in CFD post-processing[J]. Chinese Journal of Aeronautics, 2013, 26(3): 501-513. DOI:10.1016/j.cja.2013.05.001 |
| [2] |
Moretti G, Salas M D. Numerical analysis of viscous one-dimensional flows[J]. Journal of Computational Physics, 1970, 5(3): 487-506. DOI:10.1016/0021-9991(70)90076-8 |
| [3] |
Moretti G, Abbett M. A time-dependent computational method for blunt body flows[J]. AIAA Journal, 1966, 4(12): 2136-2141. DOI:10.2514/3.3867 |
| [4] |
Rawat P S, Zhong X L. On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-disturbance interactions[J]. Journal of Computational Physics, 2010, 229(19): 6744-6780. DOI:10.1016/j.jcp.2010.05.021 |
| [5] |
Prakash A, Parsons N, Wang X, et al. High-order shock-fitting methods for direct numerical simulation of hyper-sonic flow with chemical and thermal nonequilibrium[J]. Journal of Computational Physics, 2011, 230(23): 8474-8507. DOI:10.1016/j.jcp.2011.08.001 |
| [6] |
Moretti G. Thirty-six years of shock fitting[J]. Com-puters & Fluids, 2002, 31(4/7): 719-723. |
| [7] |
Paciorri R, Bonfiglioli A. A shock-fitting technique for 2D unstructured grids[J]. Computers & Fluids, 2009, 38(3): 715-726. |
| [8] |
Paciorri R, Bonfiglioli A. Shock interaction computations on unstructured, two-dimensional grids using a shock-fitting technique[J]. Journal of Computational Physics, 2011, 230(8): 3155-3177. DOI:10.1016/j.jcp.2011.01.018 |
| [9] |
Bonfiglioli A, Grottadaurea M, Paciorri R, et al. An unstructured, three-dimensional, shock-fitting solver for hypersonic flows[J]. Computers & Fluids, 2013, 73: 162-174. |
| [10] |
Bonfiglioli A, Paciorri R, Campoli L. Unsteady shock-fitting for unstructured grids[J]. International Journal for Numerical Methods in Fluids, 2016, 81(4): 245-261. DOI:10.1002/fld.v81.4 |
| [11] |
Salas M D. A shock-fitting primer[M]. Boca Raton: CRC Press, 2009, 327-369.
|
| [12] |
Liou S P, Mehlig S, Singh A, et al. An image analysis based approach to shock identification in CFD. AIAA 1995-0117, 1995. http://arc.aiaa.org/doi/abs/10.2514/6.1995-117
|
| [13] |
Lovely D, Haimes R. Shock detection from computational fluid dynamics results. AIAA 1999-3285, 1999. http://arc.aiaa.org/doi/pdf/10.2514/6.1999-3285
|
| [14] |
Darmofal D L. Hierarchal visualization of three-dimen-sional vortical flow calculations. Cambridge: Massachusetts Institute of Technology, 1991.
|
| [15] |
Ma K L, Van Rosendale J, Vermeer W. 3D shock wave visualization on unstructured grids. Proceedings of 1996 Symposium on Volume Visualization, San Franci-sco, CA: IEEE, 1999: 87-104.
|
| [16] |
Glimm J, Grove J W, Kang Y, et al. Statistical Riemann problems and a composition law for errors in numerical solutions of shock physics problems[J]. SIAM Journal on Scientific Computing, 2004, 26(2): 666-697. DOI:10.1137/S1064827503427534 |
| [17] |
Glimm J, Grove J W, Kang Y, et al. Errors in numerical solutions of spherically symmetric shock physics problems[J]. Contemporary Mathematics, 2005, 371: 163-179. DOI:10.1090/conm/371 |
| [18] |
Kanamori M, Suzuki K. Shock wave detection in two-dimensional flow based on the theory of characteristics from CFD data[J]. Journal of Computational Physics, 2011, 230(8): 3085-3092. DOI:10.1016/j.jcp.2011.01.007 |
| [19] |
刘君, 邹东阳, 徐春光. 基于非结构动网格的非定常激波装配法[J]. 空气动力学学报, 2015, 33(1): 10-16. Liu J, Zou D Y, Xu C G. An unsteady shock-fitting technique based on unstructured moving grids[J]. Acta Aerodynamica Sinica, 2015, 33(1): 10-16. (in Chinese) |
| [20] |
刘君, 邹东阳, 董海波. 动态间断装配法模拟斜激波壁面反射[J]. 航空学报, 2016, 37(3): 836-846. Liu J, Zou D Y, Dong H B. A moving discontinuity fitting technique to simulate shock waves impinged on a straight wall[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 836-846. (in Chinese) |
| [21] |
刘君, 邹东阳, 董海波. 基于非结构变形网格的间断装配法原理[J]. 气体物理, 2017, 2(1): 13-20. Liu J, Zou D Y, Dong H B. Principle of new disconti-nuity fitting technique based on unstructured moving grid[J]. Physics of Gases, 2017, 2(1): 13-20. (in Chinese) |
| [22] |
刘君, 徐春光, 白晓征. 有限体积法和非结构动网格[M]. 北京: 科学出版社, 2016, 22-106. Liu J, Xu C G, Bai X Z. Finite volume methods and unstructured dynamic grids technique[M]. Beijing: Scie-nce Press, 2016, 22-106. (in Chinese) |



