2. 上海船舶运输科学研究所,上海 200135;
3. 浙江大学能源工程学院化工机械研究所,浙江杭州 310027
2. Shanghai Ship and Shipping Research Institute, Shanghai 200135, China;
3. Institute of Process Equipment, College of Engineering, Zhejiang University, Hangzhou 310027, China
对于水中航行体而言, 摩擦阻力在总阻力中占有较大的比例, 例如在低速航行时摩擦阻力约占总阻力的70%~80%, 高速航行时占据40%~50%的份额[1], 如何减小固体壁面与流体介质间的摩擦阻力, 提高能源利用效率, 一直是国内外学者研究的热点.目前, 减小摩擦阻力的有效途径主要有:优化线型、降低航行体附近流体的黏性系数及改变边界层内湍流的结构等, 由此形成了柔性壁减阻、高分子减阻、涂层减阻、肋条减阻以及微气泡减阻等减阻方法.其中微气泡减阻方法对潜艇、鱼雷等水下航行器具有良好的应用前景.
微气泡减阻技术是最经济、无污染的减阻方法, 其基本作用原理是将气相介质引入固体表面, 在近壁区形成气液两相混合流, 降低壁面边界层附近的流体密度, 改变流体的流动状态, 将部分固液界面转变为无剪切应力的滑移气液界面, 从而降低固体壁面的摩擦阻力.根据微气泡生成方式的不同, 微气泡法又分为电解法、涂层法和喷气法, 这3种方法中喷气法减阻效果最为显著.
自20世纪70年代以来, 世界各国针对微气泡减阻技术的开发进行了大量的理论分析和实验研究, 取得了重要进展, 见文献[1-3].许多实验结果表明, 微气泡能够有效降低水中运动平板、回转体及平底船等所受的摩擦阻力, 可使湍流边界层摩擦阻力下降20%~80%[1-3]. McCormick等的实验表明通过电解法生成微气泡减阻效果较好, 在船身长度为0.91 m, 流动速度为2.6 m/s时获得的净减阻率近40%[4]. Bogdevich等早期的研究, 观察到减阻峰值出现在紧临喷气注入点的下游处; 然而, 再往下游, 摩阻恢复正常水平[5].从那时起, 学者们开始进行大量的实验以研究影响减阻的参数. Kodama等的实验沿展向测量减阻率, 结果表明均匀性很差, 从模型中心线的最大值沿展向递减, 在外边缘几乎为零.这一结果与气体从测试模型下表面逸出的概念吻合[6]. Hassan等研究了减阻机理, 阐明了边界层内微气泡的影响, 结果表明微泡浓度的增加有助于减小边界层Reynolds应力并抑制湍流的生成[7]. Jacob等还开展了直径小于100 μm微气泡减少摩擦阻力的实验.在他们的研究中测量微泡的浓度, 并用粒子图像测速技术观察微气泡的运动, 发现微气泡减少Reynolds应力, 并改变湍流边界层中的流动速度梯度[8]. Hara等应用图像分析技术研究了微气泡在槽道湍流减少摩擦阻力, 实验发现在垂直方向上振荡运动减少壁面附近的Reynolds应力, 并且这种影响对上游比下游更有作用[9]. Fukagata等通过理论方法研究表明近壁面Reynolds应力是影响摩阻预测和控制的关键[10]. Ferrante等用直接数值模拟(DNS)方法研究了Reynolds数对空间发展湍流边界层的影响[11].他们的报告指出, 动量厚度的增加挤压准流向涡结构朝向壁面, 而微气泡则使流向涡远离壁面.
我国也有一批学者和单位长期活跃在微气泡减阻技术的研究领域, 他们或者进行了微气泡减阻理论研究[12], 或者开展了微气泡控制湍流边界层减阻的方法研究[13], 或者从两相流体相互作用的角度研究了微气泡减阻的规律和机理[14].这些实验或计算的速度都较低, 在本实验研究中实现高Reynolds数大于106(基于自由流速度和模型的长度), 用应变天平测量了摩擦阻力, 且应用高速摄影可视化技术观察近壁面微气泡的流动结构.实验发现微气泡浓度(即气体流量)在湍流边界层对摩擦阻力减少的影响占主导地位.
1 实验装置和方法实验是在上海船舶运输科学研究所的空泡水洞进行的.该水洞的工作段是方形截面, 尺寸为0.6 m×0.6 m, 工作段长2.6 m.最大水流速度可达12 m/s, 水流速度不均匀性小于1%, 水流速度不稳定性小于1%.在实验测试中工作段的静压力保持大气压力.喷气用的空气是由一台空气压缩机供给的.
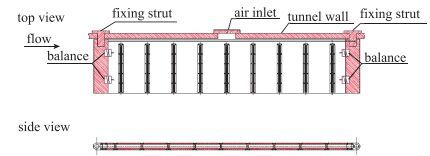
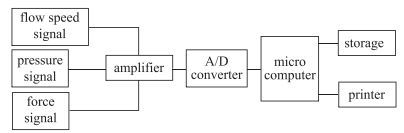
仿照空气中微吹气减阻的思想, 设计加工了一个多孔喷气平板模型, 研究水中微喷气对阻力的影响.将光滑的铝制平板水平放置在水洞的实验段, 该平板材料是LY12铝合金.为最大限度地提高其平整度, 并尽量减少扭曲或弯曲对流动的影响, 平板前后两端由两个半圆柱形整流支柱支持, 实验模型在水洞中的安装照片如图 1所示.平板的长度为1 510 mm, 宽度为305 mm, 厚度为40 mm.在平板的上下表面顺着来流的方向各布置9个喷气孔槽, 作为缓冲空腔以保证喷气均匀, 每个槽上方的盖板各有25个直径为1 mm的小孔, 气体通过小孔排放到边界层. 图 2给出了实验模型的示意图, 4个单分量阻力应变天平分别安装在X/L=0.053和X/L=0.947(X指距平板前缘的距离, L为平板的长度)处, 用于测量平板的摩擦阻力, 具体位置见图 2.应变天平的精度为0.2%, 首先将天平输出的电信号放大并进行低通滤波, 然后用LabVIEW软件进行数据采集分析.实时数据采集系统如图 3所示.

|
| 图 1 实验模型在水洞中的安装照片 Fig.1 Photo of experimental model in water tunnel |
|
| 图 2 平板模型示意图 Fig.2 Schematic diagram of flat plate model |
|
| 图 3 数据采集框图 Fig.3 Flowchart of data sampling |
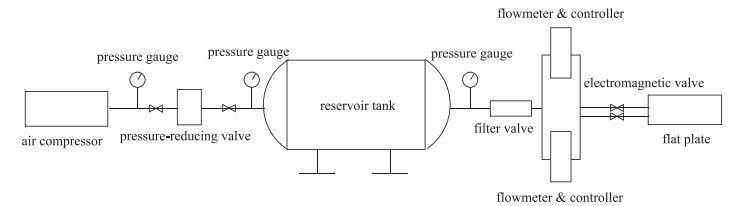
图 4给出了喷气系统控制组成示意图.压缩机产生的气体经减压阀储存在储气罐, 然后通过过滤减压阀和流量计, 最后通过电磁阀接在18个通气管上.电磁阀用来控制各个管路的开合, 通气管为直径为2.5 mm的塑料管.
|
| 图 4 喷气系统组成图 Fig.4 Set-up of air-jet system |
为了阐明微气泡减阻机理, 采用流动可视化技术观察平板边界层内的微气泡分布规律, 研究微气泡的微观行为.实验中我们用高分辨率的高速摄像机捕捉气泡图像.可视化高速摄像机布置如图 5所示.该装置包括一个高速摄像机(NAC Memrecam HX-4)、微距镜头(60 mm, Nikon AF Nikkor)和一个500 W冷光照明灯.以每秒6 000帧的速率拍摄气泡图像, 像素的分辨率为1 280×480.

|
| 图 5 高速摄影系统组成图 Fig.5 High speed camera set-up |
众所周知, 区分层流与湍流的关键参数是流体的Reynolds数(Re∞=ρUL/μ), 平板边界层的临界Reynolds数一般认为在3×105~3×106区间, 当Re < 3×105, 该流动被认为是层流, 而在Re > 3×106时, 一般使用湍流边界层理论. Re在3×105~3×106范围被认为是混合边界层, 平板的阻力可以根据边界层理论[15]预测:
层流阻力系数: Cfl=1.328(μ/ρUL)1/2
湍流阻力系数: Cft=0.074(μ/ρUL)1/2
其中, ρ和μ分别代表水的密度和动力黏度.
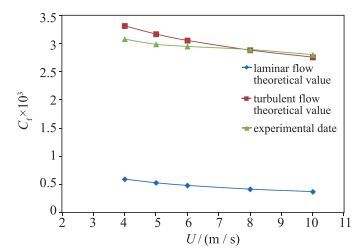
图 6给出了无微气泡时平板阻力系数的实验数据与层流和湍流理论值对比曲线, 可以看出, 实验数据与湍流理论值吻合得较好, 尤其在水速U>6 m/s时实验值与理论值几乎重合.一方面表明, 实验测试的流动已经是湍流; 另一方面, 也证明实验中测量阻力的方法是有效的.
|
| 图 6 不同水速平板阻力系数变化曲线 Fig.6 Skin friction coefficients of flat plate versus flow velocities |
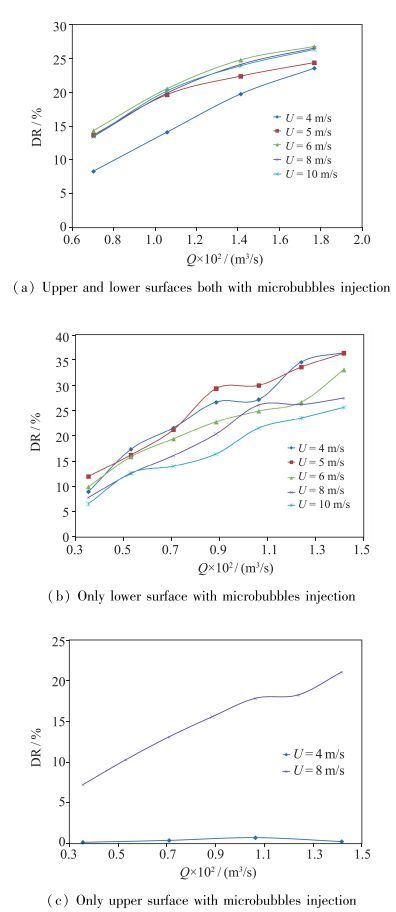
实验中, 在每个水流速度下改变喷气量大小观测阻力变化情况. 图 7对比了不同水速喷气前后阻力的减少, 减阻率定义如下:
|
| 图 7 微气泡减阻率比较曲线 Fig.7 Comparisons of drag reduction ratio with microbubbles |
| $\text{DR}=(\frac{{{C}_{\text{f-nobubble}}}-{{C}_{\text{f-bubble}}}}{{{C}_{\text{f-nobubble}}}})\times 100\%$ |
图 7(a)给出了气体体积流量Q=0.007, 0.010 6, 0.014, 0.017 m3/s, 水速U=4, 5, 6, 8, 10 m/s, 上下表面同时通气时减阻率变化曲线, 可以看出, 相同通气量, 随着水速的增加, 减阻率先增加然后降低; 但随气体流量的增加, 减阻率增加. 图 7(b)给出了气体体积流量Q=0.003 5, 0.005 3, 0.007, 0.008 8, 0.010 6, 0.012 4, 0.014 m3/s, 水速U=4, 5, 6, 8, 10 m/s, 仅下表面通气时减阻率变化曲线, 可以看出最大减阻率出现在水速U=4~5 m/s, Q=0.014 m3/s区间, 大约为36%.随着流速的进一步增加, 减阻率逐渐降低.主要是因为随流速的增加, 边界层的厚度变薄, 造成边界层中的微气泡数量减少, 从而导致减阻率降低; 同样也看到相同现象, 减阻率随空气流量的增加而增加. 图 7(c)给出了气体体积流量Q=0.003 5, 0.005 3, 0.007, 0.008 8, 0.010 6, 0.012 4, 0.014 m3/s, 水速U=4, 8 m/s, 仅上表面通气时减阻率变化曲线, 可以看出对于水速U=4 m/s工况, 减阻率几乎为零(实验只做了Q=0.003 5, 0.007, 0.010 6, 0.014 m3/s这4个工况), 明显与上表面的规律不同.这主要因为浮力迫使气泡贴近下表面, 并远离上表面.从图 8可以明显看出这种现象. 图 8显示了水速U=4 m/s, 流量Q=0.014 m3/s, 普通相机拍摄的一个典型气泡流态.还须特别指出气泡云的外形是不依赖于水流速度的.

|
| 图 8 典型气泡流态(U=4 m/s, Q=0.014 m3/s) Fig.8 Typical bubbly flow image (U=4 m/s, Q=0.014 m3/s) |
图 9~10显示了在本实验中高速摄像机所捕获的典型气泡图像, 这些确定壁面附近气泡特征的图像是从距平板前缘x=325 mm处拍摄的. 图 9给出了只有下表面喷气水速U=4 m/s, 气体体积流量Q=0.003 5, 0.007, 0.010 6, 0.014 m3/s的气泡图像, 可以看出, 随着空气流量的进一步增加, 在浮力作用下, 下表面逐渐形成一层气膜.在近壁面流动气泡的大小和形状表明, 随着气泡向下游移动, 气泡分裂不占主导地位, 反而气泡合并是更普遍的现象.当浮力迫使大量的气泡接近表面, 摩阻明显减少.

|
| 图 9 典型气泡图像(下表面U=4 m/s) Fig.9 Typical bubble images (lower surfaces U=4 m/s) |

|
| 图 10 典型气泡图像(上表面U=4 m/s) Fig.10 Typical bubble images (upper surfaces U=4 m/s) |
图 10给出了只有上表面喷气水速U=4 m/s, 气体体积流量Q=0.003 5, 0.007, 0.010 6, 0.014 m3/s的气泡图像, 从图像中观察到浮力使气泡远离固体表面, 而且随着气体流量的增加, 气泡尺寸增大.
3 结论开展了将气体引射到平板湍流边界层来实现减小摩擦阻力的实验, 测量了平板表面的剪切应力, 并观察了近壁面微气泡的特性, 得出了如下结论:
(1) 实验用天平测量了微气泡减阻的效果, 证实了微气泡在高Reynolds数(Re=106)流动中减少摩擦阻力作用是有效的.
(2) 摩擦阻力减阻率随着气体流量的增加而逐渐增加.
(3) 随着水流速度增加, 对于上下表面同时通气的工况, 减阻率先增大后减小; 仅下表面通气减阻率逐渐降低; 而对于上表面通气减阻率是逐渐增加的.
(4) 实验中最大减阻率出现在下表面通气, 水速U=4~5 m/s, 气体流量Q=0.014 m3/s区域, 大约为36%.
(5) 对于下表面, 随着气体流量的增加, 在浮力作用下边界层逐渐形成空气膜.通过观察高速摄像机拍摄的近壁流气泡的大小和形状, 随着气泡向下游移动, 气泡分裂不占主导地位, 反而气泡合并是更普遍的现象.当浮力迫使大量的气泡接近表面, 摩阻明显减少.
(6) 对于上表面, 高速摄像机观察到的浮力迫使气泡远离固壁表面; 随着气体流量的增加, 气泡尺寸增大.
| [1] | Madavan N K, Deutsch S, Merkle C L. Reduction of turbulent skin friction by microbubbles[J]. Physics of Fluids, 1984, 27(2): 356-363. DOI:10.1063/1.864620 |
| [2] | Guin M M, Kato H, Yamaguchi H, et al. Reduction of skin friction by microbubbles and its relation with near-wall bubble concentration in a channel[J]. Journal of Marine Science and Technology, 1996, 1(5): 241-254. DOI:10.1007/BF02390723 |
| [3] | Kato H, Miura K, Yamaguchi H, et al. Experimental study on microbubble ejection method for frictional drag reduction[J]. Journal of Marine Science and Technology, 1998, 3(3): 122-129. DOI:10.1007/BF02492919 |
| [4] | McCormick M E, Bhattacharyya R. Drag reduction of a submersible hull by electrolysis[J]. Naval Engineers Journal, 1973, 85(2): 11-16. DOI:10.1111/nej.1973.85.issue-2 |
| [5] | Bogdevich V G, Malyuga A R. The distribution of skin friction in a turbulent boundary layer of water beyond the location of gas injection[J]. Investigations of Boundary Layer Control, 1976: 62 |
| [6] | Kodama Y, Kakugawa A, Takahashi T, et al. Microbub-bles:drag reduction mechanism and applicability toships[C]. 24th Symposium on Naval Hydrodynamics, Fukuoka, 2002. |
| [7] | Hassan Y A, Gutierrez-Torres C C. Investigation of drag reduction mechanism by microbubble injection within a channel boundary layer using particle tracking velocimetry[J]. Nuclear Engineering and Technology, 2006, 38(8): 763-778. |
| [8] | Jacob B, Olivieri A, Miozzi M, et al. Drag reduction by microbubbles in a turbulent boundary layer[J]. Physics of Fluids, 2010, 22(11): 115104 DOI:10.1063/1.3492463 |
| [9] | Hara K I, Suzuki T, Yamamoto F. Image analysisapplied to study on frictional-drag reduction by electrolytic microbubbles in a turbulent channel flow[J]. Experiments in Fluids, 2011, 50(3): 715-727. DOI:10.1007/s00348-010-0970-5 |
| [10] | Fukagata K, Iwamoto K, Kasagi N. Contribution of Rey-nolds stress distribution to the skin friction in wall-bounded flows[J]. Physics of Fluids, 2002, 14(11): 73-76. DOI:10.1063/1.1516779 |
| [11] | Ferrante A, Elghobashi S. Reynolds number effect on drag reduction in a microbubble-laden spatially developingturbulent boundary layer[J]. Journal of Fluid Mechanics, 2005, 543: 93-106. DOI:10.1017/S0022112005006440 |
| [12] |
梁志勇. 微气泡减少平板摩擦阻力的数值模拟[J].
船舶力学, 2002, 6(4): 14-23. Liang Z Y. Numerical simulation of the friction resistance of a flat plate by micro-bubbles[J]. Journal of Ship Mechanics, 2002, 6(4): 14-23. |
| [13] |
张木, 谭俊杰, 何快. 气泡减阻实验研究[J].
船海工程, 2009, 4: 13-16. Zhang M, Tan J J, He K. Experiment study on drag reduction with air bubble[J]. Ship & Ocean Engineering, 2009, 4: 13-16. DOI:10.3963/j.issn.1671-7953.2009.z1.004 |
| [14] |
傅慧萍. 平板微气泡减阻数值模拟及影响因素分析[J].
哈尔滨工程大学学报, 2015, 36(10): 1297-1301. Fu H P. Numerical simulation of microbubble drag reduction in a plate and factors influencing its practicality process[J]. Journal of Harbin Engineering University, 2015, 36(10): 1297-1301. |
| [15] | Schlichting H, Gersten K, Krause E, et al. Boundary-layer theory[M]. 8th Edition. New York:Springer, 2000. |



