2. 香港理工大学,中国香港 999077
2. The Hong Kong Polytechnic University, Hong Kong 999077, China
长期以来, 层流向湍流的转捩一直是流体力学中最重要的前沿问题之一.从理论研究角度来说, 转捩过程是经典物理学遗留的最具挑战性的问题, 它是从简单分层稳定状态到复杂混沌湍流状态的过程, 是一个多因素耦合影响的强非线性复杂流动物理现象, 转捩问题与湍流问题一起被称为“百年(或世纪)难题”[1-2].另一方面, 边界层转捩预测与控制在航空航天领域具有广泛的应用背景, 这主要是因为层流流动和湍流流动在摩擦阻力、噪声、热交换和掺混等方面有巨大差别, 以空天飞机为例, 表面保持层流时有效载荷与总质之比是全湍流时的2倍以上[3].同样值得关注的是, 边界层流态对高超飞行器气动热环境的影响显著, 湍流区气动加热远大于层流区, 而热流峰值一般出现在流动转捩区, 高超声速时可达层流热载荷的3倍, 从而须配置额外的热防护系统、主动冷却技术或者进行弹道调整, 造成高超飞行器成本与重量增加[4].因此, 为降低飞行阻力, 增加有效载荷比, 如何有效抑制转捩成为国内外高超声速领域的研究热点.一般来说, 高超声速飞行器使用尖前缘和尽量光滑的蒙皮表面可以抑制由粗糙元引起的旁路转捩以及横流不稳定性, 但无法控制由Mack第1模态/第2模态诱发的转捩[5-6].而且由于高超声速飞行器的冷壁效应, Mack第1模态通常会被抑制, 但会激发第2模态.因此对高超声速飞行器自然转捩抑制的研究, 主要集中在如何更为有效地抑制边界层内Mack第2模态的发展[7].
鉴于高超声速飞行器严峻的气动力热环境, 转捩主动控制技术(例如吹吸气、激励器、微机电控制等)很难投入实际工程应用, 而被动控制技术(声学超表面、波状外形等)由于不需要附加的机构设置, 技术简单, 是国内外研究热点.其中, 声学超表面在不影响主流的前提下, 通过自身的声学特性设计, 能够有效抑制Mack第2模态的发展, 是最有可能投入工程实践的技术之一.微型多孔覆盖层[8-12]是超表面的一种具体结构形式, 已经在高超风洞实验中证实了能够显著延迟转捩, 并作为技术储备授权于美国Boeing公司(美国专利号588471, 1999年).微型多孔覆盖层是在壁面加工一系列远小于扰动波长的缝/孔, 通过孔内黏性来耗散吸收扰动波的能量, 从而达到抑制Mack第2模态发展的目的.然而需要注意的是, 声学超表面的特性不仅仅局限于吸声性能, 还具有诸多与常规材料不同的声学特性, 例如零阻抗, 各向异性阻抗, 可控反射/折射方向等.
本文首先推导超表面微结构-声场-流场耦合理论模型, 计及声波高阶衍射模态, 提高对声场频率的预测精度, 并针对超表面的吸声特性与阻抗特性, 分别进行优化设计, 通过对Mach 6高超声速平板流动进行数值模拟, 证实超表面对Mack第2模态的抑制效果.
1 理论模型国外对微结构-声场-流场耦合的理论模型进行了一定程度的研究. 2001年, Fedorov等[11]推导了细长孔的声学特性, 给出单孔对流场和声场的作用模型:v′=Ap′, 其中,v′为壁面法向脉动速度, p′为壁面声场压力, A为导纳,并由电力线理论类比给出. 2005年, Maslov[13]指出当微孔直径与分子自由程同量级时, 必须考虑稀薄气体效应, 并得出当Knudsen数Kn=0.588时, 扰动模态的增长率有15%~20%的降低; 同年, Kozlov等[14]给出了不同截面形状的微孔导纳表达式.需要注意的是, 上述理论模型基于单孔声学特性推导, 并未计及开孔处实体壁面引起的高阶模态散射, 也未计及孔与孔之间的干扰, 从而降低了模型的预测精度. 2010年, Brès等[15]指出这种简化导致预测的吸声频率发生偏移, 他们随后(2013年)建议使用壁面滑移速度来模化孔与孔之间的干扰, 但同时指出模型中存在过多的拟合参数, 须进一步改进[16].与以往研究不同, 本文以超表面微结构周期性单元为研究对象, 计及反射波的高阶衍射模态, 从而考虑到孔与孔的干扰作用, 提高对声场频率的预测精度.
1.1 超表面微结构如图 1所示, 本文研究的超表面由简单的槽道(二维周期孔)组成, 孔深度为H, 孔宽度为2b, 微结构的周期为s.由上述参数组合而成的无量纲参数:孔隙率ϕ=2b/s,宽深比为Ar=2b/H.
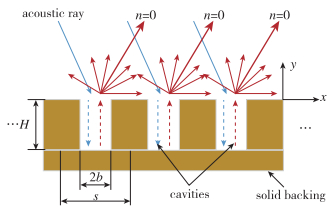
|
| 图 1 高阶散射模态示意图[17] Fig.1 Schematic drawing of reflection of acoustic waves from equally spaced two-dimensional cavities |
平面声波入射到此类超表面产生的声场环境与阻抗特性可通过平面波展开法获得, 具体推导过程可参考文献[17], 第n阶衍射波的反射系数如下所示
| $ {{R}_{n}}={{\delta }_{n, 0}}+\frac{2j\tan ({{k}_{\text{c}}}H)\phi \frac{{{\rho }_{\text{w}}}}{{\tilde{\rho }}}{{S}_{n}}\frac{{{k}_{\text{c}}}}{k_{y}^{\left( n \right)}}}{1-j\tan ({{k}_{\text{c}}}H)\phi \frac{{{\rho }_{\text{w}}}}{{\tilde{\rho }}}\sum\limits_{m=-\infty }^{+\infty }{\frac{{{k}_{\text{c}}}}{k_{y}^{\left( m \right)}}}S_{m}^{2}} $ |
其中, δn, 0为Kronecker函数, 当n=0时δn, 0=1;当n≠0时δn, 0=0. Sn为n阶衍射模态与孔内主导模态的重叠积分
| $ {{S}_{n}}={{(2b)}^{-1}}\int_{-b}^{b}{{{\text{e}}^{jk_{x}^{(n)}x}}\text{d}x}=\text{sinc(}k_{x}^{(n)}b\text{)} $ |
其中, kx(n)=kx+2πn/s, ky(n)=[k02-(kx(n))2]1/2, n∈Z. k0=ω/cw为波数, ω为圆频率, kx为x方向动量.动力等效密度
| $ \begin{align} & \tilde{\rho }={{{\rho }_{\text{w}}}}/{{{\psi }_{\text{v}}}}\;,\tilde{C}=\frac{\gamma -(\gamma -1){{\psi }_{t}}}{{{\rho }_{\text{w}}}c_{\text{w}}^{2}} \\ & k_{\text{c}}^{2}={{\omega }^{2}}\tilde{\rho }\tilde{C}=k_{0}^{2}\frac{\gamma -(\gamma -1){{\psi }_{t}}}{{{\psi }_{\text{v}}}} \end{align} $ |
其中, ρw和cw分别为壁面处流场密度与声速, 其中,ψi=1-tan(kib)/kib.
| $ k_{i}^{\text{2}}=\left\{ \begin{align} &k_{{\rm{v}}}^{\text{2}}=j\omega \frac{{{\rho }_{\text{w}}}}{\mu }, \text{ }\ \ \ \ \ \ \ 黏性波数\text{ } \\ &k_{{\rm{t}}}^{\text{2}}=j\omega \frac{{{\rho }_{\text{w}}}{{C}_{{\rm{p}}}}}{\kappa }, \text{ }\ 热力学波数 \\ \end{align} \right.\ $ |
其中,下标i可分别代表黏性相关项(下标v)或者热传导相关项(下标t).假设孔周期远小于入射声波波长s < < λacs, 同时假定Mack第2模态为垂直入射[15], 该超表面的特征阻抗可推导为
| $ \begin{align} &Z={{\left. \frac{p}{v} \right|}_{y=0}}=\frac{{{s}^{-1}}\int_{-s/2}^{s/2}{{{\left. \left( {{p}_{{\rm{i}}}}+\sum\limits_{n=-\infty }^{+\infty }{p_{r}^{(n)}} \right) \right|}_{y=0}}\text{d}x}}{{{s}^{-1}}\int_{-s/2}^{s/2}{{{\left. \left( {{v}_{{\rm{i}}}}+\sum\limits_{n=-\infty }^{+\infty }{v_{r}^{(n)}} \right) \right|}_{y=0}}\text{d}x}}\ \\ &\ =\frac{\int_{-s/2}^{s/2}{\left( 1+\sum\limits_{n=-\infty }^{+\infty }{{{R}_{n}}{{\text{e}}^{j\frac{2\pi n}{s}x}}} \right)\text{d}x}}{\int_{-s/2}^{s/2}{\left(-\frac{{{k}_{0}}}{{{\rho }_{\text{w}}}\omega }+\sum\limits_{n=-\infty }^{+\infty }{\frac{\sqrt{k_{0}^{2}-{{\left( \frac{2\pi n}{d} \right)}^{2}}}}{{{\rho }_{\text{w}}}\omega }{{R}_{n}}{{\text{e}}^{j\frac{2\pi n}{s}x}}} \right)\text{d}x}} \\ &=\frac{\int_{-s/2}^{s/2}{({{R}_{0}}+1)\text{d}x}}{\frac{{{k}_{0}}}{{{\rho }_{\text{w}}}\omega }\int_{-s/2}^{s/2}{({{R}_{0}}-1)\text{d}x}}={{\rho }_{\text{w}}}{{c}_{\text{w}}}\frac{{{R}_{0}}+1}{{{R}_{0}}-1}\ \end{align} $ | (1) |
其中, 下标i代表入射波,r代表反射波,R0为镜面反射模态
| $ {{R}_{0}}=1+\frac{2j\tan ({{k}_{\text{c}}}H)\phi \frac{{{\rho }_{\text{w}}}}{{\tilde{\rho }}}\frac{{{k}_{\text{c}}}}{{{k}_{0}}}}{1-j\tan ({{k}_{\text{c}}}H)\phi \frac{{{\rho }_{\text{w}}}}{{\tilde{\rho }}}\sum\limits_{m=-\infty }^{+\infty }{\frac{{{k}_{\text{c}}}}{\sqrt{k_{0}^{2}-{{\left( \frac{2\text{ }\pi\text{ }m}{s} \right)}^{2}}}}}S_{m}^{2}} $ | (2) |
相应地, 无量纲化的Z*为
| $ {{Z}^{*}}=\rho _{\text{w}}^{*}c_{\text{w}}^{*}\frac{{{R}_{0}}+1}{{{R}_{0}}-1} $ |
其中, ρw*和cw*分别由远场密度ρ∞和声速c∞进行无量纲处理.
1.3 预测性能如图 2所示, 将本文提出的模型与Fedorov模型[11, 14]预测的反射系数和COMSOL有限元结果进行对比[17], 可以发现, 本文提出的模型与COMSOL结构吻合较好, 而Fedorov模型由于未计及高阶衍射模态, 预测的反射系数在高频范围内出现漂移.

|
| 图 2 超表面微结构不同参数组合下理论模型预测的反射系数对比, facs=fH/cw为无量纲的入射频率 Fig.2 Reflection coefficient amplitudes at normal incidence, facs=fH/cw is the normalized incidence-wave frequency |
以往对于微型多孔覆盖层的研究, 主要利用微孔内黏性耗散Mack第2模态扰动波, 即利用超表面的吸声特性.基于方程(2), 本文使用数值方法优化超表面微结构参数, 使得|R0|最小.优化空间:loop 1:0.2≤ϕ≤0.8, loop 2:0.06 ≤Ar≤ 0.3, loop 3:0.1 < facs < min(ϕ/Ar, 1.5), 参数范围考虑了工程可实现性[16]以及模型的精度极限(facs < ϕ/Ar).
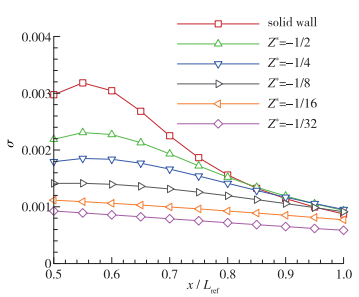
2.2 阻抗型超表面与以往研究不同, 由方程(1)可知, 壁面处Mack第2模态扰动强度p=Z·v.直观上, 若Z→0, 则p→0, 即此时超表面并无耗散作用, 只是入射声波与反射声波在该处的相位相反, 强度互相叠加为0, 从而也能达到抑制壁面处Mack第2模态的作用.为验证该设想, 使用线性稳定性分析(linear stability theory, LST)方法直接对不同阻抗值(常数)的超表面作用效果进行分析.验证算例为图 3所示的高超声速二维平板边界层流动[17], 来流条件与扰动添加方法参考文献[17-18].如图 4所示, 随着阻抗值的降低, Mack第2模态的增长率得到明显抑制.

|
| 图 3 超表面对高超声速边界层稳定性的影响(超表面安装在平板后半段) Fig.3 Schematic drawing of stabilization of hypersonic boundary-layer flow by acoustic metasurface with constant effective impedances |
|
| 图 4 不同阻抗值对Mack扰动模态增长率的影响(Lref=0.2 m为平板长度) Fig.4 Growth rate distributions of Mack second mode by acoustic metasurface with constant effective impedances (Lref=0.2 m is the length of the plate) |
使用2.1节所述的优化方法对图 1所示的超表面进行优化设计, 分别获取吸声型超表面(优化目标为反射系数最小)与阻抗型超表面(优化目标为阻抗最小).优化结果如表 1~2所示, 可以发现, 阻抗型超表面反射系数要远大于吸声型超表面.
| 下载CSV 表 1 不同优化目标下超表面微结构参数 Tab.1 Optimized shape parameters for absorptive and impedance metasurfaces |
| 下载CSV 表 2 不同优化目标下超表面阻抗值和反射系数 Tab.2 Optimized values of reflection coefficient and impedance for absorptive and impedance metasurfaces |
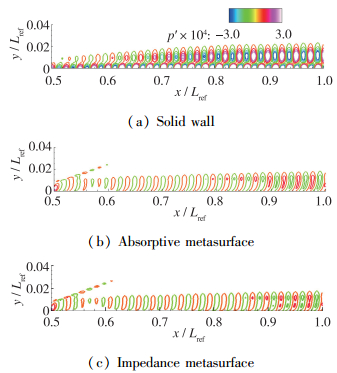
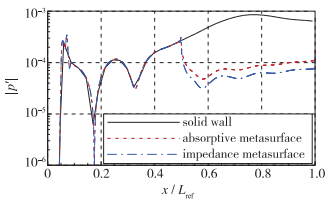
将上述优化设计的两种超表面用于图 4算例中, 使用数值模拟方法[18]获得流场脉动压力分布, 如图 5所示.可以看到两种超表面都能够抑制扰动强度, 实现抑制Mack第2模态的目的.对比图 5(b)和(c), 扰动强度在阻抗型超表面上更小一些. 图 6对比了两种超表面上脉动压力的幅值, 可以看到阻抗型超表面对扰动的抑制效果更佳.
|
| 图 5 压力脉动云图(p′以ρu∞2进行无量纲) Fig.5 Comparisons of fluctuating pressure contour with different metasurfaces(p′ was normalized by ρu∞2) |
|
| 图 6 壁面压力幅值对比(p′以ρu∞2进行无量纲) Fig.6 Amplitude distributions of pressure perturbation along the wall(p′ was normalized by ρu∞2) |
本文提出一种计及高阶衍射模态的声学超表面理论模型, 基于该模型提出超表面优化设计方法, 并揭示阻抗型超表面对Mack第2模态的抑制效果要优于以往研究的吸声型超表面.主要结论如下:
(1) 通过在理论模型中计及高阶衍射模态, 可提高对反射频率的预测精度, 并能够准确捕捉到相邻结构干扰产生的耦合模态.
(2) 通过优化超表面微结构形状参数, 可获得吸声型超表面与阻抗型超表面.研究表明, 阻抗型超表面通过调制壁面处声波相位, 可获得比吸声型超表面更优的抑制效果.
致谢 感谢国家自然科学基金(11872116)的资助,感谢中国科学院力学研究所李新亮研究员提供高精度数值模拟程序以及相关建议.| [1] |
陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. Chen J Q, Tu G H, Zhang Y F, et al. Hypersnonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. DOI:10.7638/kqdlxxb-2017.0030 (in Chinese) |
| [2] |
沈清, 杨武兵, 庄逢甘. 航天飞行器中的湍流问题[J]. 现代防御技术, 2012, 40(1): 21-25. Shen Q, Yang W B, Zhuang F G. Turbulence of Aeros-pacecraft[J]. Modern Defence Technology, 2012, 40(1): 21-25. DOI:10.3969/j.issn.1009-086x.2012.01.005 (in Chinese) |
| [3] |
李锋, 解少飞, 毕志献, 等. 高超声速飞行器中若干气动难题的实验研究[J]. 现代防御技术, 2014, 42(5): 1-7. Li F, Xie S F, Bi Z X, et al. Experimental study of several on aerodynamic problems on hypersonic vehicles[J]. Modern Defence Technology, 2014, 42(5): 1-7. DOI:10.3969/j.issn.1009-086x.2014.05.001 (in Chinese) |
| [4] |
Bertin J J, Cummings R M. Critical hypersonic aerothermodynamic phenomena[J]. Annual Review of Fluid Mechanics, 2006, 38: 129-157. DOI:10.1146/annurev.fluid.38.050304.092041 |
| [5] |
Schneider S P. Hypersonic laminar-turbulent transition on circular cones and scramjet forebodies[J]. Progress in Aerospace Sciences, 2004, 40(1/2): 1-50. |
| [6] |
Weihs H, Longo J, Turner J. The sharp edge flight experiment SHEFEX Ⅱ, a mission overview and status[C]. Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, International Space Planes and Hypersonic Systems and Technologies Conferences, Dayton: AIAA, 2008.
|
| [7] |
Mack L M. Boundary-layer linear stability theory[R]. Special course on stability and transition of laminar flow advisory group for aerospace research and development, AGARD Report No.709, 1984.
|
| [8] |
Fedorov A. Transition and stability of high-speed boun-dary layers[J]. Annual Review of Fluid Mechanics, 2011, 43: 79-95. DOI:10.1146/annurev-fluid-122109-160750 |
| [9] |
Zhong X L, Wang X W. Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers[J]. Annual Review of Fluid Mechanics, 2012, 44(1): 527-561. DOI:10.1146/annurev-fluid-120710-101208 |
| [10] |
Fedorov A V. Prediction and control of laminar-turbulent transition in high-speed boundary-layer flows[J]. Procedia IUTAM, 2015, 14: 3-14. DOI:10.1016/j.piutam.2015.03.017 |
| [11] |
Fedorov A V, Malmuth N D, Rasheed A, et al. Stabilization of hypersonic boundary layers by porous coatings[J]. AIAA Journal, 2001, 39(4): 605-610. DOI:10.2514/2.1382 |
| [12] |
Rasheed A, Hornung H G, Fedorov A V, et al. Experiments on passive hypervelocity boundary-layer control using an ultrasonically absorptive surface[J]. AIAA Journal, 2002, 40(3): 481-489. DOI:10.2514/2.1671 |
| [13] |
Maslov A A. Experimental and theoretical studies of hypersonic laminar flow control using ultrasonically absorptive coatings (UAC)[R]. Report ISTC, 2003, 2172-2001.
|
| [14] |
Kozlov V F, Fedorov A V, Malmuth N D. Acoustic properties of rarefied gases inside pores of simple geometries[J]. The Journal of the Acoustical Society of America, 2005, 117(6): 3402-3412. DOI:10.1121/1.1893428 |
| [15] |
Brès G A, Colonius T, Fedorov A V. Acoustic properties of porous coatings for hypersonic boundary-layer control[J]. AIAA Journal, 2010, 48(2): 267-274. DOI:10.2514/1.40811 |
| [16] |
Brès G A, Inkman M, Colonius T, et al. Second-mode attenuation and cancellation by porous coatings in a high-speed boundary layer[J]. Journal of Fluid Mechanics, 2013, 726: 312-337. DOI:10.1017/jfm.2013.206 |
| [17] |
Zhao R, Liu T, Wen C Y, et al. Theoretical modeling and optimization of porous coating for hypersonic laminar flow control[J]. AIAA Journal, 2018, 56(8): 1-5. |
| [18] |
Zhao R, Wen C Y, Tian X D, et al. Numerical simulation of local wall heating and cooling effect on the stability of a hypersonic boundary layer[J]. International Journal of Heat and Mass Transfer, 2018, 121: 986-998. DOI:10.1016/j.ijheatmasstransfer.2018.01.054 |



