目标发出的光束受到高速飞行器光学接收窗口附近的气动光学效应干扰, 使得光的传播方向和相位发生随机抖动, 引起目标图像模糊、偏移以及抖动, 给目标识别和成像制导带来诸多麻烦[1-4].
研究气动光学效应的影响因素, 对实施气动光学效应预测与校正的意义重大, 已经得到诸多学者的认同. Fitzgerald等[5]在AEDC的试验条件下, 对弱压缩模型进行了相关试验研究, 得出了可以预测改变高度、Mach数等飞行条件时的比例关系式; Gilbert[6]基于KC-135模型的试验数据, 提出光程差(optical path difference, OPD)空间均方根值(spatial root-mean-square of OPD, OPDrms)与动压和δ4/3成线性关系; 1985年, Craig等[7]同样基于KC-135模型, 阐述了气动光学的相似准则, 其中也提到小光学孔径会有利于Strehl比(strehl ratio, SR)更大; Masson等[8]认为, OPDrms应该用ρeMe2来标度, 其中e表示边界层边缘, 通过对Gilbert的数据进行最小二乘拟合, 获取了一个经验关系式.
2009年, Wyckham等[9]对高超声速及跨声速湍流边界层气动光学OPDrms的相似准则新方法进行了探讨推导, 很有借鉴意义; 2014年, Gordeyev等[10]对亚声速湍流边界层的气动光学效应进行了深入的实验研究, 并且分析影响OPDrms的诸多因素, 提出了可以与Wyckham的OPDrms相似律统一的计算公式, 并对其进行了实验验证.
目前, 随着相关项目研究的不断推进, 如何在高Reynolds数条件下研究Reynolds数对气动光学效应的影响成为重要命题.本文设计的变Reynolds数气动光学效应实验平台, 模拟单位Reynolds数可以在7.2×106~2.2×108 m-1范围内变化.利用背景纹影(background oriented schlieren, BOS)技术进行波前测量, 搭配双腔Nd-YAG激光器以及跨帧CCD, 通过同步控制器实现6 ns的时间分辨能力, 从而实现流场波前信息瞬态测量, 测量的空间分辨率达到0.082 mm/pixel.通过对近场条件下利用BOS测量波前方法进行适应性改进, 以便满足实验测试要求.通过对测试图像的随机点密度进行检测, 发现包含随机点数目在10个以上的查问区数量占到查问区总数的97.2%, 验证了测试光路采集的随机点阵图像用于互相关计算的可用性.在相同光路条件下, 利用此系统测量了标准平凸透镜的波前数据, 实验测量结果与理论计算结果的误差在±4%以内, 验证了测量光路与近场改进的正确性.最后对9个不同Reynolds数下的超声速气膜的气动光学效应进行测量, 并对结果进行了相关分析.
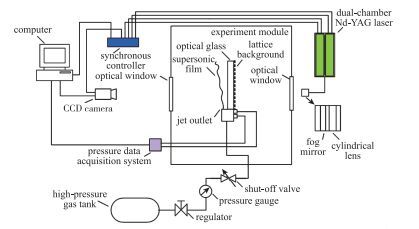
1 实验装置与测试技术研究 1.1 变Reynolds数气动光学效应实验平台设计图 1为变Reynolds数气动光学效应实验平台示意图, 设计此实验平台的原因主要在于普通风洞完成高Reynolds数下的气动光学实验比较困难, 并且Reynolds数的变化范围较小, 较难模拟真实飞行状态下的Reynolds数.变Reynolds数设计的依据来源于混合层压力匹配的概念, 易仕和等[11]的研究结果证明, 通过保持环境压强与喷流出口静压相等, 可以有效地抑制出口处波系结构, 减小气动光学效应的影响, 工程应用价值显著.
|
| 图 1 变Reynolds数气动光学效应实验平台示意图 Fig.1 Schematic diagram of variable Reynolds number aero-optics experimental platform |
波前测试技术采用以粒子图像测速(particle image velocimetry, PIV)模式工作的BOS技术, 主要由以下几部分组成:
(1) 随机背景点阵;
(2) 光源:双腔Nd-YAG激光器, 单脉冲持续时间为6 ns, 决定了系统拍摄的时间分辨率为6 ns.由于激光器经导光臂出射光束为圆形, 并且具有较强的衍射斑, 不利于整个二维区域的均匀照亮, 通过利用一个柱面镜将光束展宽, 再利用雾面镜来提高光束的均匀性, 以满足背景照明需求;
(3) 采用跨帧CCD相机, 最小跨帧时间间隔为0.2 μs, 图像分辨率为2 048 pixel×2 048 pixel, 配置Nikon 105 mm定焦镜头;
(4) 利用同步控制器对激光器和CCD相机的时序进行控制, 同步控制器时间控制精度为ps量级, 实现单帧实际曝光时间6 ns, 实测空间分辨率为0.082 mm/pixel.
1.2 基于BOS技术进行波前测量及其适应性改进研究BOS作为一项经典的流场定量测试方法, 自2000年Meier[12]在其申请的专利中首次提出以来, 该方法已经得到了广泛的应用; Tian等[13], Bichal等[14]创造性地利用此方法对流场气动光学波前进行了测量, 为利用BOS技术进行波前测量提供了思路. BOS方法的工作模式主要分成两种:一种以纹影模式工作, 另一种以PIV模式工作.比较而言, 后者的光路布置更加简单, 但是由于缺少了远场条件假设, 通常需要人为增加随机背景点阵与待测流场之间的距离, 以便近似得到远场条件[15].
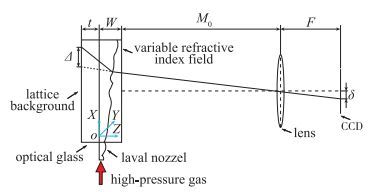
如图 2所示, 由于采用PIV模式的BOS, 且待测区域与随机背景点阵之间的距离较小, 因此不满足远场条件, 需要进行近场BOS修正才能提高结果的准确度.通过借鉴van Hinsberg等[16]在近场条件下利用BOS技术进行流场密度测量的思路, 结合实验条件进行适应性改进, 实现近场条件下利用BOS技术进行气动光学波前测量.
|
| 图 2 BOS测量原理示意图 Fig.2 Schematic diagram of BOS measuring principle |
根据Dalziel等[17]于2000年提出的背景上随机点的位移与折射率分布关系式:
| $\left\{ {\begin{array}{*{20}{l}} {\Delta \xi \left( {{x_i},{y_i}} \right) = \frac{1}{{{C_{{\rm{corr}}}}}}W\left( {W + 2{L_0}} \right) \cdot \frac{1}{{{n_0}}}\frac{{\partial {n_i}}}{{\partial {x_i}}}}\\ {\Delta \zeta \left( {{x_i},{y_i}} \right) = \frac{1}{{{C_{{\rm{corr}}}}}}W\left( {W + 2{L_0}} \right) \cdot \frac{1}{{{n_0}}}\frac{{\partial {n_i}}}{{\partial {y_i}}}} \end{array}} \right.$ |
随机背景点阵与待测流场之间的距离L0=t+0.5W, W为待测折射率场宽度.
此公式对远场、近场条件都适应, 其中Ccorr为系数, 当L0≫W时, Ccorr=2, 即与远场条件下的形式相同. n0=1+ρ0KGD, ρ0为每个状态下对应的实验舱环境密度, KGD为Gladstone Dale常数.
对整个光线传播路径进行积分, 可以获得对应每个随机点的最终位移结果:
| $\left\{ {\begin{array}{*{20}{l}} {\xi \left( {{x_i},{y_i}} \right) = \frac{1}{{{C_{{\rm{corr}}}}}}W\left( {W + 2{L_0}} \right) \cdot \int_{{z_0}}^{{z_0} + W} {\frac{1}{{{n_0}}}\frac{{\partial {n_i}}}{{\partial {x_i}}}} {\rm{d}}z}\\ {\zeta \left( {{x_i},{y_i}} \right) = \frac{1}{{{C_{{\rm{corr}}}}}}W\left( {W + 2{L_0}} \right) \cdot \int_{{z_0}}^{{z_0} + W} {\frac{1}{{{n_0}}}\frac{{\partial {n_i}}}{{\partial {y_i}}}} {\rm{d}}z} \end{array}} \right.$ | (1) |
光线穿过流场的流程称为光程(optical path length, OPL), 由式(2) 表示:
| ${\rm{OPL}}\left( {{x_i},{y_i}} \right) = \int_{{s_1}}^{{s_2}} {n{\rm{d}}s = \int_{{z_0}}^{{z_0} + W} {{n_i}} } {\rm{d}}z$ | (2) |
通过对式(2) 求偏导, 之后联立式(1) 可得:
| $\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\rm{OPL}}\left( {{x_i},{y_i}} \right)}}{{\partial {x_i}}} = \int_{{z_0}}^{{z_0} + W} {\frac{{\partial {n_i}}}{{\partial {x_i}}}} {\rm{d}}z = \frac{{{n_0}{C_{{\rm{corr}}}}}}{{W\left( {W + 2{L_0}} \right)}}\xi \left( {{x_i},{y_i}} \right)}\\ {\frac{{\partial {\rm{OPL}}\left( {{x_i},{y_i}} \right)}}{{\partial {y_i}}} = \int_{{z_0}}^{{z_0} + W} {\frac{{\partial {n_i}}}{{\partial {y_i}}}} {\rm{d}}z = \frac{{{n_0}{C_{{\rm{corr}}}}}}{{W\left( {W + 2{L_0}} \right)}}\zeta \left( {{x_i},{y_i}} \right)} \end{array}} \right.$ | (3) |
van Hinsberg等[16]研究结果表明:
| ${C_{{\rm{corr}}}} = f\left( {{L_0},W\left( {x,y} \right)} \right) = \frac{2}{{1 + W/{L_0}}}$ | (4) |
将式(4) 带入式(3) 可得:
| $\begin{array}{l} \frac{{\partial {\rm{OPL}}\left( {{x_i},{y_i}} \right)}}{{\partial {x_i}}} = \int_{{z_0}}^{{z_0} + W} {\frac{{\partial {n_i}}}{{\partial {x_i}}}} {\rm{d}}z\\ \quad \quad \quad \quad \quad \quad = \frac{{2{n_0}}}{{W\left( {W + 2{L_0}} \right)\left( {1 + W/{L_0}} \right)}}\xi \left( {{x_i},{y_i}} \right)\\ \frac{{\partial {\rm{OPL}}\left( {{x_i},{y_i}} \right)}}{{\partial {y_i}}} = \int_{{z_0}}^{{z_0} + W} {\frac{{\partial {n_i}}}{{\partial {y_i}}}} {\rm{d}}z\\ \quad \quad \quad \quad \quad \quad = \frac{{2{n_0}}}{{W\left( {W + 2{L_0}} \right)\left( {1 + W/{L_0}} \right)}}\zeta \left( {{x_i},{y_i}} \right) \end{array}$ | (5) |
由于式(5) 为光程的偏导数形式, 须要进行积分计算, 常用的积分运算方法主要有梯形积分算法、多项式拟合法以及Southwell算法, 目前精度最高的是Southwell算法[14].
令H=W(W+2L0), 那么
| $\left\{ {\begin{array}{*{20}{l}} {{\rm{OPL}}\left( {{x_i},{y_i}} \right) = {\rm{OPL}}\left( {{x_i},{y_{i - 1}}} \right) - \frac{{\Delta x}}{{2H}}\left[ {\xi \left( {{x_i},{y_{i - 1}}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right]}\\ {{\rm{OPL}}\left( {{x_i},{y_i}} \right) = {\rm{OPL}}\left( {{x_i},{y_{i + 1}}} \right) + \frac{{\Delta x}}{{2H}}\left[ {\xi \left( {{x_i},{y_{i + 1}}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right]}\\ {{\rm{OPL}}\left( {{x_i},{y_i}} \right) = {\rm{OPL}}\left( {{x_{i - 1}},{y_i}} \right) + \frac{{\Delta y}}{{2H}}\left[ {\xi \left( {{x_{i - 1}},{y_i}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right]}\\ {{\rm{OPL}}\left( {{x_i},{y_i}} \right) = {\rm{OPL}}\left( {{x_{i + 1}},{y_i}} \right) - \frac{{\Delta y}}{{2H}}\left[ {\xi \left( {{x_{i + 1}},{y_i}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right]} \end{array}} \right.$ |
式中, Δx为x方向的网格步长, Δy为y方向的网格步长.
对以上4个OPL(xi, yi)进行加权平均得到:
| $\begin{gathered} {\text{OPL}}\left( {{x_i},{y_i}} \right) = \hfill \\ \frac{{{\omega _{\left( {{x_i},{y_{i - 1}}} \right)}}{\text{OPL}}\left( {{x_i},{y_{i - 1}}} \right) + {\omega _{\left( {{x_i},{y_{i + 1}}} \right)}}{\text{OPL}}\left( {{x_i},{y_{i + 1}}} \right) + {\omega _{\left( {{x_{i - 1}},{y_i}} \right)}}{\text{OPL}}\left( {{x_{i - 1}},{y_i}} \right) + {\omega _{\left( {{x_{i + 1}},{y_i}} \right)}}{\text{OPL}}\left( {{x_{i + 1}},{y_i}} \right)}}{{{\omega _{\left( {{x_i},{y_{i - 1}}} \right)}} + {\omega _{\left( {{x_i},{y_{i + 1}}} \right)}} + {\omega _{\left( {{x_{i - 1}},{y_i}} \right)}} + {\omega _{\left( {{x_{i + 1}},{y_i}} \right)}}}} + \hfill \\ \;\left\{ { - \frac{{\Delta x}}{{2H}}{\omega _{\left( {{x_i},{y_{i - 1}}} \right)}}\left[ {\xi \left( {{x_i},{y_{i - 1}}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right] + \frac{{\Delta x}}{{2H}}{\omega _{\left( {{x_i},{y_{i + 1}}} \right)}}\left[ {\xi \left( {{x_i},{y_{i + 1}}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right]} \right. + \hfill \\ \frac{{\Delta y}}{{2H}}{\omega _{\left( {{x_{i - 1}},{y_i}} \right)}}\left[ {\xi \left( {{x_{i - 1}},{y_i}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right] - \frac{{\Delta y}}{{2H}}{\omega _{\left( {{x_{i + 1}},{y_i}} \right)}}\left. {\left[ {\xi \left( {{x_{i + 1}},{y_i}} \right) + \zeta \left( {{x_i},{y_i}} \right)} \right]} \right\}/ \hfill \\ \left( {{\omega _{\left( {{x_i},{y_{i - 1}}} \right)}} + {\omega _{\left( {{x_i},{y_{i + 1}}} \right)}} + {\omega _{\left( {{x_{i - 1}},{y_i}} \right)}} + {\omega _{\left( {{x_{i + 1}},{y_i}} \right)}}} \right) \hfill \\ \end{gathered} $ |
其中, ω表示权重系数.
实际上, OPD是比OPL更加重要的参数, 且更容易测量, OPD定义为
| ${\rm{OPD}}\left( {{x_i},{y_i}} \right) = {\rm{OPL}}\left( {{x_i},{y_i}} \right) - \overline {{\rm{OPL}}\left( {{x_i},{y_i}} \right)} $ |
其中, 上横线表示光学孔径上的空间平均.
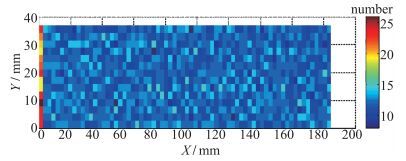
2 验证性实验结果与分析由于互相关运算中查问区尺寸的选取以及随机点密度(每个查问区内包含的粒子数)对计算精度影响很大, 所以在进行互相关计算之前, 需要确定合适的查问区尺寸以及验证随机点密度是否满足要求.通过预先测试实验, 确定喷流导致的位移分布主要集中在10 pixel以内, 考虑到一般位移量不超过查问区域的1/4, 确定查问区域尺寸为32 pixel×32 pixel.为了确定实验测试系统记录的随机点密度是否满足测试要求, 对计算区域的随机点密度进行研究, 获得如图 3所示的密度分布图, 图中的每一个马赛克对应一个查问区.
|
| 图 3 每个查问区内随机点数量分布图 Fig.3 Distribution of random points number in each inquire area |
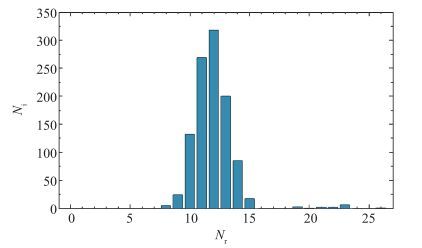
如图 4所示, 其中Ni表示查问区数量, Nr表示每个查问区内随机点数量.包含随机点数目在10个以上的查问区数量占到查问区总数的97.2%.满足了田立丰[18]提出的每个查问区内至少要有10~20个随机点的要求.
|
| 图 4 随机点密度分布示意图 Fig.4 Distribution of random points density |
为了验证系统的测试可靠性, 选取大恒光电出品的K9平凸透镜, 其直径为76.2 mm, 像方焦距f=1 000 mm, 折射率Nd=1.52.将透镜平面一侧利用透明胶带固定在与待测流场相同的位置(紧贴玻璃板), 保证系统参数与流场测量时相同.
根据透镜曲率半径计算公式:
| $1/f\left( {Nd - 1} \right) \cdot \left( {1/{r_1} + 1 / {r_2}} \right)$ |
其中, r1和r2分别表示透镜的前后曲率半径.由于平凸透镜, 所以r2→∞, 计算得到:
r1=516.8 mm(对应图 5中的OB)
|
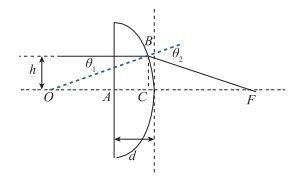
| 图 5 平凸透镜理论波前计算示意图 Fig.5 Schematic diagram of theory wavefront calculation |
光线从平凸透镜的平面一侧入射, 假设光线只有经过透镜第2个面时才会发生偏折.
设平行入射光距离光轴的距离为h, 那么入射角为
| $\sin {\theta _1} = h/R$ |
根据折射定律可得:
| $\sin {\theta _2} = Nd \times \sin {\theta _1}$ |
透镜到背景点阵距离为G, 那么穿过透镜的理论光程差可以表示为
| $S = \left[ {G + \left( {R - \sqrt {{R^2} - {h^2}} } \right)} \right] \times \left[ {\frac{1}{{\cos \left( {{\theta _2} - {\theta _1}} \right)}} - 1} \right]$ |
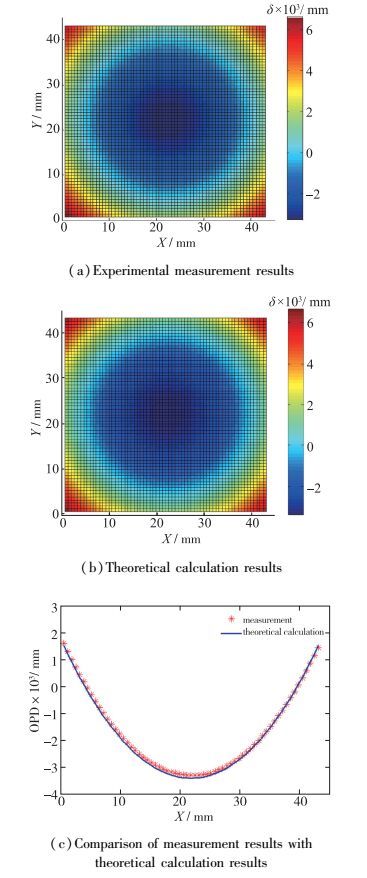
由于平凸透镜具有波前连续变化的特点, 从圆心到边缘逐渐递增, 冷却喷流波前畸变尺度位于波前变化范围内.为了更清晰呈现实验测量结果与理论计算结果之间的偏差, 考虑到圆形透镜的对称性, 任选一个方向, 绘制如图 6所示的OPD对比曲线.
|
| 图 6 平凸透镜波前实验测量结果与理论计算结果比较 Fig.6 Comparison of plane convex lens between measurement results and theoretical calculation results |
从图 6中可以看出, 利用此光路可以较好地测量透镜的波前结果, 实验测量结果与理论计算结果的误差在±4%以内.
3 超声速气膜实验及其结果分析实验研究对象为超声速气膜, 气流沿光学玻璃壁面从二维喷管中射出, 喷管宽度为104 mm, 高度为5 mm, Mach数为3.05, 喷流总温300 K.实验舱与真空罐相连, 利用真空泵可以连续调节实验舱压强从0~0.1 MPa变化.喷流的气源储存在高压气罐中, 通过压气机进行气源补充, 气罐最大容许压强为25 MPa, 高压气体经过减压器减压, 获得压力匹配条件下喷管驻室所需的总压, 此总压通过驻室压力传感器获取, 减压器下游的压力表仅用于粗略读数.系统测试区域位于喷管出口下游10~190 mm处, 测试流向长度为180 mm, 展向宽度为41 mm.激光单脉冲持续时间6 ns, 使得获得结果具有瞬态特性, 满足流场冻结条件假设.每个状态共获取30组结果, 共测试了9个状态, 具体状态参数见表 1.其中, P表示实验舱静压, P0表示实验喷流名义总压, P′0表示实验喷流喷管驻室实测总压, Re表示喷流单位Reynolds数.
| 下载CSV 表 1 测试状态汇总表 Tab.1 Test status summary |
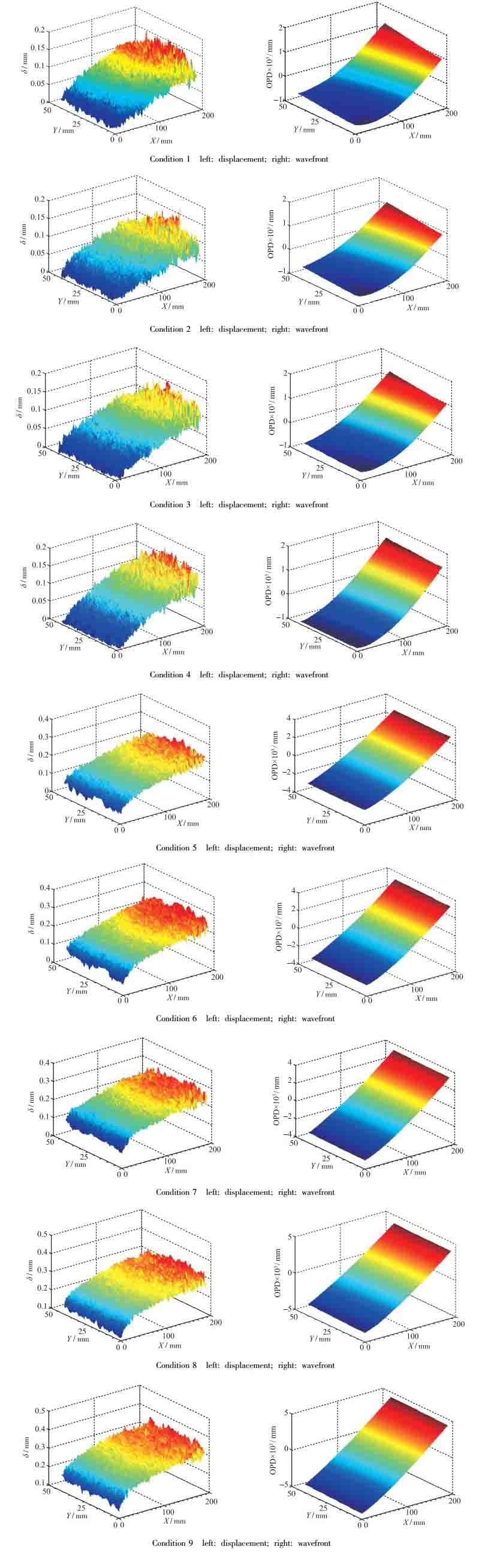
测量的9个状态下的瞬态合位移δ及瞬态波前结果如图 7所示.
|
| 图 7 不同Reynolds数下超声速气膜气动光学效应导致的瞬态合位移及其波前分布图 Fig.7 Distributions of transient displacement and corresponding wavefront produced by supersonic film aero-optics under different Reynolds conditions |
波前畸变程度通常利用波前的均方根值和SR来描述, 而两者之间又可以利用大孔径近似(large aperture approximation, LAA)建立联系, 所以这里仅选取波前的均方根值OPDrms作为波前畸变程度的评价指标, 其值越大, 畸变越严重.由于超声速气膜流动模型相较边界层模型较为复杂, 当前对气动光学相似律的推导还是空白.从边界层气动光学相似律出发, 结合实验特点, 对超声速气膜气动光学相似准则进行探索.通过比较Wyckham等[9]和Gordeyev等[10]关于湍流边界层的气动光学推导结果发现, 其结果可以统一表示为如下形式:
| ${\text{OP}}{{\text{D}}_{{\text{rms}}}} \propto {K_{{\text{GD}}}}\rho \delta {M^2}\sqrt {{C_{\text{f}}}} G\left( M \right)$ | (6) |
根据Re=ρul/μ, 将其带入式(6) 可得:
| ${\text{OP}}{{\text{D}}_{{\text{rms}}}} \propto {K_{{\text{GD}}}}\frac{\mu }{{ul}}\delta {M^2}\sqrt {{C_{\text{f}}}} G\left( M \right)Re$ | (7) |
在相同大气环境条件下, KGD随着波长的增加而减少, 针对空气而言,
| ${K_{{\rm{GD}}}}2.224\;4 \times {10^{ - 4}}\left[ {1 + {{\left( {6.713\;2 \times {{10}^{ - 8}}/\lambda } \right)}^2}} \right]{{\rm{m}}^3}/{\rm{kg}}$ |
而光源发出的光线波长可看作常量, 所以KGD可以看做常数.由于不同Reynolds数条件下, 喷流总温和Mach数不变, 故喷流的静温不变, 根据Sutherland公式可知, 黏性系数μ主要由温度决定, 所以也可以看成常数.在边界层相似准则的研究中, δ通常定义为边界层厚度, 这里用混合层厚度代替, 长期研究结果表明, 混合层的增长速度主要由Mc(对流Mach数)决定, 由于实验舱流动速度近似为0, 那么Mc可以表示为喷流Mach数M的函数:
| ${M_{\rm{c}}} = \frac{M}{{1 + \sqrt {1 + \frac{{\gamma - 1}}{2}{M^2}} }}$ |
考虑到M=3.05, Mc=1.14, 所以, 在此认为不同实验状态下δ值相同, 这一点在纹影实验中也得到了验证.同理, M2G(M)也可以看成常量.针对湍流边界层而言[19], 壁面摩擦系数Cf∝Re-1/5, 结合以上的分析, 可以将式(7) 简化为
| ${\rm{OP}}{{\rm{D}}_{{\rm{rms}}}} \propto R{e^{0.9}}$ |
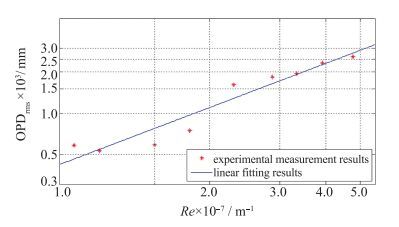
将实验测量获得的每个状态下的30组OPDrms结果取平均值, 形成一个数据点, 共有9个数据点, 对其进行函数拟合, 结果如图 8所示.幂函数拟合结果显示:
|
| 图 8 不同单位Reynolds数下的OPDrms结果分布 Fig.8 Experiment and linear fitting results of OPDrms under different unit Reynolds number |
| ${\rm{OP}}{{\rm{D}}_{{\rm{rms}}}} = 2.87 \times {10^{ - 10}} \times R{e^{0.88}}$ |
幂指数0.88与推导结果0.9基本相同.这说明, 在压力匹配条件下, 随着超声速喷流Reynolds数的增加, OPDrms不断增大, 即气动光学效应不断加剧.
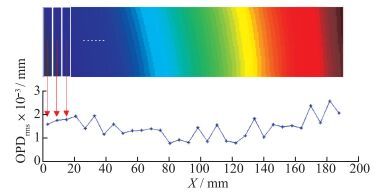
3.2 超声速气膜气动光学效应沿流向分布特性通过计算超声速气膜沿流向的OPDrms分布有助于研究流向不同位置处气动光学效应的变化情况.由于不同状态下OPDrms沿流向分布具有一定的相似性, 这里选取状态9为例, 研究OPDrms沿流向的分布特征.如图 9所示, 上图为状态9对应的OPD分布, 沿流向设置一定的宽度, 计算整个白框内OPD的均方根值作为代表此部分的OPDrms数据点. 图 9为选取流向宽度间隔为5.98 mm获取的OPDrms沿流向分布结果.
|
| 图 9 超声速气膜OPDrms沿流向分布计算示意图 Fig.9 Schematic diagram of supersonic film OPDrms distributions along the flow direction |
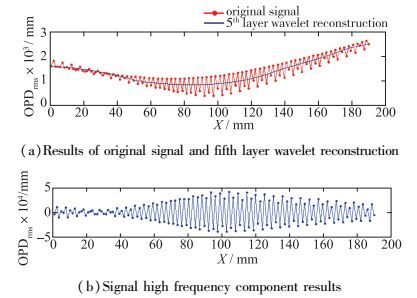
通过减小计算区域沿流向尺寸, 可以更精确地研究OPDrms沿流向的变化情况, 图 10(a)所示的原始信号为选取流向尺寸为1.33 mm的计算区域对应的计算结果.通过小波的多尺度分析, 可将信号分解为反映信号整体趋势的低频分量和反映信号细节的高频分量[20].使用db4小波作为小波基进行小波变换, 为了获得较好的观测效果, 选择5层小波分解, 获得了如图 10(a)中的第5层小波重构结果, 进而提取出信号的高频分量, 如图 10(b)所示.
|
| 图 10 超声速气膜OPDrms沿流向分布小波分析结果 Fig.10 Wavelet analysis result of supersonic film OPDrms distributions along flow direction |
第5层小波重构结果主要反映了信号整体的变化趋势, OPDrms沿流向先逐渐减小, 后基本保持不变, 最后逐渐增大, 但是增大的幅度逐渐减小.这说明在喷管出口处, 流场的气动光学效应较强, 主要是唇口的波系结构导致, 这一点已经通过纹影结果得到了验证.之后OPDrms相干结构逐渐减小并趋缓, 但是此处对应的信号高频分量震荡幅度较大, 主要由于大尺度涡结构对波前的影响相对较强, 此部分可能对应流场的转捩区域, 大尺度涡结构在不同区域内分布的不均性是信号震荡的主要成因.最后流场可能已经充分发展, 气动光学效应最强, 所以OPDrms主体结构数值不断增大, 后逐渐趋缓, 与此对应, 涡结构已经充分破碎, 涡空间分布上的均匀性相对增加, 所以OPDrms在空间分布上的差异减小, 即震荡幅度减小.
4 结论基于压力匹配的概念设计了变Reynolds数气动光学效应实验平台, 测试Reynolds数可以在7.2×106~2.2×108 m-1范围内变化.对近场条件下利用BOS技术进行波前测量做出了适应性改进, 通过测量标准平凸透镜的波前并与其理论值对比, 确定测量结果相比于理论计算结果的误差在±4%以内, 验证了测试技术的可靠性.
测量了9种不同Reynolds数下的超声速气膜瞬态波前数据, 分析结果表明:在高Reynolds数条件下, Reynolds数对于超声速气膜气动光学效应的影响比较明显, 通过对实验数据进行函数拟合发现OPDrms∝Re0.88, 与推导结果OPDrms∝Re0.9十分接近; 利用小波分析方法研究了高Reynolds数条件下气动光学效应沿流向的分布特征, 发现OPDrms的低频部分(信号的主体)呈现先降低后升高, 但是高频部分的震荡幅度呈现先升后降.初步分析认为OPDrms的低频部分主要受到流场整体结构的影响, 而高频部分更多地与流场内涡的空间分布特性有关, 随着涡结构随流向的不断发展、破碎, 高频部分出现如此结果.
| [1] |
李桂春.气动光学[M].北京:国防工业出版社, 2006:7.
Li G C. Aero optics[M]. Beijing:National Defence Industry Press, 2006:7(in Chinese). |
| [2] |
张天序, 洪汉玉, 张新宇.气动光学效应校正——原理、方法与应用[M].合肥:中国科学技术大学出版社, 2014:15.
Zhang T X, Hong H Y, Zhang X Y. Aero-optical effect correction:principles, methods and applications[M]. Hefei:Press of University of Science and Technology of China, 2014:15(in Chinese). |
| [3] |
王乃祥, 徐钰蕾, 史磊, 等. 高马赫飞行器迎风面与攻角对光学窗口周围流场的影响分析[J].
红外与激光工程, 2015, 44(4): 1267-1272. Wang N X, Xu Y L, Shi L, et al. Analysis of the impact of windward and angle of attack to the flow field around the optical window on high Mach condition[J]. Infrared and Laser Engineering, 2015, 44(4): 1267-1272. |
| [4] |
朱杨柱, 易仕和, 陈植, 等. 带喷流超声速光学头罩流场气动光学畸变试验研究[J].
物理学报, 2013, 62(8): 084219 Zhu Y Z, Yi S H, Chen Z, et al. Experimental investigation on aero-optical aberration of the supersonic flow passing through an optical dome with gas injection[J]. Acta Physica Sinica, 2013, 62(8): 084219 |
| [5] | Fitzgerald E J, Jumper E J. Scaling aero-optic aberrations due to propagation through compressible shearlayers[R]. AIAA 2000-2354, 2000. |
| [6] | Gilbert K G. KC-135 aero-optical turbulent boundary-layer/shear-layer experiments[J]. Aero-Optical Phenomena, 1982, 80: 306-324. |
| [7] | Craig J E, Rose W C. Laser propagation from airborne platforms-a review of aero-optics scaling[C]. 18th Fluid Dynamics and Plasmadynamics and Lasers Conference, Cincinnati, 1985:1628. |
| [8] | Masson B, Wissler J, Mcmackin L. Aero-optical study of a NC-135 fuselage boundary layer[C]. 32nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, 1994:277. |
| [9] | Wyckham C M, Smits A J. Aero-optic distortion in transonic and hypersonic turbulent boundary layers[J]. AIAA Journal, 2009, 47(9): 2158-2168. DOI:10.2514/1.41453 |
| [10] | Gordeyev S, Smith A E, Cress J A, et al. Experimental studies of aero-optical properties of subsonic turbulent boundary layers[J]. Journal of Fluid Mechanics, 2014, 740(2): 214-253. |
| [11] |
易仕和, 侯中喜, 赵玉新.超声速自由旋涡气动窗口及其光学质量[M].长沙:国防科学技术大学出版社, 2005:216.
Yi S H, Hou Z X, Zhao Y X. Supersonic free-vortexaerowindow and its optical quality[M]. Changsha:Press of National University of Defense Technology, 2005:261(in Chinese). |
| [12] | Meier G E. Hintergrund-schlierenme β verfahren für räumliche dichtefelder:German, 19942856[P]. 2000. |
| [13] | Tian L F, Yi S H, Zhao Y X, et al. Aero-optical wavefront measurement technique based on BOS and its applications[J]. Chinese Science Bulletin, 2011, 56(22): 2320-2326. DOI:10.1007/s11434-011-4583-z |
| [14] | Bichal A, Thurow B S. On the application of background oriented schlieren for wavefront sensing[J]. Measurement Science and Technology, 2013, 25(1): 015001 |
| [15] | Zhao Y, Yi S H, Tian L F, et al. An experimental study of aero-optical aberration and dithering of supersonic mixing layer via BOS[J]. Science China Physics Mechanics and Astronomy, 2010, 53(1): 81-94. DOI:10.1007/s11433-010-0111-4 |
| [16] | Van Hinsberg N P, Rösgen T. Density measurements using near-field background-oriented schlieren[J]. Experiments in Fluids, 2014, 55(4): 1720 DOI:10.1007/s00348-014-1720-x |
| [17] | Dalziel S B, Hughes G O, Sutherland B R. Whole-field density measurements bysynthetic schlieren'[J]. Experi-ments in Fluids, 2000, 28(4): 322-335. DOI:10.1007/s003480050391 |
| [18] |
田立丰. 超声速光学头罩流场精细结构及其气动光学效应的机理研究[D]. 长沙: 国防科学技术大学, 2011.
Tian L F. Mechanism study of fine structures and aero-optical effects of supersonic flow around an optical dome[D]. Changsha:National University of Defense Techno-logy, 2011. |
| [19] | Anderson Jr J D. Fundamentals of aerodynamics(5th edi-tion)[M]. Beijing:Aviation Industry Press, 2014. |
| [20] |
叶昊, 王桂增, 方崇智. 小波变换在故障检测中的应用[J].
自动化学报, 1997, 23(6): 736-741. Ye H, Wang G Z, Fang C Z. Application of wavelet transform to fault detection[J]. Acta Automatica Sinica, 1997, 23(6): 736-741. |



