2. 中国空气动力研究与发展中心空气动力学国家重点实验室, 四川绵阳 621000
2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China
近年来, 临近空间高超声速飞行成为新的研究热点, 在此空域的飞行器具有复杂升力体外形、气动加热时间长、热流高等特点[1], 为获得良好气动特性, 一般采取保形的非烧蚀热防护技术. 大面积的热防护材料需要在中高温度(1 000~1 600 K)、有氧环境、长时间(约3 000 s)服役, 对材料抗烧蚀性能提出了苛刻要求. 为此, 迫切需要发展新型防热材料, 或改善传统防热材料, 以满足在严酷的热环境中维持外形的要求. C/SiC复合材料作为一种低/非烧蚀防热材料近年来颇受关注[2-3], 研究发现, C/SiC复合材料在高温环境下会与氧气发生化学反应, 在材料表面形成凝相抗氧化膜, 并能在较宽的温度范围内维持, 从而有效阻止氧气与防热材料的直接接触, 显著降低烧蚀量. 液态氧化物可填补表面损伤缺陷, 实现自愈合抗氧化行为[4], 它以表面材料氧化生成氧化膜实现材料抗烧蚀, 属于一种典型的惰性氧化.
国内外研究C/SiC复合材料抗烧蚀性能主要采取实验手段, 应用多种测量仪器对氧化行为进行表征. 氧化机理和建模建立在实验研究的基础上, 然而在复合材料抗氧化烧蚀建模方面的研究仍远远不够, 亟待加强. 对此, 韩杰才等[5]认为建立复合材料高温氧化过程的理论模型是迫切需要.
C/SiC复合材料是采用C粉末和SiC粉末制备的一种基体热防护材料, 继承了碳基材料的优点并采用SiC改善碳基材料易氧化的不足, 它的抗氧化研究很自然地继承了SiC抗氧化研究的成果. SiC材料存在活性氧化和惰性氧化, 以及它们之间的转换, Jacobson等[6-7]、Yoshinaka等[8]和Harder等[9]在2011—2013年对SiC的氧化行为进行了很好的总结.
C/SiC复合材料氧化不同于SiC涂层-C基体材料的氧化损伤[10-11]; 也不同于碳纤维增强SiC基体复合材料的碳纤维优先氧化[12-13], 它具有整体抗烧蚀特性, 基本保持原材料表面同步氧化.
直接针对C/SiC复合材料建模, 相关的报道很少[14, 17], 对于烧蚀型材料和热解材料, Milos等[18]基于热化学平衡方法提出了通用计算方法并开发出相应的程序, 国内邓代英等[19]和张红军等[20]采用类似方法建立了烧蚀模型, 预测值与C/SiC复合材料电弧风洞实验结果吻合较好.
C/SiC复合材料抗烧蚀的惰性氧化几乎都是基于表层生成的液态SiO2氧化膜, 建立氧气溶解-扩散-反应模型[14]. 这类模型背后的机理最早源自Deal等[15]研究Si氧化生成液态膜, 提出了著名氧化膜厚度抛物形方程; 接着, Stern[16]将其拓展到SiC惰性氧化, 认为二者的主要差别在于活化能; 后来, Yoshinaka等[8]考虑了SiC离解为Si和C元素, 在模型中加入了它们在液态氧化膜中的扩散速率. 高温型石英的熔点为(1 696±50)K[21], 因此在中低温(1 696 K)下, C/SiC复合材料氧化可能生成固态SiO2, 在表面形成一层薄薄的多孔氧化膜, 如图 1所示. 氧化膜中的孔隙主要是C元素氧化生成的气态CO聚集并向外逸出形成的弯弯曲曲的通道. 氧化物里的孔隙随着C组分含量的增加而增大.

|
| 图 1 C-27% SiC在1 673 K空气中氧化2 h后截面形貌 Fig.1 Cross-section morphology of C-27% SiC after oxidation in the air at 1 673 K for 2 h |
在中低温区间里, C/SiC复合材料在表面形成固态氧化膜, 其中的孔隙为氧气进入和CO逸出提供了快速通道, 因此, 气体输运主要为扩散形式. 建立相应的新氧化模型, 反映氧气的侵入和描述氧化膜的演化规律, 不仅具有现实理论意义, 还可为材料的防热性能评估和应用提供参考依据.
1 C/SiC复合材料低温氧化行为 1.1 氧化机理当温度超过约700 K, 纯C物质氧化开始[22]; SiC氧化起始温度约为1 100 K[23], 当温度超过1 255 K, SiC氧化较为明显[24], C在此温度下的氧化行为属于扩散控制动力学[13]. C/SiC复合材料氧化起始温度与SiC接近, 惰性氧化速率由氧气在氧化膜孔隙中扩散速率控制, 材料中的两种组分消耗速率基本相当, 即C和SiC氧化后退速率一致, 如图 2所示, C/SiC复合材料在1 273 K空气中氧化2 h后的EDX(energy dispersive X-ray spectroscopy)表征的元素分布. 氧化层和原始基材的分界线较为平直, 可以认为C组分和SiC组分烧蚀后退量基本一致, 因此, 它们的氧化反应又可以记为
| $ \begin{gathered} \mathrm{C}_{m_{1}}(\mathrm{SiC})_{m_{2}}(\mathrm{~s})+\left(0.5 m_{1}+1.5 m_{2}\right) \mathrm{O}_{2}(\mathrm{~g}) \rightarrow \\ m_{2} \mathrm{SiO}_{2}(\mathrm{~s})+\left(m_{1}+m_{2}\right) \mathrm{CO}(\mathrm{g}) \end{gathered} $ |

|
| 图 2 C-25% SiC在1 273 K空气中氧化2 h后元素分布 Fig.2 Distribution of element of C-25% SiC afteroxidation in the air at 1 273 K for 2 h |
其中, m1和m2分别为材料中C组分和SiC组分的摩尔分数. 由化学反应及其计量数可知
| $ -\frac{1}{\dot{n}_{\mathrm{C} / \mathrm{SiC}}}=-\frac{0.5 m_{1}+1.5 m_{2}}{\dot{n}_{\mathrm{O}_{2}}}=\frac{m_{1}+m_{2}}{\dot{n}_{\mathrm{CO}}}=\frac{m_{2}}{\dot{n}_{\mathrm{SiO}_{2}}} $ | (1) |
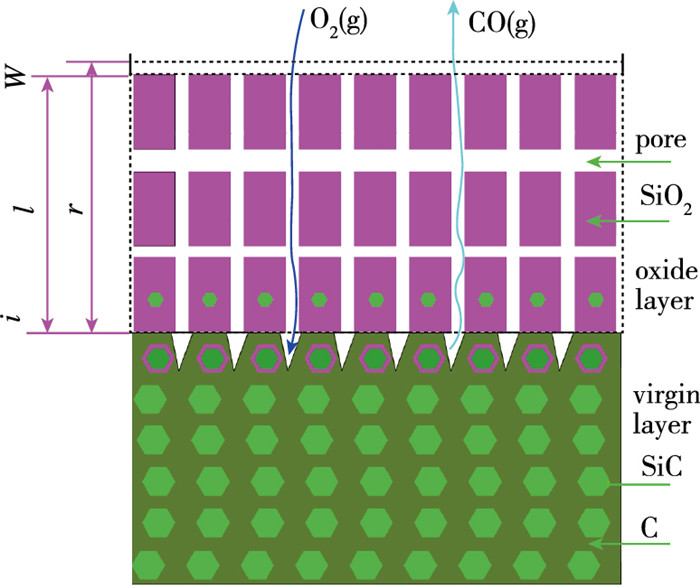
C和SiC在SiO2-SiC界面被通过孔隙扩散而来的氧气氧化, 由于上面SiO2层和下面C/SiC层的阻挡, SiC氧化生成的SiO2优先侵占C氧化留下的空洞区间, 反映出氧化膜区域的孔隙情况与C组分含量密切相关. SiC的密度约为3 200~3 250 kg·m-3, SiO2的密度约为2 200 kg·m-3, 氧化前后体积的膨胀, 会侵占一部分C氧化后形成的空洞. 固态SiO2与基材的黏附性较强, 具有一定的抗冲刷能力, 然而正因为流动性不足, 不能形成高致密度的氧化膜, 存在孔隙在所难免. 不同于氧气在充满液相物质的孔隙中的溶解-扩散行为[25], 氧气在无填充孔隙中主要以气体扩散方式通过固态氧化膜. 环境氧气以扩散方式通过孔隙到达底层, 与C/SiC反应, 生成SiO2增厚氧化膜, 生成的气态CO逆扩散通过孔隙向外逸出. 基于此, 建立了如图 3所示的C/SiC复合材料氧化模型.
|
| 图 3 C/SiC氧化微观结构示意图 Fig.3 Sketch of oxidation microstructure of C/SiC |
为简化建模, 物理-化学过程做如下假设:
(1) 氧化反应为稳态过程, 氧气消耗率与扩散而来的氧气流率相同;
(2) 氧化反应速率由氧气在孔隙中的扩散速率和氧化层-原始层界面反应速率共同控制;
(3) C/SiC复合材料的C组分和SiC组分氧化后退速率一致;
(4) 表面氧化情况一致, 只须考虑深度方向.
1.2 气体输运模型氧气主要以孔隙中的气体扩散方式通过固态氧化膜, 氧气流率为
| $ \dot{n}_{\mathrm{O}_{2}}=J_{\mathrm{O}_{2}}+x_{\mathrm{O}_{2}} \dot{N}=-f_{\mathrm{p}} D_{\mathrm{O}_{2}} c \frac{\mathrm{d} x_{\mathrm{O}_{2}}}{\mathrm{~d} y}+x_{\mathrm{O}_{2}}\left(\dot{n}_{\mathrm{O}_{2}}+\dot{n}_{\mathrm{CO}}\right) $ | (2) |
式中, fp和L分别为SiO2氧化物的孔隙率和厚度; JO2为O2在孔隙里以扩散方式向内传输的流率; xO2为孔隙里当地氧气摩尔浓度百分数. c为空气的浓度. 等式右边第1项反映的是分子扩散运动, 第2项为混合气体整体运动所携带的氧气流动. 将(1)式带入(2)式, 整理可得
| $ \dot{n}_{\mathrm{O}_{2}}=-\frac{f_{\mathrm{p}} D_{\mathrm{O}_{2}} c}{1-b x_{\mathrm{O}_{2}}} \frac{\mathrm{d} x_{\mathrm{O}_{2}}}{\mathrm{~d} y}, \quad b=\frac{-m_{1}+m_{2}}{m_{1}+3 m_{2}} $ |
分别在氧化膜两侧积分, 可得
| $ \int_{0}^{l} \dot{n}_{\mathrm{O}_{2}} \mathrm{d} y=\int_{x_{\mathrm{O}_{2}, \mathrm{i}}}^{x_{\mathrm{O}_{2}, \mathrm{w}}}-\frac{f_{\mathrm{p}} D_{\mathrm{O}_{2}} c}{1-b x_{\mathrm{O}_{2}}} \mathrm{~d} x_{\mathrm{O}_{2}} $ |
式中, l为氧化膜的厚度, xO2, i和xO2, w分别为氧化层-原始层交界面上(下标i标识)和外界环境(下标w标识)的氧气浓度百分数. 假定DO2, c为常数, 积分可得
| $ \dot{n}_{\mathrm{O}_{2}}=\frac{D_{\mathrm{O}_{2}} c}{l} \frac{f_{\mathrm{p}}}{b} \ln \left(\frac{1-b x_{\mathrm{O}_{2}, \mathrm{w}}}{1-b x_{\mathrm{O}_{2}, \mathrm{i}}}\right) $ | (3) |
由于材料发生热化学反应消耗氧气, 物面处的氧气浓度很小, Taylor级数展开取第1项, 可得ln(1-bxO2, i)≈-bxO2, i.
若C/SiC复合材料的氧化反应采用一级反应, 则氧气流率还可表达为
| $ \dot{n}_{\mathrm{O}_{2}}=-k_{\mathrm{ox}} c x_{\mathrm{O}_{2}, \mathrm{i}} $ | (4) |
式中, kox为氧化反应速率常数.
联立式(3), (4), 消去xO2, i, 可得
| $ \dot{n}_{\mathrm{O}_{2}}=\frac{c}{l / D_{\mathrm{O}_{2}}+f_{\mathrm{p}} / k_{\mathrm{ox}}} \frac{f_{\mathrm{p}}}{b} \ln \left(1-b x_{\mathrm{O}_{2}, \mathrm{w}}\right) $ |
由此可知, C/SiC复合材料的氧化主要由扩散动力学和反应动力学控制, 前者可以根据Chapman-Enskog公式求出, 后者由Arrhenius公式求出, 它们都是温度和氧分压的函数.
1.3 氧化情况描述根据反应方程式的化学计量数, 由质量守恒可获得SiO2氧化膜厚度增长方程
| $ \frac{\mathrm{d} l}{\mathrm{~d} t}=-\frac{1}{1-f_{\mathrm{p}}} \frac{m_{2}}{0.5 m_{1}+1.5 m_{2}} \dot{n}_{\mathrm{O}_{2}} \frac{M_{\mathrm{SiO}_{2}}}{\rho_{\mathrm{SiO}_{2}}} $ |
式中, t为氧化时间,MSiO2和ρSiO2分别为SiO2的摩尔质量和密度.
由于氧化, C/SiC复合材料逐渐被消耗, 后退量为
| $ \frac{\mathrm{d} r}{\mathrm{~d} t}=\frac{1}{0.5 m_{1}+1.5 m_{2}} \dot{n}_{\mathrm{O}_{2}}\left(0.5 m_{1} \frac{M_{\mathrm{C}}}{\rho_{\mathrm{C}}}+1.5 m_{2} \frac{M_{\mathrm{SiC}}}{\rho_{\mathrm{SiC}}}\right) $ |
式中, r为原材料后退量,MC和ρC分别为C的摩尔质量和密度,MSiC和ρSiC分别为SiC的摩尔质量和密度.
C/SiC复合材料因氧化而消耗, 生成SiO2而增重, 氧化前后单位面积的质量变化为
| $ \frac{\Delta m}{A}=l\left(1-f_{\mathrm{p}}\right) \rho_{\mathrm{SiO}_{2}}-r\left(f_{\mathrm{C}} \rho_{\mathrm{C}}+f_{\mathrm{SiC} } \rho_{\mathrm{SiC}}\right) $ |
式中, fC和fSiC分别为原材料中C组分和SiC组分的体积分数
| $ f_{\mathrm{C}}=\frac{m_{1} M_{\mathrm{C}} / \rho_{\mathrm{C}}}{m_{1} M_{\mathrm{C}} / \rho_{\mathrm{C}}+m_{2} M_{\mathrm{SiC}} / \rho_{\mathrm{SiC}}} $ |
| $ f_{\mathrm{SiC}}=\frac{m_{2} M_{\mathrm{SiC}} / \rho_{\mathrm{SiC}}}{m_{1} M_{\mathrm{C}} / \rho_{\mathrm{C}}+m_{2} M_{\mathrm{SiC}} / \rho_{\mathrm{SiC}}} $ |
孔隙大小及孔隙率直接影响孔隙中气体的扩散. 对于微米级的中孔, 适合采用压汞法测量. 压汞法原理可表述为Washburn方程[26-27]
| $ d=\frac{2 \sigma \cos \theta}{p} $ |
式中, d为毛细管的孔径, [m]; σ为汞表面张力, [μN·m-1]; θ为汞和毛细管表面的接触角; p为外界施加的压力, [μN].
2 扩散-反应动力学模型 2.1 扩散动力学模型孔隙中气体输运主要由分子扩散和Knudsen扩散主导. 某一组分在混合气体中分子浓度差异造成的分子扩散系数可近似表达为[28]
| $ D_{1,(2, \cdots, i)}=\frac{1}{\sum\nolimits_{i}^{i \neq 1}\left(x_{i} / D_{1-i}\right)} $ |
| $ x_{i}=\frac{n_{i}}{\sum\nolimits_{j}^{j \neq 1} n_{j}} $ |
式中, xi和ni分别为组分i的摩尔分数和摩尔数,D1, (2, …, i)为组分1在混合气体中的扩散系数,D1-i为组分1与组分i的双组份扩散系数[29]
| $ D_{1-2}=\frac{18.583 T^{3 / 2} \sqrt{\left(1 / M_{1}\right)+\left(1 / M_{2}\right)}}{\sigma_{12}^{2} \varOmega_{D} p} $ |
式中, D1-2为气体分子扩散系数; M1为组分1的相对分子量; p为混合气体总的压力; σ12=0.5(σ1+σ2), σ为碰撞直径; ΩD为碰撞对扩散的积分, 为无量纲量, 它与气体分子的分子间作用力相关, 可由下式计算[29]
| $ \begin{aligned} \varOmega_{D}=& \frac{1.060\ 36}{T^{* 0.156\ 10}}+\frac{0.193\ 000}{\exp \left(0.476\ 35 T^{*}\right)}+\\ & \frac{1.035\ 87}{\exp \left(1.529\ 96 T^{*}\right)}+\frac{1.764\ 74}{\exp \left(3.894\ 11 T^{*}\right)} \end{aligned} $ |
式中, T*为无量纲温度, T*=kT/ε12, k为Boltzmann常数,
气体组分在孔隙中的Knudsen扩散系数为
| $ D_{\mathrm{K}}=\frac{4}{3}\left(\frac{8 R T}{{\rm{ \mathsf{ π} }} M}\right)^{1 / 2} \frac{r}{2} $ |
式中, DK为Knudsen扩散系数; M为摩尔质量; r为孔隙的等效半径; R为通用气体常数. 考虑上述两种扩散的综合扩散系数由Bosanquet公式给出[30]
| $ D_{\mathrm{com}}=\left(D_{\mathrm{K}}^{-1}+D_{1-2}^{-1}\right)^{-1} $ |
该式获得的扩散系数是基于等直圆柱矩阵排列的条件获得[31]. 氧化膜孔隙内部形状多变、走向弯曲(见图 1), 气体有效扩散面要比规则孔隙的横截面小很多, 距离也更长, 考虑这种效应后的有效扩散系数为[32-33]
| $ D_{\mathrm{eff}}=\frac{f_{\mathrm{p}}}{\tau} D_{\mathrm{com}} $ |
式中, Deff为有效扩散系数; τ为孔隙弯曲因子, 反映孔隙里的气体运动相对于无约束空间中的运动, 由于障碍的存在而使得连通的路径更长, 它的数值可以通过孔隙率关联来获得[34]. 孔隙中的气体组分在混合气体中的有效扩散系数由分子扩散、Knudsen扩散、孔隙率、孔隙弯曲因子等综合确定.
2.2 反应动力学模型反应动力学根据文献[35]给出, 线性率(B/A, [μm/h])和抛物性率(B, [μm2/h])分别为
| $ \frac{B}{A}=5.808\ 7 \times 10^{6} \exp \left(-\frac{195\ 800}{R T}\right) $ |
| $ \left\{\begin{array}{l} B=524.19 \exp \left(-\frac{119\ 244}{R T}\right), & T \leqslant 1\ 673 \mathrm{~K} \\ B=1.505 \times 10^{6} \exp \left(-\frac{230\ 000}{R T}\right), & T>1\ 673 \mathrm{~K} \end{array}\right. $ |
其中
| $ B=2 D_{\mathrm{O}_{2}} c_{\mathrm{O}_{2}} \frac{\gamma M_{\mathrm{SiO}_{2}}}{\rho_{\mathrm{SiO}_{2}}}, \quad A=\frac{2 D_{\mathrm{O}_{2}}}{k_{\mathrm{ox}}} $ |
可得
| $ k_{\mathrm{ox}}=2 D_{\mathrm{O}_{2}} \frac{B / A}{B} $ |
式中, γ为材料里Si元素的质量百分数
| $ \gamma=\frac{m_{2} M_{\mathrm{Si}}}{m_{1} M_{\mathrm{C}}+m_{2} M_{\mathrm{SiC}}} $ |
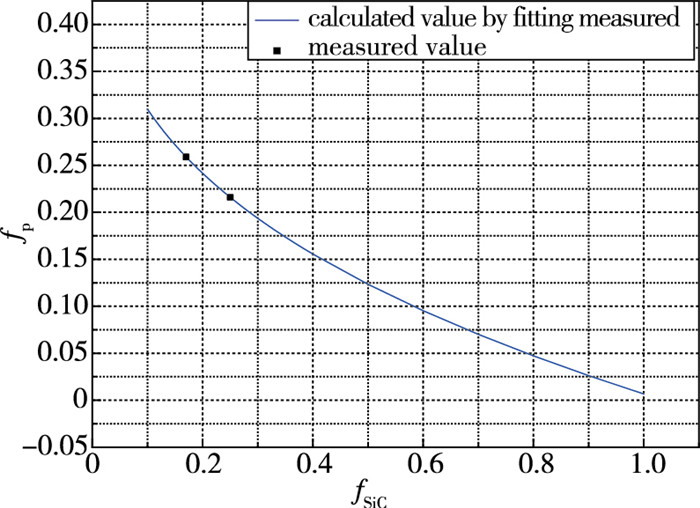
氧化膜中的孔隙情况是模型中极为重要的参数, 主要包括孔隙率、孔径和弯曲因子等. 采用压汞法获得了氧化膜里孔隙的弯曲因子和孔径, 其中, C-17% SiC氧化膜中二者分别为1.965和5.09 μm, C-25% SiC氧化膜中二者分别为2.139和2.71 μm. 图 4给出了孔隙率与SiC组分之间的关系. 黑色实心点为测量值; 蓝色线根据测量值公式拟合. 随着SiC组分含量的增加, 孔隙率逐渐减小, 当为纯SiC时, 蓝色线表示的值接近0, 即氧化膜非常致密. 下面计算采用蓝色线表示的拟合公式方法.
|
| 图 4 不同组分含量C/SiC氧化后氧化物孔隙率 Fig.4 Oxide porosity after oxidation of C/SiC composites with different component contents |
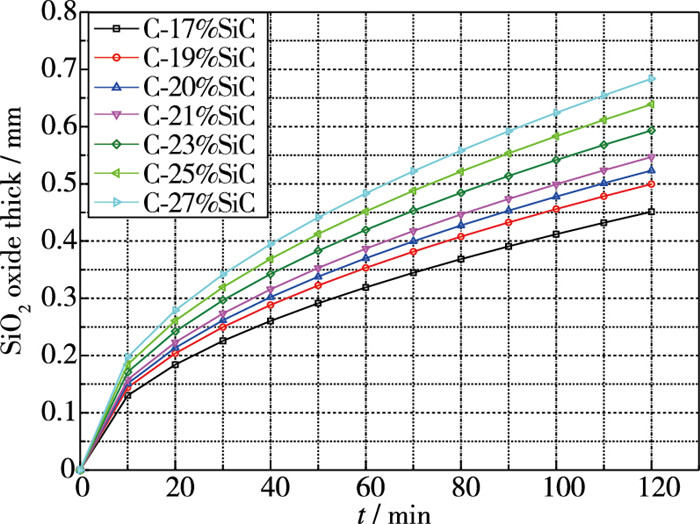
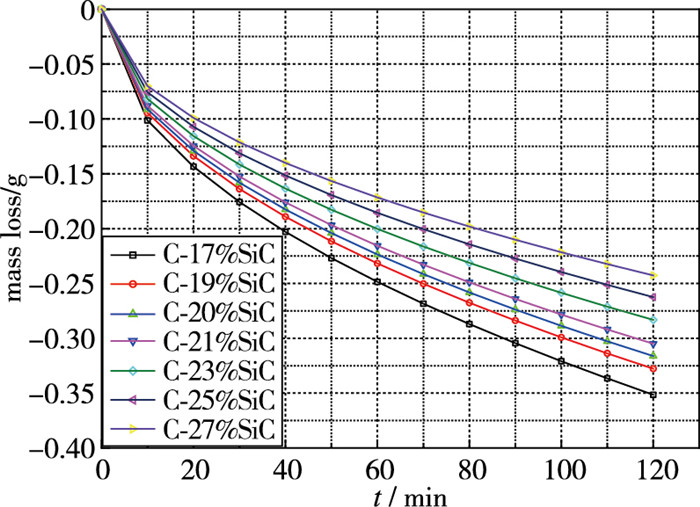
C/SiC复合材料的抗氧化性能与组分密切相关, 图 5, 6分别给出了氧化膜厚度与失重的计算值, 由图可知, 氧化膜厚度和失重均与时间成抛物型关系, 随着SiC组分含量的增加, 氧化膜厚度增加, 这说明在孔隙情况变化不大的情况下, C组分消耗留下的空间越小, 越有利于SiO2氧化物厚度的增加, 同时也抵消了部分C损失的质量, 降低了材料的整体失重的量.
|
| 图 5 不同组分含量C/SiC氧化后氧化膜厚度 Fig.5 Oxide film thickness after oxidation of C/SiC composites with different component contents |
|
| 图 6 不同组分含量C/SiC氧化后失重 Fig.6 Mass loss after oxidation of C/SiC composites with different component contents |
表 1给出了不同组分配比C/SiC复合材料在管式炉1 673 K下氧化2 h后的结果. 包括计算值与测量结果. 其中,CS17表示SiC的体积含量为17%. 在本次C/SiC复合材料配比范围内, C组分代表的原材料表面后退量与组分含量的关系不大, 计算获得的最大差量约0.06 mm. 氧化锋面实际上并不是一个平整的面, 存在一定深浅分布, 与氧化膜厚度计算值随SiC含量增加而增加的规律不同, 测量值基本上是先增加后降低、最后又增加的趋势. 试样失重测量值同样存在与氧化膜厚度变化类似的规律. 氧化膜厚度的计算值与测量值比较接近, 而失重的计算值约为测量值的一半, 建模计算表明, 它与材料后退量关系密切.
| 下载CSV 表 1 不同组分含量C/SiC复合材料氧化情况 Tab.1 Oxidation characterization of C/SiC composites with different component contents |
在原材料氧化后退大致相同的情况下, 由表 1给出的实验测量值可知, CS25氧化后形成较薄的氧化膜和造成较低的质量损失, 抗氧化性能相对较好, 选作考察不同温度影响的材料配方.
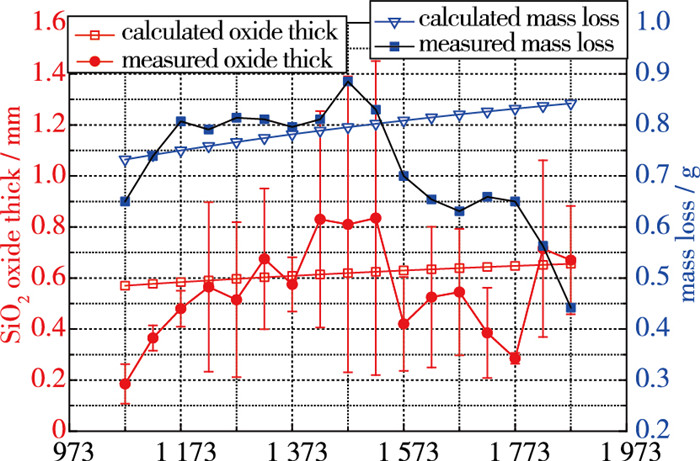
表 2给出了计算值与测量结果的对比, 图 7展示了变化规律. 计算表明, 随着温度升高, 氧化程度加强, 氧化膜厚度增加, 氧化膜随温度变化较为平缓, 当温度从1 073 K升高到1 873 K, 氧化膜厚度从0.57 mm增加到0.66 mm. 实验测试显示, 当氧化温度为1 573 K和1 673 K时, 表面氧化皮与基材由于热膨胀系数差异而开裂; 当氧化温度为1 823 K和1 873 K时, 材料表面凹凸不平, 只有部分氧化物残留. 氧化膜深度测量误差主要来源于氧化锋面的凹凸不同; 失重计算误差主要来源于试样表面积测量和厚度测量, 误差大约为其值的10%. 计算结果大致能反映出测量结果. 在1 673 K以后, 失重计算值与测量值偏差大, 测试结果发现, 在1 573 K及更高温度下, 氧化膜开裂, 甚至当温度高于1 773 K, 很难形成氧化膜, 已不再满足固态氧化膜-孔隙抗烧蚀的建模条件. 当温度为1 823 K和1 873 K时, 质量损失预测值与测量值相差较大, 计算值约为测量的2倍.
| 下载CSV 表 2 C-25%SiC复合材料不同温度下氧化情况 Tab.2 Oxidation characterization of C-25%SiC composites at different temperatures |
|
| 图 7 不同温度下C-25%SiC氧化计算值与测量值比较 Fig.7 Comparison of calculated and measured values of C-25%SiC composites at different temperatures |
在管式加热炉实验和微观形貌电镜表征中发现, C/SiC复合材料在中低温下可以氧化形成多孔固态SiO2氧化物, 提出基于固态氧化膜-孔隙的惰性氧化模型. 当氧化物在材料表面形成致密氧化膜时, 新型模型的计算氧化膜厚度的精准度较好.
C/SiC复合材料随着SiC组分含量增加, 材料的抗氧化性能呈现增强趋势. 厚度计算精准度优于质量损失的精准度.
C/SiC复合材料氧化随着温度升高而加剧. 当温度超过1 773 K后, 由于氧化膜难以存在, 后续还须研究材料反应生成全气态氧化产物的机理, 进一步提升模型在更大温度范围内的精准度.
| [1] |
崔尔杰. 近空间飞行器研究发展现状及关键技术问题[J]. 力学进展, 2009, 39(6): 658-673. Cui E J. Research statutes, development trends and key technical problems of near space flying vehicles[J]. Advances in Mechanics, 2009, 39(6): 658-673. DOI:10.3321/j.issn:1000-0992.2009.06.007 (in Chinese) |
| [2] |
Fahrenholtz W G, Wuchina E J, Lee W E, et al. Ultra-high temperature ceramics: materials for extreme environment applications[M]. Hoboken: Wiley, 2014.
|
| [3] |
Johnson S M. Ultra high temperature ceramics (UHTCs)[R]. NASA-Ames Research Center, 2015.
|
| [4] |
张伟刚, 成会明, 周龙江, 等. 纳米陶瓷/炭复合材料自愈合抗氧化行为[J]. 材料研究学报, 1997, 11(5): 487-490. Zhang W G, Cheng H M, Zhou L J, et al. SELF-Healing behavior of nano-ceramics/carbon composites during oxidation[J]. Chinese Journal of Materials Research, 1997, 11(5): 487-490. (in Chinese) |
| [5] |
韩杰才, 梁军, 王超, 等. 高超声速飞行器两类典型防热材料的性能表征与评价[J]. 力学进展, 2009, 39(6): 695-715. Han J C, Liang J, Wang C, et al. Material characterization and behavior evaluation of two typical thermal protection materials for hypersonic aircrafts[J]. Advances in Mechanics, 2009, 39(6): 695-715. DOI:10.3321/j.issn:1000-0992.2009.06.010 (in Chinese) |
| [6] |
Jacobson N S, Myers D L. Active oxidation of SiC[J]. Oxidation of Metals, 2011, 75(1): 1-25. DOI:10.1007/s11085-010-9216-4 |
| [7] |
Jacobson N, Harder B, Myers D. Oxidation transitions for SiC part I. active-to-passive transitions[J]. Journal of the American Ceramic Society, 2013, 96(3): 838-844.
|
| [8] |
Yoshinaka T, Kubota Y, Hatta H. Evaluation of passive and active oxidation transition of CVD-SiC by numerical calculation[R]. AIAA 2012-3007, 2012.
|
| [9] |
Harder B, Jacobson N, Myers D. Oxidation transitions for SiC part Ⅱ. passive-to-active transitions[J]. Journal of the American Ceramic Society, 2013, 96(2): 606-612. DOI:10.1111/jace.12104 |
| [10] |
Jacobson N S, Roth D J, Rauser R W, et al. Oxidation through coating cracks of SiC-protected carbon/carbon[J]. Surface and Coatings Technology, 2008, 203(3/4): 372-383. |
| [11] |
周述光, 刘骁, 国义军. 涂层孔隙对基体碳/碳材料的氧化损伤模拟[J]. 中国表面工程, 2019, 32(2): 154-162. Zhou S G, Liu X, Guo Y J. Simulation of oxidation damage of coating crack on carbon/carbon matrix materials[J]. China Surface Engineering, 2019, 32(2): 154-162. (in Chinese) |
| [12] |
Eckel A J, Cawley J D, Parthasarathy T A. Oxidation kinetics of a continuous carbon phase in a nonreactive matrix[J]. Journal of the American Ceramic Society, 1995, 78(4): 972-980. DOI:10.1111/j.1151-2916.1995.tb08424.x |
| [13] |
Halbig M C. The oxidation kinetics of continuous carbon fibers in a cracked ceramic matrix composite[D]. Cleveland: Army Research Lab, 2001.
|
| [14] |
国义军, 桂业伟, 童福林, 等. C/SiC复合材料烧蚀机理和通用计算模型研究[J]. 空气动力学学报, 2012, 30(1): 34-38. Guo Y J, Gui Y W, Tong F L, et al. Thermochemical ablation mechanisms and general relationship for C/SiC material oxidation[J]. Acta Aerodynamica Sinica, 2012, 30(1): 34-38. (in Chinese) |
| [15] |
Deal B E, Grove A S. General relationship for the thermal oxidation of silicon[J]. Journal of Applied Physics, 1965, 36(12): 3770-3778. DOI:10.1063/1.1713945 |
| [16] |
Stern K H. Oxidation of silicon, silicon carbide (SiC) and silicon nitride (Si3N4)[R]. NRL 5774, 1986.
|
| [17] |
邓代英, 罗晓光, 陈思员, 等. C/SiC材料主被动氧化转换机理及工程预测方法[J]. 中国科学: 技术科学, 2013, 43(7): 801-806. Deng D Y, Luo X G, Chen S Y, et al. The active-to-passive oxidation transition mechanism and engineering prediction method of C/SiC composites[J]. Sci China Tech Sci, 2013, 43(7): 801-806. (in Chinese) |
| [18] |
Milos F, Marschall J. Thermochemical ablation model for TPS materials with multiple surface constituents[C]. AIAA 94-2042, 1994.
|
| [19] |
邓代英, 陈思员, 俞继军, 等. C/SiC材料主动氧化烧蚀计算研究[J]. 空气动力学学报, 2011, 29(4): 496-500. Deng D Y, Chen S Y, Yu J J, et al. Calculation study of the active oxidation ablation of C/SiC[J]. Acta Aerodynamica Sinica, 2011, 29(4): 496-500. DOI:10.3969/j.issn.0258-1825.2011.04.017 (in Chinese) |
| [20] |
张红军, 康宏琳. C/SiC材料主被动氧化烧蚀机理及计算方法研究[J]. 宇航学报, 2019, 40(2): 223-230. Zhang H J, Kang H L. Investigation of thermochemical ablation model for active/passive oxidation transition mechanism of C/SiC composite[J]. Journal of Astronautics, 2019, 40(2): 223-230. (in Chinese) |
| [21] |
Malcolm W C Jr. NIST-JANAF thermochemical tables 4th Ed[M]. Monograph No.9: Physical and Chemical Reference Data, 1998: P1754.
|
| [22] |
Essenhigh R H, Froberg R W. The carbon-oxygen reaction an experimental study of the oxidation of suspended carbon spheres[R]. Deffense documentation center defense supply agency, Technical Reprot FS67-2(U), 1967.6.
|
| [23] |
Hatta H, Sohtome T, Sawada Y, et al. High temperature crack sealant based on SiO2-B2O3 for SiC coating on carbon-carbon composites[J]. Advanced Composite Mat-erials, 2003, 12(2/3): 93-106. |
| [24] |
Medford J. Prediction of oxidation performance of reinforced carbon-carbon material for space shuttle leading edges[C]. AIAA 75-0730, 1975.
|
| [25] |
周述光, 国义军, 刘骁. 恒温环境中ZrB2氧化行为模拟[J]. 无机材料学报, 2019, 34(6): 660-666. Zhou S G, Guo Y J, Liu X. Simulation of ZrB2 oxidation behavior at constant temperature ambient[J]. Journal of Inorganic Materials, 2019, 34(6): 660-666. (in Chinese) |
| [26] |
Wshburn E W. The dynamics of capillary flow[J]. Physical Review, 1921(17): 273-283. |
| [27] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 201650.1-2008/ISO 15901-1: 2005压汞法和气体吸附法测定固体材料孔径分布和孔隙度第1部分: 压汞法[S]. 北京: 中国标准出版社, 2008. GB/T 201650.1-2008/ISO 15901-1: 2005, IDT. Pore size distribution and porosity of solid materials by mercury porosimetry and gas adsorption-Part 1: mercury porosim-etry[S]. Beijing: Standards Press of China, 2008. |
| [28] |
Welty J R, Wilson C E, Wilson R E. Fundamentals of momentum heat and mass transfer[M]. New York: John Wiley & Sons, 1984.
|
| [29] |
Bird R B, Stewart W E, Lightfoot E L. Transport pheno-mena[M]. New York: John Wiley, 2002.
|
| [30] |
Szekely J, Evans J W, Sohn H Y. Gas-solid reactions[M]. New York: Academic Press, 1976.
|
| [31] |
Welty J R, Rorrer G L, Foster D G. Fundamentals of momentum, heat, and mass transfer[M]. 6th ed.. Hoboken: John Wiley & Sons, Inc, 2014: 454.
|
| [32] |
Wakao N, Smith J M. Diffusion in catalyst pellets[J]. Chemical Engineering Science, 1962, 17(11): 825-834. |
| [33] |
Satterfield C N. Mass transfer in heterogenous catalysis[M]. Cambridge: The MIT Press, 1969.
|
| [34] |
Zalc J M, Reyes S C, Iglesia E. The effects of diffusion mechanism and void structure on transport rates and tortuosity factors in complex porous structures[J]. Chemical Engineering Science, 2004, 59(14): 2947-2960. |
| [35] |
Zheng Z, Tressler R E, Spear K E. Oxidation of single-crystal silicon carbide: part Ⅱ. Kinetic mode[J]. Journal of The Electrochemical Society, 1990, 137(9): 925-930. |



