磁流体发电是将热能直接转换成电能的新型发电方式[1-2].它的基本工作原理仍是Faraday电磁感应定律, 不同的是用导电流体代替固体导体, 并使导电流体以一定速度通过与流动方向相互垂直的磁场, 切割磁力线而感生电动势, 从而产生电能.气体工质具有较高的电导率, 直接关系到发电机的热电转换效率, 是实现有价值的惰性气体磁流体发电机的重要因素之一, 基于此, 本文针对高温惰性气体等离子体的性能进行分析, 探讨影响因素.
在高温气体电离度的计算方法上, 陈栋泉等[3]提出了一种近似计算方法, 并进一步得到了高温气体状态方程和电离度的解析表达式, 计算了8种元素的电子浓度、各级离子浓度和相应的热力学量, 与文献值吻合很好, 同时也指出了该种方法的缺陷.针对文献[4-5]大都报道了300~30 000 K温度范围的等离子物性数据, 王海兴等[6]报道了利用双温度模型计算氦等离子的电导率等输运性质, 采用Saha方程计算等离子体组分, 采用基于将Chapman-Enskog方法扩展到高阶近似的方法, 计算获得电子温度不等于重粒子温度的情形下, 在300~40 000 K的温度范围内氦等离子体的电导率等参数.该研究结果表明压力和热力学非平衡参数对氦等离子的电导率等输运性质有较大影响.
本文首先介绍了3种典型的电导率计算模型(Spitzer模型、Z&L模型、M&G模型);然后描述了惰性气体添加种子的等离子体组分, 并建立了适合于惰性气体的电导率计算模型;最后研究了温度、压力等参数对等离子性能的影响.
1 电导率模型 1.1 Spitzer模型对于低密度、弱耦合等离子体, 往往采用Spitzer公式[7-8]计算电导率, 其表达式如下
| $ {\sigma _{{\rm{sp}}}} = \frac{1}{{6.53 \times {{10}^3}}}\frac{{{T^{3/2}}}}{{\ln \mathit{\Lambda }}} $ |
式中, σsp为采用Spitzer公式计算的理想等离子电导率, 单位为S/m, T为绝对温度, lnΛ为Coulomb对数.该公式可以通过Fokker-Planck方程、包含Boltzmann碰撞积分的Chapman-Enskog展开以及Sonine多项式展开等多种解析方法得到.
1.2 Z&L模型Zollweg和Liebermann[9]分析了Spitzer公式的推导过程, 考虑非理想区域的影响, 对Coulomb对数进行了修正, 改进的电导率模型为:
| $ {\sigma _{{\rm{zl}}}} = \frac{{{\gamma _\varepsilon }{T^{3/2}}}}{{38Z\ln {{(1 + 1.4\mathit{\Lambda }_{\rm{m}}^2)}^{1/2}}}} $ |
式中, σzl为Z&L模型计算的电导率, 单位为S/m, γε为考虑电子与电子碰撞对电导率的修正系数, Z为平均粒子电荷, lnΛm为Coulomb对数.
1.3 M&G模型Mohanti和Gilligan[10]采用更精确的非Debye屏蔽半径, 考虑了短程力的作用, 并修正了电子态密度.对Spitzer公式进行了修正, 得出的电导率方程为:
| $ \frac{{{\sigma _{{\rm{el}}}}}}{{{\sigma _{{\rm{sp}}}}}} = \delta \exp \left( {\frac{{\Delta \mu }}{{kT}}} \right)\left[{1-\frac{{{{\left( {\omega /kT} \right)}^4}}}{{{{\left( {\omega /kT + 0.8} \right)}^3}}}} \right] $ |
式中, σel为非理想等离子电导率, k为Boltzmann常数, Δμ为电子与离子间短程力作用引起的化学势. ω为由于屏蔽半径内电子的振荡而引起的能量耗散.
成剑等[11]对以上3种电导率模型进行了比较计算, 就它们在弱非理想区域的应用进行了分析.分析表明, 现有的典型等离子体模型对低温、高密度的弱非理想等离子体不能完全适用, 须进一步考虑电子与中性粒子的碰撞, 这也为本文的研究提供了参考思路.
2 惰性气体磁流体电导率 2.1 惰性气体等离子体的组成要实现磁流体发电, 首先必须使气体导电, 要使气体导电, 则必须至少使气体部分电离.惰性气体作为磁流体发电机的常用工质, 常通过预电离或添加种子的方式电离, 提高等离子体的电导率.
在惰性气体磁流体发电中, 发电工质一般选Ar, He等惰性气体, 添加易电离的种子有碱金属种子K, Cs等[12];在预电离方式中添加的气体种子可以使用惰性气体Xe[13-14].在这些等离子体中包含有各种粒子, 种子处于接近完全电离的状态, 工质气体处于弱电离的状态, 各种粒子都处于不断的热运动中.以Ar和Cs为例, 等离子体中有Ar原子、Ar离子、Cs原子、Cs离子和电子5种成分.
2.2 惰性气体等离子体的电导率宏观上看, 整个等离子体是呈电中性的, 亦即等离子体内粒子所带的正电荷总和等于粒子所带负电荷的总和, 即有:
| $ {n_{\rm{e}}} = \sum\limits_i^{ion} {n_i^ + } $ |
式中, ne为电子数密度, ni+为i组分的一次电离离子数密度,
不同组分的粒子还应满足分压定律和压力方程原则.
由电子碰撞引起的各种粒子数的密度可以通过Saha方程进行描述:
| $ \frac{{{n_{\rm{e}}}n_i^ + }}{{{n_i}}} = 2\frac{{g_i^ + }}{{{g_i}}}{\left( {\frac{{2{\rm{ \mathsf{ π} }}{m_{\rm{e}}}k{T_{\rm{e}}}}}{{{h^2}}}} \right)^{3/2}}\exp \left( {-\frac{{{\varepsilon _i}}}{{k{T_{\rm{e}}}}}} \right) $ |
式中, ni为i组分原子数密度, gi, gi+分别为i组分中性原子基态和离子基态的统计权重, me为电子的质量, k为Boltzmann常数, h为Planck常数, Te为电子温度, εi为i组分的电离电位, 单位为eV.
电导率采用标准形式的表达式:
| $ \sigma = \frac{{{n_{\rm{e}}}{e^2}}}{{{m_{\rm{e}}}{v_{\rm{e}}}}}, {v_{\rm{e}}} = \sum\limits_i {{n_i}{Q_{{\rm{e}}i}}{c_{\rm{e}}}}, {c_{\rm{e}}} = \sqrt {\frac{{8k{T_{\rm{e}}}}}{{{\rm{ \mathsf{ π} }}{m_{\rm{e}}}}}} $ |
式中, ve为电子与其他粒子的平均碰撞频率, ce为电子的Maxwell分布的情况下平均热速度, Qei为电子与i组分粒子的碰撞截面, 以惰性气体Ar为例, 电子与不同组分的碰撞截面为[15]:
| $ \begin{array}{l} {Q_{{\rm{e- Ar}}}} = \frac{4}{3} \times (0.46 \times {10^{- 23}}{T_{\rm{e}}}- 0.32 \times {10^{ - 20}})\\ {Q_{{\rm{e - ion}}}} = 6{\rm{ \mathsf{ π} }}{\left( {\frac{{{e^2}}}{{12{\rm{ \mathsf{ π} }}{\varepsilon _0}k{T_{\rm{e}}}}}} \right)^2}\ln \left[{12{\rm{ \mathsf{ π} }}{{\left( {\frac{{{\varepsilon _0}k}}{{{e^2}}}} \right)}^{3/2}}\sqrt {\frac{{T_{\rm{e}}^3}}{{{n_{\rm{e}}}}}} } \right] \end{array} $ |
式中, ε0为真空介电常数, e为电子电量.
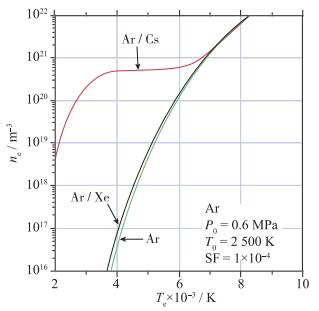
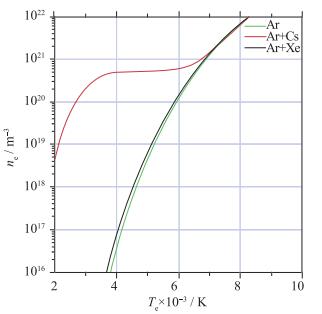
3 惰性气体磁流体等离子体性能分析采用以上惰性气体磁流体电导率模型, 针对滞止压力0.6 MPa, 滞止温度2 500 K, Xe和Cs作为种子时的含量为0.000 1, 研究了Ar的电离情况[13], 得到了电子数密度和电子温度的变化关系.其中本文计算的电子数密度如图 1所示, 文献[13]的计算结果如图 2所示, 图中P0, T0分别表示工质的滞止压力和滞止温度, SF表示种子的分数.对比可以得出, 两者结果一致性较好.
|
| 图 1 Ar工质的电子数密度(本文计算) Fig.1 Electron number density of argon(Liu′s) |
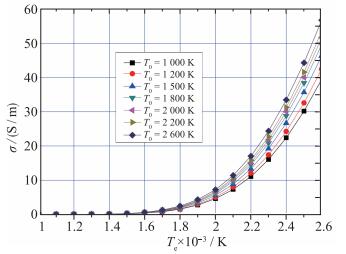
气体滞止压力为0.565 MPa, Ar在添加种子Cs的情况下, 不同气体温度下的电导率σ与电子温度Te关系如图 3所示.
|
| 图 3 Ar工质的电导率与电子温度的关系 Fig.3 Relationship between electrical conductivity and electron temperature of argon |
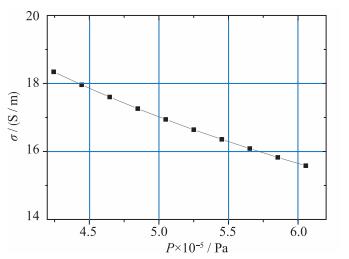
气体滞止温度为2 200 K, Ar在添加种子Cs的情况下, 不同压力P下的电导率σ变化关系如图 4所示.
|
| 图 4 工质电导率与压力的关系(2 200 K) Fig.4 Relationship between electrical conductivity and pressure(2 200 K) |
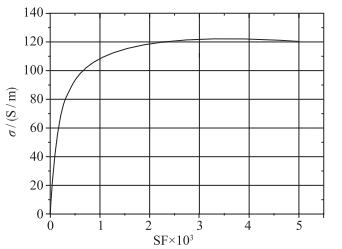
气体滞止压力为0.565 MPa, 滞止温度为2 200 K, Ar在添加种子Cs的情况下, 种子分数SF与电导率σ之间的关系如图 5所示.
|
| 图 5 工质电导率与Cs种子分数关系图 Fig.5 Relationship between electrical conductivity and seed fraction |
本文介绍了3种典型电导率计算模型(Spitzer模型、Z&L模型、M&G模型);描述了惰性气体添加种子电离后形成的等离子组分, 从电导率标准形式出发建立了适合于高温惰性气体的电导率计算模型, 并经文献验证了模型的合理性;分析研究了温度、压力等参数对等离子体性能的影响.本文为惰性气体磁流体发电技术的研究提供了参考.
| [1] |
居滋象, 吕友昌, 荆伯弘. 开环磁流体发电[M]. 北京: 北京工业大学出版社, 1998, 1-34. Ju Z X, LYU Y C, Jing B H. Open cycle MHD power generation[M]. Beijing: Beijing University of Technology Press, 1998, 1-34. (in Chinese) |
| [2] |
沙次文, 居滋象, 陈元利, 等. 开环磁流体发电工质-燃气等离子体的化学平衡组成及热力和电物理性质[J]. 工程热物理学报, 1980, 1(4): 329-336. Sha C W, Ju Z X, Chen Y L, et al. Chemicalcomposition in equilibrium, thermodynamic and electrical physical properties of combustion gas plasma used as working substance for open cycle MHD power generators[J]. Journal of Engineering Thermophysics, 1980, 1(4): 329-336. (in Chinese) |
| [3] |
陈栋泉, 陈湘涛. 高温气体电离度的近似计算方法[J]. 计算物理, 1985, 2(2): 148-160. Chen D Q, Chen X T. Approximate solution of the ionization degrees for high temperature gases[J]. Chinese Journal of Computational Physics, 1985, 2(2): 148-160. (in Chinese) |
| [4] |
Aubreton J, Elchinger M F, Rat V, et al. Two-temperature transport coefficients in argon-helium thermal plasmas[J]. Journal of Physics D:Applied Physics, 2004, 37: 34-41. DOI:10.1088/0022-3727/37/1/007 |
| [5] |
Aubreton J, Elchinger M F, Fauchais P, et al. Thermodynamic and transport properties of a ternary Ar-H2-He mixture out of equilibrium up to 30000 K at atmospheric pressure[J]. Journal of Physics D:Applied Physics, 2004, 37: 2232-2246. DOI:10.1088/0022-3727/37/16/004 |
| [6] |
王海兴, 孙素蓉, 陈士强. 双温度氦等离子体输运性质计算[J]. 物理学报, 2012, 61(19): 195203. Wang H X, Sun S R, Chen S Q. Calculation of two-temperature transport coefficients of helium plasma[J]. Acta Physica Sinica, 2012, 61(19): 195203. DOI:10.7498/aps.61.195203 (in Chinese) |
| [7] |
Spitzer L. Physics of fully ionized gasses[M]. New York: Interscience, 1956, 30-125.
|
| [8] |
宁烨, 颜君, 王建国. 等离子体中电子弹性散射截面及电导率计算[J]. 原子与分子物理学报, 2007(S1): 75-78. Ning Y, Yan J, Wang J G. Calculation of electron elastic scattering cross section and conductivity in plasma[J]. Journal of Atomic and Molecular Physics, 2007(S1): 75-78. (in Chinese) |
| [9] |
Zollweg R J, Liebermann R W. Electrical conductivity of nonideal plasmas[J]. Journal of Applied Physics, 1987, 62(9): 3621-3627. DOI:10.1063/1.339265 |
| [10] |
Mohanti R B, Giiligan J G. Electrical conductivity and thermodynamic functions of weakly nonideal plasma[J]. Journal of Applied Physics, 1990, 68(10): 5044-5051. DOI:10.1063/1.347092 |
| [11] |
成剑, 栗保明. 弱非理想等离子体电导率模型比较研究[J]. 中国科学技术大学学报, 2003, 33(3): 276-281. Cheng J, Li B M. Compare and study of electrical conductivity on nonideal plasmas[J]. Journal of University of Science and Technology of China, 2003, 33(3): 276-281. (in Chinese) |
| [12] |
Kabashima S, Yamasaki H. Recent progress in closed cycle non-equilibrium MHD power generation[C]. Proceedings of the 15th International Conference on MHD Energy Conversion, Moscow, 2005: 238-246.
|
| [13] |
Harada N. Closed cycle MHD power generation system without alkali-metal seed[C]. Proceedings of the 31st Intersociety Energy Conversion Engineering Conference, Washington, IEEE, 1996: 824-829. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=553804
|
| [14] |
Litchford R J, Harada N. Multi-MW closed cycle MHD nuclear space power via nonequilibrium He/Xe working plasma[C]. Proceedings of Nuclear and Emerging Technologies for Space 2011, Albuquerque, 2011: 3349. http://ntrs.nasa.gov/search.jsp?R=20110009914
|
| [15] |
Kobayashi H, Satou Y, Okuno Y. Numerical study on performance of disk MHD generator using frozen inert gas plasma[J]. IEEE Transaction on Plasma Science, 2002, 30(6): 2152-2159. DOI:10.1109/TPS.2002.806616 |