引言

飞行器几何外形的参数化方法在气动外形优化设计中有非常重要的作用, 参数化方法的性质^[1]对计算时间和设计空间的本质特性与范围有十分深刻的影响, 从而大大影响了气动外形优化的效率.常用的参数化方法^[2]在表达复杂曲面时, 为保证表达精度, 参数的个数会大量增加^[3], 优化过程中参数变量的随意变化还会导致不规则或不可控外形的产生, 影响优化设计的正常实现. Kulfan等提出了一种使用类别函数和形状函数表示几何外形的类别形状函数(class and shape transformation, CST)法^[4], CST方法设计变量少, 具有良好的可控性和表达精度, 是一种简洁高效的参数化方法.近年来, CST方法在很多方面得到了应用, 包括超临界翼型设计^[5]、机翼减阻优化^[6]、增升装置的表达^[7]等, 相关学者还实现了飞翼布局^[8]和乘波体机身^[9]的CST参数化表示, 并对其进行了B样条修正^[10].这些工作主要是对翼型、机翼或简单飞行器的外形表达, 很少涉及复杂飞行器外形的表达, 难以实现复杂气动外形的统一参数化建模.为了扩展CST方法对飞行器外形曲面的表达能力, 本文提出了分块CST方法, 实现了复杂曲面分块的光滑连接, 完成了飞行器的全机参数化建模.

气动外形优化设计是一个多学科的研究领域, 它将参数化表示方法、最优化理论、气动分析模型整合在一起, 因此需要综合考虑这3方面因素对优化结果的影响.一般情况下, 参数化表示方法、最优化理论及气动分析模型是同等重要的, 任何一方面因素的失当都可能导致优化设计的失败.气动外形优化的设计者必须熟悉每一个模块, 并能够针对不同的物理问题进行合理的分析.对于优化设计中复杂的多点设计问题, 线性加权和Pareto策略是常用的处理方法, 有时竞争型的Nash均衡理论也可以引入处理此类问题.本文结合Pareto遗传算法^[11]、气动力快速计算方法^[12]和分块CST方法, 以某类乘波翼身组合体飞行器为例验证了它在高超声速气动外形优化设计中的作用.

1 分块类别形状函数变换法 1.1 CST方法的基本原理

本文以翼型为例, 阐述CST方法的基本原理.一般翼型的几何外形用CST方法表示为

$ \zeta \left( \psi \right){\rm{ = }}C_{{N_2}}^{{N_1}}\left( \psi \right)S\left( \psi \right){\rm{ + }}\psi {\zeta _{\rm{R}}}. $

其中，ζ=z/c为翼型无量纲z坐标, ψ=x/c为翼型的无量纲x坐标, ζ_R为无量纲后缘厚度, c为翼型弦长.类别函数$ C_{{N_2}}^{{N_1}}\left( \psi \right) $定义为

$ C_{{N_2}}^{{N_1}}\left( \psi \right) = {\psi ^{{N_1}}}{\left( {1 - \psi } \right)^{{N_2}}}. $

其中, N₁和N₂定义了几何外形的类别^[4].

形状函数S(ψ)有多种方法定义, 本文采用n阶Bernstein多项式的加权组合作为S(ψ)的表达形式, 如式(1):

$ \left\{ \begin{array}{l} S\left( \psi \right) = \sum\limits_{i = 0}^n {{b_i}B_n^i\left( \psi \right)}, \\ B_n^i\left( \psi \right) = \frac{{n!}}{{i!\left( {n - 1} \right)!}}{\psi ^i}{\left( {1 - \psi } \right)^{n - i}}. \end{array} \right. $

(1)

其中, $ B_n^i\left( \psi \right) $为n阶Bernstein多项式的分项, b_i(i=0, 1, …, n)为多项式的权重因子, 也是CST方法中需要确定的参数.

对于任意平面形状的曲面进行CST参数化建模, 可以通过坐标变换将曲面块在x-y平面的两个方向进行单位化处理, 采用Bernstein多项式对曲面块进行描述, 同时在曲面块的特征方向上增加类别函数, 得到曲面块的CST方法表示形式为

$ \zeta \left( {\psi, \eta } \right) = C_{{N_2}}^{{N_1}}\sum\limits_{i - 0}^{{N_x}} {\sum\limits_{j = 0}^{{N_y}} {{b_{i, j}}B_m^j\left( \eta \right)B_n^i\left( \psi \right)} } . $

(2)

其中，ψ为无量纲的x坐标, η为无量纲的y坐标, ζ为无量纲的曲面z坐标. $ C_{{N_2}}^{{N_1}} $为类型函数, 当特征方向选取x或y时, 类型函数分别为$ C_{{N_2}}^{{N_1}}\left( \psi \right) $或$ C_{{N_2}}^{{N_1}}\left( \eta \right) $.$ {B_n^i\left( \psi \right)} $和$ {B_m^j\left( \eta \right)} $为两方向的Bernstein多项式函数, b_i,j是曲面控制参数.坐标变换的表达式为

$ \psi = \frac{{x - {x_{\rm{L}}}}}{{{x_{\rm{R}}} - {x_{\rm{L}}}}}, \eta = \frac{{y - {y_{\rm{D}}}}}{{{y_{\rm{U}}} - {y_{\rm{D}}}}}. $

(3)

其中，x_R, x_L为曲面块在x-y平面上x方向的边界, y_U, y_D为曲面块在x-y平面上y方向的边界.式(3) 将曲面块在x-y平面的自变量区域变为ψ-η平面上的单位正方形区域.当特征方向沿y方向时, 式(2) 中的ζ与曲面块z坐标的变换关系为

$ \zeta = \frac{{z - \eta {z_{\rm{U}}} - \left( {1 - \eta } \right){z_{\rm{D}}}}}{{{y_{\rm{U}}} - {y_{\rm{D}}}}}. $

其中z_U与z_D分别是曲面块位于y_U与y_D边界处轮廓线的z坐标.轮廓线是一条三维曲线, 可以采用二维CST方法分别表示轮廓线在x-y和x-z平面的投影，即

$ \begin{array}{l} \vartheta \left( \psi \right) = C_{{N_2}}^{{N_1}}\left( \psi \right){S_y}\left( \psi \right) + \left( {1 - \psi } \right){\vartheta _{\rm{L}}} + \psi {\vartheta _{\rm{R}}}, \\ \varsigma \left( \psi \right) = C_{{N_2}}^{{N_1}}\left( \psi \right){S_z}\left( \psi \right) + \left( {1 - \psi } \right){\varsigma _{\rm{L}}} + \psi {\varsigma _{\rm{R}}}. \end{array} $

其中$ {\vartheta _{\rm{L}}} $与$ {\vartheta _{\rm{R}}} $以及$ {\varsigma _{\rm{L}}} $与$ {\varsigma _{\rm{R}}} $分别为轮廓线起点与终点偏离原点的位置.

1.2 分块处理及曲面接合方法

飞行器的外形复杂, 机翼机身很难用一整块曲面表示, 即使同一曲面的性质和复杂程度在不同区域也不同, 因此采用分块处理是十分重要和必要的.本文根据气动力和几何形状的不同性质将飞行器曲面划分为不同的区域, 每个曲面块区域分别采用CST方法进行参数化描述, 组合所有曲面块形成一个完整的飞行器曲面.

在分块单独采用CST方法进行描述时, 很难在相邻块边界保证相接曲面块的连续和光滑, 因此需要增加相应的约束来保证曲面块在交接处的连续光滑性.本文分析了CST曲面在边界处取值和导数的特性, 推导了CST曲面在边界处取值和导数值与特定参数的关系, 给出了保证相邻曲面块连续光滑的参数约束条件.

由n阶Bernstein多项式(1) 推导导数公式，即

$ B{{_{n}^{i}}^{\prime }}\left( \psi \right)=\left\{ \begin{align} & -n{{\left( 1-\psi \right)}^{n-1}}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=0 \\ & n\left[B_{n-1}^{i-1}\left( \psi \right)-B_{n-1}^{i}\left( \psi \right) \right], i=1, \cdot \cdot \cdot, n-1 \\ & n{{\psi }^{n-1}}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=n \\ \end{align} \right. $

由Bernstein多项式及其导数的数学性质可知, Bernstein多项式在边界处由$ B_{n}^{0}\left( \psi \right) $和$ B_{n}^{i}\left( \psi \right) $控制, 其导数值由$ B{{_{n}^{0}}^{\prime }}\left( \psi \right), B{{_{n}^{1}}^{\prime }}\left( \psi \right) $和$ B{{_{n}^{n-1}}^{\prime }}\left( \psi \right), B{{_{n}^{n}}^{\prime }}\left( \psi \right) $确定.这种特性便于确定CST曲面在边界处的值和导数值, 从而可以控制相应的参数保证邻近曲面块的连续和导数连续.

以特征方向为ψ方向举例, 考虑η方向的边界连续条件.边界处η=0和η=1, 此时式(2) 简化为

$ \begin{array}{l} {\zeta _{\eta = 0}} = C_{{N_2}}^{{N_1}}\left( \psi \right)\sum\limits_{i = 0}^{{N_x}} {{b_{i, 0}}B_n^i\left( \psi \right)}, \\ {\zeta _{\eta = 1}} = C_{{N_2}}^{{N_1}}\left( \psi \right)\sum\limits_{i = 0}^{{N_x}} {{b_{i, {n_y}}}B_n^i\left( \psi \right)} . \end{array} $

只要控制b_i,j的首行参数即可保证η=0处的边界条件, 控制末行参数可保证η=1处的边界条件.

下面讨论CST曲面在边界处的导数连续条件. CST曲面在η方向的导数为

$ {{{\zeta }'}_{\eta }}=C_{{{N}_{2}}}^{{{N}_{1}}}\left( \psi \right)\sum\limits_{i=0}^{{{N}_{x}}}{\sum\limits_{j=0}^{{{N}_{y}}}{{{b}_{i, j}}B{{_{m}^{j}}^{\prime }}B_{n}^{i}\left( \psi \right)}}. $

当η=0时,

$ B{{_{{{N}_{y}}}^{j}}^{\prime }}{{\left( \eta \right)}_{\eta =0}}\left\{ \begin{align} & -{{N}_{y}}\ \ \ \ \ \ \ \ j=0 \\ & {{N}_{y}}\ \ \ \ \ \ \ \ \ \ \ \ j=1 \\ & 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ j=2, \cdot \cdot \cdot, {{N}_{y}} \\ \end{align} \right.. $

曲面导数公式简化为

$ {{{\zeta }'}_{\eta =0}}={{N}_{y}}\cdot C_{{{N}_{2}}}^{{{N}_{1}}}\left( \psi \right)\left[\sum\limits_{i=0}^{{{N}_{x}}}{{{b}_{i, 1}}B_{n}^{i}\left( \psi \right)-\sum\limits_{i=0}^{{{N}_{x}}}{{{b}_{i, 0}}B_{n}^{i}\left( \psi \right)}} \right]. $

当η=1时,

$ B{{_{{{N}_{y}}}^{j}}^{\prime }}{{\left( \eta \right)}_{\eta =1}}=\left\{ \begin{align} & 0\ \ \ \ \ \ \ \ \ \ \ \ j=0, \cdot \cdot \cdot, {{N}_{y}}-2 \\ & -{{N}_{y}}\ \ \ \ j={{N}_{y}}-1\ \ \ \ \ \ \ \\ & {{N}_{y}}\ \ \ \ \ \ \ \ \ j={{N}_{y}} \\ \end{align} \right., $

曲面导数公式简化为

$ {{{\zeta }'}_{\eta =1}}={{N}_{y}}\cdot C_{{{N}_{2}}}^{{{N}_{1}}}\left( \psi \right)\left[\sum\limits_{i=0}^{{{N}_{x}}}{{{b}_{i, {{N}_{y}}}}}B_{n}^{i}\left( \psi \right)-\sum\limits_{i=0}^{{{N}_{x}}}{{{b}_{i, {{N}_{y}}-1}}B_{n}^{i}\left( \psi \right)} \right]. $

由此可以看到b_i,j两端的两行系数决定了边界处的导数值.连续性条件已确定首行或末行的系数, 因此仅需调整第2行或倒数第2行的参数即可满足导数连续条件.

2 Pareto遗传算法及气动力评估模型

本文从参数化方法出发, 结合优化算法和气动力预测方法, 建立了气动外形优化设计平台.下面介绍本文使用的优化和气动力预测方法.

2.1 Pareto遗传算法

多目标问题(multi-objective optimization problem, MOP)的本质是在多数情况下, 各个子目标之间是矛盾的, 也就是说, 某个子目标性能的提升可能导致其它子目标性能的下降.这意味着很难让所有的子目标同时达到最优.多目标优化就是在各个子目标之间加以协调, 使得各个子目标达到系统所需的最优情况.

极小值的多目标无约束优化问题可以表示为

$ \min :\ \ \left\{ {{f}_{1}}\left( x \right), {{f}_{2}}\left( x \right), \cdot \cdot \cdot, \right.\left. {{f}_{n}}\left( x \right) \right\}. $

式中，f_i(x)为优化子目标函数, 其中i=1, 2, …，n.

法国经济学家Pareto最早研究了经济领域内的多目标优化问题^[11], 他的理论被称为Pareto最优性理论.多目标问题需要优化一组费用函数, 其解不是单一点, 而是一组点的集合, 称之为Pareto最优集. Pareto最优集定义如下:

对于最小化多目标优化问题, n个目标变量f_i(i=1, …, n)组成的向量$ \mathit{\boldsymbol{\bar{f}}}\left( {\bar{x}} \right)=\left( {{f}_{1}}\left( {\bar{x}} \right), {{f}_{2}}\left( {\bar{x}} \right), \cdot \cdot \cdot, {{f}_{n}}\left( {\bar{x}} \right) \right) $其中x_u∈U为决策变量, 若x_u为Pareto最优解, 满足:当且仅当, 不存在决策变量x_v∈U使得$ \mathit{\boldsymbol{v}}=\mathit{\boldsymbol{f}}\left( {{{\bar{x}}}_{v}} \right)=\left( {{v}_{1}}, \cdot \cdot \cdot, {{v}_{n}} \right) $支配$ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{f}}\left( {\bar x} \right) = \left( {{u_1}, \cdot \cdot \cdot ,{u_n}} \right) $，即不存在x_v∈U使得成立:

$ \forall i\in \left\{ 1, \cdot \cdot \cdot, \left. n \right\} \right., {{v}_{i}}\le {{u}_{i}}\ \wedge \ \exists i\in \left\{ 1, \cdot \cdot \cdot, \left. n \right\} \right., {{v}_{i}}<{{u}_{i}} $

本文的优化算法选择为遗传算法, 根据文献[13]的研究结果, 在基本遗传算法的基础上加入了基于排序的适应度分配方法和优选技术, 可以提高遗传算法的效率.基于排序的适应度分配方法是根据某一个体在种群中的顺序来确定该个体的选择概率, 这样就克服了基于比例的适应度分配方法中某一个体适应度过大而影响选择过程的问题.本文使用线性排序, 对于一个大小为N的种群, 个体的适应度可以计算如下:

$ \text{Fit}\left( {{P}_{\text{OS}}} \right)=2-\text{SP}+\frac{2\left( \text{SP}-1 \right)\left( {{P}_{\text{OS}}}-1 \right)}{N-1}. $

式中，P_OS为个体在种群中的序位；SP为选择压力, 一般取1~2之间的值.

优选技术是把父代群体及其产生的中间群体组织成一个具有2倍群体规模的大群体, 并在这个大群体中根据适应值信息进行排序, 保留适应值较大的一半群体, 使其直接进入下一代.这样就保留了到当前为止进化代中的多个优良个体, 从而使优化算法利用了更多的遗传信息来加速进化过程, 提高了遗传优化的效率.使用优选技术时, 容易陷入局部最优, 所以要使用较大的交叉概率和变异概率.

将Pareto策略应用于遗传算法, 本文开发实现了Pareto遗传算法程序处理多目标优化问题.它的具体实现是将多个目标值直接映射到适应度函数中, 在Pareto最优集的基础上提出了一种基于秩的适应度函数形式, 先将多目标函数值组成一个向量代表一个个体, 假定个体x_i在t代种群中有$ p_{i}^{t} $个个体支配它, 则它在种群内的秩为$ \text{rank}\left( {{x}_{i}}, t \right)=1+p_{i}^{t} $.对种群内的个体进行排序, rank为1者为Pareto最优个体.通过此算法即可求得多目标函数Pareto解.基于Pareto的多目标遗传算法能客观反映多目标优化问题的本质, 虽然其求秩过程复杂, 运算量较大, 但随着计算机技术的发展已经越来越广泛地应用到工程实践中.

2.2 高超声速气动力快速计算方法

飞行器的气动外形优化设计需要进行大量的气动力计算^[14], 由于成本和计算能力的限制, 不可能对每一个外形进行较广泛的风洞试验或较多机时的CFD数值计算, 因此使用高效的气动力评估方法十分必要.本文主要针对高超声速飞行器的气动设计问题, 因此介绍了高超声速的一系列快速预测方法，并分析了这些方法的特点, 将其应用于高超声速飞行器的优化设计, 并以类HTV-3X为例验证了高超声速快速计算方法的有效性.

高超声速气动力的工程算法种类繁多, 每种方法的适用工况不尽相同, 计算时需要根据不同的工况不同的几何外形选择合适的方法.因此, 要通过工程方法得到具有较高精度的解, 首先要求计算工具具有很大的灵活性, 可以对飞行器不同部件甚至是部件的不同曲面设置不同的计算方法；其次要求使用者熟悉各种方法并且具有丰富的计算经验.本文使用了两类方法计算无黏气动力, 一类基于面元法, 另一类是基于近似流线的激波膨胀波方法.黏性力对阻力贡献很大, 因此使用基于面元的黏性力计算方法.基于面元碰撞角的无黏气动力计算方法计算速度快, 只要给不同部件选择合适的计算方法, 就可以得到满意的结果.本文使用了大量的主流计算方法, 比如切楔切锥法、Newton法、Prandtl-Meyer方法等, 具体理论可见文献[12].

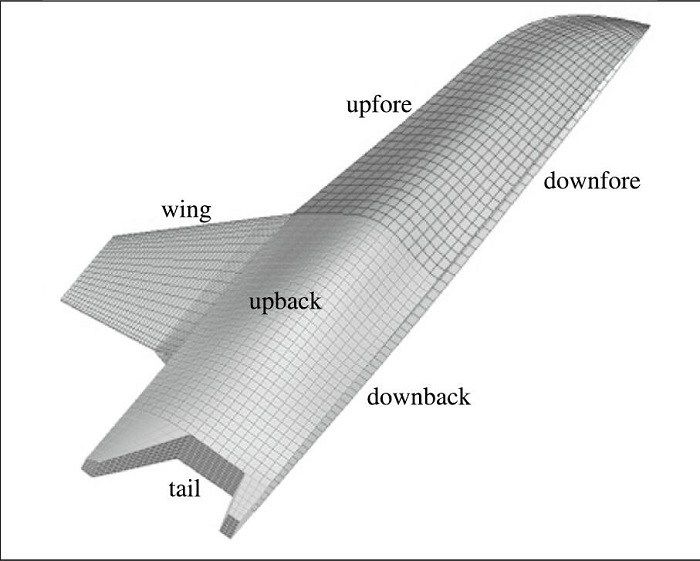
以上方法的实现均需要合适的面元网格, 使用前文所阐述的分块CST方法, 可自动生成高超声速快速计算方法需要的面元网格.划分网格时, 根据计算模型的流场特性将其分为多个部件, 如机翼、机身等, 然后再将每个部件分为多个具有简单拓扑结构的面, 最后对每个面划分面网格.这种面网格的划分策略有两个好处：第一, 最终分成的面拓扑结构简单, 在很大程度上简化了复杂外形的面网格划分工作; 第二, 将计算模型划分为多个部件, 可以根据不同部件甚至不同面的流场特性选择不同的计算方法, 大大提高了计算精度. 图 1给出了类HTV-3X飞行器的无黏计算面元网格, 黏性力使用基于面元法的Spalding-Chi方法^[15].

同时采用CFD对同一外形进行验证计算, 网格为非结构, 网格量约1.2×10⁶, 湍流模型使用S-A模型, 计算条件均为M=4.5, 高度H=30km, 攻角α=3°. 图 2给出了快速计算方法与CFD方法的压力系数对比.

从图 2可以看到压力分布吻合得很好, 对其压力进行积分得到了两种算法的气动力数据, 见表 1, 两者的误差在10%以内, 尤其是升阻比非常接近, 说明了方法的有效性.

3 类乘波翼身组合体优化设计 3.1 类乘波翼身组合体参数化建模

为了说明分块CST方法在优化设计中的作用, 本文以某类乘波翼身组合飞行器为例进行了分块CST方法建模, 并对其进行了以升阻特性为目标的优化设计.初始外形见图 3, 模型来自于美国空军Falcon计划^[16], 该飞行器的机身投影面积较机翼面积明显大很多, 机身为主要升力面.对于大多数的高超声速飞行器, 都是利用前机身的压缩产生主要升力, 因此前机身下表面需要细致设计; 机翼作为次要升力部件, 具有很大的改善空间, 也需重点设计.由初始外形的几何和气动特性确定此飞行器的分块如下:机身前部, 机身后部, 翼身融合部与机翼, 对各部分曲面进行上下分割, 整个飞行器外形曲面分为8个曲面块.

机身前部和后部曲面的建模结果见图 4, 曲面按照1.2节的接合方法对前后部机身曲面的控制参数施加约束, 保证机身表面连续光滑, 从图 4中可以看到截面形状在机身曲面块的交接处光滑连续.

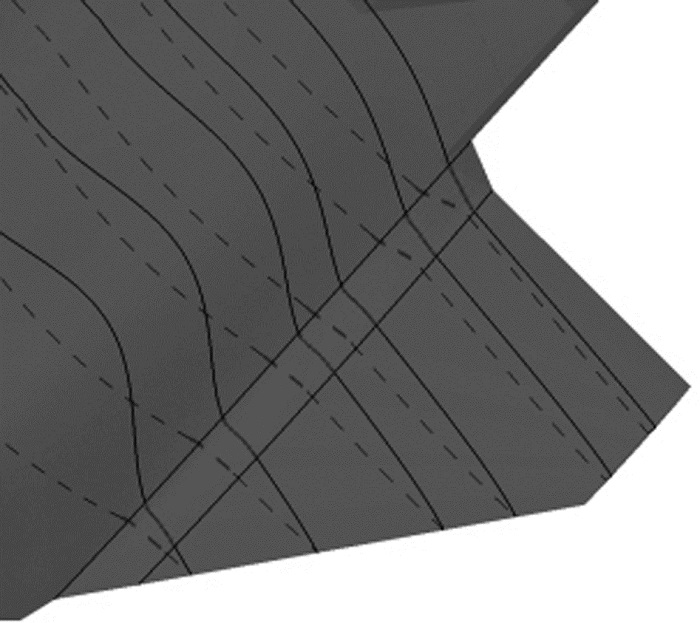
提取相邻机身和机翼曲面的边界, 按照前文介绍的接合方法, 约束曲面控制参数即可生成翼身融合面. 图 5中翼身融合面截面形状的变化与相邻曲面一致, 保证了交接区域的连续光滑.机翼采用梯形翼, 翼型选择为对称双弧翼型, 考虑机身后体减阻与发动机尾喷口放置, 参照HTV-3X高超声速飞行器^[16]采用样条插值生成了尾锥部分.

翼型选择双弧形, N₁=1.0, N₂=1.0;机身为双锥形曲面, 截面形状在边界处的斜率较小, 因此也选取N₁=1.0, N₂=1.0.飞行器的平面形状控制参数包括前后机身长度、宽度, 轮廓线参数, 机翼位置, 翼面积, 展弦比, 梢根比, 后掠角等, 总共21个; 前后机身分别选取6×5和4×4阶Bernstein多项式, 机翼使用3×2阶多项式, 考虑到相邻曲面的参数约束关系、机身曲面的对称性等, 曲面控制参数为72个.

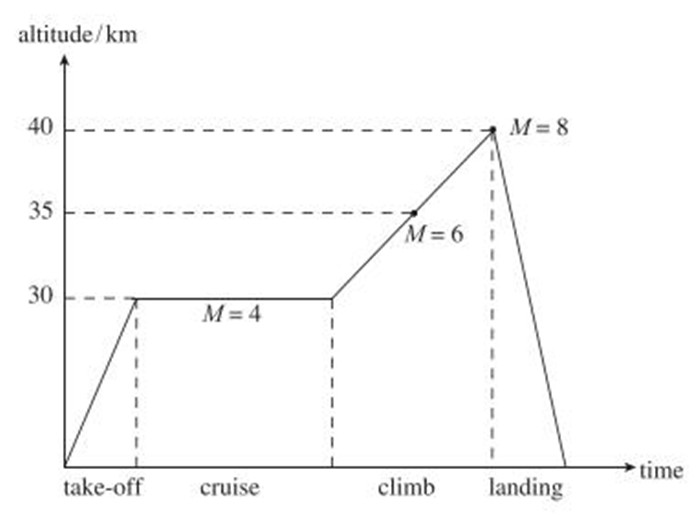
3.2 多目标优化设计及结果

本文拟设计一个上升式的高超声速飞行器，此类飞行器的飞行任务可描述如下:飞行器正常起飞后进入巡航高度, 以一定速度巡航至特定位置, 再改为爬升过程, 到达一定高度和速度后执行目标任务, 然后返回.这种飞行器要兼顾巡航和爬升性能, 其飞行任务剖面如图 6所示.

从气动力角度讲, 该飞行器在巡航时需要有好的升阻比特性.而在整个爬升过程中, 阻力尽可能小, 所以子目标定义为不同高度时的飞行器阻力最小.若考虑整个过程, 就需要处理无穷多个子目标, 实际计算时无法实现.因此, 取爬升过程的两个阶段作为优化设计时的子目标, 加上巡航时的气动特性作为另一个优化目标.因此该型飞行器可以定义3个子目标:巡航飞行时的升阻比最大, 爬升过程的阻力最小, 具体定义及相应的计算状态如表 2所示.

在优化过程中, 高超声速飞行器的容积非常重要, 本文在优化时限定容积不小于原始容积的70%.实际优化时发现, 随着飞行器性能的提高, 前体的体积会大幅度减小.为了满足体积约束, 后体的体积开始增大, 由于使用工程方法很难对底阻进行精确估算, 这进一步导致后体的厚度增大, 很容易产生类似于“圆锥”的外形, 这是不合理的.因此本文施加厚度约束, 要求前后体对接处的厚度d₁不能小于后体尾缘处的厚度d₂.从气动力角度考虑, 设计目标为升阻比, 有可能出现升力过小的情况, 因此需约束升力系数, 指定升力系数的最小值为C_Lmin.因此此类飞行器优化设计问题可以表示为

$ \begin{array}{l} \max :\;\;\;\;\;\;\;\;\;\;\;\;\;\;F\\ \;\;\;s.t.\;\;\;\;\;{\left( {{C_{\rm{L}}}} \right)_i} \ge {\left( {{C_{{\rm{L}}\min }}} \right)_i}, \;\;i = 1, 2, 3, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;V \ge {V_{{\rm{ori}}}} \times 70\%, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{d_1} \ge {d_2}. \end{array} $

同时把使用线性加权法与Pareto遗传算法的优化结果进行了对比.线性加权法的目标函数为

$ F = {\omega _1}{\left( {{f_{{\rm{cruise}}}}} \right)_1} + {\omega _2}{\left( {{f_{{\rm{climb}}}}} \right)_2} + {\omega _3}{\left( {{f_{{\rm{climb}}}}} \right)_3}. $

式中, 加权系数ω_i需要充分考虑飞行任务中各阶段所占的比重, 由飞行任务可知, 巡航飞行时间要明显大于爬升时间, 大概能占飞行时间(不考虑起飞降落)的一半, 因此本文ω₁取1/2, 爬升过程比重相近, 因此ω₂和ω₃都取1/4.线性加权法要求各子目标的目标函数数量级应该保持一致, 本文通过除以某个系数来达到上述目的.对于升阻比而言, 其量级为10, 而阻力系数的倒数量级为10², 所以分别除以10和100, 如表 2所示.

基于Pareto的多目标遗传算法, 目标函数表示为

$ F = \left\{ {{{\left( {{f_{{\rm{cruise}}}}} \right)}_1}} \right., {\left( {{f_{{\rm{climb}}}}} \right)_2}, \left. {{{\left( {{f_{{\rm{climb}}}}} \right)}_3}} \right\}. $

约束条件和设计变量的范围不变, 采用与单目标设计相同的气动力计算方法, 进化400代, 每一代耗时大约135s, 因此总的优化时间为15h.值得注意的是Pareto遗传算法并未求得明显的Pareto前沿面, 并且所得的Pareto最优解个数较少, 只有5个, 表 3给出了Pareto最优解的各子目标取值.分析原因应该是以上3个子目标变化趋同, 矛盾性不强.

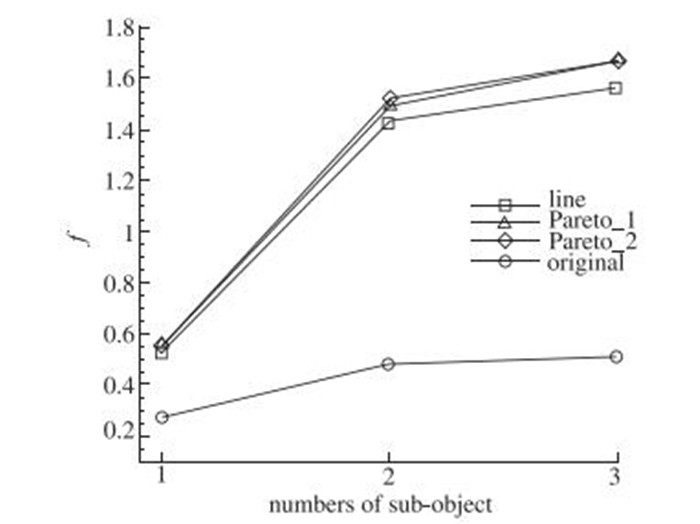
图 7给出了Pareto和线性加权法优化的子目标函数与初始值的比较, 从Pareto解中选择两个性能“最优”的结果(表 3中的最优解1和最优解2, 分别用Pareto_1和Pareto_2标示)与线性加权法得到的结果(用line标示)进行比较.由图 7可知, 线性加权法的优化设计结果和Pareto遗传算法的优化设计结果非常接近, Pareto方法的两个子目标的优化效果优于线性加权法的子目标.

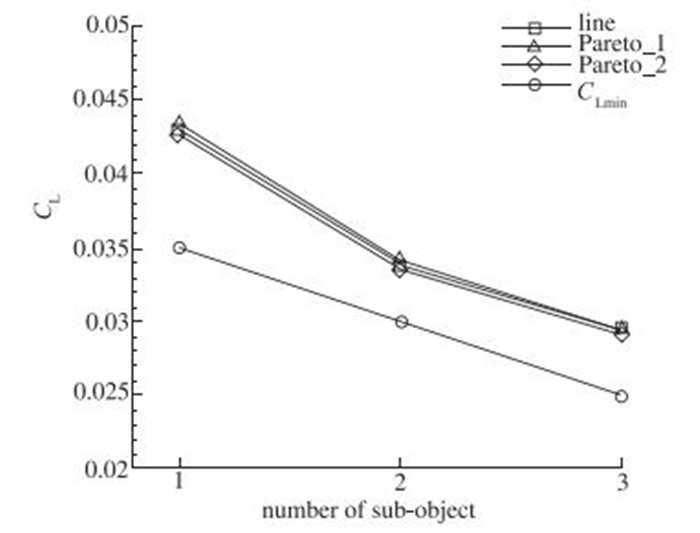
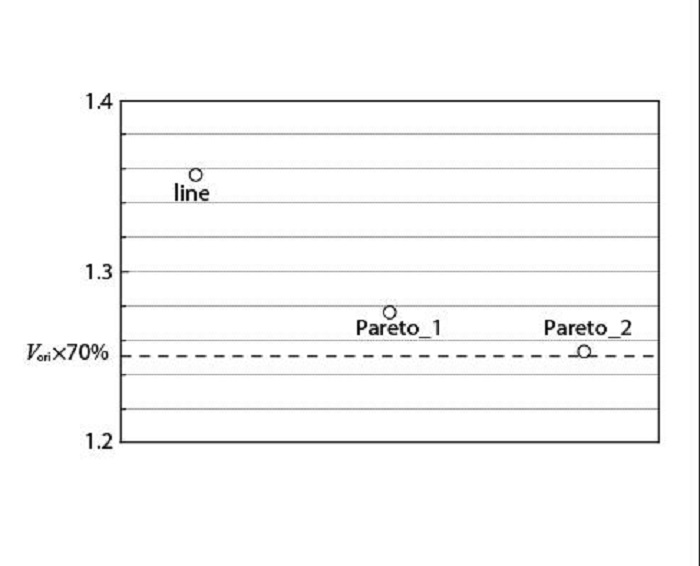
图 8给出了3个优化设计结果的升力系数与升力系数限制的比较, 可以看出3个设计结果的升力系数非常接近且都高于限制值. 图 9给出了3个优化设计结果的体积与体积限制的比较, 3个优化设计结果都满足体积约束, 线性加权法的优化设计结果体积要更大些.优化设计结果说明, 两种多目标优化设计方法对于子目标函数在数量级上有较大差异的多目标优化设计问题都是有效的.

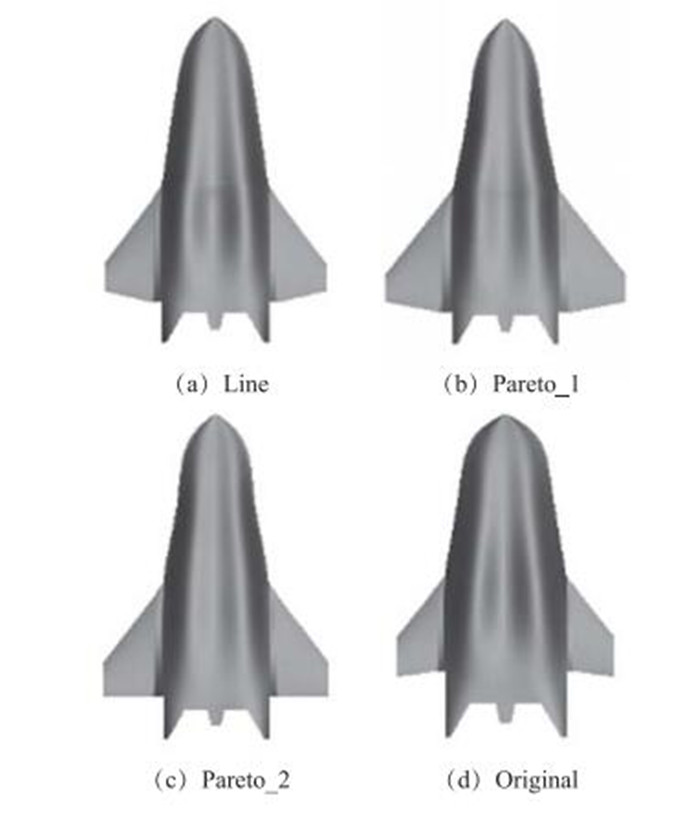
根据图 10和图 11给出的3个优化设计结果与初始外形的比较, 可以得知, 气动性能的提升同样来自前体压缩性能的提高最大机身厚度的减小以及机翼形状和位置的改变, 3个优化设计结果之间的差异不大.

3.3 应用优化设计平台的新型外形设计

3.1节中的优化设计从初始外形出发, 非常依赖初始外形的气动性能, 并且飞行器的外形大体确定, 平面形状和曲面变化不大.一个较明显的特征是飞行器外形机身两侧具有条状结构, 而在优化之后这些特征保留了下来.这些设计限制了飞行器的设计空间, 在充分测试了优化设计平台的基础上, 本文提出将设计变量的范围扩大, 使优化设计在一个较大的设计空间中自动寻优, 从而生成一系列具有较好气动性能的全新外形.这些飞行器外形不依赖于初始的飞行器外形, 仅与优化方法、参数化建模和气动力性能有关, 可以作为新型外形初步设计的工具.基于以上思路, 本文建立的优化设计平台在未指定初始外形的情况下可以作为新型飞行器初步设计的工具.

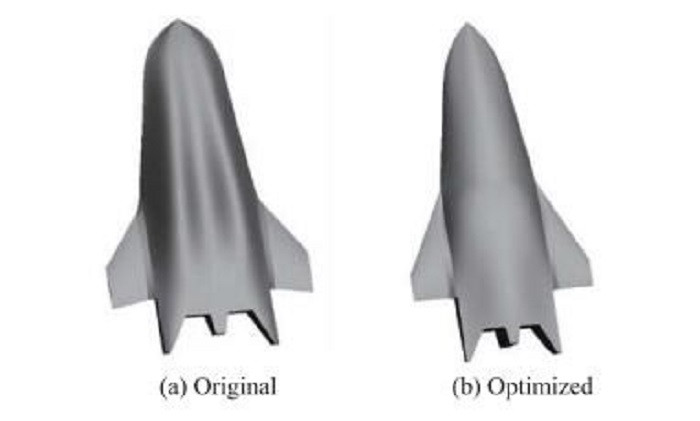
将下表面控制变量取值范围设为(-1.5, 0), 上表面取值范围设为(0, 1.5)，仍然采用多目标优化设计方法, 设计点状态和优化约束条件与3.1节中的算例类似.在最优Pareto集中选取一个升阻力较高的外形, 图 12和图 13分别是优化前后飞行器外形对比图和优化后外形的三视图.从图中可以看到飞行器外形平面形状变化不大, 而曲面形状变化较大, 机身近似为内厚外薄的乘波体构型, 机身两侧的加厚区域消失, 从而得到了新的飞行器构型.

表 4给出了优化后在第2个设计状态时的飞行器升力系数C_L阻力系数C_D和升阻比L/D.相对于3.1节中的飞行器优化外形, 此节的优化外形气动性能有所提高, 这是因为飞行器设计空间增大, 可以寻优得到气动性能更好的外形.

4 结论

通过对CST方法特性的分析, 本文提出分块CST方法, 实现了复杂飞行器曲面的参数化建模, 并结合Pareto遗传算法和气动力快速计算方法, 以类乘波翼身组合飞行器为例, 验证了其在优化设计中的应用.而对于气动外形设计中的多状态优化问题, 采用Pareto策略作为多目标优化工具.

气动外形优化算例和新型外形的设计算例表明, 基于分块CST方法、Pareto遗传优化算法和气动力快速计算方法建立的优化平台设计变量少, 具有较高的计算效率、较好优化效果与鲁棒性, 可以作为高超声速飞行器气动外形优化设计的有力工具.在下一步的工作中, 将考虑对包括气动减噪、飞行器稳定性在内的更多目标进行飞行器的工程多学科优化设计.