云是悬浮在空气中的大量小水滴和(或)冰晶共同组成的可见聚合体[1], 飞机穿过云层时水滴会撞击并贴附在其表面上, 而且由于高空温度较低, 特别是当飞机在低于冰点的结冰气象条件下飞行时, 过冷水滴碰到机体后会在机翼、进气道等部位冻结, 而其中机翼是飞机主要的升力装置, 其结冰危害性很大.风洞实验表明:在机翼前缘或上表面增加约1 mm的粗糙霜、雪和冰的沉积物可使升力减少30%以上, 阻力增加50%以上[2].为避免结冰事故的发生, 保证飞行安全, 通常会在飞机机翼上安装冰防护系统.目前大型飞机如客机已应用成熟的防除冰系统, 普遍的防除冰技术可分为液体防冰、机械除冰(气动带除冰和电脉冲除冰)、热力防除冰(电热除冰和气热防冰)3种[3-6].而对于一些小型飞行器如无人机等, 由于飞行速度低、长时间处于结冰环境且自身携带的防除冰能量有限, 防除冰问题较为严重, 亟待发展轻小型化、高效、低能耗防除冰技术.
2013年Nagappan等[7-9]提出利用底部加热的合成射流激励器进行结冰控制的思想, 该方法通过在斜劈表面下镶嵌数个加热的合成射流激励器产生周期性微型喷流, 阻碍过冷水滴与机翼表面的碰撞而实现防冰, 提供了将主动流动控制中的合成射流技术应用到防除冰领域的新思路.
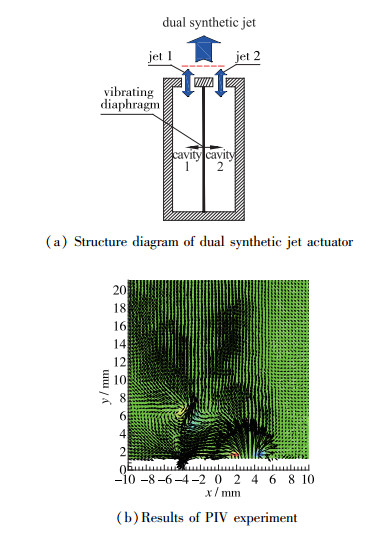
与传统防除冰技术不同, 主动控制技术通过影响水滴对防护区域的撞击特性进行防除冰, 从而阻断或减少了结冰的水滴来源, 提高了防除冰效率, 同时也兼具主动控制技术提升机翼气动性能的优点.本文利用课题组提出的合成双射流技术[10-11]对机翼水滴撞击特性进行主动流动控制, 该技术的核心元件是合成双射流激励器(如图 1所示), 由两个腔体和两个出口共享一个振动膜构成, 具有能量效率和射流频率倍增的特点, 因而在防除冰领域中的应用前景更为突出.通过流动控制在飞机易结冰区形成虚拟热气动外形, 减少或者避免过冷水滴水汽接触机体表面从而实现防除冰.
|
| 图 1 合成双射流激励器结构示意及PIV实验图 Fig.1 Structure diagram of dual synthetic jet actuator and results of PIV experiment |
由于过冷水滴是机翼结冰的主要来源, 所以计算水滴撞击量是计算结冰的基础.国内外对水滴收集系数进行了大量的实验与计算, 但都基于不加控制的水滴撞击特性, 计算方法分为两大类, 有Lag-range法和Euler法两种方法. Lagrange法在获得流场基础上对水滴建立运动方程, 计算得到每个水滴的运动轨迹, 进而得到水滴撞击特性, 但是该方法须对每个水滴进行计算, 计算量大, 不适合三维计算. Euler法将空气与水滴看作两相流, 在得到空气流场的基础上, 求解水滴相控制方程, 得到水滴分布, 该方法适合三维复杂构型的计算[12-15].
本文的工作基于Fluent软件进行, 采用Euler气液两相模型和EWF模型, 并且使用用户自定义函数(user-defined function, UDF)编写了合成双射流出口速度的UDF程序, 开展了合成射流/合成双射流对机翼的水滴撞击特性控制能力的研究.
1 控制方程与数值方法 1.1 控制方程本文采用Euler两相流计算, 其中, 空气相控制方程为不可压N-S方程[16]:
| $ \begin{array}{*{20}{c}} {\rho \left( {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla \mathit{\boldsymbol{u}}-\mathit{\boldsymbol{f}}} \right)-\nabla \cdot \mathit{\boldsymbol{\sigma }} = {\bf{0}}}\\ {\nabla \cdot \mathit{\boldsymbol{u}}{\rm{ = 0}}}\\ {\mathit{\boldsymbol{\sigma }}\left( {p, \mathit{\boldsymbol{u}}} \right) =-p\mathit{\boldsymbol{I}} + 2\mu \mathit{\boldsymbol{\varepsilon }}\left( \mathit{\boldsymbol{u}} \right)}\\ {\mathit{\boldsymbol{\varepsilon }}\left( \mathit{\boldsymbol{u}} \right) = \left( {\left( {\nabla \mathit{\boldsymbol{u}}} \right) + {{\left( {\nabla \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}} \right)/2} \end{array} $ |
式中, ρ, u, f, p, I, μ分别表示密度、速度、外部体积力、压力、特性张量和黏度, σ(p, u), ε(u)分别表示应力张量和应变率张量.
引入水滴体积分数α, 其定义为空间中水滴相所占的体积比例, 则可以建立水滴相的控制方程, 其连续方程和动量方程分别为:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{\rho _{\rm{d}}}\alpha } \right)}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{d}}}\alpha {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right) = 0}\\ {\frac{{\partial \left( {{\rho _{\rm{d}}}\alpha {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{d}}}\alpha {\mathit{\boldsymbol{u}}_{\rm{d}}} \times {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right) = {\rho _{\rm{d}}}\alpha K\left( {\mathit{\boldsymbol{u}}-{\mathit{\boldsymbol{u}}_{\rm{d}}}} \right) + {\rho _{\rm{d}}}\alpha \mathit{\boldsymbol{g}}} \end{array} $ |
其中, ρd为水滴密度, ud为水滴速度, K为惯性系数, 其表达式为:
| $ \begin{array}{*{20}{c}} {K = \frac{{18\mu }}{{{\rho _{\rm{d}}}d_{\rm{d}}^2}} \cdot \frac{{{C_{\rm{D}}}Re}}{{24}}}\\ {{C_{\rm{D}}} = \left\{ \begin{array}{l} 24\left( {1 + 0.15\;{Re^{0.687}}} \right)/Re\;Re \le 1\;000\\ 0.44\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Re > 1\;000 \end{array} \right.}\\ {Re = \rho \left| {\mathit{\boldsymbol{u}}-{\mathit{\boldsymbol{u}}_{\rm{d}}}} \right|{d_{\rm{d}}}/\mu } \end{array} $ |
其中, μ为空气动力黏性系数, dd为水滴直径, CD为水滴阻力系数, Re为相对Reynolds数.
1.2 简化假设与壁面条件处理方法实际云层内水滴的直径大小分布随机, 其形态处于动态的变化过程, 以单个水滴为对象, 它不仅与周围空气进行着热交换, 还发生着质量的变化, 例如水蒸气的凝结和蒸发等相变过程.同时, 在气动力作用下水滴也不可能保证绝对的圆球形, 且水滴之间还可能发生碰撞、融合或破裂等情况.因此进行两相流计算前须对来流水滴进行简化假设:
(1) 水滴在空气中分布均匀, 且保持球形; (2)过冷水滴的体积、质量、密度等物理参数保持不变; (3)水滴只受空气阻力、浮力和自身重力的作用, 且空气流动不受水滴运动影响.
飞行器在飞行过程中与云层中的水滴发生撞击, 进而发生水滴的收集, 在计算过程中机体表面要进行特殊的设定:对于空气, 机体表面采用无滑移边界条件; 对于水滴, 机体表面采用EWF边界条件(如图 2所示).
|
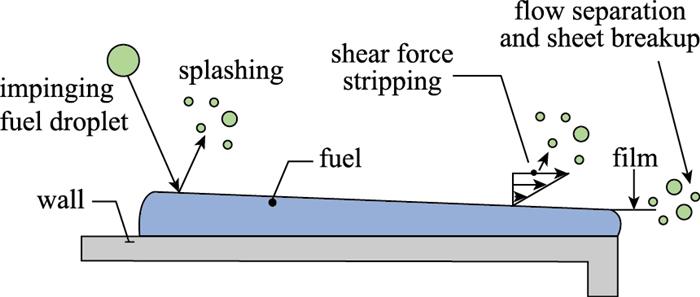
| 图 2 EWF模型 Fig.2 Eulerian wall film model |
EWF边界条件是Fluent软件为两相流计算中的离散相提供的一种固体壁面边界条件, 用于模拟单一成分的液滴撞击在壁面上形成液膜的过程, 该边界条件反映了液滴与壁面撞击的4种物理过程:黏附、反弹、展开和飞溅.其计算过程分为4步:初始液滴撞击在壁面边界上, 液滴黏附在壁面上, 计算薄膜的变化, 与空气相联结. EWF边界条件有如下假设和限制:
(1) 薄膜厚度小于500 μm, 薄膜内速度线性分布; (2)液膜表面直接与壁面接触, 热量通过壁面传导到液膜; (3)液膜温度不会超过液体的沸腾温度; (4)模拟的是瞬态过程.
使用EWF边界条件计算时, 由于既考虑了液滴与壁面的碰撞, 又考虑了液滴附着在壁面上的情况, 最接近于水滴撞击在壁面上的真实情况, 故在计算中均采用EWF边界条件.
水滴收集率的计算步骤为:首先, 采用Euler方法求解空气相与水滴相控制方程, 计算空气与水滴流场; 其次, 可获得当地水滴体积分数和水滴速度; 最后, 水滴收集率可由以下表达式得到:
| $ \beta = \frac{{\alpha {u_{{\rm{d}}n}}}}{{{\alpha _\infty }{u_\infty }}} $ |
其中, α和udn分别表示物体表面处水滴体积分数和水滴垂直于物体表面的速度, α∞和u∞分别为远端水滴体积分数和速度.物体表面每个单元单位时间收集水滴质量可以表示为:
| $ \dot m = \alpha {u_{{\rm{d}}n}}{\rho _{\rm{d}}}A $ |
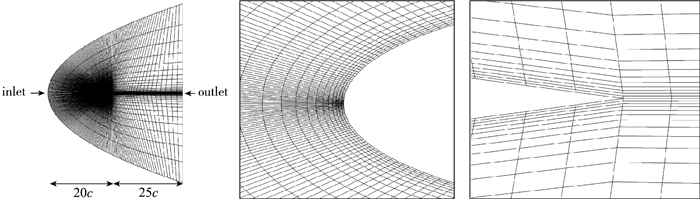
如图 3所示, 计算域为半个类椭圆区域, 由于EWF只能用于三维物面计算, 故模型Z方向设置为平直拉伸, 前锋面设置为以空气-Euler水滴为两相的入流边界, 机翼上下表面作为无滑移壁面边界条件, 且后面设置为压力出口的出流边界, 其中前端距离机翼20c, 后端距离机翼25c(c为机翼弦长).计算中由于Mach数较低, 采用不可压流动, 湍流模型选取标准k-ε模型, 利用SIMPLE算法求解Reynolds平均N-S方程得到其空气流场.
|
| 图 3 计算域及机翼前、后缘附近网格 Fig.3 Computational domain and meshes around leading edge and trailing edge |
NACA0012机翼采用的是C网格, 网格数量为115 566.机翼前缘合成射流出口处采用加密的方式, 前缘与尾缘附近网格如图 3所示.
合成射流激励器与合成双射流激励器的喷口均设置在机翼前缘, 以非定常吹、吸气边界条件的方法模拟合成射流对主流的干扰作用, 喷口设置为速度边界, 其定义为:
| $ u\left( t \right) = {u_{\rm{m}}}\sin \left( {2{\rm{ \mathsf{ π} }}ft + {\varphi _0}} \right) $ |
其中, um为合成射流速度幅值, f为合成射流入射频率, φ0为合成射流初始相位角, 定义射流入射方向与翼型弦长方向夹角为射流偏角θ, 喷口宽度为h.
来流速度为15 m/s, 喷口宽度h=2 mm, 合成射流速度幅值um=30 m/s, 施加合成射流/合成双射流的位置均在机翼前缘位置(重度结冰区域).为减少时间步长对射流流场和外流场的影响, 射流控制每周期划分为120步, 保证每个流动周期包含足够多的时间步数, 每一个时间步子迭代步数设为20步达到收敛.采用均匀来流对流场进行初始化, 先对未加控制的基准状态进行计算, 然后再加合成射流控制计算, 升阻力系数取流场呈现周期性变化特征后若干周期的平均值.
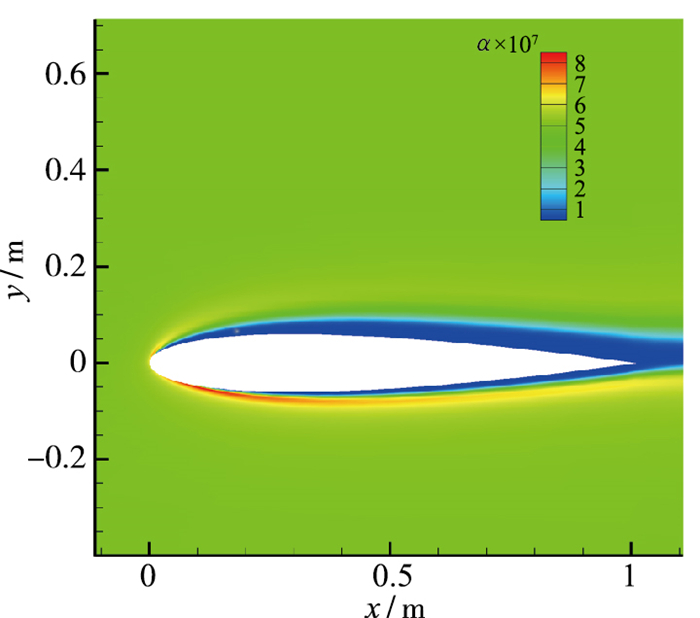
2 算例验证与参数选取 2.1 算例验证对本文选用的Fluent Euler模型和EWF模型进行验证, 计算条件为:翼型为NACA0012, 弦长为1 m, 攻角为5°, 来流速度为0.4M, 来流温度为300 K, 环境压力为101 325 Pa, 液态水含量为0.5 g/m3, 液态水体积分数为5e-7, 液滴直径为16 μm.得到的机翼附近液态水体积分数的分布图如4所示.
|
| 图 4 机翼附近区域水滴体积分数 Fig.4 Water volume fractions of area around airfoil |
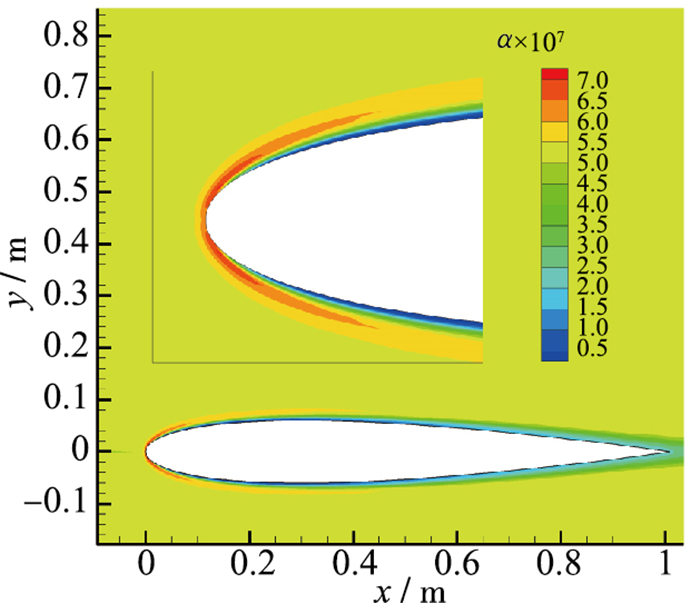
从图中可以看到机翼前缘处水滴含量较大, 水滴接近机翼后随空气偏折, 导致两侧水滴含量较大, 机翼表面只有前端有水滴碰撞, 其余部位没有水滴撞击, 机翼后方存在狭长的遮蔽区, 没有水滴存在, 主要是由于受机翼遮挡作用.
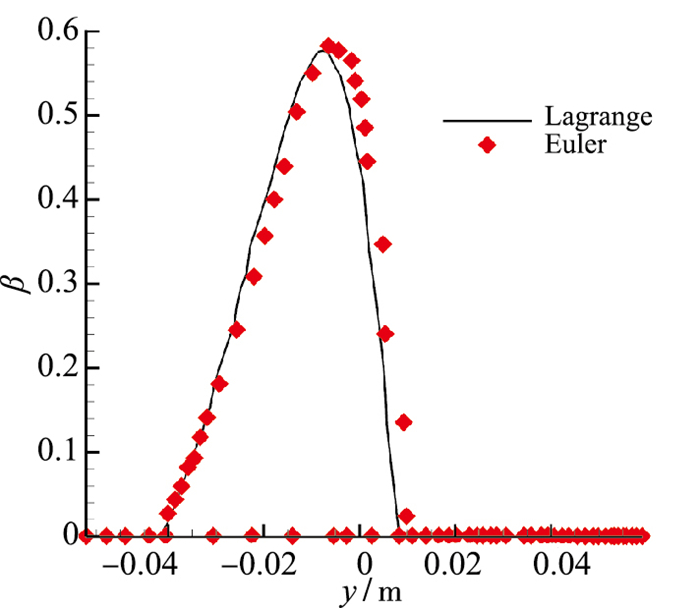
图 5为利用该方法得到的机翼表面水滴收集率分布与文献[17]采用Lagrange法计算结果的对比, 二者吻合良好, 验证了本文所使用方法与模型的准确性, 可应用于机翼水滴两相流动计算.
|
| 图 5 机翼表面水滴收集系数 Fig.5 Collecting efficiencies of airfoil surface |
本文采用合成射流/合成双射流开展了对机翼前缘水滴撞击特性的控制研究, 翼型为NACA0012, 弦长为1 m, 攻角为0°, 来流速度为15 m/s, 来流温度为300 K, 环境压力为101 325 Pa, 假设由合成射流/合成双射流激励器射流出口喷出的液态水含量也为0.5 g/m3, 液态水体积分数同为5e-7, 分别研究了合成射流/合成双射流在0°攻角时激励器频率对水滴分布的影响, 算例具体参数如表 1.
| 下载CSV 表 1 研究参数 Tab.1 Research parameters |
表 1中, 激励器分为不工作状态(baseline)、合成射流(synthetic jet, SJ)激励器工作状态和合成双射流(dual synthetic jet, DSJ)工作状态.
3 计算结果与分析 3.1 无控状态下机翼前缘水滴撞击特性在0°攻角激励器不工作时参考算例, 对应参数见表 1的case 1, 无控状态下机翼前缘水滴体积分数、前缘水滴速度和机翼表面水滴收集系数分别见图 6、图 7和图 8.
|
| 图 6 无控状态下机翼附近水滴体积分数 Fig.6 Water volume fractions of area around airfoil without jet control |
|
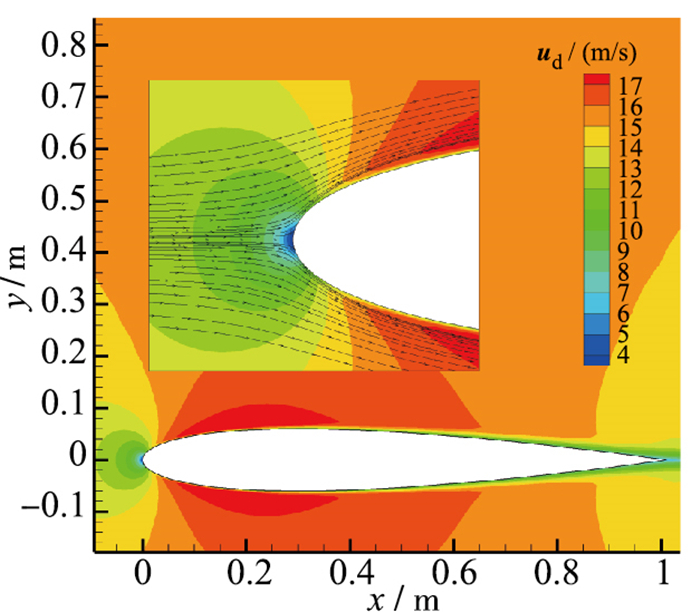
| 图 7 无控状态下机翼前缘附近水滴速度 Fig.7 Droplet velocities of area around airfoil leading edge without jet control |
|
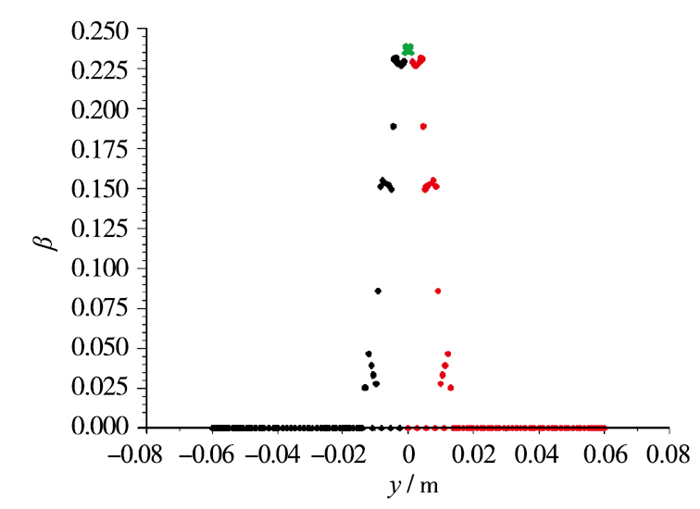
| 图 8 无控状态下机翼表面水滴收集系数 Fig.8 Collecting efficiencies of airfoil surface without jet control |
根据计算结果, 无控状态下机翼表面收集系数沿y方向的分布近似为对称的波峰, 且水滴聚集在y=±0.02 m区域, 机翼驻点处为最大收集点且收集系数约为0.24.
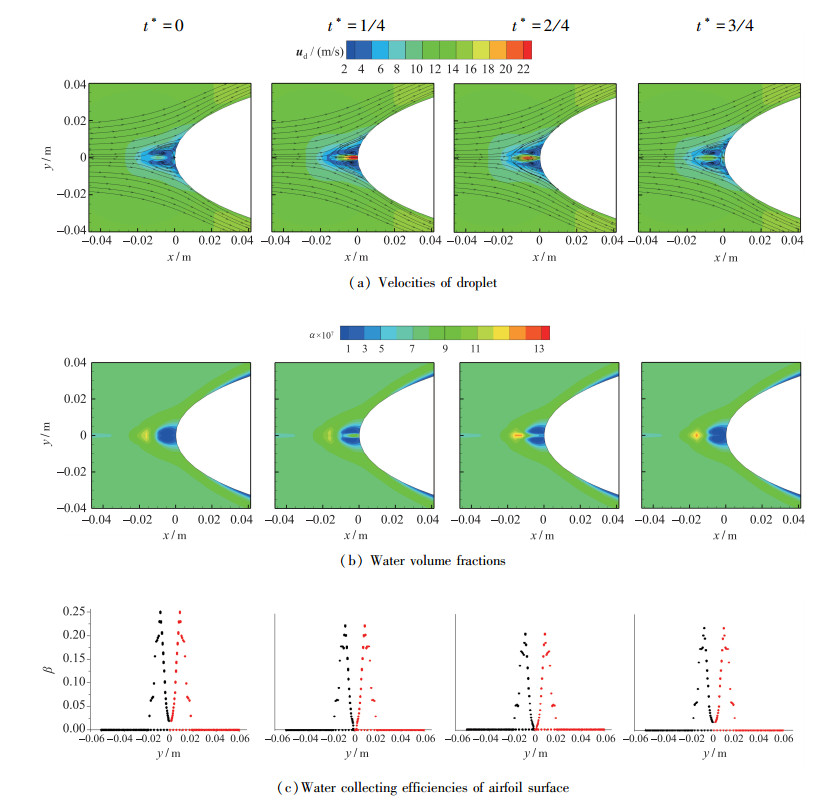
3.2 机翼前缘合成射流对水滴撞击特性的影响在0°攻角来流条件下, 分别对合成射流激励器频率为50和500 Hz的控制特性进行研究, 图 9给出了f=500 Hz时合成射流控制下的机翼前缘流场示意图, 即4个特征相位的机翼前缘水滴相速度、水滴相体积分数以及机翼表面水滴收集系数.其中, 相位t*=0定义为合成射流吹程开始时刻, 相位t*=1/4定义为合成射流吹程速度峰值时刻, 相位t*=2/4定义为合成射流吸程开始时刻, 相位t*=3/4定义为合成射流吸程速度峰值时刻.
|
| 图 9 Case 2: f=500 Hz, 合成射流控制下的机翼前缘流场 Fig.9 Case 2: f=500 Hz, flow field of area around airfoil leading edge with synthetic jet control |
在机翼前端设置喷口, 当合成射流位于吹程时, 腔体内流体被排出孔口, 并喷射出一股速度较高的射流, 逆向合成射流喷出后在机翼前缘一定距离与来流相遇形成接触面, 将含有水滴的来流与机翼前缘阻隔, 因而水滴无法直接撞击机翼前缘物面.同时, 逆向喷流在主流的作用下在喷口上下两侧诱导形成一对涡对, 并在涡对内部形成了水滴的“真空区域”; 当合成射流位于吸程时, 此时被吸入孔口的流体主要来源于上下两侧的涡对, 由水滴相的流线可知, 合成射流吸程增加了涡对的强度, 使得喷口上下两侧水滴的“真空区域”扩大, 但由于机翼喷口附近水滴的撞击速度增加, 相应也增加了水滴收集率. f=500 Hz合成射流控制下的机翼前缘水滴收集率峰值降低较少, 水滴收集率分布也从单峰改变为双峰.
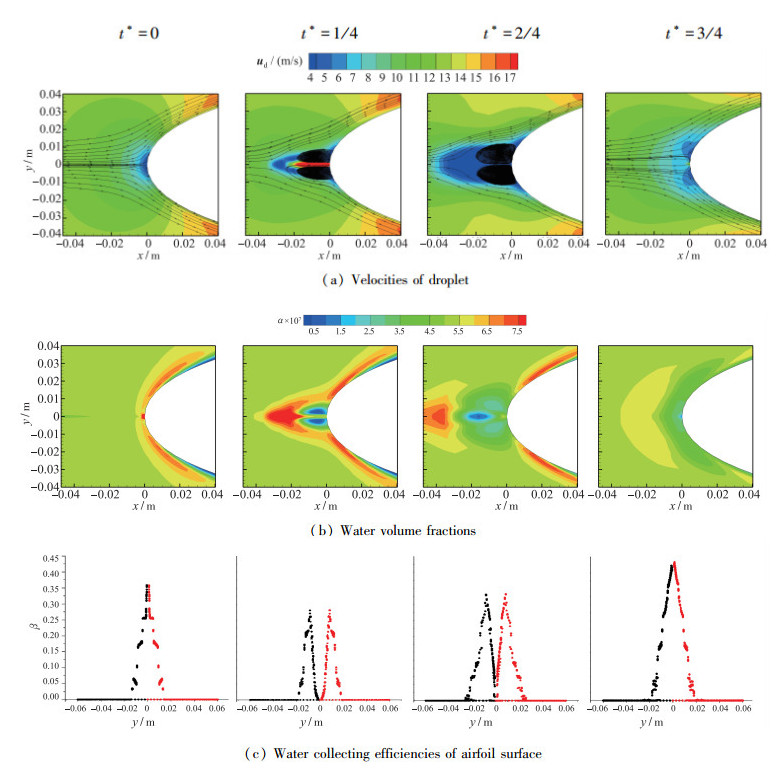
图 10给出了f=50 Hz合成射流控制下的机翼前缘流场示意图, 即4个特征相位的机翼前缘水滴相速度、水滴相体积分数以及机翼表面水滴收集系数.
|
| 图 10 Case 3: f=50 Hz, 合成射流控制下的机翼前缘流场 Fig.10 Case 3: f=50 Hz, flow field of area around airfoil leading edge with synthetic jet control |
当合成射流位于吹程时, t*=0, 来流直接撞击在机翼前缘, 由于喷口处有射流准备喷出, 故除喷口外其他位置水滴收集率分布与无控状态下机翼表面的水滴收集率分布相似, 而喷口处的水滴收集率较大; t*=1/4, 腔体内流体被排出喷口并达到速度峰值, 喷出的逆向合成射流“推开”附着在机翼前缘的来流并在机翼前缘一定距离与来流形成锥形的接触面, 同时, 逆向喷流在主流的作用下诱导产生上下两侧的一对涡对, 并在涡对内部形成了水滴的“真空区域”, 由于喷射的合成射流作用, 减小了喷口附近的水滴收集量, 故水滴收集率分布呈现“劈开”的两个波峰; 当合成射流位于吸程时, t*=2/4, 孔口处射流速度恢复为零, 在上一时刻形成的涡对继续发展并消散; t*=3/4, 孔口吸入流体速度达到最大, 来流重新撞击在机翼前缘表面, 孔口吸入的作用使得附近水滴的撞击速度增加, 相应增加了水滴收集率. f=50 Hz合成射流控制下的机翼前缘未起到改善水滴收集率的效果.
与无控状态下的水滴收集率(见图 8)相比, 布置在机翼前缘的合成射流有“劈开”来流撞击水滴的特性.合成射流频率对受控状态机翼前缘水滴收集率分布影响较大, 当处于低频状态下(与流场的特征频率同一个量级), 孔口附近流场呈现“喷-吸”的状态, 在机翼前缘上游不能形成稳定的闭合回流区, 因而不能减少机翼前缘水滴收集率; 当处于高频状态下(比流场的特征频率高一个量级), 在机翼前缘上游附近形成了一对稳定的闭合回流区, 它的基本原理是逆向喷流受到自由来流的阻挡, 反向而产生低速回流, 重新附于物面, 在上下附着点之间的区域形成了水滴的两个“真空区域”.由于回流区内部水滴速度和质量分数较低, 改变了机翼前缘的水滴收集率分布, 能够减少机翼前缘结冰程度并改变冰形, 起到了虚拟气动外形作用[18], 这种流场拓扑结构的变化类似于机翼前缘上游形成了闭式包线, 使得上游流线发生排移, 并且分别流向两侧.
3.3 机翼前缘合成双射流对水滴撞击特性的影响在0°攻角来流条件下, 采用500 Hz的合成双射流激励器对机翼前缘水滴控制特性进行了研究.两出口高度为3.6 mm, 间距为2 mm, 上下对称分布.
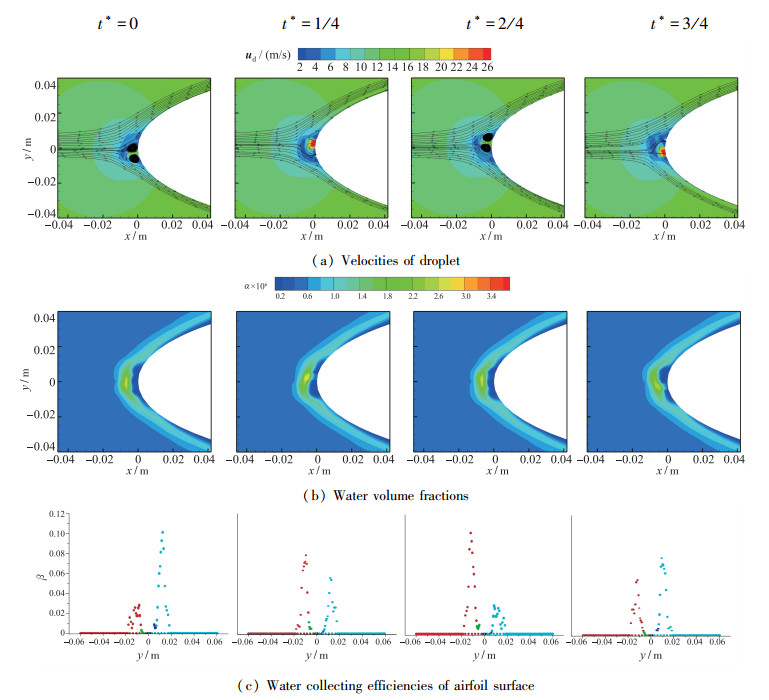
图 11给出了f=500 Hz合成双射流控制下的机翼前缘流场示意图, 即四个特征相位的机翼前缘水滴相速度、水滴相体积分数以及机翼表面水滴收集系数.
|
| 图 11 Case 4: f=500 Hz, 合成双射流控制下的机翼前缘流场 Fig.11 Case 4: f=500 Hz, flow field of area around airfoil leading edge with dual synthetic jet control |
t*=0时刻, 上喷口处有射流准备喷出, 由于前一时刻下喷口射流的喷射和来流共同的诱导作用, 在下喷口上下两侧诱导形成一对涡对; t*=1/4时刻, 上喷口处喷出射流且速度达到峰值, 喷出的逆向合成射流“推开”附着在机翼前缘的来流并在机翼前缘一定距离与来流形成接触面, 机翼前缘上游附近形成了回流区, 上喷口喷出的射流一部分向上回流, 而由于下喷口处吸入射流且速度达到峰值, 上喷口喷出的射流受到了下喷口的吸引, 故在上下喷口之间形成了“接力”的作用, 向下的回流区比向上的回流区域更大, 回流区域内部形成了水滴的“真空区域”, 且水滴速度较低; t*=2/4时刻与t*=3/4时刻分别是t*=0时刻与t*=1/4时刻的反相, 故机翼前缘水滴的流场与撞击特性分别与前两个时刻相反.
与合成射流相比, 合成双射流具有能量效率和射流频率倍增的特点, 使得合成双射流控制条件下机翼前缘的回流区域更大, 形成的虚拟气动外形的覆盖面积更广, 机翼前缘表面的水滴收集率也大幅降低, 水滴收集率峰值从无控状态下的0.24降低到了0.1, 水滴收集率分布也从幅值较高的单峰改变为幅值较低的双峰, 水滴收集量约为无控状态下的1/4, 形成了较好的防护效果.
根据相关文献[18]的结果, 还可将合成射流单出口布置在机翼上表面分离区附近, 通过向机翼分离区注入动量的方式改善上翼面的流场结构和压力分布情况, 因而在机翼大攻角下延迟流动分离.配合本文研究得到的合成射流/合成双射流改变机翼前缘水滴撞击特性的结果, 通过合理布置合成双射流两出口位置, 能够起到增升和防除冰的双重效果.
4 结论本文提出了利用合成双射流控制低速来流水滴撞击特性的新方法, 通过数值模拟, 研究了合成射流/合成双射流激励器对机翼前缘附近水滴流场控制的机理, 得出以下结论: (1)在机翼前缘布置合成射流, 合成射流处于吹程时会在前缘形成锥形的接触面, 具有“劈开”来流撞击水滴的特性.同时, 逆向喷流在主流的作用下会在喷口上下两侧诱导形成一对涡对, 并在涡对内部形成水滴的“真空区域”; (2)合成射流处于高频状态下(比流场的特征频率高一个量级), 能够在机翼前缘上游形成闭式包线, 使得上游流线发生排移, 并且分别流向两侧, 起到了虚拟气动外形作用.闭式包线内部是一对稳定的闭合回流区, 因为回流区内部水滴速度和质量分数较低, 改变了机翼前缘的水滴收集率分布; (3)合成射流处于低频状态下(与流场的特征频率同一个量级), 孔口附近流场呈现“喷-吸”的状态, 在机翼前缘上游不能形成稳定的闭合回流区, 不能减少机翼前缘水滴收集率; (4)在机翼前缘布置合成射流, 能够改变水滴撞击分布, 但水滴收集量几乎与无控状态一致, 在机翼前缘布置合成双射流, 由于其具有能量效率和射流频率倍增的特点, 能够在机翼前缘形成范围更大、更稳定的回流区, 因而大幅减少机翼前缘水滴撞击, 水滴收集量约为无控状态下的1/4, 具有较好的防护效果.
本文对于机翼前缘布置合成射流/合成双射流对水滴撞击特性的控制进行了机理分析, 对于最佳的射流频率、扰动幅值、不同攻角条件下的射流角度的选取, 以及射流温度对机翼前缘的防冰效果有待于下一步工作.
| [1] |
裘燮纲, 韩凤华. 飞机防冰系统[M]. 北京: 航空专业教材编审组, 1985. Qiu X G, Han F H. Aircraft anti-icing system[M]. Beijing: Aeronautic Specialty Textbook Read and Edit Group, 1985. (in Chinese) |
| [2] |
Lee S, Bragg M B. Investigation of factors affecting iced-airfoil aerodynamics[J]. Journal of Aircraft, 2003, 40(3): 499-508. DOI:10.2514/2.3123 |
| [3] |
马蕾, 王贤明, 宁亮. 飞机防冰涂料的研究进展[J]. 中国涂料, 2014, 29(1): 11-14, 18. Ma L, Wang X M, Ning L. Research progress of aircraft Anti-icing coatings[J]. China Coatings, 2014, 29(1): 11-14, 18. (in Chinese) |
| [4] |
李清英. 电脉冲除冰系统的实验、理论与设计研究[D]. 南京: 南京航空航天大学, 2012. Li Q Y. Research on the experiments, theories, and design of the Electro-impulse De-icing system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1014005381.htm |
| [5] |
Pellissier M, Habashi W G, Pueyo A. Design optimiza-tion of hot-air anti-icing systems by FENSAP-ICE[R]. AIAA 2010-1252, 2010.
|
| [6] |
肖春华. 飞机电热除冰过程的传热特性及其影响研究[D]. 绵阳: 中国空气动力研究与发展中心, 2010. Xiao C H. Study on heat transfer characteristics and effects of electrothermal aircraft deicing[D]. Mianyang: China Aerodynamics Research and Development Center, 2010(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90113-1011051861.htm |
| [7] |
Nagappan N, Golubev V. On icing control using thermally activated synthetic jets[C]. 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Grapevine, Texas: AIAA, 2013. http://www.researchgate.net/publication/268468059_On_Icing_Control_Using_Thermally_Activated_Synthetic_Jets
|
| [8] |
Nagappan N, Golubev V V. Parametric analysis of icing control using synthetic jet actuators[C]. 21st AIAA Computational Fluid Dynamics Conference, Fluid Dynamics and Co-located Conferences. San Diego, CA: AIAA, 2013. http://www.researchgate.net/publication/269047697_Parametric_Analysis_of_Icing_Control_Using_Synthetic_Jet_Actuators?ev=auth_pub
|
| [9] |
Nagappan N M. Numerical modeling of anti-icing using an array of heated synthetic jets[D]. Florida: Embry-Riddle Aeronautical University, 2013. https://commons.erau.edu/edt/109/
|
| [10] |
Luo Z B, Xia Z X, Liu B. New generation of synthetic jet actuator[J]. AIAA Journal, 2006, 43(10): 2418-2420. |
| [11] |
李玉杰, 罗振兵. 水滴结冰结霜及合成双射流除霜除冰实验研究[J]. 实验流体力学, 2016, 30(3): 27-32. Li Y J, Luo Z B. An experimental investigation on the process of droplet icing/frosting and defrosting/deicing using dual synthetic jet[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3): 27-32. (in Chinese) |
| [12] |
易贤, 王开春, 桂业伟, 等. 结冰面水滴收集率欧拉计算方法研究及应用[J]. 空气动力学学报, 2010, 28(5): 596-601, 608. Yi X, Wang K C, Gui Y W, et al. Study on Eulerian method for icing collection efficiency computation and its application[J]. Acta Aerodynamica Sinica, 2010, 28(5): 596-601, 608. (in Chinese) |
| [13] |
Tong X L, Luke E A. Eulerian simulations of icing collection efficiency using a singularity diffusion model[C]. 43rd AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada: AIAA, 2005. http://www.researchgate.net/publication/268567493_Eulerian_Simulations_of_Icing_Collection_Efficiency_Using_a_Singularity_Diffusion_Model
|
| [14] |
Iuliano E, Brandi V, Mingione G. Water impingement prediction on multi-element airfoils by means of Eulerian and Lagrangian approach with viscous and inviscid air flow[C]. 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada: AIAA, 2006. http://www.researchgate.net/publication/268563710_Water_Impingement_Prediction_on_Multi-Element_Airfoils_by_Means_of_Eulerian_and_Lagrangian_Approach_with_Viscous_and_Inviscid_Air_Flow
|
| [15] |
Iuliano E, Mingione G, De Domenico F, et al. An Eulerian approach to three-dimensional droplet impingement simulation in icing environment[C]. AIAA Atmospheric and Space Environments Conference, Toronto: AIAA, 2010. http://www.researchgate.net/publication/268556918_An_Eulerian_Approach_to_Three-Dimensional_Droplet_Impingement_Simulation_in_Icing_Environment
|
| [16] |
Stein K R, Benney R J, Kalro V, et al. Parachute fluid-structure interactions:3-D computation[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190(3/4): 373-386. |
| [17] |
Wirogo S, Srirambhatla S. An Eulerian method to calculate the collection efficiency on two and three dimensional bodies[C]. 41st Aerospace Sciences Meeting and Exhibit. Reno, Nevada: AIAA, 2003. http://www.researchgate.net/publication/268566438_An_Eulerian_Method_to_Calculate_the_Collection_Efficiency_on_two_and_Three_Dimensional_Bodies
|
| [18] |
Chen F J, Beeler G B. Virtual shaping of a two-dimensional NACA 0015 airfoil using synthetic jet actuator[R]. AIAA 2002-3273, 2002. http://www.researchgate.net/publication/24318180_Virtual_Shaping_of_a_Two-dimensional_NACA_0015_Airfoil_Using_Synthetic_Jet_Actuator
|



