2. 教育部流体力学实验室,北京航空航天大学,北京 100191
2. Ministry-of-Education Key Laboratory of Fluid Mechanics, Beihang University, Beijing 100191, China
随着空天技术的发展, 飞行器的高度、速度在进入21世纪以来有了巨大的突破, 人类更加快速地展开了太空科技的研究, 而往返太空与地球之间的空天载具目前而言开发难度较大, 尚未形成成熟的技术.因此, 返回舱作为载人/实验/返回地球的载具在未来很长一段时间内仍有重要作用.返回舱在进入大气至着陆期间, Apollo飞船再入速度高达11.2 km/s[1], 与空气发生剧烈摩擦会产生严重气动热现象.以第一宇宙速度7.91 km/s为例, 其单位动能为31.3 MJ/kg, 最大能流量达65 MW/m, 由对流、扩散、辐射[2]引起的加热烧蚀严重考验返回舱的性能.因此, 在设计返回舱时, 气动热的估计是非常重要的一个环节.而随着宇航技术的发展, 我国已开始进行火星着陆的研究, 对于火星而言, 其大气组分与地球不同(以CO2为主), 其气动热效应以及化学非平衡效应也有所不同[3-4].目前研究该课题的方法主要包括:风洞实验, 理论分析和数值模拟.
在高超声速条件下, 采用球冠倒锥形的返回舱有降低表面热流并提高阻力的优势, 因此目前国际上大多采用这种形式[5].各国也相继开展了对这种形式返回舱气动性能的研究. MacLean等[6]概述了高焓风洞LENS中Apollo形状的模型实验及数值模拟, 结果表明返回舱前体的受热情况最为严峻, 并且在返回舱靠近肩部的位置还会出现热流异常升高.
在进行实验的时候, 对于气动加热异常的肩部, 测热传感器的埋置会改变肩部表面的局部物面曲率, 影响局部流场, 而往往经过肩部后压力梯度骤降, 物理信息正是通过在肩部物面亚声速区向球冠传播.因此, 肩部测热传感器会引起测量的流场与原流场在肩部部分不符合.故发展数值模拟和工程算法成为必要.
目前, 求解返回舱气动热已经有一系列成熟的工程算法[7], 以Lees算法和Fay-Riddell算法为代表的驻点热流公式, 基于实际飞行数据和实验数据, 能够在可靠的精度内估计热流的数值.同时, 这些公式经过修正可以计算带有攻角的返回舱驻点和肩部气动热.除了连续流外, 还有用于计算自由分子流的Kemp-Riddell公式, 以及利用桥函数连接Lees公式和Kemp-Riddell公式得到过渡流的计算公式.但是在工程计算过程中往往以应用为主, 无法刻画流场的细节.试图精确获得高超声速全流场特性的研究早已开始, 特征线法[8]是在计算资源不发达情况下发展出来的.随着计算能力增强, 发展出一种先求解Euler方程再通过流线获得热流的方法.随着边界层方程的建立, 求解该方程获得高精度的方法也被设计出来[9].研究至今, 由于计算能力达到足够要求, 研究肩部热流机理细节的最好方法是模拟完全Navier-Stokes方程.因此, 数值模拟成为研究肩部热流机理的重要途径.
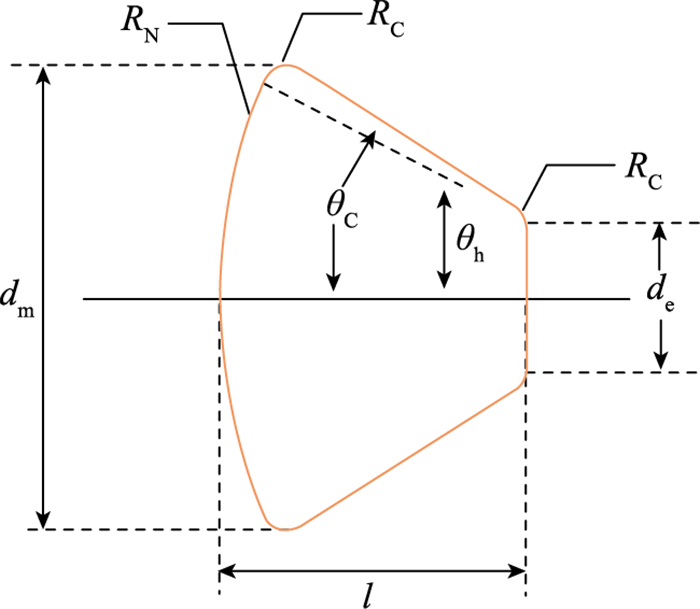
1 返回舱模型Apollo返回舱外形结构如图 1所示, 图中标注了返回舱剖面的一些参数, 其中, RN为球冠曲率半径, RC为拐角曲率半径, θC为倒锥角, θh为球冠半顶角, dm为最大截面半径, l为返回舱体长, de为返回舱小头直径.以上参数对应[6]的值列于表 1.
|
| 图 1 返回舱剖面图及几何参数 Fig.1 Dimensions of Apollo-like Reentry |
| 下载CSV 表 1 类Apollo模型几何参数 Tab.1 Geometry parameters of Apollo-like mode |
随着计算能力的提升, 目前对于高超声速可压流动问题通常采用直接数值模拟求解Navier-Stokes方程.随着数值分析的不断发展, 提出了很多高精度格式, 比如: TVD[10](total variation diminishing), ENO(essentially non-oscillatory), WENO[11](weighted essentially non-oscillatory)以及Discontinuous Galerkin等.这些格式都具有2阶以上的精度, 但是面对非线性问题以及网格不良好的情况, TVD格式会使得流场出现明显的不均匀性, 而WENO格式目前处理强激波问题时往往出现较强振荡[12], 这些鲁棒性不足的问题有时会影响解的精度和正确性.国内王发民等[13], 贺国宏等[14], 黄唐等[15]研究了格式对钝头体气动热计算的影响, 结果表明借鉴了NND(non-oscillatory and non-free-parameters dissipative)思想的格式对避免数值计算的奇异性有作用.阎超等[16]比较了Roe-FDS格式, Van-Leer-FVS格式以及AUSM+格式的热流计算分辨率, 认为驻点热流计算正确对热流分布有重要意义. AUSM+格式在同样网格下驻点热流计算较为准确, 其他格式也满足需求, 同时指出热流的计算对格式和网格比较敏感, 计算结果表明AUSM+和Roe格式由于对线性波有天然的高分辨率, 故可以获得较好的热流分布趋势.因此, Roe-FDS格式还是很多复杂问题的首选, 同时, Roe-FDS格式可以通过添加限制器提高格式精度, 对于本实验, 由于肩部热流较为复杂, 选择Roe-FDS格式作为空间离散方法比较稳妥.
以一维Euler方程为例:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} =-\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} $ |
其中, U=(ρ, ρu, e)T, F=(ρu, ρu2+p, (e+p)u)T. Roe-FDS格式对于第i个点上的差分可以写为
| $ \frac{{\partial {\mathit{\boldsymbol{U}}_i}}}{{\partial t}} =-\frac{1}{{\Delta x}}\left( {{\mathit{\boldsymbol{H}}_{i + \frac{1}{2}}}-{\mathit{\boldsymbol{H}}_{i-\frac{1}{2}}}} \right) $ |
式中, U为通量,
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_{i + \frac{1}{2}}} = \frac{1}{2}[\mathit{\boldsymbol{F}}({\mathit{\boldsymbol{U}}_{\rm{L}}}) + \mathit{\boldsymbol{F}}({\mathit{\boldsymbol{U}}_{\rm{R}}})-\\ {\mathit{\boldsymbol{R}}_{i + \frac{1}{2}}}\left| {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{{\rm{i}} + \frac{1}{2}}}} \right|\mathit{\boldsymbol{R}}_{i + \frac{1}{2}}^{-1}({\mathit{\boldsymbol{U}}_{\rm{R}}}-{\mathit{\boldsymbol{U}}_{\rm{L}}})] \end{array} $ |
式中, UL为左状态守恒变量, UR为右状态守恒变量. 1阶格式UL可以用Ui代替, UR可以用Ui+1代替, 高阶格式可以使用MUSCL等高阶重构方法获得左右状态的值. R和R-1分别代表F的左特征矩阵和右特征矩阵, Λ代表∂F/∂U的特征值.下标1/2代表平均, 可以使用算数平均或者Roe平均来获得.
3 物理模型 3.1 化学反应模型高超声速引起的高温化学非平衡效应是不可避免的一个问题, 数值计算表明:考虑化学非平衡效应的气体不仅对气动力、配平攻角有影响[17], 而且对计算热流也有重要作用.
对于来流的空气组分, 当温度达到2 500 K时氧气开始离解, 当温度达到4 000 K时氧气几乎完全离解, 这时候氮气开始离解, 当达到9 000 K时氮气几乎完全离解, 氮原子和氧原子刚开始离解[18].考虑本次实验的来流工况, 利用激波关系式可知波后温度未达到9 000 K(如果考虑化学非平衡的吸热效果, 就更不会达到这个温度), 因此本次数值模拟不会发生电离及电离温度以上的反应.
目前国内外流行的化学动力学模型有Dunn-Kang模型、Park85[19]模型、Park93模型、Park2001模型和Gupta模型, 张敏捷等[20]利用球头绕流研究了这些模型, 数值实验结果证明Park85-7组分模型精度与实验数据吻合最好, 但是Park85-5模型计算量小, 并且与7组分模型相差不大, 适合工程计算. Gupta回顾并重新构造了Dunn-Kang[21]和Bortner[22]的模型, 得到了更详细的反应模型, 其适用范围达30 000 K[23].刘茂名[24]利用ESI-CFD-FASTRAN软件模拟了类Apollo返回舱在高焓风洞[6]的实验, 计算结果表明:考虑化学非平衡效应, Gupta模型较Park模型获得的热流结果更加吻合实验结果, 在预测肩部热流的时候, Gupta模型能获得更高的热流值, 因此, 也将比较Gupta模型和Park模型的表现.
对于化学反应速率k, 通常使用Arrhenius公式拟合:
| $ k = A \cdot {T^B}\exp \left( {- \frac{{{T_{\rm{D}}}}}{T}} \right), {\left( {{{\left[{\frac{{{\rm{kmol}}}}{{{{\rm{m}}^3}}}} \right]}^{ -\alpha }}/{\rm{s}}} \right)^{ -1}} $ |
式中, A, B, TD为拟合系数, 视不同模型而不同, 列于表 2.
| 下载CSV 表 2 Park五组分模型化学反应速率拟合系数 Tab.2 Coefficients of chemical reaction rate of Park five-species model |
Park模型可以通过反应平衡比例来获得反向化学反应系数, 而Gupta模型则指定正负反应速率. 表 3中Af, Bf, TDf为正向反应速率系数的参数, Ab, Bb, TDb为逆向反应速率系数参数.
| 下载CSV 表 3 Gupta模型化学反应速率拟合系数 Tab.3 Coefficients of chemical reaction rate of Gupta model |
对于完全气体, 由Fourier定律知其热通量可以定义为
| $ {q_{\rm{w}}} =-k\left( {\frac{{\partial T}}{{\partial n}}} \right) $ |
考虑有多组分化学反应的热流通量, 可以定义为
| $ {q_{\rm{w}}} = k\left( {\frac{{\partial T}}{{\partial n}}} \right) + \sum\limits_{s = 1}^{ns} {\rho {D_s}{h_s}\frac{{\partial {Y_s}}}{{\partial n}}} $ |
式中, qw为壁面热流, k为热传导系数, ρ为混合气体总密度, Ds为组分s的扩散系数, hs为组分s的焓, Ys为组分s的分密度, (∂T/∂n)和(∂Ys/∂n)分别为温度和组分密度沿着壁面法向的梯度.其中k, Ds, ρ, hs都可以是壁面的物理性质, 可以通过经验公式计算得到[25].因此计算热流就很依赖于(∂T/∂n)和(∂Ys/∂n)的计算, 根据差分公式可以知道, 第1层网格的大小影响截断误差的大小, 因此壁面网格的尺度决定计算的精度.
4 网格数值计算[6]验证了计算网格越密, 热流的计算越精确.王浩[27]指出, 若要获得准确的热流计算结果, 物面处长宽比应该与法向网格Reynolds数同量级. Hoffman等[26], 李君哲等[28]研究了网格与气动热关系的若干问题, 满足第1层网格的网格Reynolds数经验公式如下:
| $ {Re_{{\rm{cell}}}} = \frac{{{\rho _\infty }{u_\infty }\Delta n}}{{{\mu _\infty }}} $ |
式中, Recell代表网格Reynolds数, 随具体问题而定, ρ∞代表来流密度, u∞代表来流速度, μ∞代表来流黏性系数, Δn代表壁面第1层网格高度.刘茂名[24]的数值结果表明, 对于该返回舱模型, 第1层网格Reynolds数在10以内会有比较可靠的热流计算结果.
5 工程计算赵梦熊[5]利用风洞实验和Lees及Detra-Kemp-Riddell等工程公式研究了球冠倒锥形返回舱的气动加热, 结果表明球冠的中心角大小影响热流的最大值位置.当声速点所在的角度大于球冠中心角时, 声速点位于肩部[5], 经过肩部产生一系列膨胀波, 压力下降非常剧烈, 这种效应传递到亚声速区域, 从而影响整个头部的物理场.对于一个给定的高超声速流场(Mach数大于10), 球冠中心角越小, 肩部热流相对于驻点热流就越大, 文献[5]指出当球冠中心角约为20°时, 两者基本相同.对于本课题的算例类Apollo返回舱而言, 球冠部分中心角达到32.5°, 其肩部热流有可能超过驻点热流成为关键部位.
实验测量结果[29]表明, 在带有大拐角的钝头体头部, 热流会有一个突跃, 对于方柱钝头, 在拐角处出现一个热流突跃, 这个值比方柱钝头体驻点处的热流还要高50%.理论公式[30]计算结果表明相似解理论无法准确估计热流的值.其原因在于经过拐角后的流动迅速膨胀, 流速迅速增大, 根据Fourier换热定律, 流速越大的部位换热率也越高, 因此会引起热流增大.同样, 对于返回舱也是如此, 在流经肩部的位置, 由于大拐角会出现热流快速增长的现象.许菁利用该软件模拟了Labb球头柱层流的计算[4].比较上述二者计算结果, 壁面条件取300 K或者1 000 K都可以获得准确的气动结果.
实验表明ESI-CFD-FASTRAN具有较高的鲁棒性, 并且在满足化学非平衡计算的使用要求时, 可以获得较合理的解.
6 数值研究算例比较影响肩部热流计算的因素:网格, 壁面温度的设置, 空间格式限制器, 湍流模型, 化学反应模型.分析这些因素对预测肩部热流的影响.实验采用图 1中的几何模型.实验来流工况见表 4. 表 4中h0代表来流总焓, U代表来流流速, T代表来流静温, P代表来流静压, μ代表来流黏性系数, ρN2, ρO2, ρNO, ρO, ρN分别为组分N2, O2, NO, O, N的密度.本文数值模拟都将采用该工况.
| 下载CSV 表 4 层流空气的来流条件 Tab.4 Freestream condition for laminar runs in air |
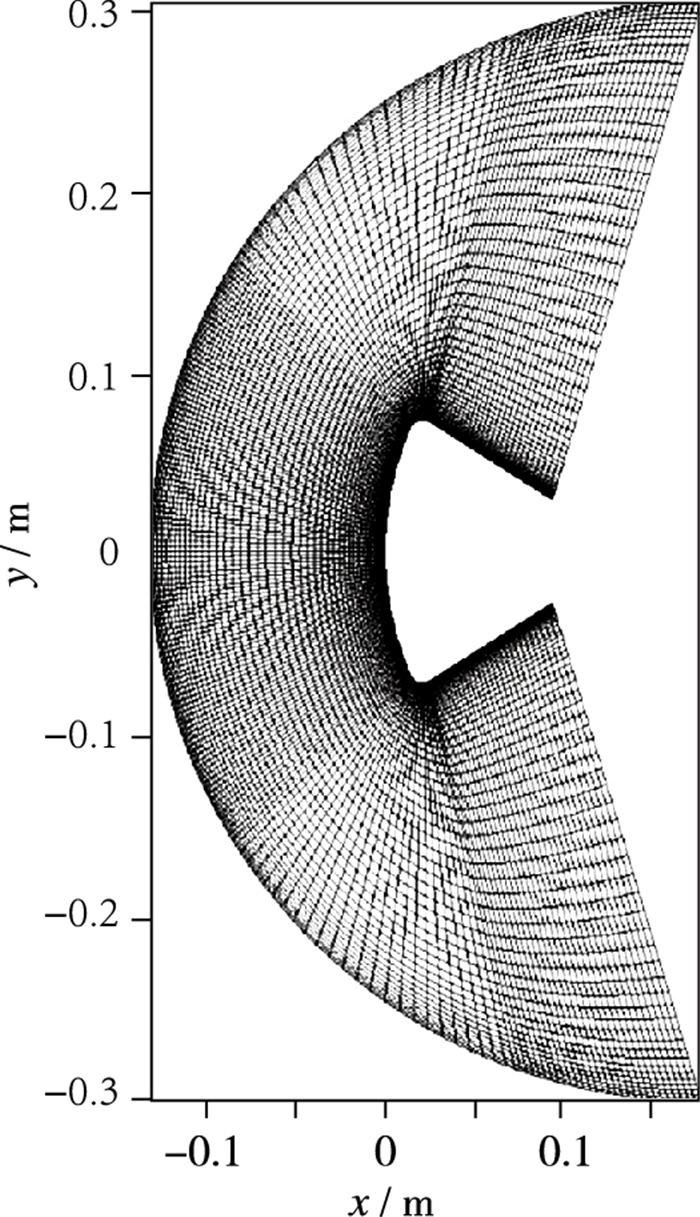
本实验主要考虑肩部周围突越热流, 为节约计算资源, 考虑以下思路:由于Navier-Stokes方程对流项特征化后存在三道特征线, 代表三道波传播的方向和传播速度, 其特征值分别为U+c, U, U-c.对于高超声速流动而言, 如果没有黏性项, 这三个特征值都为正, 即流动的影响永远往下游传播, 不会反向传播.因此, 可以只考虑把肩部包含在内的网格(满足网格Reynolds数小于10), 见图 2.
|
| 图 2 返回舱模型计算网格 Fig.2 Meshes of reentry mode |
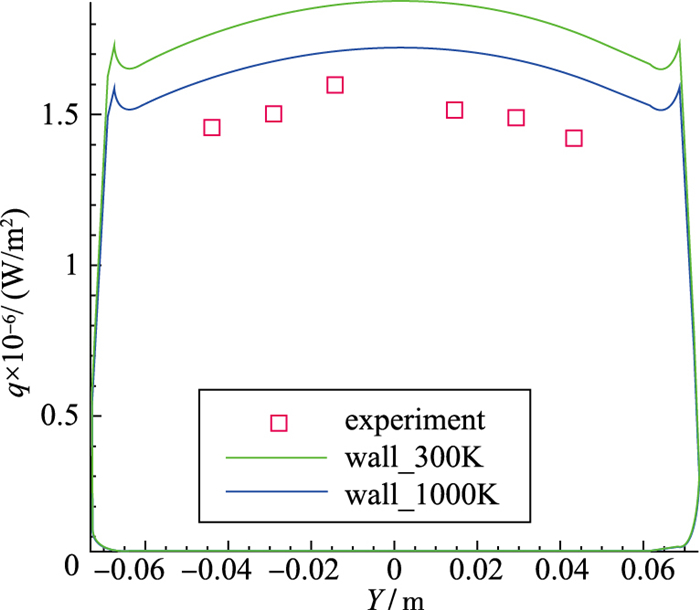
计算采用Park85模型, 空间离散使用1阶Roe-FDS格式, 时间离散使用点隐式(全隐式方法), 通常设置壁面温度为300 K, 在实验过程中, 由于热流不断加热实验装置, 因此实际温度会高于300 K.文献[4]中使用1000 K作为壁面温度获得了良好的结果, 采用较高温度壁面条件对流场分布也有影响, 故尝试使用1000 K作为壁面温度与之比较.采用1阶Roe-FDS格式, Park85化学反应模型计算获得热流分布与300 K壁温比较如图 3所示.
|
| 图 3 不同壁面温度得到的热流比较 Fig.3 Effects on heat flux of different wall temperatures |
实验结果表明温度越高热流相对就越低, 其原因在于从激波后温度降低到1000 K壁温所需要的温度梯度较降低到300 K壁温所需要的梯度低, 这样一来由温度梯度引起的热流就较低, 因此, 1000 K的壁温降低了温度梯度引起的热流.就肩部热流而言, 其计算的结果与300 K类似, 依然没有超过驻点热流.说明壁面温度的设置不影响热流的分布情况, 因此, 后续研究采用常用的300 K作为壁面温度.
6.2 网格验证为验证网格Reynolds数对准确计算热流的作用, 这里使用疏网格作为比较, 见图 4.两套网格使用了相同的网格数量, 但是沿着法向图 2所示网格在壁面处采用了加密策略, 使网格Reynolds数小于10, 其远离壁面的网格比较稀疏.

|
| 图 4 壁面疏网格 Fig.4 Coarse wall grids |
计算采用Park85模型, 空间离散使用1阶Roe-FDS格式, 时间离散使用点隐式(全隐式方法), 壁面使用300 K的等温壁面.计算流场如图 5, 图 6所示.对比疏密网格的Mach分布图, 二者基本一致, 由于壁面密网格在远离壁面处网格稀疏, 导致激波层较厚.

|
| 图 5 壁面疏网格Mach数分布图 Fig.5 Distributions of Mach of coarse wall grids |

|
| 图 6 壁面密网格Mach数分布图 Fig.6 Distributions of Mach of fine wall grids |

|
| 图 7 壁面压力分布图 Fig.7 Distributions of pressure |
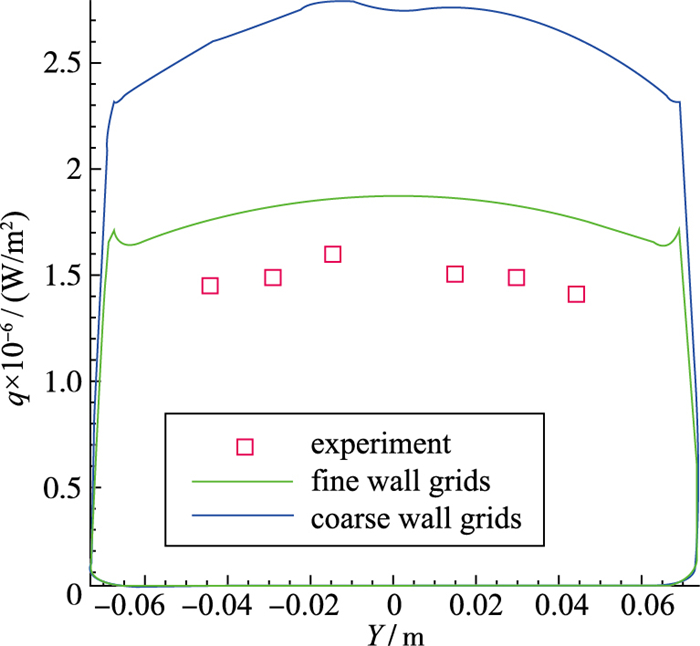
|
| 图 8 壁面热流分布图 Fig.8 Distributions of heat flux |
从图 7可以看出, 对于壁面压力, 疏网格和密网格与实验值都非常吻合, 基本上两种网格都可以获得非常精确的驻点压力值, 疏网格获得的驻点压力较壁面加密网格要更加吻合, 原因可能在于其网格在整个流场分布比较均匀, 而壁面加密的网格由于在远离壁面的地方误差比较大, 在壁面处累计误差引起的偏差相较前者大.
从图 8可以看出, 对于壁面热流, 两套网格计算结果都较实验值偏大.壁面较疏的网格获得的热流解更加偏离实验值.在肩部, 疏网格基本没有获得热流突越; 密网格在肩部获得了突越, 但是相较文献[2]和[10]获得的突越值仍然不足, 没有超过驻点热流, 分析原因, 可能在于: (1)采用1阶Roe-FDS格式精度不足; (2)网格Reynolds数不足, 壁面网格仍然较粗; (3)肩部网格沿周向分布不够, 突越值极值无法获取.
两套网格相比较而言, 在计算热流方面, 壁面加密的网格具有优势, 后续的计算分析都将采用这套网格并且以该网格的结果作为参照.
6.3 高阶空间离散: minmod限制器本节采用上述网格并在Roe-FDS格式中加入minmod限制器.
| $ {\rm{minmod}}\left( {x, y} \right) = \frac{{{\rm{sign}}\left( x \right) + {\rm{sign}}\left( y \right)}}{2}{\rm{min}}\;\left( {\left| x \right|, |y|} \right) $ |
式中
| $ {\rm{sign}}\left( x \right) = \left\{ \begin{array}{l} \;\;\;1\;\;\;\;x \ge 0\\ -1\;\;\;\;\;x \le 0 \end{array} \right. $ |
minmod限制器提供2阶的空间精度, 在计算壁面热流时, 理论上可以提高1倍精度.
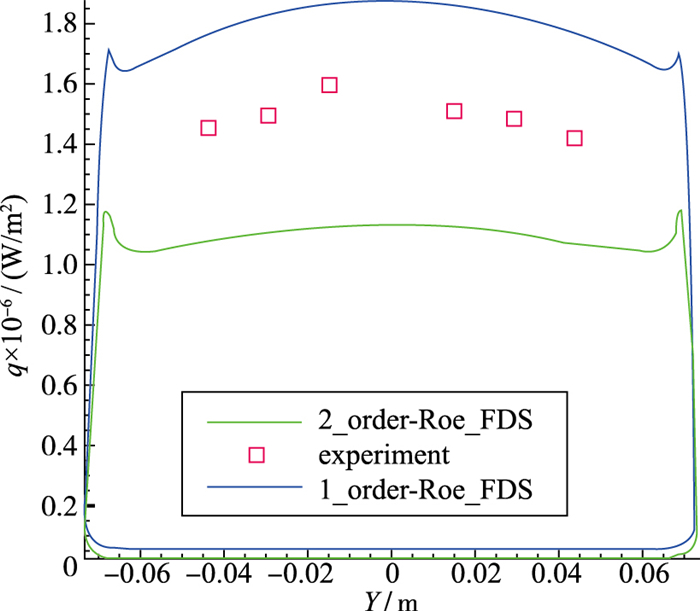
计算结果获得的压力梯度与实验值依然非常符合, 不再累述.热流计算结果对比如图 9所示.
|
| 图 9 高阶格式/1阶格式热流分布比较 Fig.9 Comparison between high order and one order heat flux |
相较1阶Roe格式, minmod 2阶格式获得的热流较低, 但肩部热流明显要高于驻点, 这个结果符合预期, 说明二阶格式在计算肩部热流时有一定优势. minmod限制器本质是限制流动梯度, 使得流动变化不会出现非物理解, 但是在这里使用可能造成温度梯度被限制, 无法获得真实的温度梯度, 进而造成热流值预测不足, 因此, 采用高阶格式对于提高肩部热流精度有重要意义.
6.4 湍流模型的影响在工程估算中[13], 湍流模型获得的工程估计公式与层流模型的公式不一样, 湍流模型工程公式认为热流极值点处于声速点位置, 而不是驻点, 因此湍流也可能影响热流的计算.这里应用Spalart-Allmaras模型, 该模型基于涡黏性的输运, 其最初是设计用于墙壁束缚流动, 在ESI-CFD-FASTRAN软件中默认加入了转捩修正因素.与层流计算结果比较如图 10所示.

|
| 图 10 湍流对热流的影响 Fig.10 Turbulence effects on heat flux prediction |
实验结果表明, 层流模型获得的热流分布与湍流获得的热流分布重合, 即湍流对热流的计算没有影响.原因可能在于在非常靠近热边界层的区域, 由于梯度非常大, 因此Spalart-Allmaras湍流模型没有对热量分布造成明显影响.
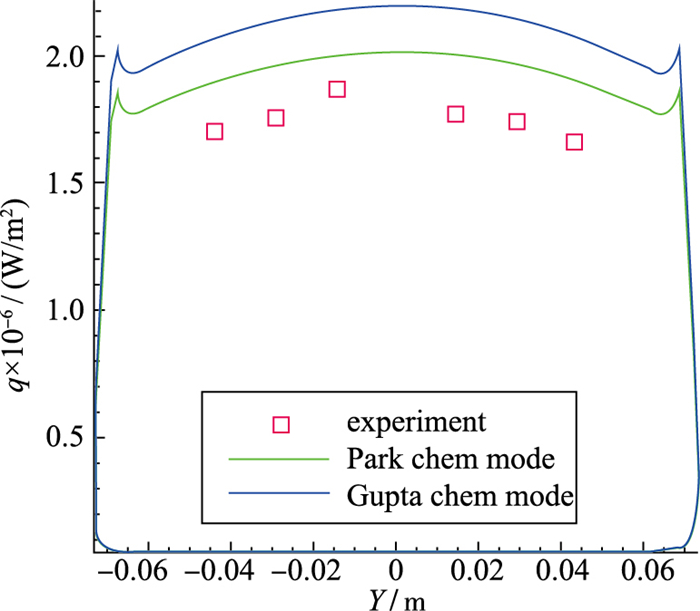
6.5 化学反应模型的影响Gupta模型和Park模型目前在不同的实践中各有优劣[5, 24-25], 除了表 4中所列工况外, 我们使用1阶Roe-FDS格式, 壁面温度设置为300 K进行比较模拟.计算热流结果如图 11所示.
|
| 图 11 不同化学反应模型比较 Fig.11 Different chemical reaction models |
实验结果表明, Gupta模型预测获得的热流值较Park模型的值高, 在肩部热流预测方面, 二者效果类似.因此, Gupta模型的结果更为保险, 工程应用中可以参考Gupta模型的结果.
7 结论本文以类Apollo模型的实验数据为参照, 采用ESI-CFD-FASTRAN软件模拟了热流在壁面的分布, 并利用该软件研究了物理模型及数值方法对肩部热流预测的影响.实验表明, 满足网格Reynolds数小于10的边界层网格可以获得高精度的热流; 高阶格式对肩部热流突越有较高的分辨率; 设置的壁面温度越高, 热流值越低, 但是不影响肩部热流相对整个壁面的分布情况; Spalart-Allmaras湍流模型与层流模型的预测结果一致, 说明湍流模型对热流的影响不是很大; 化学非平衡模型则有很大区别, Gupta模型预测获得的热流较Park模型高, 但是在肩部热流的分布情况一致.为精确计算肩部热流, 应采用满足网格Reynolds数限制的边界层网格.因此, 为准确模拟肩部热流须保证壁面网格满足网格Reynolds数, 并且采用高阶精度的格式有助于提高肩部热流的精度.
致谢: 本文工作得到了国家自然科学基金的支持(NSFC 91530325), 谨此致谢.| [1] |
Neely A J, Morgan R G. The superorbital expansion tube concept, experiment and analysis[J]. The Aeronautical Journal, 1994, 98(973): 97-105. DOI:10.1017/S0001924000050107 |
| [2] |
高铁锁, 江涛, 丁明松, 等. 辐射加热对返回舱气动热环境影响的数值研究[J]. 空气动力学学报, 2015, 33(1): 36-41. Gao T S, Jiang T, Ding M S, et al. Numerical study of radiative heating influence on aerothermal environment over a reentry capsule[J]. Acta Aerodynamica Sinica, 2015, 33(1): 36-41. (in Chinese) |
| [3] |
杨肖锋, 唐伟, 桂业伟, 等. 火星环境高超声速催化加热特性[J]. 宇航学报, 2017, 38(2): 205-211. Yang X F, Tang W, Gui Y W, et al. Hypersonic catalytic aeroheating characteristics for Mars entry process[J]. Journal of Astronautics, 2017, 38(2): 205-211. (in Chinese) |
| [4] |
许菁. 火星进入舱气动热的数值模拟[D]. 北京: 北京交通大学, 2016. Xu J. Numerical simulation of aerodynamic heat for Mars entry capsule[D]. Beijing: Beijing Jiaotong University, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10004-1016058575.htm |
| [5] |
赵梦熊. 载人飞船返回舱的气动热流率分布[J]. 气动实验与测量控制, 1996, 10(1): 1-8. Zhao M X. Aerothermal heat flux distribution on manned spacecraft reentry capsule[J]. Aerodynamic Experiment and Measurement & Control, 1996, 10(1): 1-8. (in Chinese) |
| [6] |
MacLean M, Mundy E, Wadhams T, et al. Analysis and ground test of aerothermal effects on spherical capsule geometries[C]. Proceedings of the 38th Fluid Dynamics Conference and Exhibit, Washington: AIAA, 2008. http://www.researchgate.net/publication/266097842_Analysis_and_Ground_Test_of_Aerothermal_Effects_on_Spherical_Capsule_Geometries
|
| [7] |
张鲁民. 载人飞船返回舱空气动力学[M]. 北京: 国防工业出版社, 2002, 84-122. Zhang L M. Manned spacecraft reentry capsule aerodynamics[M]. Beijing: National Defence Industry Press, 2002, 84-122. (in Chinese) |
| [8] |
Zucrow M J, Hoffman J D. Gas dynamics, Volume 2: multi-dimensional flow[M]. New York: Wiley, 1977.
|
| [9] |
White F M. Viscous fluid flow[M]. New York: McGraw-Hill, 1974.
|
| [10] |
Harten A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 49(3): 357-393. DOI:10.1016/0021-9991(83)90136-5 |
| [11] |
Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [12] |
Ding Z H, Wu S P. A study on smoothness indicator of weighted essentially non-oscillatory scheme family[C]. Proceedings of the 1st International Conference in Aerospace for Young Scientists, Beijing: Beihang University, 2016.
|
| [13] |
王民发, 沈月阳, 姚文秀, 等. 高超声速升力体气动力气动热数值计算[J]. 空气动力学报, 2001, 19(4): 439-445. Wang M F, Shen Y Y, Yao W X, et al. Aerodynamic and aerothermal numerical simulation of hypersonic lifting body configuration[J]. Acta Aerodynamica Sinica, 2001, 19(4): 439-445. (in Chinese) |
| [14] |
贺国宏, 张涵信. 高超声速钝体热流数值计算研究[C]. 第九届全国计算流体力学会议论文集, 景洪: 中国力学学会, 1998. He G H, Zhang H X. Numerical study on heat flow of hypersonic blunt body[C]. 9th Chinese National Conference for Computational Fluid Dynamics, Jinghong: Chinese Society of Theoretical and Applied Mechanics, 1998(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=101086 |
| [15] |
黄唐, 姜贵庆, 毛国亮, 等. 两种物面热流计算方法的比较[C]. 第九届全国计算流体力学会议论文集, 景洪: 中国力学学会, 1998. Huang T, Jiang G Q, Mao G L, et al. Comparison of two computational method for surface heat flux[C]. 9th Chinese National Conference for Computational Fluid Dynamics, Jinghong: Chinese Society of Theoretical and Applied Mechanics, 1998(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=244090 |
| [16] |
阎超, 李建军, 李君哲. 热流CFD计算中格式和网格效应若干问题研究[J]. 空气动力学学报, 2006, 24(1): 125-130. Yan C, Li J J, Li J Z. Scheme effect and grid dependency in CFD computations of heat transfer[J]. Acta Aerodynamica Sinica, 2006, 24(1): 125-130. (in Chinese) |
| [17] |
吕俊明, 程晓丽, 俞继军, 等. 化学非平衡效应对返回舱气动特性的影响分析[J]. 航天器环境工程, 2016, 33(4): 370-377. Lv J M, Cheng X L, Yu J J, et al. The effect of chemical non-equilibrium on aerodynamic characteristic of reentry vehicles[J]. Spacecraft Enviroment Engineering, 2016, 33(4): 370-377. (in Chinese) |
| [18] |
Anderson Jr J D. Hypersonic and high-temperature gas dynamics[M]. Yang Y, Li D, translated. Second Edition. Beijing: Aviation industry press, 2013: 385-386.
|
| [19] |
Park C. Review of chemical-kinetic problems of future NASA missions, Ⅰ: Earth entries[J]. Journal of Thermophysics and Heat Transfer, 1993, 7(3): 385-398. DOI:10.2514/3.431 |
| [20] |
张敏捷, 向树红. 高超声速三维热化学非平衡流场的数值计算对比研究[J]. 航天器环境工程, 2016, 33(1): 35-41. Zhang M J, Xiang S H. A comparative study of the computation of 3-D hypersonic flow in thermochemical nonequilibrium state[J]. Spacecraft Environment Enginee-ring, 2016, 33(1): 35-41. (in Chinese) |
| [21] |
Dunn M G, Kang S W. Theoretical and experimental studies of reentry plasmas[R]. NASA-CR-2232, 1973. http://www.researchgate.net/publication/24299381_Theoretical_and_experimental_studies_of_reentry_plasmas
|
| [22] |
Bortner M H. Suggested standard chemical kinetics for flow field calculations — a consensus opinion[C]. AMRAC Proceedings, Michigan: University of Michigan, 1966: 569-581.
|
| [23] |
Gupta R N, Yos J M, Thompson R A, et al. A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30 000 K[R]. NASA Refe-rence Publication 1232, 1990. http://www.researchgate.net/publication/24335039_A_review_of_reaction_rates_and_thermodynamic_and_transport_properties_for_an_11-species_air_model_for_chemical_and_thermal_nonequilibrium_calculations_to_30000_K
|
| [24] |
刘茂名. 类APOLLO返回舱的数值模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. Liu M M. Numerical simulatoin of an Apollo like reentry capsule[D]. Harbin: Harbin Institute of Technology, 2012(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1013038261.htm |
| [25] |
谢锦睿. 高超音速流动数值模拟与热流数值计算[D]. 北京: 北京航空航天大学, 2006. Xie J R. Numerical simulation of hypersonic flows and calculation of aerothermal heating[D]. Beijing: Beihang University, 2006(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y495124 |
| [26] |
Hoffmann K A, Siddiqui M S, Chiang S T. Difficulties associated with the heat flux computations of high speed flows by the Navier-Stokes equations[R]. AIAA 1991-0467, 1990. https://arc.aiaa.org/doi/abs/10.2514/6.1991-467
|
| [27] |
王浩. 高超音速流动数值模拟与热流数值计算[D]. 北京: 北京航空航天大学, 2002. Wang H. Numerical simulation of hypersonic flow and numerical calculatoin of heating[D]. Beijing: Beihang University, 2002(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y495124 |
| [28] |
李君哲, 阎超, 柯伦, 等. 气动热CFD计算的格式效应研究[J]. 北京航空航天大学学报, 2003, 29(11): 1022-1025. Li J Z, Yan C, Ke L, et al. Research on scheme effect of computational fluid dynamics in aerothermal[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(11): 1022-1025. DOI:10.3969/j.issn.1001-5965.2003.11.014 (in Chinese) |
| [29] |
Lees L. Laminar heat transfer over blunt-nosed bodies at hypersonic flight speeds[J]. Jet Propulsion, 1956, 26(4): 259-269. DOI:10.2514/8.6977 |
| [30] |
卞荫贵, 徐立功. 气动热力学[M]. 2版. 合肥: 中国科学技术大学出版社, 2011, 217-218. Bian Y G, Xu L G. Aerothermodynamics[M]. 2nd edition. Hefei: University of Science and Technology of China Press, 2011, 217-218. (in Chinese) |



