在高超声速飞行器的研制过程中, 风洞试验数值计算和飞行试验是获得飞行器气动性能的3种主要手段.由于飞行试验费用较高, 因此进行飞行试验的次数较少.受地面风洞设备试验条件的限制, 在风洞试验中往往需要在保证模型几何相似的情况下对模型进行适当缩比, 并且在地面风洞试验设备中不能保证试验条件与飞行环境完全一致.如何使用地面风洞试验数据预测飞行条件下的气动性能数据是高超声速飞行器设计中亟待解决的一个重要问题, 因此, 开展相关性研究十分必要.
高超声速气动热数据相关性的研究可以追溯到20世纪五六十年代.经过几十年的发展, 研究者针对该问题进行了大量的研究工作, 涉及到的模型有X-15飞机航天飞机Apollo返回舱HYFLEX及钝锥等外形.
美国Edwards空军基地飞行试验研究中心的Robert等Quinn等对X-15高超声速飞机的气动热数据相关性进行了比较系统的研究[1-3], 其使用Reynolds数将X-15飞机的飞行试验与地面风洞试验获得的Stanton数进行了关联.
1976年, Bertin等[4]在进行航天飞机的气动热数据相关性研究时, 考虑到模型表面热流由表面黏性流动状态决定, 而表面流动状态直接由激波后的流动参数决定, 因此首先提出并使用正激波后Reynolds数Rens进行气动热数据的相关性研究.但是参数Rens并不能反映无黏流动中熵梯度和黏性边界层发展长度对热流的影响, 因此Bertin等又采用基于激波后流动参数和驻点到测点位置距离计算获得的参数Renl对Apollo返回舱的风洞试验数据[5]和飞行试验数据[6]进行了关联性研究, 结果表明, Stanton数与(Renl)n成比例关系. 1983年, Throckmorton等[7]采用正激波后的Reynolds数Rens将航天飞机下表面的飞行试验和风洞试验获得的Stanton数进行了关联, 发现飞行试验和风洞试验获得的Stanton数随Reynolds数的变化趋势一致, 但是由于飞行条件和风洞条件下模型表面边界层流态不同(飞行条件下为层流, 风洞条件下为湍流)使得表面热流数值存在较大差异. 1984年, Haney[8]使用Reynolds数将航天飞机多次飞行试验获得的热传导系数比进行了关联, 并与地面风洞试验数据[9-15]和飞行预测数据进行了对比, 发现该方法只在航天飞机表面无涡流区域关联性较好, 在存在流动分离的区域关联性很差.
模型表面热流不仅受真实气体效应的影响, 还受到黏性干扰效应和模型前缘钝度引起的熵吞效应影响. 1985年, Miller等[16]首先采用黏性干扰系数V*和激波前后密度比对Stanton数进行了修正, 使用修正后的Stanton数StR对双锥模型的气动热数据进行了相关性研究. 1993年, Olivier等[17]采用Miller的方法对Stanton数进行了修正, 并对3种不同模型(双椭圆模型Hermes模型和ELAC模型)的气动热数据进行了相关性研究, 结果表明:采用这种方法可以对不同风洞不同来流条件下的气动热数据进行关联, 关联效果很好. 1995年, 德国的Legge[18]采用黏性干扰系数V*对钝锥模型在3座不同风洞中获得的驻点Stanton数进行关联, 发现驻点Stanton数与黏性干扰系数V*近似成线性关系.
除真实气体效应熵吞效应和黏性干扰效应外, 模型表面热流还受壁面焓值的影响, 2001年, Hozumi等[19]使用无量纲焓差Sw(Sw=1-Hw/H0)对黏性干扰系数V*进行了修正, 使用修正的黏性干扰系数V*/Sw对HYFLEX模型在3座不同风洞中的气动热数据开展了相关性研究, 研究结果表明:使用修正的黏性干扰系数V*/Sw可以对受熵吞效应影响较小的机身区域气动热数据进行关联, 在模型鼻部位置由于受到熵吞效应的影响, 需要使用V*/Sw/(ρ1/ρ2)n对气动热数据进行关联.
国内在高超声速气动热数据相关性方面的研究工作起步较晚, 中国空气动力研究与发展中心的李明等[20]针对某高超声速带翼飞行器模型在高超声速低密度风洞和激波风洞中的气动热试验数据进行了相关性尝试, 并取得了一定的研究结果.
本文以一平板-锥组合体模型为研究对象, 开展高超声速气动热数据相关性研究工作, 尝试了3种不同的方法, 对不同缩比模型不同来流条件下的风洞试验数据进行了相关性研究.最后基于相关性研究结论和理论分析, 提出了一种描述模型表面传热现象的数学模型.
1 模型及风洞试验该组合体模型(见图 1)上表面为半锥面, 下表面为平面, 中间采用圆弧过渡, 共有3个不同缩比的钢制模型(缩比分别为1:2,1:3和1:4), 试验在FD-20高超声速脉冲风洞(见图 2)中进行, 试验状态如表 1所示, 采用薄膜电阻温度计测量模型表面热流.测点分别布置在模型驻点和上下表面中心线上, 每条母线上分别布置7个测点, 具体测点位置如表 2所示.
|
| 图 1 平板-锥模型及测点位置示意图 Fig.1 Schematic of the plate-cone configuration |

|
| 图 2 FD-20脉冲风洞 Fig.2 FD-20 impulse tunnel |
| 下载CSV 表 1 实验状态参数表 Tab.1 Testing conditions |
| 下载CSV 表 2 测点位置表 Tab.2 Locations of the thermometers |
在相关性研究中选择在所有试验状态下均保持层流的模型上下表面中心线的第2个测点(X/R=2.43位置)为研究对象.
2 气动热数据相关性结果及分析使用3种不同的方法对不同缩比模型不同来流条件下的风洞试验数据进行了相关性尝试, 并对相关性结果进行了分析.
2.1 基于正激波后Reynolds数Rens[4]的关联方法模型表面热流由表面流动状态决定, 表面流态直接由激波后的流动参数决定, 而不是激波前的来流参数, 因此使用激波后的流动参数能够更加准确反映模型表面的流动状态.正激波后Reynolds数Rens定义如下:
| $ \mathit{R}{\mathit{e}_{{\rm{ns}}}}{\rm{ = }}{\mathit{\rho }_{{\rm{ns}}}}{\mathit{u}_{{\rm{ns}}}}{\mathit{r}_{{\rm{ref}}}}{\rm{/}}{\mathit{\mu }_{{\rm{ns}}}}{\rm{.}} $ |
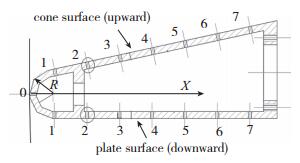
图 3给出了Stanton数与正激波后Reynolds数Rens的关联结果.图中的直线为使用最小二乘法拟合获得.由图可知, 不同缩比模型、不同来流状态下的Stanton数与参数1/Rens关联性较好, Stanton数随参数1/Rens的增大而增大, Stanton数与参数1/Rens近似成正比例关系.在10°攻角时, 以及模型其他测点位置也发现了同样的规律.该规律与文献[4]的研究结论并不完全一致, 可能是由于模型不同或者模型表面边界层流动状态不同引起的.
|
| 图 3 模型上/下表面中心线X/R=2.43位置数据关联性(α=0°) Fig.3 Correlations of heat-transfer data for the location X/R=2.43 of the upward/downward surface centre line(α=0°) |
模型表面热流不仅受到真实气体效应的影响还受到黏性干扰效应和熵吞效应的影响.
参数StR的定义如下:
| $ \mathit{S}{\mathit{t}_{\rm{R}}}{\rm{ = }}\mathit{St}\frac{{{{{\rm{(}}{\mathit{\rho }_{\rm{2}}}{\rm{/}}{\mathit{\rho }_{\rm{1}}}{\rm{)}}}^\mathit{n}}}}{{{\mathit{V}^{\rm{*}}}}}{\rm{.}} $ |
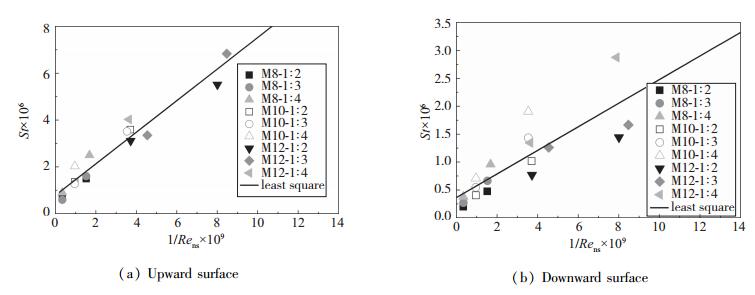
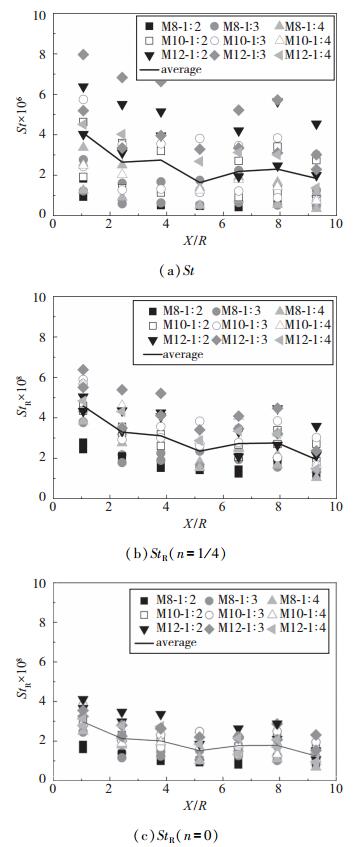
该参数中包含了黏性干扰系数Stanton数和激波前后密度比等, 使用该参数尝试进行模型表面全局气动热数据的关联, 根据已有结论, n值分别取0(无熵吞效应影响)和1/4(有熵吞效应影响)进行数据关联, 并与直接使用Stanton数的关联效果进行对比. 0°攻角下的气动热数据关联结果如图 4和图 5所示.对比发现, 相对于Stanton数, 使用StR使得各测点数据的分散度有所减小, 数据更加紧凑, 该规律在模型上下表面中心线前3个测点表现最为突出, 在模型后部的几个测点, 使用StR反而会使得热流数据的分散程度加大.可能是由于在有些来流条件下, 模型后部逐渐发生边界层转捩, 边界层进入湍流状态, 使得模型表面热流增加.激波前后密度比代表的是模型头部激波强度, 反映了模型头部位置熵吞效应的影响, n=0时的数据关联效果比n=1/4时的关联效果更好, 说明在本次研究中的测点位置流动状态受熵吞效应的影响很小或者不受熵吞效应影响. 10°攻角下的气动热数据相关性呈现同样的规律.
|
| 图 4 模型上表面中心线气动热数据关联性(α=0°) Fig.4 Correlations of heat-transfer data for the centre line of the upward surface(α=0°) |
|
| 图 5 模型下表面中心线气动热数据关联性(α=0°) Fig.5 Correlations of heat-transfer data for the centre line of the downward surface(α=0°) |
除真实气体效应黏性干扰效应和熵吞效应外, 模型壁面热流还受到壁面温度的影响.
黏性干扰系数V*为
| $ {\mathit{V}^{\rm{*}}}{\rm{ = }}{\mathit{M}_\infty }\sqrt {{\mathit{C}^{\rm{*}}}} {\rm{/}}\sqrt {\mathit{R}{\mathit{e}_{{\rm{L}}\infty }}} {\rm{.}} $ |
其中,C*为Chapman-Rubesin因子, ReL∞为测点位置当地Reynolds数.
| $ \begin{array}{l} {\mathit{C}^{\rm{*}}}{\rm{ = }}{\mathit{\mu }^{\rm{*}}}{\mathit{T}_{\rm{0}}}{\rm{/(}}\mathit{\mu }{\mathit{T}^{\rm{*}}}{\rm{)}}{\rm{.}}\\ {\mathit{T}^{\rm{*}}}{\rm{ = }}{\mathit{T}_{\rm{2}}}{\rm{/6}}{\rm{.0 \times (1 + 3}}{\mathit{T}_{\rm{w}}}{\rm{/}}{\mathit{T}_{\rm{2}}}{\rm{)}}{\rm{.}} \end{array} $ |
无量纲焓差Sw为
| $ {\mathit{S}_{\rm{w}}}{\rm{ = 1 - }}\frac{{{\mathit{H}_{\rm{W}}}}}{{{\mathit{H}_{\rm{0}}}}}{\rm{.}} $ |
其中,Hw为壁面焓值, H0为来流总焓值.
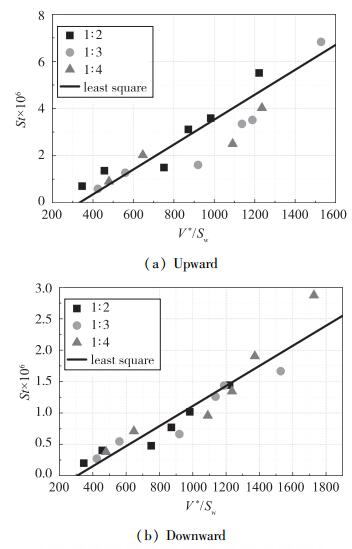
为了研究不同试验状态下不同缩比模型上某一点热流数据的相关性, 将相同模型姿态时不同来流条件下不同缩比模型上一点的热流数据使用Stanton数与V*/Sw进行相关性研究.以0°攻角时模型上下表面中心线X/R=2.43两个位置为例进行相关性分析, 数据关联结果如图 6所示.图中实线为使用最小二乘法拟合获得的线性曲线.由图可知, 在模型上下表面两个不同位置上, 不同来流条件下不同缩比模型的Stanton数与修正的黏性干扰系数V*/Sw呈现很好的线性关系, Stanton数随V*/Sw的增加而增加.在10°攻角时, 以及模型其他测点位置也呈现同样的规律.该研究结论与文献[19]的结论相同.
|
| 图 6 0°攻角X/R=2.43处气动热试验数据关联性曲线 Fig.6 Correlations of heat-transfer data for the location X/R=2.43 of the centre line at 0° of attack |
为了验证该数据关联方法的正确性, 又开展了数值模拟计算热流数据的相关性研究工作.
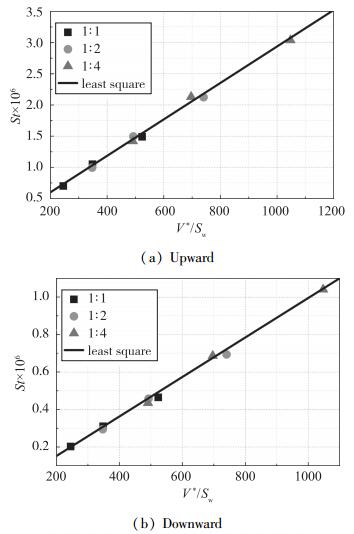
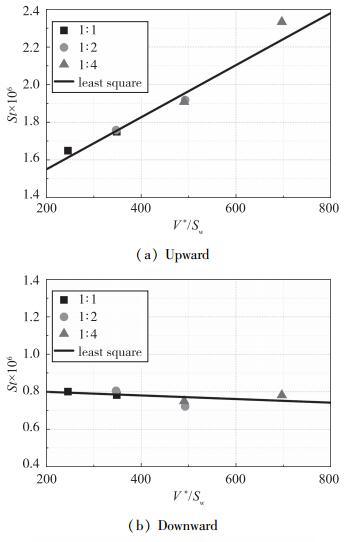
以图 2中的模型为研究对象, 采用数值模拟的方法[21-22]对模型表面的热流进行计算, 计算状态如表 3所示.以模型上下表面X/R=2.43位置为研究对象, 采用修正的黏性干扰系数V*/Sw对不同来流条件下不同缩比模型的Stanton数进行相关性研究. 图 7和图 8为层流和湍流情况下模型上下表面气动热数据相关性结果.由图可知, 模型上下表面的数据关联性较好, Stanton数与修正的黏性干扰系数V*/Sw呈现很好的线性关系.
| 下载CSV 表 3 数值模拟计算状态表 Tab.3 Numerical simulation conditions |
|
| 图 7 层流解的气动热数据关联结果 Fig.7 Correlations of heat-transfer data from numerical simulation in laminar flow |
|
| 图 8 湍流解的气动热数据关联结果 Fig.8 Correlations of heat-transfer data from numerical simulation in turbulent flow |
由修正的黏性干扰系数的定义式可以看出, 在修正的黏性干扰系数V*/Sw中包含了来流Mach数来流Reynolds数气流黏性和壁温比等参数, 因此使用该修正的黏性干扰系数可以很好地反映测点位置的流动状态. Stanton数是一种表征模型表面热流的无量纲参数.使用修正的黏性干扰系数和Stanton数进行关联是模型表面流动状态和表面热流关联的一种具体表现形式.
3 模型表面热传导建模在高超声速飞行中, 由周围气体介质向模型壁面传热主要有两个途径, 一是模型周围气体与模型壁面的对流传热, 二是周围气体向模型表面的辐射传热.
| $ {\mathit{q}_{\rm{w}}}{\rm{ = }}{\mathit{q}_{{\rm{w1}}}}{\rm{ + }}{\mathit{q}_{{\rm{w2}}}}{\rm{.}} $ |
其中, qw为周围气体向模型壁面的总传热量, qw1为模型周围气流与模型壁面的对流传热量, qw2为周围气体向模型壁面的辐射传热量.
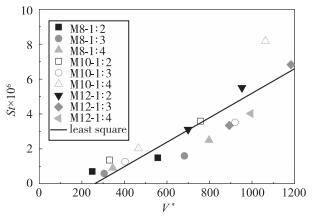
文献[18]研究表明, 模型驻点Stanton数与黏性干扰系数V*成正比.在本文2.3节的研究中, 发现模型表面的Stanton数与修正的黏性干扰系数V*/Sw也近似成正比关系.由于在风洞试验中模型壁面温度保持为室温, 只有来流总温变化, 参数Sw的变化区间为0.7~0.8, 变化范围很小, 因此推测Stanton数与黏性干扰系数V*亦近似成正比关系. 图 9为组合体模型上表面中心线X/R=2.43位置Stanton数与黏性干扰系数V*的相关性曲线, 图中直线为使用最小二乘法拟合获得, 由图可知Stanton数与黏性干扰系数V*近似成正比关系.
|
| 图 9 上表面中心线X/R=2.43位置数据相关性(α=0°) Fig.9 Correlations of heat-transfer data for the location X/R=2.43 of the upward surface centre line(α=0°) |
基于以上气动热数据相关性研究结果, 及文献[18]的研究结论Stanton数与黏性干扰系数V*近似成正比,假设Stanton数与黏性干扰系数V*的关系式为St=aV*+b, 则模型周围气流与模型壁面的对流传热量为
| $ \begin{array}{l} {\mathit{q}_{{\rm{w1}}}}{\rm{ = }}\mathit{St} \cdot {\mathit{\rho }_\infty }{\mathit{v}_\infty }{\rm{(}}{\mathit{H}_{\rm{0}}}{\rm{ - }}{\mathit{H}_{\rm{W}}}{\rm{)}}\\ \;\;\;\;\;{\rm{ = }}{\mathit{\rho }_\infty }{\mathit{v}_\infty }{\rm{(}}\mathit{a}{\mathit{V}^{\rm{*}}}{\rm{ + }}\mathit{b}{\rm{)(}}{\mathit{H}_{\rm{0}}}{\rm{ - }}{\mathit{H}_{\rm{W}}}{\rm{)}}{\rm{.}} \end{array} $ |
周围气体向模型壁面的辐射传热量[23]为
| $ {\mathit{q}_{{\rm{w2}}}}{\rm{ = }}\mathit{\varepsilon \sigma }{\rm{(}}\mathit{T}_0^4{\rm{ - }}\mathit{T}_{\rm{W}}^4{\rm{)}}{\rm{.}} $ |
可得周围气体向模型壁面的总传热量为
| $ {\mathit{q}_{\rm{w}}} = {\mathit{\rho }_\infty }{\mathit{v}_\infty }{\rm{(}}\mathit{a}{\mathit{V}^{\rm{*}}}{\rm{ + }}\mathit{b}{\rm{)(}}{\mathit{H}_{\rm{0}}}{\rm{ - }}{\mathit{H}_{\rm{W}}}{\rm{) + }}\frac{{\mathit{\varepsilon \sigma }}}{{\mathit{C}_{\rm{p}}^4}}{\rm{(}}\mathit{H}_0^4{\rm{ - }}\mathit{H}_{\rm{W}}^4{\rm{)}}{\rm{.}}\ $ |
假设H0-Hw=0, 则qw恒为0, 即模型壁面与周围气体的总焓差为0, 则不会产生向模型壁面的传热.
假设H0-Hw>0, 则周围气体向模型壁面的传热量主要由两部分组成, 分别为对流传热和辐射传热.
综上所述, 周围气体和模型壁面的总焓差是产生传热的前提.在气流总焓高于模型壁面总焓的情况下, 向模型内部的传热量主要由两部分组成, 分别为模型周围气体与模型壁面的对流传热和周围气体向模型表面的辐射传热.
4 结论本文以一平板-锥组合体模型为研究对象, 开展了不同缩比模型、不同来流条件下的风洞测热试验, 使用3种不同的方法进行了气动热试验数据的相关性研究工作.最后基于气动热数据相关性研究结果及理论分析, 提出了一种描述模型表面传热现象的数学模型.结果表明:
(1) 使用正激波后Reynolds数Rens可以将Stanton数进行关联, 关联性较好, 两者近似成反比例关系; 使用参数StR可以将不同缩比模型不同来流条件下的风洞试验数据进行关联, 但数据关联性较差, 模型上下表面测点位置受熵吞效应影响较小; 使用修正的黏性干扰系数V*/Sw可以将不同来流条件下不同缩比模型上下表面的Stanton数进行很好地关联, 且Stanton数随V*/Sw的增加而增加, 两者近似成线性关系, 该关联方法得到了风洞试验数据和数值模拟计算数据的验证.
(2) 基于气动热数据相关性研究结论和对模型表面传热现象的分析, 提出了一种描述模型表面传热现象的数学模型, 该模型的正确性有待进一步分析验证.
致谢 感谢中国航天空气动力技术研究院的陈星林键和姚大鹏等在风洞试验方面的帮助, 感谢张学军在数值模拟计算方面的指导和有益的讨论.| [1] |
Robert D Q, Kuhl A E. Comparison of flight-measured and calculated turbulent heat transfer on the X-15 airplane at Mach numbers from 2.5 to 6.0 at low angles of attack[R]. NASA TM X-939, 1964.
|
| [2] |
Quinn R D, Palitz M. Comparison of measured and calculated turbulent heat transfer on the X-15 airplane at angles of attack up to 19.0°[R]. NASA TM X-1291, 1966.
|
| [3] |
Quinn R D, Olinger F V. Heat-transfer measurements obtained on the X-15 airplane including correlations with wind-tunnel results[R]. NASA TM X-1705, 1969.
|
| [4] |
Bertin J J, Goodrich W D. Effects of surface temperature and Reynolds number on leeward shuttle heating[J]. Journal of Spacecraft and Rockets, 1976, 13(8): 473-480. DOI:10.2514/3.57111 |
| [5] |
Bertin J J. Wind-tunnel heating rates for the Apollo spacecraft[R]. NASA TMX-1033, 1965.
|
| [6] |
Lee D B, Bertin J J, Goodrich W D. Heat-transfer rate and pressure measurements obtained during Apollo orbital entries[R]. NASA TN D-6028, 1970.
|
| [7] |
Throckmorton D A, Zoby E V. Orbiter entry leeside heat transfer data analysis[J]. AIAA 1983-0484, 1983.
|
| [8] |
Haney J W. Orbiter entry heating lessons learned from development flight test program[R]. NASA-198400 02081, 1984.
|
| [9] |
Herrera B J. An investigation of entry heating on the 0.0175 scale space shuttle orbiter(model 60-0) in the AEDC VKF tunnel B (OH39A/B)[R]. NASA CR-160 490, 1980.
|
| [10] |
Dye W H. Results of heat transfer tests on a 0.0175-scale space shuttle orbiter model(56-0) in the AEDC VKF 'B' hypersonic wind tunnel(OH74)[R]. NASA CR-144596, 1976.
|
| [11] |
Foust J W. Results of heat transfer test in the Arnold Engineering Development Center von Karman facility tunnels A and B utilizing space shuttle orbiter thin skin thermocouple models 56-0, 60-0, and 83-0 tests: OH-84B, OH-105, IH-102[R]. NASA CR-160828, 1981.
|
| [12] |
Gee J, Nakamoto J. Test results from the NASA/Rockwell International Space Shuttle 0.0175-scale orbiter models 56-0/60-0 and 0.04-scale orbiter forebody model 83-0 conducted in the AEDC/VKF-B 50-inch hypersonic wind tunnel(tests OH109 and OH109B)[R]. NASA CR-167349, 1982.
|
| [13] |
Berthold C L. Results of the transatlantic abort maneuver testing using the 0.0175 scale 56-0 and 60-0, and the 0.04 scale 83-0 thin skin thermocouple models in the AEDC VKF tunnel B hypersonic wind tunnel (OH111)[R]. NASA CR-167380, 1982.
|
| [14] |
Gee J. Test results from the NASA/Rockwell International Space Shuttle 0.0175-scale orbiter models 56-0/60-0 and 0.04-scale orbiter forebody model 83-0 conducted in the NASA/ARC 3.5-foot hypersonic wind tunnel(test OH110)[R]. NASA CR-160844, 1981.
|
| [15] |
Berthold C L, Marroquin J. Results of tests on a 0.0175-scale model (60-0) of the space shuttle orbiter to determine re-entry mode convective heat transfer rates on the upper wing surface and SSME nozzles in the AEDC VKF 'B' hypersonic wind tunnel (OH98)[R]. NASA CR-160501, 1980.
|
| [16] |
Miller C G, Micol J R, Gnoffo P A. Laminar heat-transfer distributions on biconics at incidence in hypersonic-hypervelocity flows[R]. NASA TP-2213, 1985.
|
| [17] |
Olivier H, Gronig H. Hypersonic model testing in a shock tunnel[R]. AIAA 1993-5004, 1993.
|
| [18] |
Legge H. Experiments on a 70 degree blunted cone in rarefied hypersonic wind tunnel flow[R]. AIAA 1995-2140, 1995.
|
| [19] |
Hozumi K, Yamamoto Y, Masson A, et al. A study for prediction of flight aerodynamic heating using HYFLEX flight and wind tunnel data[R]. AIAA 2001-1826, 2001.
|
| [20] |
李明, 廖俊必, 曾学军, 等. 风洞气动热试验外推关联参数初步研究[J]. 空气动力学学报, 2010, 28(5): 513-517. Li M, Liao J B, Zen X J, et al. Preliminary study on correlative parameters of extrapolation-to-flight of aerodynamic heating from wind tunnels[J]. Acta Aerodynamica Sinica, 2010, 28(5): 513-517. (in Chinese) |
| [21] |
Roe P L. Approximate Riemann solvers, parameter vectors and differences schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [22] |
张亮, 程晓丽, 艾邦成, 等. 高超声速钝球柱外形表面热流分布研究[J]. 航天返回与遥感, 2014, 35(1): 13-20. Zhang L, Cheng X L, Ai B C, et al. Heat flux distribution research of hypersonic blunt sphere-cylinder model[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1): 13-20. (in Chinese) |
| [23] |
杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 1998: 8-12. Yang S M, Tao W Q. Heat transfer[M]. Beijing: Higher Education Press, 1998: 8-12. (in Chinese) |



