2. 高速水动力航空科技重点实验室,湖北荆门 448035
2. Aviation Key Scientific and Technological Laboratory of High Speed Hydrodynamic, Jingmen 448035, China
水陆两栖飞机是指能在水面上滑行、起飞、降落和停泊的水面飞行器, 同时也具备在陆地上起降的能力.水陆两栖飞机水面高速滑行过程中的运动响应较大, 且伴随着船体首部大喷溅、自由液面大变形和破碎等流场特征, 使得流场的速度梯度、压力梯度、湍流度、气液相分布等变得十分复杂, 属于强非线性问题, 对这种水陆两栖飞机水面高速滑行过程中的水动性能进行分析时, 主要以物理水池试验为主, 但随着计算机性能的提高, CFD在水陆两栖飞机水动性能设计、优化和预报方面的作用日益增强, 逐渐变成与物理水池试验并驾齐驱的研究手段.目前, 针对这种水陆两栖飞机水面高速滑行6自由度运动问题的数值计算, 主要采用传统动网格技术、整体运动网格技术、滑移网格技术、重叠网格技术或网格自适应技术等方法进行分析.本文基于传统动网格技术, 提出了一种"状态预估-精确计算"的数值模拟方法, 对水陆两栖飞机静水面高速滑行性能进行数值计算与试验分析, 研究其在静水面滑行时的阻力、姿态、升沉和流场特征.
1 数值方法及计算 1.1 数值方法控制方程:
(1) 连续方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho v}}{{\partial y}} + \frac{{\partial \rho w}}{{\partial z}} = 0 $ |
(2) 动量方程
| $ \begin{array}{l} \;\rho (\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}}) = - \frac{{\partial P}}{{\partial x}} + \mu (\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}})\\ \;\;\rho (\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}}) = - \frac{{\partial P}}{{\partial y}} + \mu (\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}})\\ \rho (\frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}}) = g - \frac{{\partial P}}{{\partial z}} + \mu (\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial {y^2}}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}) \end{array} $ |
式中, u, v, w分别为x, y, z方向上的速度分量, μ为动力黏性系数, P为流体压力, ρ为流体密度, g为重力加速度, t为时间.
计算时, 通过求解三维黏性不可压多相流体的Reynolds平均N-S方程结合运动方程来模拟飞机静水面滑行时的流场特征和运动特性, 数值模拟方法为隐式有限体积法, 具有2阶空间和时间精度.动量方程离散采用GDS格式, 自由液面捕捉采用BRICS离散格式.湍流模型采用k-ω(SST Menter)结合壁函数进行处理, 自由液面捕捉采用VOF方法. VOF方法根据各个时刻流体在网格单元中所占体积函数F来构造和追踪自由面, 若在某时刻网格单元中F=1, 则说明该单元全部为指定相流体所占据, 为流体单元; 若F=0, 则该单元全部为另一相流体所占据, 相对于前相流体则称为空单元.当0<F < 1时, 则该单元为包含两相物质的交界面单元. F函数的控制方程在形式上可以写成
| $ \frac{{\partial F}}{{\partial t}} + u\frac{{\partial F}}{{\partial x}} + v\frac{{\partial F}}{{\partial y}} + w\frac{{\partial F}}{{\partial z}} = 0 $ |
由于VOF方法追踪的是网格中的流体体积, 而不是流体质点的运动, 因而具有容易实现、计算量小和精度高等优点, 并且可以处理自由面的大变形和自由面的拓扑结构发生变化等复杂三维情况.
1.2 几何模型某轻型水陆两栖飞机是我国自行设计、制造的, 其起飞、降落滑跑距离短, 陆上可在水泥、沥青等简易跑道或现有机场起降; 水上可在海湾、江河、湖泊等水域起降, 地区适应性广, 是平原、有水域地带和边远山区便捷的作业和交通工具.该轻型水陆两栖飞机为单船身、悬臂式中上单翼布局形式, 发动机高置在机身背上.
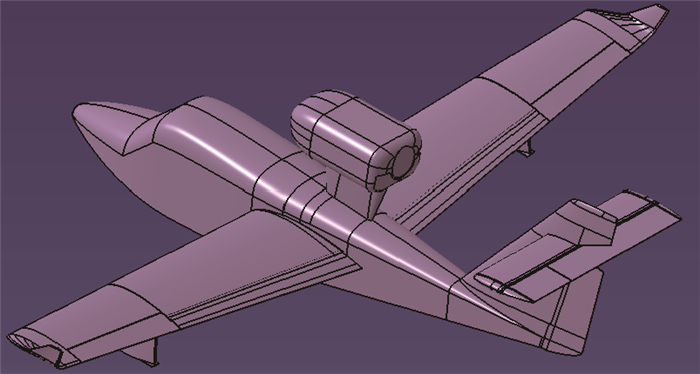
轻型水陆两栖飞机三维示意图见图 1.
|
| 图 1 轻型水陆两栖飞机示意图 Fig.1 Light amphibious aircraft |
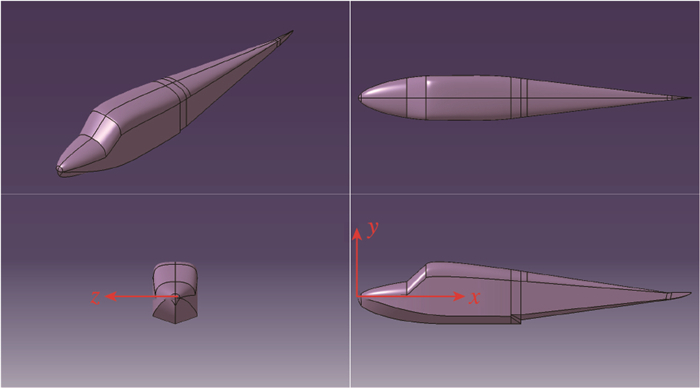
数值计算和试验分析时, 将飞机进行简化, 采用单船身为研究模型, 并通过施加砝码来模拟机翼的气动升力; 单船身具有航向、俯仰和垂荡3个自由度.
|
| 图 2 单船身示意图 Fig.2 Amphibious aircraft hull |
施加的砝码重量可按如下公式进行计算
| $ {W_L} = W{(\frac{V}{{{V_{\rm{t}}}}})^2} $ |
式中, WL为砝码重量(kg), 下标L表示升力(life); W为飞机排水量(kg); V为飞机航速(m/s); Vt为飞机离水速度(m/s), 下标t表示起飞(take off).
1.3 问题描述及解决方案该轻型水陆两栖飞机重量较轻、船体斜升角较小、后体细长等特征, 导致其在水面高速滑行过程中的姿态和升沉较大, 采用传统动网格技术和传统数值模拟方法对其水动性能进行数值计算时, 往往会因为网格的过度拉伸和变形而导致计算精度不高甚至计算终止.针对这一问题, 本文提出了一种"状态预估-精确计算"的数值模拟方法对其进行分析:
(1) 状态预估:采用很粗的网格(飞机表面和自由液面网格较大, 且无边界层网格)对飞机在不同航速下的姿态和升沉进行快速预估, 为精确网格的划分和计算方法的选取提供依据;
(2) 精确计算:将飞机置于预估状态下进行精确网格划分, 数值计算时, 先将飞机纵摇和垂荡两个自由度固定进行计算, 直至残差收敛或阻力趋于稳定时, 再将纵摇和垂荡两个自由度放开进行计算, 直至残差收敛和监测值趋于稳定.
1.4 状态预估计算网格采用非结构六面体网格布局形式, 取半模进行网格划分和计算, 计算域大小如下(L为模型长度):
(1) 飞机首部离前边界: 1L;
(2) 飞机尾部离后边界: 3L~5L;
(3) 自由液面离上边界: 1L;
(4) 自由液面离下边界: 2L;
(5) 飞机对称面离侧边界: 1L~2L.
飞机沿航向布置约250个网格, 自由液面处的网格大小为X=Y=50Z=50×L/250, 对飞机局部地方网格适当进行细化, 无边界层网格, 最终网格量约为5×105.粗网格示意图见图 3.

|
| 图 3 粗网格示意图 Fig.3 Coarse grids |
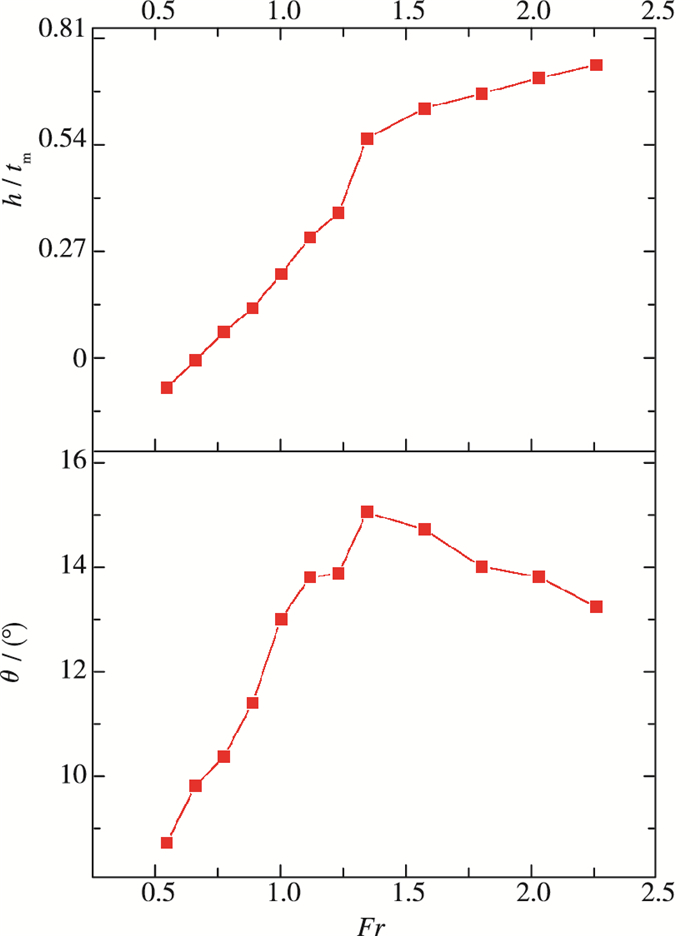
状态预估时, 模型壁面设置成滑移边界, 即不考虑黏性, 最大非线性迭代次数为8~10, 时间步长选取ΔT=0.01L/V.每个航速的平均计算时间约为5 h, 实现了快速预估.状态预估结果见图 4~5, 其中, Fr为长度Froude数, θ为姿态(°), h为重心处升沉(mm), tm为静浮时的断阶吃水(mm), z为z向位置(m).
|
| 图 4 状态预估结果 Fig.4 State prediction results |

|
| 图 5 状态预估流场示意图(Fr=2.288) Fig.5 Flow field of state prediction(Fr=2.288) |
精确计算时, 在粗网格基础上按状态预估结果对飞机的姿态和自由液面位置进行调整, 飞机沿航向布置约500个网格, 自由液面处的网格大小为X=Y=50Z=50×L/1 000, 对飞机尾部流场进行加密, 捕捉"鸡尾流", 飞机局部地方网格适当进行细化, 添加边界层网格, Y+(边界层第1层网格的无量纲大小)取40.最终网格量约为3×106~4×106(不同航速边界层网格不一样).网格示意图如图 6所示.

|
| 图 6 精确网格示意图 Fig.6 Fine grids |
精确计算时, 模型壁面设置成无滑移边界, 即考虑黏性, 最大非线性迭代次数为15~20, 时间步长选取ΔT=0.005 L/V.
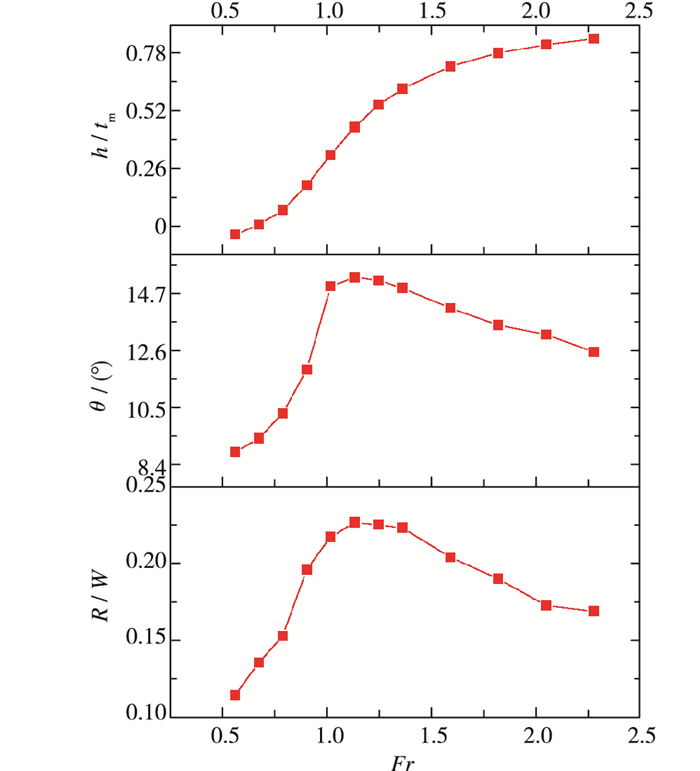
|
| 图 7 精确计算结果 Fig.7 Accurate calculation results |
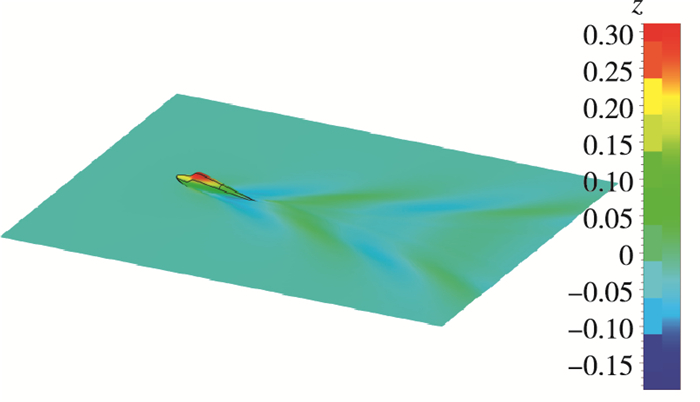
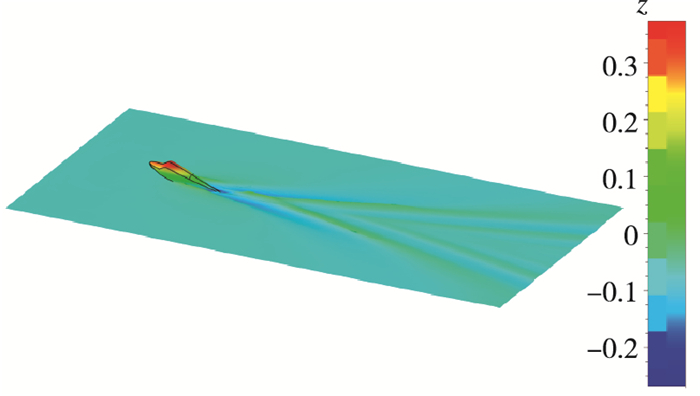
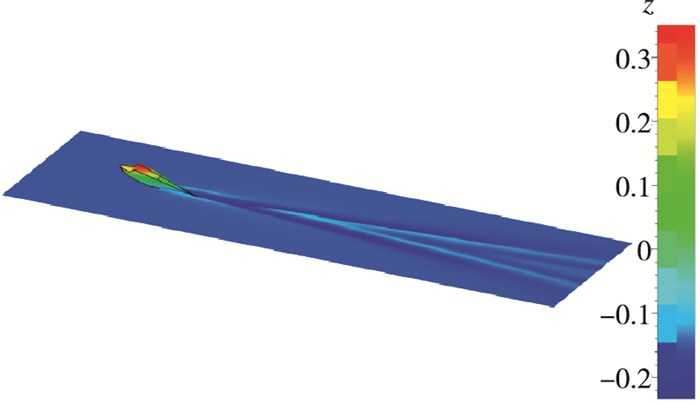
由图 8~19可得, 水陆两栖飞机单船身在静水面滑行时, 姿态较大且尾部有明显的"鸡尾流"和Kelvin尾流场; 随着航速的增大, 升沉逐渐增大, Kelvin尾流场逐渐变细变窄, 阻力和姿态有明显峰值.
|
| 图 8 流场示意图(Fr=0.572) Fig.8 Flow field(Fr=0.572) |
|
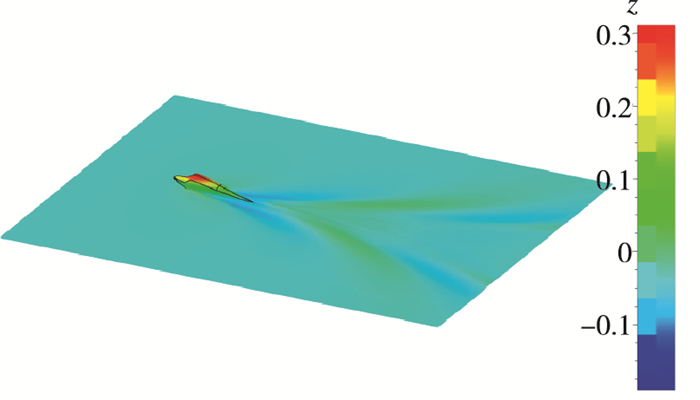
| 图 9 流场示意图(Fr=0.686) Fig.9 Flow field(Fr=0.686) |
|
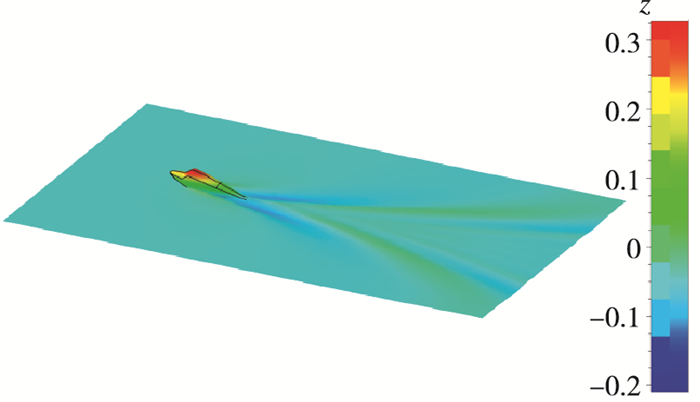
| 图 10 流场示意图(Fr=0.801) Fig.10 Flow field(Fr=0.801) |
|
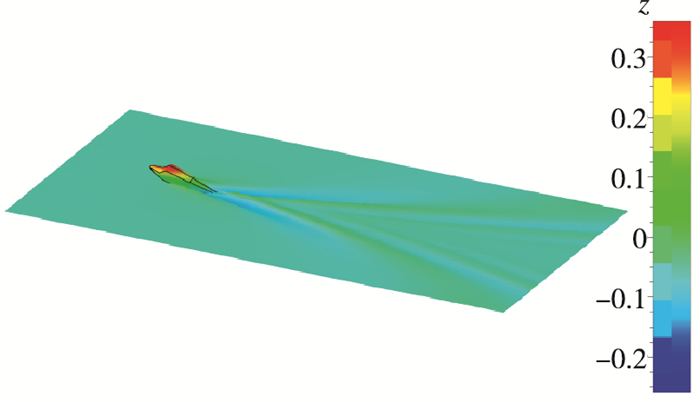
| 图 11 流场示意图(Fr=0.915) Fig.11 Flow field(Fr=0.915) |
|
| 图 12 流场示意图(Fr=1.030) Fig.12 Flow field(Fr=1.030) |
|
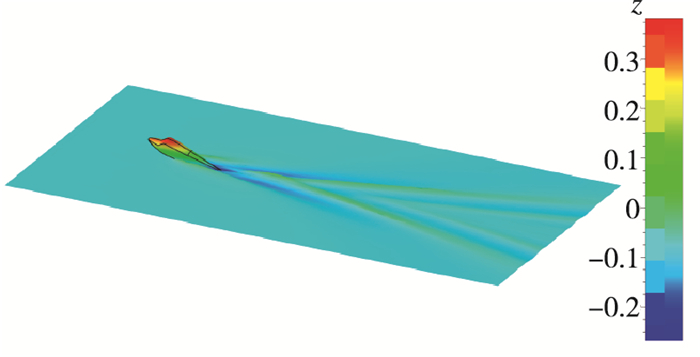
| 图 13 流场示意图(Fr=1.144) Fig.13 Flow field(Fr=1.144) |
|
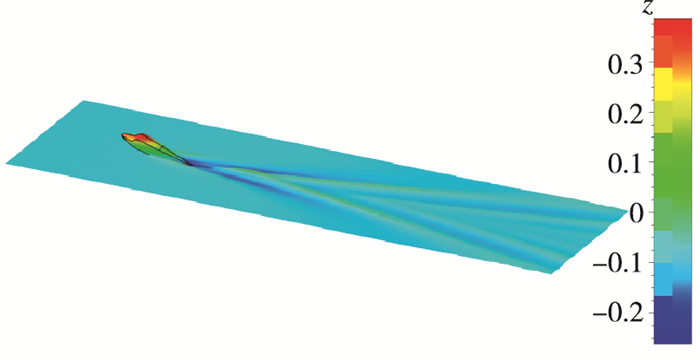
| 图 14 流场示意图(Fr=1.258) Fig.14 Flow field(Fr=1.258) |
|
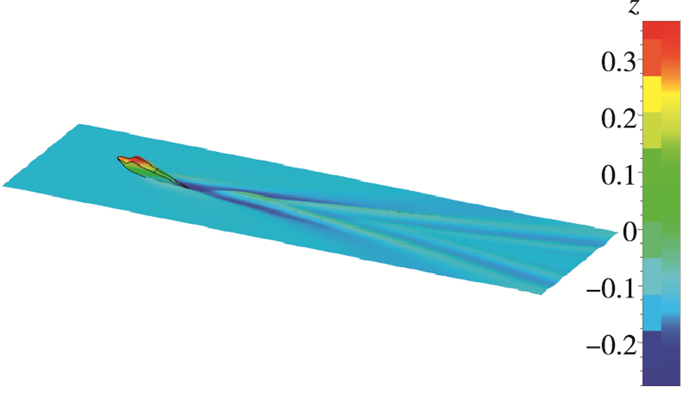
| 图 15 流场示意图(Fr=1.373) Fig.15 Flow field(Fr=1.373) |

|
| 图 16 流场示意图(Fr=1.602) Fig.16 Flow field(Fr=1.602) |

|
| 图 17 流场示意图(Fr=1.831) Fig.17 Flow field(Fr=1.831) |

|
| 图 18 流场示意图(Fr=2.059) Fig.18 Flow field(Fr=2.059) |
|
| 图 19 流场示意图(Fr=2.288) Fig.19 Flow field(Fr=2.288) |
为了验证数值模拟方法的精度和可行性, 按Froude数相似准则开展了飞机模型加工与水池静水拖曳试验.水池试验模型采用红松进行加工, 模型表面经过打磨、光顺和喷漆处理, 在安装必要的试验装置和仪器后, 按飞机理论重量、重心和惯量对模型进行调试, 将调试完成后的模型安装到拖车上进行静水拖曳试验, 通过施加砝码来模拟机翼气动升力.安装阻力传感器、倾角传感器和位置传感器分别测量飞机静水面航行时的阻力、姿态和升沉.试验示意图如图 20所示.

|
| 图 20 模型水池试验示意图(Fr=2.288) Fig.20 Tank test(Fr=2.288) |
通过水池试验观测可得, 试验时模型尾部有明显的"鸡尾流"和Kelvin流场.
3 结果对比及结论 3.1 结果对比通过以上数值计算研究和水池试验研究得到了飞机单船身在一系列航速下的滑行水动性能, 监测了飞机静水面滑行过程中的阻力、姿态、升沉和流场特征.数值计算和水池试验结果对比见图 21~23.
|
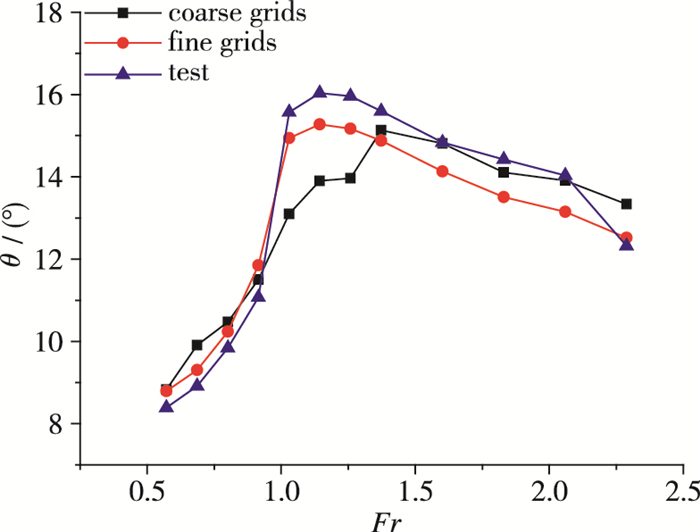
| 图 21 数值计算与水池试验结果对比(姿态) Fig.21 Comparisons of numerical results with tank test results(attitude) |
|
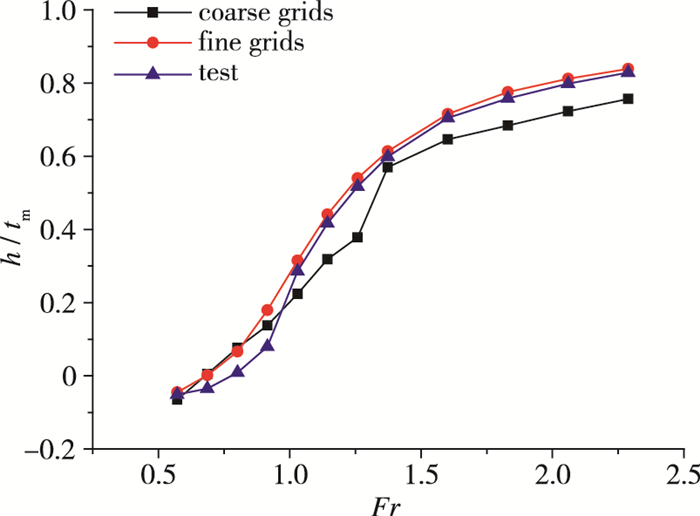
| 图 22 数值计算与水池试验结果对比(升沉) Fig.22 Comparisons of numerical results with tank test results(heave) |
|
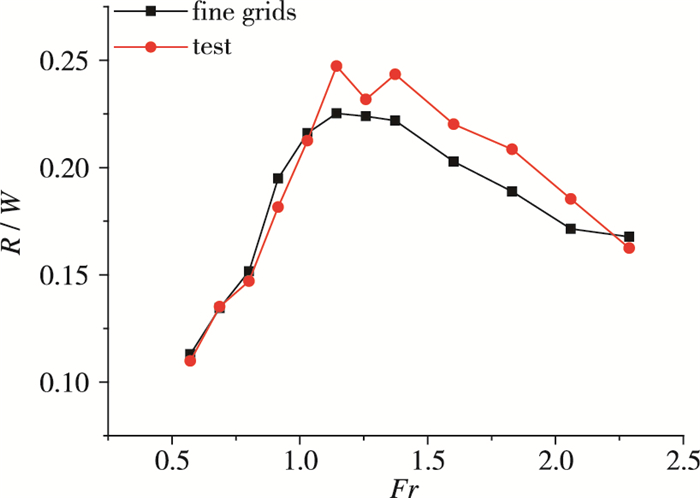
| 图 23 数值计算与水池试验结果对比(阻力) Fig.23 Comparisons of numerical results with tank test results(resistance) |
(1) 采用粗网格对飞机静水滑行最终状态进行预估的效率较高, 精度约75%;
(2) 随着航速的增大, 升沉逐渐增大, 尾部流场逐渐变细变窄, 姿态在Fr=1.144时达到最大, 阻力有明显峰值;
(3) 精确计算与水池试验的流场特征均有明显的"鸡尾流"和Kelvin流场, 且阻力、姿态和升沉的计算精度达到90%, 验证了数值模拟方法的可行性.
| [1] |
褚林塘. 水上飞机水动力设计[M]. 北京: 航空工业出版社, 2014: 1-8. Chu L T. Collected works of seaplane[M]. Beijing: Aviation Industry Press, 2014: 1-8. (in Chinese) |
| [2] |
胡问鸣. 通用飞机[M]. 北京: 航空工业出版社, 2018: 216. Hu W M. General aviation aircraft[M]. Beijing: Aviation Industry Press, 2018: 216. (in Chinese) |
| [3] |
唐彬彬, 张家旭, 李成华, 等. 水陆两栖飞机模型喷溅峰点分析方法研究[J]. 航空计算技术, 2015, 45(6): 45. Tang B B, Zhang J X, Li C H, et al. Study on analytical method for spray peaks of amphibious aircraft[J]. Aeronautical Computing Technique, 2015, 45(6): 45. DOI:10.3969/j.issn.1671-654X.2015.06.011 (in Chinese) |
| [4] |
张师帅. 计算流体动力学及其应用[M]. 武汉: 华中科技大学出版社, 2011. Zhang S S. Computational fluid dynamics and applica-tion[M]. Wuhan: Huazhong University of Science & Technology Press Co. Ltd, 2011. (in Chinese) |
| [5] |
王丽丽, 李新颖, 黄淼, 等.基于重叠网格的水陆两栖飞机浮筒水动性能研究[C].第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集, 北京: 海洋出版社, 2017: 1248. Wang L L, Li X Y, Huang M, et al. Hydrodynamics research of amphibious aircraft float based on overset mesh[C]. Proceedings of the 14th National Congress on Hydrodynamics & the 28th National Conference on Hydrodynamic, Beijing: China Ocean Press, 2017: 1248(in Chinese). |
| [6] |
李新颖, 贾力平, 吴彬. 水陆两栖飞机单船身静水面滑行数值模拟[J]. 军民两用技术与产品, 2015(10): 10. Li X Y, Jia L P, Wu B. Numerical simulation of amphibious aircraft hull taxiing on calm water[J]. Dual Use Technologies & Products, 2015(10): 10. DOI:10.3969/j.issn.1009-8119.2015.10.009 (in Chinese) |
| [7] |
余建伟.基于CFD的船舶阻力计算与预报研究[D].上海: 上海交通大学, 2009. Yu J W. Research on calculation and prediction for ship resistance based on CFD theory[D]. Shanghai: Shanghai Jiao Tong University, 2009(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10248-2009225651.htm |
| [8] |
班长英.体积分数保持法——基于VOF方法中边界线重构的改进算法[D].南京: 河海大学, 2006. Ban C Y. Volume fraction conservation method——A modified borderline reconstruction method in VOF[D]. Shanghai: Shanghai Jiao Tong University, 2009(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y912007 |
| [9] |
刘尚民, 刘朝君, 祁圣君. 海鸥300模型起飞滑行性能估算技术研究[J]. 航空科学技术, 2015, 26(10): 6. Liu S M, Liu Z J, Qi S J. Estimated research on the performance of HO300 scaled model's take off and taxiing[J]. Aeronautical Science & Technology, 2015, 26(10): 6. DOI:10.3969/j.issn.1007-5453.2015.10.002 (in Chinese) |
| [10] |
黄技.高速船舶阻流板降阻机理分析[D].大连: 大连海事大学, 2013. Huang J. Analysis of interceptor for drag reduction theory on high speed vessel[D]. Da Lian: Dalian Maritime University, 2013(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10151-1013204603.htm |
| [11] |
张成基.船舶尾流模拟及感应磁场分布特性[D].西安: 西安工业大学, 2018. Zhang C J. Simulation and induced magnetic field distribution characteristics of ship wakes[D]. Xi'an: Xi'an Technological University, 2018(in Chinese). |
| [12] |
中国船舶工业总公司. CB/Z 244-88-1988, 滑行艇船模阻力测试方法[S]. 1988. China State Shipbuilding Corporation Limited. CB/Z 244-88-1988, Method of model resistance measurement for planning craft[S]. 1988(in Chinese). |



