引言

Kelvin-Helmholtz(K-H)不稳定性由切向速度间断引起, 是一个基础问题, 并作为一个重要领域被研究多年. K-H不稳定性机理在混合层演化及湍流转捩中起着重要作用^[1].理想的K-H不稳定性由切向速度间断发展而来, 与流体黏性物质界面流体可压缩性无关.由于理论分析只能研究初期的线性和非线性阶段, 所以数值模拟方法在理解后期强非线性特性中显现出重要作用.

对于不可压缩流动, 虽然一些相关的类似现象已被数值方法广泛研究, 如高速剪切或混合层, 但是对K-H不稳定性问题进行直接模拟时仍遇到多种挑战.一个困难是切向速度间断的数值表达及物质界面的处理; 另一个困难是为了处理激波在不稳定流动中的发展, 需要引入WENO(weighted essential non-oscillatory)等激波捕捉格式^[2].然而, 这些格式的耗散远强于在激波附近数值不稳定的对称紧致格式等中心型差分格式.例如, WENO格式的自适应机制对不需要激波捕捉的普通流动区域过于敏感.原因是被加权量调制的高效插值达到最优模板的过程非常慢, 导致无强激波的大密度变化及大剪切速度区域过度耗散.

近些年, 我们发展了一种位标集(level set)守恒锐界面(sharp-interface)方法求解可压缩流动^[3].该方法能够可靠且精确地计算复杂的物质界面演化, 已被成功应用于Richtmyer-Meshkov不稳定性问题的模拟^[4].本文将该方法与一种低耗散WENO格式结合, 用来模拟K-H不稳定性问题.当物质界面被描述成接触间断时, 本文方法可精确地求解等同于无厚度涡片的切向速度间断.它允许高波数扰动发展, 这不同于单一流体或易混界面方法, 后者使高波数模态被初始设定的有限宽度剪切层或快速数值耗散所抑制.

1 锐界面方法 1.1 方法介绍

考虑无黏可压缩流体, 在区域Ω内, 流动的控制方程可写成守恒形式:

$\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \nabla \cdot \mathit{\boldsymbol{F}} = 0.$

(1)

其中, U为质量动量总能的守恒变量, F为对应的通量项.界面Γ(t)将区域Ω分为Ω¹(t)与Ω²(t)两个子区域.对于多相流问题, 界面Γ(t)的演化由两物质Riemann问题的界面条件确定:

$R({\mathit{\boldsymbol{U}}_{{\rm{fluid}}1}},{\mathit{\boldsymbol{U}}_{{\rm{fluid2}}}}) = 0.$

(2)

根据Miller等^[5]的工作, 对网格间距为Δx和Δy的二维Descartes网格的子区域Ω¹(t)中的流体应用方程(1).在被流体占据的计算网格(i, j)的时空体积Δ_ij∩Ω¹(t)上, 通过积分方程(1) 可获得有限体积离散形式:

$\smallint _n^{n + 1}{\rm{d}}t{\smallint ^{}}_{\Delta ij \cap {\mathit{\Omega }^1}(t)}{\rm{d}}x{\rm{d}}y\left( {\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \nabla \cdot \mathit{\boldsymbol{F}}} \right) = 0.$

(3)

式(3) 中, Δ_ij=ΔxΔy为网格单元体积. Δ_ij∩Ω¹(t)可用α_ij(t)ΔxΔy代替, 且α_ij(t)为依赖于时间的所求流体的体积分数系数, 满足0≤α≤1.通过应用Gauss定理, 可得到

$\smallint _n^{n + 1}{\rm{d}}t{\smallint ^{}}_{\Delta ij \cap {\mathit{\Omega }^1}(t)}{\rm{d}}x{\rm{d}}y\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \smallint _n^{n + 1}{\rm{d}}t{\smallint ^{}}_{\partial \Delta ij \cap \mathit{\Gamma }(t)}{\rm{d}}x{\rm{d}}y\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{n}} = 0.$

(4)

其中, ∂Δ_ij为网格在特定4个点下的4个单元面的直角截边, 即

$\begin{array}{l} ({x_i} + \Delta x/2,{y_j}),({x_i},{y_j} + \Delta y/2),\\ ({x_i} - \Delta x/2,{y_j}),({x_i},{y_j} - \Delta y/2). \end{array}$

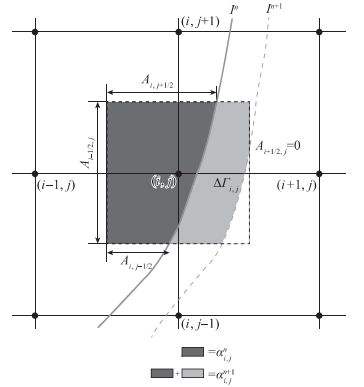
注意到图 1中界面位置Γ(t), ∂Δ_ij∩Ω¹(t)可两部分表示.一是被界面切割单元面的4段直角截边的集合, 可写为:

$\begin{array}{l} {A_{i + 1/2,j}}\left( t \right)\Delta y,{A_{i,j + 1/2}}\left( t \right)\Delta x,\\ {A_{i - 1/2,j}}\left( t \right)\Delta y,{A_{i,j - 1/2}}\left( t \right)\Delta x, \end{array}$

其中, 0≤A≤1为孔隙；另一部分是单元(i, j)内边界ΔΓ_{i, j}(t)部分.因此方程(4) 可写作

$\begin{array}{l} \quad \quad \quad \quad \alpha _{i,j}^{n + 1}\mathit{\boldsymbol{U}}_{i,j}^{n + 1} - \alpha _{i,j}^nU_{i,j}^n = \\ \smallint _n^{n + 1}{\rm{d}}t\frac{1}{{\Delta x}}[{A_{i + 1/2,j}}(t){{\mathit{\boldsymbol{\hat F}}}_{i + 1/2,j}} - {A_{i - 1/2,j}}(t){{\mathit{\boldsymbol{\hat F}}}_{i - 1/2,j}}] + \\ \smallint _n^{n + 1}{\rm{d}}t\frac{1}{{\Delta y}}[{A_{i,j + 1/2}}(t){{\mathit{\boldsymbol{\hat F}}}_{i,j + 1/2}} - {A_{i,j - 1/2}}(t){{\mathit{\boldsymbol{\hat F}}}_{i,j - 1/2}}] + \\ \quad \quad \quad \quad \smallint _n^{n + 1}{\rm{d}}t\frac{1}{{\Delta x\Delta y}}\mathit{\boldsymbol{\hat X}}\left[ {{\mathit{{ {\varGamma} }}_{i,j}}(t)} \right]. \end{array}$

(5)

其中, α_ij(t)U_{i, j}和U_{i, j}分别为所求解流体的切割单元内的守恒量和守恒量的单元平均密度. ${\mathit{\boldsymbol{\hat F}}}$ 为单元面的平均通量; $\mathit{\boldsymbol{\hat X}}\left[ {{\mathit{{{\varGamma} }}_{i,j}}(t)} \right]$ 为通过界面部分的平均动量和能量交换, 由界面接触方程(2) 决定.采用显式1阶向前的时间差分, 方程(5) 可被近似为

$\begin{array}{l} \quad \alpha _{i,j}^{n + 1}\mathit{\boldsymbol{U}}_{i,j}^{n + 1} = \alpha _{i,j}^n\mathit{\boldsymbol{U}}_{i,j}^n + \frac{{\Delta t}}{{\Delta x\Delta y}}\mathit{\boldsymbol{\hat X}}\left[ {{\mathit{{{\varGamma} }}_{i,j}}} \right] + \\ \frac{{\Delta t}}{{\Delta x}}[{A_{i - 1/2,j}}(t){{\mathit{\boldsymbol{\hat F}}}_{i - 1/2,j}} - {A_{i + 1/2,j}}(t){{\mathit{\boldsymbol{\hat F}}}_{i + 1/2,j}}] + \\ \frac{{\Delta t}}{{\Delta y}}[{A_{i,j - 1/2}}(t){{\mathit{\boldsymbol{\hat F}}}_{i,j - 1/2}} - {A_{i,j + 1/2}}(t){{\mathit{\boldsymbol{\hat F}}}_{i,j + 1/2}}]. \end{array}$

(6)

其中, Δt为时间步长.等号右边的所有项均赋予第n层时间的值.由于每一Runge-Kutta (R-K)格式子步均符合方程(6) 的形式, 所以应用了R-K格式做高阶时间推进, 同时保证离散的守恒性.

1.2 界面描述

将计算域Ω与一种符号距离函数φ(x, y, t)联系起来, 它被称作位标集函数^[6], 且 $\nabla \left| \phi \right| = 1$ .知道φ后, 可以通过寻找φ的零值以确定界面.用Γ(t)={x, y:φ(x, y, t)=0}将整个区域分割成两个子区域, 每个区域对应一种流体并带有相反的φ值符号.可见φ的持续求解等同于控制方程(7) 下的界面对流.

${\phi _t} + \mathit{\boldsymbol{v}} \cdot \nabla \phi = 0.$

(7)

其中，v为位标集的对流速度.实际应用中位标集只在接近界面的区域求解, 其中包括第1和第2最近网格层.远离界面的区域位标集被方程(8) 重新初始化^[7].

${\phi _\tau } + {\rm{sng}}\left( \phi \right)\left( {\left| {\nabla \phi } \right| - 1} \right){\rm{ = }}0.$

(8)

其中，sgn(φ)为符号函数, 用以维持位标集函数的符号距离属性.

1.3 界面重构

通过假定位标集沿单元面的线性分布，来计算单元面的孔隙.通过位标集的法向信息, 二维体积分数设定可由下式确定:

$H(\phi ,\varepsilon ) = \left\{ {\begin{array}{*{20}{l}} {0,\mathit{\Lambda } > \mathit{\Gamma },\phi ＜ 0}\\ {\frac{1}{2} + \frac{1}{{{\varepsilon ^2}}}D\phi + \frac{1}{2}\frac{{{\mathit{\Lambda }^2}}}{{\varepsilon \mathit{\Gamma }}},0 \le \mathit{\Lambda } \le \mathit{\Gamma },\phi ＜ 0}\\ {\frac{1}{2} + \frac{1}{{{\varepsilon ^2}}}D\phi ,\mathit{\Lambda } ＜ 0}\\ {\frac{1}{2} + \frac{1}{{{\varepsilon ^2}}}D\phi - \frac{1}{2}\frac{{{\mathit{\Lambda }^2}}}{{\varepsilon \mathit{\Gamma }}},0 \le \mathit{\Lambda } \le \mathit{\Gamma },\phi > 0}\\ {1,\mathit{\Lambda } > \mathit{\Gamma },\phi > 0} \end{array}} \right..$

(9)

其中,

$\begin{array}{l} D = \varepsilon {\rm{min}}(\frac{1}{{\left| {{N_x}} \right|}},\frac{1}{{\left| {{N_y}} \right|}}),\mathit{\Gamma } = \sqrt {{D^2} - {\varepsilon ^2}} ,\\ \mathit{\Lambda } = \frac{\mathit{\Gamma }}{2} + \frac{{D\left| \phi \right|}}{\varepsilon } - \frac{\varepsilon }{2}. \end{array}$

式(9) 为光滑后的Heaviside函数, 关于φ=0对称, 可变换回取值0.5的体积分数.对一种给定流体所有单元均可分为3类:体积分数大于0.5的单元为正常单元, 小于0.5但不等于0为小单元, 其他为空单元.

1.4 混合过程

对于一个小单元或空单元, 基于通过整网格CFL条件确定的时间步长可能不能够获得稳定的流体状态.因此, 应将这些单元与其附近单元合并.目标相邻单元应选作正常单元, 并由位标集的方向确定.

合并后的小单元和目标单元在x, y方向上的改变通过计算平均守恒量求得.然后界面单元附近流体的守恒量通过式(10) 求解.

$\alpha _{i,j}^{n + 1}\mathit{\boldsymbol{U}}_{i,j}^{n + 1}{\rm{ = }}{\left( {\alpha _{i,j}^{n + 1}\mathit{\boldsymbol{U}}_{i,j}^{n + 1}} \right)^*} + \sum\limits_k {{M^x} + } \sum\limits_t {{\mathit{\boldsymbol{M}}^y}} .$

(10)

式中，(α_{i, j}ⁿ⁺¹U_{i, j}ⁿ⁺¹)^*为混合前n+1时间层上的守恒量.等号右边的第2项和第3项分别综合了所有x, y方向的混合操作.注意现在的混合过程自动处理消失和新造的空单元.在以往算例中, 残余守恒量均被传入目标单元中, 最新的算例中所有新造小单元内的守恒量均传自其目标单元.

1.5 界面交换

为了获得动量和能量在界面的交换值, 求解了在沿界面方向界面区域带附近的网格点上带有界面相互作用的Riemann问题.求解界面相互作用后可获得界面压力p_Ι及法向速度v_Ι≡(u_I, v_I).因此, 对应于φ>0的流体, 传递给它的动量和能量分别为

${{\mathit{\boldsymbol{\hat X}}}^{\rm{P}}}(\Delta \mathit{\Gamma }) = {p_I}\Delta \mathit{\Gamma }{N_I},{{\mathit{\boldsymbol{\hat X}}}^{\rm{E}}}(\Delta \mathit{\Gamma }) = {p_I}\Delta \mathit{\Gamma }{\mathit{\boldsymbol{N}}_I}{v_I}.$

其中，ΔΓ和N_I分别为界面部分的长度(区域)和法向向量. ${{\mathit{\boldsymbol{\hat X}}}^{\rm{P}}} = \left( {\hat X_x^{\rm{P}},\hat X_y^{\rm{P}}} \right)$ 代表分别在x, y方向传递的动量, ${{\mathit{\boldsymbol{\hat X}}}^{\rm{E}}}$ 则代表能量传递.注意此处没有切向的动量和能量的传递, 以保证现方法在界面处恢复到精确的切向速度间断.同时, 注意到两种流体间传递的动量和能量大小相等符号相反, 所以整个流场的守恒特性得以满足.

2 低耗散WENO格式 2.1 格式介绍

目前的方法中, 通过单相流特征WENO-LLF格式^[8]及TVD R-K时间格式^[9]求解单一流体流场. WENO (2r-1) 格式可用一维对流方程描述，见式(11):

$\frac{{\partial u}}{{\partial t}} + \frac{\partial }{{\partial x}}f\left( u \right) = 0.$

(11)

方程(11) 在空间区域作离散, 即x_i=iΔx, 其中Δx为网格间距, u_i=u(x_i).方程(11) 的半离散形式为

$\frac{{{\rm{d}}u}}{{{\rm{d}}t}} = - \frac{1}{{\Delta x}}({{\hat f}_{i + 1/2}} + {{\hat f}_{i - 1/2}}).$

(12)

上式中的 ${{\hat f}_{i + 1/2}}$ 和 ${{\hat f}_{i - 1/2}}$ 为单元面左右两边通量的数值近似.当式(12) 等号右边项被赋值, 则可使用TVD R-K格式作时间推进迭代求解.单元面处的数值通量通过通量分裂方法求出：

${{\hat f}_{i + 1/2}} = \hat f_{i + 1/2}^ + + \hat f_{i + 1/2}^ - .$

(13)

其中, $\hat f_{i + 1/2}^ + $ 和 $\hat f_{i + 1/2}^ - $ 分别为正负通量.这些通量通过下面数值通量插值, 如Lax-Friedrichs (LLF)通量通过临近单元平均求得.

例如, 通过从迎风r阶模板重构候选插值函数 $\hat f_k^ + \left( x \right)$ 计算得到一个值的凸组合，构造获得 $\hat f_{i + 1/2}^ + $ , 即

$\hat f_{i + 1/2}^ + = \sum\limits_{k = 0}^{r - 1} {{\omega _k}} \hat f_k^ + ({x_{i + 1/2}}).$

其中, 插值函数通过列表系数确定, 如

$\hat f_k^ + ({x_{i + 1/2}}) = \sum\nolimits_{j = 0}^{r - 1} {{c_{k,j}}} \hat f_{i - k + j}^ + .$

加权数ω_k被α_k标准化, 公式如下：

${\alpha _k} = \frac{{{d_k}}}{{{{({\beta _k} + \varepsilon )}^p}}}.$

(14)

其中, 由于生成(2r-1) 阶中心-迎风格式，d_k被称作优化加权系数, ε>0以防止除数为0, β_k为光滑性指标, 定义为

${\beta _k} = \sum\limits_{k = 1}^{r - 1} {\Delta {x^{2k - 1}}} \smallint _{{x_{i - 1/2}}}^{{x_{i + 1/2}}}{\left[ {\frac{{{{\rm{d}}^k}}}{{{\rm{d}}{x^k}}}\hat f_k^ + (x)} \right]^2} + {\rm{d}}x.$

并在间断出现时在候选模板中变大, p=1, 2, 用于在解的不光滑部分调整特定的权.

类似地, $\hat f_{i + 1/2}^ - $ 可通过改变模板中的一个网格点至右边及反转迎风方向求得.注意, 尽管优化加权数对于单一的正负通量给出(2r-1) 阶中心-迎风格式, 但由于联立了方程(13) 的通量分裂, 实际对于方程(12) 中的 ${{\hat f}_{i + 1/2}}$ 生成了2r阶中心格式^[10].

2.2 参考光滑指标

尽管方程(14) 定义的加权量展现出很好的激波捕捉性能, 但它们极易触发自适应, 使其作用效果退化.为克服这一困难, Borges等^[11]引入了另一加权形式, 即WENO 5阶(r=3) 格式:

${\alpha _k} = {d_k}\left[ {1 + \left( {\frac{{{\tau _5}}}{{{\beta _{3,{\rm{ }}k}} + \varepsilon }}} \right)} \right],{\rm{ }}k = 0,1,2.$

(15)

其中β_{3, k}为3阶模板的常规第k个光滑指标, 即由τ₅=|β_{3, 0}-β_{3, 2}|给定一个高阶的光滑指标, 并被认为在普通流场中远小于β_{3, k}.事实上, 方程(15) 的常规光滑指标通过一个参考量的标准化.由于τ₅为3阶模板中不同光滑指标的联合, 所以不清楚在另一些精度的WENO格式中是否或能否找到类似组合.

为了扩展WENO格式的参考光滑指标思想至任意阶精度, 定义如下加权量:

${\alpha _k} = {d_k}\left( {a + \frac{{{\beta _{2r - 1,0}}}}{{{\beta _{r,k + \varepsilon }}}}} \right).$

(16)

其中, a=10, β_{r, k}为r阶模板的常规光滑指标, 参考量β_{2r-1, 0}为优化(2r-1) 阶模版的光滑指标.此时, 计算的复杂性增长, 计算β_{2r-1, 0}的代价很小.式(16) 的基本作用原理是, 由于加权量试图使其在候选模板和优化模板之间自适应, 所以一种直接的参考光滑指标的选取是优化模板的光滑指标.通过这种选取, 在普通流场中因β_{2r-1, 0}消除了高阶导数而接近β_{r, k}, 并因此生成了构成优化值所需的差别很小的加权量.为保证相同光滑指标下优化模板相对于其他候选模板的优势地位, 方程(16) 中a值取较大值.

3 算例验证

3.1节两个一维算例用于验证上文方法的计算能力.分别使用了5阶校正WENO-LLF格式及3阶TVD R-K格式对空间和时间进行求解.若不作特别指明, 所有求解中的CFL数均设定为0.6.

3.1 波-界面干扰

考虑波界干扰问题, 初始条件如下:

$\begin{array}{l} \quad \quad \quad \quad \quad (\rho ,u,p,\gamma ) = \\ \left\{ {\begin{array}{*{20}{l}} {(1,0.5{\rm{sin}}\left[ {{\rm{\pi }}\left( {1 - 0.5x} \right)} \right],1,1.4),x ＜ 0.5}\\ {(1,0.5{\rm{sin}}\left[ {{\rm{\pi }}\left( {1 - 0.5x} \right)} \right],1,1.8),x > 0.5} \end{array}} \right.. \end{array}$

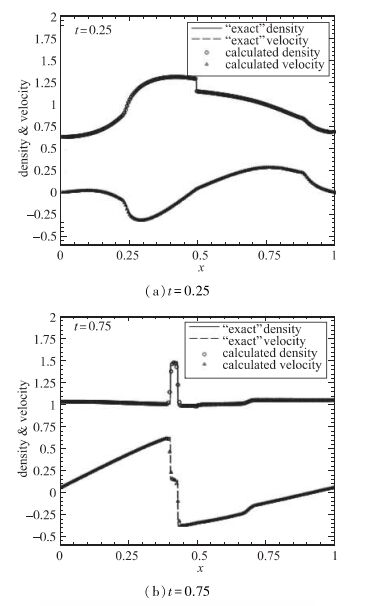
x=0及x=1处为反射壁面边界条件, 算例计算至时间t=1, 将1600个网格点作为精确的参考解以验证数值解. 图 2展现了t=0.25, 0.75时计算出的速度和密度外型, 可看出计算结果与精确解符合得很好.

研究求解结果用于评估本文方法的数值收敛性.在t=0.2, 0.64处测定熵误差为

${E_{s}} = \left| {{s^t} - {s^{{\rm{exact}}}}} \right|/{s^{{\rm{exact}}}},$

以上分别对应连续流动中熵极值及激波穿过界面两个时间点.熵误差E_s-和E_sT分别对应左部介质和总的介质, R_c为收敛平均阶数, 均在表 1中给出.我们发现连续流中可获得高阶精度的结果.然而, 当存在激波, 特别是激波穿过界面时, 误差较大, 且整体收敛性下降1阶.

3.2 激波-密度场-波干扰

冲击熵波相互作用问题^[9]的初始条件可设为Mach数为3的激波和一个扰动密度场的交互作用问题, 如下

$\begin{array}{l} \quad \quad \quad (\rho ,u,p,\gamma ) = \\ \left\{ {\begin{array}{*{20}{l}} {(3.857,2.629,10.333,1.4),0 \le x ＜ 1}\\ {(1 + 0.2{\rm{sin}}\left( {5x} \right),0,1,1.4),1 ＜ x \le 10} \end{array}} \right.. \end{array}$

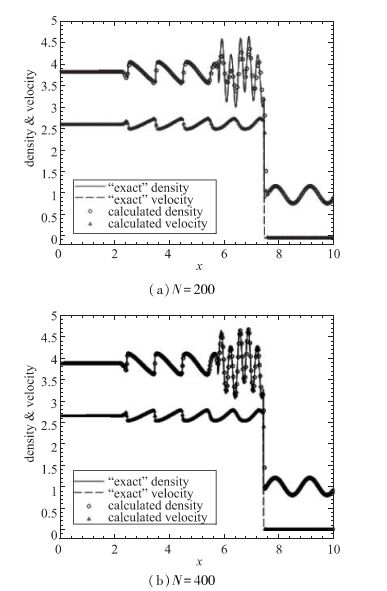
在x=0, 10处, 边界条件为0梯度.这个问题的解由位于右行激波后的一些小激波及细微结构组成. 图 3给出了t=1.8时, 不同数量网格点求解出的密度和速度外型.使用修正的WENO格式求解1600个网格点的结果作为参考精确值. 图 3(a)显示较少网格点下, 相比原始格式, 修正WENO格式能捕捉更多的细微结构, 特别是激波后的高频波.本文可获得与Kim等^[12]的混合格式相当的小耗散量.

4 直接模拟结果

本节研究了不同对流Mach数下无黏K-H不稳定性问题的二维非线性演化, 初始条件如下

$\begin{array}{l} \quad \quad \quad \quad (\rho ,u,v,p,\gamma ) = \\ \left\{ {\begin{array}{*{20}{l}} {({\rho _u},\frac{1}{2} + \tilde u,\tilde v,{p_0},{\gamma _u})\quad {\rm{upper\;flow}}}\\ {({\rho _b}, - \frac{1}{2} - \tilde u,\tilde v,{p_0},{\gamma _b})\quad {\rm{down\;flow}}.} \end{array}} \right. \end{array}$

且位标集

$\phi = - \frac{1}{2} + y.$

求解区域在[0, 1]×[0, 1]中.引入初始扰动, 并细微修正含切向速度间断的薄层的速度外型, 例如, 速度振动

$\begin{array}{l} \tilde u = \frac{1}{{10}}{\rm{cos}}\left[ {2k{\rm{\pi }}\left( {x - \frac{1}{2}} \right)} \right]{\rm{exp}} - \left( {2k{\rm{\pi }}\left| {y - \frac{1}{2}} \right|} \right)\\ \tilde v = \frac{1}{{10}}{\rm{sin}}\left[ {2k{\rm{\pi }}\left( {x - \frac{1}{2}} \right)} \right]{\rm{exp}} - \left( {2k{\rm{\pi }}\left| {y - \frac{1}{2}} \right|} \right). \end{array}$

通过调整不同的初始压力p₀以获得不同的对流Mach数 ${M_{\rm{c}}} = \sqrt {{\gamma _u}{p_0}/{\rho _u}} $ .通过调整低层流体的密度和比热比以获得不同的密度比ρ_c=ρ_u/ρ_b及比热比γ_c=γ_u/γ_b.计算采用了200×200的网格.水平方向采用周期条件, 垂直方向采用滑移壁面边界条件.

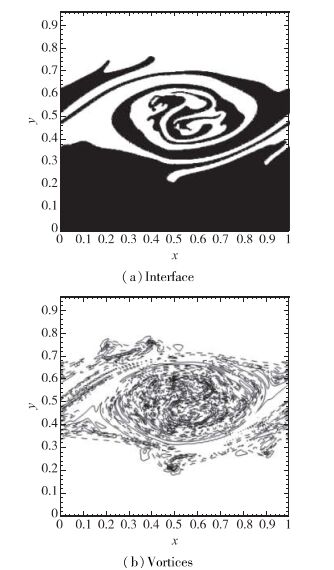
图 4给出了对流Mach数M_c=0.387, 密度比ρ_c=1, 比热比γ_c=1, 单模态扰动下, t=4时刻, 求解出的界面位置和涡型分布.与之前Després等^[13]的单一流体模型的结果比较, 基本特征符合得很好, 而现在的结果比Després等使用500×500网格的结果能反映出更多的细节.这也在意料之中, 因为他们的方法抑制了高波数扰动的发展, 这些特征在1000×1000的网格时能够部分反映.另一重要现象是如图 5所示的明显扭曲界面, 尽管所给扰动是有区域波长的单模态, 由于速度型上微小的初始数值误差, 高波数扰动未被抑制而在初期快速发展.由图 4可以看出, 这些扰动并未进一步发展而是在后期变光滑.这与采用涡点法模拟的结果有很大的不同, 涡点法中若人工扰动不足够高, 则高波数扰动会失控地增长.可以发现涡量区存在大量噪音, 这表明大量小结构的涡从界面扩散.由于我们的数值方法中没有直接的涡发散机制, 所以产生斜压部分是由于高扭曲界面不能由位标集求解而引发界面附近密度梯度及压力梯度的不匹配.当涡从界面扩散时, 可生成一个厚度增长的剪切层, 并将抑制高波数扰动的增长.另一方面界面由于伸展而变平, 如由于单一模态的发展而卷起.这些现象表明, 尽管高波数扰动开始时增长很快, 但由于耗散机制, 其增长率下降也很快, 高波数不稳定性被低波数不稳定性消除.

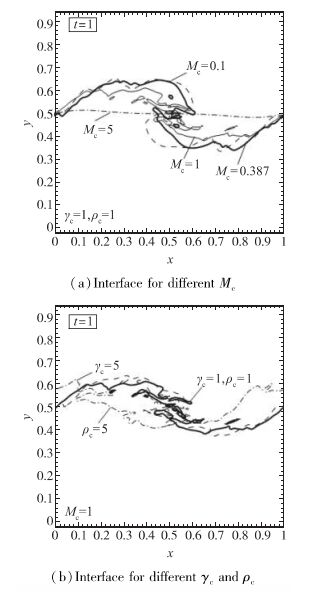
图 5展现了压缩性对增长率的影响.可以发现, 若上下层流体具有相同的压缩性(即相同的密度和比热比), 单一模态的增长随M_c单调递减, 并在M_c=5时几乎为0.这一特征和有限厚度的剪切层的线性理论相符, 但与理想K-H不稳定性不符.对于高波数的扰动, M_c＜1时, 增长率随M_c增长, 随后当M_c=5时下降至0.这一特征与理想K-H不稳定性的线化理论相符.若上下层流体有不同的压缩性(通过增长下层流体的密度和比热比), 可发现单一模态扰动的增长率没有太大改变, 较高波数的扰动却一致降低, 再次反映高波数扰动随M_c增加而较快增长.

5 结论

本文介绍了一种锐界面方法, 成功地将其与低耗散WENO格式结合, 实现了对可压缩K-H不稳定性问题的直接模拟.结果表明, 该方法允许高波数扰动发展, 且高波数扰动展现了与以往模拟结果和已有理想K-H不稳定性理论不同的特征, 但与有限厚度的剪切层结果相符.