2. 中国航天空气动力技术研究院, 北京 100074
2. China Academy of Aerospace Aerodynamics, Beijing 100074, China
高超声速飞行技术是21世纪航空航天领域的研究热点之一.高超声速流动边界层转捩会使飞行器表面摩擦阻力和表面热流大幅增加, 从而对高超声速飞行器的气动设计和结构设计等产生重要影响.因此, 对边界层转捩位置的预测是高超声速飞行器设计必须考虑的问题.
探测转捩的方法有很多.比较直观的转捩探测方法是流动显示法, 比如升华法等; 较为直接的测量方法就是通过对模型表面的平均速度剖面进行测量, 利用层流和湍流边界层速度剖面的不同来判断转捩位置; 其他的技术大多是利用流动中某些特征参量发生剧烈变化来作为判断转捩区[1-9]的准则.这些方法均有优点和局限性.
在高超声速实验方面, 探测转捩的主要手段有热流探测方法和光学探测方法.其中, 热流探测方法测量边界层内的St数, 通过St数的变化来确定转捩区.光学探测方法通过观察边界层内部的涡结构, 通过涡结构的发展来判断转捩区.但这些方法均不宜应用在飞行实验中.
文献[11]提出, 回转体转捩区内会出现壁面脉动压力均方根的峰值, 并说明利用模型表面脉动压力均方根值的特征参数可以判断转捩.文献[11]发展的基于脉动压力方法进行转捩判断的主要依据是:相比层流区和湍流区, 转捩区内脉动压力均方根值(root mean square, RMS)会出现峰值.
在超声速和高超声速领域, 当M≥4时, 除了涡的不稳定性(第1模态不稳定), 又出现了新的声波不稳定性(第2模态不稳定性)[12], 并且第2模态在高超声速转捩过程中起主导地位. Roediger等[13]研究了Mach数为6和12条件下的锥体流动.研究表明利用脉动压力的方法可以在一定条件下判定转捩, 但是受到的干扰因素比较多, 在动态校准及数据处理方面还需要进一步研究.
本征正交分解(proper orthogonal decomposition,POD)方法可以将相干结构及其所包含的能量联系起来, 即从能量的角度对样本空间进行辨识分解, 认为样本空间可以用一组正交基来重构, 不同正交基含有的能量不同.在空气动力学领域, 样本空间一般选为速度场, 关于POD的原理与应用已经有许多文献[15-17]介绍.
在高超声速实验中, 噪声对数据的影响很大.本文将脉动压力场作为样本空间进行分解[18], 根据已有的经验:高超声速转捩由第2模态主导, 因此利用含有较多第2模态的正交基对数据进行重构, 就对实验数据起到了滤波的作用.本文使用重构后的数据进行分析, 获得了转捩的特征.
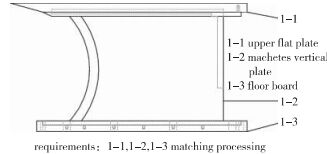
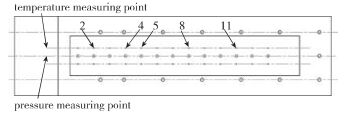
1 实验 1.1 实验模型实验选用平板模型.第1个测压孔位置距平板前缘77.5mm, 两个测压孔之间间隔20mm.模型示意图见图 1,图 2.
|
| 图 1 模型正视图 Fig.1 Front view of the model |
|
| 图 2 模型俯视图及测压孔示意图 Fig.2 Vertical view of the model and pressure hole schematic diagram |
实验在中国航天空气动力技术研究院的FD-03风洞中进行.高压气源提供高达20MPa的压缩空气.这是一座封闭式的自由射流暂冲式压力-引射的常规高超声速风洞, 主要模拟的参数是Mach数和部分Reynolds数.风洞配备的5副二元喷管, 出口尺寸为170mm×170mm, Mach数为5, 6, 7, 8和9, 通过更换喷管的方法改变Mach数.
脉动压力采集系统为HS4数据采集卡,如图 3所示.本次实验采样率为625kHz/14bit, 采样时间为0.16 s.实验选用了3个PCB-132(PCB采用的信号调理器为MODEL 482C SERIES)压力传感器, 位置分别在x=97.5,157.5,197.5mm处.同时, 使用时均纹影仪来观察流场,见图 4.

|
| 图 3 数据采集卡 Fig.3 Data acquisition card |

|
| 图 4 时均纹影仪 Fig.4 Time-average schlieren device |
本文进行了自然转捩和人工转捩的测量.自然转捩实验条件为M=5, 迎角α=0°, 单位Reynolds数Re=1.77×107, 1.99×107, 2.21×107/m.固定转捩的实验条件为M=5, 迎角α=0°, Re=2.21×107/m.固定转捩实验采用宽为12 mm, 厚度为0.24mm的胶带作为粗糙带, 位置如图 5所示.

|
| 图 5 模型及粗糙带 Fig.5 Model and roughness |
传统的数据处理方法有很多, 例如求脉动量的均值均方根值和基于FFT (fast Fourier transform)变换的频谱分析等, 这些方法已有很多文献进行了详细介绍[9, 11, 18], 在此不再赘述.下面详细介绍本文发展的单点POD分析方法.
2.1 POD原理设有一个压力场{P}, 寻找一组正交基{φj}, 使得{P}中的元素pi可由下式表示:
| ${\mathit{\boldsymbol{p}}_i} = \sum\limits_{j = 1}^{j = N} {{a_j}{\mathit{\boldsymbol{\varphi }}_j}} .$ |
其中, i=1, 2, …, N, N为某位置处采集到的压力信息数量.
当选择{PT}的右奇异值向量为k维基向量φj时, 既满足最优性条件, 也有最小误差, 误差为{PT}的最后N-k个奇异值的平方和[19].
但当N较大时, 为了求解{PT}的右奇异值向量, 需要求解一个庞大的矩阵(N×N阶), 这是极为困难的.为此, Sirovich[20]提出了一个解决方案, 被称为snapshots方法.
经推导, 正交基φj可表示为
| ${\mathit{\boldsymbol{\varphi }}_j} = \sum\limits_{k = 1}^M {{\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{P}}_k}} .$ |
其中M为压力场中测压点数量.对于A, 满足本征方程:
| $\mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{A}} = \lambda \mathit{\boldsymbol{A}}.$ |
其中C=PT·P.
对于重构系数aj, 可由下式求出:
| ${a_j} = \frac{{({\mathit{\boldsymbol{p}}_i},{\mathit{\boldsymbol{\varphi }}_j})}}{{({\mathit{\boldsymbol{\varphi }}_j},{\mathit{\boldsymbol{\varphi }}_j})}}.$ |
在脉动压力处理方面, 本文使用POD方法对传感器采集到的脉动压力信号进行处理, 具体做法如下:
(1) 构造样本空间.对于高超声速实验而言, 风洞的环境噪声不是一个小量, 噪声与表征边界层流态的脉动压力信息在一个量级上, 因此必须选取足够大的样本空间, 这样才能将边界层中表征流态的数据信息在噪声信息中提取出来.为此, 本文使用以下方法构造高超声速实验的样本空间{P}:
设高超声速实验中测压点i采集到的脉动压力时间序列为[p]i:
| ${\left[ \mathit{\boldsymbol{p}} \right]_{i}} = {\rm{ }}[{p_{{t_{{\rm{start}}}}}},{p_{{t_2}}}, \ldots \ldots ,{p_{{t_{{\rm{end}}}}}}]_{i}^{\rm{T}}.$ |
其中,i为测压点位置, [p]i中每个元素为该测压点位置在某瞬时ti时刻的瞬时压力值.针对该位置处的时间序列, 构造第j维样本空间如下:
| ${\left\{ \mathit{\boldsymbol{P}} \right\}_{i,j}} = [{p_{{t_j}}},{p_{{t_{j + 1}}}}, \ldots \ldots {p_{{t_{n - m + j}}}}]_{i}^{\rm{T}}.$ |
其中,i为测压点位置, tj为第j个时间点, m为样本空间大小, 本文中m=200.这样得到的样本空间为如下式所示的矩阵:
| ${\left\{ \mathit{\boldsymbol{P}} \right\}_i} = {\left\{ {\begin{array}{*{20}{c}} {{p_{{t_1}}}} & {{p_{{t_2}}}} & { \cdots \cdots } & {{p_{{t_j}}}} & {{p_{{t_m}}}}\\ {{p_{{t_2}}}} & {{p_{{t_3}}}} & { \cdots \cdots } & {{p_{{t_{j + 1}}}}} & {{p_{{t_{m + 1}}}}}\\ { \cdots \cdots } & { \cdots \cdots } & { \cdots \cdots } & { \cdots \cdots } & { \cdots \cdots }\\ {{p_{{t_{n - m + 1}}}}} & {{p_{{t_{n - m + 2}}}}} & { \cdots \cdots } & {{p_{{t_{n - m + j}}}}} & {{p_{{t_n}}}} \end{array}} \right\}_i}.$ |
相较于文献[18]中的全局POD分析方法, 本文为单点POD分析方法.
(2) 使用POD方法对原始数据进行重构.使用snapshots方法对(1) 中的样本进行POD分析.
在高超声速实验中, 由于噪声的能量很大, 因此要选取可以表征高超声速流动边界层信息的正交基.一般认为, 诱发高超声速流动边界层转捩的是第2模态不稳定扰动, 因此, 本文使用含有第2模态不稳定扰动能量较多的正交基进行重构.
(3) 对重构数据进行时域分析.
由于重构过程中使用的是含有较多第2模态的正交基, 因此重构数据的频率成分集中在第2模态附近.所以本文对(2) 重构后的数据进行时域分析, 例如求取RMS值等.
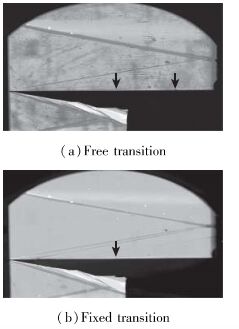
3 数据处理结果及讨论 3.1 纹影结果图 6为这两种实验状态下的时均纹影图像, 可视范围为x=0~190mm, 其中图 6(a)为自然转捩结果, 两个箭头所示位置分别为x=97.5mm与x=157.5mm; 图 6(b)为固定转捩结果, 箭头所示位置为x=97.5mm.
|
| 图 6 自然转捩与固定转捩的纹影图像 Fig.6 Schlieren images of free transition and fixed transition |
可见自然转捩时, 在x=97.5mm处边界层厚度呈现线性增长的特征, 并且没有明显变厚的过程, 这是典型的层流边界层的特征; 在x=97.5mm与x=157.5mm之间, 边界层明显变厚, 这是边界层发生转捩的明显特征.固定转捩时, 在箭头所示位置, 边界层有明显变厚的过程, 即该位置发生转捩.
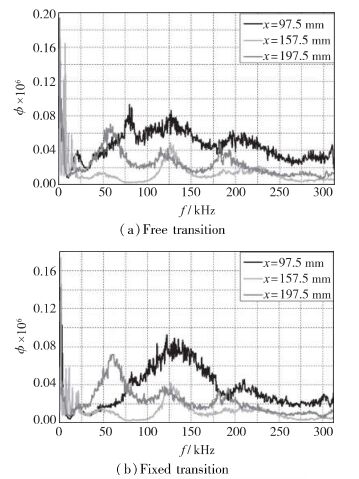
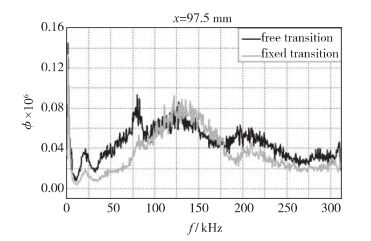
3.2 传统方法数据处理的结果图 7为两种实验状态的功率谱分析, 其中图 7(a)为自然转捩时不同位置处的功率谱, 图 7(b)为固定转捩时不同位置处的功率谱. 图 8为x=97.5mm处自然转捩与固定转捩的功率谱对比.
|
| 图 7 自然转捩与固定转捩的功率谱对比 Fig.7 Power spectrum comparisons between free transition and fixed transition |
|
| 图 8 x=97.5mm处自然转捩与固定转捩功率谱对比 Fig.8 Power spectrum comparison between free and fixed transition at x=97.55mm |
由图 7(a)可见, 在自然转捩情况下, x=97.5mm处各阶模态的扰动均已激发出来, 其中第1模态和第2模态的不稳定扰动已充分发展; x=157.5mm处, 第2模态不稳定扰动占据大部分能量; 扰动传播至x=197.5mm处, 能量在各阶模态扰动中均匀分配, 体现了湍流的流动特征.但由于x=97.5mm和x=157.5mm处第2模态扰动均已充分发展, 功率谱上不能说明具体哪个位置处于转捩区.
由图 7(b)可见, 在粗糙带的作用下, x=97.5mm处第2模态不稳定扰动的能量非常明显, 占据支配地位, 这将导致该位置发生转捩; 扰动发展到x=157.5mm处, 第2模态不稳定扰动能量逐渐减小, 相对的第1模态与高阶模态的不稳定扰动能量变大; 当扰动进一步发展到x=197.5mm处, 第2模态不稳定扰动逐渐退化为第1模态不稳定扰动, 发展为湍流.
由图 8可见, 在x=97.5mm处, 自然转捩时第1模态不稳定扰动能量较为集中, 第2模态不稳定扰动已经发展, 高阶模态不稳定扰动也已经逐渐激发出来; 当在x=97.5mm处前面加粗糙带之后, 第2模态不稳定扰动迅速被激发出来, 并且能量非常大, 在第2模态不稳定扰动的作用下, 该处发生边界层转捩.
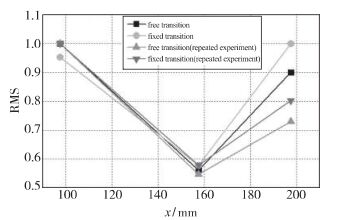
图 9为这两种实验状态原始数据的RMS值随位置的变化曲线.可见, 这两种实验状态及其重复实验的RMS值呈现一致的变化特征: x=157.5mm处的RMS均是最小值.可见使用原始数据的RMS值不能表征转捩位置.
|
| 图 9 自然转捩与固定转捩的RMS曲线 Fig.9 Curves of RMS values of free transition and fixed transition |
通过上述分析, 在原始数据的功率谱上可以观察到各阶模态不稳定扰动的传播与发展, 但不能明确给出转捩位置.对原始数据求取RMS值, 其峰值位置不能表征转捩位置.
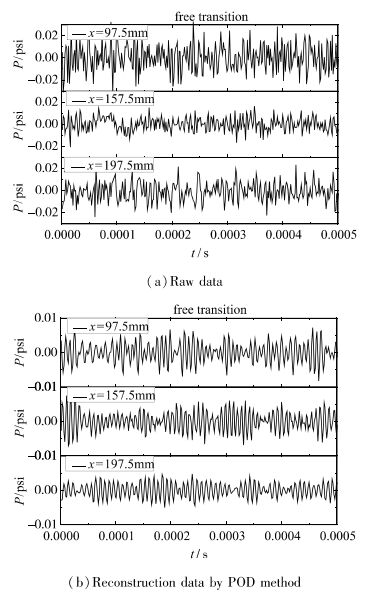
3.3 单点POD分析结果图 10为原始数据与重构数据在自然转捩情况下的波形.可见POD重构后的数据对原始数据起到了一定的滤波作用.同时, 在重构数据的波形中可以观察到明显的间歇现象.
|
| 图 10 原始数据与POD重构数据的波形对比 Fig.10 Waveshape comparisons between original data and reconstruction data |
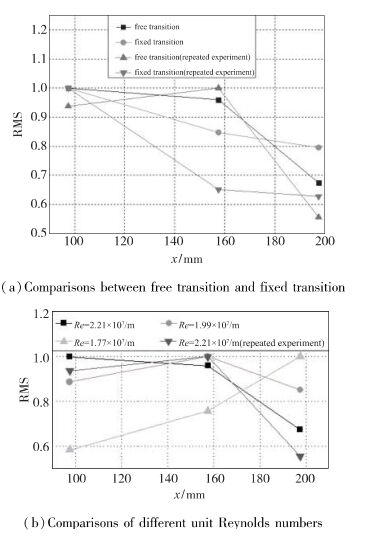
图 11为POD重构数据的RMS值随位置的变化曲线, 其中图 11(a)为自然转捩与固定转捩对比, 图 11(b)为不同单位Reynolds数的对比.
|
| 图 11 POD重构数据的RMS值 Fig.11 RMS value of reconstruction data by POD method |
由图 11(a)可以看到, 自然转捩时, x=97.5mm与x=157.5mm处的RMS极为接近, x=197.5mm处的RMS值最小, 认为在x=97.5mm与x=157.5mm之间发生转捩, 这与时均纹影的结果是一致的.固定转捩时, POD重构数据的RMS值在x=97.5mm处取得峰值, 认为x=97.5mm处发生转捩, 这与时均纹影的结果也是一致的.
由图 11(b)可以看到, Re=1.77×107,1.99×107/m时, RMS峰值位置分别为x=197.5,157.5mm, 这与纹影上的转捩位置是一一对应的. Re=2.21×107/m时, 上文已作出分析, 转捩位置在x=97.5mm与x=157.5mm之间.可见RMS峰值位置随单位Re变大而前移, 这与转捩的基本特征是一致的.
可见, 本文使用单点POD分析方法对高超声速边界层脉动压力时间序列进行分析, 重构后数据的RMS峰值位置可以表征转捩位置.
4 结束语本文对平板模型进行了M=5的高超声速边界层转捩位置测量实验.将POD分析方法引入高超声速脉动压力数据处理中, 发展了单点POD分析方法.使用本方法重构数据的RMS值峰值位置可表征转捩位置, 方法实用性强.
| [1] |
Ellsworth R H, Mueller T J. Airfoil boundary layer measurements at low Re in an accelerating flow from a nonzero velocity[J]. Experiments in Fluids, 1991, 11(6): 368-374. |
| [2] |
Vavra A J, Solomon W D, Drake A. Comparison of boundary layer transition measurement techniques on a laminar flow wing[R]. AIAA 2005-1030, 2005.
|
| [3] |
卞於中, 徐铁军, 范洁川, 等. 边界层综合诊断技术研究[J]. 流体力学实验与测量, 2000, 14(4): 7-13. Bian Y Z, Xu T J, Fan J C, et al. Investigation of synthetic diagnosis techniche of boundary layer[J]. Experiments and Measurements in Fluid Mechanics, 2000, 14(4): 7-13. (in Chinese) |
| [4] |
Schubauer G B, Skramstad H K. Laminar boundary layer oscillations and transition on a flat plate[R]. NACA TR. 909, 1948.
|
| [5] |
Joussot R, Hong D, Weber-Rozenbaum R, et al. Modification of the laminar-to-turbulent transition on a flat plate using a DBD plasma actuator[R]. AIAA 2010-4708, 2010.
|
| [6] |
Richards J, Barrett R V. Investigation of acoustic transition detector with application to boundary layer control by suction[A]. //Proceedings of 1st European Forum on Laminar Flow Technology[C]. Hamburg, 1992.
|
| [7] |
Barrett R V. Transition detection for laminar flow aircraft using microphones beneath the surface of laser drilled suction panels[J]. Proceedings of Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2000, 214(3): 143-155. DOI:10.1243/0954410001531971 |
| [8] |
Molin S, Dolfi D, Doisy M, et al. Experimental study for the detection of the laminar-turbulent aerodynamic transition on a wing aircraft, using fiber optic sensors[A]. // 4th European Workshop on Optical Fibre Sensors[C]. Porto: International Society for Optics and Photonics, 2010.
|
| [9] |
王猛. 风洞实验中边界层转捩的快速判别方法研究[D]. 西安: 西北工业大学, 2012. Wang M. Rapid discrimination method research of boundary layer transition in wind tunnel experiment[D]. Xi, an: Northwestern Polytechnical University, 2012(in Chinese). |
| [10] |
Vavra A J, Solomon W D, Drake A. Comparison of boundary layer transition measurement techniques on a laminar flow wing[R]. AIAA 2005-1030, 2005.
|
| [11] |
Huang T T, Hannan D E. Pressure fluctuations in the regions of flow transition[R]. DA022935, 1975.
|
| [12] |
Gurley K, Kijewski T, Kareem A. First-and higher-order correlation detection using wavelet transforms[J]. Journal of Engineering Mechanics, 2003, 129(2): 188-201. DOI:10.1061/(ASCE)0733-9399(2003)129:2(188) |
| [13] |
Roediger T, Knauss H, Smorodsky B V, et al. Hypersonic instability waves measured on a circular cone at M=12 using fast response surface heat-flux and pressure gauges [A]. //7th IUTAM Symposium on Laminar-Turbulent Transition[C]. Stockholm, 2010.
|
| [14] |
Casper K M, Beresh S J, Henfling J F, et al. Hypersonic wind-tunnel measurements of boundary-layer pressure fluctuations[R]. AIAA 2009-4054, 2009.
|
| [15] |
Graftieaux L, Michard M, Grosjean N. Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows[J]. Measurement Science and Technology, 2001, 12(9): 1422-1429. DOI:10.1088/0957-0233/12/9/307 |
| [16] |
Patte-Rouland B, Lalizel G, Moreau J, et al. Flow analysis of an annular jet by particle image velocimetry and proper orthogonal decomposition[J]. Measurement Science and Technology, 2001, 12(9): 1404-1412. DOI:10.1088/0957-0233/12/9/305 |
| [17] |
Pedersen J M, Meyer K E. POD analysis of flow structures in a scale model of a ventilated room[J]. Expriments in Fluids, 2002, 33: 940-949. DOI:10.1007/s00348-002-0514-8 |
| [18] |
魏斌斌, 高永卫. 基于POD方法的低速流动边界层转捩判断研究[A]. //第五届近代实验空气动力学会议[C]. 大连, 2015. Wei B B, Gao Y W. Study of judgment in low speed flow boundary layer transition based on the method of POD[A]. //The 5th Conference on Modern Experimental Aerodynamics[C]. Dalian, 2015(in Chinese). |
| [19] |
蒋耀林. 模型降阶方法[M]. 北京: 科学出版社, 2010: 200-203. Jiang Y L. Model order reduction method[M]. Bejing: Science Publishing Company, 2010: 200-203. (in Chinese) |
| [20] |
Sirovich L. Turbulence and the dynamic of coherent structures part Ⅰ: coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571. DOI:10.1090/qam/1987-45-03 |



