2. 香港科技大学深圳研究院, 广东深圳 518057
2. Shenzhen Research Institute, The Hong Kong University of Science and Technology, Shenzhen 518057, China
钱学森按照流动的稀薄程度由低至高(或流动特征长度由宏观至微观), 以Knudsen数(Kn:分子平均自由程与流动特征长度的比值)将流动定性地分为连续流(Kn < 0.001)、滑移流(0.001<Kn < 0.1)、过渡流(0.1<Kn < 10)以及自由分子流(Kn>10)这4个流域.从流动数值预测角度上讲, 以Navier-Stokes(N-S)方程为基础的常规计算流体力学方法适用于空域范围和宏观尺度的连续流动, 而以直接模拟Monte Carlo(direct simulation Monte Carlo, DSMC)[1]方法为代表的建立在稀薄气体动力学上的模型分子方法非常适合稀薄流动和微尺度流动.
在科学和工程实践中, 常遇到大量的单一流场中的多流域问题, 或称局部稀薄问题.例如, 在航天器姿控发动机喷管内推进剂呈现连续流动, 而离开喷管后会迅速膨胀为稀薄气体流动, 此过程中可能对航天器的结构以及附带的光学仪器产生严重影响; 在钝头体再入过程的临近空间段, 存在头部压缩的连续流动和尾部膨胀的稀薄流动并存的复杂情况; 在微机电系统中, 也存在整体的宏观流动与局部微尺度流动并存的情况.
这类问题的复杂性在于:一方面流场中存在多个流域,须应用多种流动模型, 这给分析和预测工作带来困难; 另一方面除非将网格尺度减小至分子自由程尺度, 并引入巨大的计算量, 则很难说滑移流和过渡流有准确的流动模型方程.对该类问题的处理包括连续/稀薄求解器的搭接方法以及使用气体动理学Boltzmann模型方程的统一方法这两个大类.统一方法又可分为以确定论方式求解离散气体动理学分布函数、并以数值积分得到宏观流场信息的确定论方法, 以及通过统计粒子刻画非平衡分布函数的统计粒子方法.以下对统一方法中确定论方法和统计粒子方法的研究现状进行回顾和分析.
1 确定论方法研究进展确定论的统一方法包括香港科技大学Xu等提出的统一气体动理学格式(unified gas-kinetic scheme, UGKS)[2-3]、中国空气动力研究与发展中心李志辉等提出的气体动理学统一算法(gas-kinetic unified algorithm, GKUA)[4-5]、以及华中科技大学Guo等提出的离散统一气体动理学格式(discrete unified gas-kinetic scheme, DUGKS)[6-7]. 3种方法同样使用Boltzmann模型方程, 区别在于分布函数通量不同的构造方式.其中, Li等根据GKUA发展出了一套能够模拟真实气体分子的跨流域三维复杂外形绕流的大规模高性能计算方法, 并在国家多个航天型号的设计和优化工作中发挥着重要的作用(见图 1)[5]. UGKS和DUGKS在通量计算中分别通过模型方程的解析解(时间积分解)和特征线差分解, 实现了粒子在输运过程中迁移和碰撞行为的耦合, 因此在连续流和近连续流计算中对黏性输运行为的预测非常准确, 二者可以认为是同一类方法, 以下对其最新研究进展进行回顾.
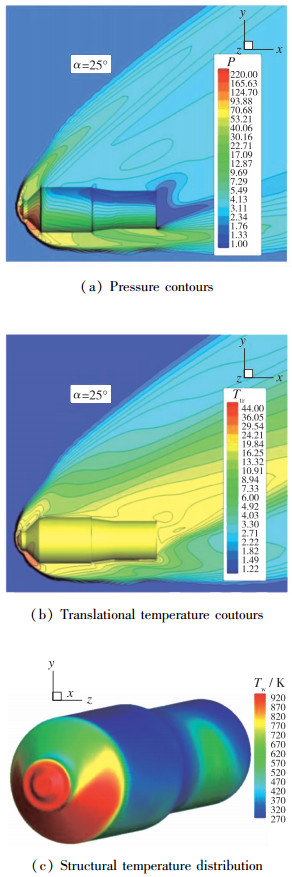
|
| 图 1 天宫的双舱结构在海拔62 km处GKUA提供的流场和物面信息[5] Fig.1 Flow field and object information of the two-capsule vehicle of Tiangong-1 spacecraft at altitude 62 km predicted by the GKUA[5] |
作为求解Boltzmann方程及其模型方程的经典确定论方法, 离散速度法(discrete velocity method, DVM)[8-12]在过去十几年间广泛用于求解稀薄非平衡流动问题.其解耦的分子迁移和碰撞机制, 一方面使得格式非常简洁, 另一方面却给近连续流动预测引入了额外的耗散, 同时导致数值时间步和网格间距受限.
2010年香港科技大学Xu等提出了UGKS [2, 13].在该方法中, 气体分子的迁移和碰撞过程通过BGK类方程[14]的解析解得以耦合如下
| $ \begin{array}{l} f(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{u}}, t) = \frac{1}{\tau }\int_0^t g \left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{u}}\left( {t - {t^\prime }} \right), \mathit{\boldsymbol{u}}, {t^\prime }} \right){{\rm{e}}^{ - \left( {t - {t^\prime }} \right)/\tau }}{\rm{d}}{t^\prime } + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{ - t/\tau }}f(\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{u}}t, \mathit{\boldsymbol{u}}, 0) \end{array} $ | (1) |
其中,分布函数f是坐标x、分子速度u和时间t的函数, 用以表示t时刻以速度u到达坐标x的分子的数密度; g是气体分子平衡态分布函数, 其参数完全依赖于宏观物理量(密度、速度和温度); τ为松弛时间, 与分子平均碰撞时间具有相同量级.当观测时间t≪τ时(自由分子流), 分布函数中初始非平衡分布f(x-ut, u, 0)占主导, 输运行为表现为完全的自由迁移, 且与DVM的过程一致.当t≫τ时(连续流), 分布函数通过平衡态g及其时空导数得到, 其对宏观输运的贡献与N-S方程一致.可见, 解析解实际上将主导稀薄流的自由迁移机制和主导连续流的分子碰撞机制通过权重有机地联系起来, 实现了流动模型在网格时/空上的自适应[3, 15].更细节的计算流程参见文献[2].
鉴于其优秀的多尺度性质, UGKS方法目前已广泛应用于从连续至稀薄、从亚声速至高超声速的全流域/全速域流动预测.在低速、微尺度流动模拟方面, UGKS已经应用在热流逸[16]、热蠕变流[16]、缝隙流[17]、微槽道流[18-19]等诸多方面[20-22].在超/高超声速流动方面, UGKS在强非平衡激波内部结构[13, 23]、返回舱再入问题、全流域圆柱绕流[17, 20]等问题中都取得了优秀的计算效果.
在真实气体模拟方面, 考虑到分子平动能量和转动能量具有不同的松弛效率, 西北工业大学刘沙、香港科技大学于普兵等引入Rykov模型[24], 以标量的转动能量描述分子转动自由度, 形成了包含分子平动、转动自由度的UGKS方法[25-26], 对氮气激波结构、氮气高超声速钝头体绕流,Apollo返回舱再入大气层等算例进行了成功的模拟.在此基础上西北工业大学张贺[27],Wang等[28]进一步考虑了具有离散能级的分子振动自由度, 构造了包含分子平动、转动、振动自由度的碰撞模型, 并将其引入UGKS方法.由于对分子振动能激发描述准确, 该方法对真实气体的高温非平衡流动进行了成功的模拟(图 2为文献[27]中对返回舱温度场的模拟).
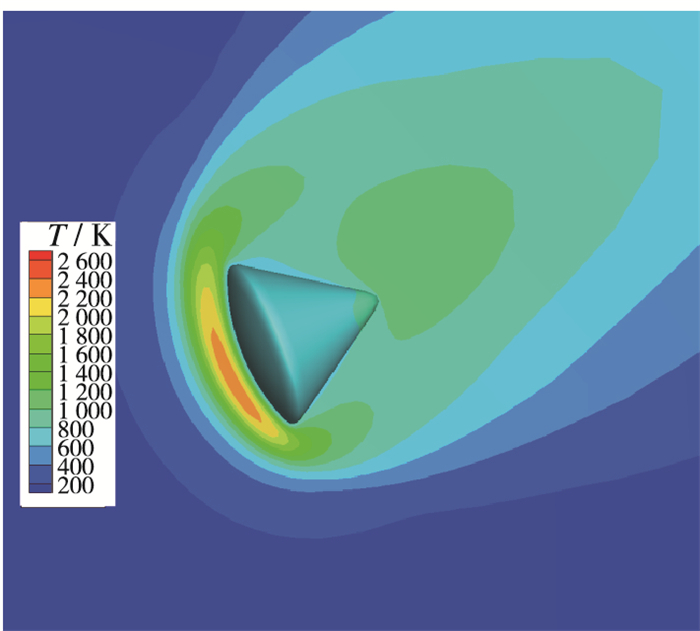
|
| 图 2 Apollo返回舱再入大气层的UGKS模拟(温度云图)[27] Fig.2 UGKS simulation of Apollo re-entry capsule (temperature contours)[27] |
在湍流模拟方面, 清华大学Li等利用UGKS优秀的多尺度性质, 以直接数值模拟的方式, 探索了流动非平衡性对湍流的影响[29].研究发现相对于UGKS直接数值模拟方法, 粗粒度的N-S直接数值模拟方法不仅在湍动能耗散曲线上与UGKS有所出入, 而且各时刻流场能谱曲线也存在着较大差别, 并指出这主要是由N-S方程不能准确捕捉非平衡效应所致.
在多物理流动模拟方面, 华中科技大学Chen等将运动网格技术应用到UGKS中[30-31], 对Crookes辐射计(见图 3)、高超声速椭圆绕流、稀薄环境喷流运动(见图 4)等进行了模拟, 展示了UGKS强大的跨流域多尺度计算能力.香港科技大学Wang等[32]、北京大学Xiao等[33]将BGK型的气体混合模型引入到UGKS中, 将UGKS拓展到多组分非平衡流动模拟, 并对多组分激波结构、微槽道流等成功进行了计算.香港科技大学Liu等[34]利用UGKS求解固体颗粒相, 用GKS求解气体相, 提出气体-颗粒多相系统模拟方法, 对气体中裹挟固体小颗粒的流动问题如风沙激波管、颗粒射流交叉/壁面反射(见图 5)、激波扫过颗粒床等进行了较好模拟. Xiao等提出有势力作用下满足平衡特性的UGKS方法[35-36], 用UGKS对重力作用下流动进行了系统模拟.此外, UGKS的统一建模思想还拓展应用到了各类输运问题和各类动力学方程中, 构造出了多种物理问题的多尺度数值计算格式, 例如光子辐射输运[37-40]、等离子体[41-43]等.

|
| 图 3 Crookes辐射计的动网格UGKS模拟(温度云图)[30] Fig.3 UGKS simulation of Crookes radiometer with moving mesh(temperature contours)[30] |
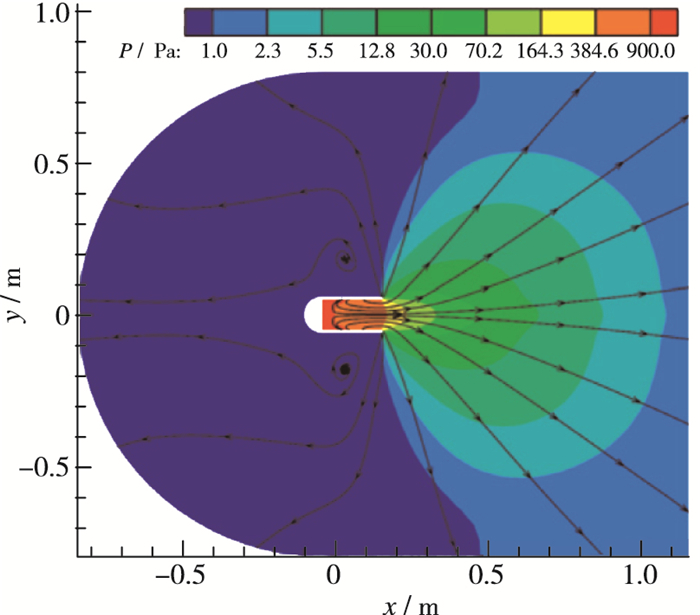
|
| 图 4 稀薄环境喷管流动问题的动网格UGKS模拟(流线和压强云图)[31] Fig.4 UGKS simulation of nozzle flow in rarefied environment with moving meshes(streamlines and pressure contours)[31] |
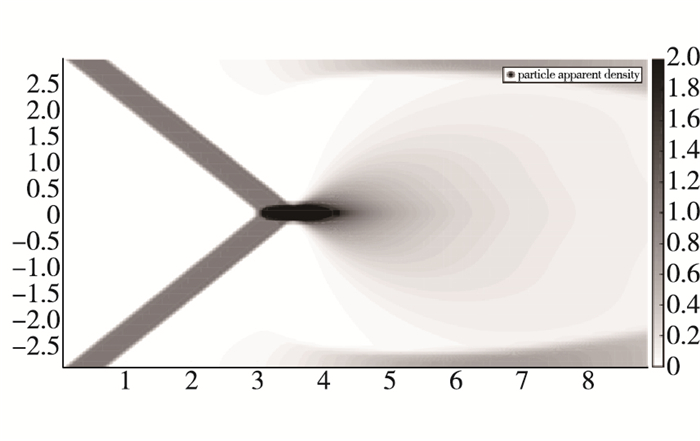
|
| 图 5 颗粒射流交叉/壁面反射的UGKS模拟[34] Fig.5 Intersection and wall reflection of particle flow predicted by UGKS[34] |
与传统CFD方法相比, UGKS方法使用了额外的离散速度空间, 因而相应的加速收敛技术尤为重要.在隐格式构造方面, 中国空气动力研究与发展中心毛枚良研究员等发展了UGKS的隐式计算方法[44], 对隐式模型方程中平衡态采用显式近似处理, 实现简单, 在大Kn数流动模拟中取得了很好的加速效果.更进一步, 香港科技大学Zhu等提出宏观量预估的思路[45-46], 利用UGKS提供的宏观量残差代入宏观隐式控制方程中求解得到预估的宏观量, 从而获得预估的平衡态代入微观隐式模型方程中, 得到了在所有流域中均有1~2个量级加速效果的定常/非定常隐式UGKS方法(表 1为隐式方法的加速效率)[45].在此基础上Zhu等还将多重网格法与宏观量预估的定常隐式UGKS进行了结合[47], 计算效率在隐式方法基础上进一步提升3~9倍.在解决内存瓶颈方面, Chen等[48]利用定常流动问题不依赖于分布函数初值的特性, 提出了定常隐式DVM框架下不储存离散分布函数信息的内存节省方案:通过一定的计算量代价(用于每一迭代步微观分布函数信息的重新计算), 将内存消耗降到一般宏观方法量级.陈松泽等人还提出了速度空间自适应的UGKS方法(adaptive unified gas-kinetic scheme, AUGKS)[31], 采用四叉树结构对不同流动区域的差异性离散速度空间进行自适应, 从而降低了计算/存储量. Xiao等则提出另一概念的自适应AUGKS方法[49], 将UGKS与基于解析形式分布函数的GKS进行了耦合搭接.该方法仅在非平衡性强的区域使用基于离散分布函数的UGKS进行计算, 其余区域则使用存储/更新宏观量信息的GKS方法进行计算, 对于局部非平衡问题具有很好的加速效果.在并行计算方面, 中国空气动力研究与发展中心江定武[50]使用UGKS结合双原子Rykov模型、隐式算法、守恒型DVM等进行了X-38飞行器缩比模型绕流等问题的并行计算.清华大学Li等[51]利用DVM框架在分子速度空间上的良好并行性[52], 开展了UGKS的物理空间/速度空间混合并行计算, 在小规模(1~16核)和大规模(729~5 832核)并行计算中均取得了接近线性的加速比.此外, Li等还推导了轴对称体系下的UGKS方法[53], 降低了轴对称三维问题的计算/存储量.
| 下载CSV 表 1 宏观量预估的隐式UGKS计算方腔流算例的加速效率[45]计算状态 Tab.1 Efficiency of the implicit UGKS with macroscopic prediction for cavity flow[45] |
DUGKS[6-7]于2013年由华中科技大学郭照立和香港科技大学徐昆提出, 是结合格子Boltzmann方法(lattice Boltzmann method, LBM)和UGKS优点发展起来的全流域流动数值预测方法, 具有渐进保持(asymptotic preserving, AP)性质. DUGKS中粒子迁移和碰撞过程的耦合, 通过特征线方向(分子速度方向)的差分解实现, 即
| $ \bar f(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{u}}, h) = {\bar f^ + }(\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{u}}h, \mathit{\boldsymbol{u}}, 0) $ | (2) |
其中, f和f+为与f相关的辅助分布函数[6], h为半个时间步长.公式(2)的物理意义为: x处半时刻u方向的分布函数f由初始时刻x-uh处(x沿特征线方向的迎风点)的分布函数f+迁移得到.
由于DUGKS与LBM存在诸多联系, 开展DUGKS与LBM在计算精度、计算效率等方面的对比研究非常具有意义.为此, 华中科技大学Wang等[54]通过数值实验详细对比了标准LBM(粒子在均匀Descartes网格上迁移和碰撞)和DUGKS在近不可压缩流动方面的数值表现, 其结论是: DUGKS与LBM精度相同, 但值稳定性更高, 且没有MRT(LBM多松弛模型)在模型参数方面的选择困难(见图 6); 均匀各向同性网格条件下, LBM单次迭代的计算效率稍高于DUGKS, 而DUGKS则可通过采用非均匀Descartes网格(或其他更灵活的网格)来大幅提高实际计算效率.标准LBM在构造过程中由于离散格子模型和物理计算网格需要耦合处理, 网格类型的限制使其在实际工程问题中面临诸多困难, 因此研究人员发展了很多非格点(off-lattice)类LBM模型(目前表现较为优异的是BKG模型[55]).华中科技大学Zhu等[56]则通过数值实验进一步对比了DUGKS和BKG模型, 其结论是:在相同的计算条件下, DUGKS的计算精度和数值稳定性均优于BKG格式(见图 7), 这种优势在高Reynolds数流动模拟中表现得更加突出.此外, 标准LBM属于有限差分方法, 主要用于低速流动的数值模拟; DUGKS则是一种有限体积方法, 网格适应性更强, 具备全流域/全速域流动数值模拟能力.
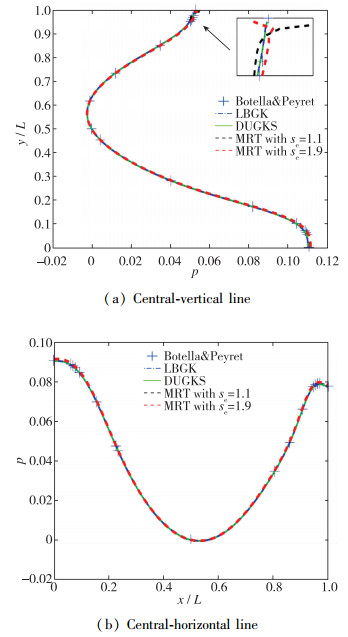
|
| 图 6 Re=1 000顶盖驱动方腔流垂直中心线和水平中心线上的压力分布对比[54] Fig.6 Pressure profiles along the central-vertical line and central-horizontal line of a lid-driven cavity flow at Re=1 000[54] |
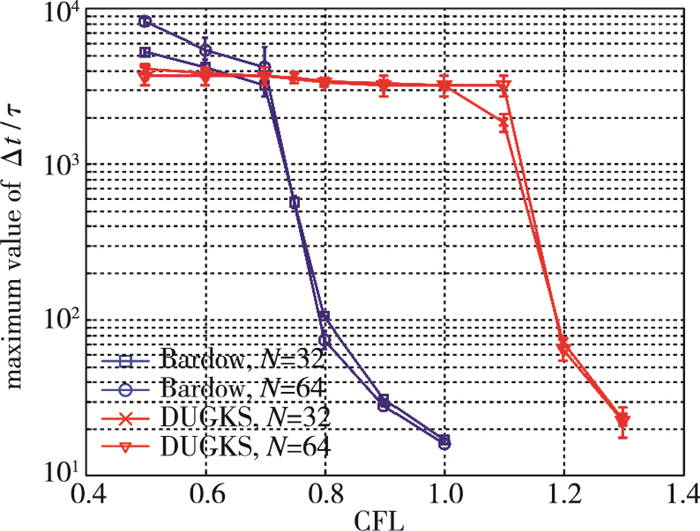
|
| 图 7 BKG和DUGKS满足顶盖驱动方腔流稳定计算所能取得的最大时间步长(Δt/τ)[56] Fig.7 Maximum time step (Δt/τ) for BKG and DUGKS in a lid-driven cavity flow[56] |
鉴于DUGKS相较于LBM具有的诸多优势、以及其通量形式简单的特点, 华中科技大学Zhu等[57]又进一步发展了非结构网格下的DUGKS方法.华中科技大学Wu等[58]发展了具有时/空3阶精度的高阶DUGKS方法, 并进一步提出了考虑体积力的DUGKS方法[59].鉴于DUGKS计算高速稀薄气体流动需要较大数量的离散分布函数, 西北工业大学Pan等[60]以及Yuan等[61], 在DUGKS形式的多尺度通量、以及Zhu等[45]的宏观量预估技术的基础上, 各自提出了全流域适用的隐式DUGKS方法.其中, Yuan等的方法是一种求解真实气体Rykov模型方程的定常隐式动理学方法, 提出了一种比传统守恒型DVM[10, 50]更高效的碰撞项守恒保持技术, 并创新地使用了非结构离散的速度空间, 使得计算效率得到了全面的优化.与显式格式相比, 这种隐式DUGKS的计算效率可以提高1~2个数量级.进一步地, Yuan等[62]还改进了宏观量预估技术, 将N-S预估格式用于宏观量预估中, 进一步提升了隐式动理学方法的收敛速度.作为气/固作用边界条件的浸入边界法[63]在模拟复杂运动边界问题时具有独特优势.为了解决连续流和稀薄流中的复杂运动边界问题, 基于浸入边界法的DUGKS也有相关工作开展[64-67].
鉴于其全流域/全速域特点, DUGKS也在多个领域得到了扩展.对于宏观流动, 目前已有湍流数值模拟[68-69], 可压缩流动[7, 70], 多元混合物流动[71-72], 固液相变[73], 多相流[74-75]等方面的工作. Wang等[68]在湍流数值模拟实践中发现DUGKS在数值稳定性和网格适应性方面表现优异.在多元混合物流动方面, 华中科技大学张月等构造了基于McCormack模型[76]的DUGKS格式[72], 对于低速流动, 该格式的计算时间快于DSMC方法两个数量级以上.对于固液相变流动模拟, 中国矿业大学Huo等提出了一种基于DUGKS的计算格式[73].鉴于LBM在模拟多相流问题时的独特优势, 以及DUGKS与LBM之间的紧密联系, 西北工业大学Yang等[75]把DUGKS应用于两相流模拟, 相比基于相场LBE模型, DUGKS可使用更宽松的CFL条件, 且数值稳定性更好.此外, DUGKS可以使用非均匀网格提高计算精度, 因而能够模拟更高黏性比和密度比的多相流. 图 8为DUGKS计算的Rayleigh-Taylor界面的时间演化过程, 两相流在破碎融合过中界面清晰[75].
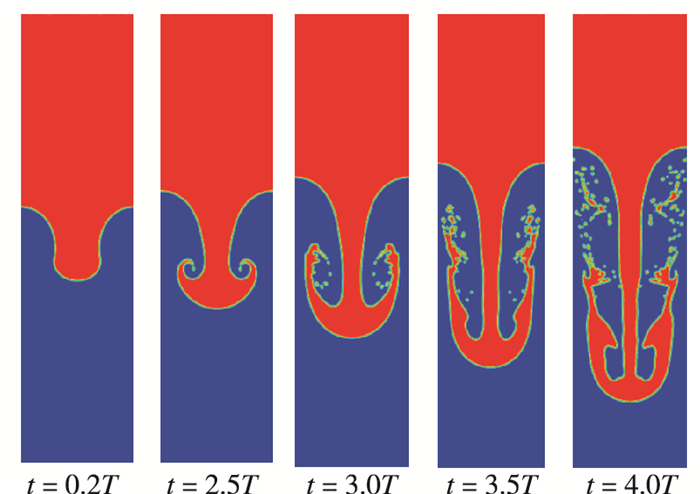
|
| 图 8 At=0.1(ρ=1.1/0.9), Re=3 000时Rayleigh-Taylor界面不稳定模式的时间演化[75] Fig.8 Evolution of interface patterns of Rayleigh-Taylor instability at At=0.1(ρ=1.1/0.9), Re=3 000[75] |
在多尺度(特别是微纳尺度)流动/传热应用方面, Guo等发展了一种基于声子Boltzmann输运方程(phonon Boltzmann transport equation, PBTE)的DUGKS方法[77].此外, 考虑色散和极化效应以及大温差情况的PBTE-DUGKS也得到了发展[78-79].在微机电系统中, 特征尺度的减小使得流动面临不同程度的稀薄效应.哈尔滨工业大学Liu等提出了一种考虑体积力的守恒型DUGKS用于低速不可压的微通道气体流动[80].对于微机电系统可能涉及的全流域运动边界问题, 西北工业大学Wang等[81]引入任意Lagrange-Euler(arbitrary Lagrange-Euler, ALE)运动边界, 成功构造了ALE-DUGKS方法. 图 9是ALE-DUGKS方法计算的一维封闭管道中单侧平板振荡引起的一维稀薄气体流动, 在平板振荡周期内, 速度型发展过程与参考解吻合良好.
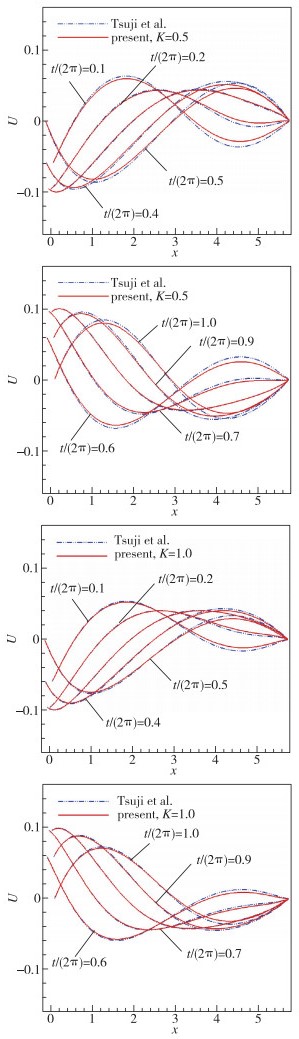
|
| 图 9 一维封闭管道中单侧平板振荡引起的一维稀薄气体流动中, 一个振荡周期不同时刻两组Knudsen数下速度型发展对比[81] Fig.9 Comparisons of velocity profiles for rarefied flow caused by one-sided plate oscillation at two different Kn[81] |
与确定论方法使用离散速度空间记录分布函数不同, 粒子方法使用模型分子的位置和速度自适应地描述分布函数.早期的统计粒子方法得到发展的原因在于同为粒子方法的DSMC方法[1]受制于算子分裂的本质, 其时间步长和空间尺度受限于分子的平均碰撞时间和平均自由程.为了增大粒子方法能够模拟的时/空尺度范围, Macrossan[82]以及Gallis等[83]独立地提出了基于BGK模型的粒子方法(stochastic particle method based on BGK model, SP-BGK).该方法的关键思想是在一个时间步长Δt内, 利用各向同性BGK方程的解析解[84]
| $ f(\Delta t) = \left( {1 - {{\rm{e}}^{ - \Delta t/\tau }}} \right)g(0) + {{\rm{e}}^{ - \Delta t/\tau }}f(0) $ | (3) |
将网格内的全体分子, 分为占比exp(-Δt/τ)的自由分子, 以及占比1-exp(-Δt/τ)的碰撞分子, 碰撞分子的出射速度根据当地平衡态分布函数g重新取样获得, 以此近似大时间步长下的分子碰撞行为.
随着方法的初步成功, 基于椭圆统计模型(ellipsoidal statistical BGK model, ESBGK)[85], Shakhov模型[86]和统一BGK模型(unified-BGK model, UBGK)[87]的模型精度更高的SP-ESBGK[88-90],SP-SBGK[88]和SP-UBGK[87]粒子方法相继被提出.
SP-BGK类方法的主要问题在于使用了各向同性(不考虑空间梯度)的BGK模型方程.其结果是参与碰撞的分子实际在经历Euler过程, 而非AP性质要求的N-S过程, 因而当时空尺度趋于连续流, 该类方法则会面临严重的黏性问题.
2.1 统一粒子方法为了克服SP-BGK类方法的不足, Fei等[91]于2018年提出了多尺度的统一粒子BGK(unified stochastic particle BGK, USP-BGK)方法, 其控制方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial f}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{x}}}} - J = \frac{1}{{{\tau _{{\rm{BGK}}}}}}\left( {{f_{\rm{G}}} - f} \right) - J}\\ {J = \frac{{{P_{\rm{E}}}}}{{{\tau _{{\rm{BGK}}}}}}\left( {g - {f^{{\rm{Grad}}}}} \right)} \end{array}} \right. $ | (4) |
即分别在BGK方程的两边添加了趋向Grad分布函数的松弛项J, 其中PE的取值范围为(0, 1), 取值下限和上限分别对应于自由分子流和连续流. Grad分布函数为Grad十三矩方程推导过程中所使用的分布函数, 实质为围绕平衡态g的Hermite展开.
USP-BGK方法的求解过程分为粒子迁移过程和碰撞松弛过程.在粒子迁移过程中, 由于附加松弛项的存在, 因而不再直接迁移初始分布函数, 而是采用类似于DUGKS的处理思路.此时, 迁移过程的演化方程可以离散为[91]
| $ \begin{array}{l} {f^*}\left( {{\mathit{\boldsymbol{x}}_{n + 1}}, \mathit{\boldsymbol{u}}, {t_{n + 1}}} \right) - f\left( {{\mathit{\boldsymbol{x}}_n}, \mathit{\boldsymbol{u}}, {t_n}} \right) = \\ \;\;\;\;\frac{{\Delta t}}{2}\left( {{J^*}\left( {{\mathit{\boldsymbol{x}}_{n + 1}}, \mathit{\boldsymbol{u}}, {t_{n + 1}}} \right) + J\left( {{\mathit{\boldsymbol{x}}_n}, \mathit{\boldsymbol{u}}, {t_n}} \right)} \right) \end{array} $ | (5) |
针对离散方程中的隐式项, 引入新的辅助分布函数
| $ \begin{array}{*{20}{l}} {{{\tilde f}^*} = {f^*} - \frac{{\Delta t}}{2}{J^*}}\\ {{{\hat f}^n} = {f^n} + \frac{{\Delta t}}{2}J} \end{array} $ | (6) |
根据辅助分布函数, 粒子迁移过程的演化方程为
| $ {\tilde f^*}\left( {{\mathit{\boldsymbol{x}}_{n + 1}}, \mathit{\boldsymbol{u}}, {t_{n + 1}}} \right) = {\hat f^n}\left( {{\mathit{\boldsymbol{x}}_n}, \mathit{\boldsymbol{u}}, {t_n}} \right) $ | (7) |
辅助分布函数的引入可以实现粒子迁移演化方程的显式更新, 并在迁移过程中耦合修正项J的影响, 使得USP-BGK方法能够在连续流域获得正确的黏性, 并具有AP性质.
碰撞松弛过程的演化方程为
| $ \begin{array}{l} {f^{n + 1}} = {f^*}{{\rm{e}}^{ - \nu \Delta t}} - \frac{{\left( {1 - {{\rm{e}}^{ - \nu \Delta t}}} \right)}}{\nu }{J^*} + \\ \;\;\;\;\;\;\;\;\;\;\left( {1 - {{\rm{e}}^{ - \nu \Delta t}}} \right)\int_{{t_n}}^{{t_{n + 1}}} {\frac{{\nu {{\rm{e}}^{\nu \left( {t - {t_n}} \right)}}}}{{\left( {{{\rm{e}}^{\nu \Delta t}} - 1} \right)}}} {f_{\rm{G}}}(t){\rm{d}}t \end{array} $ | (8) |
通过粒子迁移过程得到f*后, 即可进行粒子的碰撞过程.其中Gauss分布fG(t)的计算与SP-BGK方法不同.在SP-BGK方法中, fG(t)被认为是常数, 式(8)中的第3项可以直接积分计算.而在USP-BGK方法中, 时间步长可能远大于平均碰撞时间, 在一个时间步长Δt内, fG(t)不能被认为是常数.因此, 第3项的时间积分须采用Monte Carlo方法数值求解, 具体的过程可参考Fei等[91]的工作.
当流动处于连续流, 实际分布函数与Grad分布函数非常接近, 导致USP-BGK控制方程的右端项趋于0.此时修正项J作为一种体现N-S机制的碰撞项发挥作用, 使方法获得AP性质.而当流动处于自由分子流, 修正项J的修正作用消失, 方法退化为SP-BGK方法.综上, USP-BGK方法通过在粒子迁移过程中耦合与N-S机制相关的碰撞项, 实现了在统一计算框架下对连续流动和稀薄流动的数值模拟.
2.2 统一气体动理学波-粒子方法借鉴UGKS使用BGK类模型方程解析解耦合连续流和稀薄流的机制, 香港科技大学Liu等[92],Zhu等[93]于2018年结合统计粒子方法提出了统一气体动理学粒子(unified gas kinetic particle, UGKP)方法, 并进一步发展为统一气体动理学波-粒子(unified gas kinetic wave-particle, UGKWP)方法.
在建模思想方面, 与SP-BGK方法相比, UGKP和UGKWP使用的是完整形式BGK类模型方程的解析解, 而非SP-BGK中的各向同性BGK类模型方程的解析解, 因而时空导数以及输运过程包含在了解析解中, 并在连续流中直接对应于2阶Chapman-Enskog展开, 能够完整还原N-S方程, 也具有完整的AP性质.由于该方法使用了UGKS中的连续/稀薄耦合机制, 因而在网格时/空尺度上同样不受限于分子平均自由程和平均碰撞时间.
与SP-BGK类似, 在UGKP和UGKWP中, 粒子也被分类为自由分子和碰撞分子, 占比也近似为e-Δt/τ和1-e-Δt/τ.然而最重要的区别在于:在UGKP和UGKWP中, 粒子一旦发生碰撞, 随即融入宏观量, 其输运过程也由连续流机制进行表示, 因而在文献[92]中碰撞粒子也称为宏观流体粒子.
这里对UGKP和UGKWP的计算步骤进行简单说明. UGKP方法中的粒子分为自由迁移粒子和碰撞粒子, 相应的求解过程分为宏观和微观两个部分.宏观通量的计算分为以下两个部分:
(1) 统计粒子自由迁移穿过界面贡献的通量;
(2) 碰撞粒子对通量的贡献通过宏观量计算得到.
微观部分的粒子更新分为以下两步:
(1) 由于碰撞粒子融入宏观量并服从宏观机制, 在新的时间步中, 需要将其重新从宏观量中抽样出来, 从而完整还原流场中的所有粒子;
(2) 依照流场所处的尺度, 抽样每个粒子的首次碰撞时间, 在首次碰撞时间之前, 粒子为自由迁移, 随后融入宏观量.
这样就形成了一个完整的宏观量和微观信息演化的流程. UGKWP可看做是对UGKP方法在算法上的一次效率优化.在碰撞粒子从其对应的宏观量中再生后, 依流动尺度只有e-Δt/τ比例的粒子会成为需要记录的自由粒子.因此在UGKWP中对碰撞粒子只进行e-Δt/τ比例的抽样, 抽样后直接成为自由粒子.在连续流e-Δt/τ非常小的情况下, UGKWP的处理能够极大提升算法的计算效率.更加详尽的说明参见Liu等[92]、Zhu等[93]的工作.
UGKWP方法是一种多尺度高效数值方法(multiscale multi-efficiency preserving,MMP)[92]. MMP方法主要具有以下两个特征:
(1) 具有从自由分子流域到连续流域的全流域模拟能力, 并且时间和空间步长不受限于粒子平均碰撞时间和平均自由程;
(2) 计算效率和相应流域的高效率计算方法相当.即在连续流域, 计算效率和内存需求应当与N-S方法相当, 在自由分子流域, 计算效率应当与纯粒子方法相当.
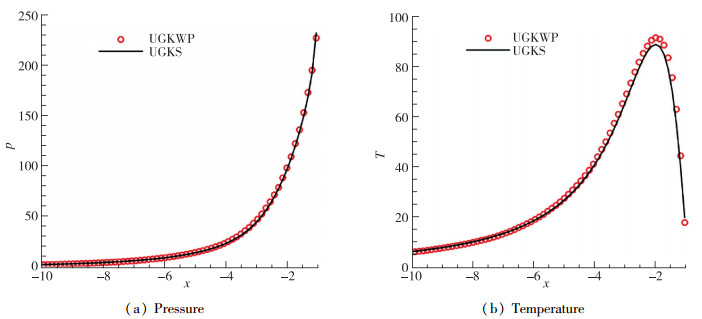
表 2给出了UGKWP方法模拟高超声速圆柱绕流(Ma=20, Kn=1)的计算时间和内存需求.相比于UGKS方法, UGKWP方法的计算效率提高了1~2个数量级, 同时内存需求减少了2个数量级. 图 10则给出了Ma=20的圆柱绕流在Kn=1情况下的计算结果, UGKWP与UGKS对流场的预测完全一致.
| 下载CSV 表 2 UGKS和UGKWP计算效率和内存需求对比(Ma=20, Kn=1)[92] Tab.2 Comparison of computational time and memory cost between the UGKS and UGKWP(Ma=20, Kn=1)[92] |
|
| 图 10 UGKS和UGKWP沿驻点线的压力和温度(Ma=20, Kn=1)[92] Fig.10 Pressure and temperature profiles along the stagnation line of cylinder predicted by UGKS and UGKWP (Ma=20, Kn=1)[92] |
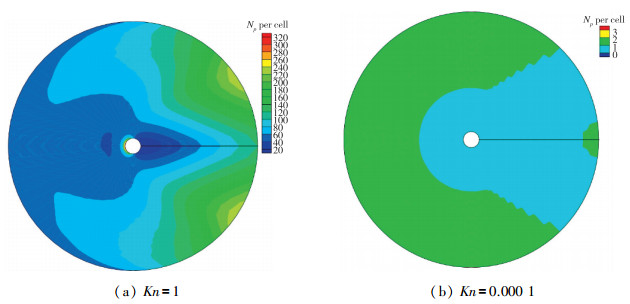
图 11给出了UGKWP在计算圆柱绕流算例时每个单元模拟粒子的数目, 在近连续流域, 每个单元只需要几个粒子, 在稀薄流域, 每个单元大概需要几十到几百个粒子.
|
| 图 11 圆柱绕流算例(Ma=20)单元模拟粒子数量[92] Fig.11 Numbers of simulation particles per cell for the cylinder flow at Ma=20[92] |
UGKWP方法通过波-粒子框架结合了确定论方法和粒子方法的优势, 实现了对全流域/全速域流动的高效求解(尤其是多维高超声速流动问题), 有望发展为求解真实外形复杂多尺度流动的高效数值工具.
3 总结与展望鉴于统一方法的跨流域多尺度模拟优势, 该类方法一经提出就迅速完成了真实气体效应的建模和计算工作, 并拓展至多相流动、多组分流动、颗粒流动, 动边界流动问题, 以及湍流研究.由于物理和力学中多尺度问题的诸多相似性, 方法还拓展至光子输运和中子输运.统一方法中的确定论与统计粒子两类方法有着各自的优势:确定论方法不存在统计涨落, 结果精确, 通过隐式加速技术以及宏观/微观协同收敛技术, 可大幅提升方法的计算效率; 统计粒子方法能够使用模型分子高效刻画速度空间, 同时不存在维度灾难, 特别适合高超声速流动问题的数值预测工作.
| [1] |
Bird G A. Molecular gas dynamics and the direct simulation of gas flows[M]. New York: Oxford University Press, 1994.
|
| [2] |
Xu K, Huang J C. A unified gas-kinetic scheme for continuum and rarefied flows[J]. Journal of Computational Physics, 2010, 229(20): 7747-7764. DOI:10.1016/j.jcp.2010.06.032 |
| [3] |
Xu K. Direct modeling for computational fluid dynamics:construction and application of unified gas-kinetic sche-mes[M]. Hackensack: World Scientific, 2015.
|
| [4] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论统一数值算法初步研究[J]. 空气动力学学报, 2000, 18(3): 255-263. Li Z H, Zhang H X. Study on gas kinetic algorithm for flows from rarefied transition to continuum[J]. Acta Aerodynamica Sinica, 2000, 18(3): 255-263. DOI:10.3969/j.issn.0258-1825.2000.03.001 (in Chinese) |
| [5] |
Li Z H, Peng A P, Ma Q, et al. Gas-kinetic unified algorithm for computable modeling of Boltzmann equation and application to aerothermodynamics for falling disintegration of uncontrolled Tiangong-No.1 spacecraft[J]. Advances in Aerodynamics, 2019, 1: 4. DOI:10.1186/s42774-019-0009-4 |
| [6] |
Guo Z L, Xu K, Wang R J. Discrete unified gas kinetic scheme for all Knudsen number flows:low-speed isother-mal case[J]. Physical Review E, 2013, 88(3): 033305. DOI:10.1103/PhysRevE.88.033305 |
| [7] |
Guo Z L, Wang R J, Xu K. Discrete unified gas kinetic scheme for all Knudsen number flows. Ⅱ. Thermal compressible case[J]. Physical Review E, 2015, 91(3): 033313. DOI:10.1103/PhysRevE.91.033313 |
| [8] |
Goldstein D, Sturtevant B, Broadwell J E. Investigations of the motion of discrete-velocity gases[R]. 1989: 100-117.
|
| [9] |
Yang J Y, Huang J C. Rarefied flow computations using nonlinear model Boltzmann equations[J]. Journal of Computational Physics, 1995, 120(2): 323-339. DOI:10.1006/jcph.1995.1168 |
| [10] |
Mieussens L. Discrete-velocity models and numerical schemes for the Boltzmann-BGK equation in plane and axisymmetric geometries[J]. Journal of Computational Physics, 2000, 162(2): 429-466. DOI:10.1006/jcph.2000.6548 |
| [11] |
Li Z H, Zhang H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193(2): 708-738. |
| [12] |
Titarev V A. Conservative numerical methods for model kinetic equations[J]. Computers & Fluids, 2007, 36(9): 1446-1459. |
| [13] |
Xu K, Huang J C. An improved unified gas-kinetic scheme and the study of shock structures[J]. IMA Journal of Applied Mathematics, 2011, 76(5): 698-711. DOI:10.1093/imamat/hxr002 |
| [14] |
Bhatnagar P L, Gross E P, Krook M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511-525. DOI:10.1103/PhysRev.94.511 |
| [15] |
Xu K, Liu C. A paradigm for modeling and computation of gas dynamics[J]. Physics of Fluids, 2017, 29(2): 026101. DOI:10.1063/1.4974873 |
| [16] |
Huang J C, Xu K, Yu P B. A unified gas-kinetic scheme for continuum and rarefied flows Ⅲ:Microflow simula-tions[J]. Communications in Computational Physics, 2013, 14(5): 1147-1173. DOI:10.4208/cicp.190912.080213a |
| [17] |
Yu P B. A unified gas kinetic scheme for all Knudsen number flows[D]. Hong Kong: Hong Kong University of Science and Technology, 2013.
|
| [18] |
Liu S, Zhong C W, Bai J. Unified gas-kinetic scheme for microchannel and nanochannel flows[J]. Computers & Mathematics with Applications, 2015, 69(1): 41-57. |
| [19] |
Wang R J, Xu X P, Xu K, et al. Onsager's cross coupling effects in gas flows confined to micro-channels[J]. Physical Review Fluids, 2016, 1(4): 044102. DOI:10.1103/PhysRevFluids.1.044102 |
| [20] |
Huang J C, Xu K, Yu P B. A unified gas-kinetic scheme for continuum and rarefied flows Ⅱ:multi-dimensional cases[J]. Communications in Computational Physics, 2012, 12(3): 662-690. DOI:10.4208/cicp.030511.220911a |
| [21] |
Wang R J, Xu K. The study of sound wave propagation in rarefied gases using unified gas-kinetic scheme[J]. Acta Mechanica Sinica, 2012, 28(4): 1022-1029. DOI:10.1007/s10409-012-0116-5 |
| [22] |
Wang R J, Xu K. Unified gas-kinetic simulation of slider air bearing[J]. Theoretical and Applied Mechanics Letters, 2014, 4(2): 022001. DOI:10.1063/2.1402201 |
| [23] |
Liu C, Xu K, Sun Q H, et al. A unified gas-kinetic scheme for continuum and rarefied flows Ⅳ:Full Boltzmann and model equations[J]. Journal of Computational Physics, 2016, 314: 305-340. DOI:10.1016/j.jcp.2016.03.014 |
| [24] |
Rykov V A. A model kinetic equation for a gas with rotational degrees of freedom[J]. Fluid Dynamics, 1975, 10(6): 959-966. |
| [25] |
Liu S, Yu P B, Xu K, et al. Unified gas-kinetic scheme for diatomic molecular simulations in all flow regimes[J]. Journal of Computational Physics, 2014, 259: 96-113. DOI:10.1016/j.jcp.2013.11.030 |
| [26] |
刘沙.统一气体动理论格式研究[D].西安: 西北工业大学, 2015. Liu S. Unified gas-kinetic scheme[D]. Xi'an: Northwestern Polytechnical University, 2015(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10699-1015581075.htm |
| [27] |
张贺.统一气体动理论格式分子振动模型研究[D].西安: 西北工业大学, 2015. Zhang H. A kinetic model with vibration for unified gas-kinetic scheme[D]. Xi'an: Northwestern Polytechnical University, 2015(in Chinese). |
| [28] |
Wang Z, Yan H, Li Q B, et al. Unified gas-kinetic scheme for diatomic molecular flow with translational, rotational, and vibrational modes[J]. Journal of Computational Physics, 2017, 350: 237-259. DOI:10.1016/j.jcp.2017.08.045 |
| [29] |
Li S Y, Li Q B. Thermal non-equilibrium effect of small-scale structures in compressible turbulence[J]. Modern Physics Letters B, 2018, 32. |
| [30] |
Chen S Z, Xu K, Lee C B. The dynamic mechanism of a moving Crookes radiometer[J]. Physics of Fluids, 2012, 24(11): 111701. DOI:10.1063/1.4765353 |
| [31] |
Chen S Z, Xu K, Lee C B, et al. A unified gas kinetic scheme with moving mesh and velocity space adapta-tion[J]. Journal of Computational Physics, 2012, 231(20): 6643-6664. DOI:10.1016/j.jcp.2012.05.019 |
| [32] |
Wang R J, Xu K. Unified gas-kinetic scheme for multi-species non-equilibrium flow[C]. AIP Conference Proceedings, 2014, 1628(1): 970-975.
|
| [33] |
Xiao T B, Xu K, Cai Q D. A unified gas-kinetic scheme for multiscale and multicomponent flow transport[J]. Applied Mathematics and Mechanics, 2019, 40(3): 355-372. DOI:10.1007/s10483-019-2446-9 |
| [34] |
Liu C, Wang Z, Xu K. A unified gas-kinetic scheme for continuum and rarefied flows Ⅵ:Dilute disperse gas-particle multiphase system[J]. Journal of Computational Physics, 2019, 386: 264-295. DOI:10.1016/j.jcp.2018.12.040 |
| [35] |
Xiao T B, Cai Q D, Xu K. A well-balanced unified gas-kinetic scheme for multiscale flow transport under gravitational field[J]. Journal of Computational Physics, 2017, 332: 475-491. DOI:10.1016/j.jcp.2016.12.022 |
| [36] |
Xiao T B, Xu K, Cai Q D, et al. An investigation of non-equilibrium heat transport in a gas system under external force field[J]. International Journal of Heat and Mass Transfer, 2018, 126: 362-379. DOI:10.1016/j.ijheatmasstransfer.2018.05.035 |
| [37] |
Sun W J, Jiang S, Xu K. An asymptotic preserving unified gas kinetic scheme for gray radiative transfer equations[J]. Journal of Computational Physics, 2015, 285: 265-279. DOI:10.1016/j.jcp.2015.01.008 |
| [38] |
Sun W J, Jiang S, Xu K, et al. An asymptotic preserving unified gas kinetic scheme for frequency-dependent radiative transfer equations[J]. Journal of Computational Physics, 2015, 302: 222-238. DOI:10.1016/j.jcp.2015.09.002 |
| [39] |
Sun W J, Jiang S, Xu K. An asymptotic preserving implicit unified gas kinetic scheme for frequency-dependent radiative transfer equations[J]. International Journal of Numerical Analysis and Modeling, 2018, 15(1/2): 134-153. |
| [40] |
Sun W J, Jiang S, Xu K. Multiscale radiative transfer in cylindrical coordinates[J]. Communications on Applied Mathematics and Computation, 2019, 1(1): 117-139. DOI:10.1007/s42967-019-0007-x |
| [41] |
Zhen Y X, Xiao M, Ni G X. Multi-scale kinetic scheme for the collisional Vlasov-Poisson system[J]. Computers & Fluids, 2016, 140: 289-296. |
| [42] |
Liu C, Xu K. A unified gas kinetic scheme for continuum and rarefied flows Ⅴ:Multiscale and multi-component plasma transport[J]. Communications in Computational Physics, 2017, 22(5): 1175-1223. DOI:10.4208/cicp.OA-2017-0102 |
| [43] |
Pan D X, Zhong C W, Zhuo C S, et al. A unified gas kinetic scheme for transport and collision effects in plasma[J]. Applied Sciences, 2018, 8(5): 746. DOI:10.3390/app8050746 |
| [44] |
毛枚良, 江定武, 李锦, 等. 气体动理学统一算法的隐式方法研究[J]. 力学学报, 2015, 47(5): 822-829. Mao M L, Jiang D W, Li J, et al. Study on implicit implementation of the unified gas kinetic scheme[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(5): 822-829. (in Chinese) |
| [45] |
Zhu Y J, Zhong C W, Xu K. Implicit unified gas-kinetic scheme for steady state solutions in all flow regimes[J]. Journal of Computational Physics, 2016, 315: 16-38. DOI:10.1016/j.jcp.2016.03.038 |
| [46] |
Zhu Y J, Zhong C W, Xu K. An implicit unified gas-kinetic scheme for unsteady flow in all Knudsen regimes[J]. Journal of Computational Physics, 2019, 386: 190-217. DOI:10.1016/j.jcp.2019.01.033 |
| [47] |
Zhu Y J, Zhong C W, Xu K. Unified gas-kinetic scheme with multigrid convergence for rarefied flow study[J]. Physics of Fluids, 2017, 29(9): 096102. DOI:10.1063/1.4994020 |
| [48] |
Chen S Z, Zhang C, Zhu L H, et al. A unified implicit scheme for kinetic model equations. Part I. Memory reduction technique[J]. Science Bulletin, 2017, 62(2): 119-129. DOI:10.1016/j.scib.2016.12.010 |
| [49] |
Xiao T B, Xu K, Cai Q D. A velocity-space adaptive unified gas kinetic scheme for continuum and rarefied flows[J]. arXiv preprint arXiv: 1802.04972, 2018.
|
| [50] |
江定武.基于模型方程解析解的气体动理学算法研究[D].绵阳: 中国空气动力研究与发展中心, 2016. Jiang D W. Study of the gas kinetic scheme based on the analytical solution of model equation[D]. Mianyang: China Aerodynamics Research and Development Center, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90113-1017018831.htm |
| [51] |
Li S Y, Li Q B, Fu S, et al. The high performance parallel algorithm for unified gas-kinetic scheme[C]. AIP Conference Proceedings, 2016, 1786(1): 180007.
|
| [52] |
陆林生, 董超群, 李志辉. 多相空间数值模拟并行化研究[J]. 计算机科学, 2003, 30(3): 129-137. Lu L S, Dong C Q, Li Z H. Research on parallelization of multiphase space numerical simulation[J]. Computer Science, 2003, 30(3): 129-137. DOI:10.3969/j.issn.1002-137X.2003.03.037 (in Chinese) |
| [53] |
Li S Y, Li Q B, Fu S, et al. A unified gas-kinetic scheme for axisymmetric flow in all Knudsen number regimes[J]. Journal of Computational Physics, 2018, 366: 144-169. DOI:10.1016/j.jcp.2018.04.004 |
| [54] |
Wang P, Zhu L H, Guo Z L, et al. A comparative study of LBE and DUGKS methods for nearly incompressible flows[J]. Communications in Computational Physics, 2015, 17(3): 657-681. DOI:10.4208/cicp.240614.171014a |
| [55] |
Bardow A, Karlin I V, Gusev A A. General characteristic-based algorithm for off-lattice Boltzmann simulations[J]. Europhysics Letters, 2006, 75(3): 434-440. DOI:10.1209/epl/i2006-10138-1 |
| [56] |
Zhu L H, Wang P, Guo Z L. Performance evaluation of the general characteristics based off-lattice Boltzmann scheme and DUGKS for low speed continuum flows[J]. Journal of Computational Physics, 2017, 333: 227-246. DOI:10.1016/j.jcp.2016.11.051 |
| [57] |
Zhu L H, Guo Z L, Xu K. Discrete unified gas kinetic scheme on unstructured meshes[J]. Computers & Fluids, 2016, 127: 211-225. |
| [58] |
Wu C, Shi B C, Shu C, et al. Third-order discrete unified gas kinetic scheme for continuum and rarefied flows:Low-speed isothermal case[J]. Physical Review E, 2018, 97(2): 023306. DOI:10.1103/PhysRevE.97.023306 |
| [59] |
Wu C, Shi B C, Chai Z H, et al. Discrete unified gas kinetic scheme with a force term for incompressible fluid flows[J]. Computers & Mathematics with Applications, 2016, 71(12): 2608-2629. |
| [60] |
Pan D X, Zhong C W, Zhuo C S. An implicit discrete unified gas-kinetic scheme for simulations of steady flow in all flow regimes[J]. Communications in Computational Physics, 2019, 25(5): 1469-1495. |
| [61] |
Yuan R F, Zhong C W. A conservative implicit scheme for steady state solutions of diatomic gas flow in all flow regimes[J]. arXiv preprint arXiv: 1810.13039, 2018.
|
| [62] |
Yuan R F, Zhong C W. A multi-prediction implicit scheme for steady state solutions of gas flow in all flow regimes[J]. arXiv preprint arXiv: 1905.06629, 2019.
|
| [63] |
Mittal R, Iaccarino G. Immersed boundary methods[J]. Annual Review of Fluid Mechanics, 2005, 37: 239-261. DOI:10.1146/annurev.fluid.37.061903.175743 |
| [64] |
Li C, Wang L P. An immersed boundary-discrete unified gas kinetic scheme for simulating natural convection involving curved surfaces[J]. International Journal of Heat and Mass Transfer, 2018, 126: 1059-1070. DOI:10.1016/j.ijheatmasstransfer.2018.04.166 |
| [65] |
Tao S, Chen B M, Yang X P, et al. Second-order accurate immersed boundary-discrete unified gas kinetic scheme for fluid-particle flows[J]. Computers & Fluids, 2018, 165: 54-63. |
| [66] |
Tao S, Zhang H L, Guo Z L, et al. A combined immersed boundary and discrete unified gas kinetic scheme for particle-fluid flows[J]. Journal of Computational Physics, 2018, 375: 498-518. DOI:10.1016/j.jcp.2018.08.047 |
| [67] |
Tao S, He Q, Wang L, et al. A non-iterative direct-forcing immersed boundary method for thermal discrete unified gas kinetic scheme with Dirichlet boundary condi-tions[J]. International Journal of Heat and Mass Transfer, 2019, 137: 476-488. DOI:10.1016/j.ijheatmasstransfer.2019.03.147 |
| [68] |
Wang P, Wang L P, Guo Z L. Comparison of the lattice Boltzmann equation and discrete unified gas-kinetic sche-me methods for direct numerical simulation of decaying turbulent flows[J]. Physical Review E, 2016, 94(4): 043304. DOI:10.1103/PhysRevE.94.043304 |
| [69] |
Bo Y T, Wang P, Guo Z L, et al. DUGKS simulations of three-dimensional Taylor-Green vortex flow and turbulent channel flow[J]. Computers & Fluids, 2017, 155: 9-21. |
| [70] |
Liu H T, Kong M C, Chen Q, et al. Coupled discrete unified gas kinetic scheme for the thermal compressible flows in all Knudsen number regimes[J]. Physical Review E, 2018, 98(5): 053310. DOI:10.1103/PhysRevE.98.053310 |
| [71] |
Zhang Y, Zhu L H, Wang R J, et al. Discrete unified gas kinetic scheme for all Knudsen number flows. Ⅲ. Binary gas mixtures of Maxwell molecules[J]. Physical Review E, 2018, 97(5): 053306. DOI:10.1103/PhysRevE.97.053306 |
| [72] |
Zhang Y, Zhu L H, Wang P, et al. Discrete unified gas kinetic scheme for flows of binary gas mixture based on the McCormack model[J]. Physics of Fluids, 2019, 31(1): 017101. DOI:10.1063/1.5063846 |
| [73] |
Huo Y T, Rao Z H. The discrete unified gas kinetic scheme for solid-liquid phase change problem[J]. International Communications in Heat and Mass Transfer, 2018, 91: 187-195. DOI:10.1016/j.icheatmasstransfer.2017.12.018 |
| [74] |
Zhang C H, Yang K, Guo Z L. A discrete unified gas-kinetic scheme for immiscible two-phase flows[J]. International Journal of Heat and Mass Transfer, 2018, 126: 1326-1336. DOI:10.1016/j.ijheatmasstransfer.2018.06.016 |
| [75] |
Yang Z R, Zhong C W, Zhuo C S. Phase-field method based on discrete unified gas-kinetic scheme for large-density-ratio two-phase flows[J]. Physical Review E, 2019, 99(4): 043302. DOI:10.1103/PhysRevE.99.043302 |
| [76] |
McCormack F J. Construction of linearized kinetic models for gaseous mixtures and molecular gases[J]. Physics of Fluids, 1973, 16(12): 2095-2105. DOI:10.1063/1.1694272 |
| [77] |
Guo Z L, Xu K. Discrete unified gas kinetic scheme for multiscale heat transfer based on the phonon Boltzmann transport equation[J]. International Journal of Heat and Mass Transfer, 2016, 102: 944-958. DOI:10.1016/j.ijheatmasstransfer.2016.06.088 |
| [78] |
Luo X P, Yi H L. A discrete unified gas kinetic scheme for phonon Boltzmann transport equation accounting for phonon dispersion and polarization[J]. International Journal of Heat and Mass Transfer, 2017, 114: 970-980. DOI:10.1016/j.ijheatmasstransfer.2017.06.127 |
| [79] |
Zhang C, Guo Z L. Discrete unified gas kinetic scheme for multiscale heat transfer with arbitrary temperature difference[J]. International Journal of Heat and Mass Transfer, 2019, 134: 1127-1136. DOI:10.1016/j.ijheatmasstransfer.2019.02.056 |
| [80] |
Liu H T, Cao Y, Chen Q, et al. A conserved discrete unified gas kinetic scheme for microchannel gas flows in all flow regimes[J]. Computers & Fluids, 2018, 167: 313-323. |
| [81] |
Wang Y, Zhong C W. An ALE-type discrete unified gas kinetic scheme for low-speed continuum and rarefied flow simulations with moving boundaries[J]. arXiv preprint arXiv: 1906.01813, 2019.
|
| [82] |
Macrossan M N. A particle simulation method for the BGK equation[C]. AIP Conference Proceedings, 2001, 585(1): 426-433.
|
| [83] |
Gallis M A, Torczynski J R. The application of the BGK model in particle simulations[R]. AIAA 2000-2360, 2000.
|
| [84] |
Zhang J, John B, Pfeiffer M, et al. Particle-based hybrid and multiscale methods for nonequilibrium gas flows[J]. Advances in Aerodynamics, 2019, 1: 12. DOI:10.1186/s42774-019-0014-7 |
| [85] |
Holway L H Jr. New statistical models for kinetic theory:methods of construction[J]. Physics of Fluids, 1966, 9(9): 1658-1673. DOI:10.1063/1.1761920 |
| [86] |
Shakhov E M. Generalization of the Krook kinetic relaxation equation[J]. Fluid Dynamics, 1968, 3(5): 95-96. |
| [87] |
Chen S Z, Xu K, Cai Q D. A comparison and unification of ellipsoidal statistical and shakhov BGK models[J]. Advances in Applied Mathematics and Mechanics, 2015, 7(2): 245-266. DOI:10.4208/aamm.2014.m559 |
| [88] |
Pfeiffer M. Particle-based fluid dynamics:comparison of different Bhatnagar-Gross-Krook models and the direct simulation Monte Carlo method for hypersonic flows[J]. Physics of Fluids, 2018, 30(10): 106106. DOI:10.1063/1.5042016 |
| [89] |
Tumuklu O, Li Z, Levin D A. Particle ellipsoidal statistical Bhatnagar-Gross-Krook approach for simulation of hypersonic shocks[J]. AIAA Journal, 2016, 54(12): 3701-3716. DOI:10.2514/1.J054837 |
| [90] |
Pfeiffer M. Extending the particle ellipsoidal statistical Bhatnagar-Gross-Krook method to diatomic molecules including quantized vibrational energies[J]. Physics of Fluids, 2018, 30(11): 116103. DOI:10.1063/1.5054961 |
| [91] |
Fei F, Zhang J, Li J, et al. A Unified stochastic particle Bhatnagar-gross-Krook method for multiscale gas flows[J]. arXiv preprint arXiv: 1808.03801, 2018.
|
| [92] |
Liu C, Zhu Y J, Xu K. Unified gas-kinetic wave-particle methods I: continuum and rarefied gas flow[J]. arXiv preprint arXiv: 1811.07141, 2018.
|
| [93] |
Zhu Y J, Liu C, Zhong C W, et al. Unified gas-kinetic wave-particle methods. Ⅱ. Multiscale simulation on unstructured mesh[J]. Physics of Fluids, 2019, 31(6): 067105. DOI:10.1063/1.5097645 |




