2. 中国航空动力机械研究所,湖南株洲 412002
2. AVIC Aviation Powerplant Research Institute, Zhuzhou 412002, China
目前航空航天领域在飞速发展, 人们对飞行器的性能提出了越来越高的要求.这就使得飞行器的几何外形及所面临的飞行环境也越来越复杂.随着巡航Mach数的不断提高, 其典型的飞行速度由低速、亚声速提高到高亚声速、跨声速, 甚至超声速, 流动状态从不可压缩已经过渡到可压缩状态, 流动也变得不再单一, 流场之间相互作用, 出现了激波、旋涡、分离等复杂流动结构.这些复杂流动相互作用, 对飞行器的气动特性产生了很大的影响[1].传统湍流模型对这些复杂流动状态的适应性大大降低, 模型计算结果与实验值有时相差较多.由于跨声速流动中流场内速度和密度等会急剧变化, 这给传统CFD计算带来了很大的困难, 因此, 跨声速等复杂流动成为近年来CFD计算领域的研究热点与难点.本文以跨声速流动为研究重点, 展开新型湍流模型的研究应用工作.
Reynolds[2]采用统计平均的方法将流场离散为平均值与脉动值之和, 对N-S方程进行平均, 产生了不封闭项, 即Reynolds应力项, 这一项反映出流场脉动量对平均量的影响, 在数值计算中, 通常用湍流模型对其进行封闭.
在现有的两方程湍流模型中, 对于湍动能方程k, 可以在RANS框架下精确得出, 而对于不封闭的ε项, 通常类比k方程的推导过程来构造输运方程进行封闭, 这就导致推导过程缺乏严格的理论指导.且k-ε湍流模型在高Reynolds数条件下, 求解附面层近壁区, 需要非常细密的网格, 但是求解精度却一般.考虑湍动能、湍流耗散率与湍流尺度之间存在一定的代数关系, 因而合理地引入湍流尺度就可封闭湍动能方程.
本文在文献[3]构造的单方程湍流模型KDO的基础上, 提出一种适用于可压缩流动的新型湍流模型, 通过模拟复杂的跨声速流动以验证新模型的性能. KDO模型用代数形式封闭ε方程, 只求解k方程, 它只含有两个可调参数.为提高KDO模型模拟跨声速等复杂流动的能力, 在其基础上进行适当可压缩修正, 构造出了一种新的湍流模型, 称为CKDO. Menter[4]提出的剪应力输运SST模型融合了k-ω和k-ε的优点, 在不可压缩流动中求解精度和鲁棒性表现很好, 但是在平衡湍流中依然保持经典关系式, 因此, 在本文中只作为一个参考对比值.典型一方程湍流模型SA[5]模型是本文另一个参考对比模型.
1 Bradshaw假设的推广在边界层流动中, 湍流主应力τ与湍动能k成正比, 即Rb=τ/k, Rb接近于一个常数[6]. Menter在其SST模型[7]中将该比值定为0.31.在许多剪切流动[6]中, 该比值常被设置在0.3左右.由于计算机技术的高速发展, 对直接数值模拟(DNS)进行更深入的研究, 大量详细的DNS数据显示, Rb不再是一个恒量.文晓庆等[8]以及刘景源[9]的研究工作表明在不同的算例条件下要对其进行相应的调整.白俊强等在文献[10]中指出在充分发展的湍流区域该比值的最大值小于0.29.根据文献[11]平板边界层在截面Reθ=4 060上的DNS数据, 将Bradshaw函数标定为
| $ \begin{align} &{{R}_{\text{b}}}=0.018{{(R{{e}_{k}}/1)}^{0.56}}\cdot {{[1+{{(R{{e}_{k}}/112)}^{2.5}}]}^{-0.51/2.5}}\cdot \\ &{{[1+{{(R{{e}_{k}}/1\text{ }070)}^{10}}]}^{-0.05/10}} \\ \end{align} $ |
新的主剪切应力公式定义为
| $ \tau =\rho {{R}_{\text{b}}}k $ |
根据两方程模型中剪切应力的计算形式
| $ \tau ={{\mu }_{\text{t}}}S $ |
推导出本文采用的涡黏性系数计算公式:
| $ {{\mu }_{\text{t}}}=\tau /S=\rho {{R}_{\text{b}}}k/S $ |
其中,
| $ \begin{array}{l} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}(\rho {\mathit{\boldsymbol{u}}_j}k) = \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {\mathit{\boldsymbol{x}}_j}}}} \right] + {P_k} - \rho \varepsilon \\ {P_k} = {\mu _{\rm{t}}}{S^2}\\ \varepsilon = {\varepsilon _1} + {\varepsilon _2}\\ {\varepsilon _1} = 2\mu \frac{{\partial \sqrt k }}{{\partial {\mathit{\boldsymbol{x}}_j}}} \cdot \frac{{\partial \sqrt k }}{{\partial {\mathit{\boldsymbol{x}}_j}}}\\ {\varepsilon _2} = {A_\varepsilon }{k^{\frac{3}{2}}}/L \end{array} $ | (1) |
| $ \begin{array}{l} {\mu _{\rm{t}}} = \rho {R_{\rm{b}}}k/S\\ L = \frac{{\sqrt {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}\cdot{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}} }}{{\sqrt {{\nabla _j}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}\cdot{\nabla _j}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}} }}, \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \nabla \times \mathit{\boldsymbol{u}} \end{array} $ | (2) |
其中,
可以看出, 式(1) 满足量纲分析, 形式上能反映出在RANS框架下, 能量从湍动能直接级串到最底层的分子耗散, 其中流体微团的位移与涡团的尺度L是同一量级, k1/2为速度尺度.在L/k1/2的时间内, 湍动能从k降低到0, 因此耗散率的量级为k/(L/k1/2)=k3/2/L.式(2) 中涡团尺度L引用徐晶磊等[12]构造的形式, 其机理为: Ωi为当地流动蕴含的势, 梯度▽jΩi认为是该势衰减最快的方向, 那么L则是该势走向0(即走出涡团)所发生的位移.对于系数Aε, 根据早期KDO湍流模型理论推出充分发展区的Aε = Cμ3/4/κ≈0.4, 该系数在描述均衡态流动的时候有较好的表现, 但是在非平衡态流动, 如湍流转捩、逆压梯度、分离等情况下需要扩充该系数的内涵.在已有的DNS中, 平板边界层的部分对数区和尾迹区流动处于该种状态, 因此选择Reθ=4 060切面的DNS数据[11]对系数Aε进行标定.由于k方程的其他项也做了模化, 因此考虑这些项模化后的误差, 以
若Rek < 10,
| $ \begin{array}{l} {\varepsilon _2} = \frac{{{A_\varepsilon }{k^{\frac{3}{2}}}}}{d}\\ {A_\varepsilon } = 2.68{\left( {\frac{{R{e_k}}}{{0.25}}} \right)^{ - 0.8}}\cdot{\left[{1 + {{\left( {\frac{{R{e_k}}}{{0.25}}} \right)}^{1.5}}} \right]^{\frac{{0.45}}{{1.5}}}}\cdot\\ {\left[{1 + {{\left( {\frac{{R{e_k}}}{{2.4}}} \right)}^{1.5}}} \right]^{\frac{{ - 0.1}}{{1.5}}}} \end{array} $ |
若Rek > 10,
| $ \begin{array}{l} {\varepsilon _2} = {\rm{min}}({A_\varepsilon }, 0.8){k^{\frac{3}{2}}}{\rm{max}}(1/L, (1-{{\rm{e}}^{ - R{e_k}/1{\rm{ }}000}})/d)\\ {A_\varepsilon } = 0.325{(R{e_k}/10)^{ - 1.7}}\cdot{[1 + {(R{e_k}/31)^4}]^{\frac{{3.3}}{4}}}\cdot\\ {[1 + {(R{e_k}/70)^5}]^{\frac{{ - 1.2}}{5}}}\cdot{[1 + {(R{e_k}/100)^6}]^{\frac{{0.65}}{6}}}\cdot\\ {[1 + {(R{e_k}/190)^{10}}]^{\frac{{ - 0.5}}{{10}}}} \end{array} $ |
该函数采用连乘形式, 每一级代表不同区域层次的流动结构, 标定函数源于She等[13]的结构系综理论, 可以表达任意形状的曲线.
3 可压缩KDO湍流模型的形式可压缩湍动能控制方程[14]为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\bar \rho k} \right) + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}(\bar \rho {{\tilde \mu }_j}k) = {P_k}-\bar \rho \varepsilon -{{\mathit{\boldsymbol{\bar u''}}}_i}\frac{{\partial \bar P}}{{\partial {\mathit{\boldsymbol{x}}_i}}} + \overline {P'\frac{{\partial {{\mathit{\boldsymbol{u''}}}_i}}}{{\partial {\mathit{\boldsymbol{x}}_i}}}} + \\ \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left[{{{\overline {{\mathit{\boldsymbol{\tau }}_{ji}}\mathit{\boldsymbol{u''}}} }_i}-\rho \mathit{\boldsymbol{u''}}\left( {\overline {{{\mathit{\boldsymbol{u''}}}_i}{{\mathit{\boldsymbol{u''}}}_i}/2} } \right)-\overline {P'{{\mathit{\boldsymbol{u''}}}_j}} } \right] \end{array} $ |
对于KDO, 方程右端各项分别模化为
| $ \begin{array}{l} {P_k} = {\mu _{\rm{t}}}{{\tilde S}^2}\\ \bar \rho \varepsilon + {{\mathit{\boldsymbol{\bar u''}}}_i}\frac{{\partial \bar P}}{{\partial {\mathit{\boldsymbol{x}}_i}}} - \overline {P'\frac{{\partial {{\mathit{\boldsymbol{u''}}}_i}}}{{\partial {\mathit{\boldsymbol{x}}_i}}}} = \bar \rho \left( {{\varepsilon _1} + {\varepsilon _2}} \right)\\ {\varepsilon _1} = 2\mu \frac{{\partial \sqrt k }}{{\partial {\mathit{\boldsymbol{x}}_j}}}\cdot\frac{{\partial \sqrt k }}{{\partial {\mathit{\boldsymbol{x}}_j}}}\\ {\varepsilon _2} = \frac{{{A_\varepsilon }{k^{\frac{3}{2}}}}}{{\tilde L}} \end{array} $ |
| $ \tilde L = \frac{{\sqrt {{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }}}_i}\cdot{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }}}_i}} }}{{\sqrt {{\nabla _j}{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }}}_i}\cdot{\nabla _j}{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }}}_i}} }}, \mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }} = \nabla \times \mathit{\boldsymbol{\tilde u}} $ | (3) |
| $ \overline {{\tau _{ji}}{{\mathit{\boldsymbol{u''}}}_i}} - \rho {{\mathit{\boldsymbol{u''}}}_j}\left( {\overline {{{\mathit{\boldsymbol{u''}}}_i}{{\mathit{\boldsymbol{u''}}}_i}/2} } \right) - \overline {P'{{\mathit{\boldsymbol{u''}}}_j}} = \left( {\mu + {\mu _{\rm{t}}}} \right)\mathit{\boldsymbol{k}}{,_j} $ |
涡黏系数μt为
| $ {\mu _{\rm{t}}} = \bar \rho {R_{\rm{b}}}k/\tilde S $ |
其中, ρ为Reynolds平均下的密度,
本文研究跨声速流动问题包含大量复杂的可压缩流动, 在式(3) 中并不包含任何可压缩流动的密度变化因素, 仅适用于不可压缩流动.若将其用于可压缩流动中, 则需要进行可压缩修正.考虑到可压缩流动特性, 提出一种新的可压缩尺度植入原模型中, 将修正后的模型称为CKDO湍流模型.基于式(3), 将其重新定义为:
| $ \tilde L = \frac{{\sqrt {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}} }}{{\sqrt {{\nabla _j}{{\widetilde {{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}}_i} \cdot {\nabla _j}{{\widetilde {{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}}_i}} }},\mathit{\boldsymbol{ \boldsymbol{\widetilde \varOmega} }} = \frac{{\nabla \times \left( {\bar \rho \mathit{\boldsymbol{\tilde u}}} \right)}}{{\bar \rho }} $ |
以上公式将密度引入新尺度
计算方法方面, 无黏项空间离散格式采用3阶Roe格式+MUSCL插值, 黏性通量空间离散格式为中心差分, 时间推进方式采用近似因子分解算法.
5 算例评估 5.1 RAE2822超临界翼型超临界翼型是目前民用干线飞机的基本支撑翼型, 这种翼型具有较高的临界Mach数, 能够有效地提高跨声速飞机的巡航Mach数, 从而维持良好的经济性.本文采用经典超临界翼型RAE2822[15]验证CKDO湍流模型对于翼型表面摩擦系数以及激波的捕捉能力.选取两个实验工况进行对比, 即M=0.73, Re=6.5×106, AOA=3.19°和M=0.75, Re=6.5×106, AOA=3.19°这两种状态.参考NASA进行湍流模型验证的计算网格, 将网格量定为25 000个, 近壁处网格进行局部加密, 设置增长率为1.2, 法向第一层网格y+=0.2, 局部计算网格见图 1.
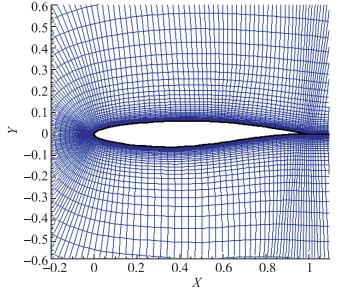
|
| 图 1 RAE2822局部计算网格 Fig.1 RAE2822 local computational grids |
图 2, 图 3分别为M=0.73, 0.75时压力系数与摩擦阻力系数的分布.从图 2(a)中可以看出, 选用的这几种湍流模型对于翼型的吸力峰值与下表面压力分布的模拟与实验值都十分接近, 相差不多, 但是在激波位置, 由于气体被剧烈压缩, 能量变化非常大, 这无疑加大了捕捉流场变化的难度.从此图中还可看出SST和KDO湍流模型的等熵压缩段较短, 这导致了激波出现过早.而CKDO模型对激波位置的捕捉与实验值吻合得很好, 说明其能合理地平衡激波处的湍动能产生.图 3(a)中各湍流模型的模拟结果相差不多, 与实验值均能较好地吻合, 但从图中可以看出CKDO模型表现得更好一些.图 2(b)和图 3(b)是翼型表面摩擦阻力系数分布, 可看出CKDO模型在翼型上表面的计算结果与实验值最接近, 而其他模型与实验值均有较多偏离, 而在下表面, 各湍流模型的计算结果相差不大, 但从图中仍能看出CKDO模型的结果要好于其他模型.
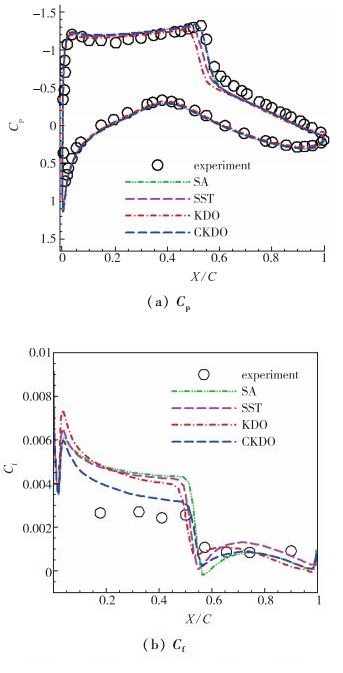
|
| 图 2 M=0.73时压力系数与摩擦阻力系数分布 Fig.2 Pressure coefficient and frictional resistance coefficient distributions at M=0.73 |
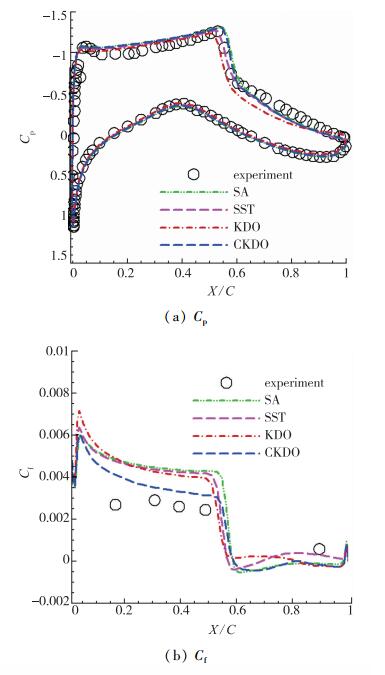
|
| 图 3 M=0.75时压力系数与摩擦阻力系数分布 Fig.3 Pressure coefficient and frictional resistance coefficient distributions at M=0.75 |
轴对称圆筒管道凸起流动是典型的分离流动, Bachalo等[16]在NASA的风洞实验室进行过该实验.在该圆筒凸起流动中不但有分离流动, 还有再附以及湍流边界层干扰等复杂流动, 这使得利用湍流模型捕捉该流场的难度加大.本文选取两种典型工况进行数值计算, 进口分别为M=0.85, 0.875这两种条件, 分别用不同的湍流模型来计算表面压力系数.轴对称圆筒管凸起局部计算网格见图 4.
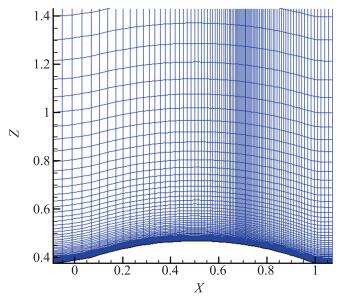
|
| 图 4 轴对称圆筒管道凸起流动局部计算网格 Fig.4 Axisymmetric bump local computational grids |
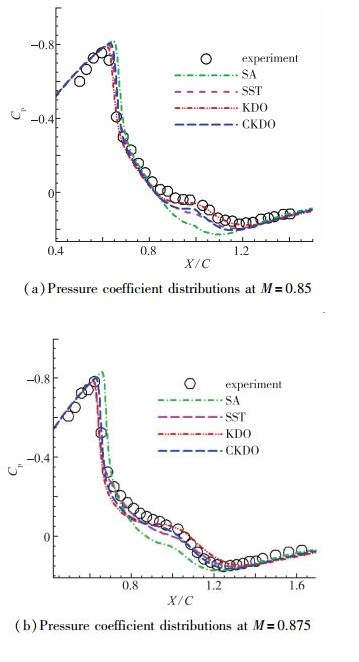
图 5(a)与(b)显示的是两个不同进口Mach数条件下管道表面压力系数分布.图 5(a)显示在M=0.85条件下未出现明显的分离流动, 但是在X/C=0.88处可以观察到压力梯度曲线的斜率发生了轻微的变化.图 5(b)中入口Mach数增大, 分离明显增强, 可以看出在分离区内CKDO模型的结果与实验值吻合得最好, 较原模型KDO结果要好很多, 这充分反映出新模型CKDO在高速分离流动中的优秀表现.在分离区外的其他各模型结果相差不多, SA模型结果最差.
|
| 图 5 表面压力系数分布 Fig.5 Surface pressure coefficient distributions |
ONERA-M6机翼实验常被用来验证湍流模型的准确度, 是一个比较经典的实验案例. Schmitt等[17]对该型机翼进行过实验研究.实验的特点在于该机翼表面存在一个λ形激波, 在几个典型位置处, 该实验给出了压力分布以便对比.本文选取两个较为典型的实验工况做对比, 计算条件为: (a)M=0.839 5, Re=11.72×106, AOA=3.06°; (b)M=0.880 9, Re=11.77×106, AOA=3.06°.网格分布为285×65×49, 法向第1层网格的y+=0.2.图 6为ONERA-M6计算网格.图 7、图 8分别为M=0.839 5, 0.880 9时不同位置机翼表面的压力系数.图中B代表全展长, Y代表机翼展向坐标.

|
| 图 6 ONERA-M6计算网格 Fig.6 ONERA-M6 computational grids |
|
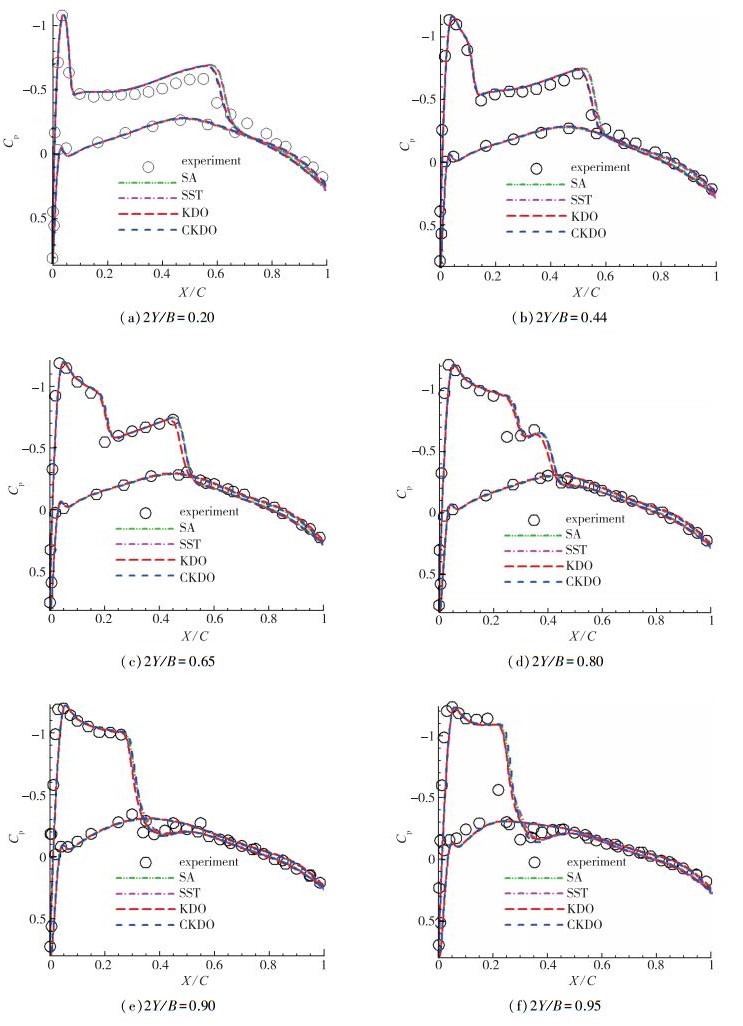
| 图 7 M=0.839 5时不同位置机翼表面的压力系数Fig. 7 Pressure coefficients of wing surface at M=0.839 5 Fig.7 Pressure coefficients of wing surface at M=0.839 5 |
|
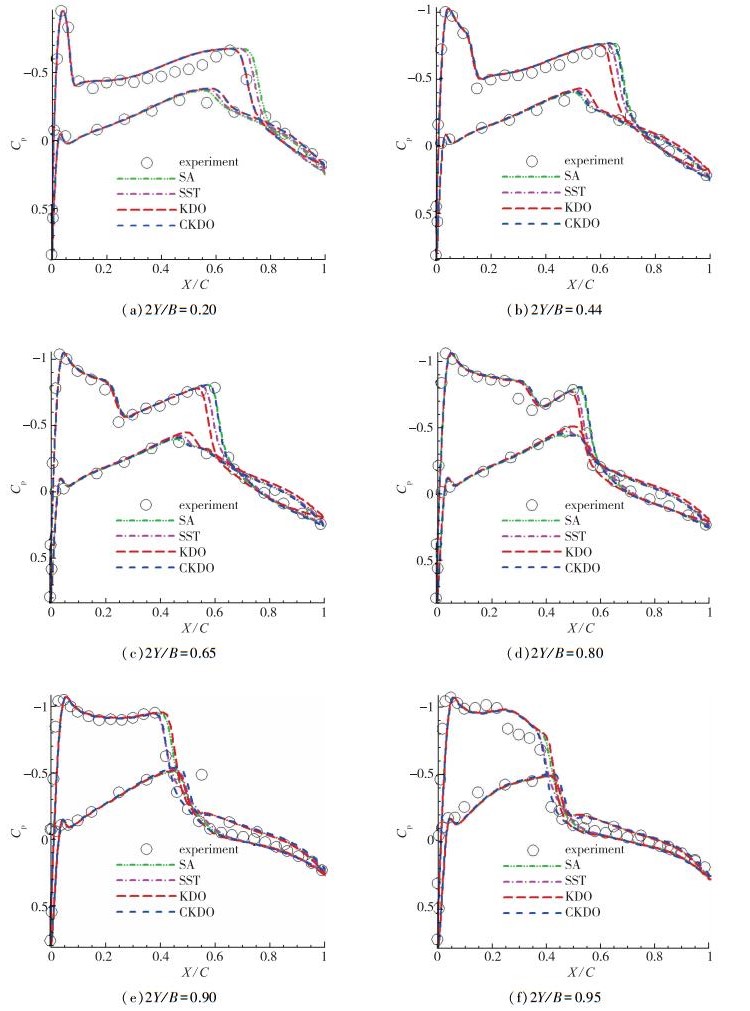
| 图 8 M=0.880 9时不同位置机翼表面的压力系数 Fig.8 Pressure coefficients of wing surface at M=0.880 9 |
从图 7可以看出, 在前两个站位上, 这几种湍流模型的模拟精度基本一致, 相差很小, 对于激波和吸力峰值的捕捉能力相当.但是在靠近翼尖截面的压力分布在一定程度上有所不同, CKDO模型与KDO模型在反映激波后压力恢复的极值以及恢复处的斜率上效果要比SA模型与SST模型好一些.在后4个站位上, 可以看出CKDO模型模拟结果要比原KDO模型结果好一些, 尤其是在激波处以及激波后压力恢复区内.
从图 8可以看出, 在几乎所有站位上, CKDO模型的模拟结果与实验值均吻合得最好, 相比原KDO模型, 精度提高了不少, SA模型次之.总体上, 新模型CKDO能够较为准确地捕捉机翼整个表面的压力分布, 能够合理地平衡流动中湍动能能量的变化, 这表明该模型在跨声速机翼绕流计算中的优越性.
6 结论本文提出的CKDO模型基于湍动能方程, 通过代数模化方式对该方程进行封闭, 保证整个推导过程在N-S方程的严格控制下.通过分析跨声速等可压缩流动的特性, 在原KDO模型的基础上引入可压缩湍流尺度来平衡整个流动过程的湍动能能量, 构造出新型湍流模型CKDO.
通过二维算例RAE2822超临界翼型、轴对称圆筒管道凸起流动以及三维算例ONERA-M6机翼绕流这3个算例研究了新模型CKDO对于壁面压力系数分布、翼型的吸力峰值以及激波位置等的模拟情况, 模拟结果均与实验值吻合较好.
以上算例表明, CKDO模型对于跨声速这种复杂流动的流动现象有较好的模拟, 且CKDO模型控制方程能够较为简便地植入其他传统模型中, 有助于提高计算精度, 因此CKDO模型具有一定的工程应用价值.今后, 将重点研究不同类型的跨声速及超声速等复杂流动问题, 并且深入研究其作用机理, 以便进一步完善该CKDO模型.
| [1] |
武宇, 易仕和, 陈植, 等. 超声速层流/湍流压缩拐角流动结构的实验研究[J].
物理学报, 2013, 62(18): 184702 Wu Y, Yi S H, Chen Z, et al. Experimental investigations on structures of supersonic laminar/turbulent flow over a compression ramp[J]. Acta Physica Sinica, 2013, 62(18): 184702 DOI:10.7498/aps.62.184702 |
| [2] | Reynolds O. On the dynamical theory of incompressible viscous fluids and the determination of the criterion[J]. Proceedings of the Royal Society of London, 1894, 56(336-339): 40-45. DOI:10.1098/rspl.1894.0075 |
| [3] | Xu J L, Zhang Y, Bai J Q. One-equation turbulence model based on extended Bradshaw assumption[J]. AIAAJournal, 2015, 53(6): 1433-1441. |
| [4] | Menter F. Improved two-equation k-ω turbulence models for aerodynamic flows[R]. NASA-TM 103975, 1992. |
| [5] | Spalart P, Allmaras S. A one-equation turbulence model for aerodynamic flows[R]. AIAA 1992-0439, 1992. |
| [6] | Harsha P T, Lee S C. Correlation between turbulent shear stress and turbulent kinetic energy[J]. AIAA Journal, 1970, 8(8): 1508-1510. DOI:10.2514/3.5932 |
| [7] | Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [8] |
文晓庆, 柳阳威, 方乐, 等. 提高k-ω SST模型对翼型失速特性的模拟能力[J].
北京航空航天大学学报, 2013, 39(8): 1127-1132. Wen X Q, Liu Y W, Fang L, et al. Improving the capability of k-ω SST turbulence model for predicting stall characteristics of airfoil[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(8): 1127-1132. |
| [9] |
刘景源. SST湍流模型在高超声速绕流中的改进[J].
航空学报, 2012, 33(12): 2192-2201. Liu J Y. An improved SST turbulence model for hypersonic flows[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2192-2201. |
| [10] |
白俊强, 张扬, 徐晶磊, 等. 新型单方程湍流模型构造及其应用[J].
航空学报, 2014, 35(7): 1804-1814. Bai J Q, Zhang Y, Xu J L, et al. Construction and its application of a new one-equation turbulence model[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1804-1814. |
| [11] | Schlatter P, Örlü R. Assessment of direct numerical si-mulation data of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2010, 659: 116-126. DOI:10.1017/S0022112010003113 |
| [12] |
徐晶磊, 阎超. 一个一方程scale-adaptive simulation模型的构造[J].
气体物理—理论与应用, 2010, 5(1): 78-82. Xu J L, Yan C. A one-equation scale-adaptive simulation model[J]. Physics of Gases—Theory and Applications, 2010, 5(1): 78-82. |
| [13] | She Z S, Chen X, Wu Y, et al. New perspective in statistical modeling of wall-bounded turbulence[J]. Acta Mechanica Sinica, 2010, 26(6): 847-861. DOI:10.1007/s10409-010-0391-y |
| [14] | Wilcox D C. Turbulence modeling for CFD[M]. California: DCW Industries, Inc, 2006: 243-261. |
| [15] | Cook P H, Firmin M C, McDonald M A. Aerofoil RAE2822: pressure distributions, and boundary layer and wake measurements[R]. AGARD AR-138, 1979. |
| [16] | Bachalo W D, Johnson D A. Transonic, turbulent boun-darylayer separation generated on an axisymmetric flow model[J]. AIAA Journal, 1986, 24(3): 437-443. DOI:10.2514/3.9286 |
| [17] | Schmitt V, Charpin F. Pressure distributions on the ONERA-M6-wing at transonic Mach numbers[A]. //Experimental Data Base for Computer Program Assessment[R]. AGARD-AR-138, 1979. |



