动力系统作为水下航行器的“心脏”一直是国内外学者研究的重点对象.近年来, 随着减阻技术和结构优化的快速发展, 高性能舰船及水下航行器的速度得到大幅提升, 同时也对水下推进装置提出了更高要求.按照推进方式的不同可将水下兵器推进系统分为叶片式与喷射式两种, 由于叶片在高转速下会产生“空化”现象, 导致螺旋桨丧失部分推力, 推进效率严重降低, 同时也会造成叶片的空蚀损伤, 70 Knot也就成为采用螺旋桨推进方式的水下兵器不可逾越的速度极限[1].
根据喷射工质的不同, 喷射推进可分为喷水推进与喷气推进两种.喷水推进的基本原理是向航行器后方喷射经泵等设备加速后的水流, 依靠产生的反作用力产生推力[2].目前, 泵喷推进发动机是国内外舰艇的主流推进装置, 其核心部件为轴流泵、混流泵或离心泵, 具有震动小、噪声较低、附体阻力小、抗空化能力强、推进效率较高等优点, 但也存在结构复杂, 体积庞大, 尚未完全解决空化、空蚀等一系列问题[3].水下喷气推进最初是指将火箭发动机技术应用于水下导弹的发射[4], 具有结构简单、紧凑轻量、较高单位体积功率等优点, 但是推进效率极低, 并且需要携带氧化剂, 从而限制了其水下航程. 20世纪90年代初, 以俄罗斯“暴风雪”号超高速鱼雷动力系统为代表的金属/水反应冲压发动机的问世极大提高了水下航行器的性能, 其利用外界海水作为氧化剂, 有效提高了发动机的比冲和能量密度, 但是依然存在效率较低的问题.
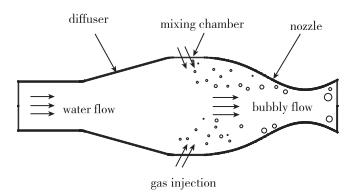
气液两相冲压发动机作为一种新型水下推进技术日益受到全世界学者的关注, 其基本原理如图 1所示:来流通过扩张段的冲压作用减速增压, 使其部分动能变为压力势能, 保证气体与水流在一定压强下混合.高压气体通过一定的分散装置(如多孔材料)形成气泡并在混合腔中与水混合形成气液两相流, 随后进入喷管不断加速.泡状流在加速过程中, 由于顺压梯度的作用气体不断膨胀并对液体做功, 将气相的压力势能转化为两相流的动能, 从而产生推力.气液两相冲压发动机结构简单、推进效率高、比冲大, 由于没有旋转部件, 不会发生空化, 不受空蚀破坏, 同时静音性能优良, 适用于水下兵器的高速巡航[5].
|
| 图 1 气液两相推进装置原理图 Fig.1 Schematic diagram of underwater two-phase propulsor |
Mottard等[6]首先提出了以压缩空气为动力源的水下冲压发动机概念, 并在拖曳水池中对一原理样机进行大量试验, 试验数据表明在所有测试工况下发动机均有正推力产生, 从而证实了气液两相冲压发动机的可行性.之后, Witte等[7]研究了发动机结构、航行速度、尾喷管长度对推进效率的影响, 并提出了一种可以自启动的发动机构型.近年来, Gany[8]研究了气液两相冲压发动机的能量循环过程, 指出该类型发动机在一定速度范围内具有较高的推进效率. Mor等[5]通过简化的一维模型得到了气液两相冲压发动机的性能曲线, 结果表明其推进效率可以达到70%~80%. Hayati等[9]利用计算流体力学的方法对气液两相冲压发动机内流场进行数值模拟研究.此外, Haustein等[10-11]提出了一种可以利用相变潜热的新型气液两相冲压发动机构想, 即将液化气(R134a)通入发动机混合腔, 由于压力突降, 液化气在水流中发生沸腾.作者认为沸腾过程中液化气的体积膨胀会对水流做功从而增大发动机推力.拖曳试验结果表明, 在所能达到最大航行速度条件下(17 m/s), 注入液化气产生的推力比注射压缩空气高约20%.
国内相关方面的研究也在迅速展开, 哈尔滨工业大学的付英杰等[12-13]、魏英杰等[14]利用双流体模型分析了航行速度、气体质量流率、发动机入口面积和气泡初始半径对气液两相冲压发动机性能的影响, 董磊等[15-16]利用数值模拟方法研究了发动机内流场随工作参数的变化情况.国防科技大学的张家瑞等[17-18]在Gany[8]研究的基础上改进了气液两相冲压发动机的热量循环模型, 指出气液两相冲压发动机的推进效率在90%以上, 这是其主要的性能优势.更进一步, 该团队首次建立了描述气液两相冲压发动机内气泡生成过程的数学模型, 根本上改进了仅根据工程经验预估气泡初始半径的发动机性能预示方法, 建立了更为完备的气液两相冲压发动机一维稳态模型[19-20].
由于实验条件的限制, 特别是观测手段的局限, 目前对气液两相冲压发动机在高速航行条件下的工作特性及可能出现的问题还没有清晰认识, 对发动机内部流动机理的研究还不够深入, 对发动机在水下高速航行时极易发生的气蚀效应还未见研究.随着计算流体力学的发展, 数值模拟已经成为研究发动机性能和内部流场结构的重要工具[15], 具有成本低廉、适用范围广阔、监测方便、能捕捉微观结构等优点.本文综合考虑湍流耗散、气液两相之间的作用力及传热、传质等因素的影响, 利用数值模拟方法对气液两相冲压发动机的内部流场结构进行分析, 重点研究高速条件下气蚀效应对气液两相冲压发动机性能的影响, 讨论不同工作参数下发动机性能的变化规律, 以期对其工作特性有更深刻的认识.
1 数值模拟方法 1.1 控制方程气液两相冲压发动机内部流动属于两相流动, 其中包含气水掺混、水的气蚀与水的蒸发与凝结等物理现象.质量守恒、动量守恒、能量守恒是支配流体运动的三大定律, 气液两相流作为一种复杂流体遵守相同的物理规律.
本文采用混合物模型作为描述气液两相冲压发动机内部流场的基本模型, 混合物模型是一种简化的多相流模型, 将每一相流体视为是连续的, 可以模拟具有不同速度的多相流动, 但是假定了在短尺度空间上的局部平衡, 通过求解混合物的质量守恒方程、动量守恒方程和能量守恒方程及离散相的体积分数方程及代数形式的相对速度方程,对多相流动进行建模.稳态条件下其主要控制方程如下:
连续方程:
| $ \nabla \cdot ({\rho _{\rm{m}}}{v_{\rm{m}}}) = 0 $ |
其中,下标m表示混合物, vm为基于质量的平均速度:
| $ {\mathit{\boldsymbol{v}}_{\rm{m}}} = \frac{{\mathop \sum \limits_{k = 1}^3 {\alpha _k}{\rho _k}{v_k}}}{{{\rho _{\rm{m}}}}} $ |
此外, ρm为混合物的平均密度:
| $ {\rho _{\rm{m}}} = \mathop \sum \limits_{k = 1}^3 {\alpha _k}{\rho _k} $ |
式中, αk表示第k相的体积分数, k=1, 2, 3分别表示液态水、空气和水蒸气.
动量方程:
| $ \begin{array}{l} \nabla \cdot ({\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}) = \nabla p + \nabla \cdot [{\mu _{\rm{m}}}(\nabla {\mathit{\boldsymbol{v}}_{\rm{m}}} + \nabla \mathit{\boldsymbol{v}}_{\rm{m}}^{\rm{T}})] + \\ {\rho _{\rm{m}}}\mathit{\boldsymbol{g}} + \mathit{\boldsymbol{F}} + \nabla \cdot (\mathop \sum \limits_{k = 1}^3 {\alpha _k}{\rho _k}{\mathit{\boldsymbol{v}}_{{\rm{dr}}, k}}{\mathit{\boldsymbol{v}}_{{\rm{dr}}, k}}) \end{array} $ |
其中, F为体积力, μm为混合物黏性系数:
| $ {\mu _{\rm{m}}} = \mathop \sum \limits_{k = 1}^3 {\alpha _k}{\mu _k} $ |
vdr, k为第k相的漂移速度:
| $ {\mathit{\boldsymbol{v}}_{{\rm{dr}}, k}} = {\mathit{\boldsymbol{v}}_k} - {\mathit{\boldsymbol{v}}_{\rm{m}}} $ |
vm为混合物平均速度.
能量方程:
| $ \nabla \cdot \mathop \sum \limits_{k = 1}^3 [{\alpha _k}{\mathit{\boldsymbol{v}}_k}({\rho _k}{E_k} + p)] = \nabla \cdot ({k_{{\rm{eff}}}}\nabla T) $ |
其中, keff为等效导热率:
| $ {k_{{\rm{eff}}}} = \mathop \sum \limits_{k = 1}^3 {\alpha _k}({k_k} + {k_t}) $ |
式中, kt为湍流导热率, 根据所选用的湍流模型决定.
本文将水流视为主相, 用下标q表示, 空气、水蒸气为次相, 用下标p表示, 次相的体积分数方程为:
| $ \nabla \cdot ({\alpha _{\rm{p}}}{\rho _{\rm{p}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}) = - \nabla \cdot ({\alpha _{\rm{p}}}{\rho _{\rm{p}}}{\mathit{\boldsymbol{v}}_{{\rm{dr, p}}}}) $ |
第k相的质量分数定义为:
| $ {c_k} = \frac{{{\alpha _k}{\rho _k}}}{{{\rho _{\rm{m}}}}} $ |
进而将漂移速度和相对速度的关系表示为:
| $ {\mathit{\boldsymbol{v}}_{{\rm{dr, p}}}} = {\mathit{\boldsymbol{v}}_{{\rm{pq}}}} - \mathop \sum \limits_{k = 1}^3 {c_k}{\mathit{\boldsymbol{v}}_{{\rm{q}}k}} $ |
相对速度的计算采用下式计算[21]:
| $ {\mathit{\boldsymbol{v}}_{{\rm{pq}}}} = \frac{{{\tau _{\rm{p}}}}}{{{f_{{\rm{drag}}}}}}\frac{{{\rho _{\rm{p}}} - {\rho _{\rm{m}}}}}{{{\rho _{\rm{p}}}}}\mathit{\boldsymbol{a}} $ |
其中, a为次相的加速度, τp为离散相的弛豫时间:
| $ {\tau _{\rm{p}}} = \frac{{{\rho _{\rm{p}}}d_{\rm{p}}^2}}{{18{\mu _{\rm{q}}}}} $ |
式中, dp为离散气泡的直径, fdrag拖曳力函数[22]
| $ {f_{{\rm{drag}}}} = \left\{ \begin{array}{l} 1 + 0.15R{e^{0.687}}\;\;\;\;Re \le 1000\\ 0.0183Re\;\;\;\;\;\;\;\;\;\;Re > 1000 \end{array} \right. $ |
本文选用混合物标准k-ε模型作为湍流模型, 即将多相流视为一连续流体, 物性参数为多相的平均值, 从而建立多相流的湍流模型, 其湍流动能方程为:
| $ \nabla \cdot ({\rho _{\rm{m}}}{v_{\rm{m}}}k) = \nabla \cdot \left( {\left( {{\mu _{\rm{m}}} + \frac{{{\mu _{t, {\rm{m}}}}}}{{{\sigma _k}}}} \right)\nabla k} \right) + {G_{k, {\rm{m}}}} - {\rho _{\rm{m}}}\varepsilon $ |
湍动能耗散率方程为:
| $ \begin{array}{l} \nabla \cdot ({\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}\varepsilon ) = \nabla \cdot \left( {\left( {{\mu _{\rm{m}}} + \frac{{{\mu _{{\rm{t, m}}}}}}{{{\sigma _k}}}} \right)\nabla \varepsilon } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\varepsilon }{k}({C_{1\varepsilon }}{G_{k, {\rm{m}}}} - {C_{2\varepsilon }}{\rho _{\rm{m}}}\varepsilon ) \end{array} $ |
其中混合物的湍流黏度按下式计算
| $ {\mu _{{\rm{t, m}}}} = {\rho _{\rm{m}}}{C_\mu }\frac{{{k^2}}}{\varepsilon } $ |
湍动能生成项按下式计算
| $ {G_{k, {\rm{m}}}} = {\mu _{t, {\rm{m}}}}(\nabla {\mathit{\boldsymbol{v}}_{\rm{m}}} + {(\nabla {\mathit{\boldsymbol{v}}_{\rm{m}}})^{\rm{T}}}) \cdot \nabla {\mathit{\boldsymbol{v}}_{\rm{m}}} $ |
在标准k-ε湍流模型中, 系数C1ε,C2ε,Cμ,σk,σε为模型常数, 根据大量的实验及模拟验证, 一般推荐取值分别为C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3.
Kim等[23]在1995年提出的非平衡流壁面函数有效解决了对存在分离流等复杂流动的近壁面区域的数值模拟问题, 该方法特别适用于处理存在剧烈压强梯度变化的复杂流动, 因此本文采用非平衡壁面函数进行计算.
1.3 气蚀模型在温度一定的情况下, 当液体的压力降至饱和蒸气压力(PV)以下, 其内部会产生蒸气或气体空泡, 该空泡产生、发展及溃灭的过程就是空化[24].空化现象广泛存在于自然界[27]及各种与流体接触的机械中, 并且对其工作性能产生显著的影响, 例如:空化会导致水下航行器表面阻力的增加、螺旋桨输出功率降低甚至失效、液体泵的水头减小等[27].此外, 空化还会导致严重的空蚀, 即对产生空化的表面造成严重的损伤, 导致螺旋桨叶片、泵的叶片寿命严重降低.
对于高速航行状态下的气液两相冲压发动机, 其表面也会产生严重的气蚀现象并对发动机性能产生一定影响, 本文采用Schnerr等[28]在2001年提出的气蚀模型对发动机进行建模, 其主要控制方程如下:
| $ \nabla \cdot ({\alpha _{\rm{v}}}{\rho _{\rm{v}}}\mathit{\boldsymbol{V}}) = {R_{\rm{e}}} - {R_{\rm{c}}} $ |
其中, 下标v表示水蒸气, Re,Rc分别表示水蒸气生成与溃灭产生的质量源项.
当Pv > P时, 水蒸气生成
| $ {R_{\rm{e}}} = \frac{{{\rho _{\rm{v}}}{\rho _{\rm{l}}}}}{{{\rho _{\rm{m}}}}}{\alpha _{\rm{v}}}(1 - {\alpha _{\rm{v}}})\frac{3}{{{R_{\rm{B}}}}}\sqrt {\frac{2}{3}\frac{{({P_{\rm{v}}} - P)}}{{{\rho _{\rm{l}}}}}} $ |
当Pv < P时, 水蒸气溃灭
| $ {R_{\rm{c}}} = \frac{{{\rho _{\rm{v}}}{\rho _{\rm{l}}}}}{{{\rho _{\rm{m}}}}}{\alpha _{\rm{v}}}(1 - {\alpha _{\rm{v}}})\frac{3}{{{R_{\rm{B}}}}}\sqrt {\frac{2}{3}\frac{{(P - {P_{\rm{v}}})}}{{{\rho _{\rm{l}}}}}} $ |
其中, RB为气泡半径.
最后, 利用单位体积内的气泡数目nb使方程封闭:
| $ {\alpha _{\rm{v}}} = \frac{{{n_{\rm{b}}}\frac{4}{3}{\rm{ \mathsf{ π} }}R_{\rm{B}}^3}}{{1 + {n_{\rm{b}}}\frac{4}{3}{\rm{ \mathsf{ π} }}R_{\rm{B}}^3}} $ |
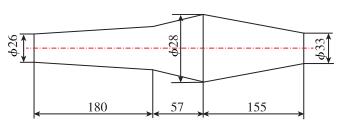
本节数值模拟研究的对象为Ovadia等[25]在以色列理工大学悬臂水池中试验的缩比发动机, 试验系统如图 2所示, 发动机结构尺寸如图 3所示.

|
| 图 2 悬臂水池试验系统 Fig.2 Photograph of a tow-pool test system |
|
| 图 3 试验发动机结构示意图(mm) Fig.3 Schematic diagram of test engine(mm) |
本文利用商业软件ICEM将拖曳水池环境及缩比发动机模型抽象并划分为二维计算域网格.通过计算气泡的Froude数(
为了检验网格划分合理性, 首先进行网格无关性验证.本小节共划分了4套不同节点数量的计算网格, 网格节点数量分别为: 214 842,506 608,852 448与1 089 608, 依次记为1,2,3,4号计算网格.现将这4套网格用于模拟Ovadia等的试验. Ovadia等在发动机模型内流道入口、混合腔出口、喷管二分之一长度处及喷管出口处安装了压力传感器, 在缩比发动机拖曳试验过程中测量了这4处压力值(分别为: 106 229 Pa, 125 430 Pa, 114 406 Pa, 101 112 Pa), 现将4套网格的计算结果与试验结果进行比对, 以验证模拟的计算精度, 求解采用Sample算法, 对于压力项离散采用的是标准差分格式, 离散则采用1阶迎风格式, 计算结果如表 1所示.
| 下载CSV 表 1 不同节点数网格的计算误差 Tab.1 Computation errors with different mesh resolution levels |
从表 1中可以看出, 当网格节点数量大于5×105时, 数值计算收敛, 计算的平均误差小于7%,在可以接受的范围之内, 并且随着网格节点数量的增大, 计算结果没有发生显著变化, 综合考虑计算准确性与经济性, 本文选用节点数量为8.5×105的网格作为数值模拟所用的计算网格.
3 结果分析 3.1 航行速度对气液两相冲压发动机性能的影响表 2所示为7个模拟工况下的数值计算结果, 在不改变其他条件的情况下, 讨论气液两相冲压发动机航行速度对其性能的影响.从表中可以看出, 随着航行速度的增加, 发动机比冲呈现先增大后减小的趋势, 说明在通入气体质量流率一定的情况下, 存在一个最优速度使得发动机性能最佳.
| 下载CSV 表 2 气液两相冲压发动机性能随航行速度的变化关系 Tab.2 Performance of underwater two-phase ramjet engine vs cruise velocity |
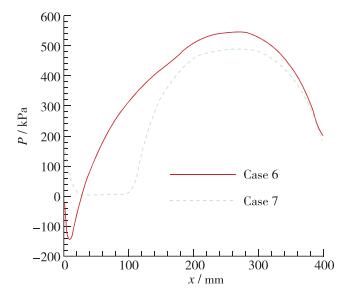
通过数值模拟可以发现, 当气液两相冲压发动机航行速度大于等于32 m/s时, 若不考虑气蚀影响, 如图 4中Case 6所示, 在发动机壁面入口附近将会出现负压, 这是不符合物理规律的, 因为在出现负压之前液态水会发生气蚀效应, 流场的压强应不小于该温度下水蒸气的饱和压力, 所以当速度较高时必须考虑气蚀的影响, 而当速度小于32 m/s时, 由于发动机内流场压力均大于水的饱和蒸气压, 无需考虑气蚀.
|
| 图 4 气蚀效应对发动机内流场压力的影响 Fig.4 Effect of cavitation on internal flow field of engine |
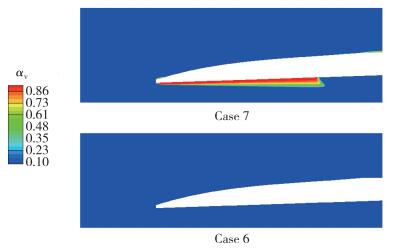
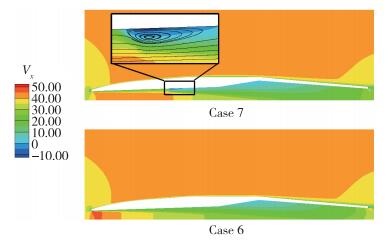
如图 5所示, 在考虑气蚀效应后, Case 7发动机入口下游附近的回流区有水蒸气产生, 该区域内的压强等于环境温度下的饱和蒸气压强.在气蚀区域内不断有气泡生成、膨胀、破裂与并聚,并造成显著的压力波动与噪声, 会对航行器表面造成严重的腐蚀.此外, 气蚀也会导致一定的总压损失, 如图 6所示, 其中, Vx为液相速度在x方向上的分量.与Case 6相比, Case 7在考虑气蚀效应后发动机内流场流体的速度总体明显降低, 并在扩张段中部发生流动分离, 导致两相流的总压严重降低.
|
| 图 5 气液两相冲压发动机入口处的气蚀现象 Fig.5 Cavitation phenomena in inlet of ramjet engine |
|
| 图 6 气蚀效应所导致的发动机内部的流动分离现象 Fig.6 Flow separation in internal flow field of ramjet engine caused by cavitation |
说明高速条件下, 气蚀对发动机性能的不利影响是十分显著的.
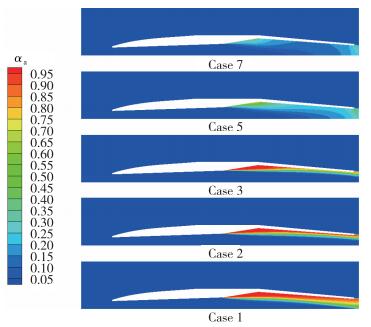
图 7为不同航行速度下发动机内气体的体积分数云图, 其中, αa表示空气的体积分数.可以发现气液两相之间存在分层现象, 低速条件下尤为显著, 说明气体并没有充分与液体混合, 这很有可能是制约气液两相冲压发动机性能的关键因素.气液两相之间产生分层的主要原因是气体的惯性远小于液体, 气体经过气泡分散装置与液体混合后难以维持原有初始速度.此外, 随着发动机航行速度的增大, 发动机内气体的体积分数逐渐降低, 说明单位体积混合物中气体的体积不断减小, 同时再结合表 2可以得到如下结论, 在气体质量流率一定的情况下, 由于航行速度的变化导致气体在发动机内部体积分布的改变,这对发动机性能有显著影响.
|
| 图 7 发动机内流场气体空隙率分布与发动机航行速度的变化关系 Fig.7 Distributions of gas volume fraction in the ramjet engine with different cruise velocities |
表 3所示为4个模拟工况下的数值计算结果, 在不改变其他条件的情况下, 讨论通入发动机的气体质量流率对其性能的影响.从表中可以看出, 在其他条件一定的情况下, 随着气体质量流率的增加, 发动机推力不断增大, 但其比冲和效率却不断降低, 这是因为随着注入高压气体质量流率的增大, 气体对发动机内部水流所做的有用功增大, 两相流在发动机出口处的速度增加, 所以推力增大.比冲及效率降低的原因可能是注入气体的质量流率偏大, 导致局部气体体积分数过高使得两相之间的能量交换效率降低.气液两相冲压发动机在航行速度为24 m/s的条件下, 最优气体质量流率应小于13.57 g/s.
| 下载CSV 表 3 气液两相冲压发动机性能随气体质量流率变化关系 Tab.3 Performance of underwater two-phase ramjet engine vs gas mass flow rate |
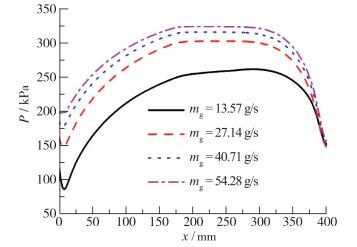
图 8为发动机内流场压力分布随气体质量流率的变化关系.可以发现随着气体质量流率的增大, 发动机内流场的压力逐渐增大.说明气体质量流率越大, 注入单位质量流率气体消耗的能量越大, 需要的气体总压也就越高, 这也是发动机效率下降的原因之一.此外, 发动机内流场压力的增大可以有效抑制气蚀现象, 所以在高速条件下通过增大气体质量流率是提高发动机推力的有效途径.
|
| 图 8 发动机内流场压力分布随气体质量流率的变化关系 Fig.8 Internal flow field pressure distributions oframjet engine |
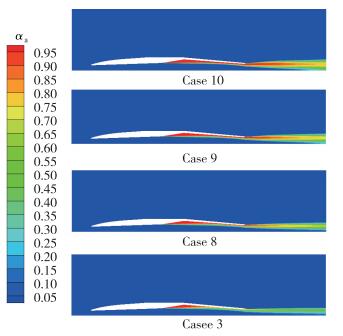
图 9为不同气体质量流率下气体体积分数在发动机内流场的分布, 从图中可以看出, 随着气体质量流率的增大, 气体传递给液体的体积功增大, 从而提高了发动机的推力, 但同时发动机内部气体所占体积也在不断增大, 气液两相之间的混合程度不断下降, 导致相界面浓度降低, 致使气液两相之间能量交换效率降低, 从而对气液两相冲压发动机的比冲及效率等经济性指标造成不利影响.
|
| 图 9 不同气体质量流率下气体体积分数在发动机内流场的分布 Fig.9 Distributions of gas volume fraction in the ramjet engine with different gas mass flow rates |
表 4所示为4个模拟工况下的数值计算结果, 在不改变其他条件的情况下, 讨论通入气体温度的变化对发动机性能的影响.需要说明的是, 为了简化计算, 本文采用等熵压缩后等压加热的方式, 所以将常温、常压的气体增温、加压所需要的能量为:
| 下载CSV 表 4 气液两相冲压发动机性能随注入气体温度的变化关系 Tab.4 Performance of underwater two-phase ramjet engine vs gas temperature |
| $ E = \frac{{\gamma R{T_0}}}{{\gamma - 1}}\left[ {1 - {{\left( {\frac{{{P_{\rm{m}}}}}{{{P_0}}}} \right)}^{\frac{{\gamma - 1}}{\gamma }}}} \right] + {C_{\rm{p}}}({T_2} - {T_0}) $ |
其中, Cp为定压比热容.那么, 发动机的效率可以表示为:
| $ \eta = \frac{{F{U_{\rm{v}}}}}{E} $ |
从表 4中可以看出, 随着气体温度的升高, 气液两相冲压发动机的推力与比冲均增大, 但是发动机效率在不断降低, 说明对注入气体进行加热可以提高发动机推力, 但是该方法的经济性较低, 导致发动机效率下降.
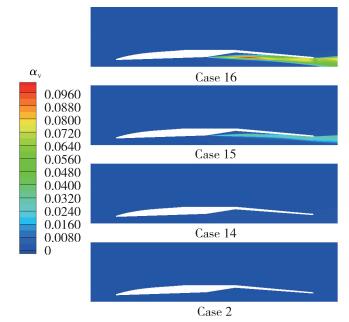
图 10为不同温度下水蒸气在发动机内流场中的分布, 通过对比可以发现, 当发动机混合腔中注入的是高温气体时, 有部分水流被加热成为水蒸气, 并进入喷管, 在顺压梯度的作用下将其内能转化为两相流的动能, 从而提高了发动机的推力.在气体质量流率一定的情况下, 注入气体的温度越高, 生成的水蒸气越多, 发动机的推力、比冲越大.但是由于水的蒸发潜热很大, 通过加热气体来提高发动机性能的方式能量利用效率较低.
|
| 图 10 不同温度下水蒸气体积分数在发动机内流场中的分布 Fig.10 Distributions of stream volume fraction in ramjet engine with different gas temperatures |
本文综合考虑湍流耗散、相间作用力及传热、传质等因素, 对气液两相冲压发动机进行了数值模拟, 分析了稳态流动条件下发动机工作参数对其内流场压力、速度、温度、气体体积分布的影响, 并着重讨论了发动机入口附近的气蚀现象, 主要结论如下:
(1) 采用壁面通气的气液两相冲压发动机内存在明显的气液分层现象, 气体不能与液体充分混合,成为限制其性能提升的重要原因.
(2) 当发动机航行速度较高时, 入口处会出现气蚀现象, 导致严重的总压损失使得扩展段中游产生流动分离, 气液两相冲压发动机的性能将会严重降低, 此外, 气蚀还可能造成严重的表面腐蚀.
(3) 发动机航行速度增大时, 发动机的比冲先增大后减小.此外, 发动机内部气相的体积分数分布情况也与航行速度有关.
(4) 随着通入发动机气体质量流率的增大, 发动机内流场的压强不断升高, 气体总压增大, 因此注入单位质量流率所需要的能量也增大, 这是发动机效率降低的原因之一.
(5) 提高注入发动机的气体的温度可以提高发动机的推力和比冲, 但是发动机效率急剧降低.
| [1] |
查志武. 鱼雷动力技术发展展望[J]. 鱼雷技术, 2005, 13(1): 1, 4-9. Zha Z W. A summary of development in torpedo power technologies[J]. Torpedo Technology, 2005, 13(1): 1-4, 9. DOI:10.3969/j.issn.1673-1948.2005.01.001 (in Chinese) |
| [2] |
李晓晖, 朱玉泉, 聂松林. 喷水推进器的发展研究综述[J]. 液压与气动, 2007(7): 1-4. Li X H, Zhu Y Q, Nie S L. The overview of development and research for waterjet propulsion[J]. Chinese Hydraulics & Pneumatics, 2007(7): 1-4. DOI:10.3969/j.issn.1000-4858.2007.07.001 (in Chinese) |
| [3] |
刘柱, 孟凡立. 船舶喷水推进技术发展[J]. 航海技术, 2004(4): 42-44. Liu Z, Meng F L. The development on technology of water jet propulsion for ship[J]. Marine Technology, 2004(4): 42-44. DOI:10.3969/j.issn.1006-1738.2004.04.025 (in Chinese) |
| [4] |
孙明芳. 水下火箭的推进原理和应用[J]. 舰载武器, 1995(4): 19-25. |
| [5] |
Mor M, Gany A. Performance mapping of bubbly water ramjet[J]. International Journal of Maritime Engineering, 2007, 149(1): 45-50. |
| [6] |
Mottard E J, Shoemaker C J. Preliminary investigation of an underwater ramjet powered by compressed air[R]. NASA TN D-991, 1961: 1-40.
|
| [7] |
Witte J. Predicted performance of large water ramjets[C]. Proceedings of the 2nd Advanced Marine Vehicles and Propulsion Meeting, Washington, US: AIAA, 1969: 69-406.
|
| [8] |
Gany A. Analysis of a new thermodynamic power cycle for a two-phase waterjet[C]. Proceedings of Waterjet Propulsion 4, London, UK: The Royal Institute of Naval Architects, 2004: 1-6.
|
| [9] |
Hayati A N, Hashemi S M, Shams M. Design and analysis of bubble-injected water ramjets with discrete injection configurations by computational fluid dynamics method[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2012, 227(9): 1945-1955. |
| [10] |
Haustein H D. Investigation of bubbly flow creation through phase change, for application in marine engine[D]. Israel: Technion-Israel Institute of Technology, 2009.
|
| [11] |
Haustein H D, Gany A, Elias E. Study of a two-phase underwater ramjet propulsor employing liquified gas boiling[C]. Proceedings of Second International Symposium on Marine Propulsors, Hamburg, Germany: SMP, 2011.
|
| [12] |
付英杰, 魏英杰, 张嘉钟, 等. 水下两相冲压喷射发动机性能的数值模拟研究[J]. 哈尔滨工业大学学报, 2010, 42(3): 343-347. Fu Y J, Wei Y J, Zhang J Z, et al. Numerical study on performance of bubbly water ramjet engine[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 343-347. (in Chinese) |
| [13] |
Fu Y J, Wei Y J, Zhang J Z. Parametric study on the thrust of bubbly water ramjet with a converging-diverging nozzle[J]. Journal of Hydrodynamics, Ser. B, 2009, 21(5): 591-599. DOI:10.1016/S1001-6058(08)60189-4 |
| [14] |
魏英杰, 付英杰, 张嘉钟. 结构参数对两相冲压发动机喷管性能影响分析[J]. 推进技术, 2009, 30(5): 544-550. Wei Y J, Fu Y J, Zhang J Z. Effect of structure parameter on nozzle performance of bubbly water ramjet engine[J]. Journal of Propulsion Technology, 2009, 30(5): 544-550. DOI:10.3321/j.issn:1001-4055.2009.05.007 (in Chinese) |
| [15] |
董磊.水下两相冲压式发动机工作机理的数值模拟研究[D].哈尔滨: 哈尔滨工业大学, 2010. Dong L. Numerical simulation of underwater two-phase ramjet working mechanism[D]. Harbin: Harbin Institute of Technology, 2010(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D269403 |
| [16] |
董磊, 张嘉钟, 魏英杰, 等. 通气参数对水下两相冲压式发动机内推力影响的数值模拟研究[J]. 振动与冲击, 2009, 28(6): 175-178. Dong L, Zhang J Z, Wei Y J, et al. Effect of aeration parameter on inner thrust of underwater two-phases ramjet[J]. Journal of Vibration and Shock, 2009, 28(6): 175-178. DOI:10.3969/j.issn.1000-3835.2009.06.042 (in Chinese) |
| [17] |
张家瑞, 夏智勋, 黄利亚.气液两相冲压发动机理论性能分析[C].中国航天第三专业信息网第三十八届技术交流会暨第二届空天动力联合会议论文集. 2017: 1544-1553.
|
| [18] |
Zhang J R, Xia Z X, Huang L Y, et al. Power cycle analysis of two-phase underwater ramjet[J]. Applied Ocean Research, 2018, 71: 69-76. DOI:10.1016/j.apor.2017.12.006 |
| [19] |
张家瑞, 夏智勋, 黄利亚.气液两相冲压发动机工作特性数值模拟研究[C].第六届冲压发动机技术交流会论文集.海南, 文昌, 2017: 248-258.
|
| [20] |
Zhang J R, Xia Z X, Huang L Y, et al. Experimental and numerical parametric studies on two-phase underwater ramjet[J]. Journal of Propulsion and Power, 2018, 34(1): 161-169. DOI:10.2514/1.B36533 |
| [21] |
Manninen M, Taivassalo V, Kallio S. On the mixture model for multiphase flow[R]. VTT Publication No. 228, 1996.
|
| [22] |
Schiller L, Naumann Z. A drag coefficient correlation[J]. Zeitschrift des Vereins Deutscher Ingenieure, 1935, 77: 318-320. |
| [23] |
Kim S E, Choudhury D. A near-wall treatment using wall functions sensitized to pressure gradient[C]. Proceedings of Separated and Complex Flows, American: ASME, 1995, 217.
|
| [24] |
Brennen C. Cavitation and bubble dynamics[M]. New York: Oxford University Press, 1995: 47-107.
|
| [25] |
Ovadia O, Strauss J. The nautical ramjet-an alternative approach[EB/OL]. 2005-09-18/2016-09-05.
|
| [26] |
Versluis M, Schmitz B, Von Der Heydt A, et al. How snapping shrimp snap:through cavitating bubbles[J]. Science, 2000, 289(5487): 2114-2117. DOI:10.1126/science.289.5487.2114 |
| [27] |
Arndt R E. Cavitation in fluid machinery and hydraulic structures[J]. Annual Review of Fluid Mechanics, 1981, 13(1): 273-328. DOI:10.1146/annurev.fl.13.010181.001421 |
| [28] |
Schnerr G H, Sauer J. Physical and numerical modeling of unsteady cavitation dynamics[C]. Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, US: ICMF, 2001.
|



