动导数是指飞行器的气动力系数和气动力矩系数对飞行器无因次旋转角速度或姿态角变化率的导数.动导数与飞行器的运动状态密切相关, 尤其对有升力面的高超声速载人飞行器及再入弹头落地过程, 是飞行器设计最重要的参数之一.在模型动导数测量方面, 有自由震荡技术、自由滚转技术、自由翻转技术、强迫振动技术及模型自由飞试验等测量技术.除模型自由飞技术外, 其他几种技术中, 模型都依赖于支撑系统, 尾支杆对绕流有直接干扰, 而有支撑系统存在时风洞堵塞度增加, 对风洞流场产生干扰[1].对支杆干扰影响的系统研究表明:支杆影响在跨声速时最为严重, 其次是高超声速; 同时, 支杆对动态测量的影响较静态测量更为严重[2].正因为如此, 模型自由飞技术在飞行器模型动稳定性测量中具有独特的优势, 得到了越来越广泛的应用.风洞模型自由飞试验技术是指以某种方式把试验模型投放到风洞的均匀流场中, 让其自由飞行, 同时利用高速相机清晰地记录模型的运动历程, 根据模型运动特征参数反演模型的气动特性[3].该试验技术也可用于模型的级间分离、抛壳及多体分离等复杂运动的研究.
本文在JF-8A高超声速脉冲风洞中开展了10°尖锥模型自由飞试验, 并以圆球模型的自由飞运动测量风洞动压, 对模型运动特征参数的数字图像提取技术及气动参数的辨识方法等关键技术进行了研究.
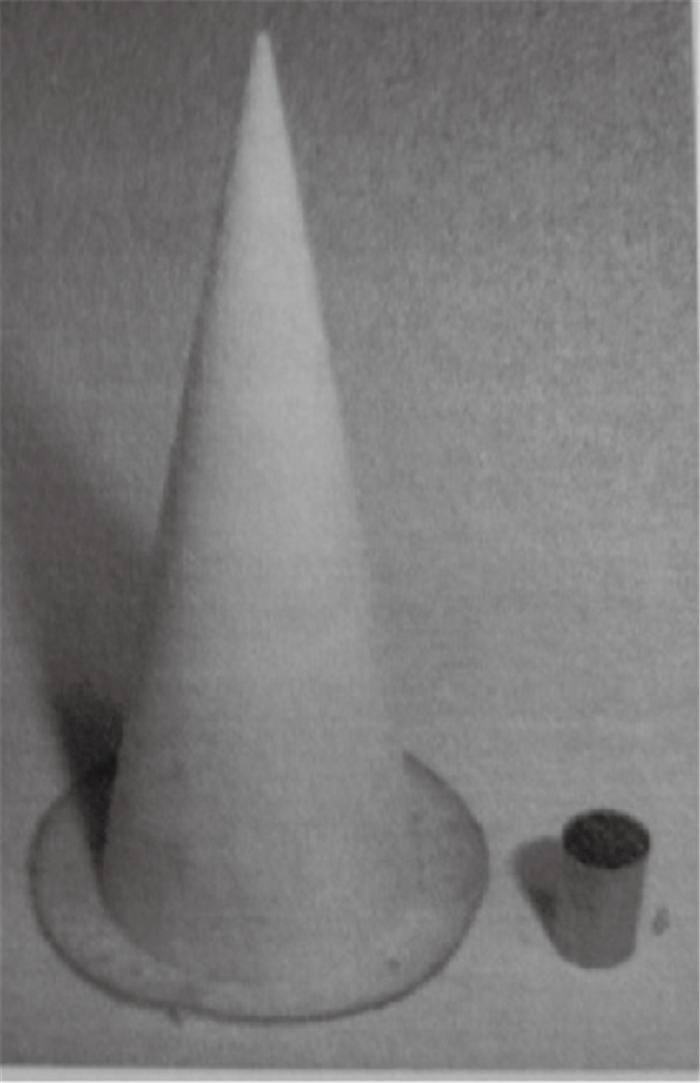
1 试验装置试验是在中国科学院力学研究所JF-8A高超声速脉冲风洞中进行的.风洞驱动段内径为150mm, 长度为9.67m;被驱动段内径为155mm, 长度17.1m;型面喷管出口直径为800mm; 试验段直径为2m.试验采用激波风洞运行方式, 流场参数如表 1所示.试验采用高超声速动态试验标准尖锥模型, 其几何形状为底部直径20mm, 半锥角10°的尖锥.模型由硬质聚氨酯泡沫塑料轻质外壳和高密度钨铈合金配重构成, 重心位置通过配重块调节, 控制在Xcg/L=0.6处.圆球模型为直径12mm的钢球. 图 1为尖锥模型照片, 左侧为外壳,右侧为配重块.
| 下载CSV 表 1 试验流场状态 Tab.1 Flow conditions |
|
| 图 1 试验模型 Fig.1 Test model |
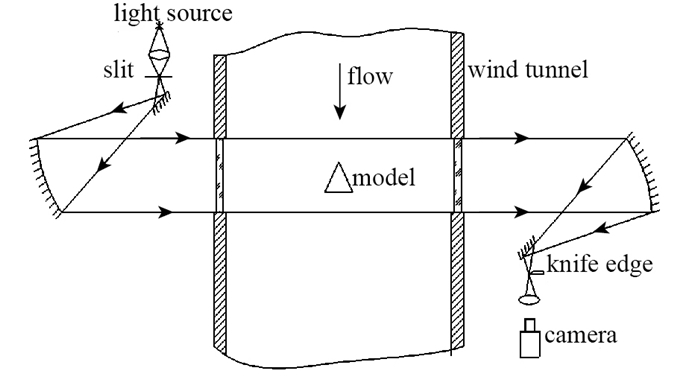
试验采用图 2所示的纹影光路记录模型的飞行历程, 高速相机通过同步控制系统实现与流场的同步.采用纹影光路可以同时记录模型头部激波结构, 用于判断试验流场结构及有效试验时间.
|
| 图 2 试验光路设置 Fig.2 Setup of optical path |
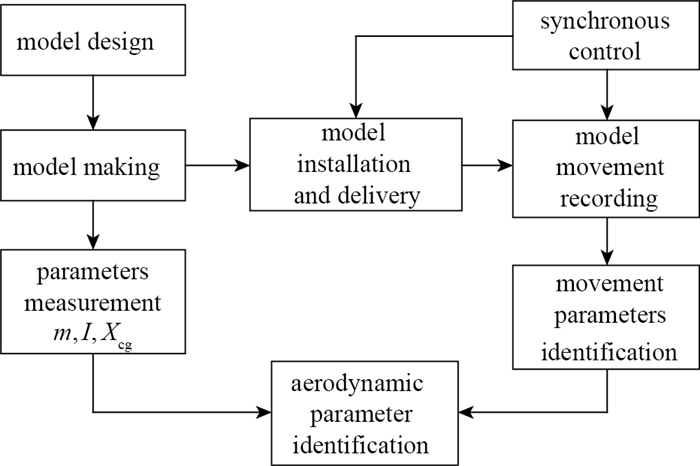
风洞模型自由飞试验流程如图 3所示, 其关键技术包括模型技术、模型投放及运动参数记录技术、运动特征参数提取技术及气动参数辨识技术等.模型设计时首先要估算模型运动状态, 列出近似的运动方程, 推算出模型质量特征参数与模型运动之间的关系式, 再根据关系式计算模型的总重量、合适的重心位置及转动惯量等, 从而确定模型结构、尺寸及材料, 模型设计可参考文献[4].本文重点讨论模型运动特征参数提取和气动参数辨识方法.
|
| 图 3 风洞模型自由飞试验流程图 Fig.3 Flow chart of free flight test in wind tunnel |
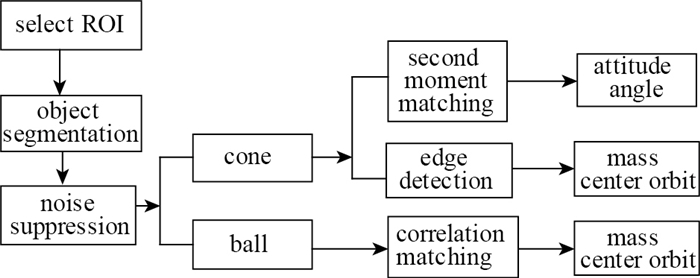
对于尖锥模型, 运动特征参数包括模型质心点的运动轨迹及姿态角;对圆球模型,运动特征参数为质心运动轨迹. 图 4为实验中获取的典型照片.本文利用Matlab数字图像处理工具箱开发了专用的图像处理算法,提取了特征参数.算法设计框图如图 5所示:首先进行目标分割、噪声抑制处理; 对于尖锥模型可选用2阶矩匹配算法得到模型的姿态角, 再利用边缘检测算法获取模型顶点位置, 结合模型姿态角和几何特征关系推算出质心位置.对于圆球模型, 先生成模型模板, 再利用相关检测算法在图像中搜寻圆球模型质心位置[5].

|
| 图 4 试验典型照片 Fig.4 Photo of typical experiment |
|
| 图 5 算法设计框图 Fig.5 Algorithm design block diagram |
目标分割是为了将试验模型与背景进行分离.对于目标物体为比较简单的灰度图像, 灰度值可以当作提取目标的判据.阈值处理在目标提取中占有重要的地位.其原理为:在任何图像f中,满足f(x, y)≥Tth的点(x, y)称为对象点, 其他点称为背景点.换言之, 阈值处理后的图像g(x, y)定义为
| $ g\left( {x, y} \right) = \left\{ \begin{array}{l} 1, f\left( {x, y} \right) \ge {T_{{\rm{th}}}}\\ 0, f\left( {x, y} \right) < {T_{{\rm{th}}}}. \end{array} \right. $ |
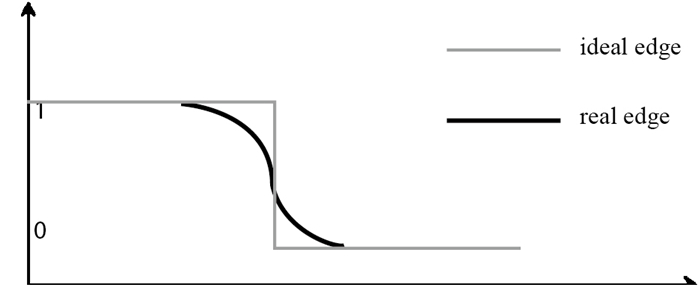
标注为1的像素对应于目标, 而标注为0的像素则对应于背景, Tth为分割阈值.在实际试验中获得的图像不可避免地存在模型边缘模糊的现象, 在边缘附近, 图像灰度值的变化与理想情况差别较大, 如图 6所示.这为准确确定边缘的位置带来困难.为保证提取精度,选用Otsu最大化类间方差方法来确定阈值.
|
| 图 6 图像边缘灰度分布 Fig.6 Gray-level distributions along image edges |
对图像f(x, y)进行归一化处理:
| $ {P_q}\left( {{r_q}} \right) = \frac{{{n_q}}}{n}, q = 0, 1, 2, \cdot \cdot \cdot, L - 1. $ |
其中, Pq(rq)表示灰度级rq出现的频数,n为图像中的像素总数, nq为灰度级为rq的像素数目, L为图像中所有可能的灰度级数.假设选定一个阈值Tth, C0是一组灰度级为[0, 1, …, Tth-1]的像素, C1是一组灰度级为[Tth, Tth+1, …, L-1]的像素.类间方差为
| $ \sigma _{\rm{B}}^2 = {w_0}{\left( {{u_0} - {u_T}} \right)^2} + {w_1}{\left( {{u_1} - {u_T}} \right)^2}. $ | (1) |
式(1) 中,
| $ \begin{array}{l} {w_0} = \sum\limits_{q = 0}^{T - 1} {{P_q}} \left( {{r_q}} \right), {u_0} = \sum\limits_{q = 0}^{T - 1} {q{P_q}} \left( {{r_q}} \right)/{w_0}, {w_1} = \sum\limits_{q = T}^{L - 1} {{P_q}} \left( {{r_q}} \right), \\ {u_1} = \sum\limits_{q = T}^{L - 1} q {P_q}\left( {{r_q}} \right)/{w_1}, {u_T} = \sum\limits_{q = 0}^{L - 1} {q{P_q}} \left( {{r_q}} \right). \end{array} $ |
迭代计算找到具有最大类间方差的阈值Tth, 并依此阈值来分割目标.
2.1.2 边缘检测边缘信息主要表现为图像局部特征的不连续性, 是图像中灰度变化比较剧烈的地方.通常将边缘划分为阶跃状和屋顶状两种类型, 阶跃边缘中边缘两侧的灰度值有明显的变化, 而屋顶状边缘中边缘位于灰度增加与减少的交界处.因此确定边缘的基本思想是使用如下两个基本准则之一在图像中找到灰度快速变化的地方:
(1) 找到灰度的1阶导数在幅值上比指定阈值大的地方;
(2) 找到灰度的2阶导数有零交叉的地方.
利用此原理开发的数字图像边缘检测算法有Soble, Prewitt, Roberts和Canny算子, 其中Canny算子是最有效的边缘检测方法.该算子处理过程如下:
(1) 图像使用带有指定标准差的Gauss滤波函数来平滑, 从而可以减少噪声.
(2) 在每一点处计算局部梯度和边缘方向.边缘点定义为梯度方向上强度最大的点.
(3) 步骤(2) 中确定的边缘点会导致梯度幅度图像中出现脊.然后, 算法追踪所有脊的顶部, 并将所有不在脊的顶部像素设定为0.脊像素使用两个阈值T1和T2作阈值处理, 其中T1小于T2.值大于T2的脊像素称为强边缘像素, T1和T2之间的脊像素称为弱边缘像素.
(4) 最后, 算法通过将8连接的弱像素集成到强像素, 执行边缘连接.
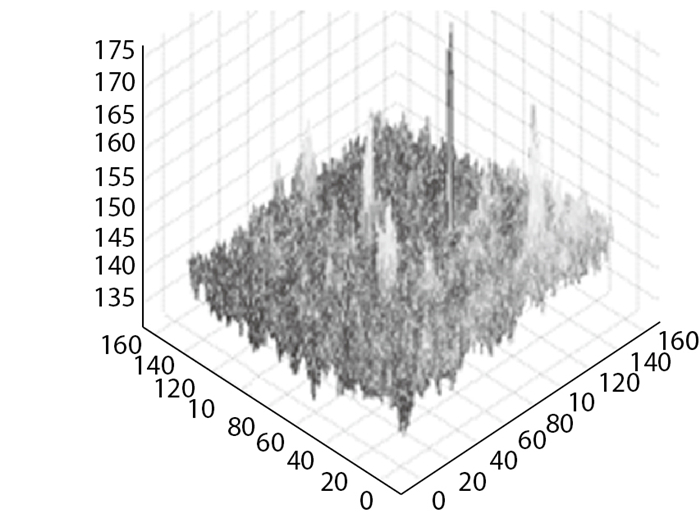
2.1.3 噪声抑制记录模型自由飞运动轨迹的图像过程中, 图像灰度分布不均匀, 含有大量的噪声. 图 7为模型上方空白图像中噪声分布情况.噪声在图像中体现为灰度值快速变化的区域, 这和模型边缘具有相似的性质.若不对噪声进行处理, 将增加边缘检测环节的难度, 影响处理结果的精度.
|
| 图 7 噪声分布情况 Fig.7 Noise distributions |
形态学滤波为非线性滤波器, 充分利用形态学开运算所具有的几何特征和良好的代数性质, 从几何形态观点进行处理, 在滤波的同时保持图像结构不被钝化.形态学滤波是对图像进行形态学腐蚀和膨胀处理的结果.
形态学中腐蚀的数学定义为
| $ A \odot B = \left\{ {z\;\left| {\;{{\left( B \right)}_z}} \right.} \right.\; \cap \;{A^{\rm{c}}}\; = \left. \phi \right\}. $ |
A、B为集合, Ac表示集合A的补集,
膨胀的数学定义为
| $ A \oplus B = \left\{ {z\;\left| {\;{{\left( {\bar B} \right)}_z}} \right.} \right.\; \cap \;{A^{\rm{c}}}\; \ne \left. \phi \right\}. $ |
A被B膨胀是所有结构元素原点位置组成的集合, 其中映射并平移后的B至少与A的某些部分重叠.形态学开运算是A被B腐蚀后再用B来膨胀的结果:
| $ A^\circ B = \left( {A \odot B} \right) \oplus B. $ |
形态学开运算完全删除了不能包含结构元素的对象区域, 平滑了对象的轮廓, 断开了狭窄的连接, 去掉了细小的突出部分.利用上述形态学开运算的性质对流场进行滤噪处理, 如图 8所示, 左图为直接进行边缘检测的结果, 模型边缘信息淹没在大量的噪声中, 并且模型边缘不连续; 右图为先进行噪声抑制再边缘检测的结果.对比结果表明:形态学滤波方法能够很好地滤除流场图像中的噪声, 滤波后边缘检测得到的模型边缘清晰、连续, 保证了边缘检测的精度.

|
| 图 8 噪声抑制前后边缘检测结果 Fig.8 Edge detection results before and after noise suppression |
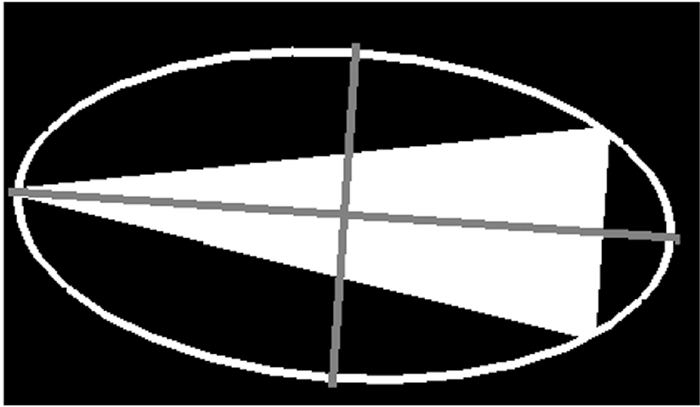
由于锥模型特殊的几何外形, 可以利用2阶矩算法确定姿态角.定义与模型区域具有相同标准2阶中心矩的最小椭圆的长轴方向为锥模型姿态角, 几何关系如图 9所示.计算时不断改变椭圆长短轴的大小及方向, 当与尖锥模型区域具有相同标准2阶中心矩时椭圆长轴的方向即为姿态角.该算法充分利用模型图像中所有像素信息, 不受模型边缘模糊效应的影响, 姿态角辨识精度更高.
|
| 图 9 尖锥模型与具有相同标准2阶矩椭圆的几何关系 Fig.9 Geometric relationships between cone model and ellipse with the same standard two order moment |
图 10为圆球经目标分割及边缘检测算法处理后的结果, 可看出圆球头部弓形激波对模型边缘形状影响严重.若直接利用边缘检测的结果进行拟合, 所得质心坐标误差较大.在此改用相关匹配算法进行圆球质心位置的辨识, 其原理如下:

|
| 图 10 图像处理结果 Fig.10 Image processing results |
给定一幅图像f(x, y), 相关匹配就是在该图像中寻找与事先给定的子图像w(x, y)(也称模板)相匹配的位置.典型情况下, 子图像比匹配图像小得多, 匹配过程为:将w(x, y)作为一个空间滤波器在f(x, y)搜寻区域中的每个位置做相关运算, 相关系数最大值出现的位置即为w(x, y)在f(x, y)中的最佳匹配点.为了减小运算量, 相关匹配过程时可利用相关定理, 将空间相关用图像f(x, y)的Fourier变换与子图像w(x, y)的Fourier变换的复共轭乘积的逆变换得到.用“°”表示相关, 用“*”表示复共轭, 相关定理表述为
| $ f\left( {x, y} \right) \circ w\left( {x, y} \right) \Leftrightarrow F\left( {u, v} \right){H^*}\left( {u, v} \right). $ |
模板利用matlab生成, 圆球尺寸与其实际尺寸相同, 整个模板大小为100×100像素, 如图 11所示.算法中设定的搜寻区域为150×150像素, 计算得到相关函数分布如图 12.

|
| 图 11 模板 Fig.11 Template |

|
| 图 12 相关系数分布 Fig.12 Correlation coefficient distributions |
风洞模型自由飞气动参数的辨识主要有三周期法[6-8](Tricyclic拟合)、Chapman-Kirk[9-11]算法(CK算法)和最大似然法[12, 13].三周期法是以方程解的形式进行拟合, 该方法适用于攻角变化幅度较小的情况, 处理大攻角时拟合精度较低. CK算法则是直接从表征运动的微分方程入手, 并不要求有封闭形式的解.最大似然法以最大似然估计值为判据, 修正的Newton -Raphson算法作为迭代算法的一种辨识算法. CK算法和最大似然法两种算法辨识精度基本一致, 均能满足工程需要, 但最大似然算法可能会在某个极值解停止运算而非最优解, 因此初值的选取会影响最终的结果.本文最终选用CK算法进行气动参数的辨识, 对算法做一般讨论如下:
| $ \ddot \alpha + {C_1}\dot \alpha + {C_2}\alpha = {C_5}. $ | (2) |
其中, C1,C2,C5为待辨识参数, 设C3和C4为0时刻变量α及其导数的初值.引入参数微分变量:
| $ {P_j} = \frac{{\partial \alpha }}{{\partial {C_j}}}, {P'_j} = \frac{{\partial {P_j}}}{{\partial t}} = \frac{{\partial \dot \alpha }}{{\partial {C_j}}}, {P''_j} = \frac{{{\partial ^2}{P_j}}}{{\partial {t^2}}} = \frac{{\partial \ddot \alpha }}{{\partial {C_j}}}. $ |
其中,j=1,2,3,4,5, 对连续函数:
| $ \frac{\partial }{{\partial {C_j}}}\left( {\frac{{\partial \alpha }}{{\partial t}}} \right) = \frac{\partial }{{\partial t}}\left( {\frac{{\partial \alpha }}{{\partial {C_j}}}} \right). $ |
式(2) 对C1微分有:
| $ {{P''}_1} + {C_1}{{P'}_1} + {C_2}{P_1} = - \dot \alpha . $ |
同理对C2~C5微分可得到微分方程组:
| $ \left\{ \begin{array}{l} {{P''}_1} + {C_1}{{P'}_1} + {C_2}{P_1} = - \dot \alpha \\ {{P''}_2} + {C_1}{{P'}_2} + {C_2}{P_2} = - \alpha \\ {{P''}_3} + {C_1}{{P'}_3} + {C_2}{P_3} = 0\\ {{P''}_4} + {C_1}{{P'}_4} + {C_2}{P_4} = 0\\ {{P''}_5} + {C_1}{{P'}_5} + {C_2}{P_5} = 1 \end{array} \right.. $ | (3) |
方程组(3) 为变系数的微分方程组, 在设定C1~C5初值后可求得数值解αi(i=1, 2, 3, …, n), 将其带入式(3) 即可得到微分参量的数值解(Pj)i(j=1~5, i=1~n).然后通过正则方程:
| $ \Delta \mathit{\boldsymbol{C}} = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}}. $ |
其中,
| $ \begin{array}{l} {A_{jk}} = \sum\limits_{i = 1}^n {\left( {\frac{{\partial \alpha }}{{\partial {C_i}}}} \right)i\left( {\frac{{\partial \alpha }}{{\partial {C_k}}}} \right)} i, \\ {B_j} = \sum\limits_{i = 1}^n {\left( {{\alpha _{\exp }} - {\alpha _{{\rm{cal}}}}} \right)i\left( {\frac{{\partial \alpha }}{{\partial {C_i}}}} \right)} i. \end{array} $ |
式中,αexp为试验测量值, αcal为按拟合所得气动参数计算给出的理论值.通过正则方程求得各系数的修正量, 重复求解整个过程直至达到精度要求.这时所得的各系数即为辨识结果. 表 2为CK算法辨识性能的验证.
| 下载CSV 表 2 算法验证 Tab.2 Algorithm verification |
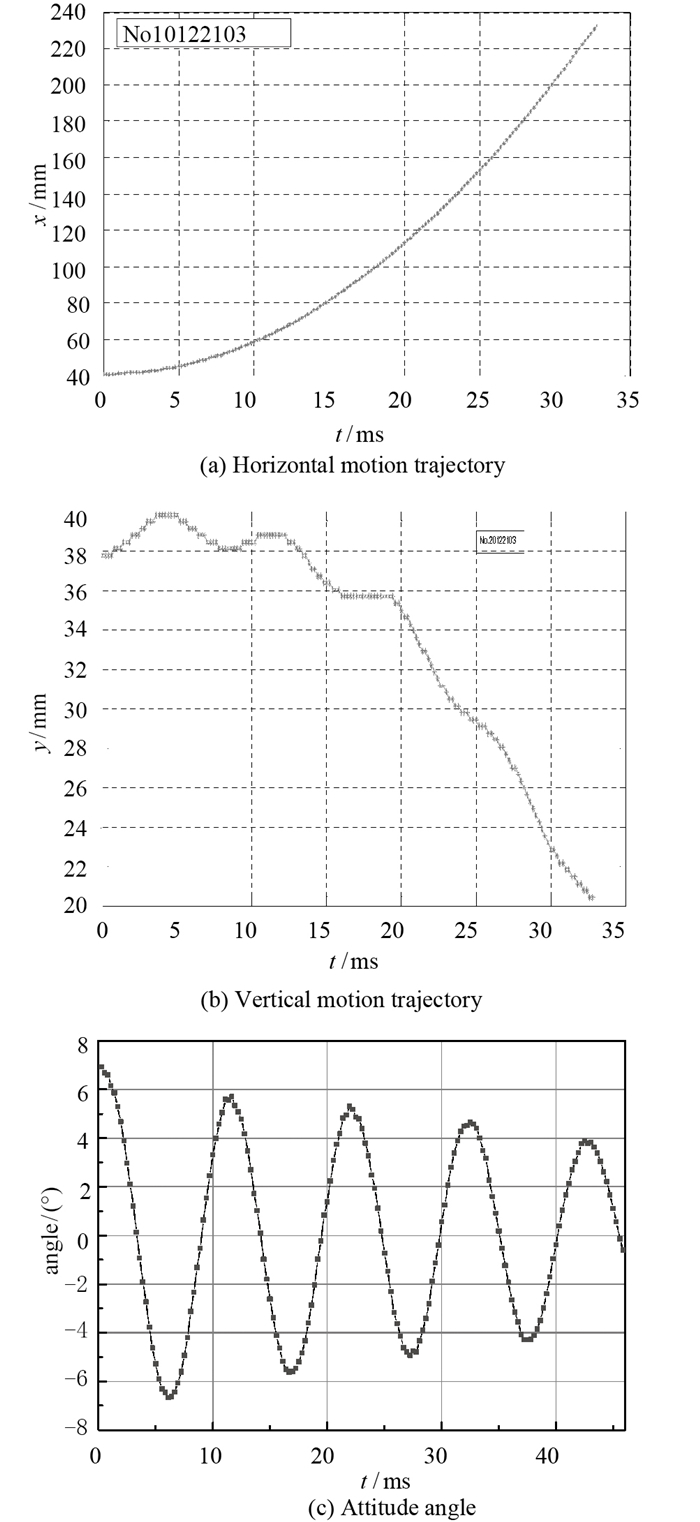
图 13为风洞模型自由飞试验获得的模型运动历程图像序列, 模型为圆球和10°尖锥模型.由于采用了纹影光路, 模型头部激波结构清晰可见.利用上述的数字图像特征提取技术对试验获得的图像序列进行处理, 结果如图 14所示.

|
| 图 13 模型运动历程 Fig.13 Motion process of models |
|
| 图 14 尖锥模型运动参数 Fig.14 Motion parameters of the cone model |
对于辨识模型的动导数, 只需要考虑模型的角运动.在速度坐标系下, 模型在俯仰平面的角运动方程可表示为
| $ I\ddot \alpha = {C_{{\text{m}}0}}qsd + {C_{{\text{m}}\alpha }}\alpha qsd + \left( {{C_{{\text{mq}}}} + {C_{{\text{m}}\dot \alpha }}} \right)\dot \alpha \frac{{qs{d^2}}}{{{V_\infty }}}. $ |
式中,Cm0为引起偏离对称位置的当量力矩系数;
利用CK算法对模型角运动方程进行参数辨识即可获得相应的气动参数. 表 3为尖锥模型3次试验的辨识结果. 3次试验尖锥模型动导数(俯仰阻尼力矩系数)都为负值, 表明模型为动稳定模型.由图 14(c)中可看出模型姿态角随时间变化震荡幅值逐渐减小, 亦表明模型为动稳定的.
| 下载CSV 表 3 气动参数辨识结果 Tab.3 Results of parameters identification |
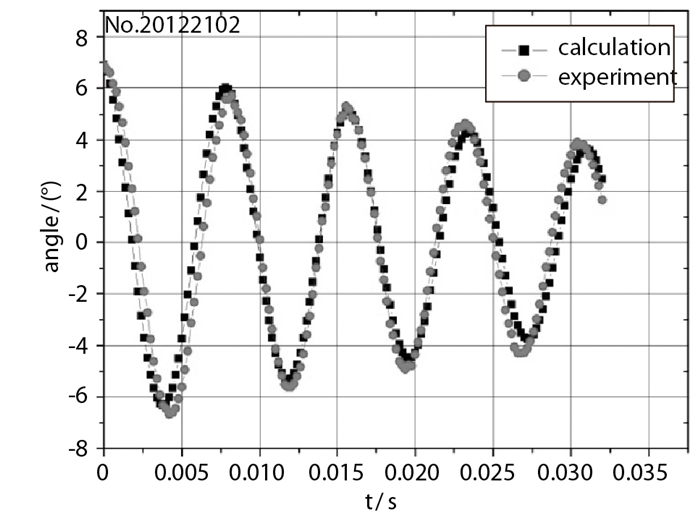
利用各参数的辨识结果代入模型的角运动控制方程即可得到模型姿态角随时间变化的理论值, 图 15为理论计算值和试验测量值的对比, 可看出两曲线震荡周期及幅值基本吻合, 证明了本文介绍的处理方法切实可靠.
|
| 图 15 尖锥姿态角变化历程 Fig.15 Time histories of the cone attitude angle |
圆球模型在流场中的运动直接与流场动压相关, 因此可以利用圆球模型的运动轨迹确定流场动压.圆球模型的自由飞运动控制方程为
| $ m\frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} = {C_{\rm{D}}} \times q \times S. $ |
其中,m为圆球质量, x为圆球水平运动距离, t为时间, CD为圆球模型阻力系数, 其值根据大量试验测定结果表明在连续流范围内几乎为一常值, 按照文献[14]可采用下列公式计算:
| $ {C_{\rm{D}}} = 0.9 + \frac{1}{2}\frac{{{M_\infty }}}{{\sqrt {R{e_{\rm{D}}}} }}. $ |
q为圆球所受动压, 而并非来流动压q∞, q应为
| $ q = \frac{1}{2}{\rho _\infty }{\left( {{V_\infty } - {V_{\rm{s}}}} \right)^2}. $ |
其中,ρ∞为流场来流密度, V∞为流场来流速度, Vs为圆球运动速度.在本文试验条件下, 圆球模型做加速运动, 试验时间结束时最大速度约为16m/s, 远远小于流场来流速度, 因此可用q来近似代表q∞.
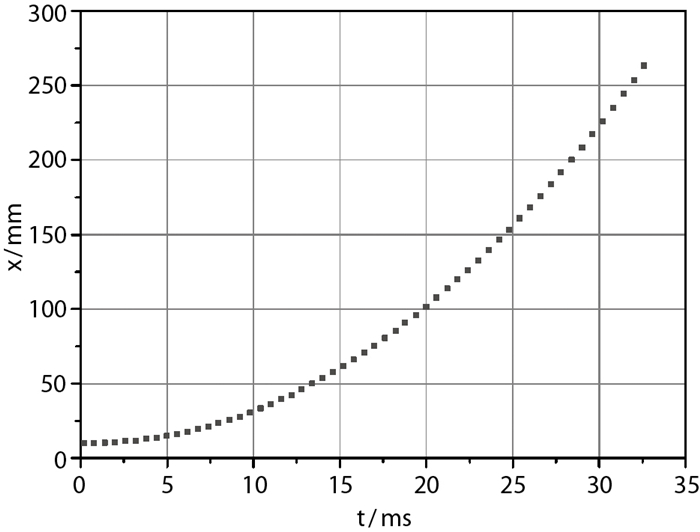
图 16为试验获得的圆球模型水平运动轨迹, 对运动轨迹进行了2次曲线拟合并求2阶导数即可获得圆球模型加速度随时间的变化关系, 结合运动控制方程即可获得来流动压. 表 4为流场动压的标定结果.
|
| 图 16 圆球水平运动轨迹 Fig.16 Horizontal motion trajectory of the ball |
| 下载CSV 表 4 流场动压标定结果 Tab.4 Results of dynamic pressure measurement |
本文在JF-8A高超声速脉冲风洞中开展了10°尖锥模型自由飞试验, 并以圆球模型的自由飞运动测量风洞动压, 对模型运动特征参数的数字图像提取技术及气动参数辨识方法等关键技术进行了研究.试验结果表明: (1) 试验所采用的10°尖锥模型为动稳定模型; (2) 开发完成的运动特征参数提取算法和气动参数辨识算法完全满足高超声速脉冲风洞模型自由飞试验的需求, 最终获取的气动参数与理论计算结果一致, 具有较高的精度.
| [1] |
李桂春. 风洞试验光学测量方法[M]. 北京: 国防工业出版社, 2008: 355-357. Li G C. Optical measurement method for wind tunnel test[M]. Beijing: National Defense Industry Press, 2008: 355-357. (in Chinese) |
| [2] |
Ericsson L E, Reding J R. Review of support interference in dynamic tests[J]. AIAA Joural, 1983, 21(12): 1652-1666. DOI:10.2514/3.60166 |
| [3] |
马家驩, 唐宗衡, 张小平. 在高超声速脉冲型风洞中测量静、动稳定性导数的模型自由飞方法[J]. 空气动力学学报, 1983(4): 77-85. Ma J h, Tang Z H, Zhang X P. Free flight method in hypersonic impulse type tunnels for static and dynamic stability study[J]. Acta Aerodynamica Sinica, 1983(4): 77-85. (in Chinese) |
| [4] |
孙英英, 潘文欣, 谷笳华, 等. 脉冲风洞自由飞动态标模设计与制作[A]. //高温气体动力学国家重点实验室夏季研讨会论文集[C]. 内蒙古, 2011: 66-69. Sun Y Y, Pan W X, Gu J H, et al. Design and manufacture of a calibration model for free flight dynamic stability study in impulse type wind tunnel [A].// Summer Symposium Proceedings of State Key Laboratory of High-temperature Gas Dynamics [C]. Inner Mongolia, 2011: 66-69(in Chinese). |
| [5] |
Gonzales R C, Woods R E, Eddins S L. 数字图像处理技术(Matlab版) [M]. 阮秋琦, 等, 译. 北京: 电子工业出版社, 2005: 255-262. Gonzales R C, Woods R E, Eddins S L. Digital image processing using matlab [M]. Translated by Ruan Q Q, et al. Beijing: Publishing House of Electronics Industry, 2005: 255-262(in Chinese). |
| [6] |
Prislin R H, Holway H P. A wind tunnel free flight testing technique for nonplanar motion of spinning models[R]. AIAA 1966-774, 1966.
|
| [7] |
Jaffe P. Nonplanar tests using the wind-tunnel free-flight technique[J]. Journal of Spacecraft and Rockets, 1973, 10(7): 435-442. DOI:10.2514/3.61905 |
| [8] |
许可法, 王凌志, 李明娟, 等. 旋转导弹风洞六自由度自由飞动导数实验研究[J]. 空气动力学学报, 1993, 11(3): 257-263. Xu K F, Wang L Z, Li M J, et al. Experimental investigation of a spinning missile model for dynamic stability coefficients in[J]. Acta Aerodynamica Sinica, 1993, 11(3): 257-263. (in Chinese) |
| [9] |
Lewis H, East R. Measurement of free-flight dynamic stability derivatives of cones in a hypersonic gun tunnel [A]. //AIAA 6th International Aerospace Planes and Hypersonics Technologies Conference[C]. Chattanooga, 1995.
|
| [10] |
Chapman G T, Kirk D B. A method for extracting aerodynamic coefficients from free-flight data[J]. AIAA Journal, 1970, 8(4): 753-758. DOI:10.2514/3.5752 |
| [11] |
马家驩, 陈素贞, 唐宗衡. 风洞中自由飞模型气动特性参数的辨识[J]. 飞航导弹, 1991(3): 23-26. Ma J H, Chen S Z, Tang Z H. Method of aerodynamic parameter identification for free flight model in wind tunnel[J]. Aerodynamic Mission Journal, 1991(3): 23-26. (in Chinese) |
| [12] |
蔡金狮. 飞行器系统辨识学[M]. 北京: 国防工业出版社, 2003: 137-156. Cai J S. Aircraft system identification[M]. Beijing: National Defense Industry Press, 2003: 137-156. (in Chinese) |
| [13] |
Jategaokar R V, Plaetschke E. Maximum likelihood parameter estimation from flight test data for general nonlinear systems[R]. DFVLR-FB 1983-14, 1983.
|
| [14] |
马家驩. 高超声速稀薄气流中球阻力系数的一种简单公式[J]. 空气动力学学报, 1985(1): 107-111. Ma J H. A simple formula of drag coefficient of sphere in rarefied hypersonic flow[J]. Acta Aerodynamica Sinica, 1985(1): 107-111. (in Chinese) |



