由于临近空间位于航天器入轨与返回的必经区域, 空间环境的特殊性决定了航天飞行器在穿过时必须考虑稀薄大气环境对飞行器气动力防隔热通讯及控制的影响.虽然临近空间的稀薄流动特征较连续流发生显著变化, 但对于传统再入钝头飞行器飞行品质影响十分有限, 因此稀薄流动精细模拟在这类飞行器的大余量工程设计中往往被忽略.但由于临近空间高超声速飞行器往往是具有尖锐前缘的乘波体外形, 如HTV-2, X-51A等飞行器翼前缘及头部尖锐前缘热环境就必须考虑稀薄气体效应影响.除气动热预测外, 过渡区稀薄气体效应对气动力的影响也不容小觑.例如高超声速滑翔飞行器在小攻角再入条件下, 飞行器各方向力矩特性压心位置及控制面舵面效率对飞行稳定性至关重要.即使稀薄气体效应对整体气动特性影响有限, 但长航时飞行条件下的扰动累积仍会对飞行姿态与弹道产生影响[1].与此同时, 高Mach数飞行条件在飞行器滞止区所产生的高温气体效应使得气体分子内部发生热力学能态激发化学反应等复杂物理过程.因此, 临近空间高超声速飞行器飞行环境同时包括了稀薄气体效应与高温气体效应的影响, 两种效应叠加对飞行器空气动力学研究提出了新的课题与挑战.
尽管以地面风洞实验和CFD为基础的气动技术作为研制航空航天飞行器的基础性关键技术, 已得到了充分的发展, 但美国前期所开展的临近空间高超声速飞行器飞行试验多次失利等与气动问题密切相关的事实仍然表明:由于临近空间高超声速空气动力学问题存在物理过程认知尚不清晰, 地面风洞试验手段对于复现临近空间高超声速低Reynolds数与高焓环境仍存在严重的挑战, 以及数值计算方法的理论模型与实验验证并不完备等诸多研究瓶颈, 气动预测精度决定飞行成败与品质仍是临近空间高超声速飞行器设计的重要准则.高超声速稀薄过渡流区气动技术作为临近空间飞行器设计的关键技术将对飞行器气动布局一体化设计能源与推进系统设计防隔热及控制系统设计等起到重要的技术支撑作用.临近空间高超声速飞行器气动特性高精度预测与精细流场仿真对数值计算方法提出了巨大的挑战与严苛的工程需求.
如果存在适定的物理模型能够近似描述稀薄非平衡条件下分子动理论中的多尺度特征, 采用成熟的基于偏微分方程组的连续模型来对流场物理量进行描述, 将极大改善目前稀薄过渡流数值方法的计算效率与计算精度.因此, 矩方法与Boltzmann方程几乎同时诞生, 并始终围绕这一目标进行应用与研究.结合本文作者多年来在稀薄气体动力学领域开展的相关工作, 本文将重点阐述Boltzmann方程与矩方程的研究意义发展历程工程应用背景及面临的挑战.
1 Boltzmann方程研究进展建立在稀薄气体动理论基础之上的Boltzmann方程对气体从自由分子流到连续流进行了统一的描述[2], 在这两种极限流动之间的流域还包含了滑移流与过渡流域.通常判断流动区域划分的依据为Knudsen数, 其基本定义为分子平均自由程与宏观参考特征尺度之比. Tsien(钱学森) [3]早在1946年就提出远程飞行器最佳飞行高度约为96km, 并根据Knudsen数将流动划分为连续流(Kn < 0.01), 滑移流(0.01 < Kn < 0.1), 过渡流(0.1 < Kn < 10) 与自由分子流(Kn > 10) 这4部分, 并提倡大力研究稀薄气体动力学.从Knudsen数定义不难发现, 流动稀薄特性与气体平均分子自由程和宏观参考特征尺度息息相关.比如, 在临近空间的高空稀薄环境, 高超声速飞行器来流分子平均自由程显著增大, 对于研究飞行器整体气动特性的宏观参考尺度而言, 飞行器绕流已满足过渡流的Knudsen数标准, 飞行器物面速度滑移温度跳跃以及Knudsen层形成使得传统的连续流计算方法对飞行器气动特性预测已然失准.再如, 即使在常温常压条件下形成的激波内部, 由于激波内分子碰撞的物理过程仅发生在数个平均分子自由程范围之内, 研究激波结构的宏观参考长度应取为激波厚度.由此所产生的微流动现象也具有较大的局部Knudsen数和稀薄过渡流动的特点, 导致高Mach数条件下传统连续流计算方法对激波厚度激波密度温度分离距离及激波对称性参数等关键激波结构参数无法准确预测.由于钱学森的Knudsen数定义只是概念上的定性划分, 临近空间滑移与过渡流飞行器绕流[1]及近年来受到广泛关注的微通道微机电系统[4] (micro electro mechanical system, MEMS)流动多具有多尺度的流动特征, 连续流中往往存在局部稀薄效应, 不能简单定义为完全连续流或过渡流动, 现实中的滑移流与过渡流域流动现象十分丰富, 稀薄气体流动数值计算所面临的挑战更为严峻.
Boltzmann方程在整个稀薄气体动力学中占据中心位置, 直接采用理论或数值方法求解Boltzmann方程是解决稀薄气体流动问题的最为统一的途径.但Boltzmann方程是一个包含多自变量与碰撞积分项的高度非线性的七维积分-微分方程, 目前为止人们仅得到了常温静止气体平衡态的Maxwell速度分布等极少数解析解, 而直接数值求解则因为方程维数(包括时间位置与速度的七维空间)过高和碰撞积分项(非线性二元无穷积分)计算困难导致研究进展缓慢, 因此人们针对不同流域发展了各自不同的简化理论与数值计算方法.通常在Knudsen数趋于0的连续流条件下, 气体可假设为连续介质并采用N-S方程进行求解; 在Knudsen数大于10的自由分子流域, 分子间的相互碰撞可以忽略不计而仅考虑分子与物面相互碰撞, 此时Boltzmann方程的碰撞积分项得到极大简化, 因此自由分子流理论在该流域获得广泛应用.而在1 < Kn < 10的过渡流域, 各种粒子仿真方法如直接模拟Monte Carlo方法(direct simulation of Monte Carlo method, DSMC)能够高效准确预测流动物理特征并证明收敛于Boltzmann方程.然而在滑移流域与0.01 < Kn < 1的过渡流领域, 传统N-S方程连续流方法的模型准确性与DSMC等粒子仿真方法的计算效率均暴露出各自的局限性.
由于Boltzmann方程实现了不同Knudsen数稀薄气体流动的统一描述, 人们仍致力于Boltzmann方程的求解, 文献[5]将Boltzmann方程的求解分为分析方法与数值方法两大类.分析方法往往是对Boltzmann方程进行各种简化与假设, 使求解得以进行.其中包括对碰撞积分项进行模型化处理的模型方程方法(例如BGK模型方程)对速度分布函数进行假设的矩方法以及Chapman-Enskog级数展开, 以及针对低速微流动小扰动线性化假设的线化Boltzmann方程方法.数值方法包括: (1) 对Boltzmann方程的直接求解, 如求解Boltzmann方程的有限差分方法(碰撞积分项采用DSMC方法进行计算)对速度空间进行间断假设以求简化的间断速度方法(或间断纵坐标法)和积分形式的Boltzmann方程积分方法; (2) 介于微观与宏观之间所谓介观层次的格子Boltzmann方法[6] (lattice Boltzmann method, LBM). LBM研究宏观充分小微观充分大流体微团的格点碰撞, 采用统计力学观点获得宏观流场特性参数, 被认为是一种简化分子动力学方法.近年来LBM也被应用于微机电系统数值仿真[7-8]及不可压缩流动, 但有学者指出LBM方法基于分子动力学方法的简化使其已经失去了物理真实性[9]且最终收敛的方程为简化BGK模型方程, 而不是Boltzmann方程本身[10]; (3) 物理意义十分明确的粒子仿真方法, 包括确定论模拟的分子动力学方法(molecular dynamics, MD), 概率论模拟的实验粒子Monte Carlo方法和DSMC方法等.在这些分析方法与数值方法中, 学术界研究的热点包括模型方程方法中的BGK模型方法间断速度方法及DSMC.事实上, 虽可以按求解思路将Boltzmann方程的求解方法分为分析方法与数值解法, 分析方法所得到的简化方程形式最终也须采用有限差分或有限体积的数值方法进行求解实现.因此实际应用中各种方法间往往互相借鉴互相包含, 最终构成了稀薄气体动力学的绚丽图景.虽然上述方法已获得广泛研究与发展, 但在滑移过渡流域(0.01 < Kn < 1) 的物理现象描述计算资源占用算法稳定性与可实现性方面均存在较大缺陷.下面简要阐述近几十年来人们发展的Boltzmann方程数值计算方法及遇到的主要困难.
(1) 在近连续流和滑移流区域采用的基于小Knudsen数的滑移边界条件N-S方程数值计算方法[11].滑移流区(0.01 < Kn < 0.1) 稀薄效应并不显著, 绝大部分流场仍可采用连续介质假设的N-S方程模型, 但物面附近Knudsen层变厚使得物面无滑移边界条件失效, 因此求解考虑滑移边界的N-S方程得到了广泛应用与研究, 其中工程计算中使用最广泛的是1阶Maxwell/Smoluchowski滑移边界条件. 1879年Maxwell [11]在研究稀薄气体运动及其黏性阻力时基于分子运动论以及小Knudsen数假设推导出了1阶Tayler展开的近似滑移本构方程, 1898年Smoluchowski发展并完善了物面滑移与温度跳跃边界条件, Maxwell/Smoluchowski滑移边界条件是目前近连续流研究应用最广泛的滑移边界条件.
但随着稀薄程度的增加, 物面Knudsen层厚度逐渐增大, 除物面出现速度滑移与温度跳跃外, Knudsen层内真实的物理本构关系与N-S方程假设差异愈发显著, 且影响区域迅速扩大.针对Maxwell滑移条件在大Knudsen数下精度下降这一缺点, Gokcen等[12], MacCormack等[13]提出了通用滑移边界条件, 即通过引入在Knudsen层外的速度, 使得在小Knudsen数条件下能够还原为Maxwell滑移本构形式.此外考虑到滑移边界条件的提出包含两条途径:一是在物面上保证滑移速度的准确而得到不准确的远壁面流场; 二是在物面处假设虚假的滑移速度而保证远壁面流场的正确性. Lockerby等[14-15]通过使用类似湍流中的壁面函数修正Knudsen层内黏性的方法来修正Knudsen层内速度分布也推导得到了另一种滑移条件. Lofthouse等[16]针对圆柱绕流对上述3种滑移条件进行了计算并与DSMC结果进行了对比, 认为Gokcen的滑移条件更为全面与准确. Sharipov等[17]重点研究了Maxwell滑移条件中的速度与温度调节系数的变化规律, 归纳给出了一般情况下采用的调节系数.为扩展N-S方程描述稀薄气体流动的适用范围. Cercignani [18], Deissler [19], Beskok等[20], Karniadakis等[21]和Hsia等[22]都在Maxwell本构方程的基础上进行了2阶滑移条件的尝试.国内中科院谢翀等[23]就比较研究了3种具有代表性的2阶速度滑移模型, 发现Cercignani提出的2阶滑移模型效果较好, 但是2阶滑移模型的物面速度分布在Knudsen数0.1附近明显偏离DSMC方法和IP(information preservation)方法的结果.由于2阶条件的引入增加了计算难度与计算量, 但并未改变N-S方程线性本构关系的局限性, 与1阶模型相比虽有改善, 但效果有限, 所以在工程应用中广泛使用的仍是1阶滑移边界条件.
滑移边界条件为滑移流域数值计算提供了十分重要的计算方法与途径, 并已在工程计算中得到广泛应用.但是, N-S方程线性本构关系的特点决定了滑移边界条件对Knudsen层内非线性速度分布的物理描述不足, 特别是对多尺度流动中非物面附近流场如激波结构流动分离及飞行器底部流场等局部稀薄效应显著区域, 通过滑移边界条件对N-S方程修正的处理方法则显得束手无策.
(2) 以DSMC [24-25]方法为代表的粒子仿真方法. DSMC是Bird [24-25]基于分子碰撞真实物理过程且严格遵循分子动理论提出的模型分子直接模拟方法, 方法的物理可信度与准确度较高, Wagner [26]在文章中证明DSMC方法收敛于Boltzmann方程. DSMC方法的核心思想是模拟分子的运动与碰撞, 通过追踪仿真分子的时空信息, 最终采用统计方法获得流场的宏观物理量. DSMC首先应用于模拟均匀气体的一维激波结构和松弛问题, 后来逐渐拓展到二维和三维流动数值计算中, 并开始考虑流动的热力学与化学非平衡过程. Bird [25]在他的专著中列出了一些基于可变径硬球模型(variable hard sphere, VHS)计算的激波结构结果, 但只给出了与N-S方程以及Burnett方程结果对比. Erwin等[27]研究了Mach数为1.9~9来流条件下氦气与氩气的激波结构, 并与实验数据进行了对比, 其激波内分子速度分布函数的计算结果与实验测量结果基本一致. Vogenitz等[28]采用DSMC方法对稀薄条件下高超声速0°攻角平板流动进行了计算仿真, 并与实验数据进行了校对, 但由于实验数据不精确, 并未达到预期验证目标.在复杂流动的模拟研究中, DSMC方法被广泛应用并模拟了AFE(aeroassisted flight experiment)飞船相交钝楔带攻角平板流尖前缘平板流发动机羽流及全尺寸航天飞机单级入轨(single-stage-to-orbit, SSTO)飞行器火星“探测者号”等外形的流场. DSMC化学反应流模拟的流动介质多为N-O混合物或O2-CO2混合物. Moss等[29]模拟了包含化学反应的火星探测器头部绕流, 计算采用了变径硬球分子模型, 同时包含了5组元化学反应及Borgnakke-Larsen转动能松弛模型, 并与飞行实验数据和N-S方程计算结果进行了比对.目前, DSMC方法已在稀薄气体动力学研究尤其是过渡区流动仿真取得广泛的研究与应用.但是, 由于DSMC方法计算效率受限于分子平均碰撞时间与分子平均自由程的时间与空间计算尺度, 其准确度依赖于仿真分子自由移动与分子间碰撞解耦假设合理性仿真分子的数量是否足够描述所研究的流动以及仿真分子理化模型的可信度, DSMC方法的应用与发展始终受限于方法本身的计算效率与计算机的运算速度和内存大小.在目前计算条件下, 准确模拟近连续流域所需的仿真分子数目占用的海量计算机内存和碰撞统计所消耗的漫长计算时间使DSMC方法的工程应用受限十分严重, 极大地降低了DSMC方法在临近空间飞行器设计工程领域的可用性.例如在Columbia号航天飞机失事调查报告[30]中仅对91~100km高度的气动环境采用DSMC方法进行了流场复现, 91km以下由于计算效率低与飞行器外形复杂等原因基本无法开展.另外, Koppenwallner [31]发现在模拟返回舱过渡流时, 如果采用较少的仿真分子数量便无法获得准确的飞行器纵向俯仰力矩结果.同时, DSMC方法对多尺度流动中局部稠密效应(如发动机羽流污染)等问题亦无法获得令人满意的计算效率和计算精度.
为克服粒子仿真方法与连续流计算方法各自的不足与缺陷, 稀薄与连续流求解器的耦合方法自然而然受到学界关注与发展.其中较为热门和成熟的是连续流N-S方程求解器与稀薄流DSMC方法的耦合[32-33], 其主要思想是采用分区求解, 各区交界面实现信息交换, 稀薄区域用DSMC方法求解, 而连续区数值求解N-S方程.根据N-S/DSMC交界面两侧的信息传递频率不同, 可分为解耦或非耦合[34-35]弱耦合[36]强耦合[37-38]这3种方式进行.非耦合方法是N-S和DSMC子区都达到稳态之后才进行信息交换, 而弱耦合方法则增加了信息交换的频率, 强耦合方法在每个时间步上都进行N-S与DSMC各区之间的信息交换. N-S/DSMC耦合算法研究内容主要分为两部分:一是N-S方程失效性准则研究, 二是过渡区和连续区交界面的确定及信息传递方式研究. Boyd等[39]针对典型激波和边界层流动, 利用基于当地特征量梯度的局部Knudsen数作为连续性假设失效参数进行判断.根据N-S/DSMC交界面两侧信息传递方式的不同, 可分为基于通量和基于状态参数的两种N-S/DSMC耦合方法. Sun等[40]的研究发现, 应用基于通量的N-S/DSMC耦合方法的前提是计算网格中存在大量的模拟分子, 一旦计算网格中没有足够的粒子, 计算程序可能崩溃. Schwartzentruber等[41]也指出, 基于通量的耦合方法所带来的统计涨落与基于状态参数的耦合方法所带来的统计涨落之间的关系是Eflux=Estate/Kn, 而在交界面处Kn≈0.01, 这样就导致基于通量的耦合方法所带来的统计误差是基于状态参数的耦合方法的100倍.国内也开展了相应的工作, 刘靖[42]应用弱耦合方法开展了过渡流区的基于非结构化网格的N-S/DSMC算法的研究和算例的验证工作, 徐珊姝[43]也针对过渡区推进器的流场开展了N-S/DSMC算法的研究和验证工作.但是, 由于国内外N-S/DSMC耦合算法研究目前尚处于起步阶段, 关键问题在于连续流求解方法本质上是确定论方法, 而粒子仿真方法是概率论方法, 两种本质截然不同的方法进行耦合必然存在许多亟待解决的科学和工程问题, 例如在交界面上如何控制DSMC方法统计涨落并保证提供给N-S方程的边界条件足够光滑[39], N-S/DSMC耦合算法收敛难度大及计算效率偏低复杂外型适应性以及程序鲁棒性等多个方面仍面临较大挑战, 其技术的工程应用前景有待进一步明朗.
(3) 简化Boltzmann方程的BGK模型方程及间断速度法. 1954年, Bhatnagar等[44]提出了BGK模型, 它采用简化碰撞模型替代了Boltzmann方程碰撞积分项, 其核心思想是假设在平衡态附近速度分布函数回归平衡态的速率与偏离平衡态程度成正比.由于化简后方程易于求解, 且同时表征了Boltzmann方程所描述的气体分子碰撞松弛及统计特性而获得广泛应用与发展.采用Chapman-Enskog方法在Maxwell平衡分布附近进行0阶矩1阶矩及2阶矩展开即可得到BGK形式的Euler, N-S及Burnett方程. BGK模型方程自从提出以来, 作为Boltzmann方程的简化方程被广泛应用于各种数值计算方法.但是由于采用Chapman-Enskog方法展开的原始BGK方程Prandtl数为1, 因此在解决动量与能量交换问题上尤其是物面热流与摩阻的预测上, 该方法存在较大缺陷, 针对这一缺陷就需要对BGK模型方程进行Prandtl数修正, 其中以ES-BGK模型[45]以及Xu [46]所提出的1阶Chapman-Enskog展开BGK模型方程的修正方法最为成功.
间断速度法又称为间断纵坐标法, 其基本思想是采用有限个间断的速度来代替整个速度空间使得Boltzmann方程得到极大近似与简化.其中最著名的形式为Broadwell [47]提出的八速度气体模型以及Cabannes [48]提出的十四速度模型等. 1994年Bobylev等[49]曾证明均匀网格的间断速度方法收敛于Boltzmann方程, 这是间断速度法发展史上重要的里程碑, 证明该方法发展前景广阔.国内学者对间断速度法也进行了深入研究, 有力地推动了国内稀薄气体动力学的发展.如中国空气动力学发展中心李志辉所提出的气体运动论统一数值算法正是基于间断速度法对Boltzmann方程的简化模型, 即修正BGK模型方程的基础上进行了数值求解, 并获得了较为广泛的数值验证[50-54].但是, 作为从自由分子流到连续流跨流域的统一算法及工程化的发展目标, 目前采用的计算方法多是围绕如何简化Boltzmann方程的积分碰撞项展开, 且间断速度法的研究对象还仅限于简单几何外形和理想气体分子模型[5], 其特殊的物理与化学模型处理往往存在各自的假设和缺陷, 工程应用前景有待进一步深入研究.
(4) 以Burnett方程55]和Grad十三矩方程[56]为代表的矩方法.矩方法以求解Boltzmann方程的矩方程形式为目标, 而矩方程则是将Boltzmann方程乘以分子的某个量后在速度空间积分所得到的, 从而得到的宏观物理量守恒方程组, 但该方程组不封闭.矩方法核心思想是将分布函数通过简化表达为宏观物理量的函数, 从而封闭守恒方程组.矩方法希望能够获得高阶流体力学方程对热力学非平衡现象进行准确描述, 其中包括扩展流体力学方程(extended hydrodynamics equations, EHE)与广义流体力学方程(generalized hydrodynamics equations, GHE).扩展流体力学方程方法中最为重要的一类就是Chapman-Enskog展开[57]方法. Chapman-Enskog方法将分布函数展开为基于Knudsen数的幂级数, 其中0阶展开与1阶展开所得到的应力张量与热流通量分别为连续流Euler与N-S方程本构关系, 而其2阶与3阶分布函数幂级数展开将得到可以应用于更大Knudsen数范围的Burnett与super-Burnett方程.从数学性质上来讲, 虽然幂级数展开并不会在Kn>1时给出满意的解, 但Tsien [3]等均指出高超声速滑移过渡流区域数值计算采用Burnett方程能够给出优于N-S方程的计算结果.且N-S方程与Burnett方程同属Chapman-Enskog展开, 属于理论意义上的连续性方法, 流动宏观量空间与时间连续, 且可用一组非线性偏微分方程进行描述, 其显著特点为已发展的数值计算方法成熟, 计算效率高.但是, Burnett方程求解的稳定性与高阶边界条件仍有待深入细致地开展研究, 尤其是部分形式的Burnett方程线性失稳与违背热力学第二定律的缺点极大地阻碍了该方法的发展与应用. Grad十三矩方程是扩展流体力学方程(EHE方法)中另一类直接求解矩方程的方法, 它以获得13个未知量的13个矩方程为目标, 将速度分布函数展开为密度压力速度应力与热流的Hermite多项式并代入Boltzmann方程求矩, 联立质量动量与能量守恒方程获得13个独立输运方程[56]. Grad十三矩方程与Burnett方程经历了同一个时期的发展与讨论, 且开始由于与Burnett方程一样无法获得高Mach数条件下的激波解, 在当时均不被学术界重视.但随着时间相关法发展, Burnett方程很快突破了Mach数限制获得了高超声速激波解, 但十三矩方程仍与其定常解法一样无法取得突破, 且被证明违背Gibb′s关系[58-59].由于该多项式展开被证明当来流Mach数大于1.85时发散[60], 以及没有得到DSMC方法与实验进一步的验证与支持. Levermore等指出Grad十三矩方程违反熵关系[61]后提出Gauss闭合法[62]. Gauss闭合法是在有限维度线性子空间里将矩方程变换为双曲型方程进行求解, Groth等[63]则基于Gauss闭合法也发展了相关计算模型, 但是由于该方法的解无法获得热流, 导致其应用大大受限.此外, Brown [64]还发展了更为复杂的三十五矩方程, 但目前仍没有获得大于Mach数2的仿真结果.目前三维十三矩方程与三十五矩方程计算尚存在较大缺陷, 无法开展数值求解与计算.为克服扩展流体力学方程(EHE)物理与数值求解过程中的困难, Myong [65]基于Eu方程提出了广义流体力学方程, 由于Eu方程[66]是基于非平衡正则分布函数及Boltzmann方程碰撞项累积展开, 严格满足热力学第二定律, 因此较为有效地解决了一些一维条件下的过渡流问题, 但应用该方法求解二维与三维条件下的过渡流问题仍需要进一步研究与突破.
2 矩方程研究进展完整的无穷矩方程是Boltzmann方程描述的另一类表达形式, 若考虑基于完整的函数空间的所有矩输运方程, 该方程与Boltzmann方程所采用的速度分布函数描述完全等价.但由于任意阶矩方程的不可封闭性(方程包含更高一阶矩), 研究重点往往集中在有限矩(如五矩十三矩等)方程的封闭与数值方法.
2.1 Chapman-Enskog展开与Burnett方程Chapman-Enskog方法最早从Boltzmann方程推导出N-S方程, 其基本思路是将分子质量动量与能量乘以Boltzmann方程各项并对整个速度空间进行积分, 由此所得到的方程被称为矩方程或Maxwell输运方程.所得到的矩方程包含质量动量与能量守恒方程式, 但方程组本身并不封闭, 需要对应力与热流张量本构关系进行封闭. Chapman与Enskog通过将速度分布函数基于Knudsen数进行了级数展开, 其中0阶近似取平衡态Maxwell速度分布, 求得应力张量与热流张量为0时得到Euler方程组.对应的1阶近似得到N-S方程, 2阶近似得到Burnett方程.从基于Knudsen数正幂次级数展开的数学本质来看, 虽然Chapman-Enskog展开方法所得到的结果不会在Kn>1时得到明显改善, 但已有研究表明Burnett方程的高阶应力张量与热流张量明显能提供比N-S方程失效边界更大的Knudsen数范围.按照钱学森关于流动领域的划分, 过渡流Knudsen数定义为0.1~10之间.考虑到当Kn>1时的流动已经充分稀薄, 在通常定义的临近空间(20~100km)范围内不论是考察来流Knudsen数还是考察各类局部Kn>1的高超声速飞行器绕流流场并不多见, 且对于Kn>1的流动应用已充分发展的DSMC方法就能够较高效地获得更为真实的流场物理描述和计算结果, 同时Kn>1也已超出了Chapman-Enskog级数展开中关于Kn < 1的限制, 因此作为延伸至稀薄滑移与过渡流域的连续流方法, Burnett方法具有十分重要的研究价值并得到了学术界广泛关注与研究.
1936年Burnett研究了速度分布函数的Chapman-Enskog 2阶展开, 并得到了对应2阶热流与应力张量[55], 获得了原始Burnett方程.随后, Chapman等[57]将原始Burnett方程中的物质导数进行了Euler形式的描述, 获得了常规Burnett方程(conventional Burnett equations), 考虑到Euler方程N-S方程与Burnett方程均为Chapman-Enskog各阶展开, 因此将原始Burnett方程中的物质导数替换成Euler或N-S方程空间导数的形式是合理的.常规Burnett方程一经提出就获得了广泛关注与研究, 在过去60年里, 国内外学者对常规Burnett方程的热情远远高于原始方程形式. Tsien [3]在1946年就将Burnett方程2阶项与Navier-Stokes-Fourier方程中的1阶项进行了对比, 提出对于高超声速滑移过渡流区域数值计算应采用Burnett方程, 但Burnett方程需要提供更为复杂的边界条件.在Burnett方程提出后, 一维激波结构问题普遍被学术界认为是Burnett方程优于N-S方程最强有力的证明, 但对于任意Mach数条件下Burnett方程求解的困难使得研究者十分困惑. 1948年, Wang等[67]试图采用Burnett方程求解Mach数1.2以上激波结构, 但最终无法稳定求解. Sherman等[68]对N-S方程与Burnett方程激波结构进行了对比分析, 但仍无法获得Burnett方程Mach数2.0以上的激波结构, 并认为N-S方程对于弱激波仍然适用, 且Burnett方程在弱激波条件下并未表现出明显优点.而对于来流Mach数2.5以上的激波结构, Burnett方程可能存在理论上的缺陷, 无法获得稳定求解. Foch [69]也在计算定常Burnett方程时遇到了所谓的Mach数障碍, 同时研究了超Burnett方程, 但均无法获得任意Mach数下的激波结果. 1964年, Holway [58]研究Burnett方程后认为基于Boltzmann矩方程所获得的流动控制方程对高Mach数条件下激波结构求解无能为力.但随后Bulter等[70]发现通过修改矩方程Maxwell权函数可以获得稳定的高超声速激波解.由于稀薄气体动力学实验与理论有时采用N-S方程反而获得了优于Burnett方程的结果, 且复杂的方程形式与边界条件难于程序化处理, 学术界对Burnett方程研究一度陷入低谷. 1976年Vestner [71]将边界层效应与Burnett贡献分辨开, 获得了黏性磁场热流并由Hermans等[72]设计的实验进行了验证.自此2阶Chapman-Enskog展开近似才获得了较为严谨的实验确认, 奠定了Burnett方程研究重要的里程碑.随后Fiscko在自己的博士论文[73]及和Chapman [74]采用时间相关法求解控制方程, 充分验证了一维激波结构中Burnett方程比N-S方程模拟结果与DSMC吻合得更好, 同时也发现了Burnett方程在细密网格中的不稳定性.更为重要的是, 他们所得到的结果证明了Chapman-Enskog展开所获得的2阶Burnett方程与3阶超Burnett方程本身不存在所谓Mach数障碍, 而是数值求解方法限制了计算Mach数范围与计算稳定性, 极大提振了人们对于研究Burnett方程的信心与热情, 这成为Burnett方程研究历史上最重要的转折点.随后, Lin等[75]采用高阶滑移边界条件求解Burnett方程并与实验数据进行比对, 当Kn < 0.25时获得了十分满意的圆柱与Couette流动仿真结果, 明显优于滑移边界的N-S方程. Burnett方程对于小波长扰动的不稳定性已得到广泛证实, 其导致当流场区域内网格尺度小于平均分子自由程时计算发散. Bobylev [76]研究发现小波长下一维Burnett方程的线性不稳定性, Zhong等[77]后来采用Bobylev的稳定性分析方法通过研究后提出了增广Burnett方程, 具体方程形式是在3阶展开后得到的热流与应力项中取部分项放入常规Burnett方程之中, 并采用1阶滑移边界条件计算了圆柱绕流球头椭球与低密度喷管流动, 取得了较为满意的仿真结果. Agarwal等[78]通过研究也证明了增广Burnett方程的稳定性与相比N-S方程更准确的模拟精度, 但增广Burnett方程在模拟钝头体尾流及平板边界层过程中计算难以收敛, 且方程本构关系中所增加的线性超Burnett方程项的必要性遭到质疑.此外, 尽管Burnett方程的推导起初仅局限于单原子气体分子仿真, 但Lumpkin [79]证明对于双原子气体的氮气分子激波结构, 考虑转动能非平衡效应的Burnett方程也能够提供优于N-S方程的结果.
在Burnett方程稳定性研究方面, Uribe等[80]发现并重新解释了硬球分子模型下原始Burnett方程的不稳定性, 并给出了稳定Knudsen数范围. Soderholm [81]证明原始Burnett方程存在奇异点, 且构造了混合常规-原始Burnett方程并证明其线性稳定性. Jou等[82]构造了能反映Burnett项影响的高阶流体力学方程, 并采用Bobylev方法进行了线性稳定性分析. Welder等[83]认为在较大Knudsen数条件下仅仅对常规Burnett方程进行线性稳定性分析是不够的, 由于忽略了高阶本构关系中的非线性项, 线性稳定只能作为方程计算稳定的必要条件. Comeaux等[84]与Jin等[85]均研究了常规Burnett方程与热力学第二定律的相容性, 认为是由于违背了热力学第二定律导致了方程对于小波长扰动的不稳定, 同时Jin等[85]还在文章中首次提出了正则Burnett方程.为了克服这一缺点, Balakrishnan等[86-88]及Welder等[83]分别提出了BGK Burnett方程, 其基本思路是采用1954年Bhatnagar所提出的Bhatnagar-Gross-Krook(BGK) [44]模型对Boltzmann方程中的碰撞积分项进行了替代, 所得到的BGK Burnett方程被证明满足Boltzmann-H定理, 一维线性稳定分析也表明该方程线性稳定, 但是原始BGK模型不能获得正确的流场输运系数, 如前所述需要进行修正. 3阶Chapman-Enskog展开所得到的超Burnett方程(super Burnett equations)与更高阶展开所获得的方程由于数学性质与物理意义均存在较大争议, 因此考虑其数值方法目前还没有理论与应用价值[78]. Reese等[89]和Woods [90]认为Burnett方程本构关系中并未区分扩散项和对流项, 通过推导将Burnett本构关系中对流项进行了消元, 得到了Woods方程.除上述方程外, 最近的一组Burnett方程形式是在2013年由Dadzie [91]推导得到的, 且推导过程避免了Chapman-Enskog展开. Burnett方程中的应力与热流项中3阶以上导数需要额外的边界条件才能使得方程获得定解, 不同的边界取值会导致不同的方程计算结果[92].国内Wang等[93-94]研究了2阶Burnett方程热流项与1阶N-S热流项在驻点处的比值, 提出了非Fourier换热的稀薄效应准则, 并发展了对应的桥函数, 获得了与DSMC较为一致的驻点热流预测结果. Bao等[95-96]采用Bobylev线性稳定性分析方法对不同类型一维及二维Burnett方程进行了数学分析, 证明了部分方程的线性稳定性质.
虽然理论上Burnett方程求解需要比N-S方程更高阶的边界条件, 但目前文献中Burnett方程的物面边界条件主要采用1阶Maxwell/Smoluchowski滑移边界条件与2阶滑移边界条件.热化学非平衡流动的Burnett方程研究目前国内外文献尚很少见, 相关研究工作目前还仅限于多组元无化学反应Burnett方程计算研究[97].除Descartes坐标系下的Burnett方程外, 圆柱坐标系下的Burnett方程也有学者进行了推导与数值计算, 并获得了相应数值解.如Zhong等[98]采用柱坐标系增广Burnett方程计算了轴对称钝头体高超声速绕流, Yang等[99]推导了柱坐标系条件下Burnett方程应力项, Singh等[100]推导了三维柱坐标下增广Burnett方程并求解了三维等温Poiseuille流动.此外在低速微流动与微机电研究中, 学术界也采用Burnett方程获得了较为丰富的数值仿真结果.如Agarwal等[78], Bao等[101], Xue等[102], Uribe等[103], Singh等[104-105]均采用增广Burnett方程计算得到了令人满意的稀薄条件下平板Couette和Poiseuille流场结果.
Burnett方程自1936年首次提出以来, 虽受到学术界广泛研究与关注, 但在高超声速流动中的应用始终不太顺利. Zhong等[77]总结其主要原因在于: (1) 边界条件难于准确描述气体分子与壁面的相互作用; (2) Chapman-Enskog级数展开收敛特性未知; (3) Burnett方程熵增性质未得到证明; (4) 在转动坐标系中Burnett方程表现出坐标系相关[90]; (5) 纵向扰动下Burnett方程线性失稳.针对Burnett方程遇到的上述问题, 经过多方面分析总结后可以发现:
(1) 关于Burnett方程边界条件:边界条件对于偏微分方程求解的影响毋庸置疑, 但即使在连续流区域采用典型无滑移边界条件, N-S方程解的唯一性学术界仍存在争议, 从数学上对N-S方程边界条件进行准确分类还存在一定差距, 因此对Burnett方程进行严格边界条件定义理论上还尚不可及.虽然学术界一致认为包含高阶应力与热流项的Burnett方程对边界条件提出了更高需求, 但目前为止几乎所有Burnett方程数值计算文献均采用较为成熟的1阶与2阶滑移边界条件, 且获得了准确稳定的数值计算结果.因此本文认为对于Burnett方程边界条件数学描述难于突破的前提下, 建议数值求解Burnett方程时仍沿用已有的较为成熟的1阶与2阶滑移边界条件, 同时须进一步开展1阶与2阶滑移边界条件对比研究与相关工作的总结.
(2) 关于Chapman-Enskog方法收敛性问题: N-S方程与Euler方程也同属Chapman-Enskog展开, 因此收敛性问题属Chapman-Enskog展开共性问题.目前Chapman-Enskog级数展开收敛性尚未证明, 且关于正则化方法及Grad方法收敛性证明研究都较为缺乏, 学术界关于收敛性问题还存在较大争议.由于这个问题属于Chapman-Enskog方法自身特点, 本文不展开深入研究.
(3) 关于熵增问题, 由于没有充足证据证明Burnett方程具有非负耗散函数并满足热力学第二定律, 因此目前关于熵增的讨论还在继续, 且已被证明由于违背热力学第二定律导致了方程对于小波长扰动的不稳定; 一些发展和修正的Burnett方程(如BGK-Burnett方程)也被证明满足热力学第二定律, 因此数学和计算证明方程的熵条件显得十分必要.
(4) 关于坐标系相关性问题, Truesdell等[106]认为虽然BGK模型方程通过简化获得了坐标系无关性, 但Boltzmann方程本身却并非一定强调坐标系无关.因此Burnett方程在旋转坐标系下的坐标相关性是否影响其方程应用价值还值得商榷.
(5) 关于线性方程小扰动失稳, 从工程角度人们更加关心Burnett方程究竟能否稳定准确地给出优于N-S方程的结果.因此Burnett方程的稳定性问题才是目前困扰该方程发展应用的瓶颈和最有希望解决的问题, 方程稳定性得不到保障, Burnett方程就不可能被工程界广泛应用与发展.正因为上述问题困扰, 流体力学界曾有人认为Burnett方程研究价值与意义不大, 直到Fiscko与Chapman将其在高超声速流动中进行了里程碑式的应用.
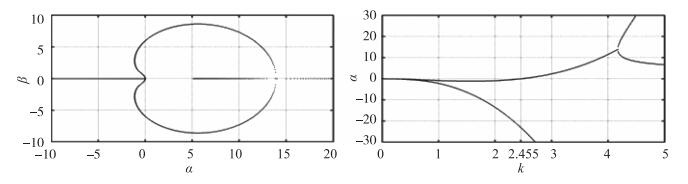
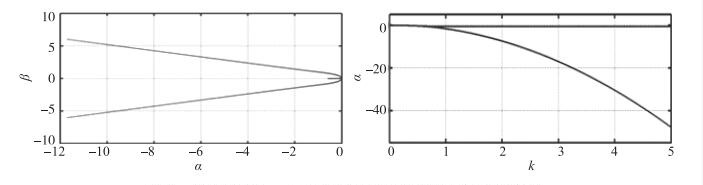
为验证Burnett方程线性失稳的特点, 图 1与图 2分别给出了常规Burnett方程及简化常规Burnett方程根轨迹与增长系数随波数变化图[107].若方程线性稳定, 则根轨迹所有点都应当落在α=0轴左侧.从图 1可以看出一维常规Burnett方程存在线性不稳定, 与文献结论一致, 图 2代表的SCB方程表现出一维线性稳定的特点.此外增长系数随波数变化曲线还给出了方程线性失稳的边界.
|
| 图 1 常规Burnett方程根轨迹与增长系数随波数变化图 Fig.1 inear stability diagram in (α, β) plane and (α, k) diagram for conventional Burnett equations |
|
| 图 2 简化常规Burnett方程根轨迹与增长系数随波数变化图 Fig.2 Linear stability diagram in (α, β) plane and (α, k) diagram for simplified conventional Burnett equations |
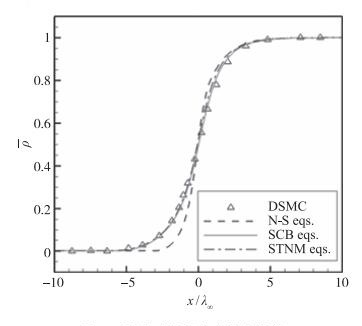
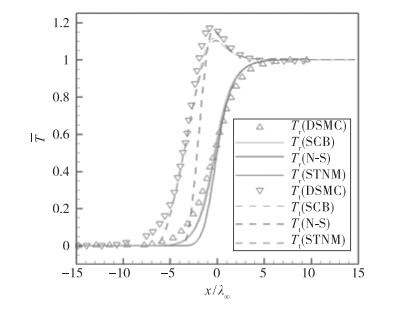
图 3与图 4则分别给出了Mach数为10来流条件下激波无量纲密度与温度分布曲线, 可以看出SCB方程较N-S方程能够获得更趋近于DSMC方法的计算结果[108]
|
| 图 3 激波无量纲密度分布曲线 Fig.3 Normalized density profiles for shock structure in Nitrogen (M=10) |
|
| 图 4 激波无量纲平动(Tt)与转动(Tr)温度分布曲线 Fig.4 Normalized translational(Tt) and rotational(Tr) temperature profiles for shock structure in Nitrogen (M=10) |
Grad矩方法将速度分布函数在平衡态附近进行Hilbert展开, 得到分布函数Hermite多项式表达形式[56]. Grad方法可以对包含应力张量热流及更高阶矩的输运方程进行封闭并耦合求解, 其中最为常见的包括Grad十三矩方程与Grad二十六矩方程.然而, 原始Grad矩方法与Burnett方程一样, 存在十分明显的理论缺陷:首先由于Grad方程表现出双曲型特点, 因此存在激波结构仿真的最大Mach数范围, 来流条件超过这个Mach数很难得到光滑与稳定的激波结构, 例如Grad十三矩方程的最大Mach数仅为1.65, 且这个最大Mach数仅随着方程矩数的增大而缓慢增大[109], 这一方程数学特性缺陷极大制约了Grad类矩方程的发展.其次, 由于高阶矩方程边界条件普遍存在的适定性问题, 目前文献中考虑边值问题的Grad方程求解十分困难, 已有的数值结果寥寥.此外, 例如Knudsen层描述准确度与Grad方程中矩的阶数相关性问题[110]高Mach数条件下速度分布函数多项式展开小于零[111]等问题也使得该方程研究与应用充满挑战.
Struchtrup等[112]针对十三矩Grad方程进行了正则化处理, 得到了正则化十三矩方程(R-13方程), 正则化通过在原始Grad输运方程上增加2阶导数项描述Boltzmann方程多尺度耗散特点, 最终得到的方程形式克服了原始Grad十三矩方程双曲型的缺点, 能够获得全Mach数稳定光滑的激波结构.由于Grad分布函数并非和Maxwell分布函数一样在Boltzmann方程中有明确的物理含义, R-13方程假设非平衡气体向平衡态过渡时首先达到一个伪平衡中间态, 且这个松弛时间较达到平衡态的松弛时间要小得多, 这个伪平衡态条件的速度分布函数即为Grad分布函数, 正则化的的思想同样被广泛应用于其他矩方法之中[85, 113-114].将R-13方程采用基于Knudsen数Chapman-Enskog展开可以发现, 2阶Burnett方程与3阶super-Burnett方程被包含进来, 而传统Grad十三矩方法不能包括super-Burnett阶精度.同时R-13方程能够保证任意波长与频率的线性稳定, 这比传统线性稳定性分析仅考虑扰动时间稳定性要求更为苛刻(例如增广Burnett方程仅克服了原始Burnett方程时间线性失稳的缺陷, 然而空间仍存在线性不稳定).因此, Torrilhon等[115]针对激波结构问题将R-13方程与Burnett与super-Burnett方程进行了详细对比与讨论, 并对Grad速度分布函数保正性进行了研究.
2.3 非线性本构关系理论为了提供一种可靠的能够实现稳定计算的高阶流体动力学模型, Eu从广义的流体动力学理论出发, 结合非平衡集成方法, 提出了一组一般化的流体动力学方程(GHE) [116-117].他采用不可逆的扩展热力学作为理论工具, 为统计力学提供了一个坚实可靠的基础.这套理论最非凡之处在于巧妙地构建了一个非平衡态分布函数.这个分布函数只是形态定义, 并非严格具体的表达式, 作为一座桥梁, 把从非平衡态到平衡态演化的熵增特性和宏观非守恒量的耗散演化的过程紧密联系起来, 使得这套理论从一开始的介观分布函数层面就强制确保满足H定理.为了完成对高阶非守恒量输运方程的封闭, Eu对其碰撞项进行累积量展开, 消去高阶展开式, 保留了1阶项.该1阶项是宏观非守恒量的双曲正弦函数, 在近平衡态附近演化成Rayleigh-Onsager耗散函数.一般化的流体动力学方程已经成功地被运用到高Mach数的一维激波结构[118]和声波吸收散布问题[119]的研究当中.
但是, 当上升到多维问题的研究时, GHE的应用受到限制.这主要是由于GHE方程形式复杂, 高阶非守恒量之间强非线性耦合所致.为此, Myong在GHE基础上发展了一套有效的多维计算动力学模型, 并为之提出一套行之有效的解耦求解算法[120].该模型由GHE在Eu的绝热假设和封闭假设条件下, 通过对高阶非守恒量时间项和对流项的简化处理得到.该模型是一组非线性耦合代数方程, 通过解耦求解算法能有效地结合双曲守恒律控制方程, 实现对流动的数值模拟.目前, 该模型, 也就是非线性耦合本构关系, 简称NCCR模型, 在单原子气体的一维激波结构和二维平板钝头绕流等问题得到了验证[121], 初步表明了其在高速稀薄流域流动机理模拟的潜力.随后, 该模型考虑了和体积黏性有关的附加体积应力, 通过引入附加体积应力这个高阶非守恒量演化方程, 拓展到了双原子气体流动问题的模拟方面上来, 并成功应用到了二维高超稀薄钝头绕流的模拟问题的研究当中[122].由于在非平衡流动问题取得巨大的成功, NCCR模型受到关注, 并在多方面得到拓展性的研究, 包括在微机电系统下的研究[123], 结合间断Galerkin计算方法的高精度算法研究[124]以及平板Couette流和一维Poiseuille流的理论分析研究[125]等问题.
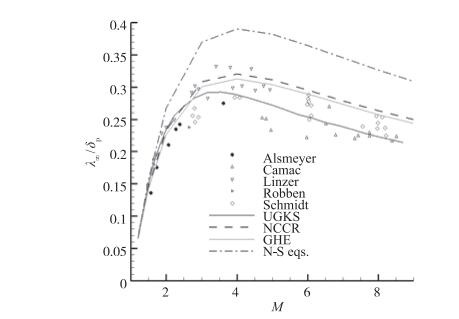
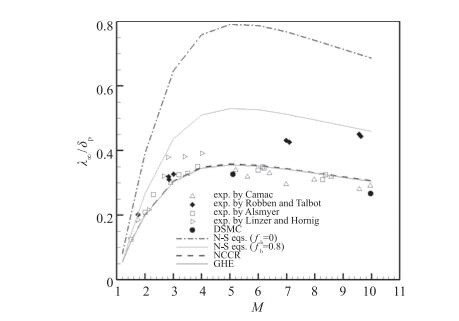
激波内部由于存在十分强烈的非平衡效应, 一直以来被广泛用于测试非平衡方法的准确性. 图 5和图 6分别给出了单双原子氩气与氮气激波密度厚度随Mach数变化曲线, 从图中可以看出GHE方程与NCCR本构关系较N-S方程均能够获得更为准确的激波结构参数[126].
|
| 图 5 单原子氩气激波厚度随Mach数变化曲线 Fig.5 Inverse density thicknesses of shock structure in Argon |
|
| 图 6 双原子氮气激波厚度随Mach数变化曲线 Fig.6 Inverse density thicknesses of shock structure in Nitrogen |
此外, 在稀薄气体动力学中, 分子动理论从分子水平碰撞描述了气体流动, 但往往高超声速流动还伴随着分子内能激发离解电子能级跃迁及化学反应等十分复杂的分子内部结构物理过程, 即热化学非平衡效应.上述分子内部结构变化改变了气体属性与状态方程, 影响了流场激波结构与分离区大小, 直接关系到飞行器受力与受热情况.由于滑移过渡区稀薄效应对分子平均碰撞时间的影响, 在连续流条件下假设平衡的平动-转动松弛过程发生改变, 转动能非平衡效应凸显.因此, 在多原子分子Burnett方程中还需考虑平动-转动非平衡所产生的松弛过程影响, 其非平衡方程表现形式稳定性及碰撞参数影响与规律值得进行讨论与总结.此外, 在热化学非平衡数值方法研究中, 化学反应源项求解刚性问题各能态间能量交换与松弛问题化学反应模型的不完备及稀薄效应与热化学非平衡效应耦合影响等问题使其研究具有较大的难度与挑战性.同时将稀薄气体效应与热化学非平衡效应考虑进来, 不仅包含了前述非平衡流动共性问题, 还需要将分子内部结构变化与稀薄条件下分子宏观运动结合进行耦合研究, 使得流动问题复杂程度大大增加.
3 结论建立在稀薄气体动理论基础之上的Boltzmann方程对气体从自由分子流到连续流进行了统一的描述, 在这两种极限流动之间的流域还包含了滑移流与过渡流域.直接采用理论或数值方法求解Boltzmann方程是解决稀薄气体流动问题的最为统一的途径.但Boltzmann方程是一个包含多自变量与碰撞积分项的高度非线性的七维积分-微分方程, 目前为止仅得到了如平衡态Maxwell速度分布等极少数解析解, 而直接数值求解则因为方程维数(包括时间位置与速度的七维空间)过高和碰撞积分项(非线性二元无穷积分)计算困难导致研究进展缓慢, 只能针对不同流域发展不同的简化理论与数值计算方法.矩方程是Boltzmann方程描述的另一类宏观表达形式, 若考虑基于完整的函数空间的所有矩输运方程, 该方程与Boltzmann方程所采用的速度分布函数描述完全等价且现有CFD计算理论十分成熟, 但由于方程形式和数学特性十分复杂, 其理论研究进展缓慢, 工程应用成果寥寥.
本文从Boltzmann方程和稀薄气体动力学基本概念出发, 并结合本文作者近年来开展的一系列工作, 对经典Chapman-Enskog展开Burnett方程Hilbert展开十三矩方程及近年来发展的非线性本构关系理论进行了全面介绍与分析.通过对不同类型矩方程国内外研究进展取得的最新进展及面临的主要问题与挑战进行概述, 表明矩方程作为经典的稀薄气体动力学方法具有十分显著和不可替代的计算效率与工程应用优势, 深入研究基于宏观描述矩方法对于拓展稀薄气体动力学与计算流体力学应用领域提升气动力学细观研究水平具有十分重要的意义.
致谢 本文研究工作获得国家重点基础研究发展计划(2014CB340201), 国家自然科学基金青年基金(11502232), 中央高校基本科研业务费专项资金资助支持,谨此致谢.| [1] |
Ivanov M S, Gimelshein S F. Computational hypersonic rarefied flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 469-505. DOI:10.1146/annurev.fluid.30.1.469 |
| [2] |
Vincenti W G, Kruger C H. Introduction to physical gas dynamics[M]. New York : Wiley, 1965 : 538. https://www.coursehero.com/file/p6o9e8t/110-W-G-Vincenti-and-C-H-Kruger-Introduction-to-Physical-Gas-Dynamics-John/
|
| [3] |
Tsien H S. Superaerodynamics, mechanics of rarefied gases[J]. Journal of the Aeronautical Sciences, 1946, 13(12): 653-664. DOI:10.2514/8.11476 |
| [4] |
Gad-El-Hak M. The fluid mechanics of microdevices —the freeman scholar lecture[J]. Journal of Fluids Engineering, 1999, 121(1): 5-33. DOI:10.1115/1.2822013 |
| [5] |
Shen Q. Rarefied gas dynamics[M]. Beijing: National Defend Industry Press, 2003: 321.
|
| [6] |
Mcnamara G R, Zanetti G. Use of the Boltzmann-equation to simulate lattice-gas automata[J]. Physical Review Letters, 1988, 61(20): 2332-2335. DOI:10.1103/PhysRevLett.61.2332 |
| [7] |
Lim C Y, Shu C, Niu X D, et al. Application of lattice Boltzmann method to simulate microchannel flows[J]. Physics of Fluids, 2002, 14(7): 2299-2308. DOI:10.1063/1.1483841 |
| [8] |
Nie X B, Doolen G D, Chen S Y. Lattice-Boltzmann simulations of fluid flows in MEMS[J]. Journal of Statistical Physics, 2002, 107(1/2): 279-289. DOI:10.1023/A:1014523007427 |
| [9] |
Wolf-Gladrow D A. Lattice-gas cellular automata and lattice Boltzmann models : an introduction[M]. Berlin : Springer-Verlag, 2000 : 308. http://link.springer.com/book/10.1007/b72010
|
| [10] |
Chen S Y, Doolen G D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 329-364. DOI:10.1146/annurev.fluid.30.1.329 |
| [11] |
Maxwell J C. On stresses in rarified gases arising from inequalities of temperature[J]. Philosophical Transactions of the Royal Society of London, 1879, 170: 231-256. DOI:10.1098/rstl.1879.0067 |
| [12] |
Gokcen T, MacCormack R W. Nonequilibrium effects for hypersonic transitional flows using continuum approach[R]. AIAA 1989-461, 1989. http://www.academia.edu/16327453/Real_Gas_Effects_on_a_Planetary_Re-entry_Capsule
|
| [13] |
MacCormack R W, Chapman D R, Gokcen T. Computational fluid dynamics near the continuum limit[R]. AIAA 1987-1115, 1987. https://link.springer.com/article/10.1007/BF02697944
|
| [14] |
Lockerby D A, Reese J M, Emerson D R, et al. Velocity boundary condition at solid walls in rarefied gas calculations[J]. Physical Review E : Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2004, 70(1): 17303. |
| [15] |
Lockerby D A, Gallis M A, Reese J M. Capturing the Knudsen layer in continuum-fluid models of nonequilibrium gas flows[J]. AIAA Journal, 2005, 43: 1391-1393. DOI:10.2514/1.13530 |
| [16] |
Lofthouse A J, Scalabrin L C, Boyd I D. Velocity slip and temperature jump in hypersonic aerothermodynamics[J]. Journal of Thermophysics and Heat Transfer, 2008, 22(1): 38-49. DOI:10.2514/1.31280 |
| [17] |
Sharipov F, Kalempa D. Velocity slip and temperature jump coefficients for gaseous mixtures. I. Viscous slip coefficient[J]. Physics of Fluids, 2003, 15: 1800. DOI:10.1063/1.1574815 |
| [18] |
Cercignani C. The Boltzmann equation and its applications[M]. Berlin : Springer-Verlag, 1988 : 455. https://link.springer.com/content/pdf/10.1007%2F978-3-642-50235-4_1.pdf
|
| [19] |
Deissler R G. An analysis of second-order slip flow and temperature-jump boundary conditions for rarefied gases[J]. International Journal of Heat and Mass Transfer, 1964, 7(6): 681-694. DOI:10.1016/0017-9310(64)90161-9 |
| [20] |
Beskok A, Karniadakis G E, Trimmer W. Rarefaction and compressibility effects in gas microflows[J]. Journal of Fluids Engineering, 1996, 118(3): 448-456. DOI:10.1115/1.2817779 |
| [21] |
Karniadakis G, Beskok A, Aluru N. Microflows and nanoflows : fundamentals and simulation[M]. New York : Springer, 2005 : 817. http://www.springer.com/us/book/9780387221977
|
| [22] |
Hsia Y T, Domoto G A. An experimental investigation of molecular rarefaction effects in gas lubricated bearings at ultra-low clearances[J]. Journal of Tribology, 1983, 105(1): 120-129. |
| [23] |
谢翀, 樊菁. Navier-Stokes方程二阶速度滑移边界条件的检验[J]. 力学学报, 2007(1): 1-6. Xie C, Fan J. Assessment of second-order velocity-slip boundary conditions of the Navier-Stokes equations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007(1): 1-6. (in Chinese) |
| [24] |
Bird G A. Molecular gas dynamics[M]. Oxford : Clarendon Press, 1976 : 238. http://www.worldcat.org/title/molecular-gas-dynamics/oclc/2462695
|
| [25] |
Bird G A. Molecular gas dynamics and the direct simulation of gas flows[M]. Oxford : Clarendon Press, 1994 : 458. http://www.worldcat.org/title/molecular-gas-dynamics-and-the-direct-simulation-of-gas-flows/oclc/29797920
|
| [26] |
Wagner W. A convergence proof for Bird′s direct simulation Monte Carlo method for the Boltzmann equation[J]. Journal of Statistical Physics, 1992, 66(3): 1011-1044. |
| [27] |
Erwin D A, Pham-Van-Diep G C, Muntz E P. Muntz E P. Nonequilibrium gas-flows. I : A detailed validation of Monte Carlo direct simulation for monatomic gases[J]. Physics of Fluids A : Fluid Dynamics, 1991, 3(4): 697-705. DOI:10.1063/1.858075 |
| [28] |
Vogenitz F W, Bird G A, Broadwell J E, et al. Theoretical and experimental study of rarefied supersonic flows about several simple shapes[J]. AIAA Journal, 1968, 6(12): 2388-2394. DOI:10.2514/3.4999 |
| [29] |
Moss J N, Price J M, Dogra V K, et al. Comparison of DSMC and experimental results for hypersonic external flows[R]. AIAA 1995-2028, 1995. http://www.academia.edu/30013793/Experimental_and_numerical_study_of_the_laminar_separation_in_hypersonic_flow
|
| [30] |
Gehman H W, Barry J L, Deal D W, et al. Report of Columbia accident investigation board[R]. NASA Technical Report, 2003. https://www.researchgate.net/publication/276854195_RIT_by_Cavity
|
| [31] |
Koppenwallner G, Ing P D. Low Reynolds number influence on aerodynamic performance of hypersonic lifting vehicles[R]. Aerodynamics of Hypersonic Lifting Vehicles, 1987, CP-428(AGARD) : 11. https://ar.scribd.com/document/241885999/Shock-Wave-Boundary
|
| [32] |
Oran E S, Oh C K, Cybyk B Z. Direct simulation Monte Carlo : Recent advances and applications[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 403-441. DOI:10.1146/annurev.fluid.30.1.403 |
| [33] |
Roveda R, Goldstein D B, Varghese P L. Hybrid Euler/particle approach for continuum/rarefied flows[J]. Journal of Spacecraft and Rockets, 1998, 35(3): 258-265. DOI:10.2514/2.3349 |
| [34] |
Hash D B, Hassan H A. A decoupled DSMC/Navier-Stokes analysis of a transitional flow experiment[R]. AIAA 1996-0353, 1996. http://www.oalib.com/paper/4250030
|
| [35] |
Lumpkin III F E, Stuart P C, Le Beau G J. Enhanced analysis of plume impingement during Shuttle-Mir docking using a combined CFD and DSMC methodology[R]. AIAA 1996-1877, 1996.
|
| [36] |
Hash D B, Hassan H A. Assessment of schemes for coupling Monte Carlo and Navier-Stokes solution methods[J]. Journal of Thermophysics and Heat Transfer, 1996, 10(2): 242-249. DOI:10.2514/3.781 |
| [37] |
Wadsworth D C, Erwin D A. Two-dimensional hybrid continuum/particle approach for rarefied flows[R]. AIAA 1992-2975, 1992. https://www.researchgate.net/publication/23927829_Two-dimensional_hybrid_continuumparticle_approach_for_rarefied_flows
|
| [38] |
Wadsworth D C, Erwin D A. One-dimensional hybrid continuum/particle simulation approach for rarefied hypersonic flows[R]. AIAA 1990-1690, 1990. https://www.researchgate.net/publication/23588803_One-dimensional_hybrid_continuumparticle_simulation_approach_for_rarefied_hypersonic_flows
|
| [39] |
Boyd I D, Chen G, Candler G V. Predicting failure of the continuum fluid equations in transitional hypersonic flows[J]. Physics of Fluids, 1995, 7(1): 210-219. DOI:10.1063/1.868720 |
| [40] |
Sun Q H, Boyd I D, Candler G V. A hybrid continuum/particle approach for modeling subsonic, rarefied gas flows[J]. Journal of Computational Physics, 2004, 194(1): 256-277. DOI:10.1016/j.jcp.2003.09.005 |
| [41] |
Schwartzentruber T E, Boyd I D. Detailed analysis of a hybrid CFD-DSMC method for hypersonic non-equilibrium Flows[R]. AIAA 2005-4829, 2005. https://experts.umn.edu/en/publications/detailed-analysis-of-a-hybrid-cfd-dsmc-method-for-hypersonic-non-
|
| [42] |
刘靖. 高超声速近连续流的混合算法研究[D]. 长沙: 国防科学技术大学, 2009. Liu J. Research on the hybrid algorithm of hypersonic near-continuum flow[D]. Changsha : National University of Defense Technology, 2009(in Chinese). http: //cpfd. cnki. com. cn/Article/CPFDTOTAL-AGLU200908008085. htm |
| [43] |
徐珊姝. 过渡区飞行器流场的数值模拟研究[D]. 北京: 清华大学, 2008. Xu S S. Numerical simulation of flows for vehicle flying in the transitional regime[D]. Beijing : Tsinghua University, 2008(in Chinese). http: //www. cnki. com. cn/Article/CJFDTotal-JRKR201118036. htm |
| [44] |
Bhatnagar P L, Gross E P, Krook M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511. DOI:10.1103/PhysRev.94.511 |
| [45] |
Holway Jr L H. Kinetic theory of shock structure using an ellipsoidal distribution function[M]. Toronto: Academic, 1965.
|
| [46] |
Xu K. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J]. Journal of Computational Physics, 2001, 171(1): 289-335. DOI:10.1006/jcph.2001.6790 |
| [47] |
Broadwell J E. Study of rarefied shear flow by the discrete velocity method[J]. Journal of Fluid Mechanics, 1964, 19(3): 401-414. DOI:10.1017/S0022112064000817 |
| [48] |
Cabannes H. Couette-flow for a gas with a discrete velocity distribution[J]. Journal of Fluid Mechanics, 1976, 76(2): 273-287. DOI:10.1017/S0022112076000633 |
| [49] |
Bobylev A V, Palczewski A, Schneider J. Discretization of the Boltzmann equation and discrete velocity models[M]. Oxford: Oxford University Press, 1995: 857-863.
|
| [50] |
Li Z H, Zhang H X. Numerical investigation from rarefied flow to continuum by solving the Boltzmann model equation[J]. International Journal for Numerical Methods in Fluids, 2003, 42(4): 361-382. DOI:10.1002/(ISSN)1097-0363 |
| [51] |
Li Z H, Zhang H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193(2): 708-738. DOI:10.1016/j.jcp.2003.08.022 |
| [52] |
李志辉. 从稀薄流到连续流的气体运动论统一数值算法研究[D]. 绵阳: 中国空气动力研究与发展中心, 2001. Li Z H. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[D]. Mianyang : China Aerodynamics Research and Development Center, 2001(in Chinese). http: //cpfd. cnki. com. cn/Article/CPFDTOTAL-ZGKQ200300001051. htm |
| [53] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论统一数值算法初步研究[J]. 空气动力学学报, 2000, 18(3): 255-263. Li Z H, Zhang H X. Study on gas kinetic algorithm for flows from rarefied transition to continuum[J]. Acta Aerodynamica Sinica, 2000, 18(3): 255-263. (in Chinese) |
| [54] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论模型方程算法研究[J]. 力学学报, 2002, 34(2): 145-155. Li Z H, Zhang H X. Study on gas kinetic algorithm for flows from rarefied transition to continuum using Boltzmann model equation[J]. Acta Mechanica Sinica, 2002, 34(2): 145-155. (in Chinese) |
| [55] |
Burnett D. The distribution of molecular velocities and the mean motion in a non-uniform gas[J]. Proceedings of the London Mathematical Society, 1936. |
| [56] |
Grad H. On the kinetic theory of rarefied gases[J]. Communications on Pure and Applied Mathematics, 1949, 2(4): 331-407. DOI:10.1002/(ISSN)1097-0312 |
| [57] |
Chapman S, Cowling T G. The mathematical theory of non-uniform gases : an account of the kinetic theory of viscosity, thermal conduction and diffusion in gases[M]. Cambridge: Cambridge University Press, 1970: 423.
|
| [58] |
Holway L H. Existence of kinetic theory solutions to the shock structure problem[J]. Physics of Fluids, 1964, 7: 911-913. DOI:10.1063/1.1711307 |
| [59] |
Weiss W. Comments on "Existence of kinetic theory solutions to the shock structure problem", 911 (1964)][J]. Physics of Fluids, 1996, 8(6): 1689-1690. DOI:10.1063/1.868947 |
| [60] |
Schaaf S A, Chambré P L. Flow of rarefied gases : fundamentals of gas dynamics[M]. Princeton: Princeton University Press, 1958: 687-739.
|
| [61] |
Levermore C D. Moment closure hierarchies for kinetic theories[J]. Journal of Statistical Physics, 1996, 83(5/6): 1021-1065. |
| [62] |
Levermore C D, Morokoff W J. The Gaussian moment closure for gas dynamics[J]. Journal on Applied Mathematics, 1998, 59(1): 72-96. |
| [63] |
Groth C P T, Roe P L, Gombosi T I, et al. On the nonstationary wave structure of a 35-moment closure for rarefied gas dynamics[R]. AIAA 1995-2312, 1995. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.322.4796
|
| [64] |
Brown S L. Approximate Riemann solvers for moment models of dilute gases[D]. Ann Arbor : The University of Michigan, 1996. https://www.researchgate.net/publication/226712342_Application_of_the_10-Moment_Model_to_MEMS_Flows
|
| [65] |
Myong R. A new hydrodynamic approach to computational hypersonic rarefied gas dynamics[R]. AIAA 1999-3578, 1999. http://www.annualreviews.org/doi/citedby/10.1146/annurev.fluid.30.1.469
|
| [66] |
Eu B C. Kinetic theory and irreversible thermodynamics[M]. New York: John Wiley & Sons, Inc, 1992: 732.
|
| [67] |
Wang Chang C S. On the theory of the thickness of weak shock waves[R]. University of Michigan : Research, APL/JHU, CM-503, 1948. https://link.springer.com/article/10.1007/BF03185039
|
| [68] |
Sherman F S, Talbot L. Structure of weak shock waves in a monatomic gas[R]. NASA Technical Report, 1959. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19980228372.pdf
|
| [69] |
Foch Jr J D. On higher order hydrodynamic theories of shock structure[M]. New York: Springer Verlag, 1973: 123-140.
|
| [10] |
Butler D S, Anderson W M. Shock structure calculations by an orthogonal expansion method[A]. //Proceedings of the fifth International Symposium Oxford[C]. Oxford : 1967.
|
| [71] |
Vestner H. Theory of the viscomagnetic heat flux[J]. Zeitschrift fuer Naturforschung, 1976, 31: 540-552. |
| [72] |
Hermans L J, Eggermont G E, Knaap H F, et al. The use of a magnetic field in an experimental verification of transport theory for rarefied gases[A].// Rarefied Gas Dynamics : Proceedings of the Eleventh International Symposium Cannes[C]. Cannes : 1979.
|
| [73] |
Fiscko K A. Study of continuum higher order closure models evaluated by a statistical theory of shock structure[D]. Stanford : Stanford University, 1988. http://web.stanford.edu/group/frg/seminars/index.html
|
| [74] |
Fiscko K A, Chapman D R. Comparison of Burnett, super-Burnett and Monte Carlo solutions for hypersonic shock structure[M]. asadena: AIAA, 1988: 374-395.
|
| [75] |
Lin T C, Street R E. Effect of variable viscosity and thermal conductivity on high-speed slip flow between concentric cylinders[J]. NACA Technical Report, 1954. |
| [76] |
Bobylev A V. The Chapman-Enskog and Grad methods for solving the Boltzmann equation[J]. Soviet Physics Doklady, 1982, 27(1): 29-31. |
| [77] |
Zhong X L, MacCormack R W, Chapman D R. Stabilization of the Burnett equations and application to hypersonic flows[J]. AIAA Journal, 1993, 31(6): 1036-1043. DOI:10.2514/3.11726 |
| [78] |
Agarwal R K, Yun K Y, Balakrishnan R. Beyond Navier-Stokes : Burnett equations for flows in the continuum-transition regime[J]. Physics of Fluids, 2001, 13(10): 3061-3085. DOI:10.1063/1.1397256 |
| [79] |
Lumpkin F E. Development and evaluation of continuum models for translational-rotational nonequilibrium[D]. Stanford : Stanford University, 1990. http://www.jsce.or.jp/nctam/forchairmans/NCTAMVol-54/GS/2G09.pdf
|
| [80] |
Uribe F J, Velasco R M, Garcia-Colin L S. Bobylev′s instability[J]. Physical Review E : Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2000, 62(4): 5835-5838. |
| [81] |
Soderholm L H. Hybrid Burnett equations : a new method of stabilizing[J]. Transport Theory and Statistical Physics, 2007, 36(4/6): 495-512. |
| [82] |
Jou D, Casas-Vazquez J, Madureira J R, et al. Higher-order hydrodynamics : extended Fick′s Law, evolution equation, and Bobylev′s instability[J]. Journal of Chemical Physics, 2002, 116(4): 1571-1584. DOI:10.1063/1.1426416 |
| [83] |
Welder W T, Chapman D R, MacCormack R W. Evaluation of various forms of the Burnett equations[J]. AIAA 1993-3094, 1993. |
| [84] |
Comeaux K A, Chapman D R, MacCormack R W. An analysis of the Burnett equations based on the second law of thermodynamics[J]. AIAA 1995-0415, 1995. |
| [85] |
Jin S, Slemrod M. Regularization of the Burnett equations via relaxation[J]. Journal of Statistical Physics, 2001, 103(5): 1009-1033. |
| [86] |
Balakrishnan R. An approach to entropy consistency in second-order hydrodynamic equations[J]. Journal of Fluid Mechanics, 2004, 503: 201-245. DOI:10.1017/S0022112004007876 |
| [87] |
Balakrishnan R, Agarwal R K. Numerical simulation of Bhatnagar-Gross-Krook-Burnett equations for hypersonic flows[J]. Journal of Thermophysics and Heat Transfer, 1997, 11(3): 391-399. DOI:10.2514/2.6253 |
| [88] |
Balakrishnan R, Agarwal R K, Yun K Y. BGK-Burnett equations for flows in the continuum-transition regime[J]. Journal of Thermophysics and Heat Transfer, 1999, 13(4): 397-410. DOI:10.2514/2.6464 |
| [89] |
Reese J M, Woods L C, Thivet F, et al. A 2nd-order description of shock structure[J]. Journal of Computational Physics, 1995, 117(2): 240-250. DOI:10.1006/jcph.1995.1062 |
| [90] |
Woods L C. An introduction to the kinetic theory of gases and magnetoplasmas[M]. New York: Oxford University Press, 1993: 300.
|
| [91] |
Dadzie S K. A thermo-mechanically consistent Burnett regime continuum flow equation without Chapman-Enskog expansion[J]. Journal of Fluid Mechanics, 2013, 716. |
| [92] |
Banach Z, Larecki W, Zajaczkowski W. Stability analysis of phonon transport equations derived via the Chapman-Enskog method and transformation of variables[J]. Physical Review E : Statistical Nonlinear and Soft Matter Physics, 2009, 80. |
| [93] |
Wang Z H, Bao L, Tong B G. Variation character of stagnation point heat flux for hypersonic pointed bodies from continuum to rarefied flow states and its bridge function study[J]. Science in China Series G : Physics Mechanics & Astronomy, 2009, 52(12): 2007-2015. |
| [94] |
Wang Z H, Bao L, Tong B G. Rarefaction criterion and non-Fourier heat transfer in hypersonic rarefied flows[J]. Physics of Fluids, 2010, 22(12): 126103. DOI:10.1063/1.3525289 |
| [95] |
Bao F B, Lin J Z. Linear stability analysis for various forms of one-dimensional Burnett equations[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(3): 295-303. |
| [96] |
Bao F B, Zhu Z H, Lin J Z. Linearized stability analysis of two-dimension Burnett equations[J]. Applied Mathematical Modelling, 2012, 36(5): 1902-1909. DOI:10.1016/j.apm.2011.07.078 |
| [97] |
Galkin V S. Burnett′s equations for multicomponent mixtures of polyatomic gases[J]. Journal of Applied Mathematics and Mechanics, 2000, 64(4): 569-582. DOI:10.1016/S0021-8928(00)00083-6 |
| [98] |
Zhong X L, Furumoto G H. Augmented Burnett-equation solutions over axisymmetric blunt bodies in hypersonic flow[J]. Journal of Spacecraft and Rockets, 1995, 32(4): 588-595. DOI:10.2514/3.26657 |
| [99] |
Yang Z, Garimella S V. Rarefied gas flow in microtubes at different inlet-outlet pressure ratios[J]. Physics of Fluids, 2009, 21(5): 711-715. |
| [100] |
Singh N, Agrawal A. The Burnett equations in cylindrical coordinates and their solution for flow in a microtube[J]. Journal of Fluid Mechanics, 2014, 751: 121-141. DOI:10.1017/jfm.2014.290 |
| [101] |
Bao F B, Lin J Z. Burnett simulation of gas flow and heat transfer in micro Poiseuille flow[J]. International Journal of Heat and Mass Transfer, 2008, 51(15): 4139-4144. |
| [102] |
Xue H, Ji H M. Prediction of flow and heat transfer characteristics in micro-Couette flow[J]. Microscale Thermophysical Engineering, 2003, 7(1): 51-68. DOI:10.1080/10893950390150430 |
| [103] |
Uribe F J, Garcia A L. Burnett description for plane Poiseuille flow[J]. Physical Review E : Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1999, 60(4): 4063-4078. |
| [104] |
Singh N, Dongari N, Agrawal A. Analytical solution of plane Poiseuille flow within Burnett hydrodynamics[J]. Microfluidics and Nanofluidics, 2014, 16(1/2): 403-412. |
| [105] |
Singh N, Gavasane A, Agrawal A. Analytical solution of plane Couette flow in the transition regime and comparison with direct simulation Monte Carlo data[J]. Computers & Fluids, 2014, 97: 177-187. |
| [106] |
Truesdell C, Muncaster R G. Fundamentals of Maxwell′s kinetic theory of a simple monatomic gas[J]. Journal of Fluid Mechanics, 1980, 104(1): 655-662. |
| [107] |
赵文文. 高超声速流动Burnett方程稳定性与数值计算方法研究[D]. 杭州: 浙江大学, 2014. Zhao W W. Linearized stability analysis and numerical computation of Burnett equations in hypersonic flow[D]. Hangzhou : Zhejiang University, 2014(in Chinese). http: //www. cnki. com. cn/Article/CJFDTotal-HKXB201605003. htm |
| [108] |
Zhao W, Chen W, Liu H, et al. Computation of 1D shock structure in a gas in rotational non-equilibrium using a new set of simplified Burnett equations[J]. Vacuum, 2014, 109: 319-325. DOI:10.1016/j.vacuum.2014.05.011 |
| [109] |
Weiss W. Continuous shock structure in extended thermodynamics[J]. Physical Review E : Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1995, 52(6). |
| [110] |
Reitebuch D, Weiss W. Application of high moment theory to the plane Couette flow[J]. Continuum Mechanics and Thermodynamics, 1999, 11(4): 217-225. DOI:10.1007/s001610050112 |
| [111] |
Struchtrup H. Macroscopic transport equations for rarefied gas flows[M]. Berlin: Springer Berlin Heidelberg, 2005: 245.
|
| [112] |
Struchtrup H, Torrilhon M. Regularization of Grad′s 13-moment equations : derivation and linear analysis[J]. Physics of Fluids, 2003, 15(9): 2668-2680. DOI:10.1063/1.1597472 |
| [113] |
Karlin I V, Gorban A N, Dukek G, et al. Dynamic correction to moment approximations[J]. Physical Review E : Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1998, 57(2): 1668-1672. |
| [114] |
Muller I, Reitebuch D, Weiss W. Extended thermodynamics-consistent in order of magnitude[J]. Continuum Mechanics and Thermodynamics, 2003, 15(2): 113-146. DOI:10.1007/s00161-002-0106-0 |
| [115] |
Torrilhon M, Struchtrup H. Regularized 13-moment equations : shock structure calculations and comparison to Burnett models[J]. Journal of Fluid Mechanics, 2004, 513: 171-198. DOI:10.1017/S0022112004009917 |
| [116] |
Eu B C. Nonequilibrium statistical mechanics[M]. Dordrecht: Kluwer Academic Publishers Group, 1998.
|
| [117] |
Eu B C. Kinetic Theory and Irreversible Thermodynamics[M]. New York: Wiley, 1992: 752.
|
| [118] |
Alghoul M, Eu B C. Generalized hydrodynamics and shock waves[J]. Physical Review E : Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1997, 56(3A): 2981-2992. |
| [119] |
Eu B C, Ohr Y G. Generalized hydrodynamics, bulk viscosity, and sound wave absorption and dispersion in dilute rigid molecular gases[J]. Physics of Fluids, 2001, 13(3): 744-753. DOI:10.1063/1.1343908 |
| [120] |
Myong R S. Thermodynamically consistent hydrodynamic computational models for high-Knudsen-number gas flows[J]. Physics of Fluids, 1999, 11(9): 2788-2802. DOI:10.1063/1.870137 |
| [121] |
Myong R S. A computational method for Eu′s generalized hydrodynamic equations of rarefied and microscale gasdynamics[J]. Journal of Computational Physics, 2001, 168(1): 47-72. DOI:10.1006/jcph.2000.6678 |
| [122] |
Myong R S. A generalized hydrodynamic computational model for rarefied and microscale diatomic gas flows[J]. Journal of Computational Physics, 2004, 195(2): 655-676. DOI:10.1016/j.jcp.2003.10.015 |
| [123] |
Myong R S. Coupled nonlinear constitutive models for rarefied and microscale gas flows : subtle interplay of kinematics and dissipation effects[J]. Continuum Mechanics and Thermodynamics, 2009, 21(5): 389-399. DOI:10.1007/s00161-009-0112-6 |
| [124] |
Le N T, Xiao H, Myong R S. A triangular discontinuous Galerkin method for non-Newtonian implicit constitutive models of rarefied and microscale gases[J]. Journal of Computational Physics, 2014, 273: 160-184. DOI:10.1016/j.jcp.2014.05.013 |
| [125] |
Myong R S. A full analytical solution for the force-driven compressible Poiseuille gas flow based on a nonlinear coupled constitutive relation[J]. Physics of Fluids, 2011, 23: 012002. DOI:10.1063/1.3540671 |
| [126] |
Zhao W, Jiang Z, Chen W. Computation of 1D shock structure using nonlinear coupled constitutive relations and generalized hydrodynamic equations[A]. // 30th International Symposium on Rarefied Gas Dynamics[C]. Victoria, 2016. http://wrap.warwick.ac.uk/view/publications_funders/Engineering_and_Physical_Sciences_Research_Council_=28EPSRC=29_.creators_name.html
|



