动稳定性导数是飞行器稳定性和可控性分析与设计的关键参数, 对飞行器的控制系统设计和飞行品质有着重要影响.随着导弹武器系统向高速化、精确化方向的不断发展, 对高超声速巡航导弹、高性能战术导弹和再入飞行器等各类高速飞行器设计的性能要求不断提高, 无论在巡航阶段还是在大幅机动阶段都须要对飞行器开展精确控制, 且高超声速飞行器气动力对姿态变化和扰动的响应极快, 控制系统有效调整时间极短, 因此, 动稳定性导数的精确测量变得尤为重要[1-2].
常规动导数风洞试验主要有自由振动和强迫振动两种试验方法.欧美和俄罗斯等对以上两类常规动导数试验技术的研究起步较早, 在从低速到高超声速的各类风洞内都发展了相配套的动导数试验设备, 并且已成为各类航空、航天飞行器研制过程中所必需的试验技术[3].经过几十年的发展, 国内动导数试验技术也相对比较成熟, 并在主流的低速、亚跨超声速风洞内发展了相应的动导数试验系统.高超声速动导数试验技术的相关文献主要基于Φ 0.5 m高超声速风洞[4-9], 而关于Φ 1 m量级高超声速风洞动导数试验技术研究的文献较少[3].
自由振动和强迫振动两种试验方法各有特色, 但对于再入弹头、返回舱等类型飞行器, 自由振动试验方法更具优势.就试验能力而言, 自由振动试验方法只能够测量直接导数, 强迫振动试验方法既能够测量直接导数, 也能够测量交叉导数; 就系统特点而言, 自由振动试验系统属于能量开放系统, 试验系统简单, 连接环节少, 能够在试验过程中直接反映气动阻尼影响效应, 最终获得的动导数为直接量.而强迫振动试验系统属于能量封闭系统, 系统相对复杂, 连接环节较多, 最终获得的动导数为间接量.因此, 由长期经验总结可知, 对于战斗机等气动阻尼强、交叉导数不能忽略的飞行器, 适合采用强迫振动试验方法; 而对于导弹、弹头、返回舱等直接导数占主导, 且气动阻尼较弱的飞行器, 自由振动试验技术具备更高的测量精度.目前, 国内除中国航天空气动力技术研究院长期重视发展自由振动试验技术以外, 其他主要气动研究单位均以发展强迫振动试验技术为主.
随着国内大尺度高超声速风洞的持续建设, 在为自由振动试验技术发展提供更大空间的同时, 也带来了一系列新的问题与矛盾, 其中气动载荷与频率模拟之间的矛盾最为突出.具体而言, 较之于Φ 0.5 m量级风洞, Φ 1 m量级风洞中模型尺寸可增加1倍, 更有利于飞行器局部细节的模拟, 但作用于模型的气动载荷则呈平方倍数关系增加, 且对应风洞试验需模拟的振动频率呈倍数关系降低.而随着对飞行器有效突防需求的提高, 高机动能力的要求使得飞行器静稳定度及自然频率进一步降低, 进而导致兼顾减缩频率相似和系统强度要求的难度进一步增大.
针对上述问题, 研究团队专门研制了可用于低频、大载荷高超声速飞行器的组合式俯仰动导数自由振动天平系统.其中, 低阻尼滚动轴承在放开俯仰通道自由度的同时, 承载模型的轴向力和法向力, 确保模型在弹性应变梁断裂时不受破坏; 可拆卸弹性梁可根据试验要求更改结构尺寸, 调整系统振动频率及应变片输出信号的质量.试验过程中通过采集弹性梁上应变片的动态信号, 获得模型的静、动态力矩特性.应用该系统, 于2014年在中国航天空气动力技术研究院FD-07风洞完成前期试验验证, 并成功获得了弹头端头在不同烧蚀量情况下的俯仰动稳定性导数及小俯仰力矩变化量[8-9].
本文工作在总结前期试验技术经验的基础上, 进一步针对Φ 1 m量级高超声速风洞进行了天平系统的优化升级, 并以10°半锥角、3种不同钝度比的圆锥标模为试验对象, 对试验系统的俯仰动导数测量能力进行了专门考核.最终的风洞试验结果表明, 本文发展的自由振动试验技术能够准确获得不同钝度圆锥标模的动稳定性变化规律, 并且能够精确测量该标模较小的俯仰动导数量值.本试验技术重复性好, 技术可靠, 试验精度满足相关飞行器对俯仰动导数的测量需求.
1 风洞试验设备、自由振动天平和标模 1.1 试验设备标模验证试验在中国空气动力研究与发展中心Ф 1 m高超声速风洞(FD-30)进行.该高超声速风洞采用高压下吹-真空抽吸的运行方式.试验Mach数范围为4~10, 喷管出口直径为1 m, 最高设计压力为8.0 MPa, 运行时间≥30 s.风洞试验段内流场品质指标满足国军标GJB4399-2002《高超声速风洞气动力试验方法》和GJB6758-2009《常规高超声速风洞测压试验方法》中流场均匀性指标要求, 最大Mach数偏差<1%.
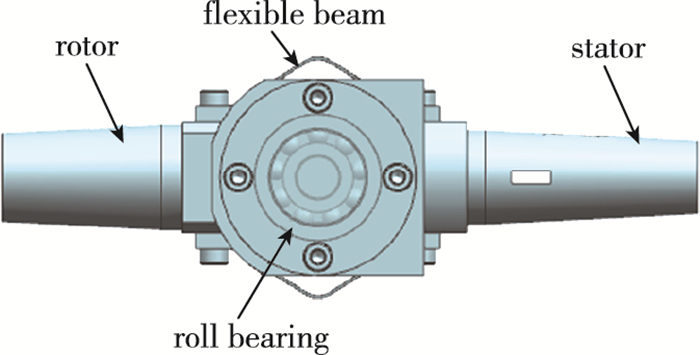
1.2 自由振动天平轴对称弹头类飞行器在高超声速风洞动态试验中具有气动载荷大、阻尼小、试验振动频率低的特点.若采用传统一体式动态天平, 弹性应变梁厚度应足够大以满足高承载能力要求.然而弹性应变梁厚会导致振动频率高, 机械阻尼大, 无法兼顾减缩频率相似和小气动力精确测量的要求.为此, 专门设计如图 1所示组合式动态天平, 两组轴承承载试验模型的轴向和径向气动载荷, 弹性应变梁仅提供弹性回复力, 从而最大限度减小弹性应变梁厚度, 在降低系统机械阻尼的同时更有利于模拟系统的低频振动特性.
|
| 图 1 组合式动态天平 Fig.1 Combinatory dynamic balance |
较之于一体式天平, 组合式动态天平部件多, 装配精度要求严格, 部件加工精度、装配误差、结构不对称性及轴承摩擦等均会对高精度气动力测量造成较大影响.因此, 在总结前期试验技术应用经验的基础上, 组合式动态天平选用高精度、低摩擦的进口轴承, 且轴承转动中心与上下两片弹性梁几何中心重合, 在减小摩擦力的情况下保证弹性梁两端应变片变形的一致性; 其次, 加工过程中轴承安装孔和转轴均严格根据轴承内外圈尺寸配作, 满足滑动配合要求, 避免轴承内外圈因受挤压而导致摩擦力变大; 同时, 转轴上设计有专用定位部件, 保证装配后铰接式天平的固定端与自由端轴线共面, 避免弹性梁受到侧向的扭转力.最后, 根据上述技术要求设计装配步骤, 保证各部件装配位置可调, 系统装配精度可控. 图 2为新设计组合式动态天平的地面振动曲线与理论仿真曲线对比.由图 2可知, 两者在用于计算系统机械阻尼的较大振幅曲线段(0.7~2.5°)重合度较好, 证明了通过方案优化设计以及对加工和装配的精度控制, 组合式天平无额外次频及机械阻尼引入, 满足动导数试验要求.

|
| 图 2 地面振动曲线与理论曲线对比 Fig.2 Contrasts between oscillating and theoretic curve |
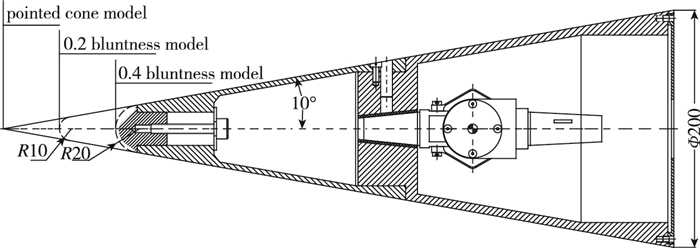
为了验证试验技术的可行性和可靠性, 采用高超声速弹头标模在Ф 1 m高超声速风洞进行风洞试验.在国内现有的国军标准[10]中, 仅有对于动导数试验的技术要求, 而并没有统一的、经标准化认证的动导数试验数据参考, 这也是本文研究的重要意义所在.因此, 结合本次标模试验需求, 考虑到半锥角较大时, 流动分离点和转捩点对风洞试验条件不敏感, 气动力数据重复性好, 试验选用国际通用的10°锥角尖锥标准模型(HSCM-2模型)和两种10°锥角不同头部钝度模型.如图 3所示, 尖锥模型全长564 mm, 底部直径为Ф 200 mm, 半锥角为10°, 质心距尖锥头部长度为全长的70%.两种钝度比分别为: 2×R10/Ф200=0.1, 2×R20/Ф200=0.2.
|
| 图 3 试验标模外形 Fig.3 Testing standard model |
标模试验对比数据从文献[11]中提取.文献试验中实际Mach数为6.85, 试验Reynolds数1.45×106~2.17×106, 以2倍模型长度为参考量的减缩频率范围为0.001 8~0.009 2, 自由振动最大振幅约1°.上述文献数据已被多个研究团队引用, 数据可靠, 可以使用.
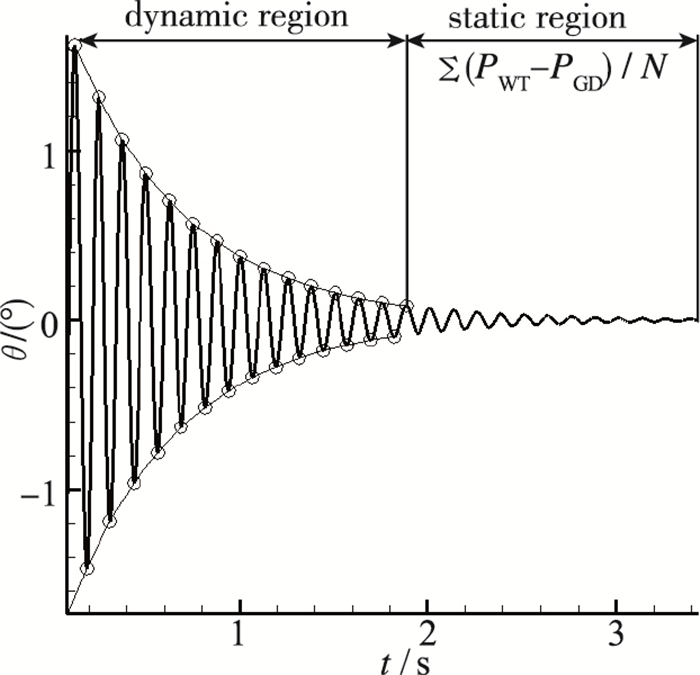
2 试验原理及方法本试验技术可同时获得系统俯仰阻尼导数和静力矩系数.风洞试验过程中, 利用气缸激励动态天平产生初始角位移, 释放后系统进行自由振动.对采集到的弹性元件动态应变信号, 从幅值衰减明显的大振幅区间中提取阻尼导数, 对于幅值变化平缓的小振幅区间, 认为试验模型已形成绕平衡位置的小扰动运动, 采用数值平均的方法从整周期振动信号中获得平衡状态静力矩, 如图 4所示[8-9].
|
| 图 4 试验原理示意 Fig.4 Principle sketch of test |
阻尼导数计算方法详见文献[1].对于静力矩测量而言, 如文献[13]所述的静态小俯仰力矩测量是建立在大量对称性试验基础之上的, 其原理是以尽可能多的数据平均来消除系统随机误差, 以提高风洞测量的精度[14].文献[15]的研究亦指出, 多个周期数据的平均, 能够很好地消除模型惯性力影响, 获得满意的静态气动数据.因此, 本试验技术对于小振幅数据的大量平均能够极大程度地消除常规天平单次试验所带来的随机误差, 从而有效提高对俯仰力矩微小变化量的测量精度, 且其测量效果已通过风洞试验验证[8-9].本文重点关注对于俯仰动稳定性导数的测量, 有关静力矩测量及数据处理可重点参见文献[8]和文献[15].
3 试验结果与讨论风洞试验的名义Mach数为7, 实际Mach数为6.85, 前室总压P0=3 MPa, 前室总温T0=632 K, 动压q∞=23 795 Pa, 单位Reynolds数Re=1.27×107/m, 以底部直径为参考长度的Reynolds数为Reb =2.54×106, 与文献[11], [12]Reynolds数上限一致.模型-天平系统的地面振动频率f=7.6 Hz, 对应以2倍模型长度为参考量的减缩频率为0.012 6, 与上述文献减缩频率上限基本一致, 量值略高.本次标模试验模型自由振动的最大振幅约为1.7°.参考长度为试验模型全长0.564 m, 参考面积为模型底部面积0.031 4 m2.由于标模为弹头类外形, 动导数无量纲化参数取V∞/(q∞SL2).
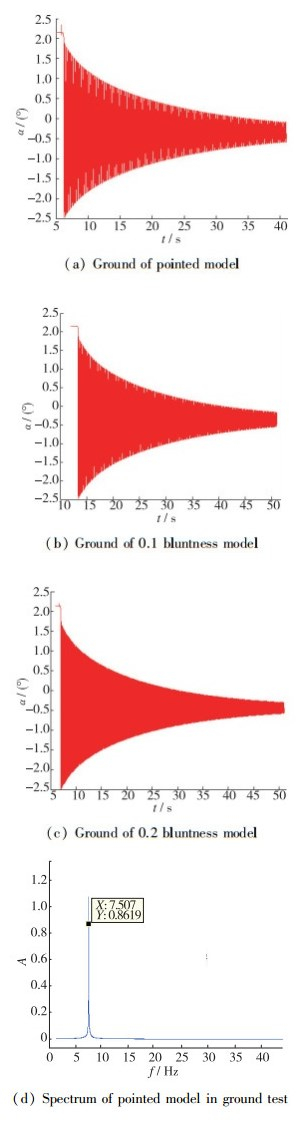
由于系统在风洞上的安装误差, 且系统处于动态运动的状态, 可能导致系统机械阻尼的偏差.为确定系统的工作状态是否正常, 并较精确地给出每次风洞试验的机械阻尼, 在每次风洞试验吹风前后均在风洞上重新测试系统的机械阻尼. 图 5为3种标模典型状态的地面振动曲线及对应频谱图, 由该图可知, 各试验状态吹风前后的有量纲机械阻尼变化较小, 均在2.74×10-2~2.90×10-2 N·m·s/rad之间, 且无额外次频引入.
|
| 图 5 标模无风振动曲线及频谱 Fig.5 Wind-off oscillating curves and frequency spectrum of the standard model |
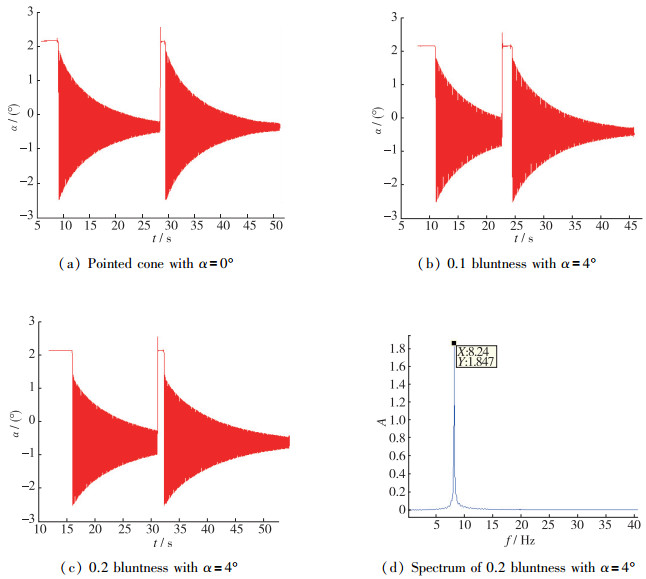
图 6为3种标模典型状态的风洞试验曲线及频谱图.可以看出, 风洞试验过程中, 试验系统振动曲线光滑、同一试验状态重复性较好, 结果随攻角变化规律明确, 亦无额外次频引入.同时可见, 由于静、动态气动力影响, 风洞试验过程中自由振动频率较地面状态略有增大, 约为8.2 Hz, 这与常规自由振动试验规律一致.由于动态天平相对于常规测力天平刚度较低, 弹性应变梁在气动力和重力作用下会发生一定变形, 试验数据处理过程中进行了弹性角修正, 确保了测量结果的可靠性.
|
| 图 6 典型状态风洞试验振动曲线及频谱 Fig.6 Wind-on oscillating curves and frequency spectrum of the standard model |
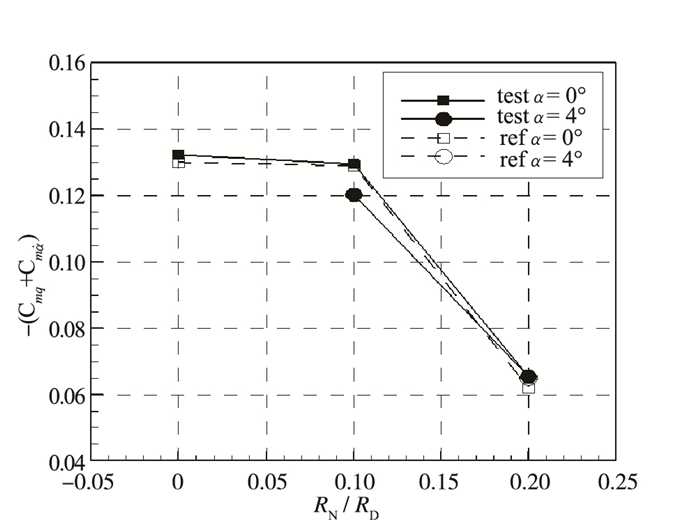
表 1和图 7分别给出了本文试验结果与文献[11]结果对比数据及曲线.由表 1和图 7可见, 本次标模俯仰动导数试验结果与文献结果趋势一致, 量值吻合良好, 除钝度比0.2模型的相对误差在5.63%以外, 其余3个可对比状态的动导数相对误差均低于2%.这是由于, 随模型钝度增大, 气动阻尼大幅降低, 测量误差随之增大.综合而言, 4个可对比状态的平均相对误差为2.11%.由以上试验数据量化分析可知, 本次标模试验较为成功, 文中所述试验系统满足风洞动态试验的精度要求.
|
| 图 7 本文试验结果与文献[17]结果对比曲线 Fig.7 Pitching damps between test and reference[17] results |
进一步由图 7可见, 无翼弹头外形在高超声速状态下的气动阻尼较低, 俯仰动导数量值对头部钝度较敏感, 且随头部钝度增大而降低.详细分析可见, 在零攻角状态下, 相较头部尖锥模型, 钝度比0.2的小钝锥外形气动阻尼大幅降低, 降低幅度约为50%.同时可见, 在攻角0~4°范围内, 动导数随攻角变化较小, 且变化趋势无明确规律, 这与文献[11]给出结果的规律一致.对应工程应用可知, 在采用烧蚀热防护情况下, 随着弹体端头烧蚀后退量的不断增大, 其动稳定性明显降低.因此, 对于有控飞行器, 应当在控制增稳设计中重点考虑此动稳定性的动态变化规律; 而对于无控的弹道式再入飞行器, 也须将飞行中烧蚀量的变化与动导数的变化过程进行耦合建模, 以提高气动设计及落点精度评估的可靠性.
4 结论动导数的精确测量是未来新型高超声速飞行器研制和发展的重要基础.为适应高超声速地面试验设备尺度不断增大的趋势, 本文进一步发展了组合式俯仰动导数自由振动天平系统, 并以10°半锥角、3种不同钝度的圆锥标模为考核对象, 完成了在Ma=7, 低振动频率及大气动载荷条件下的高超声速风洞俯仰动导数考核试验.试验结果显示, 本文发展的试验技术能够准确获得不同钝度圆锥标模的动稳定性变化规律, 并且能够对高超声速状态下较小的俯仰动导数量值进行精确测量, 从而有效解决了自由振动试验技术在大尺度高超声速风洞中面临的气动载荷大, 天平-模型系统刚度、阻尼和振动频率难以兼顾的问题.本文试验技术成熟可靠, 可用于相关飞行器动导数测量, 文中试验结果亦可供相关试验技术及数值模拟方法验证参考使用.
致谢: 感谢中国航天空气动力技术研究院李潜研究员、毕志献研究员、秦永明研究员以及二所科技处在工作开展过程中给予的关心、指导与帮助!感谢气动中心超高速所许晓斌研究员、谢飞高工及何超工程师在风洞试验过程中给予的密切配合与支持!| [1] |
李周复. 风洞特种试验技术[M]. 北京: 航空工业出版社, 2010. Li Z F. Special technique of wind tunnel test[M]. Beijing: Aviation Industry Press, 2010. (in Chinese) |
| [2] |
唐志共, 许晓斌, 杨彦广, 等. 高超声速风洞气动力试验技术进展[J]. 航空学报, 2015, 36(1): 86-97. Tang Z G, Xu X B, Yang Y G, et al. Research progress on hypersonic wind tunnel aerodynamic testing techni-ques[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 86-97. (in Chinese) |
| [3] |
郭雷涛. ϕ1m高超声速风洞动导数试验技术研究[D]. 绵阳: 中国空气动力研究与发展中心, 2013. Guo L T. Investigation on dynamic derivative test technique in ϕ1m hypersonic wind tunnel[D]. Mian-yang: China Aerodynamics Research and Development Center, 2013(in Chinese). |
| [4] |
赵忠良, 任斌, 黄叙辉, 等. 跨超、高超声速风洞模型动导数试验技术研究[J]. 航空学报, 2000, 21(1): 52-55. Zhao Z L, Ren B, Huang X H, et al. Investigation on model dynamic stability derivatives test techniques in trans-, supers-, hypersonic wind tunnels[J]. Acta Aeronautica et Astronautica Sinica, 2000, 21(1): 52-55. (in Chinese) |
| [5] |
李潜. 不同半锥角钝锥动导数研究[R]. 北京: 北京空气动力研究所, 2003. Li Q. Research of blunt conical for different half conical angle[R]. Beijing: Beijing Institute of Aerodynamics, 2003(in Chinese). |
| [6] |
白葵, 冯明溪, 付光明. 小不对称再入体滚转气动力测量技术[J]. 流体力学实验与测量, 2002, 16(3): 63-67, 72. Bai K, Feng M X, Fu G M. Experimental technique for rolling aerodynamic of slight asymmetric re-entry body[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(3): 63-67, 72. (in Chinese) |
| [7] |
赵俊波, 梁彬, 付增良, 等. 机动式再入弹头小滚转气动力风洞试验技术[J]. 空气动力学学报, 2016, 34(1): 53-58. Zhao J B, Liang B, Fu Z L, et al. Experimental techni-que for micro rolling aerodynamics of a maneuvering reentry body[J]. Acta Aerodynamica Sinica, 2016, 34(1): 53-58. (in Chinese) |
| [8] |
赵俊波, 付增良, 梁彬, 等. 再入弹头小不对称俯仰气动特性测量技术研究[J]. 实验流体力学, 2015, 29(5): 55-59. Zhao J B, Fu Z L, Liang B, et al. Research on the wind tunnel test techniques for micro-pitching-aerodynamics of re-entry body[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(5): 55-59. (in Chinese) |
| [9] |
赵俊波, 付增良, 梁彬, 等. 再入弹头小气动力风洞试验技术[C]. 中国航天空气动力技术研究院第二研究所第二届风洞试验与测试技术交流会论文集, 北京: 2015: 1-8. Zhao J B, Fu Z L, Liang B, et al. Experimental tech-nique in wind tunnel for micro-aerodynamics of re-entry body[C]. The Second Session Wind Tunnel Experiment and Testing Technique of 2nd Academic Institute of CAAA, Beijing: 2015: 1-8(in Chinese). |
| [10] |
GJB 4399-2002. 高超声速风洞气动力试验方法[S]. 2002. GJB 4399-2002. Aerodynamic test method in hypersonic wind tunnel[S]. 2002(in Chinese). |
| [11] |
East R A, Hutt G R. Comparison of predictions and experimental data for hypersonic pitching motion stability[J]. Journal of Spacecraft and Rockets, 25(3): 225-233. DOI:10.2514/3.25975 |
| [12] |
East R A, Qasrawi A M, Khalid M. An experimental study of the hypersonic dynamic stability of pitching blunt conical and hyperballistic shapes in short running time facility[R]. AGARD-CP-235 Paper 12, 1978.
|
| [13] |
吕治国, 刘洪山, 张雁, 等. 烧蚀端头锥模型激波风洞试验研究[J]. 流体力学实验与测量, 2003, 17(1): 6-8, 14. LUV Z G, Liu H S, Zhang Y, et al. The balance test in shock tunnel for the war-head with ablation nose[J]. Experiments and Measurements in Fluid Mechanics, 2003, 17(1): 6-8, 14. (in Chinese) |
| [14] |
恽起麟. 风洞实验数据的误差与修正[M]. 北京: 国防工业出版社, 1996, 3-21. Yun Q L. Wind tunnel experiment data error and correction[M]. Beijing: National Defense Industry Press, 1996, 3-21. (in Chinese) |
| [15] |
刘云峰, 汪运鹏, 苑朝凯, 等. JF12长实验时间激波风洞10°尖锥气动力实验研究[J]. 气体物理, 2017, 2(2): 1-7. Liu Y F, Wang Y P, Yuan C K, et al. Aerodynamic force measurements of 10° half-angle cone in JF12 long-test-time shock tunnel[J]. Physics of Gas, 2017, 2(2): 1-7. (in Chinese) |




