2. 中国科学院大学工程科学学院,北京 100049
2. School of Engineering Sciences, University of Chinese Academy of Sciences, Beijng 100049, China
常规高超声速风洞的实验气流总温低声速低, 忽略了热化学反应这一高超声速流动的关键特征.因此, 在地面高超声速实验中, 如何研究真实气体效应对气动力和力矩的影响是一个非常困难的问题, 一度成为了“未知”问题[1].在航天飞机首次入轨飞行中发现, 在预测的配平攻角下, 有明显的俯仰力矩增量.在首次飞行前, Woods等[2]基于气体动力学设计数据手册预测, 在40°的再入攻角下, 襟翼的配平角是7.5°.但实际飞行表明, 飞机的襟翼需要转过一个更大的转角, 约为16°, 比理想气体的预测值增大了1倍.该转角非常接近飞机襟翼的设计极限, 若需要更大的转角, 将会导致严重的飞行事故.后来的研究表明, 该上仰异常现象的主要原因是高Mach数下的真实气体效应[3].从此, 产生了一门新的学科——高温气体动力学.
对于高超声速飞行器, 当来流总焓升高到3 MJ/kg时, 激波波后的空气分子将会发生振动激发离解和电离等热化学反应过程.这些热化学过程将会吸收热量, 引起空气比热比降低和压缩系数升高, 导致压力分布发生变化[4], 从而引起高超声速飞行器气动力特性发生变化.为了更精确地设计高超声速飞行器, 必须准确研究真实气体效应对气动力特性的影响.为验证这些设计参数的有效性, 就必须进行风洞实验[5].由于发生了热化学反应, 高超声速实验并不像低速风洞一样在理论上存在相似准则, 必须真实复现飞行器的来流参数.而为了产生所需温度Mach数和Reynolds数下的实验气流, 这样的风洞必须能够提供很高的总焓和总压[6-7].
为了提高地面实验数据的精准度, 国内外发展了很多先进的高超声速实验设备[8], 其中一个研究目的是测量高超声速飞行器的气动力和力矩.然而, 没有一个地面实验设备拥有复现高超声速飞行条件的能力, 不同的设备分别研究了高超声速飞行器设计问题的不同方面[9].激波风洞具有产生高温气流的能力, 但实验时间极短, 仅用于气动热研究, 难以进行气动力研究.由于实验时间短, 惯性力的影响难以消除, 即使采用了加速度补偿的方法, 实验数据仍然难以满足工程需要的精准度.
2012年, 在国家重大科研装备研制项目的支持下, 中科院力学所成功研制了基于反向爆轰的大型爆轰驱动激波风洞[10-11], 即JF12长实验时间激波风洞.它拥有复现25~50 km飞行高度Mach数5~9的纯净空气气流的能力, 有效实验时间超过了100 ms, 成为世界上第一座能够直接使用传统应变天平进行气动力和力矩测量的激波风洞.而世界上第二大激波风洞LENS Ⅱ激波风洞, 有效实验时间为30 ms[12], 目前还没有公开发表的在LENS Ⅱ上开展的气动力研究结果.
真实气体效应对高超声速飞行器气动力特性的影响是JF12激波风洞长期和主要的研究内容之一.作为第1步, 在复现35 km, 总焓2.5 MJ/kg, Mach数7.0的高超声速来流条件下, 对半锥角为10°的尖锥标模开展气动力实验研究, 给出了实验结果, 并与常规高超声速风洞的气动力测量结果进行了比较, 同时还给出了JF12气动力测量的特点和相关实验技术.
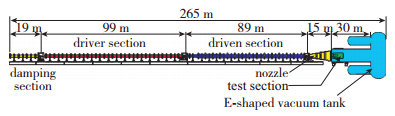
1 实验条件和模型图 1给出了JF12激波风洞的结构图, 图 2是风洞照片.它的总长度为265 m, 包括6个主要部分, 从右到左分别是E-型真空罐实验段喷管被驱动段, 驱动段和卸爆段.其中, 真空罐的总长度为40 m, 内径为3.5 m, 容积为600 m3, 高背压产生的反射激波在风洞起动200 ms以后返回实验段, 从而可以保证风洞最大有200 ms的实验时间.实验段的长度为7 m, 内径为3.5 m.型面喷管的长度为15 m, 出口直径为2.5 m, 名义Mach数为5~7, 喉道是可更换的.
|
| 图 1 JF12长实验时间激波风洞结构图 Fig.1 Schematic of JF12 long-test-time shock tunnel |

|
| 图 2 JF12长实验时间激波风洞照片 Fig.2 Photo of JF12 long-test-time shock tunnel |
被驱动段长度为89 m, 内径为720 mm.驱动段长度为99 m, 内径为400 mm.驱动段和被驱动段之间通过过渡段和夹膜机连接, 即管道直径是从720 mm逐渐降到400 mm的, 主膜片在驱动段一侧.采用反向爆轰驱动模式, 即爆轰是在驱动段的右端点火, 然后往左传播的.卸爆段位于设备的最左端, 长度为19 m, 直径为400 mm, 实验前抽真空, 用于降低爆轰波的反射压力, 避免爆轰波对设备产生破坏.所以与常规轻气体驱动的激波风洞不同, JF12驱动段末端返回的是反射激波而不是稀疏波.
实验模型是半锥角为10°的尖锥标模, 有大量的常规高超声速风洞的实验结果用于比较.模型的长度为1.5 m, 质量为50 kg, 采用铝合金制成.该模型对于高超声速风洞的测力结构而言是相当大和相当重的. 图 3是安装在JF12激波风洞中的实验模型.

|
| 图 3 10°尖锥模型 Fig.3 10° half-angle cone model |
采用了专为JF12激波风洞设计的六分量应变天平, 图 4是该气动天平的实物图, 天平的最大直径为106 mm.在激波风洞实验过程中, 模型天平和支杆的振动在100 ms的实验时间内不会发生很明显的阻尼衰减.在激波风洞进行天平测力,由于实验时间短,模型无法稳定,都采用惯性补偿方法[13]. JF12的气动力实验没有采用加速度补偿方法.为了从耦合了测力系统惯性力和模型气动力数据的输出信号中重构模型的气动力和力矩, 必须确保在100 ms实验时间内获得至少3~4个完整的振动周期.因此, 将天平的刚度设计得很大, 同时对模型支撑系统的强度也进行了加强.目前, JF12激波风洞共有5只不同量程的杆式和盒式天平, 用于不同模型的气动力实验研究.

|
| 图 4 六分量应变天平 Fig.4 Six-component strain balance |
在实验中, 喷管的名义Mach数为7.0, 总焓为2.5 MJ/kg, 总压为3.0 MPa, 实验条件复现35 km高空的飞行条件.在每次实验中都采用Pitot探头测量Pitot压力.假设自由来流处于热化学平衡状态, 考虑真实气体效应, 计算得到喷管出口的自由流参数.模型攻角分别为-5, 0, 5, 10和14°, 侧滑角为0°.为了获得JF12激波风洞测力结果的不确定度, 在5°攻角下进行了6次重复性实验, 而在其他攻角下分别进行了3次重复性实验.
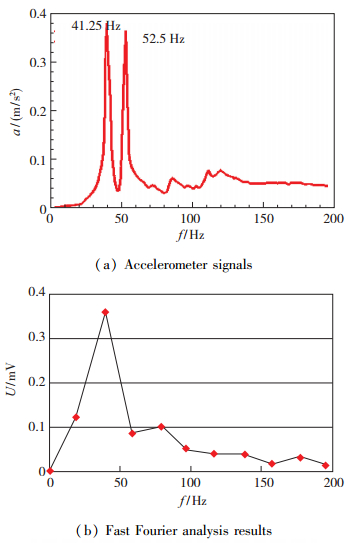
2 结果与讨论在实验前, 先采用拉线熔断法或橡皮锤敲击法, 对模型支撑系统的振动频率进行动态校准, 以确定最低振动频率.模型支撑系统包括了模型天平支杆和其他支撑设备, 其中支杆是用合金钢制成的, 直径为100 mm, 大弯刀的回转半径为2.4 m.法向方向上的振动频率采用加速度计进行测量. 图 5(a)给出了加速度计的测量结果, 图 5(b)给出了加速度信号的快速Fourier分析结果.从图中可以看出, 测力系统的1阶振动频率为41.25 Hz, 从而可以保证100 ms的有效实验时间里, 法向力和俯仰力矩至少可以获得两个完整周期的数据.轴向力的振动频率大于100 Hz, 从而在100 ms的实验时间里可以获得10个以上的完整振动周期.
|
| 图 5 模型支撑系统的振动频率 Fig.5 Vibration frequencies of JF12 model supporting system |
理论上讲, 如果测力系统的振动频率是成倍数增长的, 就可以获得非常规律的周期性天平信号.实际上并非如此, 天平的法向力和俯仰力矩总是有两个频率非常接近的振动模态.从图 5可以看出, 实验中测力系统的1阶振动模态频率为41.25 Hz, 2阶振动模态频率为52.5 Hz, 这两个低阶振动模态的频率非常接近.这是由天平支杆弯刀模型重量共同决定的.这两个频率叠加在一起, 会使天平信号变得比较复杂.
进一步举例说明这个问题. 图 6为没有安装模型的天平的俯仰力矩信号, 可以看出天平自身的振动频率比测力系统的振动频率高1个量级.从图 6(a)可以看出, 天平的俯仰力矩信号比较复杂, 缺乏周期性.如图 6(b)和(c)所示, 这个信号中包含两个频率非常接近的低阶振动, 其中1阶频率为236.35 Hz, 2阶频率为249.76 Hz.将这两个低阶振动剔除之后, 就获得了非常平稳的气动力信号[14].

|
| 图 6 天平俯仰力矩信号 Fig.6 Balance signal of pitch moment |
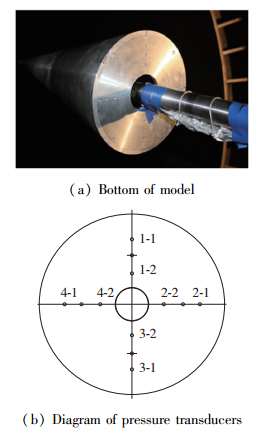
激波风洞的的非定常起动过程会对模型造成冲击, 对天平信号产生影响.为了研究激波风洞的非定常起动过程, 在模型底部安装了12个底压传感器, 上下左右各3个, 如图 7所示.模型底部安装了后端盖, 上面有螺纹孔, 压力传感器从模型内部直接安装在模型后端盖上.
|
| 图 7 模型底部底压传感器布置图 Fig.7 Pressure transducers installed on bottom surface of test model |
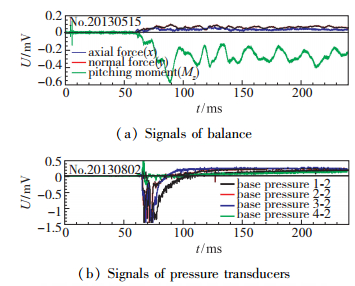
图 8给出了天平的典型输出信号, 包括了轴向力法向力和俯仰力矩数据, 以及4个底压传感器的信号.天平的输出信号可以分成两部分.在开始的30 ms里, 信号是没有规律的, 说明模型处在无规律的机械振动中, 这是由流场非定常建立过程造成的.流场建立过程的持续时间与很多因素有关, 比如模型的形状和大小攻角和Mach数等.激波风洞的非定常起动过程同样也可以从模型的压力信号中得到验证.从图 8可以看出, 在非定常起动阶段, 天平信号和底压传感器信号完全是同步的.因此, 这部分的结果不能用于气动力和力矩的计算.
|
| 图 8 天平信号和模型底压信号 Fig.8 Balance and pressure transducers output signals |
在非定常起动过程之后, 天平的输出信号变得非常有规律, 且在100 ms的有效实验时间里出现了3个以上的完整周期, 低阶振动频率同实验前的动态校准结果一致.同样, 在30 ms以后, 模型底压信号也变得非常平稳.天平信号里包括气动力信号和惯性力信号, 其中惯性力信号通过对输出信号进行平均处理就可以很容易地去除, 不需要进行加速度补偿来重构测量结果.即由于轴向力和法向力的高频振荡信号中含有足够的振动周期, 使用该天平通过简单的数据处理技术就可获得精确的实验数据.该研究表明长实验时间对激波风洞测力的重要性, 一旦JF12激波风洞的有效实验时间小于30 ms或测力系统的固有频率低于10 Hz, 测力数据的准确度将会大大降低.
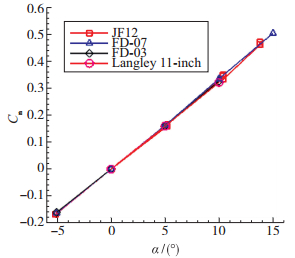
图 9~11给出了不同攻角下的法向力系数轴向力系数和压心系数.为了方便比较, 图上同时给出了FD-07, FD-03和Langley的11 in常规低焓高超声速风洞的平均结果[15]. JF12的所有实验点都画在图上, 而其他风洞只给出了平均值.从图中可见JF12激波风洞的测力结果精准度非常高, 法向力系数的不确定度小于2%, 而轴向力系数的不确定度小于5%.两大关键技术保证了高质量的实验数据.一是爆轰驱动技术,由于爆轰驱动激波风洞的运行与破膜压力无关, 它可以产生高质量的流场, 而在其他激波风洞中, 破膜压力极大地影响了流场.二是长实验时间,在超过100 ms的长实验时间里, 模型拥有3~5个完整的振动周期, 惯性力可以很简单地通过对天平信号进行平均来去除, 同时还可以消除激波风洞非定常起动过程对测量结果的影响, 从而很好地降低了实验数据的不确定度.
|
| 图 9 不同攻角下的法向力系数 Fig.9 Normal force coefficients at different attack angles |
|
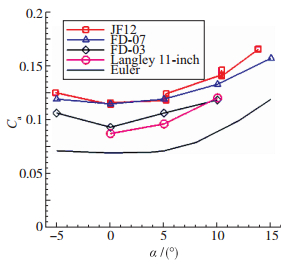
| 图 10 不同攻角下的轴向力系数 Fig.10 Axial force coefficients at different attack angles |
|
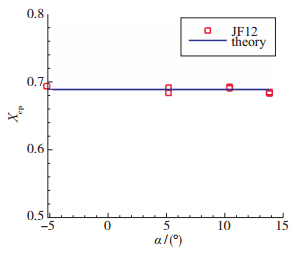
| 图 11 不同攻角下的压心系数 Fig.11 Coefficients of pressure center at different attack angles |
从图 9可见, 在JF12激波风洞中, 不同攻角下的法向力系数Cn与常规高超声速风洞的结果符合得较好, 差别小于2%.压心系数Xcp也与理论结果相符, 理论值为Xcp=0.6874.不同风洞的轴向力系数不完全相同, 这是因为轴向力系数可以分成压差阻力和摩擦阻力两部分. 图 10中同时给出了Euler方程计算得到的轴向力系数.实验数据与Euler结果的差值就是摩阻阻力对轴向力系数的贡献.对层流边界层, 摩阻系数与基于模型长度的Reynolds数ReL的平方根成反比.在当前Reynolds数下, 边界层流动都是层流.首先可以看出, FD-03风洞的轴向力系数几乎与Langley风洞的结果一致.而JF12激波风洞的轴向力系数比FD-03的轴向力系数大10%, 这是因为FD-03风洞的ReL大约是JF12激波风洞的2倍. JF12激波风洞的ReL约为1.5×106, 而FD-03风洞的ReL约为3×106.在FD-03风洞的总轴向力中, 摩阻的贡献约为10%, 而在JF12激波风洞中约为20%. JF12激波风洞的轴向力系数同FD-07风洞的轴向力系数基本相等. FD-07风洞的Reynolds数ReL约为5×106, 约为JF12的3倍, 但是, 在FD-07模型后部边界层发生了转捩[15], 因此它的轴向力系数比层流的结果更大一些.
3 结论在JF12长实验时间激波风洞中开展了半锥角10°的尖锥标模的气动力实验研究.实验结果表明, JF12激波风洞可以获得高精度的测力数据, 实验数据的不确定度小于2%.实验数据与常规高超声速风洞的结果符合得很好. JF12激波风洞与常规高超声速风洞的法向力系数的差别小于2%.而轴向力系数的差别是由于基于模型长度的Reynolds数以及边界条件的不同所导致的.对总焓2.5 MJ/kg下的10°尖锥而言, 真实气体效应对气动力特性的影响不明显.
致谢: 在此向LHD激波与爆轰物理课题组的全体成员的辛勤劳动表示感谢.该研究是在国家自然科学基金的支持下完成的, 基金号为11672312, 11532014, 在此表示感谢.| [1] | Bertin J J, Cummings R M. Critical hypersonic aerothermodynamic phenomena[J]. Annual Review of Fluid Mechanics, 2006, 38(1): 129-157. DOI:10.1146/annurev.fluid.38.050304.092041 |
| [2] | Woods W C, Arrington J P, Hamilton H H. A review of preflight estimates of real-gas effects on space shuttle aerodynamic characteristics[R]. NASA CP-2283, 1983. |
| [3] | Maus J R, Griffith B J, Szema K Y, et al. Hypersonic Mach number and real gas effects on space shuttle orbiter aerodynamic[J]. Journal of Spacecraft and Rockets, 1984, 21(2): 136-141. DOI:10.2514/3.8624 |
| [4] | Liu J, Li K, Liu W Q. High-temperature gas effects on aerodynamic characteristics of waverider[J]. Chinese Journal of Aeronautics, 2015, 28(1): 57-65. DOI:10.1016/j.cja.2014.12.004 |
| [5] |
唐志兵, 许晓斌, 杨彦广, 等. 高超声速风洞气动力试验技术进展[J].
航空学报, 2015, 36(1): 86-97. Tang Z G, Xu X B, Yang Y G, et al. Reaserch progress on hypersonic wind tunnel aerodynamic testing techniques[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 86-97. |
| [6] | Park C. Hypersonic aerothermodynamics:past, present and future[J]. International Journal of Aeronautical and Space Sciences, 2013, 14(1): 1-10. DOI:10.5139/IJASS.2013.14.1.1 |
| [7] | Park C. Evaluation of real-gas phenomena in high-enthalpy impulse test facilities:a review[J]. Journal of Thermophysics and Heat Transfer, 1997, 11(1): 10-18. DOI:10.2514/2.6217 |
| [8] | Lu F K, Marren D E. Advanced hypersonic test facilities[M]. New York:AIAA, 2002. |
| [9] | Bertin J J, Cummings R M. Fifty years of hypersonics:where we've been, where we're going[J]. Progress in Aerospace Sciences, 2003, 39(6): 511-536. |
| [10] | Jiang Z, Yu H. Experiments and development of long-test-duration hypervelocity detonation-driven shock tunnel (LHDst)[R]. AIAA 2014-1012, 2014. |
| [11] | Jiang Z L, Li J P, Zhao W, et al. Investigation into techniques for extending the test-duration of detonation-driven shock tunnels[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(5): 824-831. |
| [12] | Dufrene A T, MacLean M, Wadhams T, et al. Extension of LENS shock tunnel test times and lower Mach number capability[R]. AIAA 2015-2017, 2015. |
| [13] | Luo Y F, Bi Z X. The accelerometer force balance used in the impulse wind tunnel[J]. Aerodynamic Experiment and Measurement and Control, 1996, 10(1): 59-64. |
| [14] | Luo C T, Wang Y P, Wang C, et al. Wave system fitting:a new method for force measurements in shock tunnels with long test duration[J]. Mechanical Systems and Signal Processing, 2015, 62-63: 296-304. DOI:10.1016/j.ymssp.2015.02.024 |
| [15] |
陈河梧. 超声速高超声速风洞测力数据衔接性的研究[J].
空气动力学学报, 2002, 18(3): 345-349. Chen H W. Investigation on the link-up between the aerodynamic force data measured in supersonic and hypersonic wind tunnel[J]. Acta Aerodynamica Sinica, 2002, 18(3): 345-349. |



