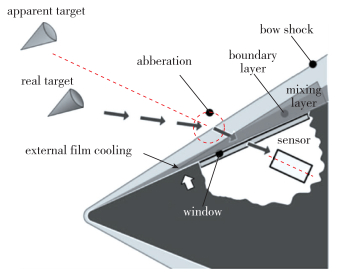
通常来说, 光学成像飞行器头部通常安装有带成像窗口的光学头罩用于目标寻的.另外, 当飞行器以高超声速在大气层中飞行时, 一般需要冷却系统来降低光学窗口表面的温度, 以免飞行器光学窗口承受的严重热负荷会造成光学窗口过热甚至损伤最终导致光学窗口失效[1-3].前期研究结果表明:窗口外部冷却喷流可以对光学窗口进行有效冷却.只是, 如图 1所示, 喷流气体和外部绕流可能会相互作用, 形成较为复杂的相互干扰湍流流场.这些复杂的干扰流场将会导致探测系统接收的目标图像出现偏移、抖动和模糊, 即我们常说的气动光学光传输效应[4].
近些年, 气动光学效应研究已经成为发展机载激光通信平台, 带光学寻的器光学头罩以及激光武器系统研制的重点之一.当前, 针对气动光学效应的研究方法主要分成:数值模拟和实验测试. Sutton等[5]采用有限差分Navier-Stokes(finite difference Navier-Stokes,FDNS)空气动力学计算程序计算了高超声速拦截器绕流流场, 研究了时均流场以及瞬态流场对机载光学传感器跟踪和成像的影响. Xu等[6]利用Reynolds平均Navier-Stokes(Reynolds-averaged Navier-Stokes, RANS)方程计算了机载侧窗光学系统的绕流结果, 研究了特定状态下非均匀流场导致的图像偏移、光线传输路径以及沿传播路径的密度分布. Morgan等[7]利用Reynolds平均Navier-Stokes/高阶隐式大涡模拟混合方法(hybrid Reynolds averaged Navier-Stokes/high-fidelity implicit large eddy simulation, hybrid RANS/LES)研究了Ma∞=0.35平窗光学头罩的气动光学效应, 获取了光学孔径上的时间平均和瞬时光程差结果. Guo等[8]利用基于Boltzman方程的直接Monte Carlo模拟方法对临近空间带喷流高超声速飞行器头罩绕流进行了计算, 结果显示, 在飞行高度高于30 km时气动光学效应已经比较弱了, 成像偏移与光线入射角密切相关. Xu等[9]提出了一种后向光线追迹方法用于一种典型钝头体飞行器气动光学效应仿真, 他们认为这种后向追迹方法以及计算停止准则可以极大地简化气动光学流场的光线追迹计算.随着计算能力的不断发展, 利用数值计算方法研究气动光学效应取得了极大的进展.但是, 面对着高Mach数, 高Reynolds数以及高精度计算的现实需求, 数值计算方法仍然对于计算资源有着无尽的渴望.
事实上, 气动光学研究目前仍然主要依赖于在不同设备中展开的地面实验. Couch等[10]设计并构建了一个实验方案, 研究了高速飞行器窗口区域湍流流动状态与气动光学畸变之间的关系. Chen等[11]利用Shack-Hartmann波前传感器测量了一个光学头罩半模超声速绕流引起的气动光学波前. Gordeyev等[12, 14], DeLucca等[13, 15]对带平窗半球形光学头罩波前畸变特性进行了比较详尽的研究.并且在实际飞行情况下测量了光学头罩的气动光学效应[16-17].基于纳米粒子平面激光散射(nano-tracer planar scattering, NPLS)技术, 朱杨柱[18]研究了有/无喷流超声速光学头罩绕流引起的光程差分布结果. Lee等[3, 19]在激波风洞中研究了外部冷却喷流以及激波的气动光学效应, 获取了风洞总压与Strehl比(Strehl ratio, SR)以及瞄视误差(bore sight error, BSE)之间的关系.
本文基于KD-01高超声速炮风洞以及背景纹影技术的波前测试技术构建了气动光学效应地面测试平台.对有/无流动控制下喷流压比与瞄视误差和高阶气动光学畸变之间的关系进行了研究.
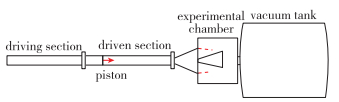
1 实验装置及测试过程 1.1 KD-01高超声速炮风洞实验主要在国防科技大学KD-01高超声速炮风洞进行.如图 2所示, 这是一个短时运行风洞, 主要由驱动段、被驱动段、实验舱以及真空罐组成.整个风洞全长42 m, 驱动段和被驱动段内径均为103 mm.喷管出口直径为500 mm, 喷管喉道可以更换, 以便实现Mach数在5~10之间调整.风洞运行采用自由活塞技术, 在当前的设置下使得风洞的运行时间可达25 ms, 并且流场具有更好的稳定性.
在当前的实验设置下, Ma∞= 6.0, 总温T0=900 K, 运行时间t≈25 ms.详细的实验状态参数见表 1, 这些参数本着尽可能接近飞行状态的原则进行设计.
| 下载CSV 表 1 实验状态参数 Tab.1 Parameters of experimental condition |
畸变波前与流场中空气的密度变化密切相关, 空气的折射率n通过Gladstone-Dale关系与密度直接相关
| $ n = 1 + {K_{{\rm{GD}}}}\rho $ |
光学波前定义为等值相位表面或者光程(optical path length, OPL).光程定义为折射率沿光线路径的积分
| $ {\rm{OPL}}\left( {x, y} \right) = \int\limits_{{z_0}{\rm{ - }}\frac{W}{2}}^{{z_0} + \frac{W}{2}} {n\left( {x, y, z} \right)} {\rm{d}}z $ |
光学孔径上相对于光程的偏差称为光程差(optical path difference, OPD).而穿过复杂畸变流场的波前畸变通常使用OPD进行定量描述, 其定义为
| $ {\rm{OPD}}\left( {x, y} \right) = {\rm{OPL}}\left( {x, y} \right) - \left\langle {{\rm{OPL}}\left( {x, y} \right)} \right\rangle $ |
其中, 角括号主要表示孔径上的空间平均.
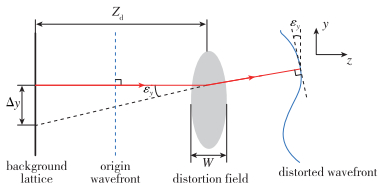
如图 3所示, Zd为背景与有效折射平面之间的距离. W为畸变场宽度(例如流场). εy为光线与主光轴之间的夹角. Δy为背景上的位移.基于BOS的波前重构思路与Shack-Hartmann波前传感器十分相似,均利用Huygens原理, 即波前传播方向与波前本身垂直.因此, 波前的斜率∂OPD/∂x和∂OPD/∂y分别与εx和εy相等.之后便可以通过适当的积分方法实现波前重构.
|
| 图 3 基于BOS方法波前传感的原理图 Fig.3 Schematic map of wavefront measurement based on BOS |
在远场情况下, 根据图 3所示的几何关系可知
| $ \frac{{\partial {\rm{OPD}}\left( {x, y} \right)}}{{\partial y}} = {\varepsilon _y} = {\tan ^{-1}}\left( {\frac{{\Delta y}}{{{Z_{\rm{d}}}}}} \right) $ |
基于相同的思路,
| $ \frac{{\partial {\rm{OPD}}\left( {x, y} \right)}}{{\partial x}} = {\varepsilon _x} = {\tan ^{-1}}\left( {\frac{{\Delta x}}{{{Z_{\rm{d}}}}}} \right) $ |
上述两个方程中的Δx, Δy可以利用互相关算法计算获得.
在波前重构算法的选择上, 由于Southwell方法对边界条件不敏感, 在波前重构中得到了较为广泛的应用[20].这里, 通过增加波前重构参考点个数以及匹配特定状态, 消除低阶偏差, 可以获得具有5阶精度的波前重构结果[21].
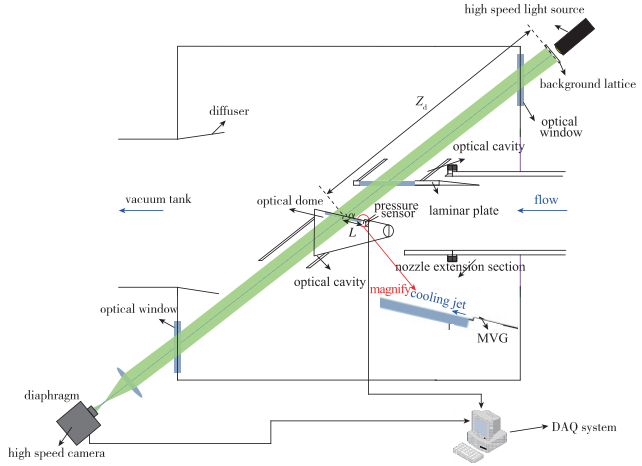
1.3 光学测试系统如图 4所示, 通过适当延长风洞喷管并且安装层流平板可以消除轴对称喷管的边界层以及菱形区波系对气动光学波前测试的影响.分别在层流平板上部和光学头罩下部安装光学空腔以消除主流以及射流边界的影响.安装在实验舱上的光学窗口可以满足光学头罩前视成像的需求.
|
| 图 4 光学测试系统示意图 Fig.4 Schematic map of the optical measurement system |
基于1.2小节论述的波前测试原理, 如图 4所示, 建立了用于光学头罩的波前测试系统.利用高速摄影光源对预先设计的随机背景点阵进行照明(实验所采用的高速摄影光源波长λ=450~465 nm, 为了方便后续进行无量纲处理, 取λ=457.5 nm).光线穿过流场及远心光路系统后被高速相机捕获.本文采用的高速相机空间分辨率为1 563 pixel×1 563 pixel, 帧频f=2 000 Hz, 曝光时间texposure=20 μs, CMOS像素线性尺寸lp=11 μm, 远心光路主光轴与窗口之间的夹角α=50.4°.远心光路主光轴与喷流出口之间的距离L=98 mm.有效测试孔径AD=56 mm.背景点阵距窗口之间的等效距离Zd=1 250 mm.详细的技术参数请见表 2.表中Ns为等效亚孔径数量,ε为实际测试灵敏度.
| 下载CSV 表 2 基于背景纹影的波前传感器技术参数 Tab.2 Technical parameters of wavefront measurement based on BOS |
如图 4所示, 实验模型为典型的带有切向射流的平窗构型光学头罩.光学头罩内构建的喷流系统可以实现Mac=3, 总温Tc, 0=300 K以及可调总压Pc, 0的切向喷流.在喷管出口上部以及喷管驻室安装有压力传感器,分别监测主流静压P∞以及喷流总压Pc, 0, 基于理想气体状态方程, 可以获得对应的喷流静压Pc,并确认对应的喷流压比(PRJ=Pc/P∞).其中, PRJ=0定义为无喷流; 0 < PRJ < 1定义为欠压; PRJ=1定义为压力匹配; PRJ>1定义为过压.流动控制主要是通过在喷流出口平台上游20 mm处布置微型涡流发生器(micro vortex generator, MVG)阵列实现.
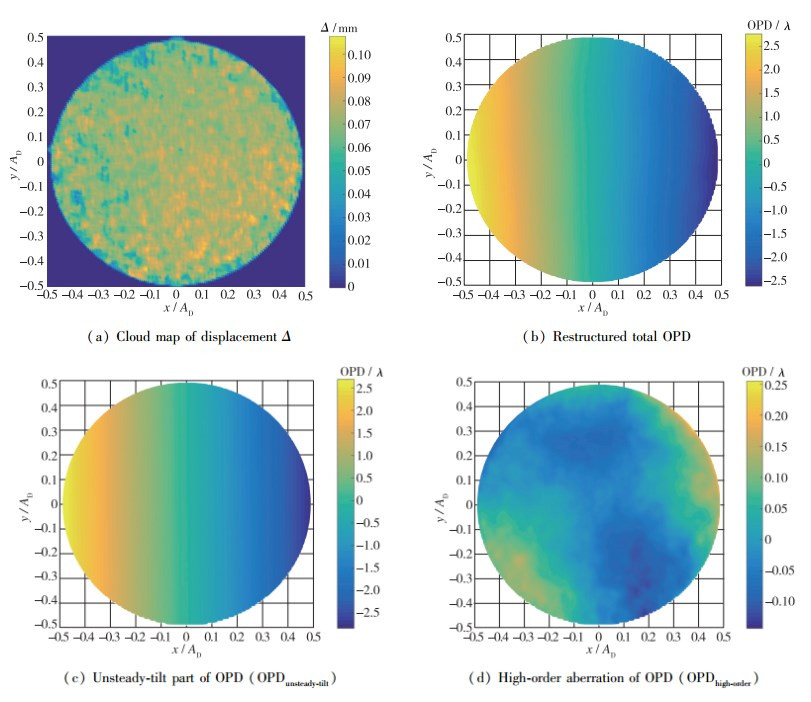
图 5为Ma∞=6.0, P0≈8.5 MPa, T0≈900 K, PRJ=0, texposure=20 μs条件下基于背景纹影的波前测试(wavefront sensor based on BOS, BOS-WS)技术获取的波前结果. 图 5(a)为位移Δ的云图, 基于此结果, 利用改进Southwell方法重构的OPD结果如图 5(b)所示.基于方程(1)和(2), OPD可以被分解为两部分, 即不稳定切斜分量(OPDunsteady-tilt, 如图 5(c)所示)以及高阶畸变部分(OPDhigh-order, 如图 5(d)所示).
|
| 图 5 BOS技术获取的位移Δ以及对应重构获取的OPD Fig.5 Displacment Δ obtained by BOS and the restructured OPD |
气动光学瞄视误差(bore sight error, BSE)是高超声速飞行器寻的、定位和制导的重要参数之一.通常而言, BSE主要由畸变波前中的倾斜分量造成, 即上文所述的不稳定倾斜部分, 将其表述为OPDunsteady-tilt, 如图 5(c)所示.虽然目前OPDunsteady-tilt可以通过自适应光学系统进行一定程度的校正, 但是研究PRJ以及MGV对BSE的影响仍然意义重大.采用最小二乘方法对方程(1)进行最小化处理以获取参数A, B, C.
| $ G=\iint\limits_{{{A}_{p}}}{{{\left[\text{OPD}\left( x, y \right)-\left( Ax+By+C \right) \right]}^{2}}\text{d}x\text{d}y} $ | (1) |
其中,AD表示光学孔径, OPD不稳定倾斜部分可以表述为
| $ \text{OP}{{\text{D}}_{\text{unsteady-tilt}}}=Ax+By+C\text{=OPD}-\text{OP}{{\text{D}}_{\text{high}-\text{order}}} $ | (2) |
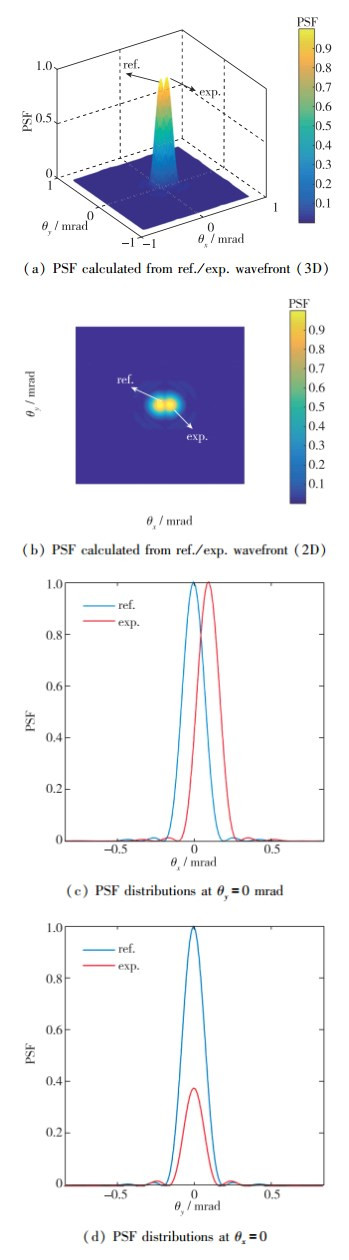
为了获取瞄视误差结果, 首先应该计算点扩散函数(point spread function, PSF). BSE定位为PSF峰值点的移动, 参考值对应的PSF是由零畸变波前计算获取的, 图 6为基于Ma∞=6.0,P0≈8.5 MPa,T0≈900 K,无流动控制,texposure=20 μs状态下获取的波前结果计算得到PSF分布.实验结果对应的PSF是由OPDunsteady-tilt计算获取的.
|
| 图 6 有零畸变波前和波前不稳定倾斜分量计算得到的归一化点扩函数 Fig.6 Normalized point spread function (PSF) calculated from undistorted wavefront (ref.) and OPDunsteady-tilt (exp.) |
图 6中实验结果的PSF分布形状以及归一化峰值与零畸变波前计算得到的PSF相比差异较小. OPD不稳定倾斜部分对图像模糊影响比较小, 主要造成图像的偏移, 或者说BSE.通过计算不稳定倾斜分量对应的OPDrms, 并将其与整体OPD计算获取的OPDrms进行对比, 可以发现由不稳定倾斜分量贡献的OPDrms占到整体的90%以上.虽然由不稳定倾斜分量引起的BSE也是气动光学效应的一部分, 但是基于此结果通过大孔径近似原理计算获取的SR值大小,可能会与我们对于气动光学效应强弱的感官体验存在差异.如图 6所示, OPDunsteady-tilt 主要引起了PSF峰值的移动, 并且主要沿x方向(流向).这与直观分析光学头罩图像偏移的结果是一致的.
当光学头罩在大气层中高速飞行时, 很难保证喷流出口上缘主流静压与喷流出口静压的恒定, 这将导致PRJ不断变化.本文将要分析PRJ对于BSE的影响, 并且对比分析有/无流动控制下的结果.
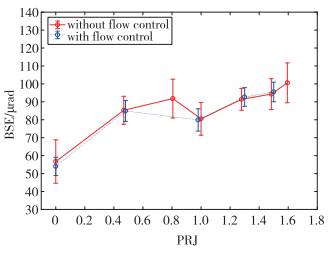
图 7为Ma∞=6.0,P0≈8.5 MPa,T0≈900 K,texposure=20 μs状态下有/无流动控制时PRJ与BSE之间的变化曲线.图中的圆点代表同一实验状态下获取的多组结果的平均值, 短横线位置表示相同状态下不同结果的均方根值, 主要用于衡量不同时刻的差异性.整体来讲, BSE的幅值在100 μrad左右, 对应10 km处目标跟踪误差在1 m左右.相对来讲, PRJ=0时BSE相对较小, 随着PRJ的不断增加, BSE倾向于不断增加, BSE在PRJ=1时存在局部小值.流场波系结构在PRJ=1时相对简单可能是导致上述结果的原因.前期研究结果证实PRJ=1时喷流一般也具有比较好的冷却效果[22-24].在这种情况下, BSE也相对比较小, 所以压力匹配可以作为带喷流光学头罩设计指标之一.当PRJ>1时, BSE随着PRJ的增加不断增加.基本上说, 在PRJ和BSE之间存在近似正比的关系(排除PRJ=1).在施加流动控制之后, 整体来讲, BSE与PRJ之间的关系并没有明显的变化.流动控制装置可以实现光学头罩主流边界层的提前转捩, 但是其对流场中时间平均结构影响相对较小, 尤其是那些波系结构, 所以其对气动光学波前中不稳定倾斜分量影响比较小.这可能表明流动控制并不能有效抑制气动光学效应中的瞄视误差.
|
| 图 7 有/无流控下BSE与PRJ相互关系曲线 Fig.7 Varying curves between BSE and PRJ with/without flow control |
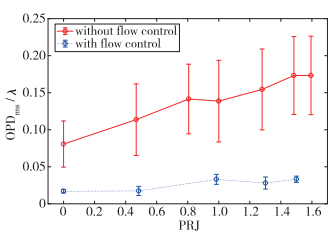
在消除了OPD中不稳定倾斜分量的影响后, 文章对PRJ与气动光学波前高阶畸变分量之间的关系进行了研究.在光学孔径上计算得到的OPD的均方根值OPDrms常被用作气动光学效应强弱的评价指标.通过计算不同状态下的OPDhigh-order对应的OPDrms结果, PRJ与OPDrms的关系曲线绘制见图 8,其中,图 8为Ma∞=6.0,P0≈8.5 MPa,T0≈900 K,texposure=20 μs状态在曝光时间texposure=20 μs时, 在高超声速流场中, 中小尺度涡结构被时间平均后可能主要影响气动光学波前中的不稳定倾斜部分.如图 8所示, OPDrms基本在亚波长范围, 实际上其对于气动光学效应的影响是比较弱的.只是这并不影响研究有/无流动控制下PRJ与OPDrms之间的关系.
|
| 图 8 OPDrms与PRJ之间的关系曲线 Fig.8 Relationship curves between OPDrms and PRJ |
有流动控制时的OPDrms小于无流动控制下的结果.与此同时, 有流动控制下的OPDrms不同时刻的差异性要小于无流动控制下的结果.主流与喷流之间的剪切混合过程可能会在窗口区域影响K-H转捩过程[25], 其中大尺度结构具有相对明显的不稳定特征, 而大尺度结构对气动光学效应影响较为显著, 这可能是无控制状态下OPDrms不同时刻差异性比较大的原因.伴随着流动控制装置的引入, 主流边界可能已经提前转捩, 存在抑制K-H转捩发展过程的可能性[26].在相同情况下, 随着PRJ的增加, OPDrms同样倾向于增加.这可能是由于随着PRJ增加, 实际上对应着喷流流量的增加, 这种增加可能会导致喷流厚度的增加, 存在引入更多涡结构进入流场的可能.
OPDhigh-order和流场的涡结构之间可能存在较为紧密的关系.为了进一步验证上述构想, 计算获得的OPD结构尺寸可以在一定程度上反映涡结构的尺度特性, 以便衡量流动控制的效果.根据下面方程, 应用空间两点相关计算方法获取结构尺度.
| $ \begin{array}{l} {R_{{\rm{OP}}{{\rm{D}}_{{\rm{high-order}}}}}}\left( {\Delta x, \Delta y} \right) = \\ \frac{{\overline {\left\langle {{\rm{OP}}{{\rm{D}}_{{\rm{high-order}}}}\left( {x, y} \right){\rm{OP}}{{\rm{D}}_{{\rm{high-order}}}}\left( {x + \Delta x, y + \Delta y} \right)} \right\rangle } }}{{\sqrt {\overline {\left\langle {{\rm{OP}}{{\rm{D}}_{{\rm{high - order}}}}^2\left( {x, y} \right)} \right\rangle } } \sqrt {\overline {\left\langle {{\rm{OP}}{{\rm{D}}_{{\rm{high - order}}}}^2\left( {x + \Delta x, y{\rm{ + }}\Delta y} \right)} \right\rangle } } }} \end{array} $ |
其中角括号表示孔径上的空间平均, 上划线表示时间平均.
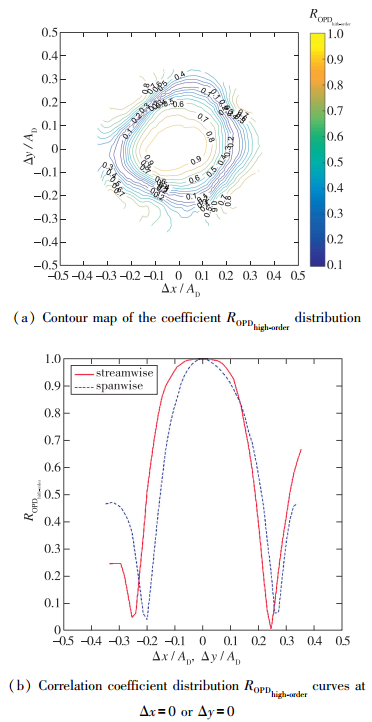
通过对波前进行空间两点相关计算可以获取流向和展向尺寸.第1个最小值位置通常被定义互相关尺寸[12]. 图 9为Ma∞=6.0,P0≈8.3 MPa,T0≈ 900 K,texposure=20 μs状态下获取的波前结果归一化互相关二维云图以及对应的Δy/AD=0和Δx/AD=0处切线.利用空间两点相关结果第1个最小值点位置定义, 无流动控制情况下结构尺寸近似为0.2AD, 施加流动控制后, 结构尺寸近似为0.1AD.
|
| 图 9 归一化OPD互相关系数ROPDhigh-order分布 Fig.9 Normalized correlation coefficient ROPDhigh-order distributions of OPD |
Ma∞=6.0,P0≈8.3 MPa,T0≈900 K,texposure=20 μs时不同PRJ下计算得到的结构尺寸Θ以及对应的结果绘制见图 10.无流动控制时, 流向和展向的结构尺寸近似为0.2AD.施加流动控制后, 流向和展向结构尺寸近似为0.1AD.流向结构尺寸与展向结构尺寸近似相等.与此同时, PRJ对结构尺寸的影响比较小, 结构尺寸随着PRJ的增加并没有出现明显的变化.结合如图 8所示的OPDrms分布, 无流动控制时, 大结构尺寸对应了比较严重的气动光学畸变, 施加流动控制后, 小结构尺寸对应了较弱的气动光学畸变.

|
| 图 10 有/无流动控制时结构尺寸与PRJ之间的关系曲线 Fig.10 Relationship curves between structure size and PRJ with/without flow control |
相对来讲, BSE在PRJ=0时比较小, 随着PRJ的增加, BSE不断增加. BSE在PRJ=1处存在局部小值. PRJ=1时流场的波系结构相对简单.当PRJ>1时, BSE随着PRJ的增加不断增加.总体来看, PRJ与BSE之间呈正相关(排除PRJ=1).在施加流动控制之后, BSE与PRJ之间的关系并没有明显变化.微型涡流发生器可以实现主流边界层的提前转捩, 但是对流场的时均结构, 尤其是波系结构影响比较小, 所以其对波前的不稳定倾斜分量影响较小.即流动控制方式并不能有效抑制气动光学效应中的BSE.流动控制下OPDrms小于无流动控制下的结构.与此同时, 流动控制下OPDrms不同时刻的差异性小于无流动控制下的结果.随着PRJ的增加, OPDrms也倾向于增加.这可能主要是因为PRJ通常对应着喷流流量.这种增加直接导致了喷流厚度的增加, 可能导致流场中的涡结构数量增加.利用互相关系数第1个最小值位置定义互相关尺寸.无流动控制时流向和展向结构尺寸近似为0.2AD.当流动控制使用后, 流向和展向的结构尺寸近似为0.1AD.流向的结构尺寸与展向的结构尺寸近似相等.与此同时, PRJ对结构尺寸的影响比较小, 随着PRJ的增加, 结构尺寸并没有出现明显的变化.无流动控制时, 大结构尺寸对应了较为严重的气动光学效应, 施加流动控制后, 小结构尺寸对应了较弱的气动光学效应.
| [1] |
Fu J, Yi S H, Wang X H, et al. Experimental study on supersonic film cooling on the surface of a blunt body in hypersonic flow[J]. Chinese Physics B, 2014, 23(10): 104702. DOI:10.1088/1674-1056/23/10/104702 |
| [2] |
朱杨柱, 易仕和, 陈植, 等. 带喷流超声速光学头罩流场气动光学畸变试验研究[J]. 物理学报, 2013, 62(8): 084219. Zhu Y Z, Yi S H, Chen Z, et al. Experimental investigation on aero-optical aberration of the supersonic flow passing through an optical dome with gas injection[J]. Acta Physica Sinica, 2013, 62(8): 084219. (in Chinese) |
| [3] |
Lee S, Yoon H, Jeung I S, et al. Super-/hypersonic aero-optical effects induced by external jet cooling[C]. Proceedings of the 30th International Symposium on Shock Waves 1, Cham: Springer, 2017.
|
| [4] |
Jumper E J, Fitzgerald E J. Recent advances in aero-optics[J]. Progress in Aerospace Sciences, 2001, 37(3): 299-339. DOI:10.1016/S0376-0421(01)00008-2 |
| [5] |
Sutton G W, Pond J E, Snow R, et al. Hypersonic interceptor aero-optics performance predictions[J]. Journal of Spacecraft & Rockets, 1994, 31(4): 592-599. |
| [6] |
Xu L, Cai Y L. Influence of non-uniform flow fields on imaging deviation of side-window airborne optical systems[C]. Proceedings of the IEEE International Conference on Imaging Systems and Techniques, May 2011. Penang, Malaysia: IEEE, 2011.
|
| [7] |
Morgan P E, White M D, Visbal M R. Simulation of aero-optics for flow over a flat-window hemispherical turret[C]. Proceedings of the 41st AIAA Fluid Dynamics Conference and Exhibit. Honolulu, Hawaii: AIAA, 2011.
|
| [8] |
Guo G M, Liu H, Zhang B. Aero-optical effects of an optical seeker with a supersonic jet for hypersonic vehicles in near space[J]. Applied Optics, 2016, 55(17): 4741-4751. DOI:10.1364/AO.55.004741 |
| [9] |
Xu L, Xue D T, Lv X Y. Computation and analysis of backward ray-tracing in aero-optics flow fields[J]. Optics Express, 2018, 26(1): 567-576. |
| [10] |
Couch L L, Kalin D A, McNeal T. Experimental investigation of image degradation created by a high-velocity flow field[C]. Characterization, Propagation, and Simulation of Sources and Backgrounds. Orlando, FL, United States: SPIE, 1991.
|
| [11] |
Chen Z Q, Fu S. Optical wavefront distortion due to supersonic flow fields[J]. Chinese Science Bulletin, 2009, 54(4): 623-627. DOI:10.1007/s11434-009-0090-x |
| [12] |
Gordeyev S, Hayden T E, Jumper E J. Aero-optical and flow measurements over a flat-windowed turret[J]. AIAA Journal, 2007, 45(2): 347-357. DOI:10.2514/1.24468 |
| [13] |
De Lucca N, Gordeyev S, Jumper E. Aero-optical environment around turrets at forward-viewing angles[C]. Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Texas: AIAA, 2013.
|
| [14] |
Gordeyev S, Jumper E, Hayden T. Aero-optical and hot-wire measurements of the flow around the hemispherical turret with a flat window[C]. Proceedings of the 35th AIAA Plasmadynamics and Lasers Conference, Portland, Oregon: AIAA, 2004.
|
| [15] |
De Lucca N, Gordeyev S, Jumper E. The study of aero-optical and mechanical jitter for flat window turrets[C]. Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee: AIAA, 2012.
|
| [16] |
Porter C, Gordeyev S, Zenk M, et al. Flight measure-ments of the aero-optical environment around a flatwin-dowed turret[J]. AIAA Journal, 2013, 51(6): 1394-1403. DOI:10.2514/1.J052067 |
| [17] |
Whiteley M R, Goorskey D J. Imaging performance with turret aero-optical wavefront disturbances[J]. Optical Engineering, 2013, 52(7): 071410. DOI:10.1117/1.OE.52.7.071410 |
| [18] |
朱杨柱.带后台阶超声速光学头罩流动机理及其气动光学效应试验研究[D].长沙: 国防科技大学, 2015. Zhu Y Z. Experimental investigation on supersonic flow over an optical dome with backward facing step and its aero-optical effects[D]. Changsha: National University of Defense Technology, 2015(in Chinese). |
| [19] |
Lee S, Jeong M C, Jeung I S, et al. Aero-optical measurement in shock wave of hypersonic flow field[C]. Proceedings of the 30th International Symposium on Shock Waves 1, Cham: Springer, 2017.
|
| [20] |
Southwell W H. Wave-front estimation from wave-front slope measurements[J]. Journal of the Optical Society of America, 1980, 70(8): 998-1006. DOI:10.1364/JOSA.70.000998 |
| [21] |
Li G H, Li Y Q, Liu K, et al. Improving wavefront reconstruction accuracy by using integration equations with higher-order truncation errors in the Southwell geometry[J]. Journal of the Optical Society of America A, 2013, 30(7): 1448-1459. DOI:10.1364/JOSAA.30.001448 |
| [22] |
Sahoo D, Desai P, Smits A J. Experimental investigation of helium injection in a hypersonic turbulent boundary layer[C]. Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Floridap: AIAA, 2010.
|
| [23] |
杨晓颖, 刘纯胜, 顾永其. 高速飞行器红外制冷头罩设计[J]. 红外与激光工程, 2004, 33(6): 576-579. Yang X Y, Liu C S, Gu Y Q. Design of the hypersonic vehicle infrared cooling dome[J]. Infrared and Laser Engineering, 2004, 33(6): 576-579. DOI:10.3969/j.issn.1007-2276.2004.06.005 (in Chinese) |
| [24] |
易司琪, 丁浩林, 龙志强. 超声速气膜冷却时的光学性能优化设计[J]. 应用光学, 2017, 38(4): 549-554. Yi S Q, Ding H L, Long Z Q. Optimal design of supersonic gaseous film cooling optical performance[J]. Journal of Applied Optics, 2017, 38(4): 549-554. (in Chinese) |
| [25] |
Zhu Y Z, Yi S H, He L, et al. Instantaneous and time-averaged flow structures around a blunt double-cone with or without supersonic film cooling visualized via nano-tracer planar laser scattering[J]. Chinese Physics B, 2013, 22(1): 014702. |
| [26] |
Yi S H, He L, Zhao Y X, et al. A flow control study of a supersonic mixing layer via NPLS[J]. Science in China Series G:Physics, Mechanics & Astronomy, 2009, 52(12): 2001-2006. |